Direction of Arrival Estimation of Generalized Nested Array via Difference–Sum Co-Array
Abstract
:1. Introduction
2. Signal Model
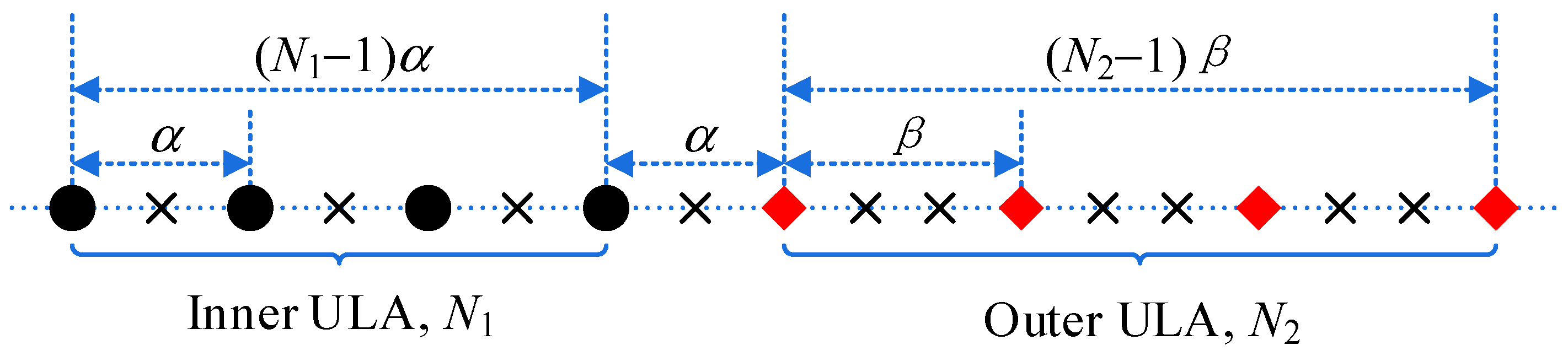
3. Generalized Nested Array
- (a)
- Self-difference: , where .
- (b)
- Cross-difference: , where , while .
- (c)
- Self-sum: , where .
- (d)
- Cross-sum: , where , while .
- (a)
- Difference co-array: .
- (b)
- Sum co-array: .
- (c)
- Difference–sum co-array: .
3.1. Review of GNA-DCA
- (a)
- When, the range of positive and negative consecutive lags can be presented asand, respectively, whereand.
- (b)
- If, the number of unique lags reaches, where.
- (c)
3.2. Proposed GNA-DSCA
- (a)
- Provided that,possesses all the consecutive lags in the range, whereand. Provided that,enjoys all the consecutive lags in the range.
- (b)
- In the case, the total number of unique lags inreaches, where.
| Maximum DOFs | |||
|---|---|---|---|
| Even | or | ||
| Odd |
4. DOA Estimation
5. Simulation Results
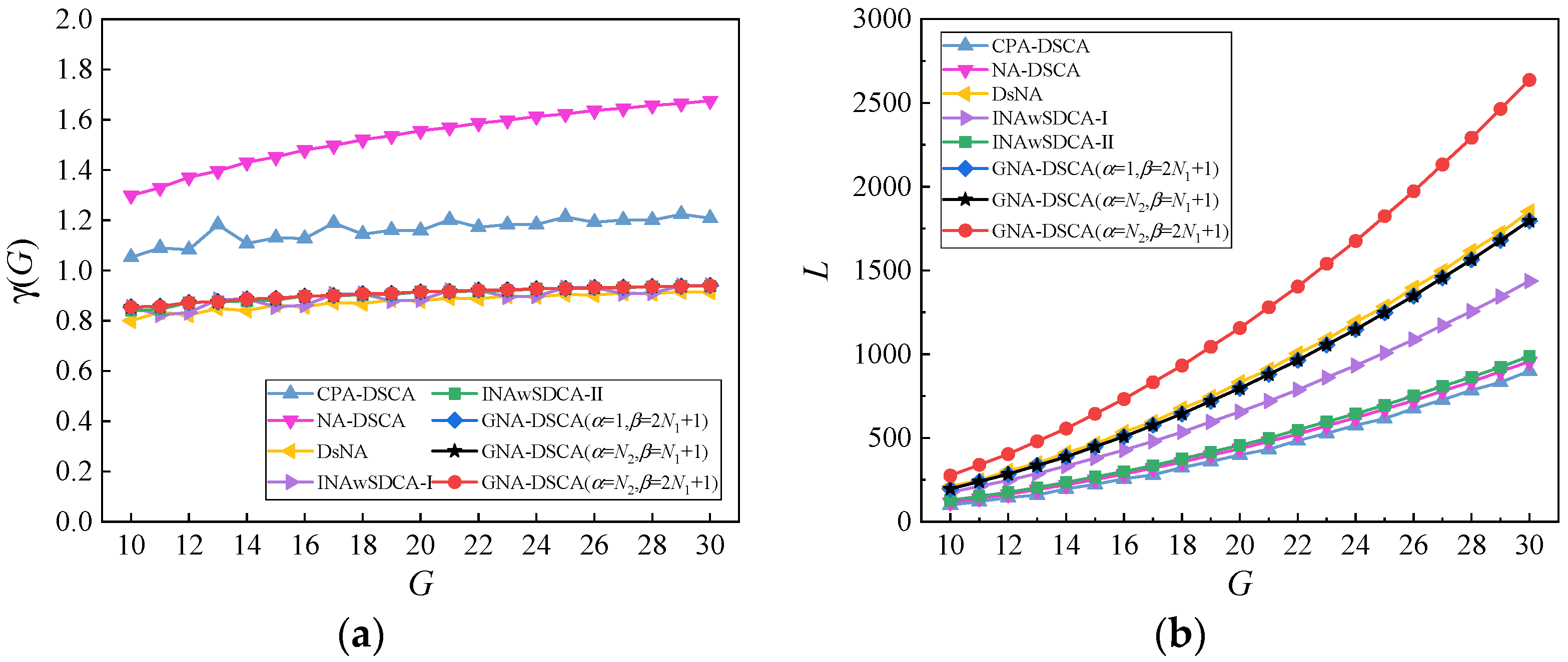
5.1. Virtual Array Properties
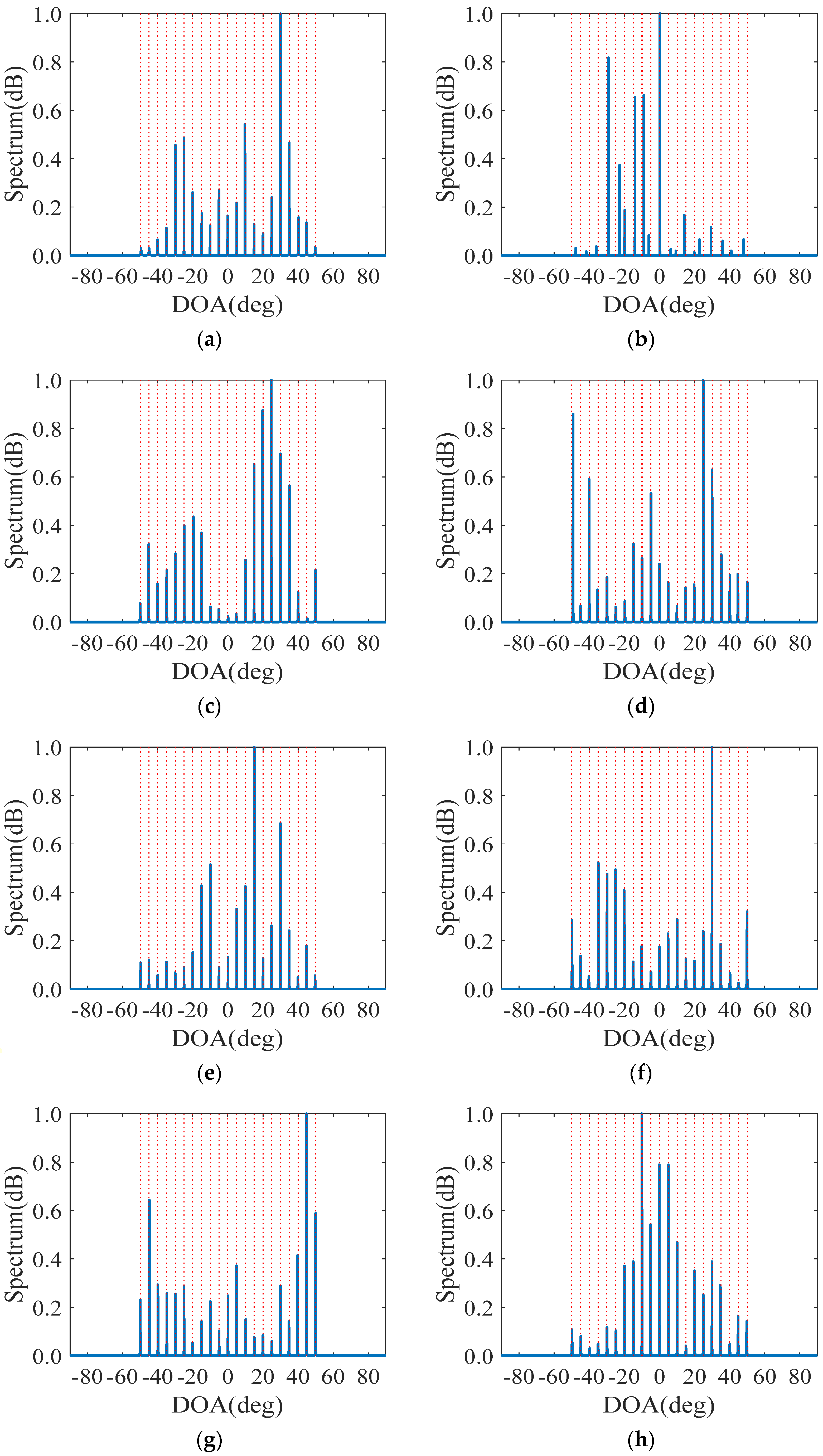
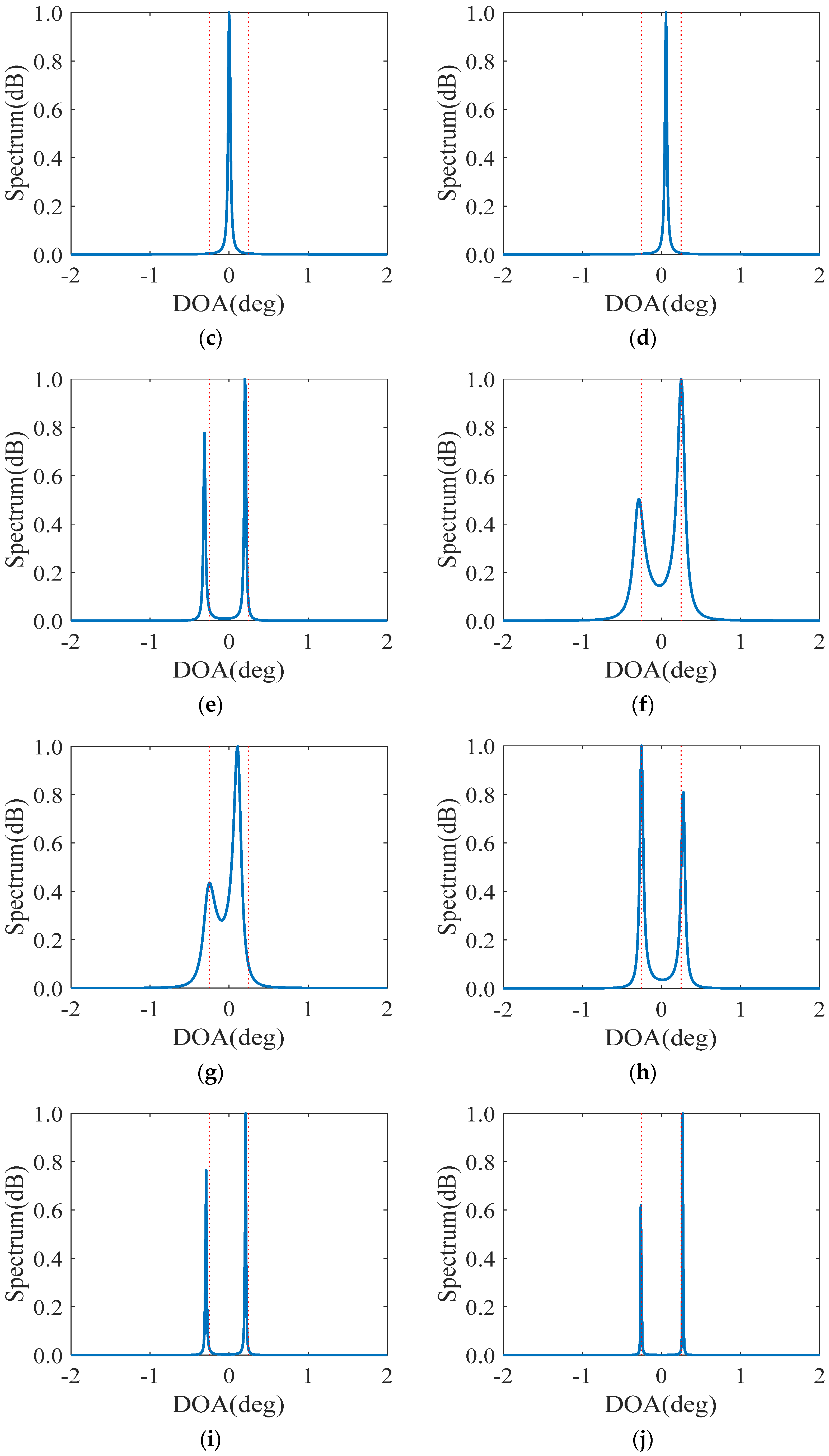
5.2. MUSIC Spectra
5.3. Root-Mean-Square Error
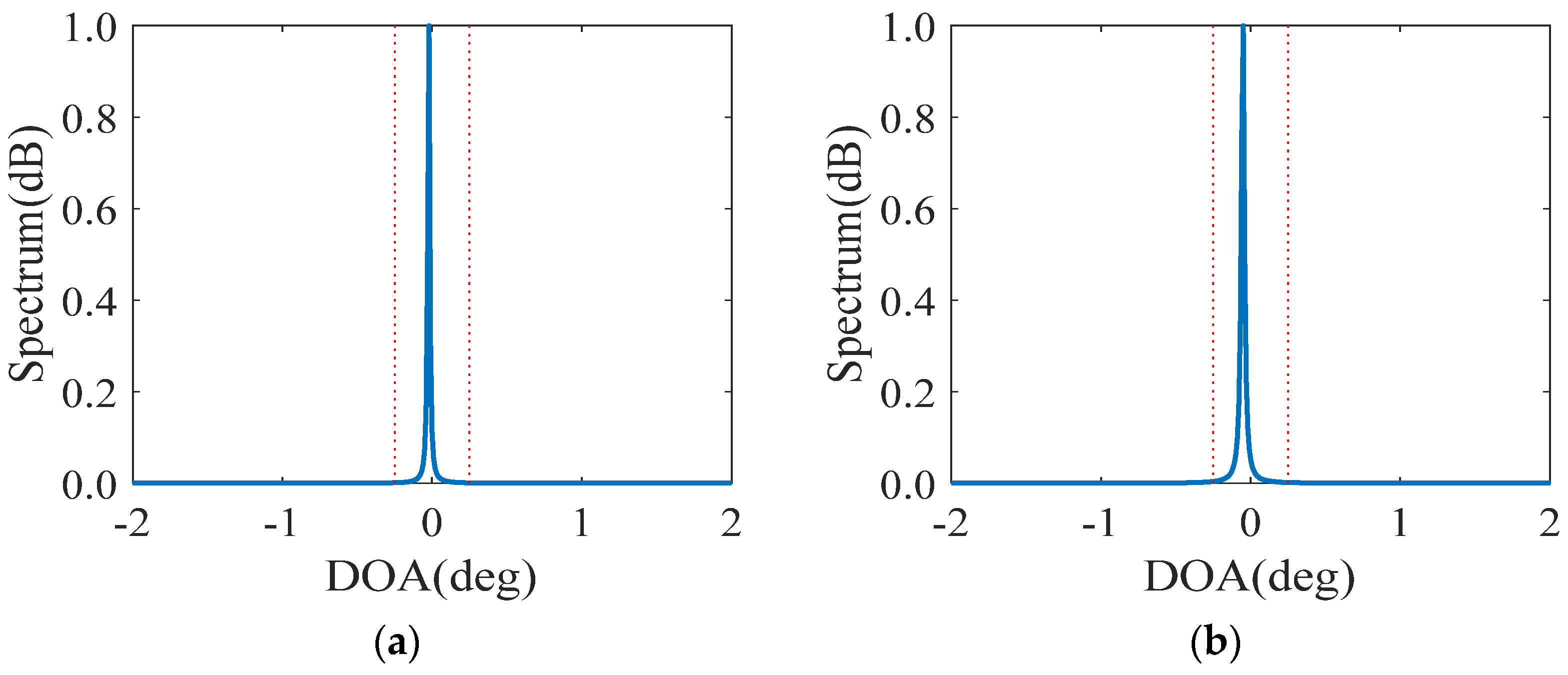
5.4. Resolution Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Lemma 2
- (a)
- For Lemma 2(a), since , we need to analyze the elements in and , respectively. The set can be expressed as [20]
- (b)
- For Lemma 2(b), we take the positive set as an example. We need proof that possesses unique lags for the case , where .

Appendix B. Solution of Equation (17)
References
- Wen, F.; Shi, J.; Zhang, Z. Closed-form estimation algorithm for EMVS-MIMO radar with arbitrary sensor geometry. Signal Process. 2021, 186, 108117. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Generalized spatial smoothing in bistatic EMVS-MIMO radar. Signal Process. 2022, 193, 108406. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Wen, F.; Shi, J. PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry. Remote Sens. 2022, 14, 2905. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Li, P.; Tang, L.; Zhang, X.; Wu, Q. Self-Position Awareness Based on Cascade Direct Localization Over Multiple Source Data. IEEE Trans. Intell. Transp. Syst. 2022, 1–9, Early Access. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, T. Nested MIMO Radar: Coarrays, Tensor Modeling, and Angle Estimation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 573–585. [Google Scholar] [CrossRef]
- Turchin, V.I.; Rodionov, A.A. Source Detection and Bearing Estimation Using Sparse Antenna Arrays. Radiophys. Quantum Electron. 2018, 61, 109–126. [Google Scholar] [CrossRef]
- Shi, J.; Yang, Z.; Liu, Y. On Parameter Identifiability of Diversity-Smoothing-Based MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1660–1675. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Deng, W.; Tang, Y.; Zhang, X.; Wu, Q. Source Direction Finding and Direct Localization Exploiting UAV Array With Unknown Gain-Phase Errors. IEEE Internet Things J. 2022, 9, 21561–21569. [Google Scholar] [CrossRef]
- Wen, F.; Wang, J.; Shi, J.; Gui, G. Auxiliary Vehicle Positioning Based on Robust DOA Estimation With Unknown Mutual Coupling. IEEE Internet Things J. 2020, 7, 5521–5532. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust., Speech, Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef] [Green Version]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Chen, T. Direction-of-Arrival Estimation Using a Sparse Representation of Array Covariance Vectors. IEEE Trans. Signal Process. 2011, 59, 4489–4493. [Google Scholar] [CrossRef]
- Ma, W.-K.; Hsieh, T.-H.; Chi, C.-Y. DOA Estimation of Quasi-Stationary Signals With Less Sensors Than Sources and Unknown Spatial Noise Covariance: A Khatri-Rao Subspace Approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef] [Green Version]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P.P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling-Part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P.P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling-Part II: High-Order Extensions. IEEE Trans. Signal Process. 2016, 64, 4203–4217. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.D.; Lu, Y.; Ren, S.; Cao, S. Augmented Nested Arrays With Enhanced DOF and Reduced Mutual Coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Zhou, H. Generalized Nested Array: Optimization for Degrees of Freedom and Mutual Coupling. IEEE Commun. Lett. 2018, 22, 1208–1211. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Raza, A.; Liu, W.; Shen, Q. Thinned Coprime Array for Second-Order Difference Co-Array Generation With Reduced Mutual Coupling. IEEE Trans. Signal Process. 2019, 67, 2052–2065. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Zhang, X.; Wang, Y.; Shen, J.; Champagne, B. Padded Coprime Arrays for Improved DOA Estimation: Exploiting Hole Representation and Filling Strategies. IEEE Trans. Signal Process. 2020, 68, 4597–4611. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Shi, J.; Zhou, H.; Zhan, C.; Zhao, F. DOA estimation of an enhanced generalized nested array with increased degrees of freedom and reduced mutual coupling. Int. J. Antennas Propaga. 2021, 2021, 7233651. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Zhang, F.; Zhou, H. Enhanced CACIS configuration for direction of arrival estimation. Electron. Lett. 2022, 58, 737–739. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, Y.; Liu, Z.; Hu, P. Enhanced and Generalized Coprime Array for Direction of Arrival Estimation. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–12, Early Access. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Sun, F.; Zhou, H. Sparsity-Based Two-Dimensional DOA Estimation for Coprime Array: From Sum-Difference Coarray Viewpoint. IEEE Trans. Signal Process. 2017, 65, 5591–5604. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Coprime sampling and the MUSIC algorithm. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P.P. Remarks on the Spatial Smoothing Step in Coarray MUSIC. IEEE Signal Process. Lett. 2015, 22, 1438–1442. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Amin, M.G.; Himed, B. Sparsity-based DOA estimation using co-prime arrays. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3967–3971. [Google Scholar] [CrossRef]
- BouDaher, E.; Jia, Y.; Ahmad, F.; Amin, M.G. Multi-Frequency Co-Prime Arrays for High-Resolution Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 3797–3808. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P.P.; Pal, P. Coprime coarray interpolation for DOA estimation via nuclear norm minimization. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 2639–2642. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Sebt, M.A. Array Interpolation Using Covariance Matrix Completion of Minimum-Size Virtual Array. IEEE Signal Process. Lett. 2017, 24, 1063–1067. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-Grid Direction-of-Arrival Estimation Using Coprime Array Interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Liu, S.; Mao, Z.; Zhang, Y.D.; Huang, Y. Rank minimization-based toeplitz reconstruction for DoA estimation using coprime array. IEEE Commun. Lett. 2021, 25, 2265–2269. [Google Scholar] [CrossRef]
- Weng, C.-C.; Vaidyanathan, P.P. Nonuniform sparse array design for active sensing. In Proceedings of the 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 1062–1066. [Google Scholar] [CrossRef]
- BouDaher, E.; Ahmad, F.; Amin, M.G. Sparsity-Based Direction Finding of Coherent and Uncorrelated Targets Using Active Nonuniform Arrays. IEEE Signal Process. Lett. 2015, 22, 1628–1632. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Sun, F. Sparsity-Based DOA Estimation of Coherent and Uncorrelated Targets With Flexible MIMO Radar. IEEE Trans. Veh. Technol. 2019, 68, 5835–5848. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Z.; Ren, S.; Cao, S. DOA estimation based on the difference and sum coarray for coprime arrays. Digit. Signal Process. 2017, 69, 22–31. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Y.; Ren, S.; Chen, Z. A Novel Nested Configuration Based on the Difference and Sum Co-Array Concept. Sensors 2018, 18, 2988. [Google Scholar] [CrossRef] [Green Version]
- Si, W.; Peng, Z.; Hou, C.; Zeng, F. Improved Nested Arrays With Sum-Difference Coarray for DOA Estimation. IEEE Sens. J. 2019, 19, 6986–6997. [Google Scholar] [CrossRef]
- Zhan, C.; Hu, G.; Zhang, Z.; Feng, Z. Increasing Utilization of Redundant Virtual Array for DOA Estimation Based on Coprime Array. Math. Probl. Eng. 2020, 2020, 8830416. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.2. January 2020. Available online: http://cvxr.com/cvx (accessed on 1 January 2020).



| Maximum DOFs | |||
|---|---|---|---|
| Even | or | ||
| Odd |
| Sparse Array | Configuration | DOFs | Virtual Aperture | Coupling Leakage |
|---|---|---|---|---|
| NA-DCA | {0, 1, 2, 3, 4, 5, 11, 17, 23, 29} | 59 | 29 | 0.5022 |
| CPA-DCA | {0, 5, 6, 10, 12, 15, 18, 20, 24, 25} | 39 | 25 | 0.2929 |
| GNA-DCA () | {0, 5, 10, 15, 20, 25, 31, 37, 43, 49} | 59 | 49 | 0.1215 |
| CPA-DSCA | {0, 5, 6, 10, 12, 15, 18, 20, 24, 25} | 95 | 50 | 0.2929 |
| DsNA | {0, 3, 5, 7, 8, 17, 26, 35, 44, 53} | 125 | 106 | 0.3187 |
| INAwSDCA−I | {0, 16, 17, 18, 19, 20, 26, 32, 38, 44} | 117 | 88 | 0.4806 |
| INAwSDCA−II | {0, 9, 15, 21, 27, 28, 29, 30, 31, 32} | 119 | 64 | 0.5022 |
| GNA-DSCA () | {0, 1, 2, 3, 4, 5, 16, 27, 38, 49} | 117 | 98 | 0.4991 |
| GNA-DSCA () | {0, 5, 10, 15, 20, 25, 31, 37, 43, 49} | 117 | 98 | 0.1215 |
| GNA-DSCA () | {0, 5, 10, 15, 20, 25, 36, 47, 58, 69} | 117 | 138 | 0.1126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hu, G.; Zhou, H.; Bai, J.; Zhan, C.; Guo, S. Direction of Arrival Estimation of Generalized Nested Array via Difference–Sum Co-Array. Sensors 2023, 23, 906. https://doi.org/10.3390/s23020906
Zhang Y, Hu G, Zhou H, Bai J, Zhan C, Guo S. Direction of Arrival Estimation of Generalized Nested Array via Difference–Sum Co-Array. Sensors. 2023; 23(2):906. https://doi.org/10.3390/s23020906
Chicago/Turabian StyleZhang, Yule, Guoping Hu, Hao Zhou, Juan Bai, Chenghong Zhan, and Shuhan Guo. 2023. "Direction of Arrival Estimation of Generalized Nested Array via Difference–Sum Co-Array" Sensors 23, no. 2: 906. https://doi.org/10.3390/s23020906
APA StyleZhang, Y., Hu, G., Zhou, H., Bai, J., Zhan, C., & Guo, S. (2023). Direction of Arrival Estimation of Generalized Nested Array via Difference–Sum Co-Array. Sensors, 23(2), 906. https://doi.org/10.3390/s23020906








