Analysis of Lidar Actuator System Influence on the Quality of Dense 3D Point Cloud Obtained with SLAM
Abstract
1. Introduction
2. Materials and Methods
2.1. State of the Art
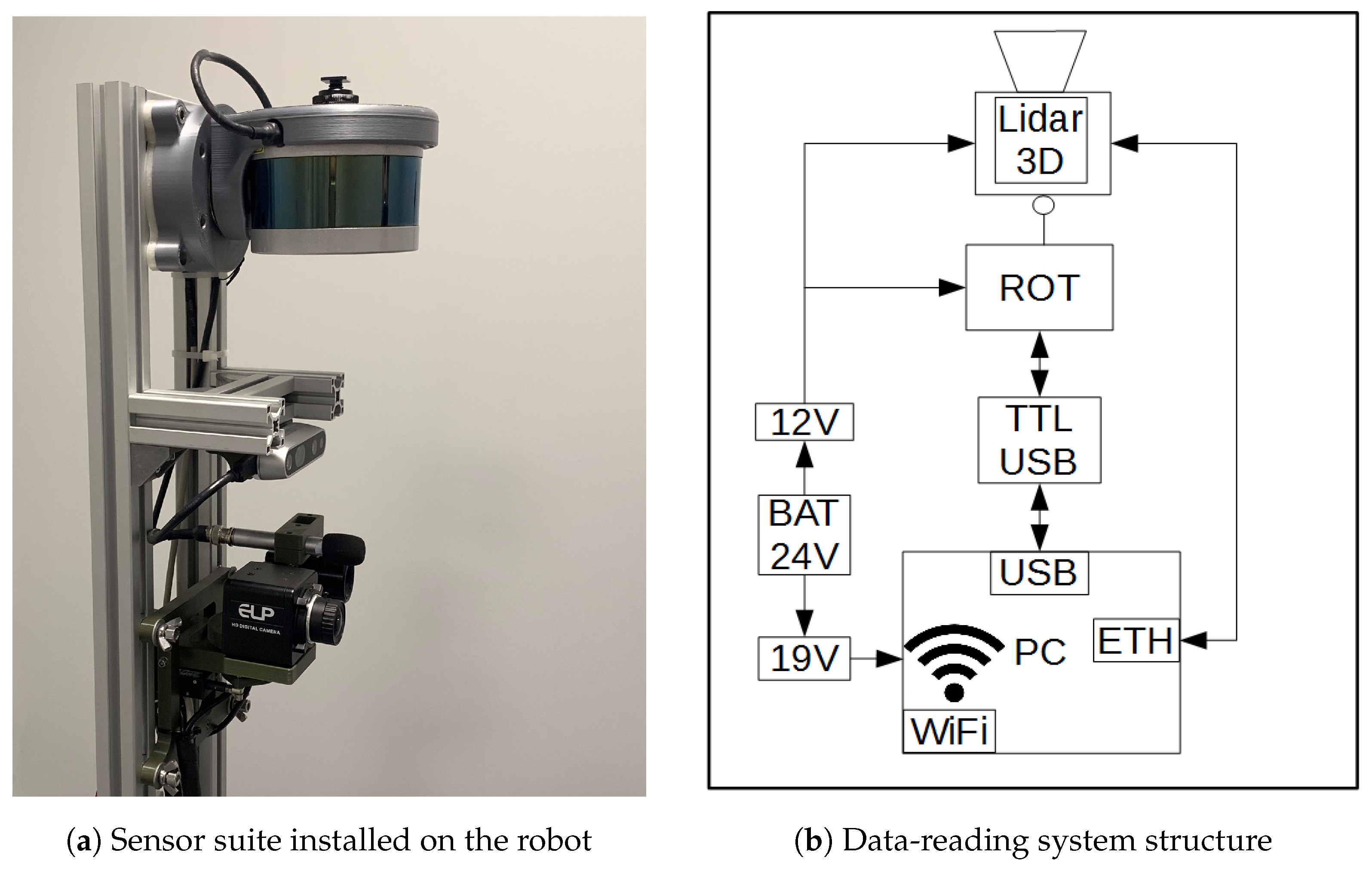
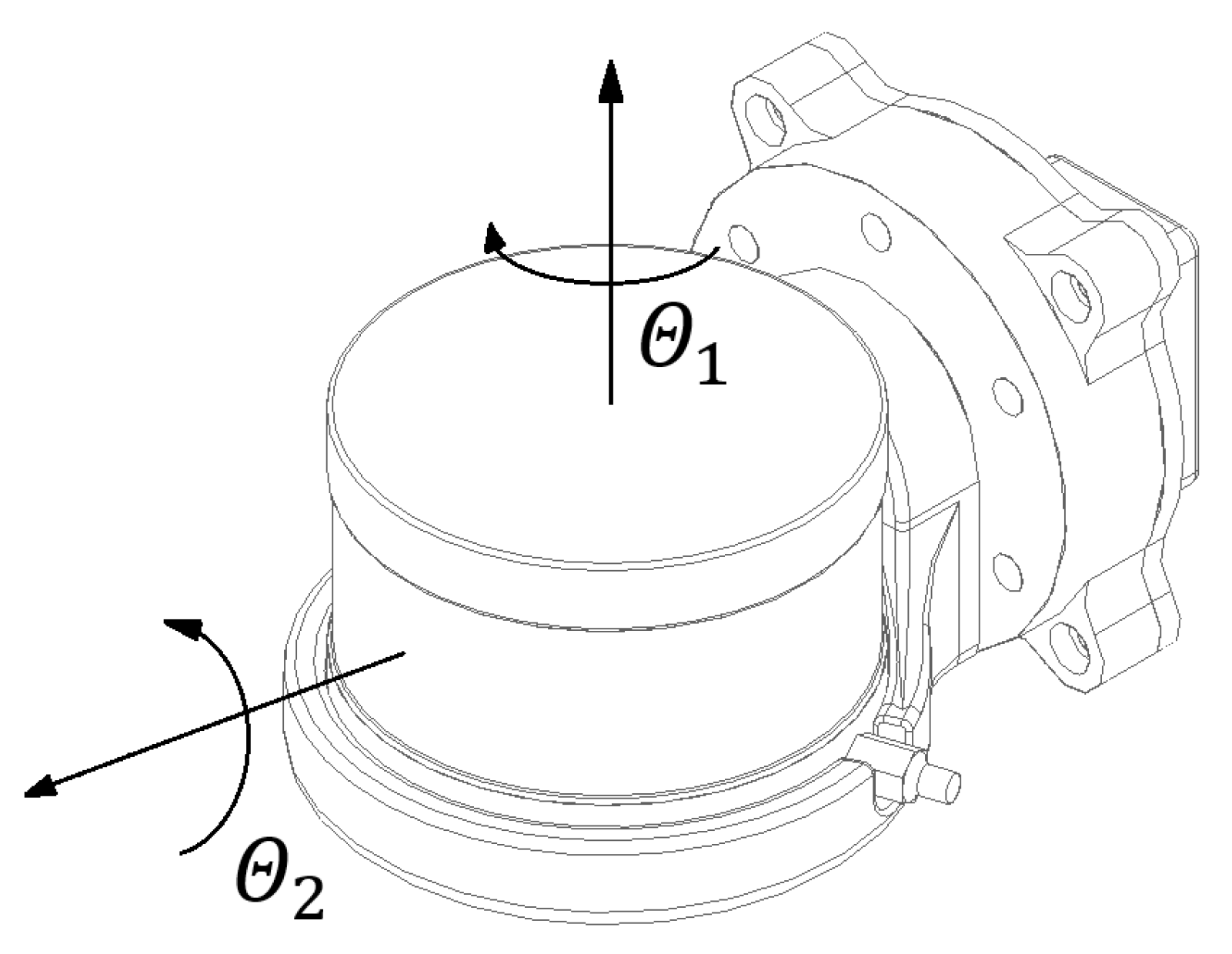
2.2. Adjustable Mapping System Design
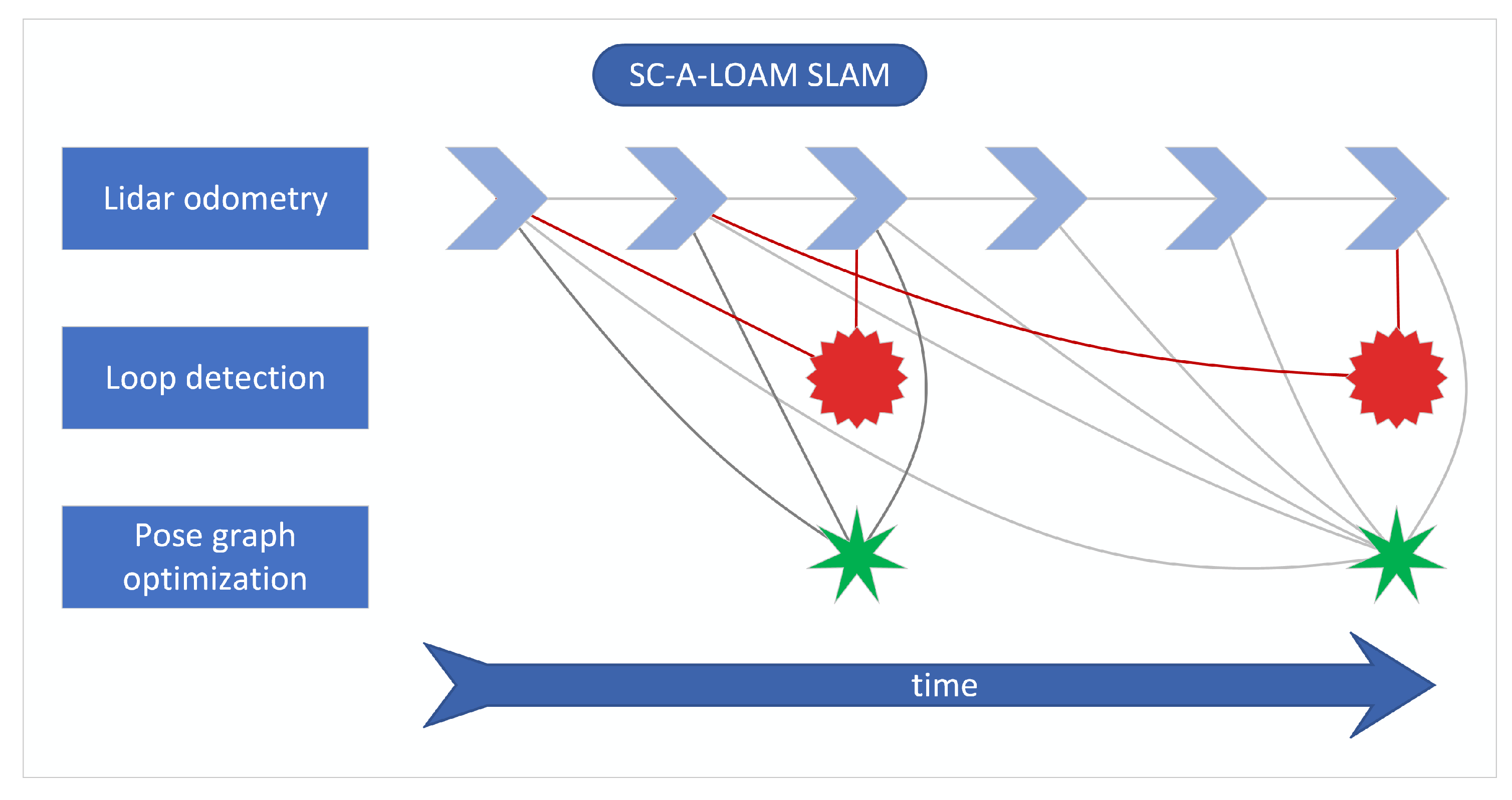
2.3. 3D Lidar SLAM
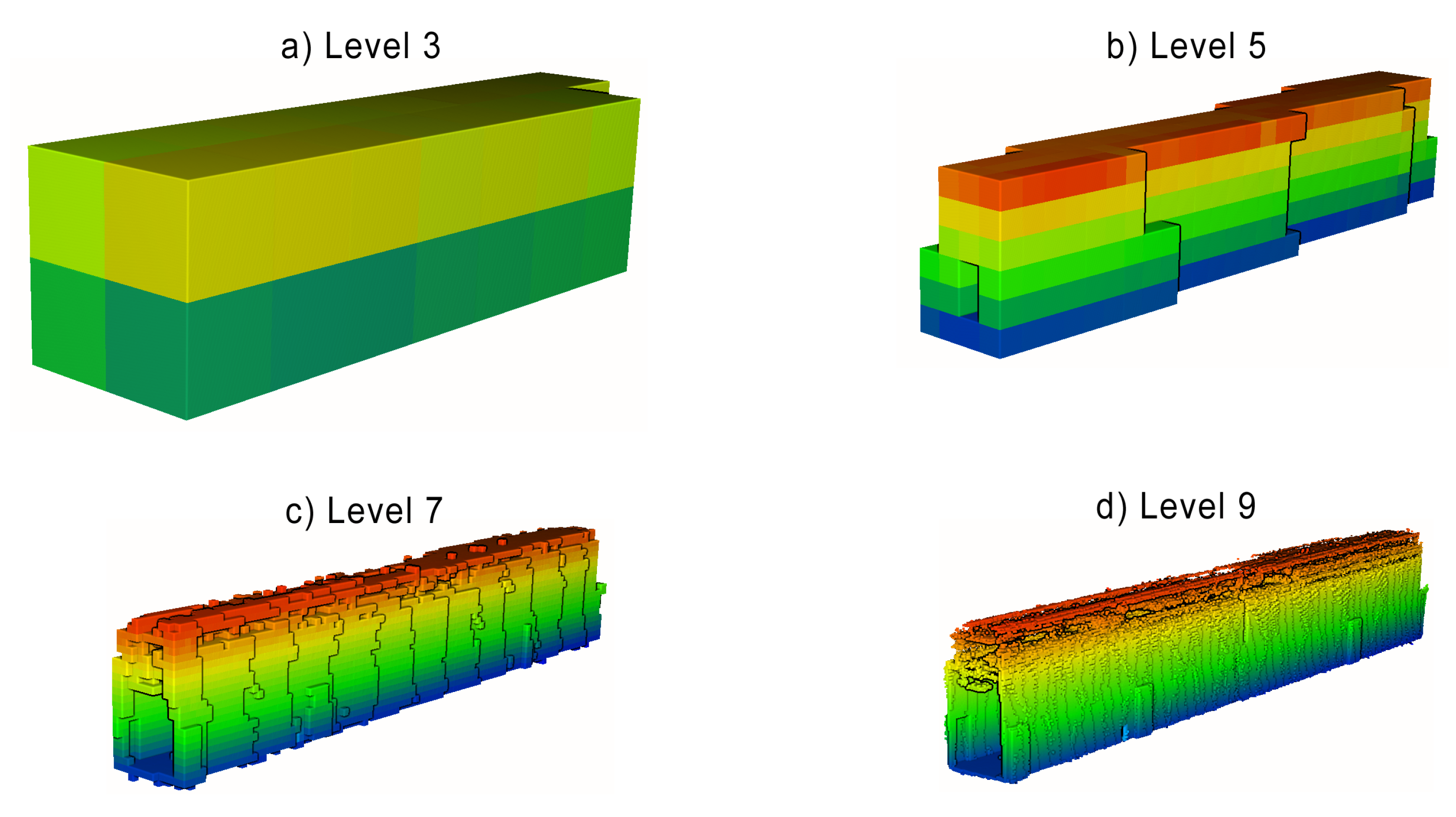
2.4. Metrics for Quality Assessment of 3D-Scene Reconstruction
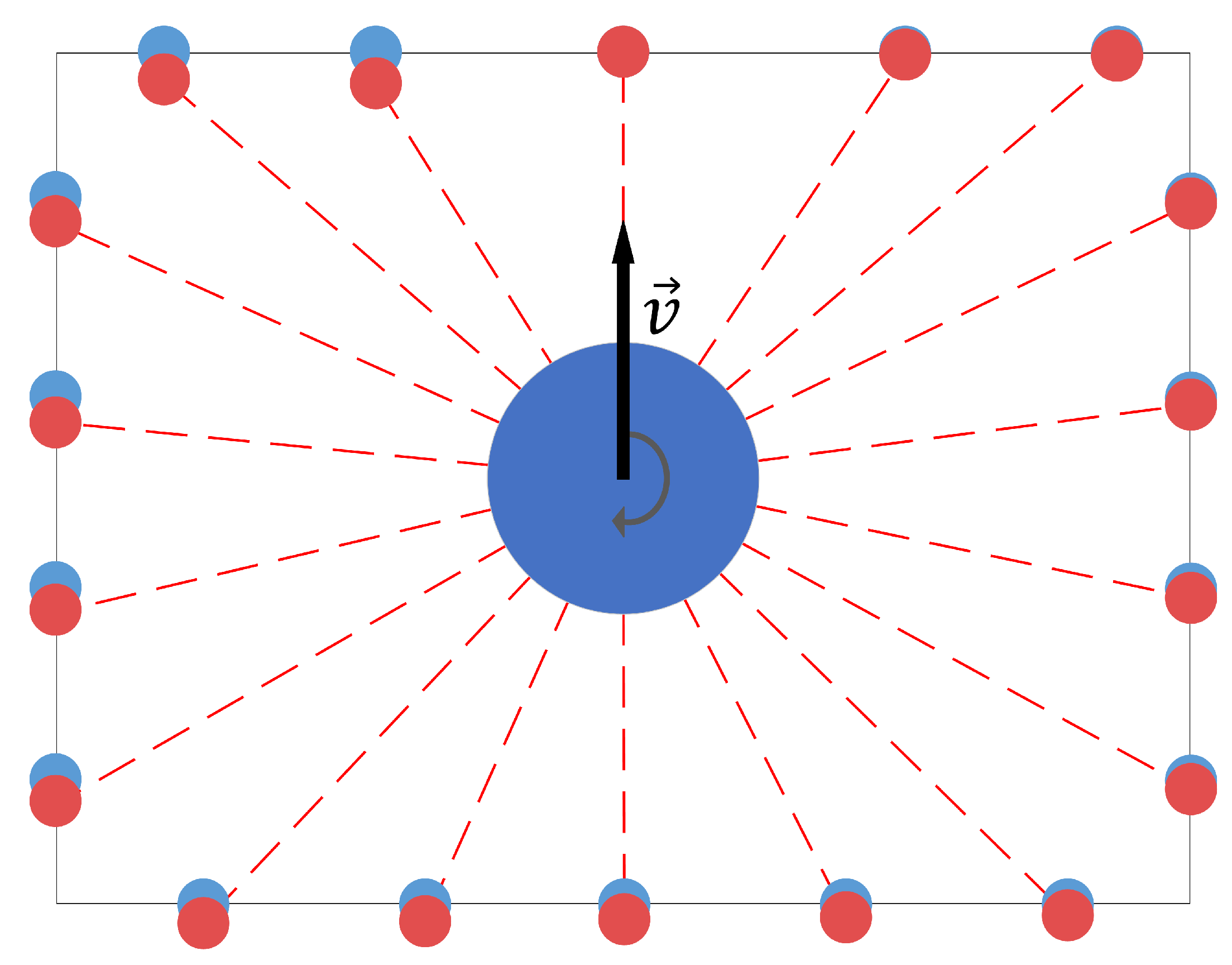
2.5. Data Acquisition Setup
- Sensor in fixed horizontal position, i.e., horizontal lidar;
- Sensor rotating in the full range from −90° to 90°, i.e., rotating lidar;
- Sensor rotating in the limited range from −45° to 45°, i.e., tilting lidar.
3. Results and Discussion
3.1. Analysis of the 3D Data Density
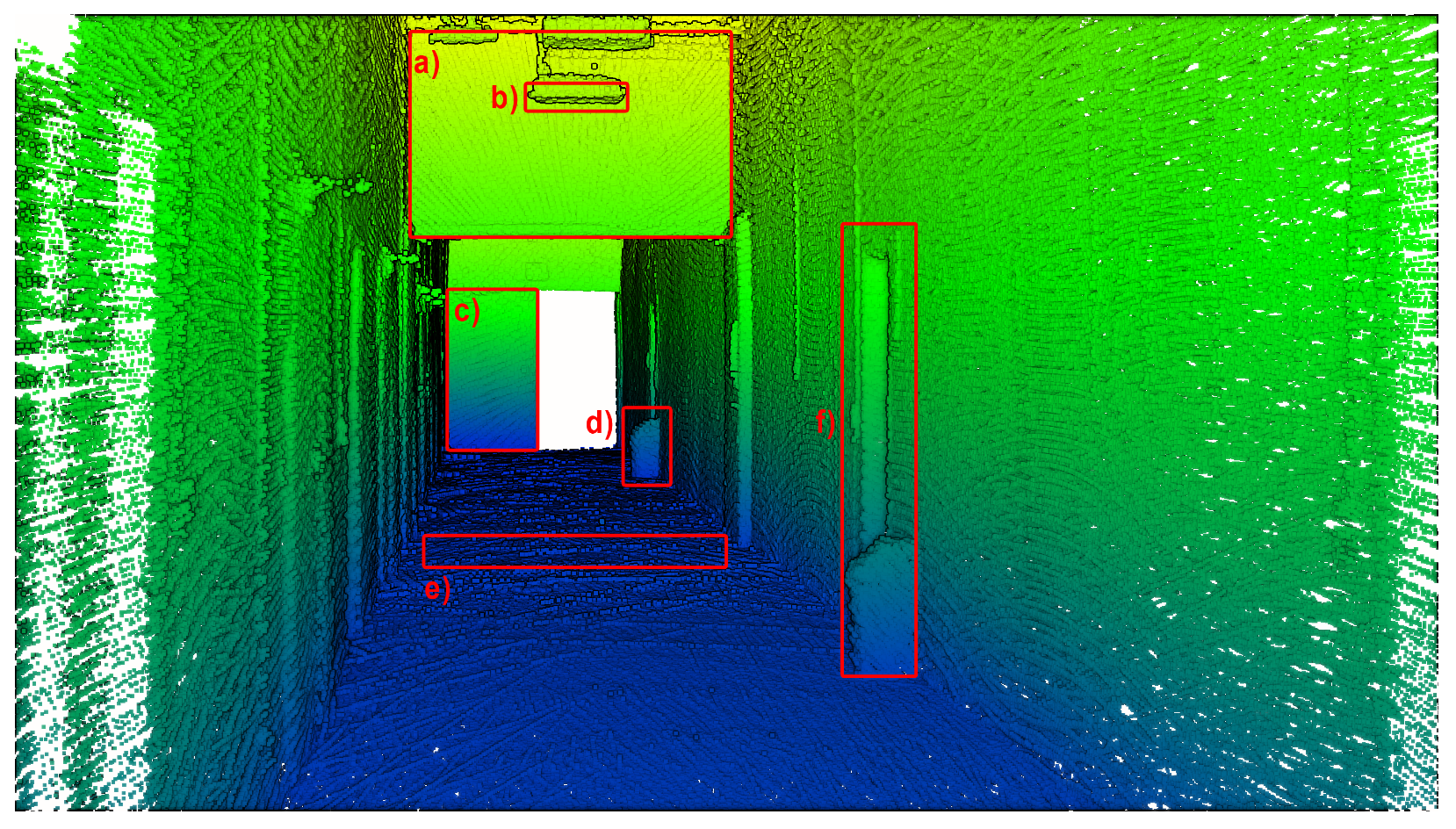
3.2. Local Point Cloud Quality
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alismail, H.; Baker, L.D.; Browning, B. Continuous trajectory estimation for 3D SLAM from actuated lidar. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May 2014–7 June 2014; pp. 6096–6101. [Google Scholar]
- Neumann, T.; Dülberg, E.; Schiffer, S.; Ferrein, A. A Rotating Platform for Swift Acquisition of Dense 3D Point Clouds. In Proceedings of the Intelligent Robotics and Applications, Tokyo, Japan, 22–24 August 2016; Kubota, N., Kiguchi, K., Liu, H., Obo, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 257–268. [Google Scholar]
- Huang, L. Review on LiDAR-based SLAM Techniques. In Proceedings of the 2021 International Conference on Signal Processing and Machine Learning (CONF-SPML), Stanford, CA, USA, 14 November 2021; pp. 163–168. [Google Scholar]
- Xu, X.; Zhang, L.; Yang, J.; Cao, C.; Wang, W.; Ran, Y.; Tan, Z.; Luo, M. A Review of Multi-Sensor Fusion SLAM Systems Based on 3D LIDAR. Remote Sens. 2022, 14, 2835. [Google Scholar] [CrossRef]
- Wei, W.; Shirinzadeh, B.; Nowell, R.; Ghafarian, M.; Ammar, M.M.A.; Shen, T. Enhancing Solid State LiDAR Mapping with a 2D Spinning LiDAR in Urban Scenario SLAM on Ground Vehicles. Sensors 2021, 21, 1773. [Google Scholar] [CrossRef] [PubMed]
- Bosse, M.; Zlot, R.; Flick, P. Zebedee: Design of a spring-mounted 3-d range sensor with application to mobile mapping. IEEE Trans. Robot. 2012, 28, 1104–1119. [Google Scholar] [CrossRef]
- Yoshida, T.; Irie, K.; Koyanagi, E.; Tomono, M. 3D laser scanner with gazing ability. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3098–3103. [Google Scholar]
- Frosi, M.; Matteucci, M. ART-SLAM: Accurate Real-Time 6DoF LiDAR SLAM. IEEE Robot. Autom. Lett. 2022, 7, 2692–2699. [Google Scholar] [CrossRef]
- Bosse, M.; Zlot, R. Continuous 3D scan-matching with a spinning 2D laser. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4312–4319. [Google Scholar]
- Alismail, H.; Browning, B. Automatic Calibration of Spinning Actuated Lidar Internal Parameters. J. Field Robot. 2015, 32, 723–747. [Google Scholar] [CrossRef]
- Ravi, R.; Lin, Y.J.; Elbahnasawy, M.; Shamseldin, T.; Habib, A. Bias impact analysis and calibration of terrestrial mobile lidar system with several spinning multibeam laser scanners. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5261–5275. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, W.; Yang, F.; Li, G. Rate-Distortion Optimized Geometry Compression for Spinning LiDAR Point Cloud. IEEE Trans. Multimed. (Early Access) 2022. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.P.; et al. Comparison of the Selected State-Of-The-Art 3D Indoor Scanning and Point Cloud Generation Methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. In Proceedings of the IEEE Visualization, 2002, VIS 2002, Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- Nurunnabi, A.; Belton, D.; West, G. Diagnostic-robust statistical analysis for local surface fitting in 3D point cloud data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-3, 269–274. [Google Scholar] [CrossRef]
- Mohammadi, M.E.; Wood, R.L.; Wittich, C.E. Non-temporal point cloud analysis for surface damage in civil structures. ISPRS Int. J. Geo-Inf. 2019, 8, 527. [Google Scholar] [CrossRef]
- Tan, Y.; Li, Y. UAV Photogrammetry-Based 3D Road Distress Detection. ISPRS Int. J. Geo-Inf. 2019, 8, 409. [Google Scholar] [CrossRef]
- Huber, D.F.; Vandapel, N. Automatic three-dimensional underground mine mapping. Int. J. Robot. Res. 2006, 25, 7–17. [Google Scholar] [CrossRef]
- Nuchter, A.; Surmann, H.; Lingemann, K.; Hertzberg, J.; Thrun, S. 6D SLAM with an application in autonomous mine mapping. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings, ICRA ’04, 2004, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, L.; Bi, L. Robust GICP-based 3D LiDAR SLAM for underground mining environment. Sensors 2019, 19, 2915. [Google Scholar] [CrossRef]
- Ferrein, A.; Scholl, I.; Neumann, T.; Krückel, K.; Schiffer, S. A System for Continuous Underground Site Mapping and Exploration. In Unmanned Robotic Systems and Applications; Reyhanoglu, M., Cubber, G.D., Eds.; IntechOpen: Rijeka, Croatia, 2020; Chapter 4. [Google Scholar]
- Zlot, R.; Bosse, M. Efficient large-scale three-dimensional mobile mapping for underground mines. J. Field Robot. 2014, 31, 758–779. [Google Scholar] [CrossRef]
- Fahle, L.; Holley, E.A.; Walton, G.; Petruska, A.J.; Brune, J.F. Analysis of SLAM-Based Lidar Data Quality Metrics for Geotechnical Underground Monitoring. Mining Metall. Explor. 2022, 39, 1939–1960. [Google Scholar] [CrossRef]
- Li, M.; Zhu, H.; You, S.; Wang, L.; Tang, C. Efficient Laser-Based 3D SLAM for Coal Mine Rescue Robots. IEEE Access 2019, 7, 14124–14138. [Google Scholar] [CrossRef]
- Ellmann, A.; Kütimets, K.; Varbla, S.; Väli, E.; Kanter, S. Advancements in underground mine surveys by using SLAM-enabled handheld laser scanners. Surv. Rev. 2021, 54, 363–374. [Google Scholar] [CrossRef]
- Ebadi, K.; Bernreiter, L.; Biggie, H.; Catt, G.; Chang, Y.; Chatterjee, A.; Denniston, C.E.; Deschênes, S.P.; Harlow, K.; Khattak, S.; et al. Present and future of slam in extreme underground environments. arXiv 2022, arXiv:2208.01787. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Kim, G.; Kim, A. Scan Context: Egocentric Spatial Descriptor for Place Recognition within 3D Point Cloud Map. In Proceedings of the Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Kim, G.; Choi, S.; Kim, A. Scan context++: Structural place recognition robust to rotation and lateral variations in urban environments. IEEE Trans. Robot. 2021, 38, 1856–1874. [Google Scholar] [CrossRef]
- Lupton, T.; Sukkarieh, S. Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions. IEEE Trans. Robot. 2012, 28, 61–76. [Google Scholar] [CrossRef]
- Carlone, L.; Kira, Z.; Beall, C.; Indelman, V.; Dellaert, F. Eliminating conditionally independent sets in factor graphs: A unifying perspective based on smart factors. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4290–4297. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation. In Proceedings of the Robotics: Science and Systems Conference, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Foote, T. tf: The transform library. In Proceedings of the 2013 IEEE Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, 22–23 April 2013; pp. 1–6. [Google Scholar]
- Kim, G.; Kim, A. Remove, then Revert: Static Point cloud Map Construction using Multiresolution Range Images. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 10758–10765. [Google Scholar]
- Olson, E.; Kaess, M. Evaluating the performance of map optimization algorithms. In Proceedings of the RSS Workshop on Good Experimental Methodology in Robotics, Seattle, WA, USA, 28 June 2009; Volume 15. [Google Scholar]
- Kümmerle, R.; Steder, B.; Dornhege, C.; Ruhnke, M.; Grisetti, G.; Stachniss, C.; Kleiner, A. On measuring the accuracy of SLAM algorithms. Auton. Robot. 2009, 27, 387–407. [Google Scholar] [CrossRef]
- He, Y.; Hu, Z.; Wu, K.; Wang, R. A Novel Method for Density Analysis of Repaired Point Cloud with Holes Based on Image Data. Remote Sens. 2021, 13, 3417. [Google Scholar] [CrossRef]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3D lidar point clouds. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2011, XXXVIII-5/W12, 97–102. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour detection in unstructured 3D point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1610–1618. [Google Scholar]
- Blomley, R.; Weinmann, M.; Leitloff, J.; Jutzi, B. Shape distribution features for point cloud analysis-a geometric histogram approach on multiple scales. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 9. [Google Scholar] [CrossRef]
- Huang, C.; Tseng, Y.H. Plane fitting methods of LiDAR point cloud. In Proceedings of the 29th Asian Conference on Remote Sensing 2008, ACRS 2008, Colombo, Sri Lanka, 10–14 November 2008; pp. 1925–1930. [Google Scholar]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graph. Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, X.; Stilla, U. Voxel-based representation of 3D point clouds: Methods, applications, and its potential use in the construction industry. Autom. Constr. 2021, 126, 103675. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3, p. 5. [Google Scholar]






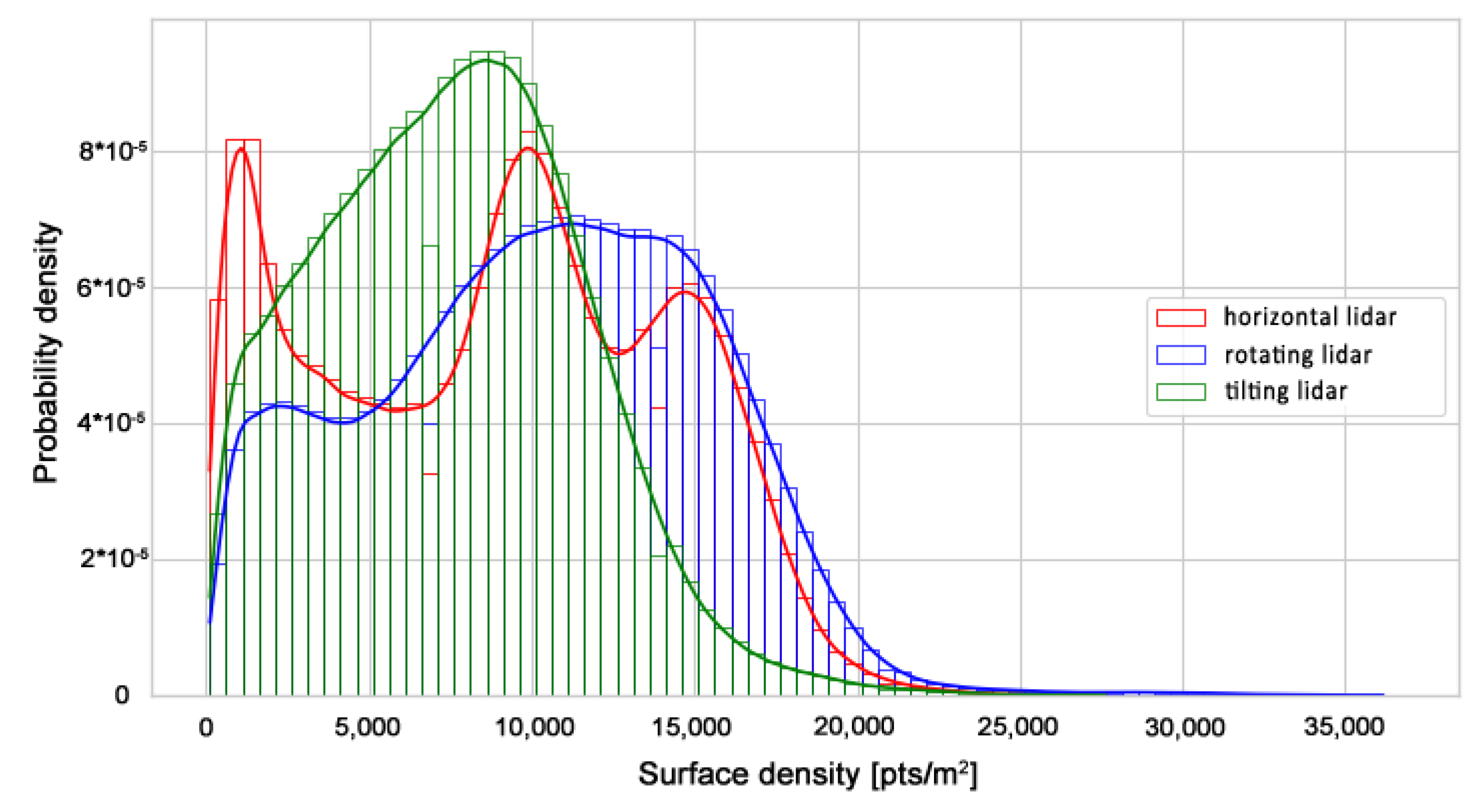
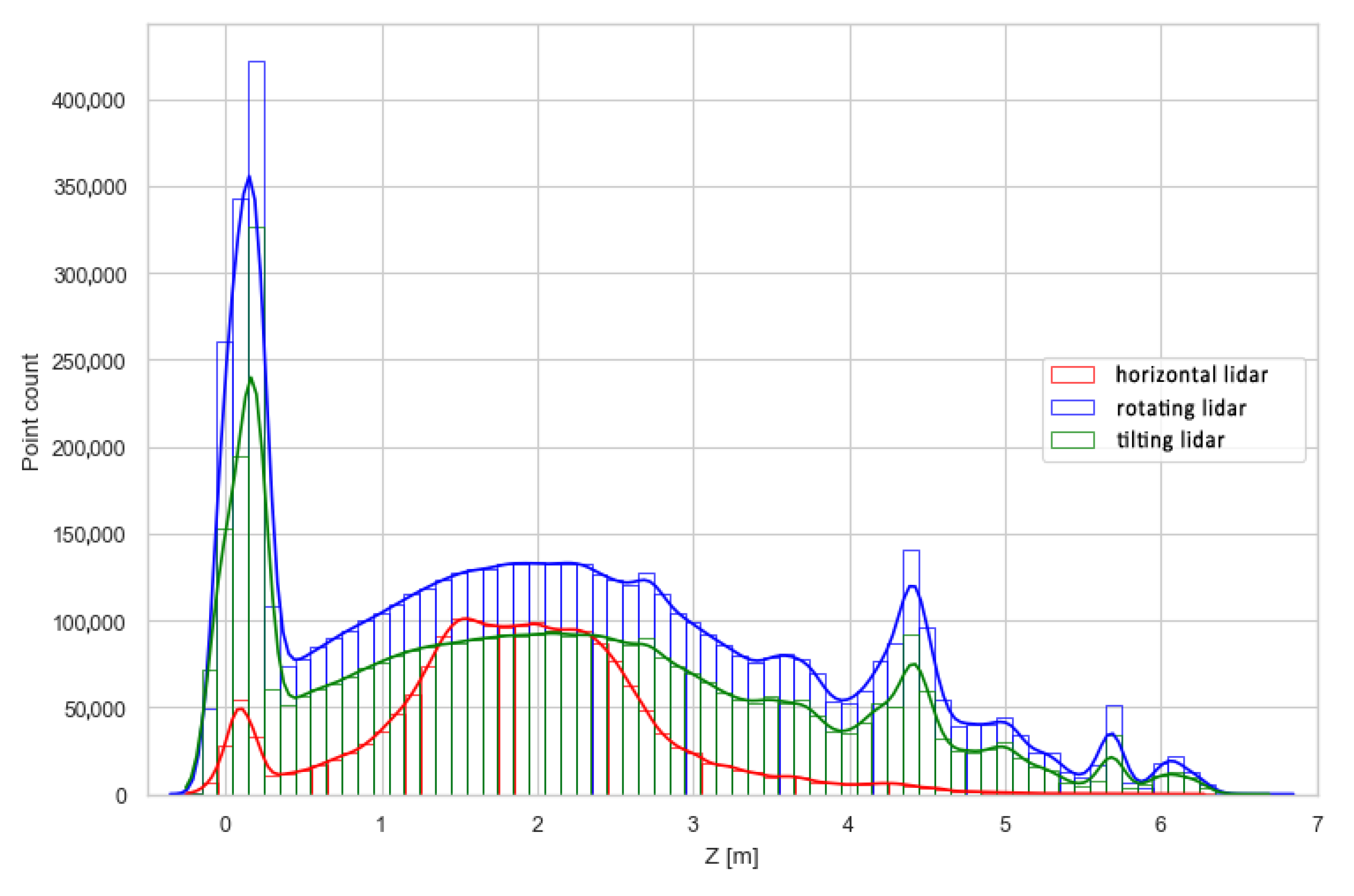



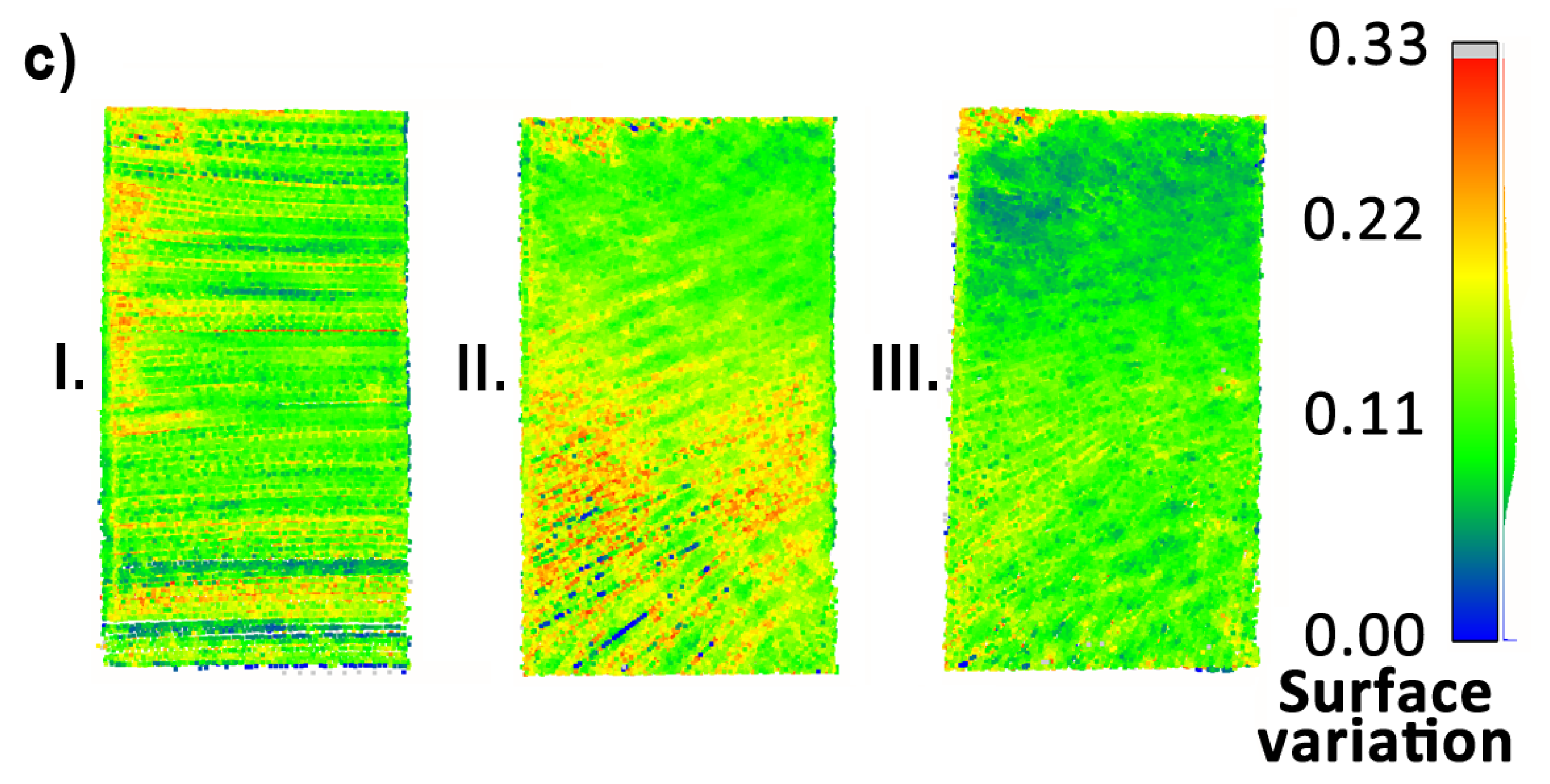



| No | Point Cloud | Mean Surface Density | Standard Deviation |
|---|---|---|---|
| I | Horizontal lidar | 8978 | 5249 |
| II | Rotating lidar | 10,230 | 5146 |
| III | Tilting lidar | 7581 | 3967 |
| No | Measurement Type | Plane Fit [mm] | ||
|---|---|---|---|---|
| (a) | (c) | (e) | ||
| I | Horizontal lidar | 47 | 28 | 20 |
| II | Rotating lidar | 30 | 36 | 12 |
| III | Tilting lidar | 42 | 52 | 14 |
| No | Measurement Type | Points per Object | |||||
|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | ||
| I | Horizontal lidar | 38,113 | 836 | 64,347 | 1432 | 6013 | 23,576 |
| II | Rotating lidar | 86,618 | 5874 | 90,425 | 6289 | 44,671 | 38,065 |
| III | Tilting lidar | 55,151 | 2286 | 70,834 | 4415 | 25,727 | 20,222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trybała, P.; Szrek, J.; Dębogórski, B.; Ziętek, B.; Blachowski, J.; Wodecki, J.; Zimroz, R. Analysis of Lidar Actuator System Influence on the Quality of Dense 3D Point Cloud Obtained with SLAM. Sensors 2023, 23, 721. https://doi.org/10.3390/s23020721
Trybała P, Szrek J, Dębogórski B, Ziętek B, Blachowski J, Wodecki J, Zimroz R. Analysis of Lidar Actuator System Influence on the Quality of Dense 3D Point Cloud Obtained with SLAM. Sensors. 2023; 23(2):721. https://doi.org/10.3390/s23020721
Chicago/Turabian StyleTrybała, Paweł, Jarosław Szrek, Błażej Dębogórski, Bartłomiej Ziętek, Jan Blachowski, Jacek Wodecki, and Radosław Zimroz. 2023. "Analysis of Lidar Actuator System Influence on the Quality of Dense 3D Point Cloud Obtained with SLAM" Sensors 23, no. 2: 721. https://doi.org/10.3390/s23020721
APA StyleTrybała, P., Szrek, J., Dębogórski, B., Ziętek, B., Blachowski, J., Wodecki, J., & Zimroz, R. (2023). Analysis of Lidar Actuator System Influence on the Quality of Dense 3D Point Cloud Obtained with SLAM. Sensors, 23(2), 721. https://doi.org/10.3390/s23020721









