Constructing Physics-Informed Neural Networks with Architecture Based on Analytical Modification of Numerical Methods by Solving the Problem of Modelling Processes in a Chemical Reactor
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Statement
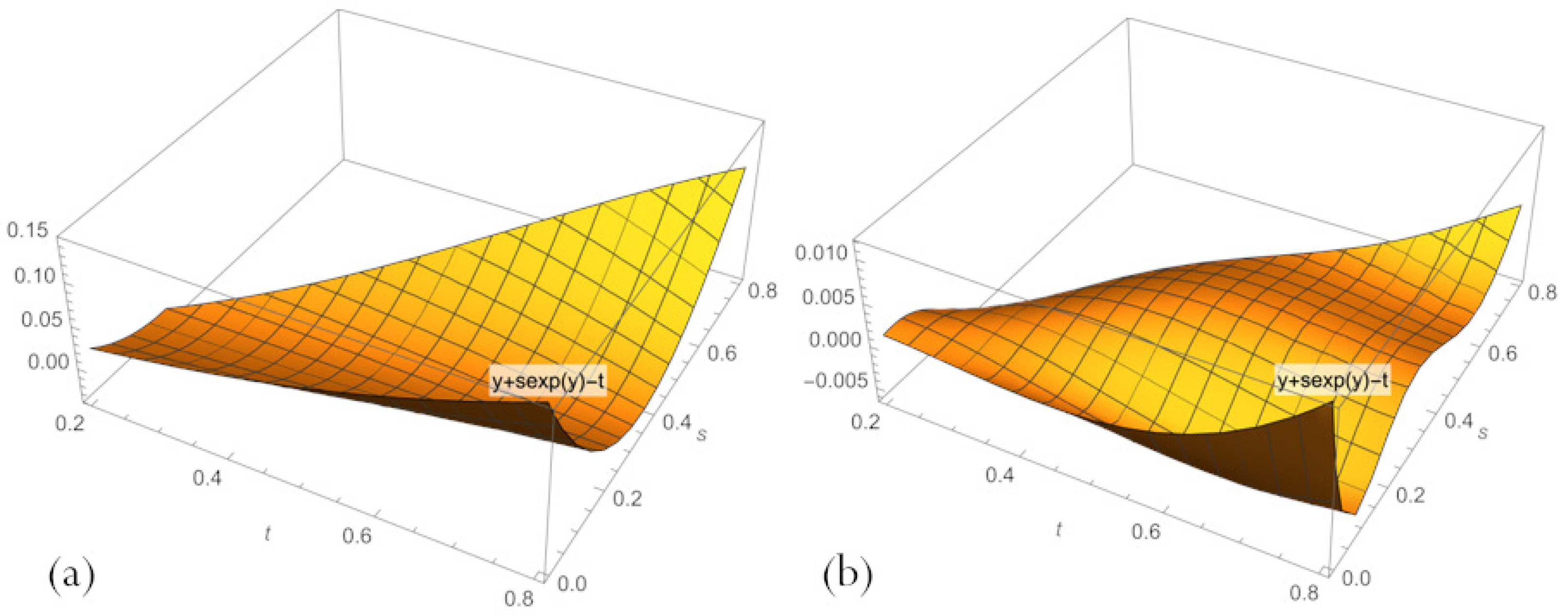
2.2. Analytical Modification of the Shooting Method and Constructing PBA Model
2.3. PBA-PINN Model Constructing
2.4. High-Fidelity Refinement PBA-PINNs Based on Sensor Data
2.5. Data-Driven Parameter Identification
3. Case Study
3.1. Problem Statement
3.2. Transformation of Equations
3.3. Embedding Neural Network in PBA Solution
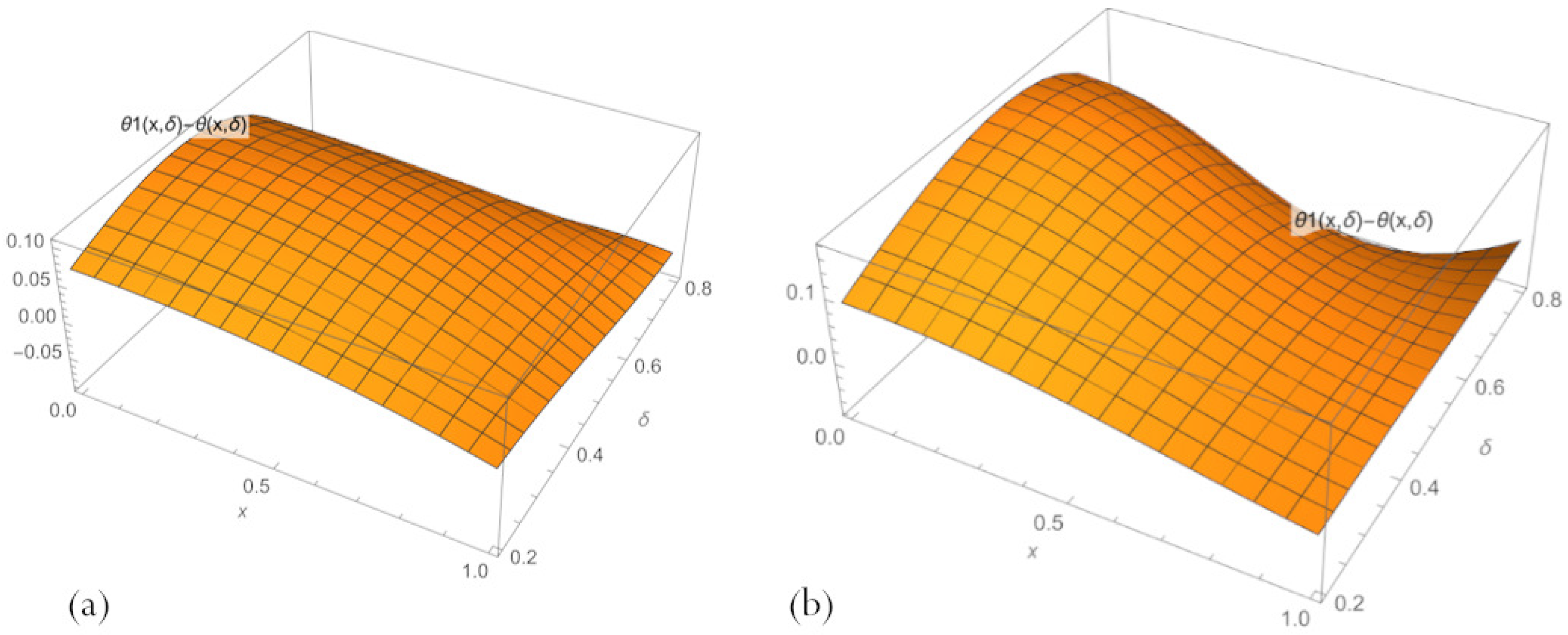
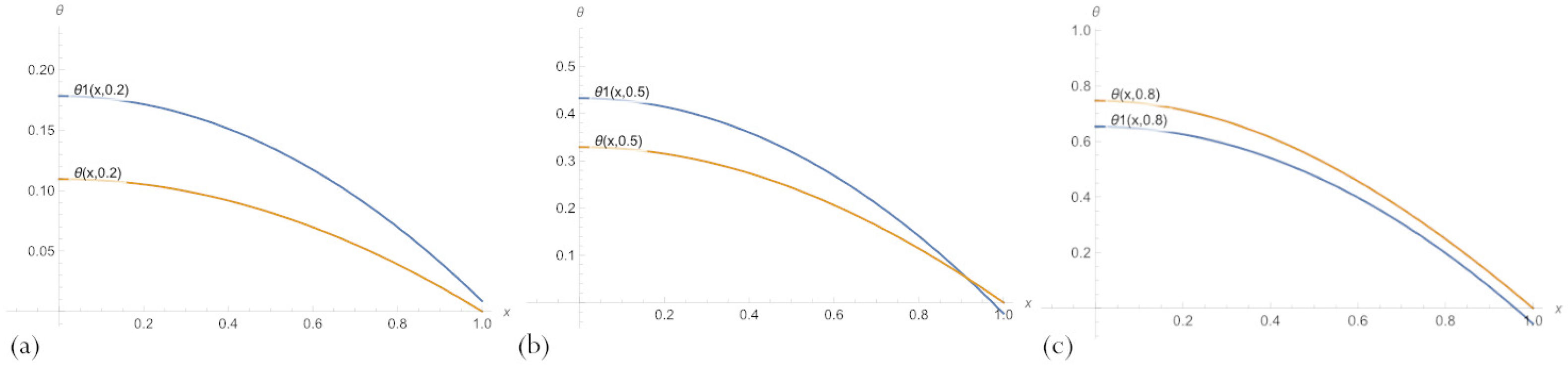
3.4. Physics-Informed Refinement of Initial PBA Neural Networks
3.5. Additional Embedding Neural Network in PBA Solution
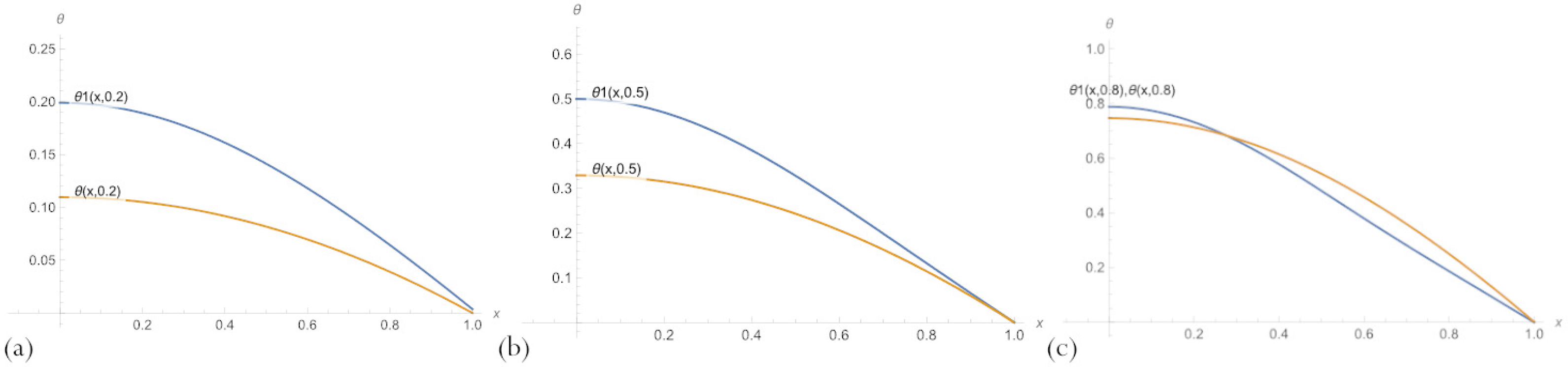
3.6. Data-Driven PBA-PINN Model Refinement and Discovery
3.6.1. Parametric PBA-PINN
3.6.2. PBA-PINN for Fixed Parameter Value
3.6.3. Parameter Identification
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Tarkhov, D.; Vasilyev, A. Parametric Neural Network Modeling in Engineering. Recent Patents Eng. 2016, 11, 1. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, L.; Guo, L.; Karniadakis, G.E. Quantifying total uncertainty in physics-informed neural networks for solving forward and inverse stochastic problems. J. Comput. Phys. 2019, 397, 108850. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Arthurs, C.J.; King, A.P. Active training of physics-informed neural networks to aggregate and interpolate parametric solutions to the Navier-Stokes equations. J. Comput. Phys. 2021, 438, 110364. [Google Scholar] [CrossRef]
- Lye, K.O.; Mishra, S.; Molinaro, R. A multi-level procedure for enhancing accuracy of machine learning algorithms. Eur. J. Appl. Math. 2021, 32, 436–469. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Zhao, X.; Gong, Z.; Zhang, Y.; Yao, W.; Chen, X. Physics-informed convolutional neural networks for temperature field prediction of heat source layout without labeled data. Eng. Appl. Artif. Intell. 2023, 117A, 105516. [Google Scholar] [CrossRef]
- Tang, S.; Feng, X.; Wu, W.; Xu, H. Physics-informed neural networks combined with polynomial interpolation to solve nonlinear partial differential equations. Comput. Math. Appl. 2023, 132, 48–62. [Google Scholar] [CrossRef]
- Goswami, S.; Yin, M.; Yu, Y.; Karniadakis, G.E. A physics-informed variational DeepONet for predicting crack path in quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2022, 391, 114587. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Malykhina, G.; Tarkhov, D. Construction of an Individual Model of the Deflection of a PVC-Specimen Based on a Differential Equation and Measurement Data. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies, FarEastCon 2020, Vladivostok, Russia, 6–9 October 2020; p. 9271144. [Google Scholar]
- Bolgov, I.; Kaverzneva, T.; Kolesova, S.; Lazovskaya, T.; Stolyarov, O.; Tarkhov, D. Neural network model of rupture conditions for elastic material sample based on measurements at static loading under different strain rates. J. Phys. Conf. Ser. 2016, 772, 012032. [Google Scholar] [CrossRef]
- Filkin, V.; Kaverzneva, T.; Lazovskaya, T.; Lukinskiy, E.; Petrov, A.; Stolyarov, O.; Tarkhov, D. Neural network modeling of conditions of destruction of wood plank based on measurements. J. Phys. Conf. Ser. 2016, 772, 012041. [Google Scholar] [CrossRef]
- Chakraborty, S. Transfer learning based multi-fidelity physics informed deep neural network. J. Comput. Phys. 2021, 426, 109942. [Google Scholar] [CrossRef]
- Huang, Y.; Hao, W.; Lin, G. HomPINNs: Homotopy physics-informed neural networks for learning multiple solutions of nonlinear elliptic differential equations. Comput. Math. Appl. 2022, 121, 62–73. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Malykhina, G.; Tarkhov, D. Physics Based Neural Networks Methods for Solving Parametrised Singular Perturbation Problem. Computation 2021, 9, 97. [Google Scholar] [CrossRef]
- Peng, P.; Pan, J.; Xu, H.; Feng, X. RPINNs: Rectified-physics informed neural networks for solving stationary partial differential equations. Comput. Fluids 2022, 245, 105583. [Google Scholar] [CrossRef]
- Lazovskaya, T.; Tarkhov, D.; Chernukha, D.; Korchagin, A.; Malykhina, G. Analysis of Predictive Capabilities of Adaptive Multilayer Models with Physics-Based Architecture for Duffing Oscillator. Int. Conf. Neuroinform. 2023, 1064, 54. [Google Scholar]
- Zobeiry, N.; Humfeld, K.D. A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications. Eng. Appl. Artif. Intell. 2021, 101, 104232. [Google Scholar] [CrossRef]
- Hlavácek, V.; Marek, M.; Kubícek, M. Modelling of chemical reactors—X Multiple solutions of enthalpy and mass balances for a catalytic reaction within a porous catalyst particle. Chem. Eng. Sci. 1968, 23, 1083–1097. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Pandey, V.S.; Khan, Z.H.; Tripathi, D. 3D free convective MHD flow of nanofluid over permeable linear stretching sheet with thermal radiation. Powder Technol. 2017, 3015, 205–215. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Afsharpanah, F.; Zamani, S.; Gholinia, M.; Ganji, D.D. A numerical investigation on ethylene glycol-titanium dioxide nanofluid convective flow over a stretching sheet in presence of heat generation/absorption. Case Stud. Therm. Eng. 2018, 12, 228–236. [Google Scholar] [CrossRef]
- Puneeth, V.; Manjunatha, S.; Makinde, O.D.; Gireesha, B.J. Bioconvection of a radiating hybrid nanofluid past a thin needle in the presence of heterogeneous-homogeneous chemical reaction. J. Heat Transf. 2021, 143, 042502. [Google Scholar] [CrossRef]
- Parker, S.S.; Newman, S.; Fallgren, A.J.; White, J.T. Physics Based Neural Networks Methods for Solving Thermophysical Properties of Mixtures of Thorium and Uranium Nitride. JOM 2021, 73, 3564–3575. [Google Scholar] [CrossRef]
- Gui, N.; Jiang, S.; Yang, X.; Tu, J. A review of recent study on the characteristics and applications of pebble flows in nuclear engineering. Exp. Comput. Multiph. Flow 2022, 2, 339–349. [Google Scholar] [CrossRef]
- Pantopoulou, S.; Ankel, V.; Weathered, M.T.; Lisowski, D.D.; Cilliers, A.; Tsoukalas, L.H.; Heifetz, A. Monitoring of Temperature Measurements for Different Flow Regimes in Water and Galinstan with Long Short-Term Memory Networks and Transfer Learning of Sensors. Computation 2022, 10, 108. [Google Scholar] [CrossRef]
- Shen, L.; Xie, F.; Xiao, W.; Ji, H.; Zhang, B. Thermal Analyses of Reactor under High-Power and High-Frequency Square Wave Voltage Based on Improved Thermal Network Model. Electronics 2021, 10, 1342. [Google Scholar] [CrossRef]
- So, S.; Jeong, N.; Song, A.; Hwang, J.; Kim, D.; Lee, C. Measurement of Temperature and H2O Concentration in Premixed CH4/Air Flame Using Two Partially Overlapped H2O Absorption Signals in the Near Infrared Region. Appl. Sci. 2021, 11, 3701. [Google Scholar] [CrossRef]
- Najeeb, A.; Sultan, F.; Alshomrani, A.S. Binary chemical reaction with activation energy in radiative rotating disk flow of Bingham plastic fluid. Heat-Transf.-Asian Res. 2020, 49, 1314–1337. [Google Scholar]
- Wang, K.; Deng, P.; Liu, R.; Ge, C.; Wang, H.; Chen, P. A Novel Understanding of the Thermal Reaction Behavior and Mechanism of Ni/Al Energetic Structural Materials. Crystals 2022, 12, 1632. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problem; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Tarkhov, D.; Vasilyev, A. Semi-Empirical Neural Network Modeling and Digital Twins Development; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Tarkhov, D.A.; Vasilyev, A.N. The Construction of the Approximate Solution of the Chemical Reactor Problem Using the Feedforward Multilayer Neural Network. Int. Conf. Neuroinform. 2020, 856, 41. [Google Scholar]
- Motsa, S.S.; Makinde, O.D.; Shateyi, S. On New High Order Quasilinearization Approaches to the Nonlinear Model of Catalytic Reaction in a Flat Particle. Adv. Math. Phys. 2013, 2013, 350810. [Google Scholar]
- Yadav, N.; Yadav, A.; Deep, K. Artificial neural network technique for solution of nonlinear elliptic boundary value problems. Adv. Intell. Syst. Comput. 2015, 335, 113–121. [Google Scholar]

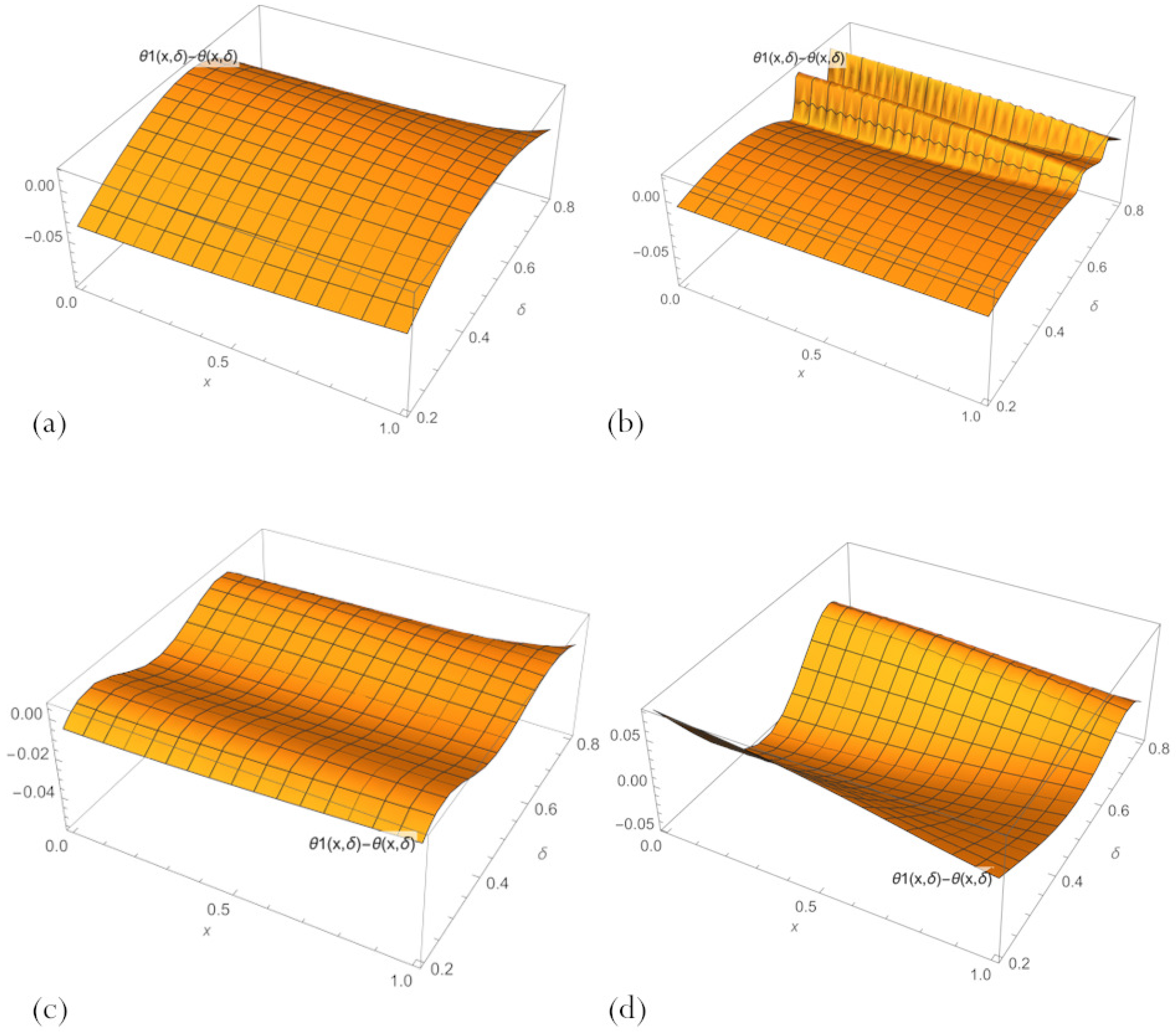
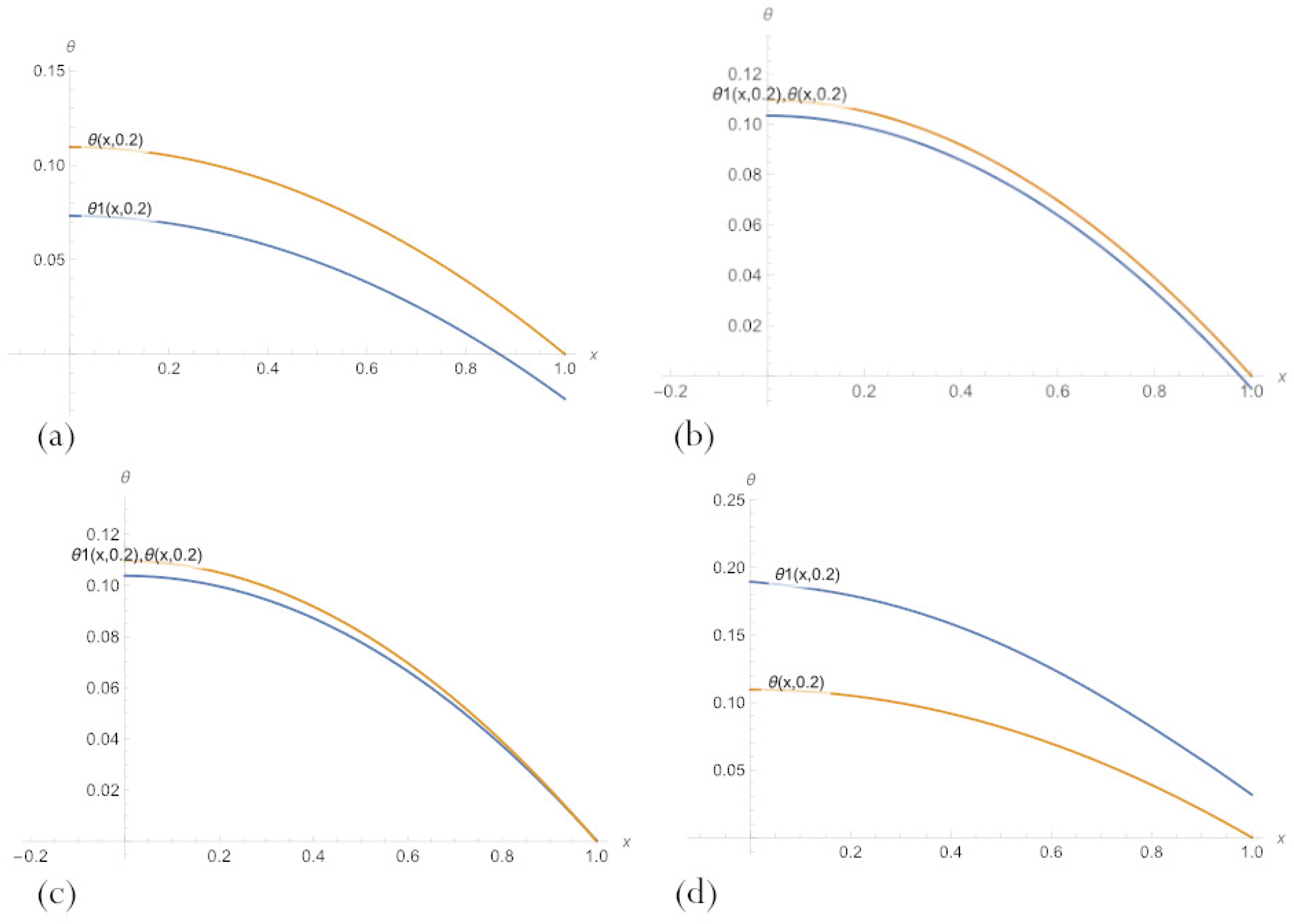
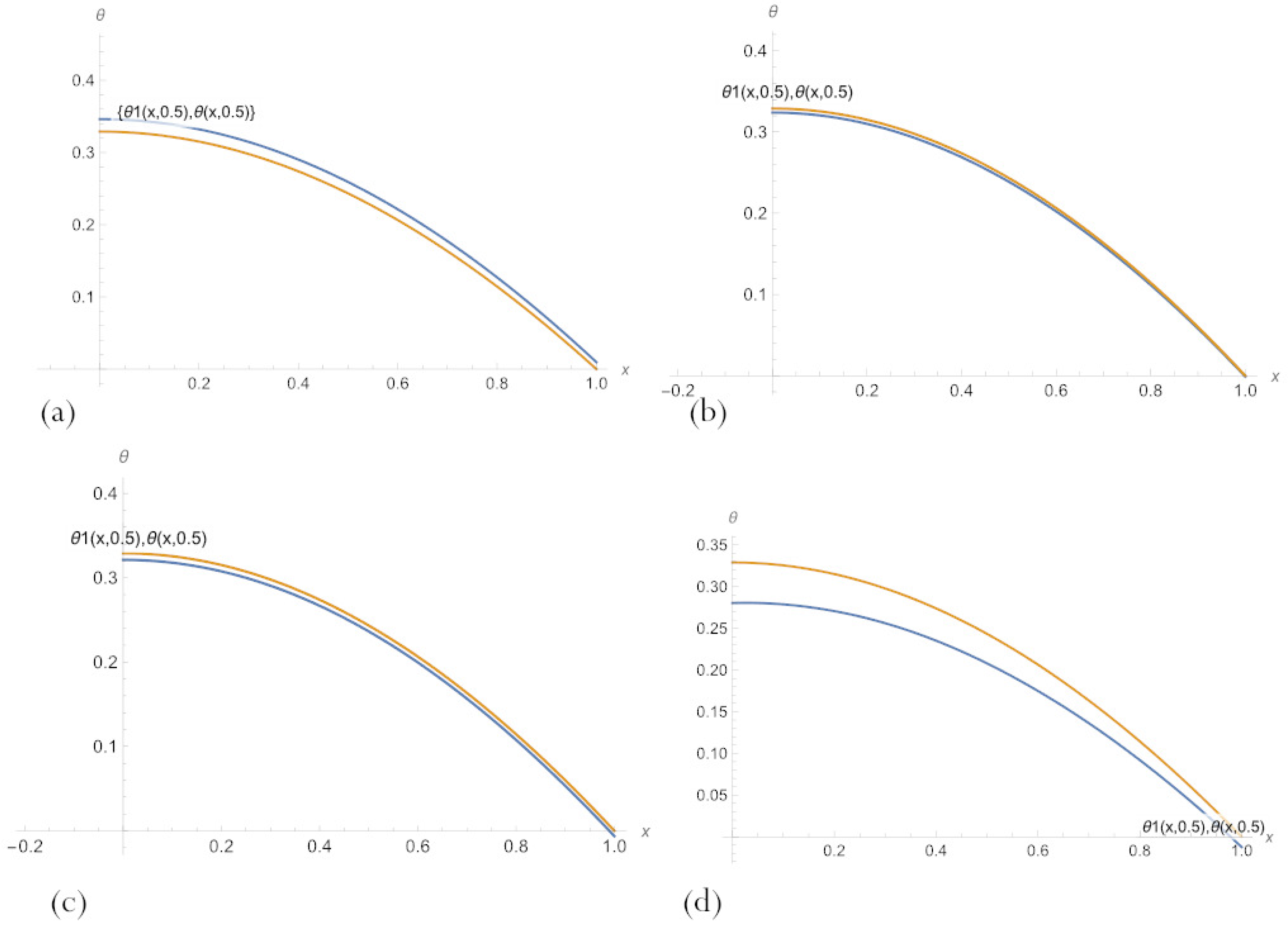

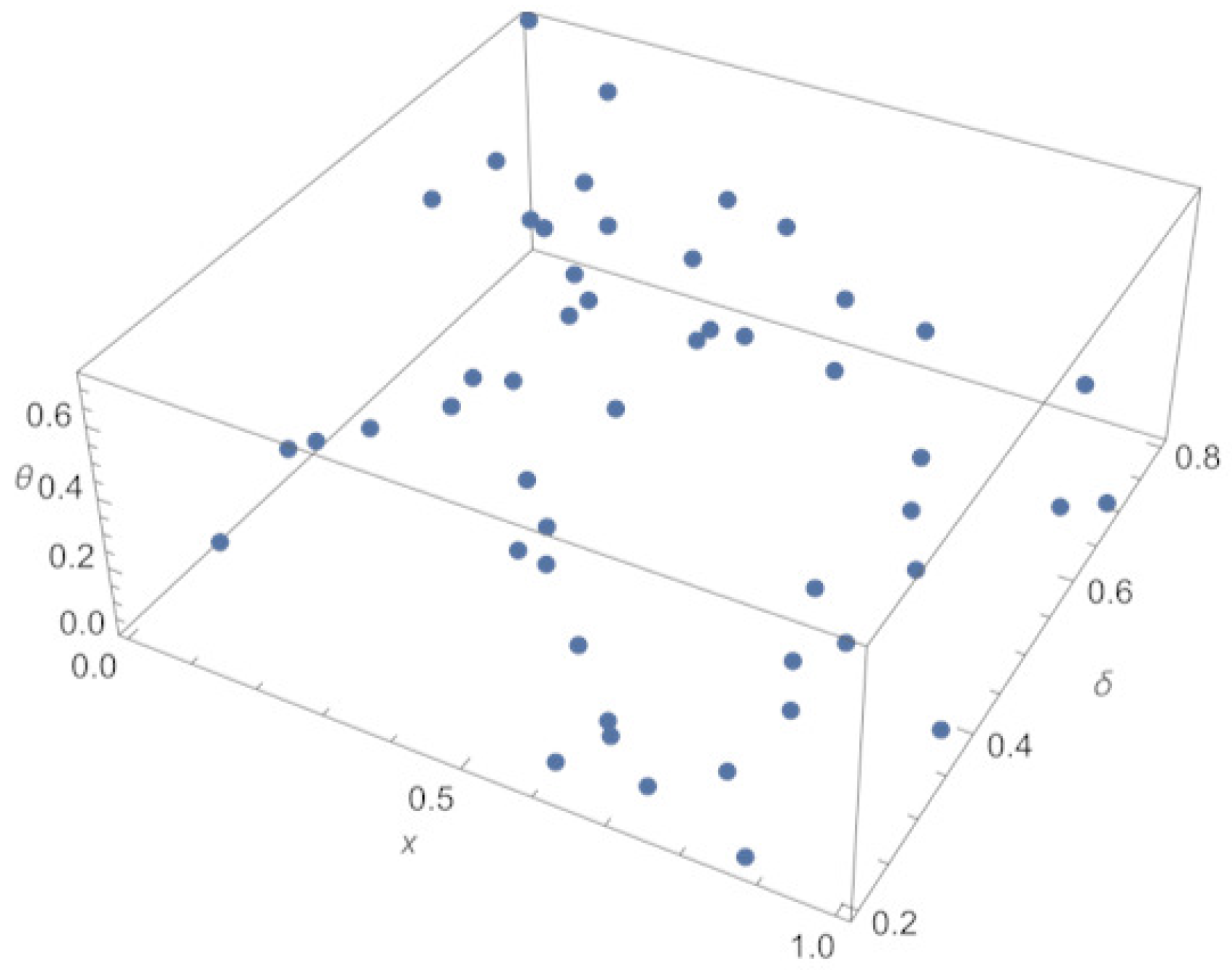
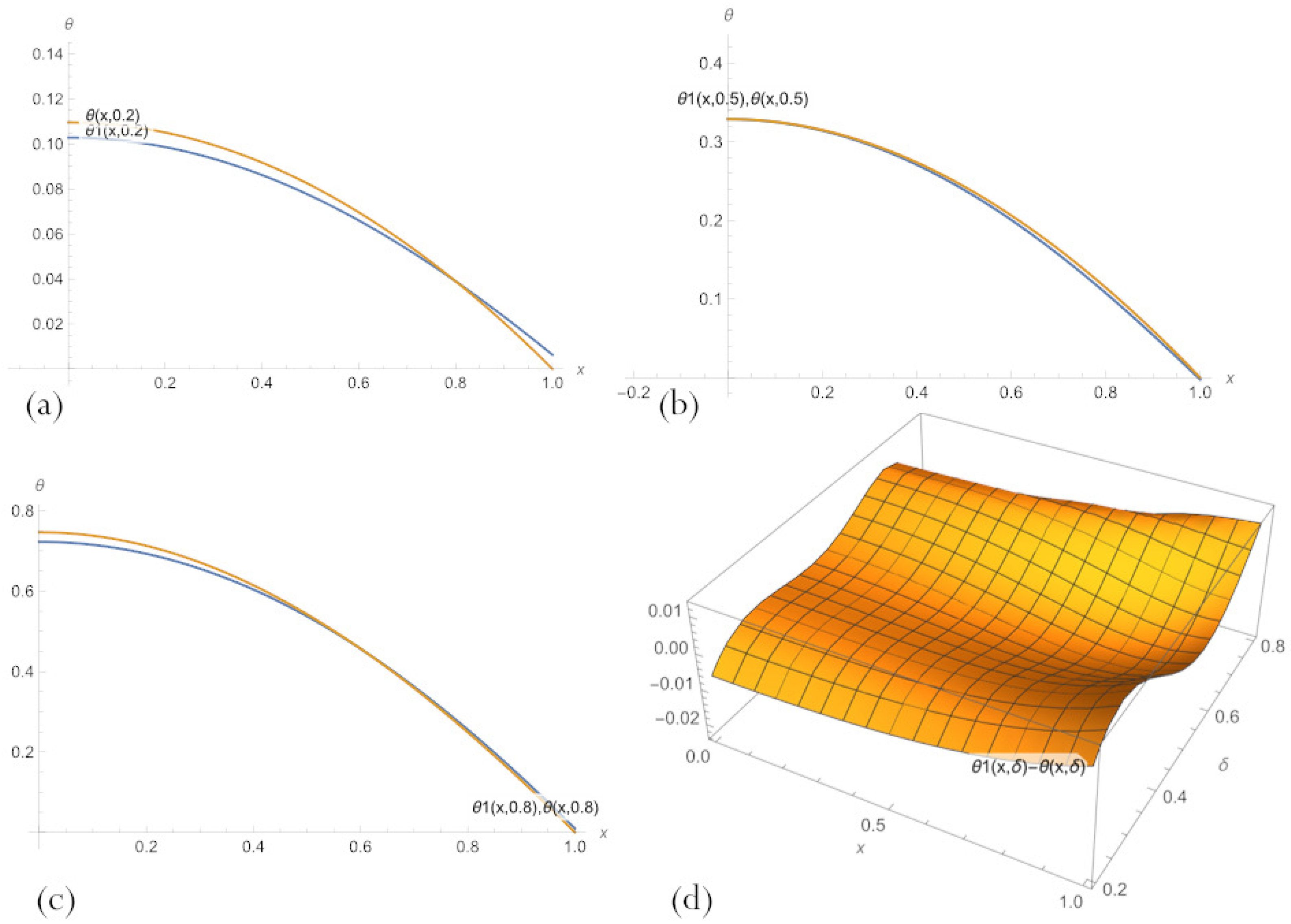
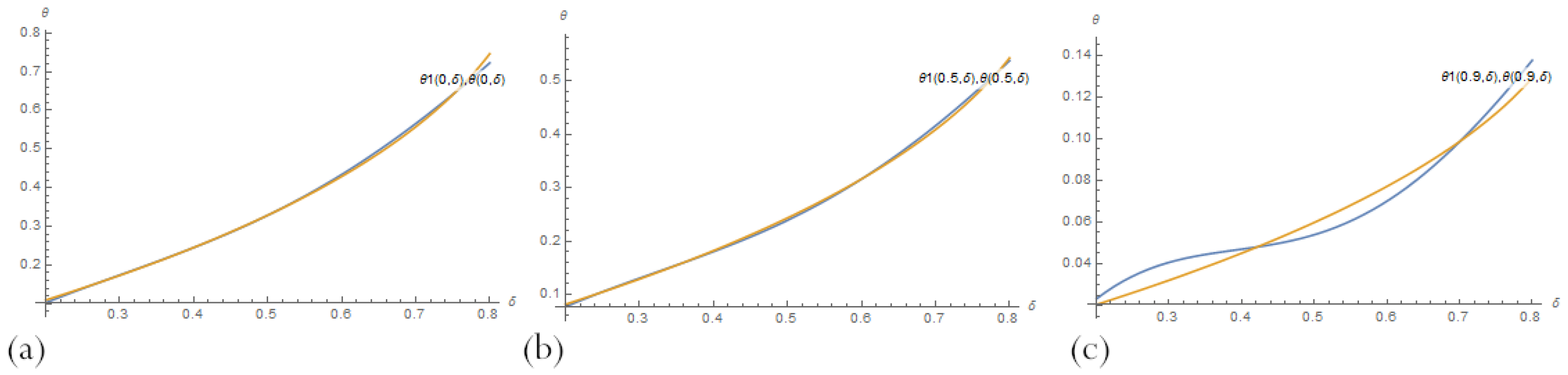
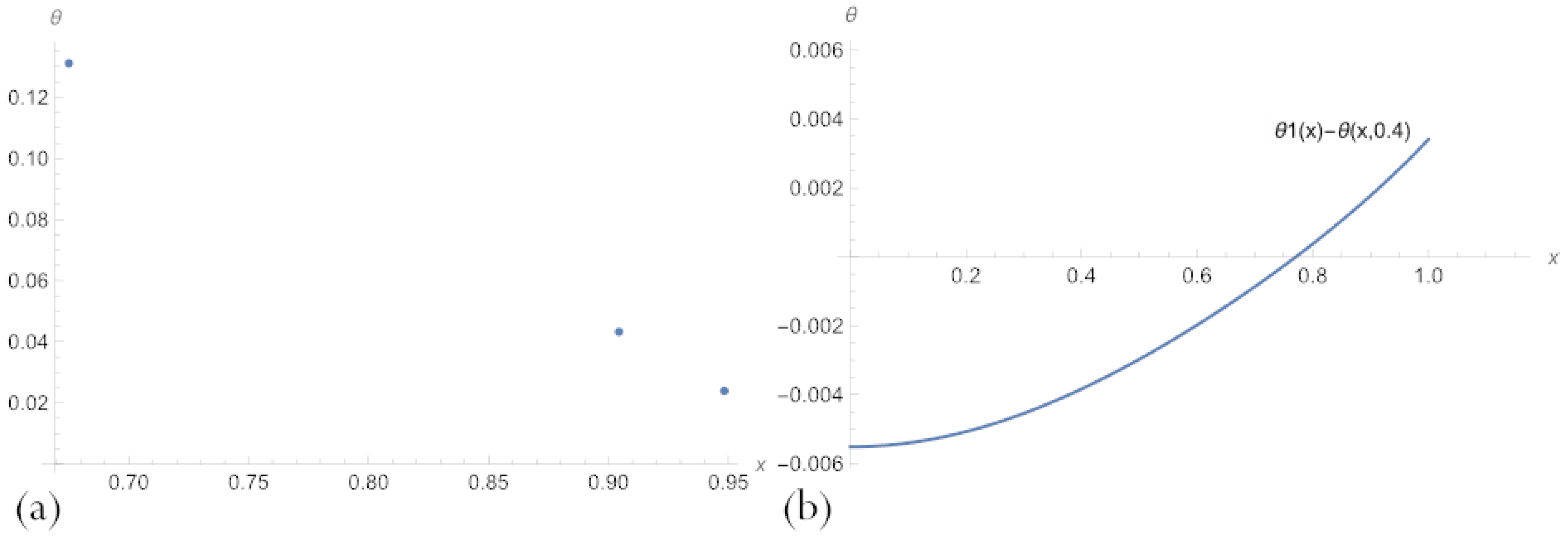
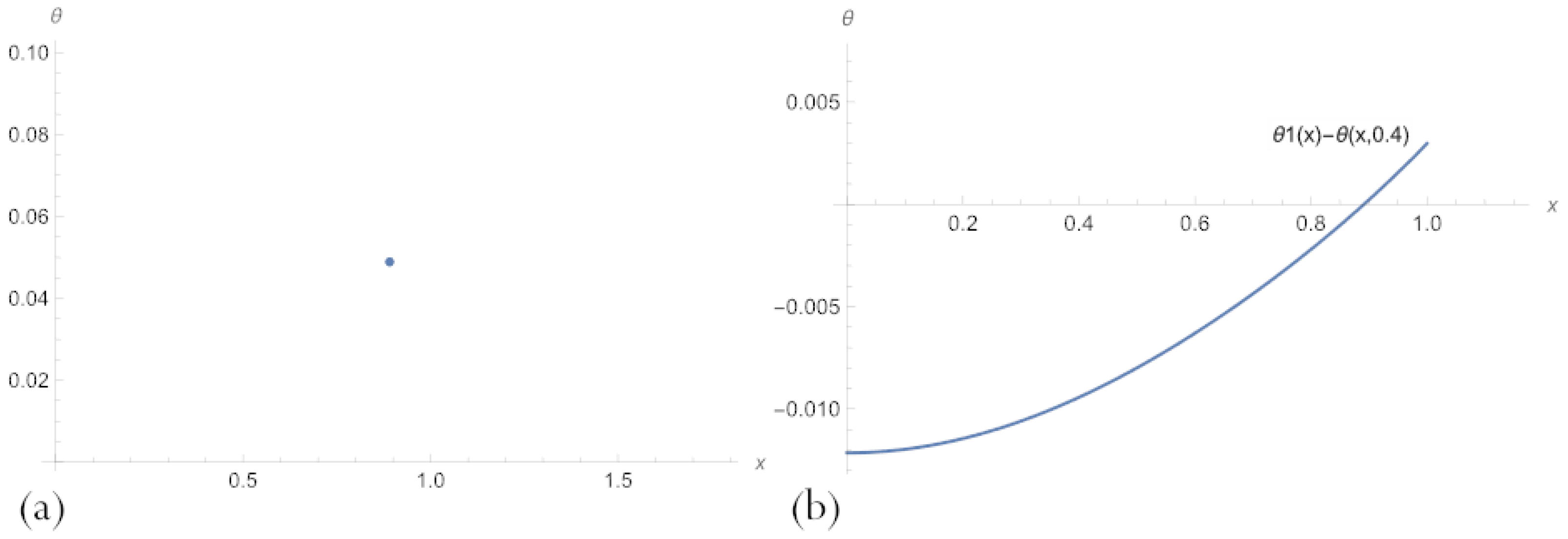
| Number of Neurons | MSE for (16) | max|Error| for (16) | MSE for (11) | max|Error| for (11) |
|---|---|---|---|---|
| 0.0259 | 0.146 | 0.0617 | 0.106 | |
| 0.00354 | 0.0238 | 0.0900 | 0.168 | |
| 0.00189 | 0.0117 | 0.0880 | 0.172 | |
| 0.00223 | 0.0100 | 0.0875 | 0.176 |
| Number of Neurons | MSE for Learned (20) | max|Error| for Learned (20) | MSE for Classical PINN | max|Error| for Classical PINN |
|---|---|---|---|---|
| 0.0192 | 0.0947 | 0.120 | 0.393 | |
| 0.0118 | 0.0678 | 0.0448 | 0.149 | |
| 0.0113 | 0.0706 | 0.0374 | 0.123 | |
| 0.0269 | 0.0792 |
| Number of Neurons | MSE | max|Error| |
|---|---|---|
| , | 0.00865 | 0.0527 |
| , | 0.00593 | 0.0437 |
| MSE for (11) | max|Error| for (11) | |
|---|---|---|
| 0.00445 | 0.0163 | |
| 0.0000456 | 0.000155 | |
| 0.000148 | 0.000272 | |
| 0.000798 | 0.00178 |
| Number of Sensor Data | Predicted | |Error| |
|---|---|---|
| 0.378 | 0.022 | |
| 0.364 | 0.046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarkhov, D.; Lazovskaya, T.; Malykhina, G. Constructing Physics-Informed Neural Networks with Architecture Based on Analytical Modification of Numerical Methods by Solving the Problem of Modelling Processes in a Chemical Reactor. Sensors 2023, 23, 663. https://doi.org/10.3390/s23020663
Tarkhov D, Lazovskaya T, Malykhina G. Constructing Physics-Informed Neural Networks with Architecture Based on Analytical Modification of Numerical Methods by Solving the Problem of Modelling Processes in a Chemical Reactor. Sensors. 2023; 23(2):663. https://doi.org/10.3390/s23020663
Chicago/Turabian StyleTarkhov, Dmitriy, Tatiana Lazovskaya, and Galina Malykhina. 2023. "Constructing Physics-Informed Neural Networks with Architecture Based on Analytical Modification of Numerical Methods by Solving the Problem of Modelling Processes in a Chemical Reactor" Sensors 23, no. 2: 663. https://doi.org/10.3390/s23020663
APA StyleTarkhov, D., Lazovskaya, T., & Malykhina, G. (2023). Constructing Physics-Informed Neural Networks with Architecture Based on Analytical Modification of Numerical Methods by Solving the Problem of Modelling Processes in a Chemical Reactor. Sensors, 23(2), 663. https://doi.org/10.3390/s23020663