Estimating the Depth of Anesthesia from EEG Signals Based on a Deep Residual Shrinkage Network
Abstract
1. Introduction
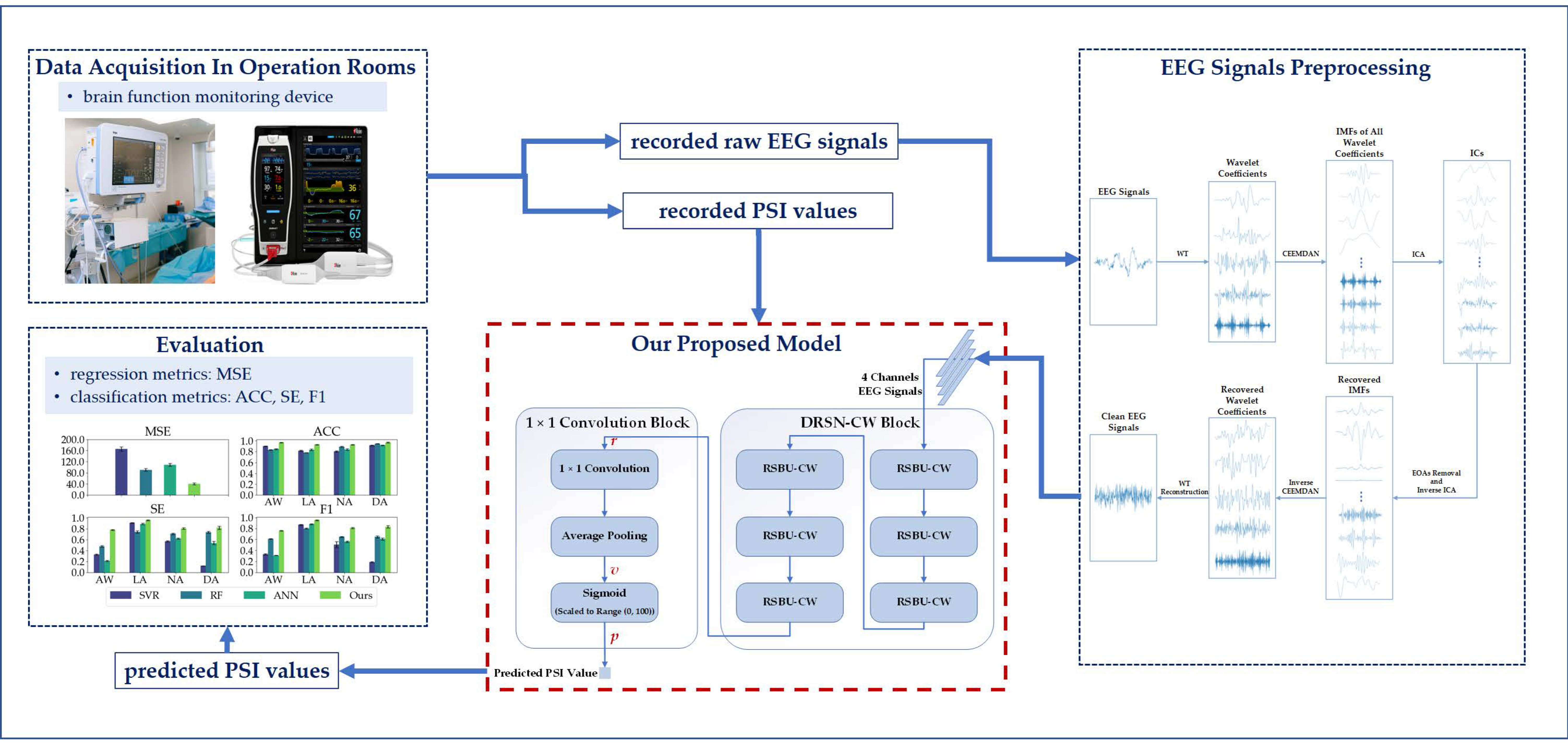
2. Materials and Methods
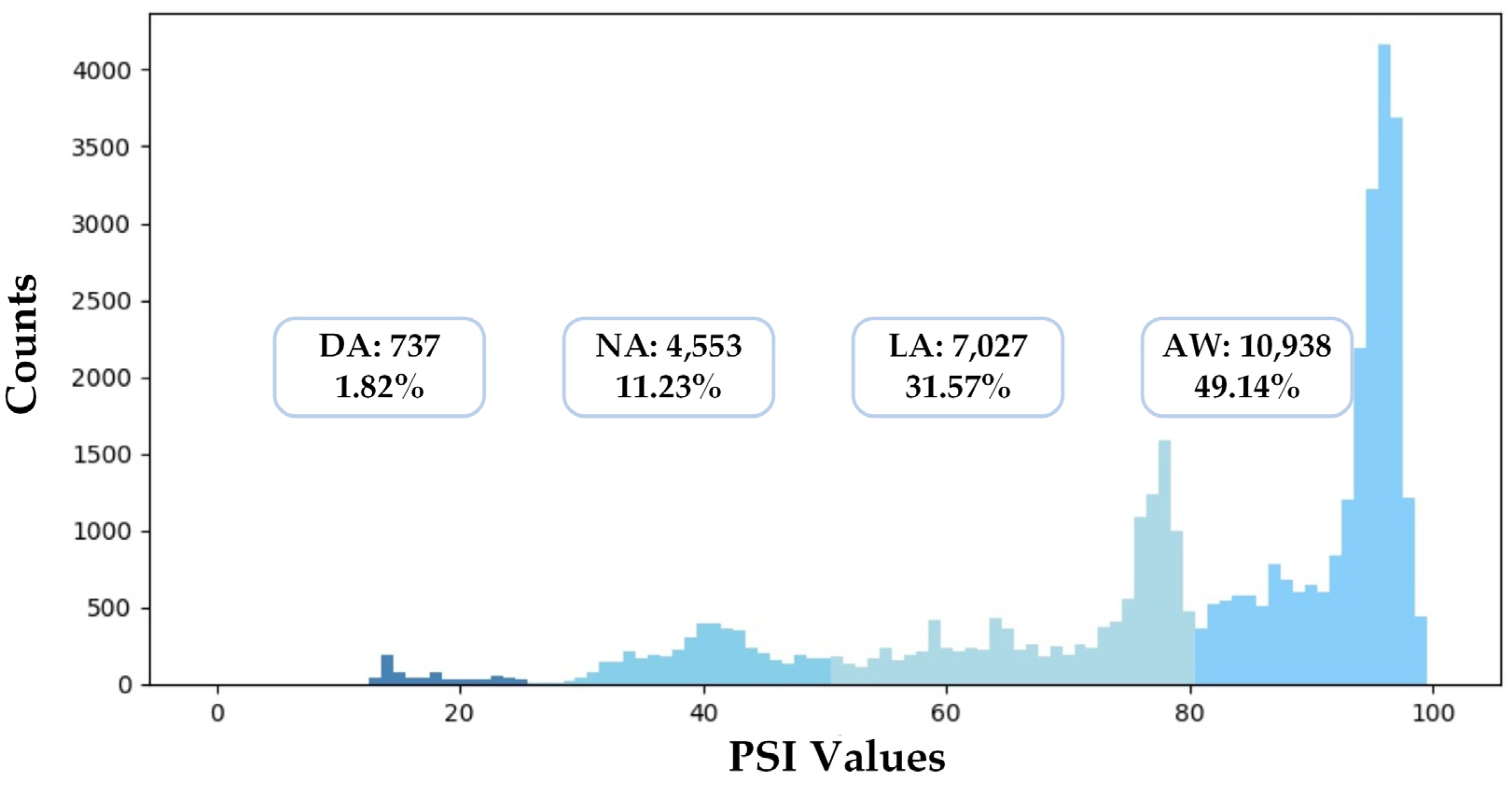
2.1. Dataset
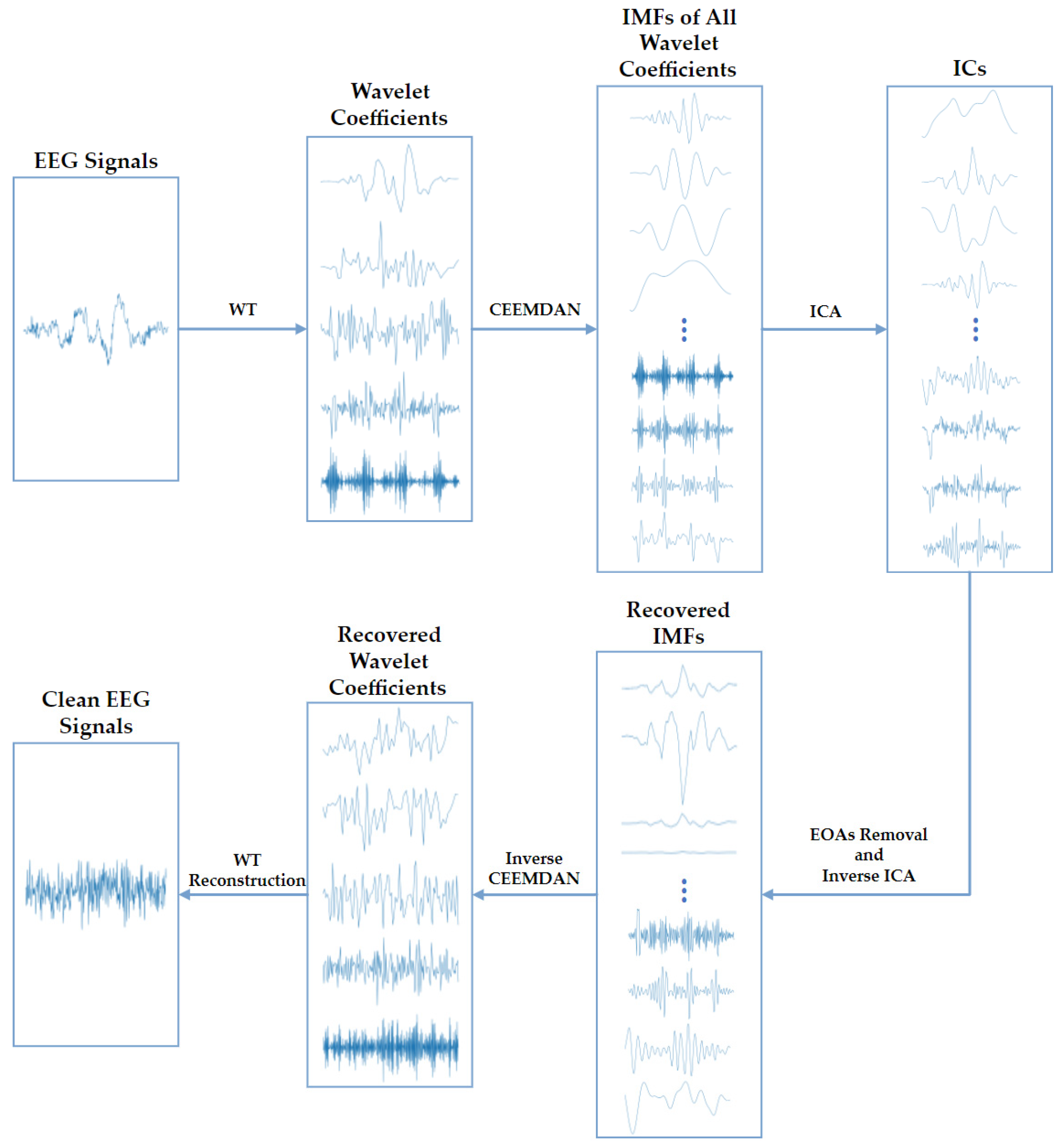
2.2. EEG Signals Preprocessing
2.3. Evaluation Metrics
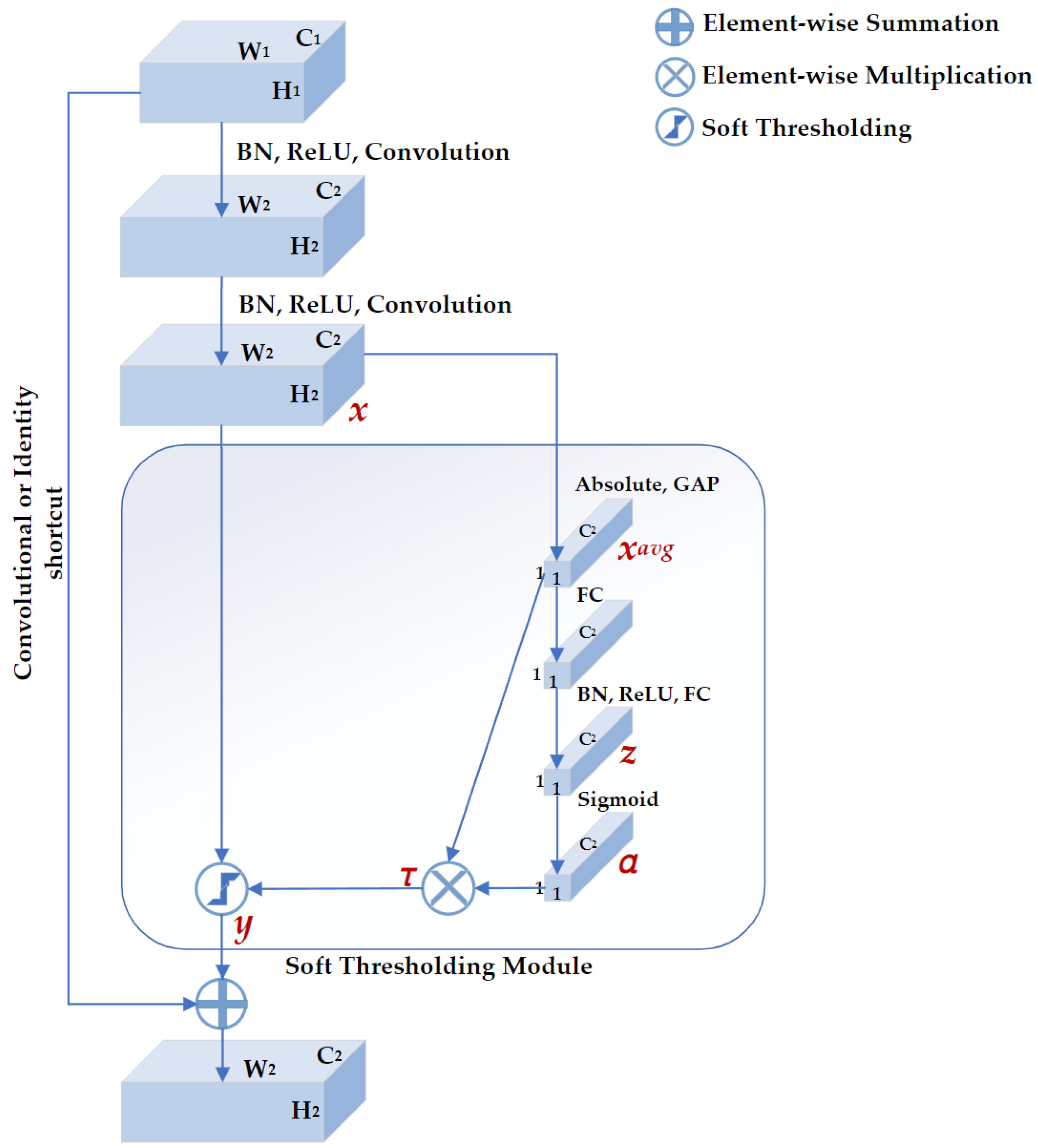
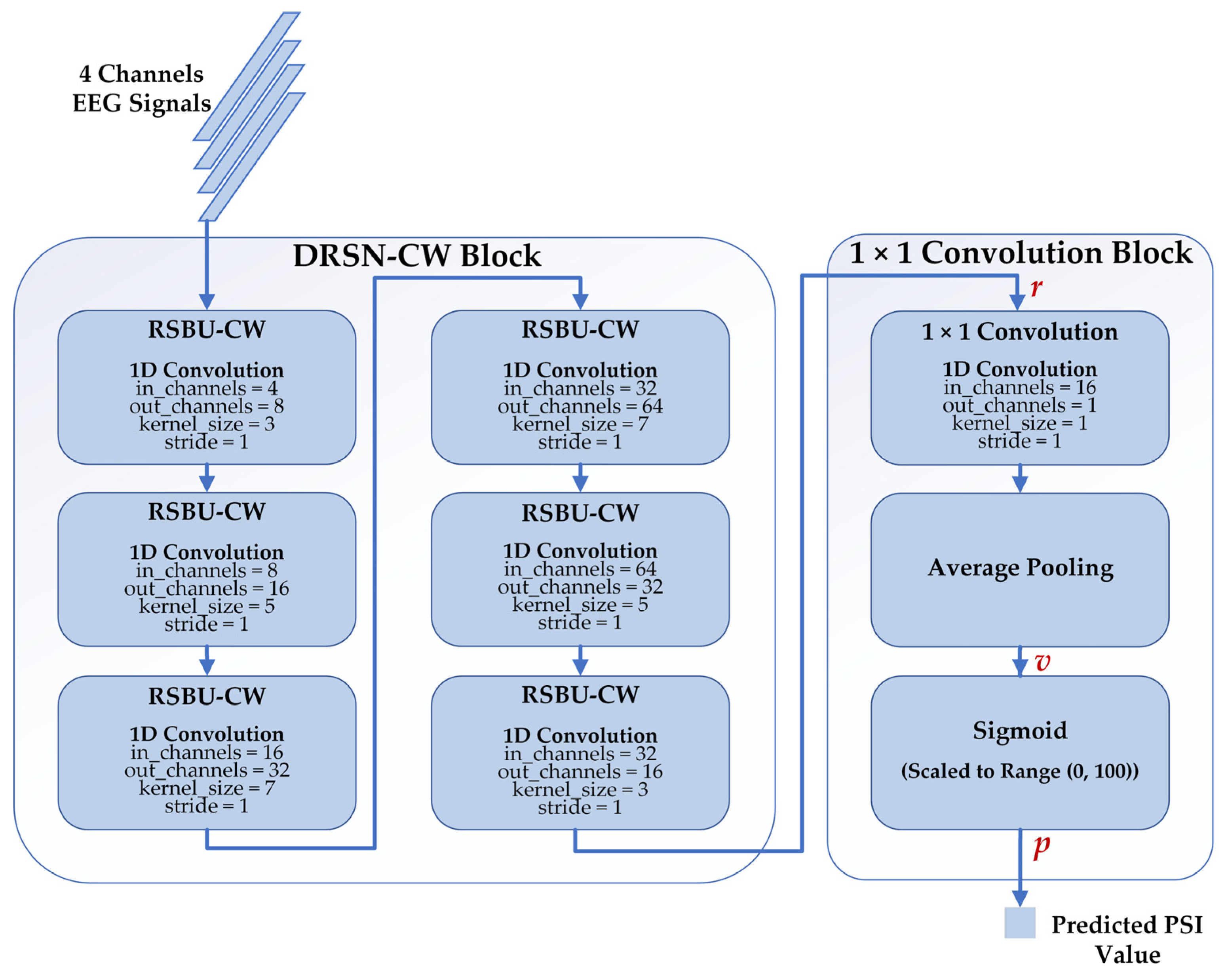
2.4. Deep Learning Model
2.4.1. Deep Residual Shrinkage Network
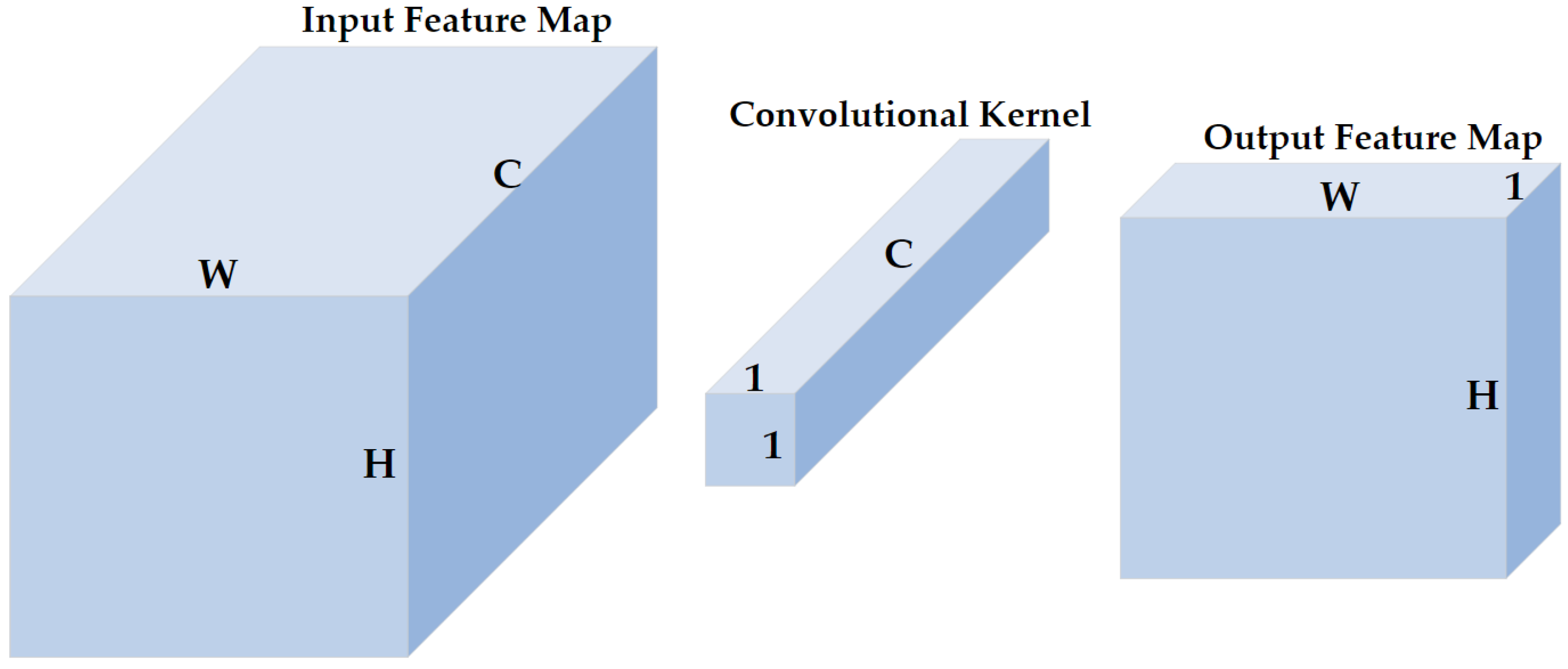
2.4.2. 1 × 1 Convolution
2.4.3. Proposed Regression Model
2.5. Conventional Models
2.5.1. Features Extraction
- Band Power
- Spectral Edge Frequency
- Sample Entropy
2.5.2. Conventional Regression Models
- Support Vector Machine
- Random Forest
- Artificial Neural Network
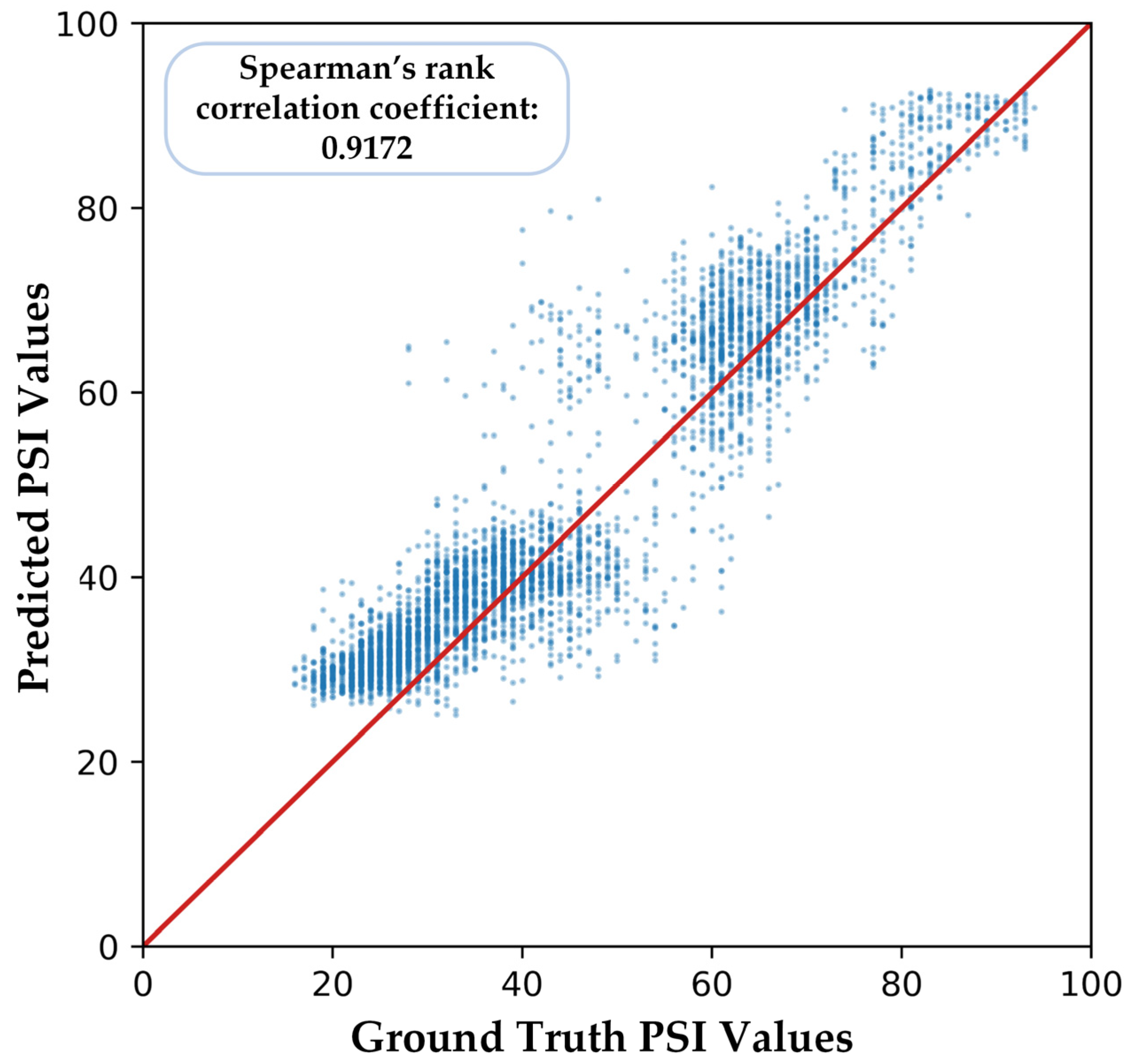
3. Results
3.1. Experimental Settings
3.2. Experimental Results
4. Discussion
- The recorded raw EEG signals are usually contaminated by electrical noise and other physiological signals. We used bandpass finite filters to remove electrical noise, and the WT-CEEMDAN-ICA algorithm to extract clean EEG signals.
- We adopted deep learning models to extract discriminative features automatically instead of extracting features manually from EEG signals.
- To improve our proposed model’s generalization ability and convergence speed, we standardized the EEG signals.
- DRSN-CW can deal with signals disturbed by noise, which is suitable for EEG-signal processing.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hajat, Z.; Ahmad, N.; Andrzejowski, J. The role and limitations of EEG-based depth of anaesthesia monitoring in theatres and intensive care. Anaesthesia 2017, 72, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Kent, C.; Domino, K.B. Depth of anesthesia. Curr. Opin. Anaesthesiol. 2009, 22, 782–787. [Google Scholar] [CrossRef] [PubMed]
- Fahy, B.G.; Chau, D.F. The technology of processed electroencephalogram monitoring devices for assessment of depth of anesthesia. Anesth. Analg. 2018, 126, 111–117. [Google Scholar] [CrossRef] [PubMed]
- Aydemir, E.; Tuncer, T.; Dogan, S.; Gururajan, R.; Acharya, U.R. Automated major depressive disorder detection using melamine pattern with EEG signals. Appl. Intell. 2021, 51, 6449–6466. [Google Scholar] [CrossRef]
- Loh, H.W.; Ooi, C.P.; Aydemir, E.; Tuncer, T.; Dogan, S.; Acharya, U.R. Decision support system for major depression detection using spectrogram and convolution neural network with EEG signals. Expert Syst. 2022, 39, e12773. [Google Scholar] [CrossRef]
- Tasci, G.; Loh, H.W.; Barua, P.D.; Baygin, M.; Tasci, B.; Dogan, S.; Acharya, U.R. Automated accurate detection of depression using twin Pascal’s triangles lattice pattern with EEG Signals. Knowl.-Based Syst. 2022, 260, 110190. [Google Scholar] [CrossRef]
- Xiao, G.; Shi, M.; Ye, M.; Xu, B.; Chen, Z.; Ren, Q. 4D attention-based neural network for EEG emotion recognition. Cogn. Neurodynamics. 2022, 16, 805–818. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.; Sun, X.; Li, D.; Voss, L.J.; Sleigh, J.W.; Li, X. EEG entropy measures in anesthesia. Front. Comput. Neurosci. 2015, 9, 16. [Google Scholar] [CrossRef]
- Saadeh, W.; Khan, F.H.; Altaf, M.A.B. Design and implementation of a machine learning based EEG processor for accurate estimation of depth of anesthesia. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 658–669. [Google Scholar] [CrossRef]
- Khan, F.H.; Ashraf, U.; Altaf, M.A.B.; Saadeh, W. A patient-specific machine learning based EEG processor for accurate estimation of depth of anesthesia. In Proceedings of the 2018 IEEE Biomedical Circuits and Systems Conference (BioCAS), Cleveland, OH, USA, 17–19 October 2018; pp. 1–4. [Google Scholar]
- Gonsowski, C.T. Anesthesia Awareness and the Bispectral Index. N. Engl. J. Med. 2008, 359, 427–431. [Google Scholar]
- Drover, D.; Ortega, H.R. Patient state index. Best Pract. Res. Clin. Anaesthesiol. 2006, 20, 121–128. [Google Scholar] [CrossRef]
- Ji, S.H.; Jang, Y.E.; Kim, E.H.; Lee, J.H.; Kim, J.T.; Kim, H.S. Comparison of Bispectral Index and Patient State Index during Sevoflurane Anesthesia in Children: A Prospective Observational Study. Available online: https://www.researchgate.net/publication/343754479_Comparison_of_bispectral_index_and_patient_state_index_during_sevoflurane_anesthesia_in_children_a_prospective_observational_study (accessed on 3 November 2020).
- Li, P.; Karmakar, C.; Yearwood, J.; Venkatesh, S.; Palaniswami, M.; Liu, C. Detection of epileptic seizure based on entropy analysis of short-term EEG. PLoS ONE 2018, 13, e0193691. [Google Scholar] [CrossRef] [PubMed]
- Olofsen, E.; Sleigh, J.W.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. BJA Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Ma, L.; Fan, S.Z.; Abbod, M.F.; Shieh, J.S. Sample entropy analysis for the estimating depth of anaesthesia through human EEG signal at different levels of unconsciousness during surgeries. PeerJ 2018, 6, e4817. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Mohammadi, A. Analyzing the EEG signals in order to estimate the depth of anesthesia using wavelet and fuzzy neural networks. Int. J. Interact. Multimed. Artif. Intell. 2016, 4, 12. [Google Scholar] [CrossRef]
- Ortolani, O.; Conti, A.; Di Filippo, A.; Adembri, C.; Moraldi, E.; Evangelisti, A.; Roberts, S.J. EEG signal processing in anaesthesia. Use of a neural network technique for monitoring depth of anaesthesia. Br. J. Anaesth. 2002, 88, 644–648. [Google Scholar] [CrossRef] [PubMed]
- Shalbaf, A.; Saffar, M.; Sleigh, J.W.; Shalbaf, R. Monitoring the depth of anesthesia using a new adaptive neurofuzzy system. IEEE J. Biomed. Health Inform. 2017, 22, 671–677. [Google Scholar] [CrossRef]
- Gu, Y.; Liang, Z.; Hagihira, S. Use of Multiple EEG Features and Artificial Neural Network to Monitor the Depth of Anesthesia. Sensors 2019, 19, 2499. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef]
- Lee, H.C.; Ryu, H.G.; Chung, E.J.; Jung, C.W. Prediction of bispectral index during target-controlled infusion of propofol and remifentanil: A deep learning approach. Anesthesiology 2018, 128, 492–501. [Google Scholar] [CrossRef]
- Afshar, S.; Boostani, R. A Two-stage deep learning scheme to estimate depth of anesthesia from EEG signals. In Proceedings of the 2020 27th National and 5th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, India, 26–27 November 2020. [Google Scholar]
- Castellanos, N.P.; Makarov, V.A. Recovering EEG brain signals: Artifact suppression with wavelet enhanced independent component analysis. J. Neurosci. Methods 2006, 158, 300. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; La Foresta, F.; Morabito, F.C. Automatic artifact rejection from multichannel scalp EEG by Wavelet ICA. IEEE Sens. J. 2012, 12, 533–542. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep residual shrinkage networks for fault diagnosis. IEEE Trans. Ind. Inform. 2019, 16, 4681–4690. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Seeck, M.; Koessler, L.; Bast, T.; Leijten, F.; Michel, C.; Baumgartner, C.; Beniczky, S. The standardized EEG electrode array of the IFCN. Clin. Neurophysiol. 2017, 128, 2070–2077. [Google Scholar] [CrossRef]
- Alexandre, G. MEG and EEG data analysis with MNE-Python. Front. Neurosci. 2013, 7, 267. [Google Scholar]
- Prerau, M.J.; Brown, R.E.; Bianchi, M.T.; Ellenbogen, J.M.; Purdon, P.L. Sleep neurophysiological dynamics through the lens of multitaper spectral analysis. Physiology 2017, 32, 60–92. [Google Scholar] [CrossRef]
- Obert, D.P.; Schweizer, C.; Zinn, S.; Kratzer, S.; Hight, D.; Sleigh, J.; Kreuzer, M. The influence of age on EEG-based anaesthesia indices. J. Clin. Anesth. 2021, 73, 110325. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample Entropy. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2004; pp. 172–184. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rodriguez-Perez, R.; Vogt, M.; Bajorath, J. Support vector machine classification and regression prioritize different structural features for binary compound activity and potency value prediction. ACS omega 2017, 2, 6371–6379. [Google Scholar] [CrossRef]
- Shahid, N.; Rappon, T.; Berta, W. Applications of artificial neural networks in health care organizational decision-making: A scoping review. PloS ONE 2019, 14, e0212356. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Chintala, S. PyTorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process Syst. 2019, 32, 8026–8037. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, É. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adeli, H.; Subha, D.P. Automated EEG-based screening of depression using deep convolutional neural network. Comput. Methods Programs Biomed. 2018, 161, 103–113. [Google Scholar] [CrossRef]



| Metric | Formula | Description |
|---|---|---|
| MSE (Regression) | Mean Squared Error | |
| ACC (Classification) | Accuracy | |
| SE (Classification) | Sensitivity | |
| PR (Not used directly in this paper) | Precision | |
| F1 (Classification) | F1-score |
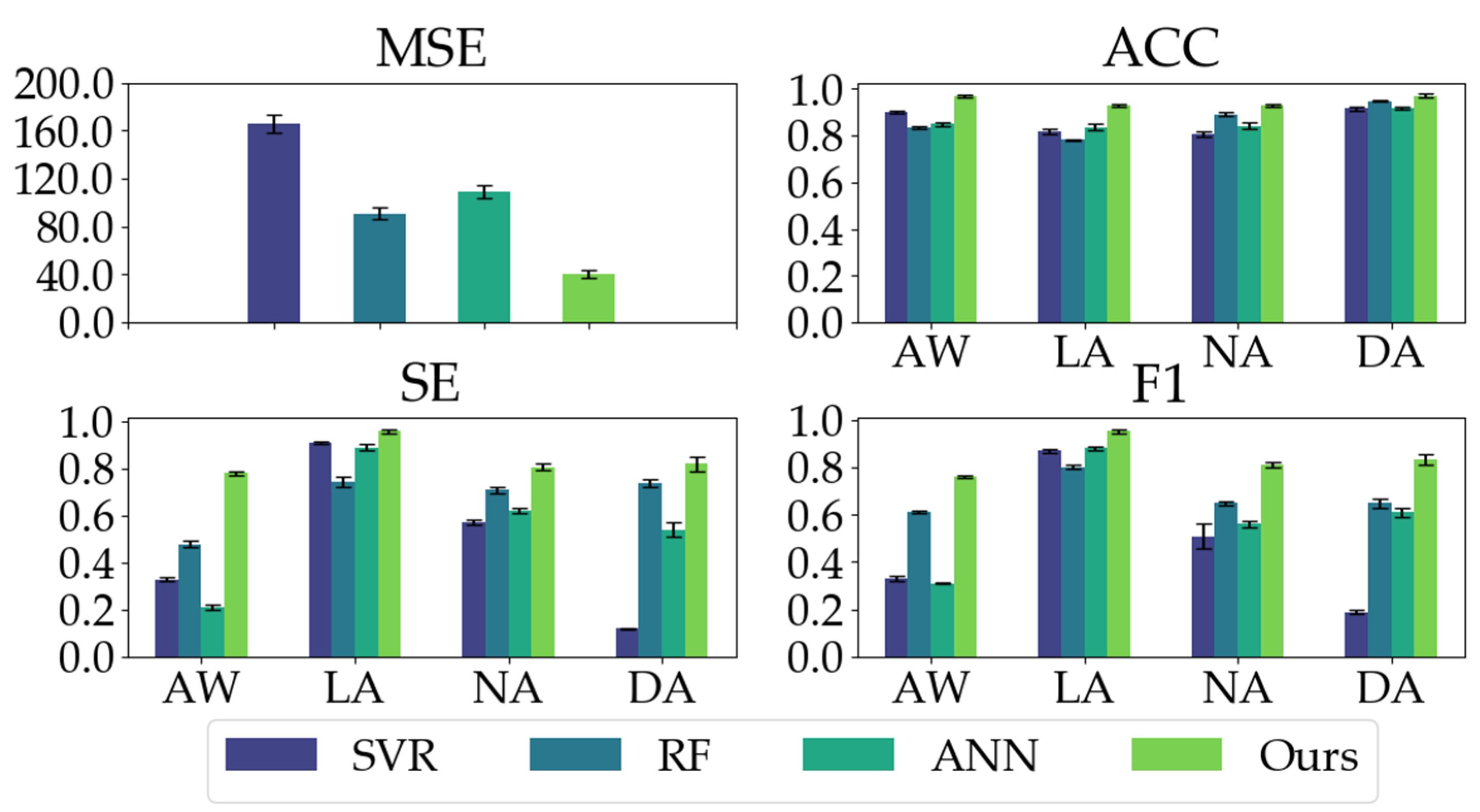
| Metrics | SVR | RF | ANN | Our Proposed Model |
|---|---|---|---|---|
| MSE | 166.02 ± 7.77 | 90.95 ± 4.88 | 109.20 ± 5.80 | 40.35 ± 3.22 |
| ACC | 0.8596 ± 0.0574 | 0.8640 ± 0.0720 | 0.8606 ± 0.0380 | 0.9503 ± 0.0224 |
| SE | 0.4825 ± 0.3391 | 0.6685 ± 0.1266 | 0.5650 ± 0.2801 | 0.8411 ± 0.0790 |
| F1 | 0.475 ± 0.2941 | 0.6770 ± 0.0840 | 0.5901 ± 0.2337 | 0.8395 ± 0.0812 |
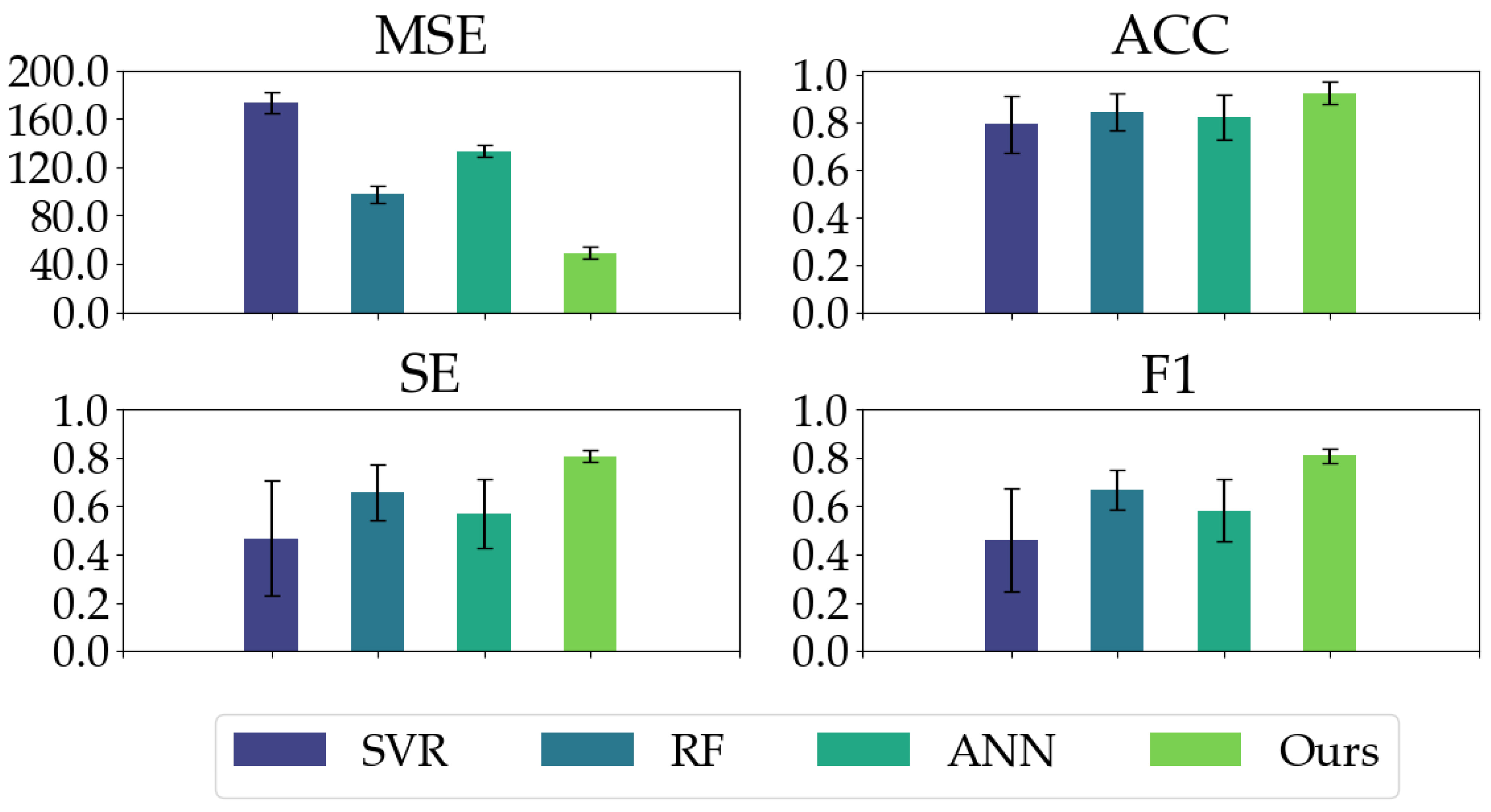
| Metrics | SVR | RF | ANN | Our Proposed Model |
|---|---|---|---|---|
| MSE | 173.22 ± 8.56 | 97.56 ± 6.88 | 133.49 ± 5.40 | 49.22 ± 4.62 |
| ACC | 0.7908 ± 0.1187 | 0.8420 ± 0.0765 | 0.8216 ± 0947 | 0.9203 ± 0.0470 |
| SE | 0.4675 ± 0.3391 | 0.6575 ± 0.1266 | 0.5700 ± 0.1414 | 0.8054 ± 0.0243 |
| F1 | 0.4599 ± 0.2132 | 0.6670 ± 0.0821 | 0.5852 ± 0.1274 | 0.8070 ± 0.0306 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, M.; Huang, Z.; Xiao, G.; Xu, B.; Ren, Q.; Zhao, H. Estimating the Depth of Anesthesia from EEG Signals Based on a Deep Residual Shrinkage Network. Sensors 2023, 23, 1008. https://doi.org/10.3390/s23021008
Shi M, Huang Z, Xiao G, Xu B, Ren Q, Zhao H. Estimating the Depth of Anesthesia from EEG Signals Based on a Deep Residual Shrinkage Network. Sensors. 2023; 23(2):1008. https://doi.org/10.3390/s23021008
Chicago/Turabian StyleShi, Meng, Ziyu Huang, Guowen Xiao, Bowen Xu, Quansheng Ren, and Hong Zhao. 2023. "Estimating the Depth of Anesthesia from EEG Signals Based on a Deep Residual Shrinkage Network" Sensors 23, no. 2: 1008. https://doi.org/10.3390/s23021008
APA StyleShi, M., Huang, Z., Xiao, G., Xu, B., Ren, Q., & Zhao, H. (2023). Estimating the Depth of Anesthesia from EEG Signals Based on a Deep Residual Shrinkage Network. Sensors, 23(2), 1008. https://doi.org/10.3390/s23021008







