Comparison of X-ray Radiant Power Absolute Measurement between a Free-Air Ionization Chamber and a Cryogenic Electrical Substitution Radiometer
Abstract
1. Introduction
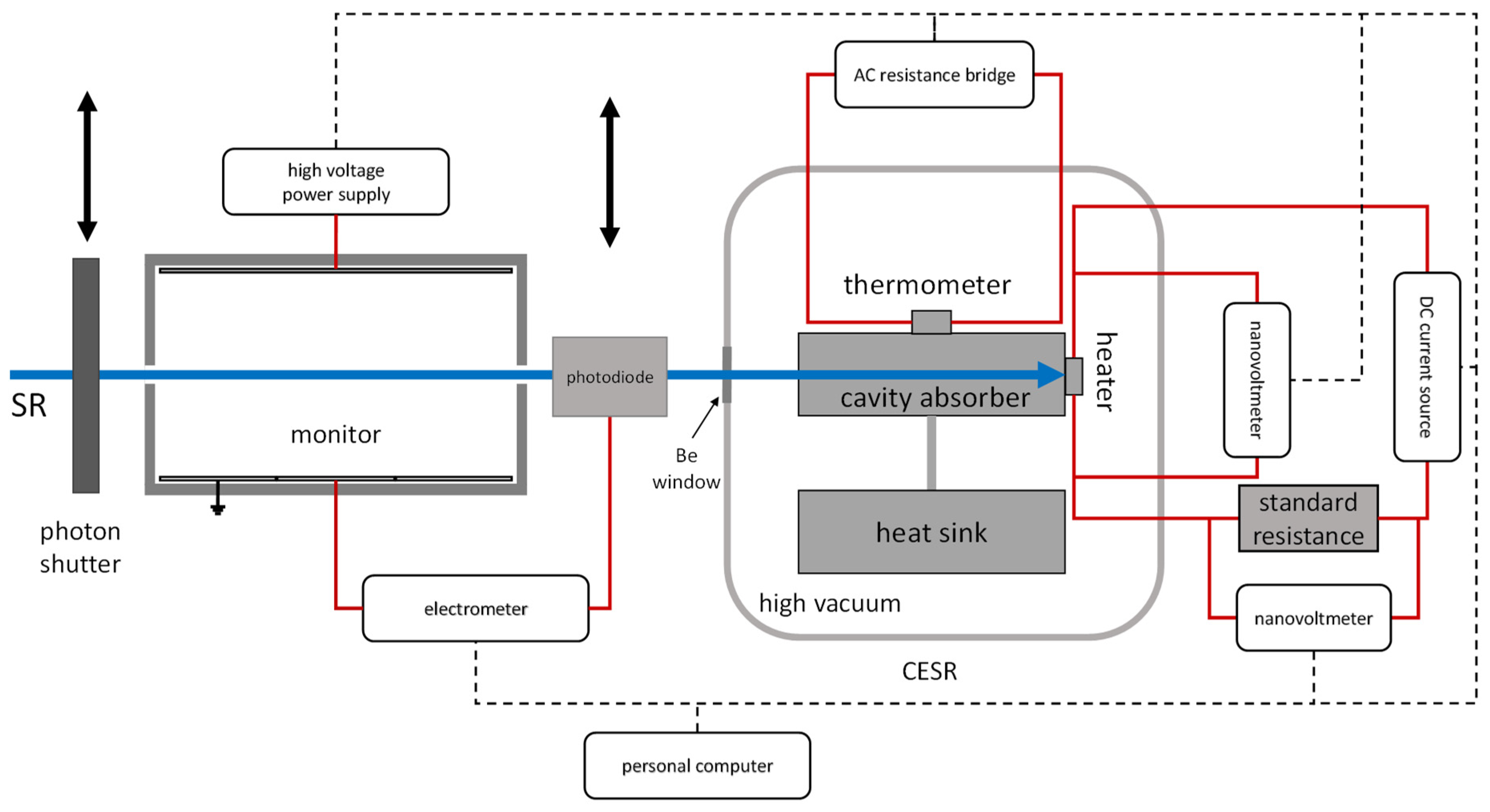
2. Method and Instrumentation
2.1. Monochromatized Synchrotron Radiation Sources
2.2. Free-Air Ionization Chamber
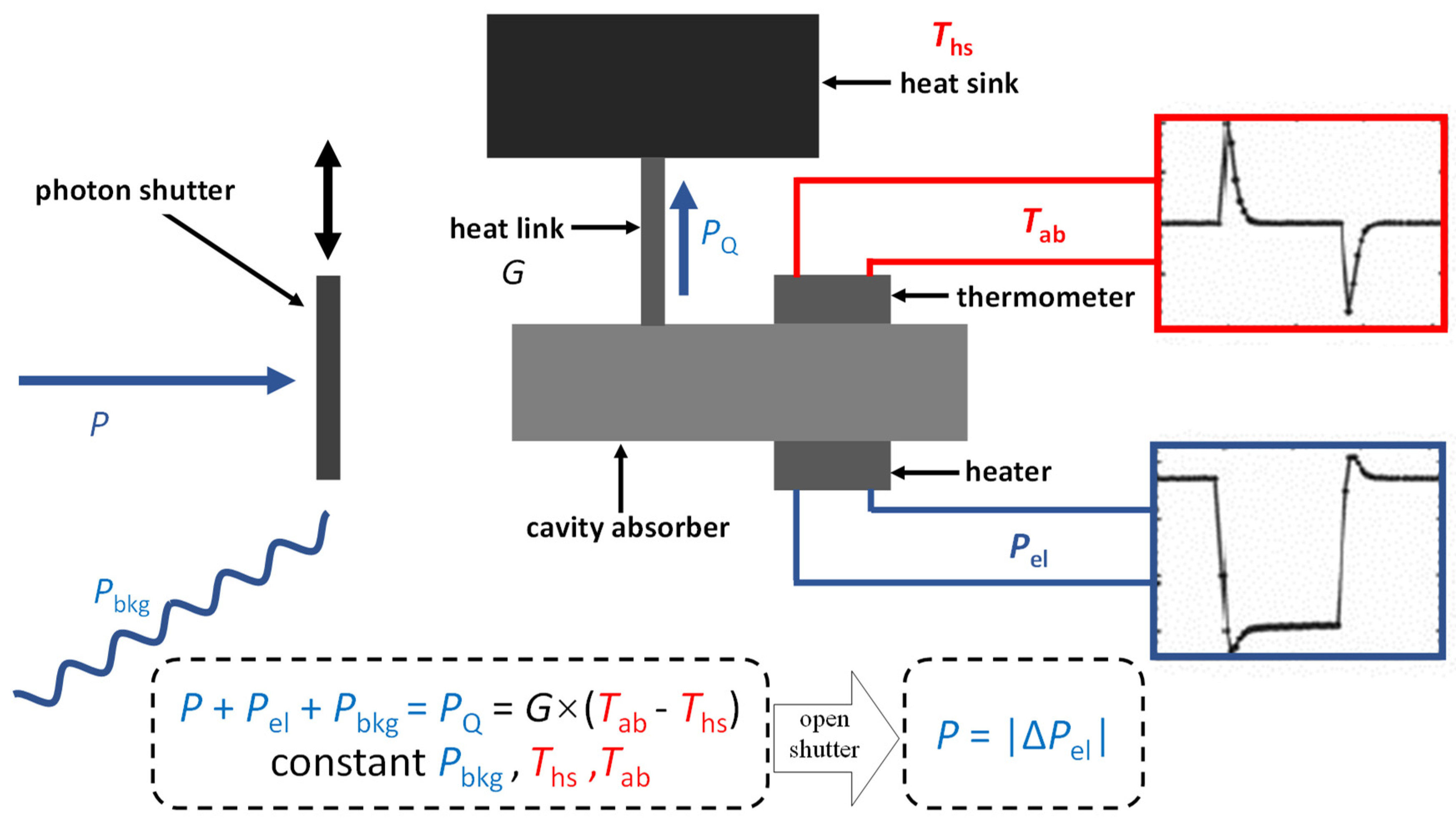
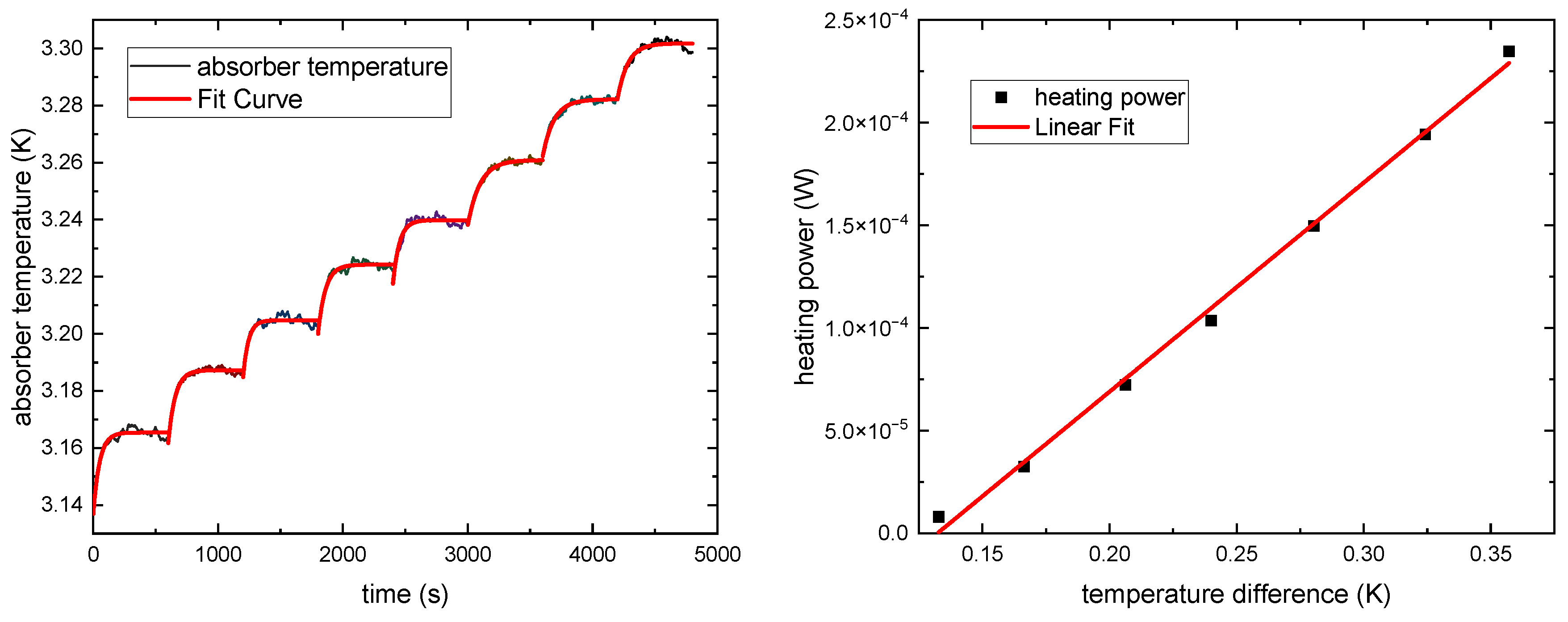
2.3. Cryogenic Electrical Substitution Radiometer
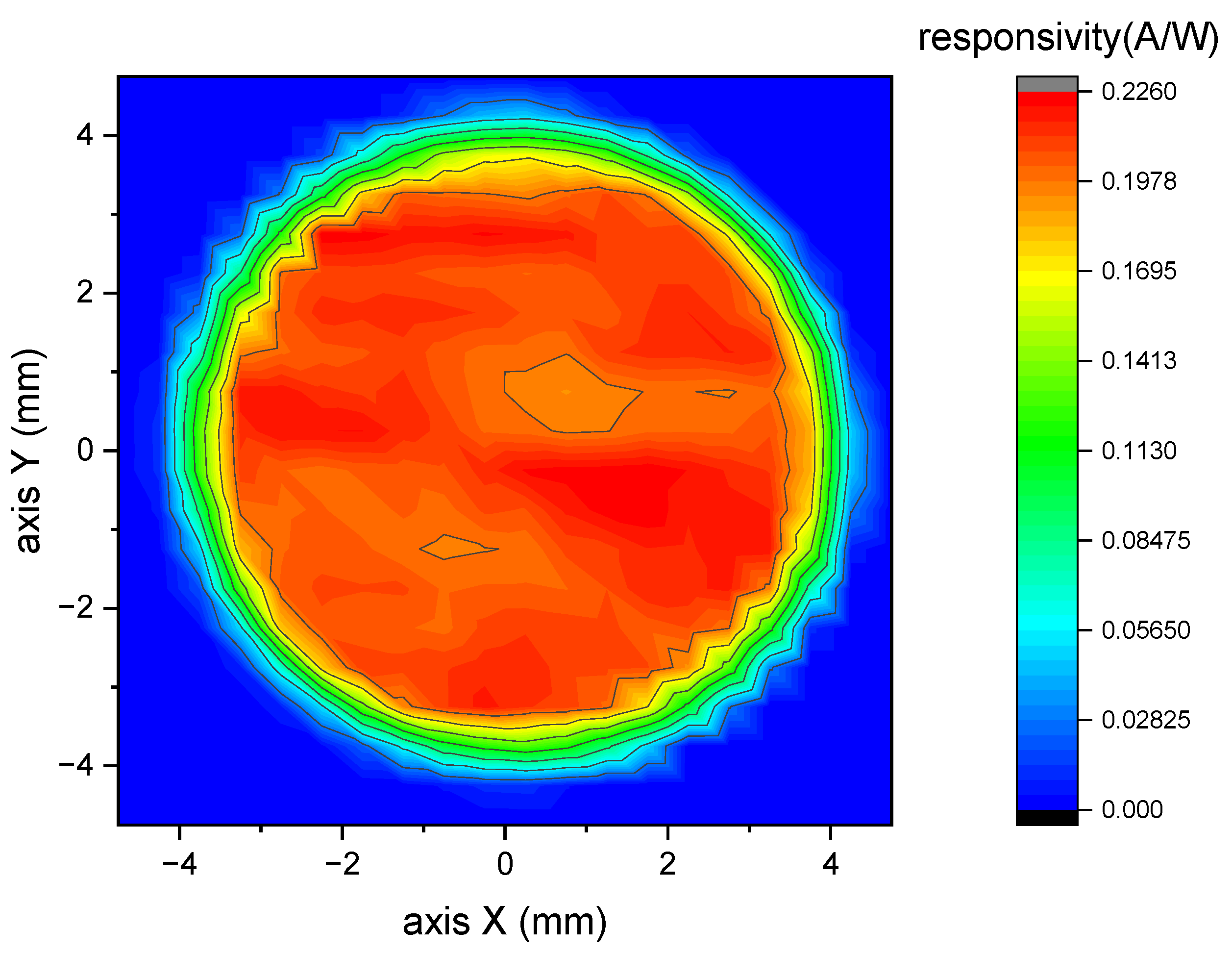
2.4. Silicon Photodiode
3. Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beckhoff, B.; Gottwald, A.; Klein, R.; Krumrey, M.; Müller, R.; Richter, M.; Scholze, F.; Thornagel, R.; Ulm, G. A quarter-century of metrology using synchrotron radiation by PTB in Berlin. Phys. Status Solidi B 2009, 246, 1415–1434. [Google Scholar] [CrossRef]
- Klein, R.; Fliegauf, R.; Kroth, S.; Paustian, W.; Reichel, T.; Richter, M.; Thornagel, R. Source-based calibration of space instruments using calculable synchrotron radiation. J. Astron. Telesc. Instrum. Syst. 2016, 2, 4. [Google Scholar] [CrossRef]
- Unterumsberger, R.; Hönicke, P.; Colaux, J.L.; Jeynes, C.; Wansleben, M.; Müller, M.; Beckhoff, B. Accurate experimental determination of gallium K- and L3-shell XRF fundamental parameters. J. Anal. At. Spectrom. 2018, 33, 1003–1013. [Google Scholar] [CrossRef]
- Kirkwood, R.K.; Moody, J.D.; Kline, J.; Dewald, E.; Glenzer, S.; Divol, L.; Michel, P.; Hinkel, D.; Berger, R.; Williams, E.; et al. A review of laser–plasma interaction physics of indirect-drive fusion. Plasma Phys. Control. Fusion 2013, 55, 27. [Google Scholar] [CrossRef]
- Zheng, L.; Zhao, Y.D.; Tang, K.; Ma, C.Y.; Hong, C.H.; Han, Y.; Cui, M.Q.; Guo, Z.Y. A new experiment station on beamline 4B7A at Beijing Synchrotron Radiation Facility. Spectrochim. Acta Part B At. Spectrosc. 2014, 101, 1–5. [Google Scholar] [CrossRef]
- Jeon, H.; Yoo, W.J.; Shin, S.H.; Kwon, G.; Kim, M.; Kim, H.J.; Song, Y.B.; Jang, K.W.; Youn, W.S.; Lee, B. Performance Evaluation of a Multichannel All-In-One Phantom Dosimeter for Dose Measurement of Diagnostic X-ray Beam. Sensors 2015, 15, 28490–28501. [Google Scholar] [CrossRef]
- Gu, L.; Shah, C.; Zhang, R. Uncertainties in Atomic Data for Modeling Astrophysical Charge Exchange Plasmas. Sensors 2022, 22, 752. [Google Scholar] [CrossRef] [PubMed]
- Owens, A. Synchrotron light sources and radiation detector metrology. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 695, 1–12. [Google Scholar] [CrossRef]
- Klein, R.; Thornagel, R.; Ulm, G. From single photons to milliwatt radiant power—Electron storage rings as radiation sources with a high dynamic range. Metrologia 2010, 47, R33. [Google Scholar] [CrossRef]
- Klein, R.; Kroth, S.; Paustian, W.; Richter, M.; Thornagel, R. PTB’s radiometric scales for UV and VUV source calibration based on synchrotron radiation. Metrologia 2018, 55, 386–391. [Google Scholar] [CrossRef]
- Rabus, H.; Persch, V.; Ulm, G. Synchrotron-radiation-operated cryogenic electrical-substitution radiometer as the high-accuracy primary detector standard in the ultraviolet, vacuum-ultraviolet, and soft-x-ray spectral ranges. Appl. Opt. 1997, 36, 5421–5440. [Google Scholar] [CrossRef]
- Krumrey, M.; Herrmann, C.; Müller, P.; Ulm, G. Synchrotron-radiation-based cryogenic radiometry in the X-ray range. Metrologia 2000, 37, 361–364. [Google Scholar] [CrossRef]
- Gerlach, M.; Krumrey, M.; Cibik, L.; Müller, P.; Rabus, H.; Ulm, G. Cryogenic radiometry in the hard x-ray range. Metrologia 2008, 45, 577–585. [Google Scholar] [CrossRef]
- Saito, N.; Suzuki, I.H. Absolute fluence rates of soft X-rays using a double ion chamber. J. Electron. Spectrosc. 1999, 101–103, 33–37. [Google Scholar] [CrossRef]
- Kato, M.; Nohtomi, A.; Morishita, Y.; Kurosawa, T.; Arai, N.; Suzuki, I.H.; Saito, N. Development of the soft X-ray intensity measurement with a cryogenic radiometer. In Proceedings of the 9th International Conference on Synchrotron Radiation Instrumentation (SRI 2006), Daegu, Republic of Korea, 28 May–2 June 2006; pp. 1129–1132. [Google Scholar]
- Tanaka, T.; Kato, M.; Kurosawa, T.; Morishita, Y.; Saito, N.; Yabashi, M.; Tono, K.; Kudo, T.; Ishikawa, T.; Shiraiwa, S. Improvement of a cryogenic radiometer for XFEL absolute intensity measurement. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 659, 528–530. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.-D.; Wang, P.-W.; Zheng, L.; Guo, S.-M.; Wang, J.; Tang, K.; Zhao, X.-J.; Li, J.-M. Absolute measurement of radiant power for synchrotron radiation monochromatized X-rays. Radiat. Detect. Technol. Methods 2019, 4, 97–105. [Google Scholar] [CrossRef]
- Li, H.P.; Zheng, W.N.; Zhao, Y.D.; Wang, P.W.; Li, F. Absolute measurement of photon flux for synchrotron radiation hard X-rays. Opt. Precis. Eng. 2017, 25, 2845–2851. [Google Scholar]
- Zhao, X.; Zhao, Y.; Tang, K.; Zhao, Y.; Li, F.; Zheng, L.; Liu, S. A soft X-ray cryogenic radiometer built on BSRF. Radiat. Detect. Technol. Methods 2018, 2, 32. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Zheng, L.; Tang, K.; Liu, S.; Zhao, X.; Zhao, Y.; Li, F. Online monitoring the detector calibration process at a synchrotron X-ray source. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 874, 1–4. [Google Scholar] [CrossRef]
- Rabus, H.; Klein, R.; Scholze, F.; Thornagel, R.; Ulm, G. Validation of the uncertainty budget for soft X-ray radiant power measurement using a cryogenic radiometer. Metrologia 2002, 39, 381–389. [Google Scholar] [CrossRef]
- Saito, N.; Juranić, P.N.; Kato, M.; Richter, M.; Sorokin, A.A.; Tiedtke, K.; Jastrow, U.; Kroth, U.; Schöppe, H.; Nagasono, M.; et al. Radiometric comparison for measuring the absolute radiant power of a free-electron laser in the extreme ultraviolet. Metrologia 2010, 47, 21–23. [Google Scholar] [CrossRef]
- Wu, Y.R.; Chao, Z.Y.; Xiao, Y.A.; Pan, J.X.; Tang, E.S. XRF experiments at BSRF. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1995, 359, 291–294. [Google Scholar] [CrossRef]
- Yuan, Q.X.; Zhang, K.; Hong, Y.L.; Huang, W.X.; Gao, K.; Wang, Z.L.; Zhu, P.P.; Gelb, J.; Tkachuk, A.; Hornberger, B.; et al. A 30 nm-resolution hard X-ray microscope with X-ray fluorescence mapping capability at BSRF. J. Synchrotron Radiat. 2012, 19, 1021–1028. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.N.; Hu, T.D.; Liu, T.; Zhang, J. The 1W1B-XAFS beam line at BSRF. Synchrotron Radiation Instrumentation, Pts 1 and 2. AIP Conf. Proc. 2007, 879, 856–859. [Google Scholar]
- Scholze, F.; Rabus, H.; Ulm, G. Mean energy required to produce an electron-hole pair in silicon for photons of energies between 50 and 1500 eV. J. Appl. Phys. 1998, 84, 2926–2939. [Google Scholar] [CrossRef]
- Gerlach, M.; Krumrey, M.; Cibik, L.; Müller, P.; Ulm, G. Comparison of scattering experiments using synchrotron radiation with Monte Carlo simulations using Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 608, 339–343. [Google Scholar] [CrossRef]
- Jiao, Y.; Xu, G.; Cui, X.H.; Duan, Z.; Guo, Y.Y.; He, P.; Ji, D.H.; Li, J.Y.; Li, X.Y.; Meng, C.; et al. The HEPS project. J. Synchrotron Radiat. 2018, 25, 1611–1618. [Google Scholar] [CrossRef] [PubMed]




| Xi | xi | u(xi) (%) |
|---|---|---|
| I | 1.51 × 10−9 A | 0.22 |
| Wair | 33.97 eV | 0.35 |
| µen/ρ | 4.60 m2kg-1 | 0.80 |
| ρ | 1.19 kgm−3 | 0.07 |
| d | 4.05 × 10−2 m | 0.01 |
| ks | 1.0015 | 0.02 |
| kh | 0.9980 | 0.03 |
| kd | 1.0000 | 0.01 |
| ke | 1.0000 | 0.05 |
| kpol | 1.0000 | 0.05 |
| ksckfl | 0.9962 | 0.10 |
| result | Value | uc (%) |
| radiant power | 2.29 × 10−6 W | 0.92 |
| Xi | μA | μB | Ci |
|---|---|---|---|
| ΔT | 3.96 × 10−5 K | - | 0.00102 W/K |
| Vstd | - | 8.7 × 10−6 V | −1.32 × 10−4 V/Ω |
| Vhtr | - | 8.7 × 10−6 V | −8.01 × 10−5 V/Ω |
| Rstd | 3.69 × 10−4 Ω | 5.9 × 10−2 Ω | 1.07 × 10−8 V2/Ω2 |
| Pbkg | - | 4.4 × 10−7 W | −1 |
| H | - | 0.001 | 4 × 10−5 W |
| result | combined standard uncertainty uc | ||
| Radiant power | 4.39 × 10−7 W | ||
| Sources | Calibration against FAC | Calibration against CESR | ||
|---|---|---|---|---|
| Value | Uncertainty (%) | Value | Uncertainty (%) | |
| Idio | 6.13 × 10−5 A | 0.13 | 9.77 × 10−5 A | 0.12 |
| P | 3.59 × 10−6 W | 0.92 | 4.09 × 10−6 W | 1.10 |
| MP/MI | - | - | - | 0.10 |
| μBe | 0.98963 | 0.01 | 0.98963 | 0.01 |
| μair | 0.83149 | 0.51 | 0.87347 | 0.41 |
| Light source | - | 0.40 | - | 0.40 |
| Type A | - | 0.01 | - | 1.21 |
| Combined | 0.20747 A/W | 1.11 | 0.20649 A/W | 1.74 |
| Sources | Value | Uncertainty (%) |
|---|---|---|
| s1 | 0.20747 A/W | 1.11 |
| s2 | 0.20649 A/W | 1.74 |
| Linearity of photodiode | - | 2.39 |
| Spatial homogeneity of photodiode | - | 1.11 |
| Combined | - | 3.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhao, Y.; Wang, P.; Tang, K.; Zheng, L. Comparison of X-ray Radiant Power Absolute Measurement between a Free-Air Ionization Chamber and a Cryogenic Electrical Substitution Radiometer. Sensors 2023, 23, 1006. https://doi.org/10.3390/s23021006
Li F, Zhao Y, Wang P, Tang K, Zheng L. Comparison of X-ray Radiant Power Absolute Measurement between a Free-Air Ionization Chamber and a Cryogenic Electrical Substitution Radiometer. Sensors. 2023; 23(2):1006. https://doi.org/10.3390/s23021006
Chicago/Turabian StyleLi, Fan, Yidong Zhao, Peiwei Wang, Kun Tang, and Lei Zheng. 2023. "Comparison of X-ray Radiant Power Absolute Measurement between a Free-Air Ionization Chamber and a Cryogenic Electrical Substitution Radiometer" Sensors 23, no. 2: 1006. https://doi.org/10.3390/s23021006
APA StyleLi, F., Zhao, Y., Wang, P., Tang, K., & Zheng, L. (2023). Comparison of X-ray Radiant Power Absolute Measurement between a Free-Air Ionization Chamber and a Cryogenic Electrical Substitution Radiometer. Sensors, 23(2), 1006. https://doi.org/10.3390/s23021006





