A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search
Abstract
1. Introduction
- (1)
- An improved BCA algorithm based on the Beetle Antennae Search (BAS) algorithm is proposed to address the shortcomings of conventional blind source separation algorithms.
- (2)
- A step decay factor is introduced to the BAS algorithm, which avoids entering local optima during the iteration process.
- (3)
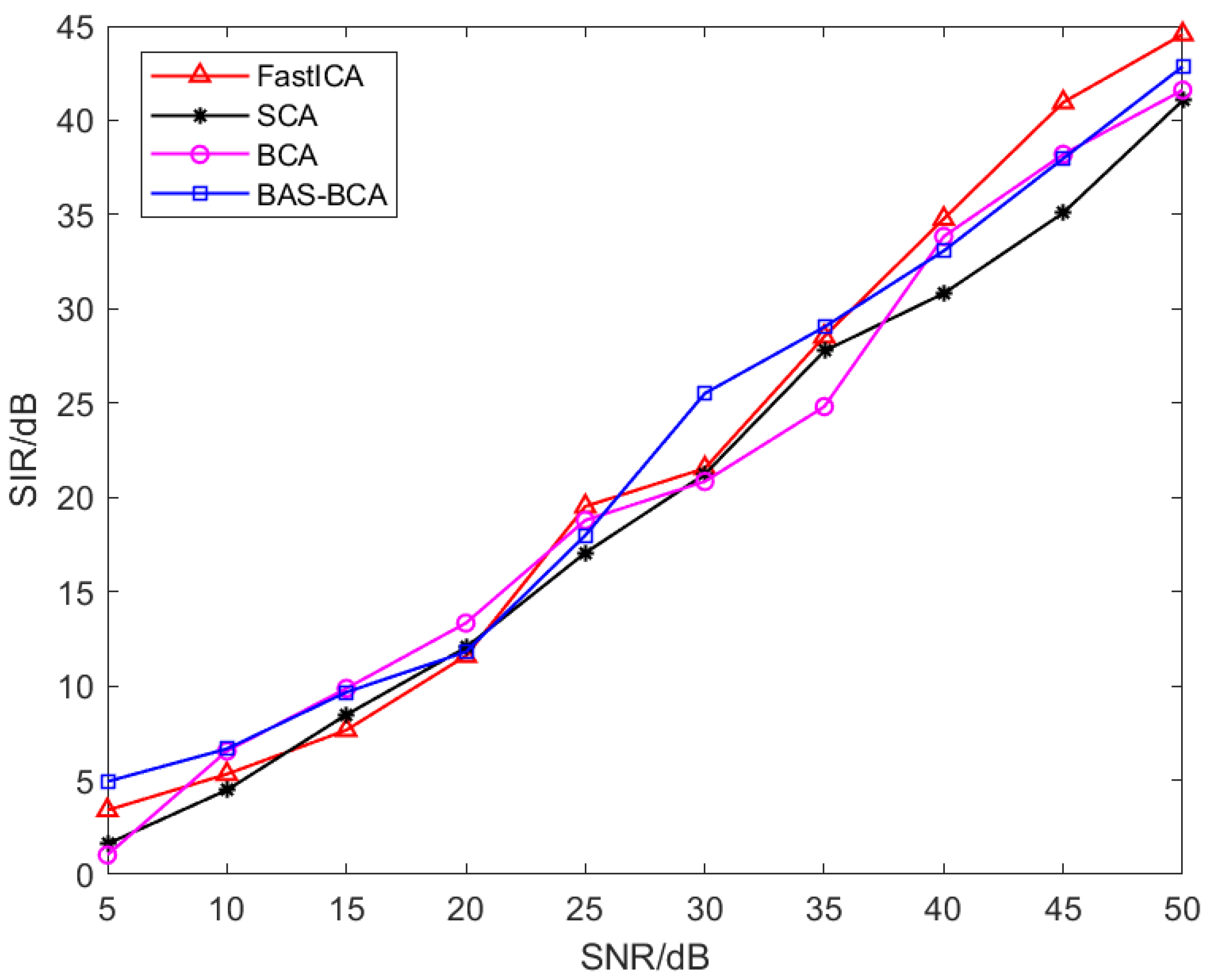
- Simulation results show that the BAS-BCA algorithm successfully separates the dependent and independent source signals. This algorithm not only has stronger universality but also has faster convergence speed and more stable precision than traditional blind source separation algorithms and BCA algorithms.
2. Theories of BSS Based on BCA
2.1. BSS
2.2. BSS Based on BCA
- (1)
- Assume that the mixing matrix A has rank n, i.e., column full rank, i.e., the number of sensors should be greater than or equal to the number of source signals.
- (2)
- Assume that the distribution of source signals is bounded.
- (3)
- Assume that the branch set S, consisting of the joint distribution of all source signals, can be expressed by the Cartesian product of the branch set Si of each source signal:where n is the number of source signals and denotes the Cartesian product.
3. Blind Source Separation Algorithm Based on BAS-BCA
3.1. BAS
- An initial position defined as X0 is given before beetle foraging.
- Determine the location of the beetle antennas. To ensure the randomness of the aspen search direction, a random factor is defined as P with the following expression.where denotes an n-dimensional random number between 0 and 1.
- 3.
- The left antenna XL and the right antenna XR are brought into the adaptation function equation to obtain the magnitude of the detected food taste concentration, which is used to update the position of the beetle.where denotes the position of the beetle in the k-th cycle, denotes the fitness function, and denotes the travel step length of the beetle. In this paper, we improve on the basic BAS algorithm by introducing a step decay factor E and using adaptive weights [28] as the decay factor.where k denotes the number of cycles and M is the maximum number of iterations.
- 4.
- Enter the loop process, and when the set maximum number of iterations M is reached, or the adaptation value reaches the set requirement, stop the iteration and output the optimal result.
| Algorithm 1 BAS |
Inputs: maximum number of iterations M, fitness function , step decay factor E, line progress length of the beetle, distance D between the left antenna and the right antenna of the beetle
|
3.2. BAS-BCA
- Pre-processing of the received mixed signal, including de-averaging and pre-whitening.
- Parameter initialization. The observed mixed signals (in the case of three signals) are used as the position information of the individual beetle X = [X1, X2, X3], the maximum number of iterations M, the step decay factor E, the travel length of the aspen , the distance between the left antenna and the right antenna of the beetle D.
- Determine the left antenna XL and right antenna XR of the beetle according to Equations (16) and (17).
- Calculate the objective function J(W) as the fitness of the beetle by Equation (15).
- Update the position of the aspen , according to Equation (19).
- Update the step decay factor using Equation (20).
- If the algorithm satisfies the termination condition, go to step 8; otherwise, repeat step 3 until it is satisfied.
- Output separation matrix W and estimate the source signal.
4. Simulation and Experimentation
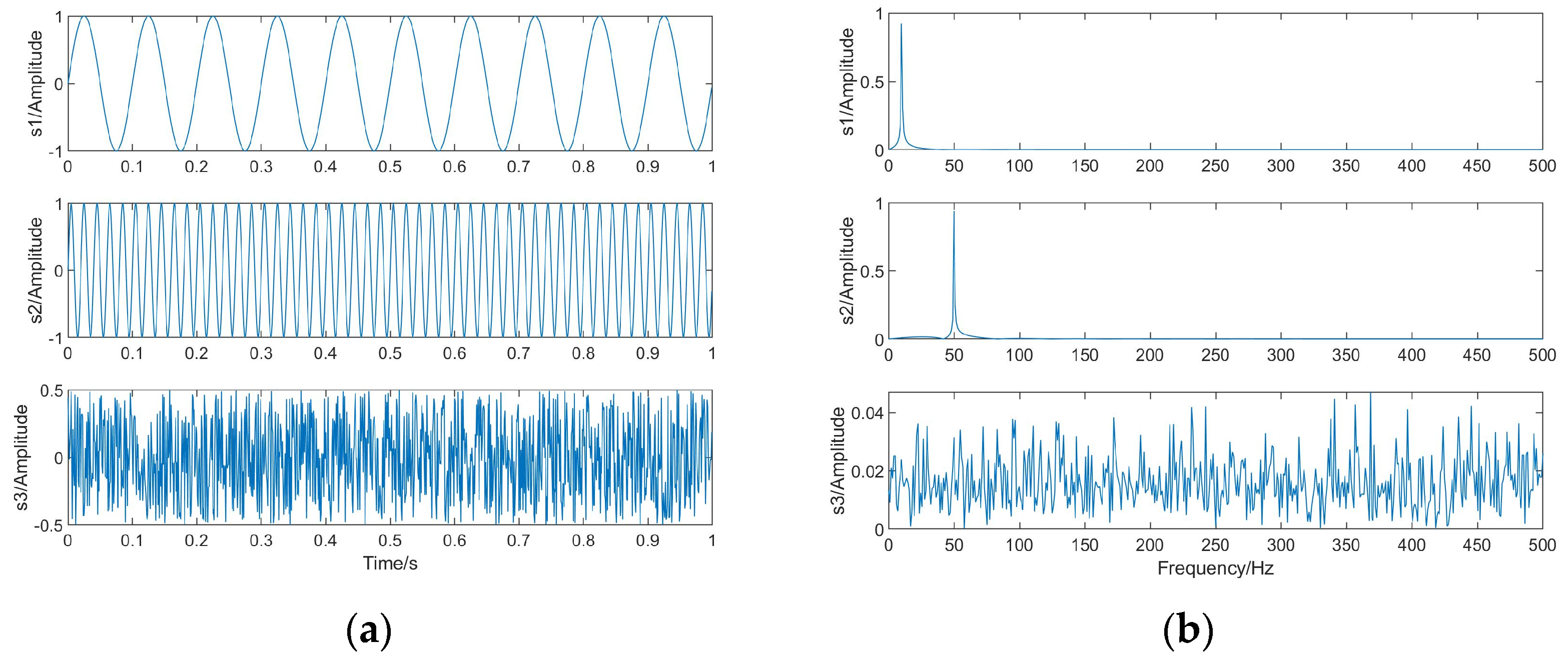
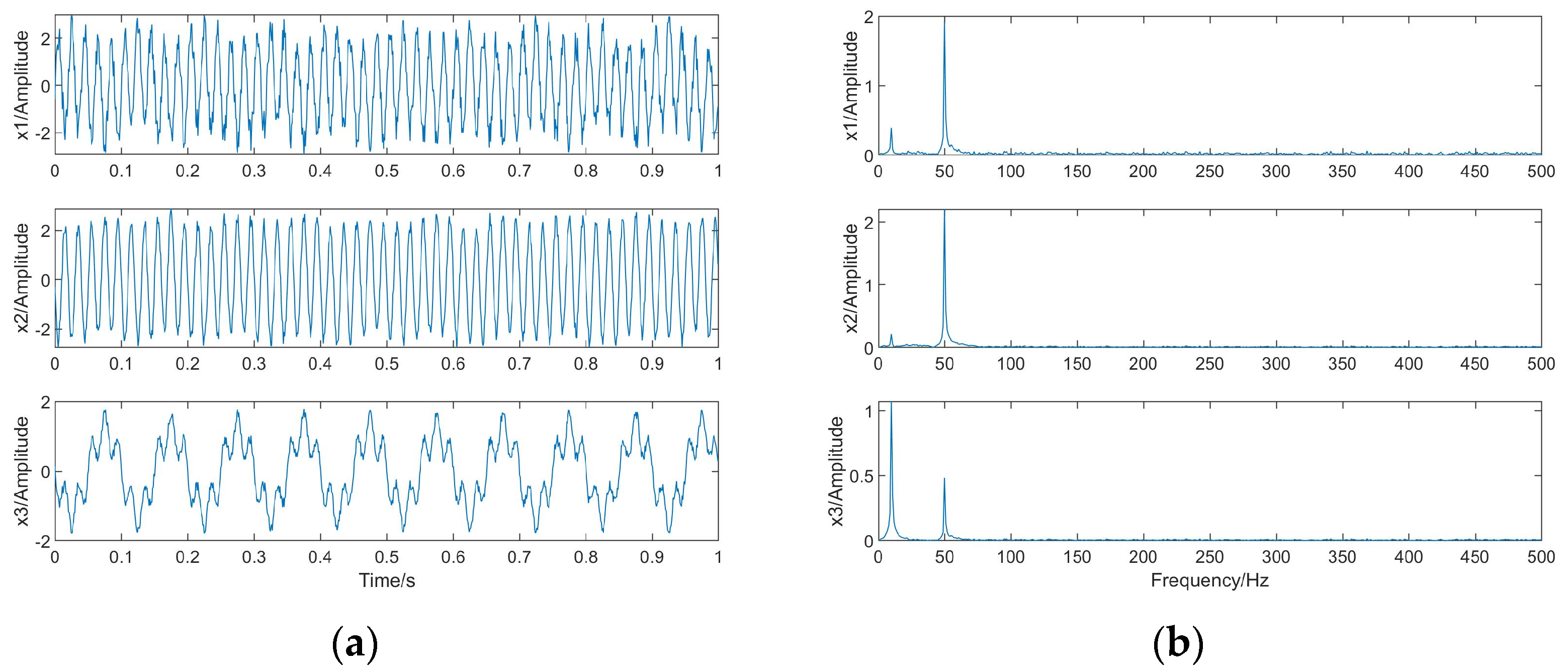
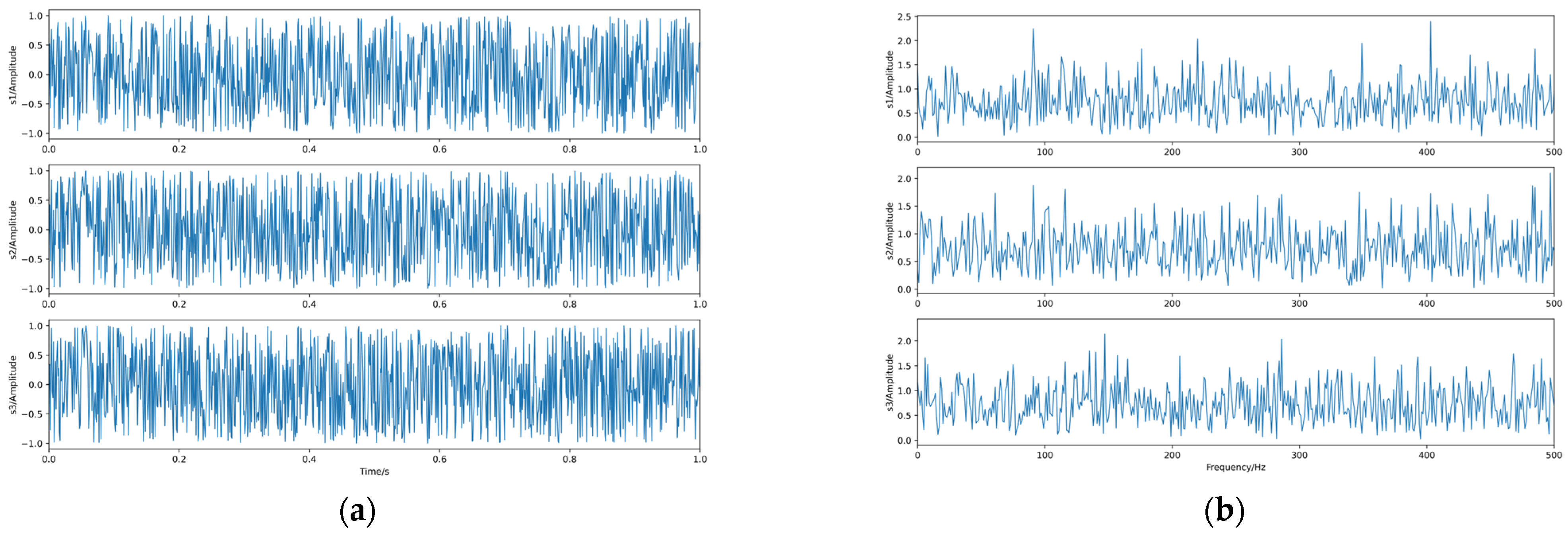
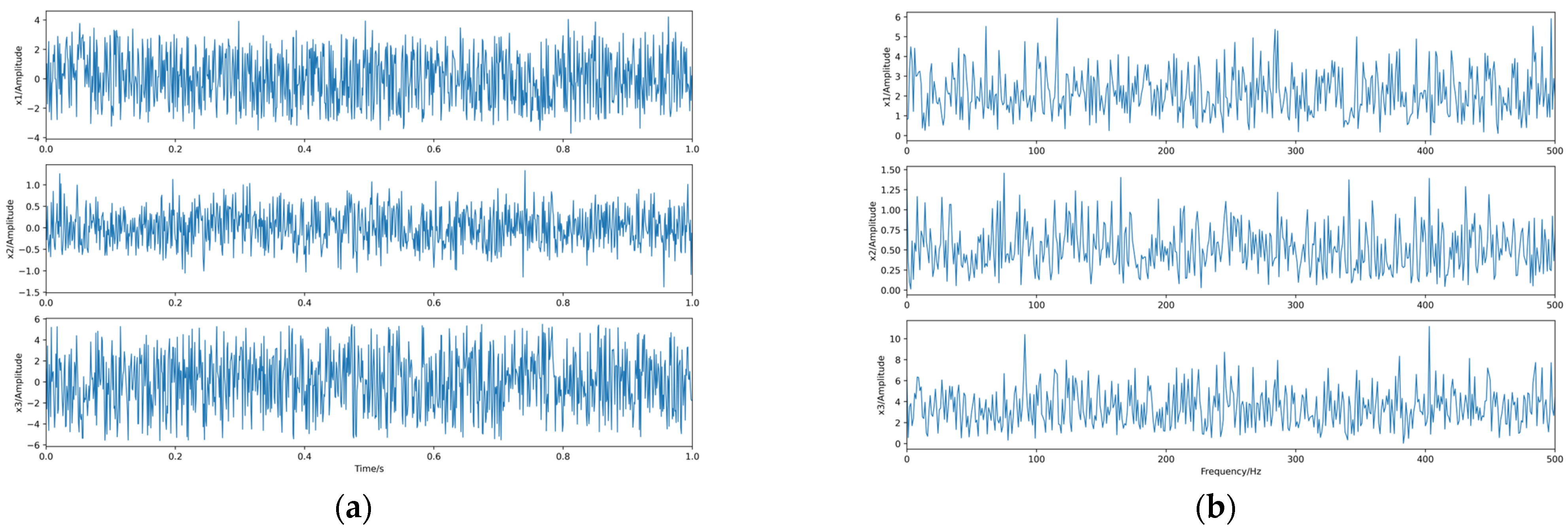
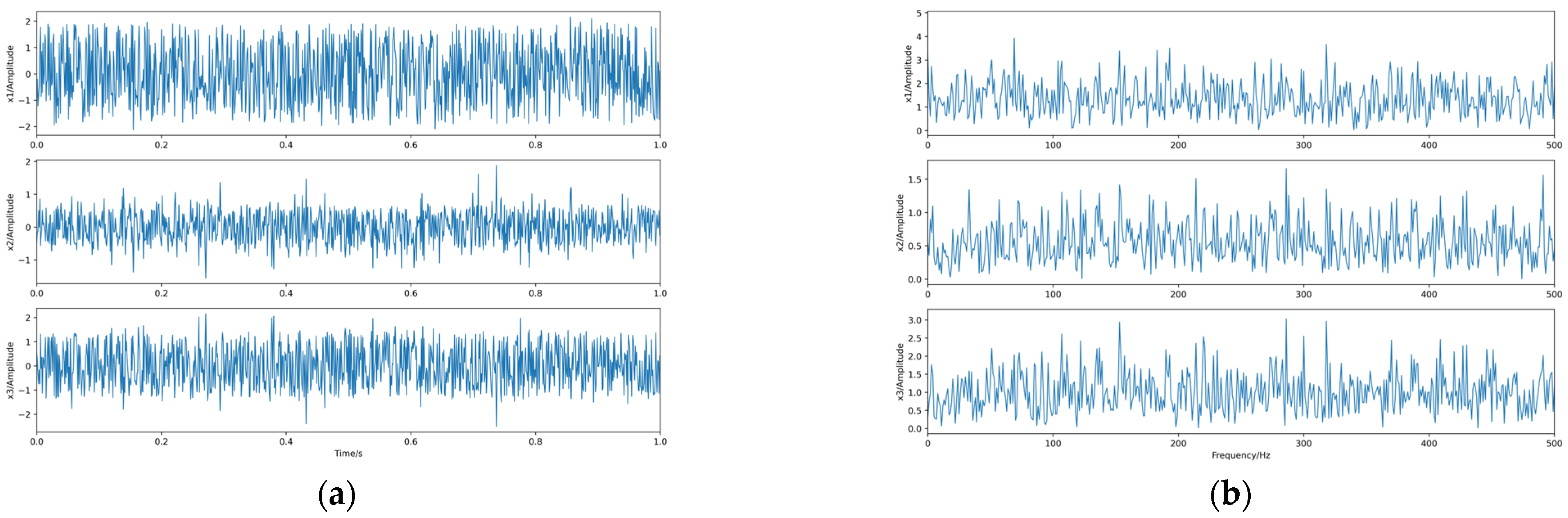
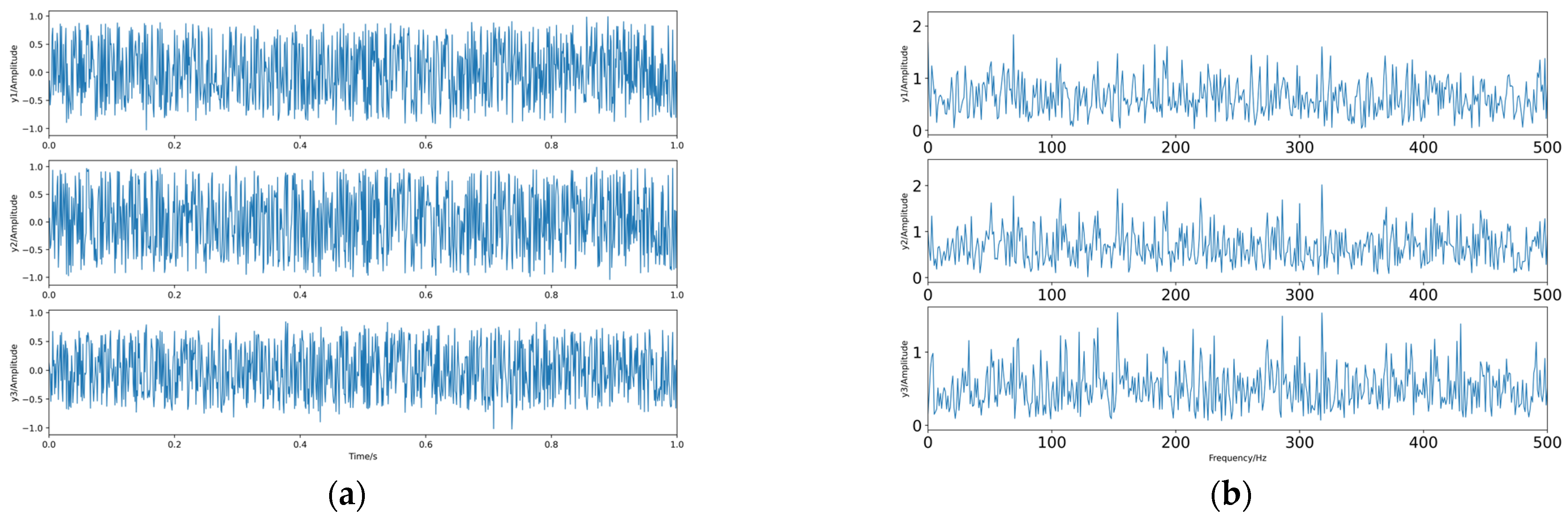
4.1. Separation of Independent Source Signals
- , represents the similarity of s and y, and the closer to 1, the more similar,
- , which means that s and y are completely similar,
- , which means s and y are not similar at all.
| y1 | y2 | y3 | |
|---|---|---|---|
| S1 | 0.97990255 | 0.01395991 | 0.00630897 |
| S2 | 0.00404252 | 0.96984297 | 0.00778653 |
| S3 | 0.00741474 | 0.00730825 | 0.94597251 |
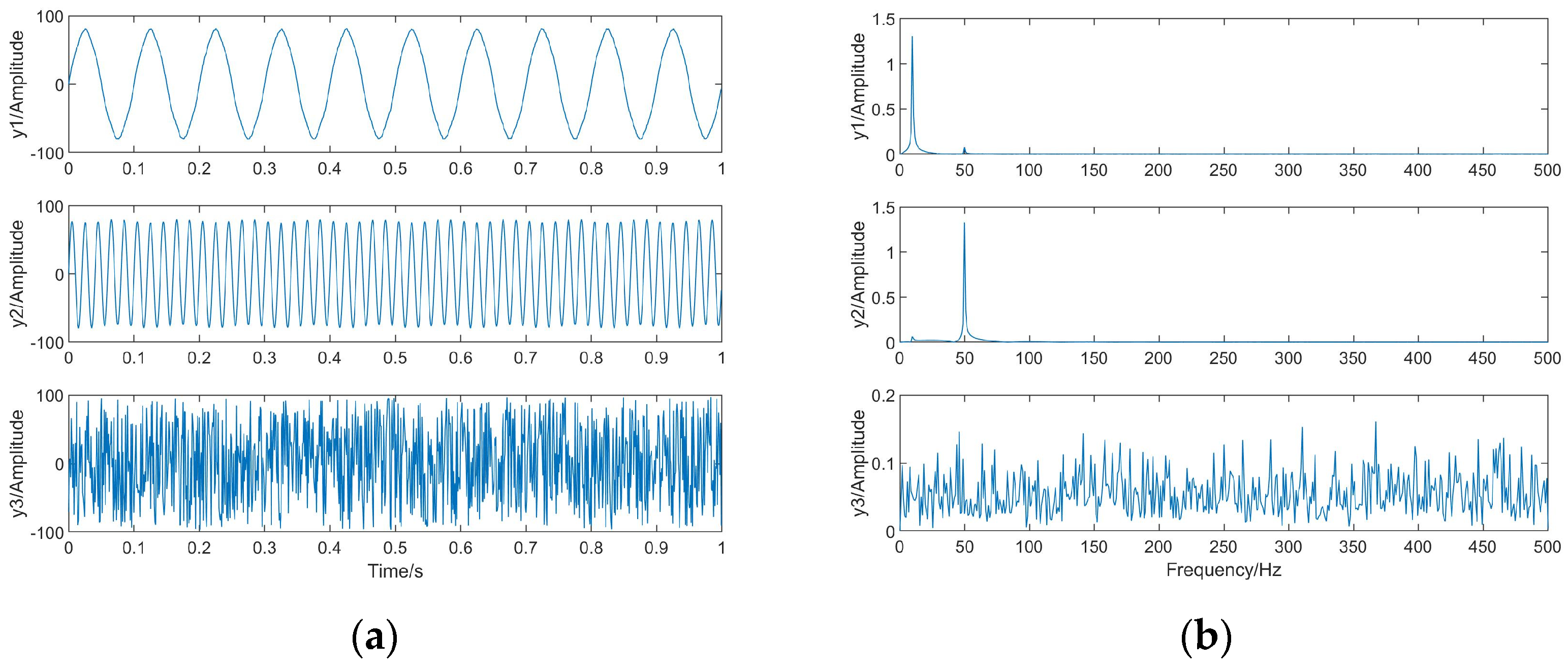
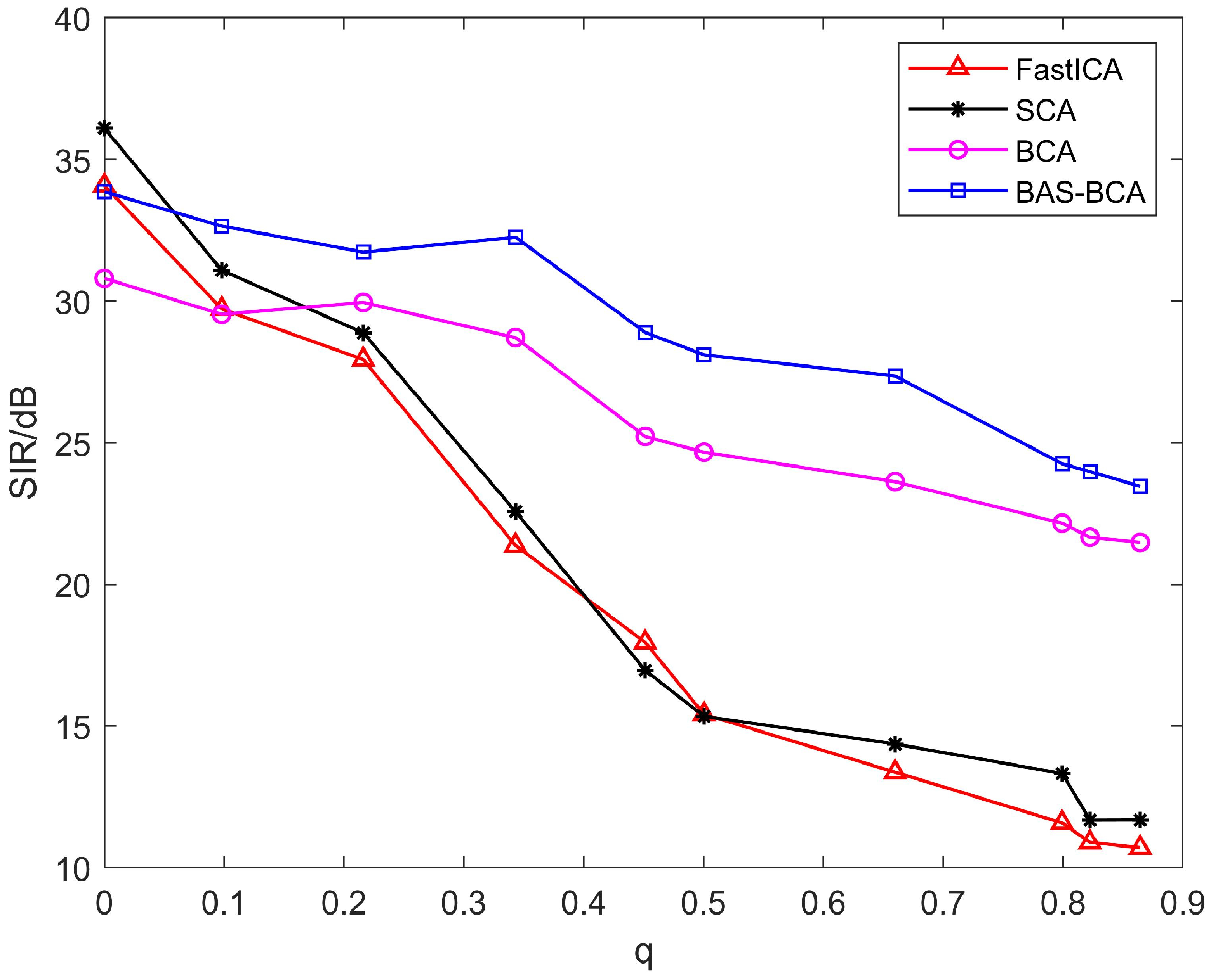
4.2. Separation of Dependent Source Signals
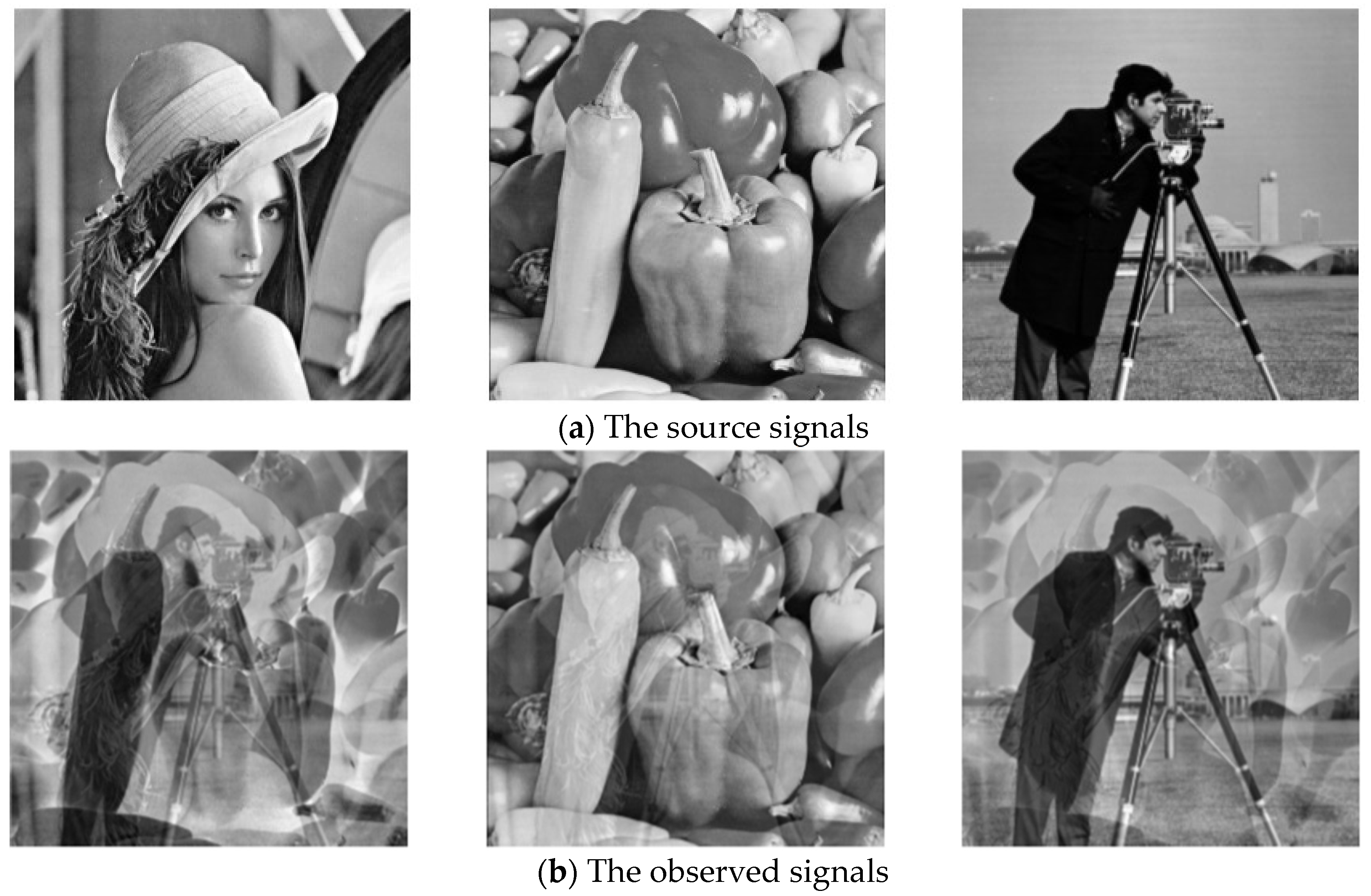
4.3. Blind Source Separation of Images
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.C.; Niu, Y.L.; Chen, Y.Y. Blind Signal Processing; National Defense Industry Press: Beijing, China, 2006. [Google Scholar]
- Bell, A.J.; Sejnowski, T.J. An information maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1004–1034. [Google Scholar]
- Cruces, S. Bounded component analysis of linear mixtures: Acriterion of minimum convex perimeter. IEEE Trans. Signal Process. 2010, 58, 2141–2154. [Google Scholar]
- Erdogan, A.T. A class of bounded component analysis algorithms for the separation of both independent and dependent sources. IEEE Trans. Signal Process. 2013, 61, 5730–5743. [Google Scholar] [CrossRef]
- Babatas, E.; Erdogan, A.T. An algorithmic framework for sparse bounded component analysis. IEEE Trans. Signal Process. 2018, 66, 5194–5205. [Google Scholar]
- Gong, T.; Zhang, Z.; Luo, X.; Li, Y. Quantitative identification of independent and dependent sources based on bounded component analysis. Meas. Sci. Technol. 2021, 32, 035009. [Google Scholar]
- Babatas, E.; Erdogan, A.T. Time and Frequency Based Sparse Bounded Component Analysis Algorithms for Convolutive Mixtures. Signal Process. 2020, 173, 107590. [Google Scholar] [CrossRef]
- Cheng, W.; Chen, S.; Song, C.; Ou, K.; Chen, X.; Wang, J.; Yan, L.; Yang, M. Convolutive blind source separation in the frequency domain of mechanical noise for gas turbines based on bounded component analysis. Meas. Sci. Technol. 2023, 34, 035002. [Google Scholar]
- Tang, Y.; Ma, W.; Chu, J.; Wei, X. In band full duplex digital self interference cancellation based on bounded component analysis. J. Electron. Inf. Technol. 2023, 45, 1619–1626. [Google Scholar]
- Vetter, R.; Celka, P.; Gruter, R.; Vesin, J.M.; Scherrer, U. Observer of the human cardiac sympathetic nerve activity using blind source separation and genetic algorithm optimization. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 30 October–2 November 1997; pp. 293–296. [Google Scholar]
- Gao, Y.; Xie, S.L. A blind source separation algorithm using particle swarm optimization. In Proceedings of the IEEE 6th Circuits and Systems Symposium on Emerging Technologies: Frontiers of Mobile and Wireless Communication, Shanghai, China, 31 May–2 June 2004; Volume 1, pp. 297–300. [Google Scholar]
- Zhang, N.; Liu, T. The application of ant colony optimization algorithm in linear-combination blind source separation problem. In Proceedings of the International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; pp. 1–4. [Google Scholar]
- Li, Z.; Huang, X. Glowworm swarm optimization and its application to blind signal separation. Math. Probl. Eng. 2016, 2016, 5481602. [Google Scholar] [CrossRef][Green Version]
- Chu, D.L.; Chen, H.; Xuan, Z.J. Blind source separation method based on improved whale optimization algorithm. J. Detect. Control 2018, 40, 76–81. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar]
- Zhang, X.; Han, Y.; Yang, Y. Independent component analysis algorithm based on genetic-lion swarm algorithm optimization. Comput. Appl. Softw. 2021, 38, 244–249. [Google Scholar]
- Cardoso, J.F. Blind Signal Separation: Statistical Principles. Proc. IEEE 1998, 86, 2009–2025. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Erdogan, A.T. A family of Bounded Component Analysis algorithms. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Inan, H.A.; Erdogan, A.T. An extended family of bounded component analysis algorithms. In Proceedings of the 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 442–445. [Google Scholar]
- Khan, A.T.; Cao, X.; Li, Z.; Li, S. Enhanced Beetle Antennae Search with Zeroing Neural Network for online solution of constrained optimization. Neurocomputing 2021, 447, 294–306. [Google Scholar]
- Chen, J.; Wang, C.; Wang, S. Evaluation of spatial straightness error based on the variable step size Beetle Swarm Optimization Algorithm. Tool Technol. 2018, 52, 136–138. [Google Scholar] [CrossRef]
- Yin, Y.M.; Liao, B.L.; Li, S.A. New Optimization Algorithm and Its Comparison on Traditional Optimization Algorithms. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 2698–2701. [Google Scholar]
- Zhang, H.; Li, Z.; Jiang, X.; Ma, X.; Chen, J.; Li, S.; Luan, Y.; Lv, Z.; Ma, S. Beetle Colony Optimization Algorithm and Its Application. IEEE Access 2020, 8, 128416–128425. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, K.; Dong, H.; Chi, S.; Chen, Z. An Improved Beetle Swarm Optimization Algorithm for the Intelligent Navigation Control of Autonomous Sailing Robots. IEEE Access 2021, 9, 5296–5311. [Google Scholar] [CrossRef]
- Guo, Z.-Z.; Wang, P.; Ma, Y.-F.; Wang, Q.; Gong, C.-Q. Whale optimization algorithm based on adaptive weights and Corsivariance. Microelectron. Comput. 2017, 34, 20–25. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Wang, W. Blind Source Separation Algorithm and Application Research; Harbin Engineering University: Heilongjiang, China, 2009. [Google Scholar]
- Ali, M.N.; Falavigna, D.; Brutti, A. Time-Domain Joint Training Strategies of Speech Enhancement and Intent Classification Neural Models. Sensors 2022, 22, 374. [Google Scholar] [CrossRef]





| Number | Function | DIM | scope | fmin |
|---|---|---|---|---|
| F1 | 30 | [−100, 100] | 0 | |
| F2 | 30 | [−10, 10] | 0 | |
| F3 | 30 | [−30, 30] | 0 | |
| F4 | 30 | [−600, 600] | 0 | |
| F5 | 30 | [−5.12, 5.12] | 0 | |
| F6 | 30 | [−32, 32] | 0 |
| Number | BAS | GWO | WOA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BEST | STD | TIME | BEST | STD | TIME | BEST | STD | TIME | |
| F1 | 8.43 × 10−9 | 1.32 × 10−9 | 0.124 | 1.28 × 10−19 | 3.39 × 10−19 | 0.176 | 0.279 | 0.13 | 0.085 |
| F2 | 4.47 × 10−14 | 0.348 | 0.092 | 2.01 × 10−9 | 3.41 × 10−9 | 0.182 | 1.24 × 10−16 | 4.82 | 0.098 |
| F3 | 22.63 | 7.06 × 10−7 | 0.096 | 0.269 × 102 | 0.601 | 0.213 | 4.14 × 102 | 5.36 × 102 | 0.103 |
| F4 | 1.01 × 10−5 | 1.11 × 10−4 | 0.085 | 1.84 × 10−3 | 4.12 × 10−3 | 0.219 | 0.038 | 0.016 | 0.089 |
| F5 | −1.92 × 10−3 | 0.136 | 0.081 | 0.398 | 0.545 × 102 | 0.198 | 1.64 × 10−2 | 0.462 × 102 | 0.079 |
| F6 | 2.35 × 10−3 | 0.542 | 0.076 | 2.19 × 10−4 | 3.54 × 10−4 | 0.192 | 5.09 × 10−3 | 1.61 | 0.073 |
| y1 | y2 | y3 | |
|---|---|---|---|
| S1 | 0.95674313 | 0.39900721 | 0.04960461 |
| S2 | 0.47858537 | 0.98699327 | 0.47763681 |
| S3 | 0.35747411 | 0.50449069 | 0.97789969 |
| FastICA | SCA | BCA | BAS-BCA | |
|---|---|---|---|---|
| similarity coefficient | 0.61478832 0.79113256 0.86792361 | 0.75382446 0.83249712 0.84562887 | 0.94112682 0.89978596 0.96120685 | 0.99913226 0.97777913 0.98947889 |
| PI | 0.37858537 | 0.33259634 | 0.18382564 | 0.09763681 |
| SIR | 17.78995818 | 18.58967436 | 23.98567492 | 27.52189291 |
| Time | 19.36 | 20.21 | 29.68 | 25.11 |
| y1 | y2 | y3 | |
|---|---|---|---|
| S1 | 0.99705728 | 0.86008656 | 0.66929815 |
| S2 | 0.87889169 | 0.99727447 | 0.82707136 |
| S3 | 0.75027519 | 0.89507997 | 0.98287344 |
| FastICA | SCA | BCA | BAS-BCA | |
|---|---|---|---|---|
| similarity coefficient | 0.52367416 0.71235987 0.79534238 | 0.76545382 0.63541287 0.77852536 | 0.93564258 0.90312354 0.95238421 | 0.99705728 0.99727447 0.98287344 |
| PI | 0.49896372 | 0.39986341 | 0.21368547 | 0.15236846 |
| SIR | 11.6689403 | 12.9658332 | 22.6854931 | 24.6235874 |
| Time | 20.68 | 21.93 | 31.42 | 26.57 |
| s1 | s2 | s3 | |
|---|---|---|---|
| s1 | 1 | 0.27858537 | 0.34960461 |
| s2 | 0.27858537 | 1 | 0.12389069 |
| s3 | 0.34960461 | 0.12389069 | 1 |
| FastICA | SCA | BCA | BAS-BCA | |
|---|---|---|---|---|
| similarity coefficient | 0.81583695 0.80563229 0.83652718 | 0.85426875 0.82156371 0.84685932 | 0.96189537 0.92678932 0.95345874 | 0.98256749 0.96585374 0.99136457 |
| PI | 0.29356417 | 0.27998659 | 0.14567789 | 0.11268894 |
| SIR | 18.1235845 | 20.2314567 | 23.2589671 | 28.9358791 |
| Time | 21.56 | 24.13 | 33.15 | 28.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Wu, Y. A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search. Sensors 2023, 23, 8325. https://doi.org/10.3390/s23198325
Tang M, Wu Y. A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search. Sensors. 2023; 23(19):8325. https://doi.org/10.3390/s23198325
Chicago/Turabian StyleTang, Mingyang, and Yafeng Wu. 2023. "A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search" Sensors 23, no. 19: 8325. https://doi.org/10.3390/s23198325
APA StyleTang, M., & Wu, Y. (2023). A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search. Sensors, 23(19), 8325. https://doi.org/10.3390/s23198325






