Performance Analysis of UAV-Assisted Hybrid FSO/RF Communication Systems under Various Weather Conditions
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation and Contributions
- To our knowledge, we, firstly, propose a multi-hop parallel hybrid FSO/RF communication system architecture with and without PE based on the UAV relay.
- New mathematical expressions for the end-to-end system in terms of average bit error rate and outage probability are derived under EW turbulence and Nakagami fading channels for four binary subcarrier modulation schemes.
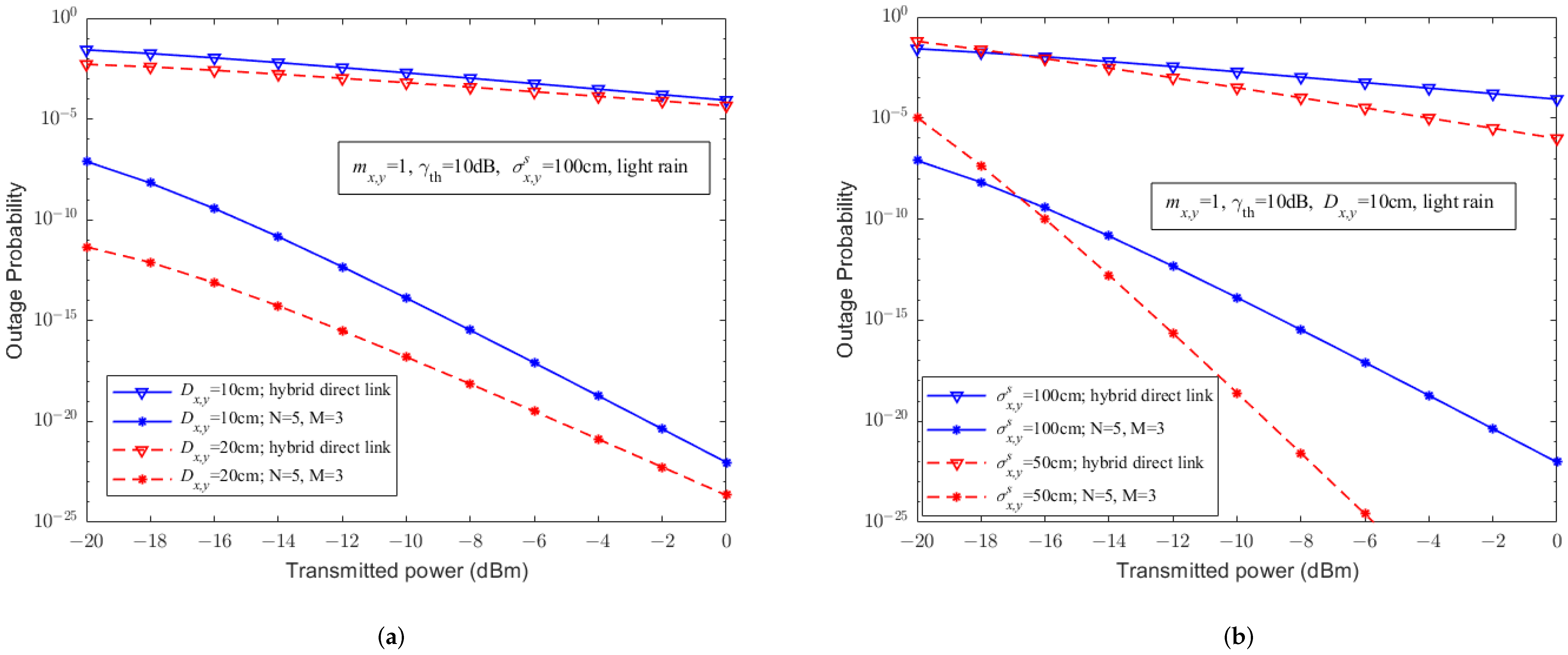
- The effects of different weather environments, modulation methods, receiver apertures, RF fading parameters, pointing errors, and relay structures on the performance of our considered systems are analyzed through numerical evaluationnumerical simulations. As far as we know, no existing work considered the impact of weather environments and aperture averaging on UAV-assisted FSO communication.
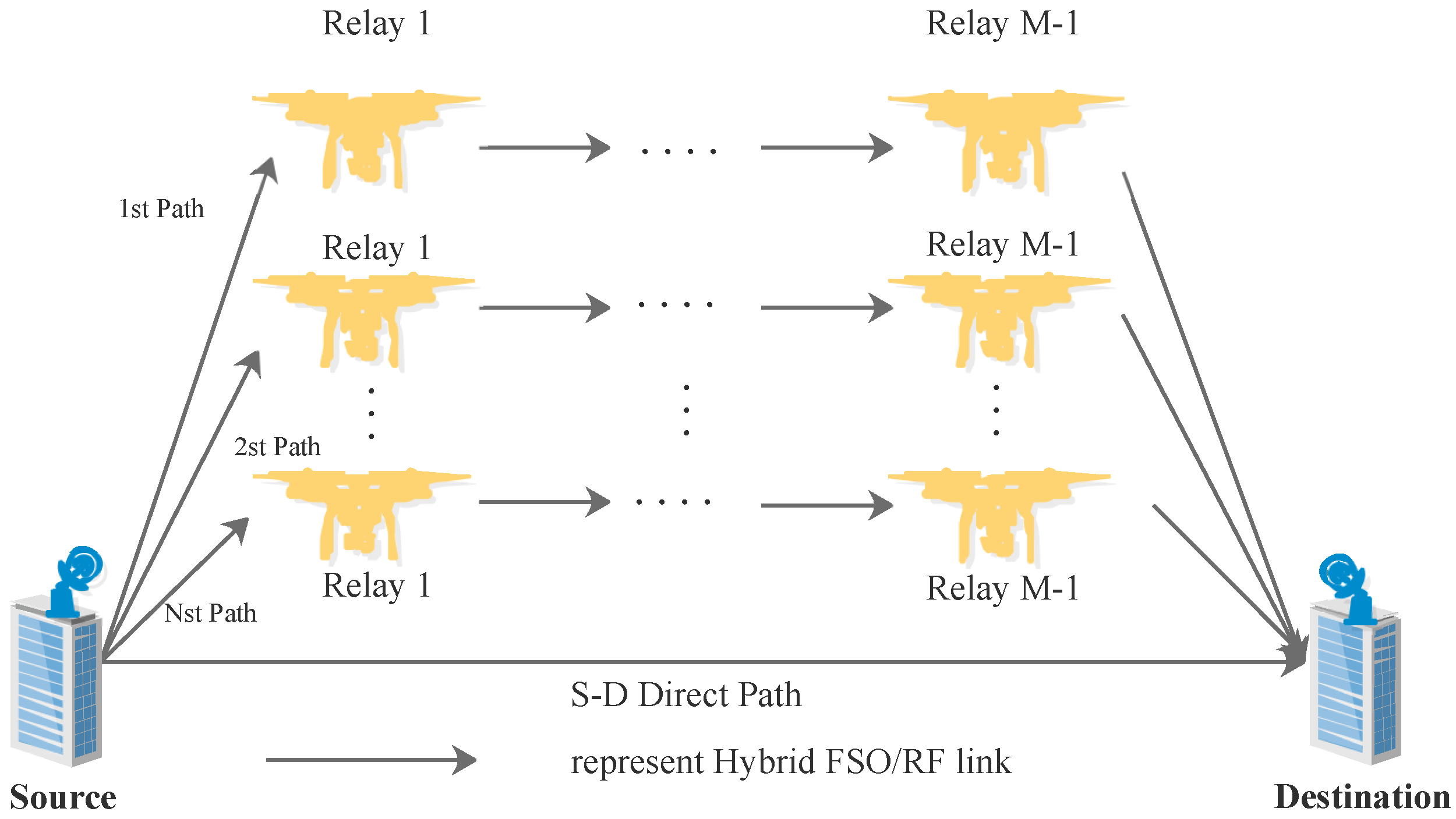
2. System and Channel Models
2.1. One-Hop FSO SublinkSubsystem under Various Weather Conditions
2.2. One-Hop RF SublinkSubsystem under Various Weather Conditions
2.3. One-Hop Hybrid FS0/RF System Based on a Selective Combination Scheme
3. System Performance Analysis
3.1. Average Bit Error Rate
3.2. Outage Probability
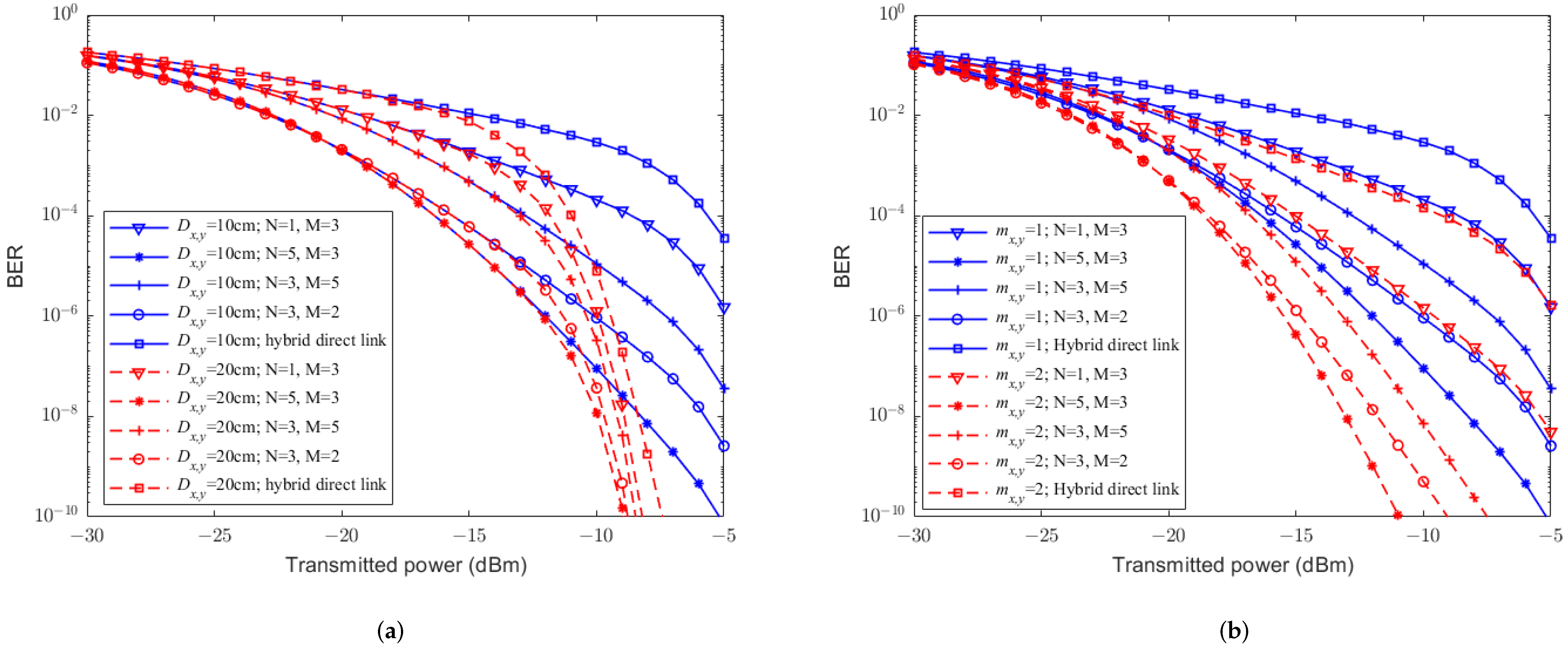
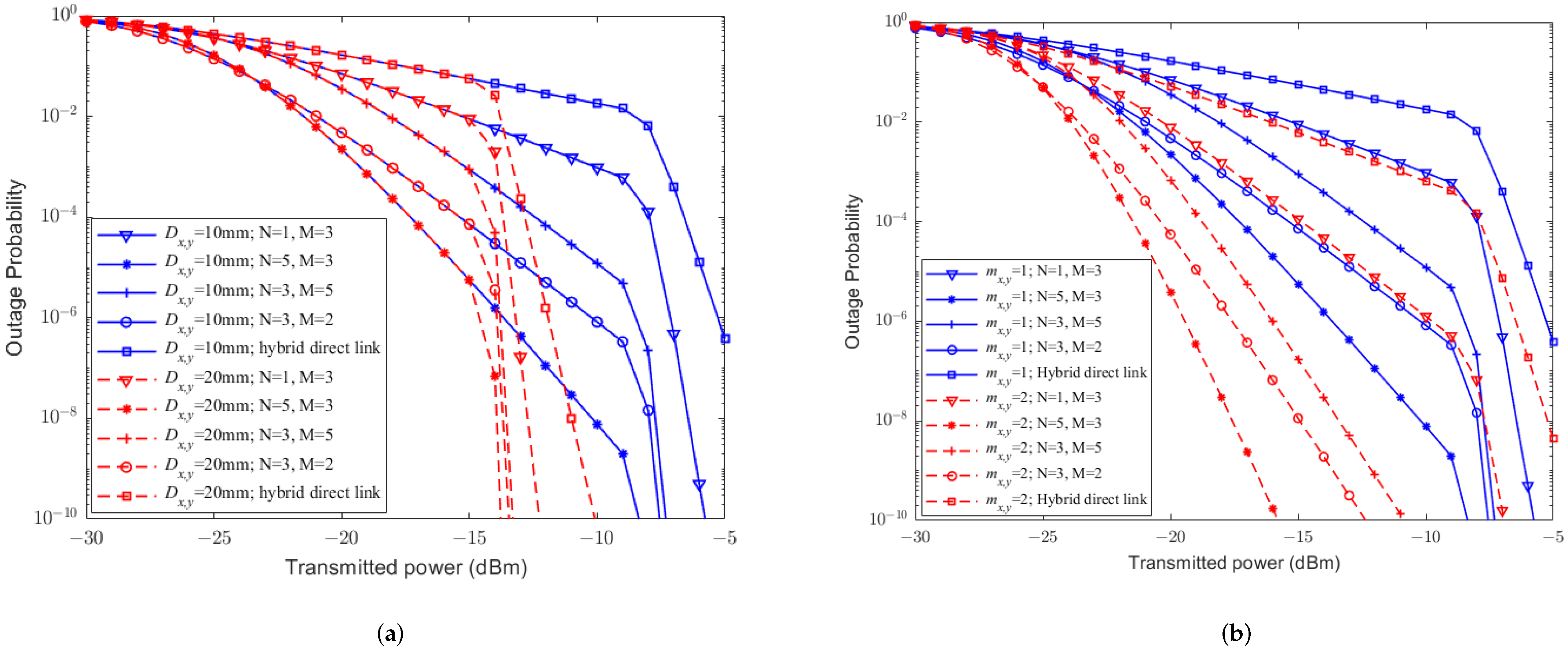
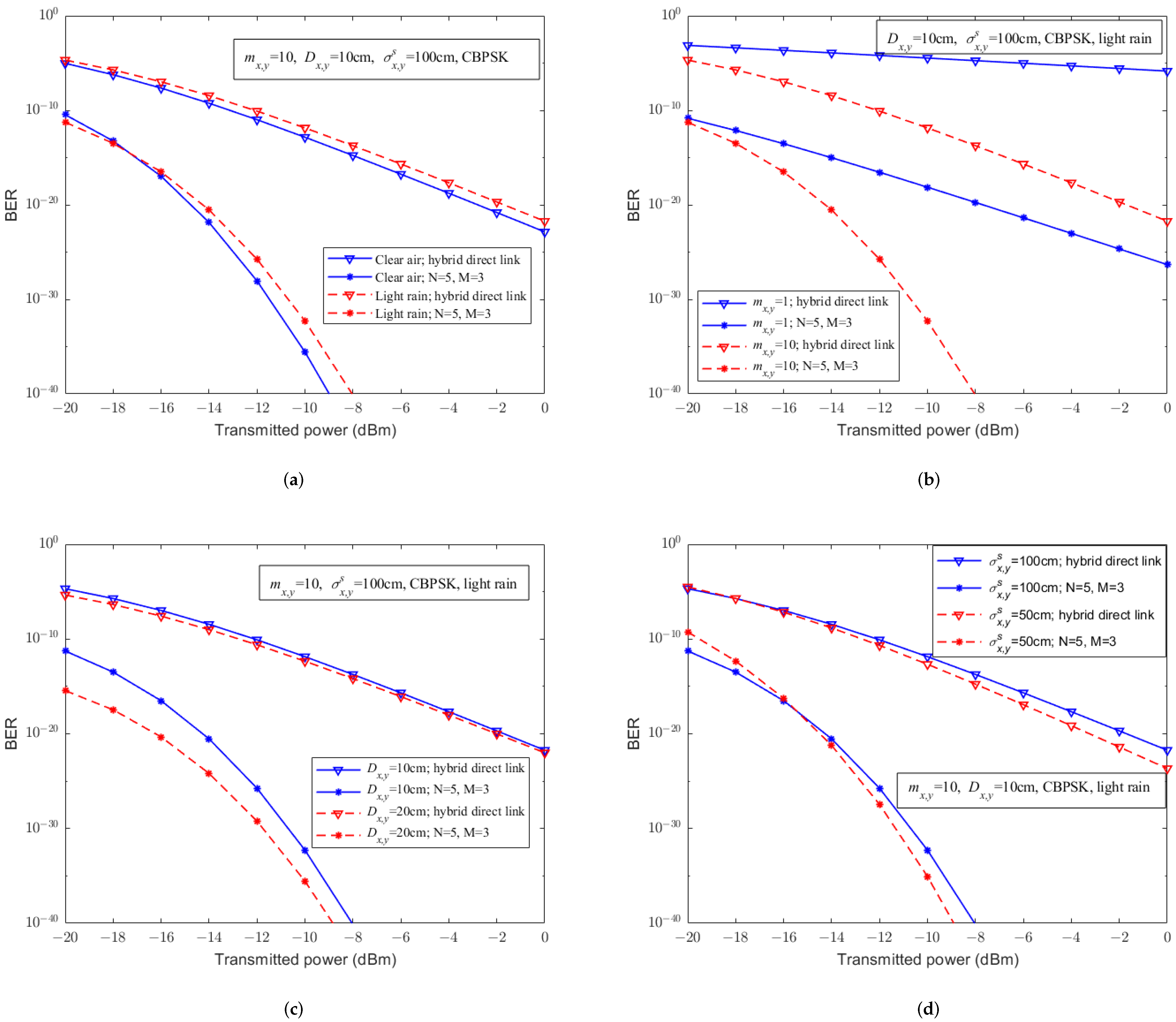
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Magidi, S.; Jabeena, A. Free space optics, channel models and hybrid modulation schemes: A review. Wirel. Pers. Commun. 2021, 119, 2951–2974. [Google Scholar] [CrossRef]
- Uysal, M.; Capsoni, C.; Ghassemlooy, Z.; Boucouvalas, A.; Udvary, E. Optical Wireless Communications: An Emerging Technology; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Safi, H.; Dargahi, A.; Cheng, J.; Safari, M. Analytical channel model and link design optimization for ground-to-HAP free-space optical communications. J. Light. Technol. 2020, 38, 5036–5047. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Laser Beam Scintillation with Applications; SPIE Press: Bellingham, WA, USA, 2001; Volume 99. [Google Scholar]
- Garcia-Zambrana, A. Error rate performance for STBC in free-space optical communications through strong atmospheric turbulence. IEEE Commun. Lett. 2007, 11, 390–392. [Google Scholar] [CrossRef]
- Samimi, H. Performance analysis of free-space optical links with transmit laser selection diversity over strong turbulence channels. IET Commun. 2011, 5, 1039–1043. [Google Scholar] [CrossRef]
- Niu, M.; Cheng, J.; Holzman, J.F. Error rate analysis of M-ary coherent free-space optical communication systems with K-distributed turbulence. IEEE Trans. Commun. 2011, 59, 664–668. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y.; Al-Habash, M. Theory of optical scintillation. J. Opt. Soc. Am. A—Opt. Image Sci. Vis. 1999, 16, 1417–1429. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Karagianni, E.A.; Tsigopoulos, A.D.; Fafalios, M.E.; Tombras, G.S. Average capacity of optical wireless communication systems over atmospheric turbulence channels. J. Light. Technol. 2009, 27, 974–979. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Puerta-Notario, A.; Awrejcewicz, J. A unifying statistical model for atmospheric optical scintillation. Numer. Simul. Phys. Eng. Process. 2011, 181, 181–205. [Google Scholar]
- Barrios, R.; Dios, F. Exponentiated Weibull distribution family under aperture averaging for Gaussian beam waves. Opt. Express 2012, 20, 13055–13064. [Google Scholar] [CrossRef]
- Barrios, R.; Dios, F. Exponentiated Weibull model for the irradiance probability density function of a laser beam propagating through atmospheric turbulence. Opt. Laser Technol. 2013, 45, 13–20. [Google Scholar] [CrossRef]
- Zedini, E.; Ansari, I.S.; Alouini, M.S. Performance analysis of mixed Nakagami-m and Gamma–Gamma dual-hop FSO transmission systems. IEEE Photonics J. 2014, 7, 1–20. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, P.; Liu, X.; Cao, T. On the performance of dual-hop mixed RF/FSO wireless communication system in urban area over aggregated exponentiated Weibull fading channels with pointing errors. Opt. Commun. 2018, 410, 609–616. [Google Scholar] [CrossRef]
- Touati, A.; Abdaoui, A.; Touati, F.; Uysal, M.; Bouallegue, A. On the effects of combined atmospheric fading and misalignment on the hybrid FSO/RF transmission. J. Opt. Commun. Netw. 2016, 8, 715–725. [Google Scholar] [CrossRef]
- Odeyemi, K.O.; Owolawi, P.A. Selection combining hybrid FSO/RF systems over generalized induced-fading channels. Opt. Commun. 2019, 433, 159–167. [Google Scholar] [CrossRef]
- Kashani, M.A.; Uysal, M. Outage performance and diversity gain analysis of free-space optical multi-hop parallel relaying. J. Opt. Commun. Netw. 2013, 5, 901–909. [Google Scholar] [CrossRef]
- Wang, P.; Liu, X.; Cao, T.; Fu, H.; Wang, R.; Guo, L. Impact of nonzero boresight pointing errors on the performance of a relay-assisted free-space optical communication system over exponentiated Weibull fading channels. Appl. Opt. 2016, 55, 7593–7603. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, P.; Liu, T.; Jia, C.; Pang, W.N.; Wang, W. Performance analysis of multi-hop parallel FSO system over double generalized gamma distribution considering two transmission beams. Optoelectron. Lett. 2021, 17, 215–220. [Google Scholar] [CrossRef]
- Fawaz, W.; Abou-Rjeily, C.; Assi, C. UAV-aided cooperation for FSO communication systems. IEEE Commun. Mag. 2018, 56, 70–75. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Sadough, S.M.S.; Ansari, I.S. Tractable optical channel modeling between UAVs. IEEE Trans. Veh. Technol. 2019, 68, 11543–11550. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Rezaee, M.; Ansari, I.S.; Yazdanian, V. Channel modeling for UAV-based optical wireless links with nonzero boresight pointing errors. IEEE Trans. Veh. Technol. 2020, 69, 14238–14246. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Sadough, S.M.S. Optimal placement of UAV-assisted free-space optical communication systems with DF relaying. IEEE Commun. Lett. 2019, 24, 155–158. [Google Scholar] [CrossRef]
- Wang, J.Y.; Ma, Y.; Lu, R.R.; Wang, J.B.; Lin, M.; Cheng, J. Hovering UAV-based FSO communications: Channel modelling, performance analysis, and parameter optimization. IEEE J. Sel. Areas Commun. 2021, 39, 2946–2959. [Google Scholar] [CrossRef]
- Lu, R.R.; Wang, J.Y.; Fu, X.T.; Lin, S.H.; Wang, Q.; Zhang, B. Performance analysis and optimization for UAV-based FSO communication systems. Phys. Commun. 2022, 51, 101594. [Google Scholar] [CrossRef]
- Xu, G.; Song, Z. Performance analysis of a UAV-assisted RF/FSO relaying systems for internet of vehicles. IEEE Internet Things J. 2021, 9, 5730–5741. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Guo, J.; Li, G.; Kong, D. Performance Analysis of a Multi-Hop Parallel Hybrid FSO/RF System over a Gamma–Gamma Turbulence Channel with Pointing Errors and a Nakagami-m Fading Channel. Photonics 2022, 9, 631. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, H.; Ma, X.; Lu, W. Performance of multi-hop parallel free-space optical communication over gamma–gamma fading channel with pointing errors. Appl. Opt. 2016, 55, 9178–9184. [Google Scholar] [CrossRef] [PubMed]
- Barrios, R.; Dios, F. Probability of fade and BER performance of FSO links over the exponentiated Weibull fading channel under aperture averaging. In Proceedings of the Unmanned/Unattended Sensors and Sensor Networks IX, Edinburgh, UK, 24–27 September 2012; SPIE: Bellingham, WA USA, 2012; Volume 8540, pp. 79–87. [Google Scholar]
- Shakir, W.M. Performance analysis of the hybrid MMW RF/FSO transmission system. Wirel. Pers. Commun. 2019, 109, 2199–2211. [Google Scholar] [CrossRef]
- Wu, Y.; Hao, Y.; Liu, H.; Zhao, L.; Jiang, T.; Deng, D.; Wei, Z. Performance improvement for wireless sensors networks by adopting hybrid subcarrier intensity modulation over exponentiated Weibull turbulence channels. IEEE Access 2020, 8, 118612–118622. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Feng, W. Performance study of wavelength diversity serial relay OFDM FSO system over exponentiated Weibull channels. Opt. Commun. 2021, 478, 126470. [Google Scholar] [CrossRef]
- Alathwary, W.A.; Altubaishi, E.S. On the performance analysis of decode-and-forward multi-hop hybrid FSO/RF systems with hard-switching configuration. IEEE Photonics J. 2019, 11, 1–12. [Google Scholar] [CrossRef]
- Kazemi, H.; Uysal, M.; Touati, F.; Haas, H. Outage performance of multi-hop hybrid FSO/RF communication systems. In Proceedings of the 2015 4th International Workshop on Optical Wireless Communications (IWOW), Istanbul, Turkey, 7–8 September 2015; pp. 83–87. [Google Scholar]
- He, B.; Schober, R. Bit-interleaved coded modulation for hybrid RF/FSO systems. IEEE Trans. Commun. 2009, 57, 3753–3763. [Google Scholar] [CrossRef]
- Chatzidiamantis, N.D.; Karagiannidis, G.K.; Kriezis, E.E.; Matthaiou, M. Diversity combining in hybrid RF/FSO systems with PSK modulation. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–6. [Google Scholar]
- Amirabadi, M.A.; Vakili, V.T. Performance comparison of two novel relay-assisted hybrid FSO/RF communication systems. IET Commun. 2019, 13, 1551–1556. [Google Scholar] [CrossRef]
- Wang, P.; Wang, R.; Guo, L.; Cao, T.; Yang, Y. On the performances of relay-aided FSO system over M distribution with pointing errors in presence of various weather conditions. Opt. Commun. 2016, 367, 59–67. [Google Scholar] [CrossRef]
- Ansari, I.S.; Al-Ahmadi, S.; Yilmaz, F.; Alouini, M.S.; Yanikomeroglu, H. A new formula for the BER of binary modulations with dual-branch selection over generalized-K composite fading channels. IEEE Trans. Commun. 2011, 59, 2654–2658. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration, 2nd ed.; Academic Press, INC.: Cambridge, MA, USA, 1984. [Google Scholar]
- Concus, P.; Cassatt, D.; Jaehnig, G.; Melby, E. Tables for the evaluation of by Gauss-Laguerre quadrature. Math. Comput. 1963, 17, 245–256. [Google Scholar]



| Weather Condition | [] | [dB/Km] | [dB/Km] | [dB/Km] |
|---|---|---|---|---|
| Clear air | 0 | 15.1 | ||
| Haze | 0 | 15.1 | ||
| Light fog | 0 | 15.1 | ||
| light rain ( mm/h) | 15.1 |
| Binary Modulation Scheme | p | q |
|---|---|---|
| Coherent binary phase shift keying (CBPSK) | 1 | |
| Differential binary phase shift keying (DBPSK) | 1 | 1 |
| Coherent binary frequency shift keying(CBFSK) | ||
| Non-coherent binary frequency shift keying (NBFSK)(NBPSK) | 1 |
| FSO Subsystem | RF Subsystem | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Wavelength, | 1550 nm | Wavelength of 60 GHz RF, | 5 mm |
| Divergence angle, | 1 mrad | Nakagami fading parameter, | 2 |
| Receiver aperture diameter, | 10 cm or 20 cm | Transmit antenna gain, | 44 dBi |
| Responsivity, | A/W | Receive antenna gain, | 44 dBi |
| Noise Variance, | Noise Variance, | dBm | |
| Transmission distance, | 1 km | Oxygen attenuation, | dB/km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Kong, D.; Wang, Q.; Li, G. Performance Analysis of UAV-Assisted Hybrid FSO/RF Communication Systems under Various Weather Conditions. Sensors 2023, 23, 7638. https://doi.org/10.3390/s23177638
Wu Y, Kong D, Wang Q, Li G. Performance Analysis of UAV-Assisted Hybrid FSO/RF Communication Systems under Various Weather Conditions. Sensors. 2023; 23(17):7638. https://doi.org/10.3390/s23177638
Chicago/Turabian StyleWu, Yan, Dejin Kong, Qian Wang, and Gang Li. 2023. "Performance Analysis of UAV-Assisted Hybrid FSO/RF Communication Systems under Various Weather Conditions" Sensors 23, no. 17: 7638. https://doi.org/10.3390/s23177638
APA StyleWu, Y., Kong, D., Wang, Q., & Li, G. (2023). Performance Analysis of UAV-Assisted Hybrid FSO/RF Communication Systems under Various Weather Conditions. Sensors, 23(17), 7638. https://doi.org/10.3390/s23177638






