Estimation of Wideband Multi-Component Phasors Considering Signal Damping †
Abstract
1. Introduction
1.1. Background and Motivations
1.2. Literature Review
1.3. Summary of Contributions
- (1)
- A concise index and criterion for identifying the number of modes in the measured signal with a non-zero damping factor is proposed. It is found to be more robust than the existing index, and its applicability is analyzed by testing the influence of various factors.
- (2)
- The signal damping factor is taken into account by the proposed WMPE algorithm, and thus the multiple phasors in the measured signal can be accurately estimated, even if the signal includes fundamental, multi-harmonic, and multi-interharmonic tones; covers the frequency range of 10–2000 Hz; and has non-zero damping factors.
- (3)
- Several test scenarios are designed according to synchrophasor standards and literature studies on wideband phasor measurement. The test signals include wideband multi-components with different damping factors, noise, amplitudes or phase modulations, frequency deviations or ramps, and different interharmonic frequencies and transient changes. The test results confirm that the proposed method can accurately estimate wideband multi-component phasors, and has a short response time in these complex signal environments.
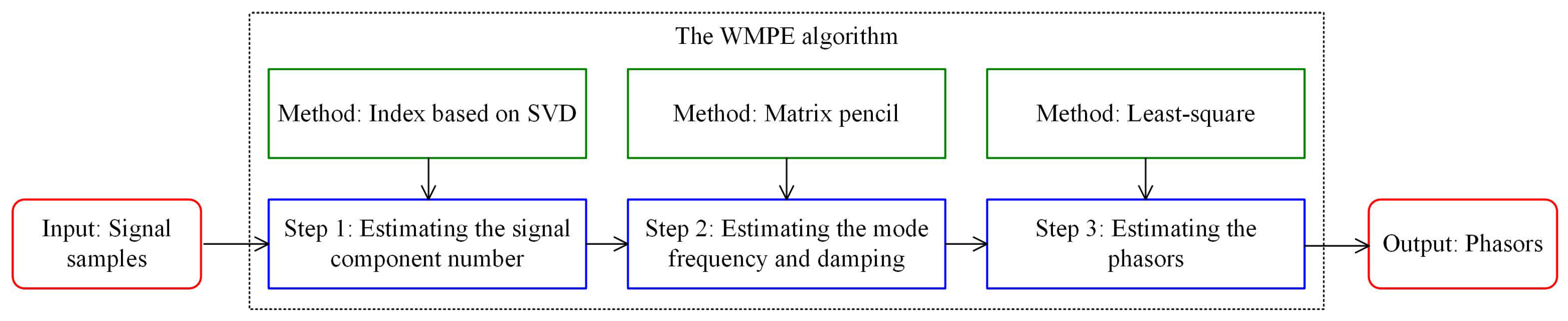
2. The Complete Process of the Proposed WMPE Algorithm
2.1. The Proposed Index for Identifying Signal Component Number
- T1: The damping ratios for all signal components, i.e., and , increase from −1 to 1 with a step of 0.2; the interharmonic amplitudes p.u., frequencies , and number ; the signal-to-noise ratio (SNR) is 60 dB; the sampling frequency kHz; and the time window . Then, this test signal contains a total of 149 signal components, i.e., the maximum component number in (4), and the minimum frequency interval is only 3 Hz.
- T2: The interharmonic tones have amplitudes p.u. with a step of 0.02 p.u.; frequencies , and number ; the damping ratios and ; the SNR is 60 dB; the sampling frequency kHz; and the time window .
- T3: The SNR changes from 50 dB to 80 dB in a step of 5 dB; the damping ratios and ; the interharmonic tones have amplitudes p.u., frequencies , and number ; the sampling frequency kHz; and the time window .
- T4: The sampling frequency increases from 5 kHz to 10 kHz with a step 1 kHz; the damping ratios and ; the interharmonic tones have amplitudes p.u., frequencies , and number ; the SNR is 60 dB; and the time window .
- T5: The time window length changes from 2 to 7 in a step of 1; the damping ratios and ; the interharmonic tones have amplitudes p.u., frequencies traverses {47}, {47, 70}, {20, 47, 70}, {20, 47, 70, 90}, and {10, 30, 47, 70, 90} for , respectively, and number , i.e., the signal contains no interharmonic when c = 2; the SNR is 60 dB; and the sampling frequency kHz.
2.2. The Signal Component Frequency and Damping Factor Estimation Based on the Matrix Pencil
2.3. The Wideband Multi-Component Phasor Estimation Based on the Modified Least-Squares Algorithm
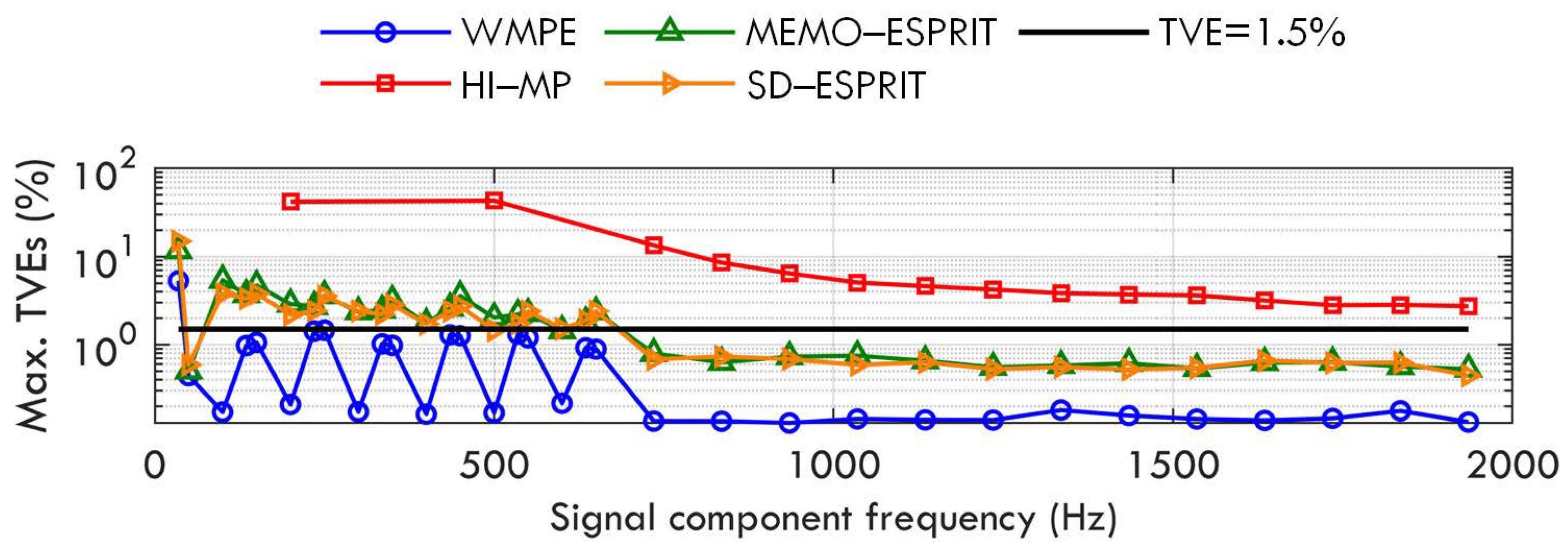
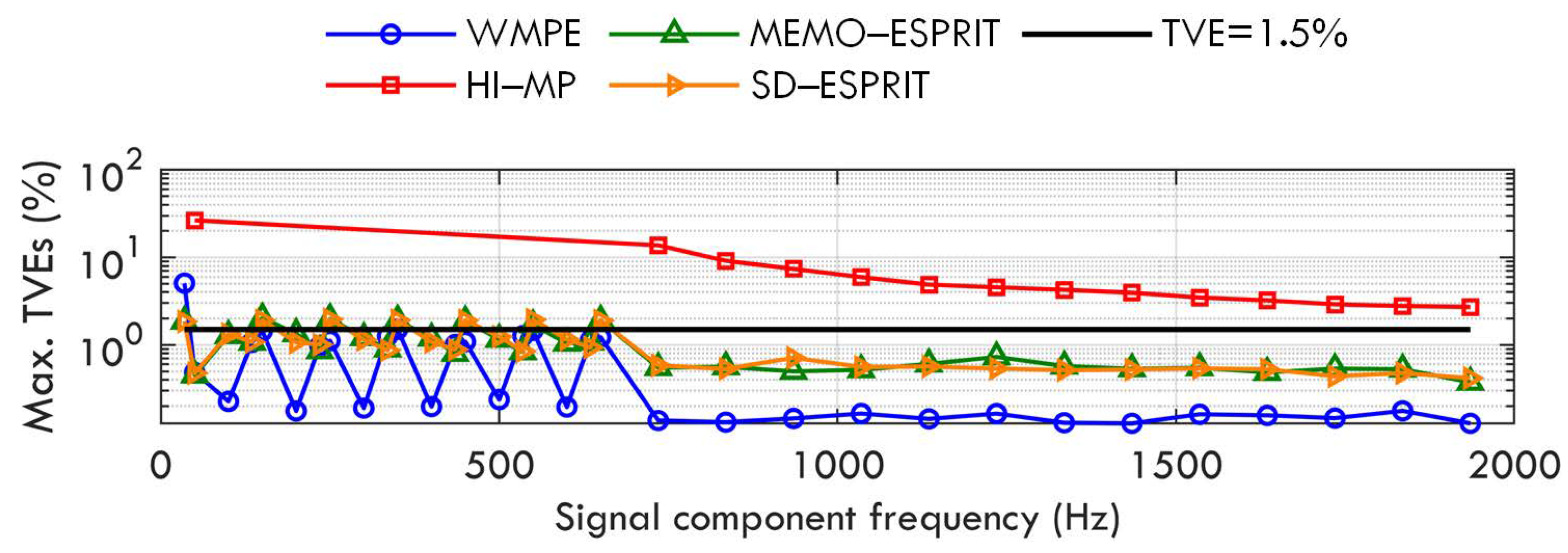
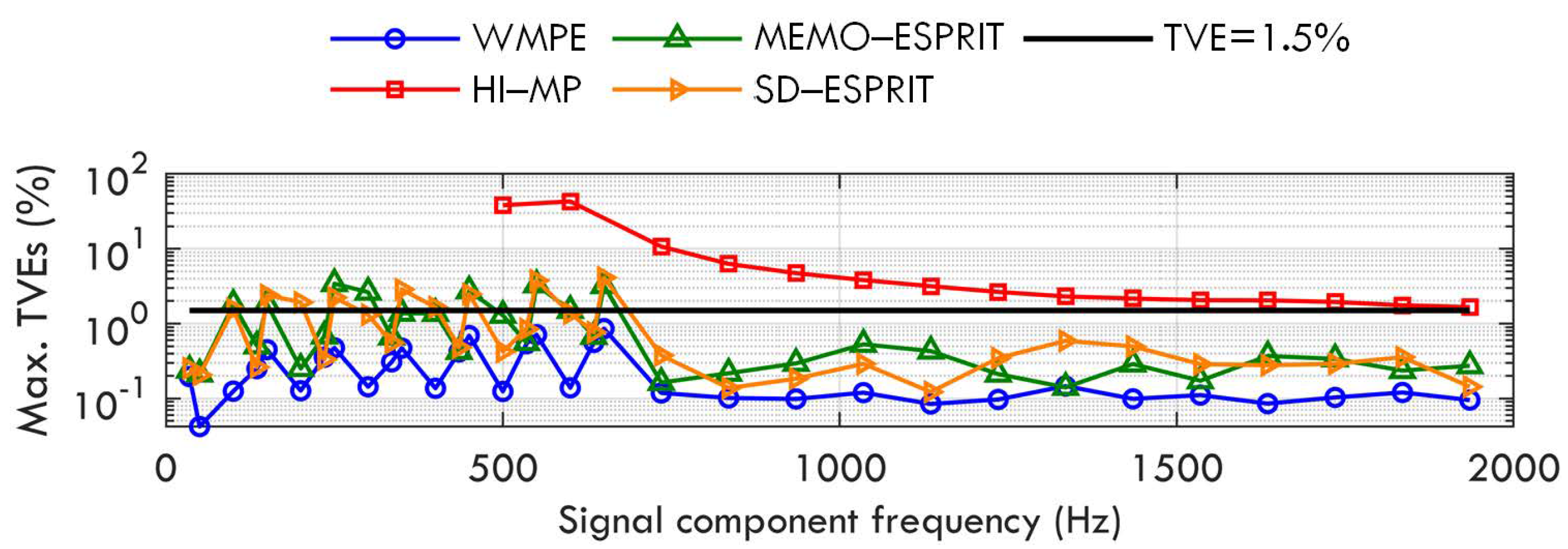
3. Numerical Tests
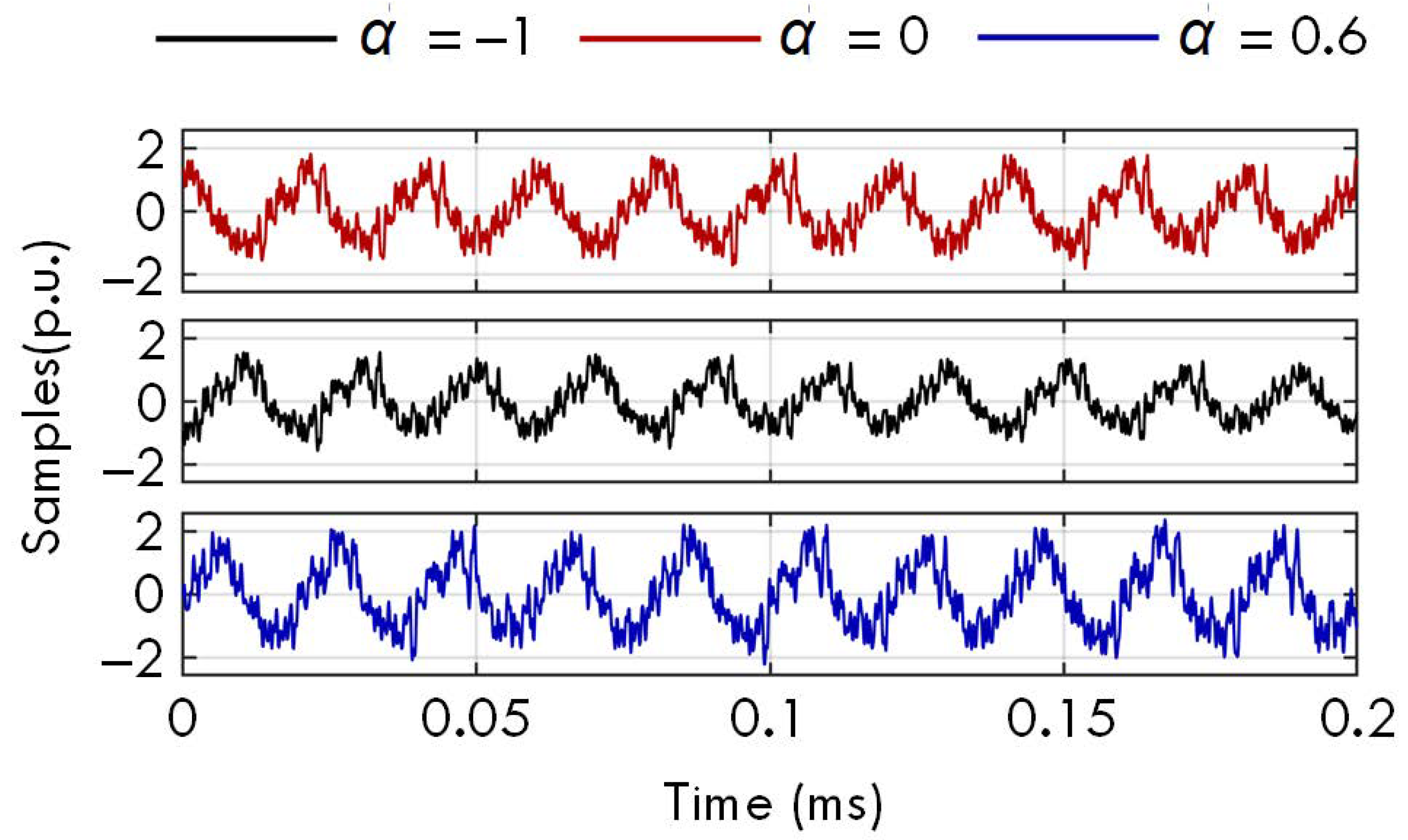
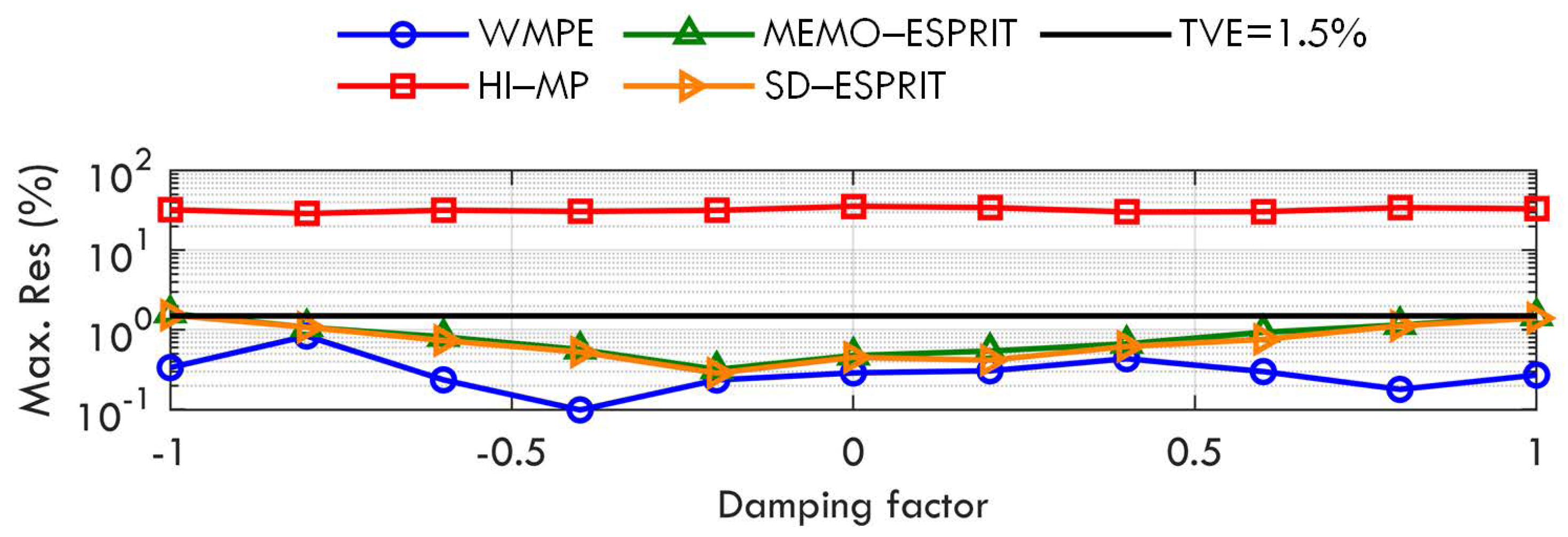
- Case A: Various damping factors
- Case B: Amplitude modulation of fundamental and harmonics
- Case C: Phase modulation of fundamental and harmonics
- Case D: Frequency deviation of fundamental and harmonics
- Case E: Frequency ramp change of fundamental and harmonics
- Case F: Different interharmonic frequency
- Case G: Transient response
4. Experimental Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PMU | Phasor measurement unit |
| FFT | Fast Fourier transform |
| DFT | Discrete Fourier transform |
| LS | Least squares |
| WMPE | Wideband multi-component phasor estimator |
| SVD | Singular value decomposition |
| SNR | Signal–noise ratio |
| Max | Maximum criterion |
| Thr | Threshold method |
| MEMO | Modified exact model order |
| ESPRIT | Estimation of signal parameters using rotational invariance technique |
| HI−MP | Harmonic and interharmonic phasor estimation using matrix pencil |
Appendix A
References
- Cheng, Y.; Fan, L.; Rose, J.; Huang, F.; Schmall, J.; Wang, X.; Xie, X.; Shair, J.; Ramamurthy, J.; Modi, N.; et al. Real-world subsynchronous oscillation events in power grids with high penetrations of inverter-based resources. IEEE Trans. Power Syst. 2023, 38, 316–330. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Xie, X.; Li, H.; Wang, K.; Shi, Z. The effect of different models of closed-loop transfer functions on the inter-harmonic oscillation characteristics of grid-connected PMSG. CSEE J. Power Energy Syst. 2021, 1–8. [Google Scholar] [CrossRef]
- Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. BorWin1-First Experiences with harmonic interactions in converter dominated grids. In Proceedings of the International ETG Congress 2015, Die Energiewende-Blueprints for the New Energy Age, Bonn, Germany, 17–18 November 2015; pp. 1–7. [Google Scholar]
- Chen, B.; Pin, G.; Ng, W.M.; Li, P.; Parisini, T.; Hui, S.Y.R. Online detection of fundamental and interharmonics in AC mains for parallel operation of multiple grid-connected power converters. IEEE Trans. Power Electron. 2018, 33, 9318–9330. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Tiwari, A.; Singh, S.N. Harmonic/Inter-harmonic Estimation: Key Issues and Challenges. In Proceedings of the 2021 IEEE 6th International Conference on Computing, Communication and Automation (ICCCA), Arad, Romania, 17–19 December 2021; pp. 842–853. [Google Scholar]
- Hao, L.; Tianshu, B.; Chang, X.; Xiaolong, G.; Lu, W.; Chuang, C.; Qing, Y.; Jinsong, L. Impacts of subsynchronous and supersynchronous frequency components on synchrophasor measurements. J. Mod. Power Syst. Clean Energy 2016, 4, 362–369. [Google Scholar]
- Chan, S.; Nopphawan, P. Multi-resolution/High-resolution Telemetry Data Sensors for Interharmonic and Oscillation Detection within a Smart Grid Implementation. In Proceedings of the 2020 8th International Conference on Condition Monitoring and Diagnosis (CMD), Phuket, Thailand, 25–28 October 2020; pp. 178–181. [Google Scholar]
- Rupasinghe, J.; Filizadeh, S.; Strunz, K. Assessment of dynamic phasor extraction methods for power system co-simulation applications. Electr. Power Syst. Res. 2021, 197, 107319. [Google Scholar] [CrossRef]
- Chen, L.; Farajollahi, M.; Ghamkhari, M.; Zhao, W.; Huang, S.; Mohsenian-Rad, H. Switch status identification in distribution networks using harmonic synchrophasor measurements. IEEE Trans. Smart Grid 2020, 12, 2413–2424. [Google Scholar] [CrossRef]
- Xie, X.; Zhan, Y.; Shair, J.; Ka, Z.; Chang, X. Identifying the source of subsynchronous control interaction via wide-area monitoring of sub/super-synchronous power flows. IEEE Trans. Power Del. 2019, 35, 2177–2185. [Google Scholar] [CrossRef]
- IEC/IEEE Standard 60255-118-1; Measuring Relays and Protection Equipment-Part 118–1: Synchrophasor for Power System-Measurements. IEEE: New York, NY, USA, 2018.
- Phadke, A.G.; Thorp, J.S.; Adamiak, M.G. A new measurement technique for tracking voltage phasors, local system frequency, and rate of change of frequency. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1025–1038. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy analysis of the multicycle synchrophasor estimator provided by the interpolated DFT algorithm. IEEE Trans. Instrum. Meas. 2013, 62, 942–953. [Google Scholar] [CrossRef]
- Derviškadić, A.; Romano, P.; Paolone, M. Iterative-interpolated DFT for synchrophasor estimation: A single algorithm for P-and M-class compliant PMUs. IEEE Trans. Instrum. Meas. 2017, 67, 547–558. [Google Scholar] [CrossRef]
- Mai, R.; He, Z.; Fu, L.; Kirby, B.; Bo, Z. A dynamic synchrophasor estimation algorithm for online application. IEEE Trans. Power Deliv. 2010, 25, 570–578. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: Theory, implementation, and validation of a PMU prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Petri, D.; Fontanelli, D.; Macii, D. A frequency-domain algorithm for dynamic synchrophasor and frequency estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2330–2340. [Google Scholar] [CrossRef]
- Vejdan, S.; Sanaye-Pasand, M.; Malik, O.P. Accurate dynamic phasor estimation based on the signal model under off-nominal frequency and oscillations. IEEE Trans. Smart Grid 2015, 8, 708–719. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic phasor estimates for power system oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. A real-valued Taylor weighted least squares synchrophasor estimator. In Proceedings of the 2014 IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–6. [Google Scholar]
- Platas-Garza, M.A.; Platas-Garza, J.; de la O Serna, J.A. Dynamic phasor and frequency estimates through maximally flat differentiators. IEEE Trans. Instrum. Meas. 2009, 59, 1803–1811. [Google Scholar] [CrossRef]
- Radulović, M.; Zečević, Ž.; Krstajić, B. Dynamic phasor estimation by symmetric Taylor weighted least square filter. IEEE Trans. Power Deliv. 2019, 35, 828–836. [Google Scholar] [CrossRef]
- Belega, D.; Fontanelli, D.; Petri, D. Dynamic phasor and frequency measurements by an improved Taylor weighted least squares algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 2165–2178. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, F.; Li, S.; Chen, L.; Zhao, W.; Huang, S. A SVD-based synchrophasor estimator for P-class PMUs with improved immune from interharmonic tones. IEEE Access 2021, 9, 151567–151577. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, Q.; Huang, S. Four harmonic analysis and energy metering algorithms based on a new cosine window function. J. Eng. 2017, 2017, 2678–2684. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, F.; Li, S.; Zhao, W.; Chen, L.; Huang, S.; Wang, S.; Li, H. An Optimization of Least-Square Harmonic Phasor Estimators in Presence of Multi-Interference and Harmonic Frequency Variance. Energies 2023, 16, 3397. [Google Scholar] [CrossRef]
- Carta, A.; Locci, N.; Muscas, C. A PMU for the measurement of synchronized harmonic phasors in three-phase distribution networks. IEEE Trans. Instrum. Meas. 2009, 58, 3723–3730. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Tramarin, F. Resolution enhancement in harmonic analysis by compressive sensing. In Proceedings of the 2013 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 25–27 September 2013; pp. 40–45. [Google Scholar]
- Platas-Garza, M.A.; de la O Serna, J.A. Dynamic harmonic analysis through Taylor–Fourier transform. IEEE Trans. Instrum. Meas. 2010, 60, 804–813. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic harmonic analysis with FIR filters designed with O-splines. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 5092–5100. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, Q.; Wang, F.; Huang, S. Dynamic harmonic synchrophasor estimator based on sinc interpolation functions. IEEE Trans. Instrum. Meas. 2018, 68, 3054–3065. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Xie, X.; Zhao, D.; Huang, S. Harmonic phasor estimation based on frequency-domain sampling theorem. IEEE Trans. Instrum. Meas. 2020, 70, 9001210. [Google Scholar] [CrossRef]
- Li, W.; Zhang, G.; Chen, M.; Zhong, H.; Geng, Y. Dynamic harmonic phasor estimator considering frequency deviation. IEEE Sens. J. 2021, 21, 24453–24461. [Google Scholar] [CrossRef]
- Liu, H.; Bi, T.; Li, J.; Xu, S.; Yang, Q. Inter-harmonics monitoring method based on PMUs. IET Gener. Transm. Distrib. 2017, 11, 4414–4421. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Xie, X.; Xiao, X.; Gao, B.; Wang, Y. Interpolated DFT-based identification of sub-synchronous oscillation parameters using synchrophasor data. IEEE Trans. Smart Grid 2019, 11, 2662–2675. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, L.; Wu, R.; Qi, Y.; Liu, H.; Bi, T. Decision Tree Based Subsynchronous Oscillation Detection and Alarm Method Using Phasor Measurement Units. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 2448–2453. [Google Scholar]
- Wu, C.; Sheng, J.; Cheng, G.; Duan, R.; Cheng, M.; Xie, X.; Li, Z. Wide-band phasor measurement unit: Design and test. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1116–1120. [Google Scholar]
- Xie, X.; Liu, H.; Wang, Y.; Xu, Z.; He, J. Measurement of sub-and supersynchronous phasors in power systems with high penetration of renewables. In Proceedings of the 2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Sun, Z.; He, Z.; Zang, T.; Liu, Y. Multi-interharmonic spectrum separation and measurement under asynchronous sampling condition. IEEE Trans. Instrum. Meas. 2016, 65, 1902–1912. [Google Scholar] [CrossRef]
- Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A general noise-resilient technique based on the matrix pencil method for the assessment of harmonics and interharmonics in power systems. IEEE Trans. Power Del. 2016, 32, 2179–2188. [Google Scholar] [CrossRef]
- Bernard, L.; Goondram, S.; Bahrani, B.; Pantelous, A.A.; Razzaghi, R. Harmonic and interharmonic phasor estimation using matrix pencil method for phasor measurement units. IEEE Sens. J. 2020, 21, 945–954. [Google Scholar] [CrossRef]
- Najmeddine, H.; Drissi, K.E.K.; Pasquier, C.; Faure, C.; Kerroum, K.; Jouannet, T.; Michou, M.; Diop, A. Smart metering by using “Matrix Pencil”. In Proceedings of the 2010 9th International Conference on Environment and Electrical Engineering, Prague, Czech Republic, 16–19 May 2010; pp. 238–241. [Google Scholar]
- Song, J.; Zhang, J.; Wen, H. Accurate dynamic phasor estimation by matrix pencil and Taylor weighted least squares method. IEEE Trans. Instrum. Meas. 2021, 70, 9002211. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, F.; Li, S.; Zhao, W.; Huang, S. A Dynamic Wideband Multi-Component Phasor Estimator Using Matrix Theory. In Proceedings of the 2022 International Conference on Smart Grid Synchronized Measurements and Analytics (SGSMA), Split, Croatia, 24–26 May 2022; pp. 1–6. [Google Scholar]
- Jain, S.K.; Jain, P.; Singh, S.N. A fast harmonic phasor measurement method for smart grid applications. IEEE Trans. Smart Grid 2016, 8, 493–502. [Google Scholar] [CrossRef]
- Banerjee, P.; Srivastava, S.C. An effective dynamic current phasor estimator for synchrophasor measurements. IEEE Trans. Instrum. Meas. 2014, 64, 625–637. [Google Scholar] [CrossRef]
- Chen, L.; Xie, X.; Song, M.; Li, Y.; Zhang, Y. Estimation of High-Frequency Oscillations Magnitude and Frequency based on Multi-tone FIR Filter. IEEE Trans. Power Syst. 2022, 38, 528–536. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Tiwari, A.; Singh, N. Harmonic and Interharmonic Estimation using Poincaré Filtering Assisted ESPRIT Method. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022; pp. 1143–1149. [Google Scholar]
- Srivastava, A.K.; Tiwari, A.; Singh, S. Harmonic/interharmonic estimation using standard deviation assisted ESPRIT method. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2021, 40, 1067–1083. [Google Scholar] [CrossRef]




| T2 () | 0.02 | 0.04 | 0.06 | 0.08–0.14 | 0.16 | 0.18 | 0.2 |
| Min | 0.3 | 14.3 | 84.7 | 100.0 | 99.9 | 98.6 | 97.2 |
| Max | 0.3 | 11.7 | 78.9 | 100.0 | 99.8 | 97.1 | 94.9 |
| Thr | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T3 (SNR) | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Min | 80.2 | 99.9 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Max | 72.8 | 99.4 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Thr | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| T4 () | 5 k | 6 k | 7 k | 8 k | 9 k | 10 k | |
| Min | 99.6 | 99.8 | 100.0 | 99.9 | 100.0 | 100.0 | |
| Max | 99.5 | 99.8 | 100.0 | 99.9 | 100.0 | 100.0 | |
| Thr | 0 | 0 | 0 | 0 | 0 | 0 | |
| T5 (c) | 2 | 3 | 4 | 5 | 6 | 7 | |
| Min | 100.0 | 96.1 | 99.9 | 100.0 | 100.0 | 100.0 | |
| Max | 100.0 | 94.0 | 99.3 | 100.0 | 100.0 | 100.0 | |
| Thr | 0 | 0 | 0 | 0 | 0 | 0 |
| Order h | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| WMPE | 58.5 | 58.6 | 58.7 | 57.9 | 58.7 | 57.9 | 58.7 |
| Order h | 8 | 9 | 10 | 11 | 12 | 13 | |
| WMPE | 57.9 | 58.7 | 57.9 | 58.7 | 57.9 | 58.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Li, S.; Wang, F.; Zhao, W.; Huang, S. Estimation of Wideband Multi-Component Phasors Considering Signal Damping. Sensors 2023, 23, 7071. https://doi.org/10.3390/s23167071
Zhao D, Li S, Wang F, Zhao W, Huang S. Estimation of Wideband Multi-Component Phasors Considering Signal Damping. Sensors. 2023; 23(16):7071. https://doi.org/10.3390/s23167071
Chicago/Turabian StyleZhao, Dongfang, Shisong Li, Fuping Wang, Wei Zhao, and Songling Huang. 2023. "Estimation of Wideband Multi-Component Phasors Considering Signal Damping" Sensors 23, no. 16: 7071. https://doi.org/10.3390/s23167071
APA StyleZhao, D., Li, S., Wang, F., Zhao, W., & Huang, S. (2023). Estimation of Wideband Multi-Component Phasors Considering Signal Damping. Sensors, 23(16), 7071. https://doi.org/10.3390/s23167071










