Three-Dimensional Image Transmission of Integral Imaging through Wireless MIMO Channel
Abstract
1. Introduction
2. Related Work
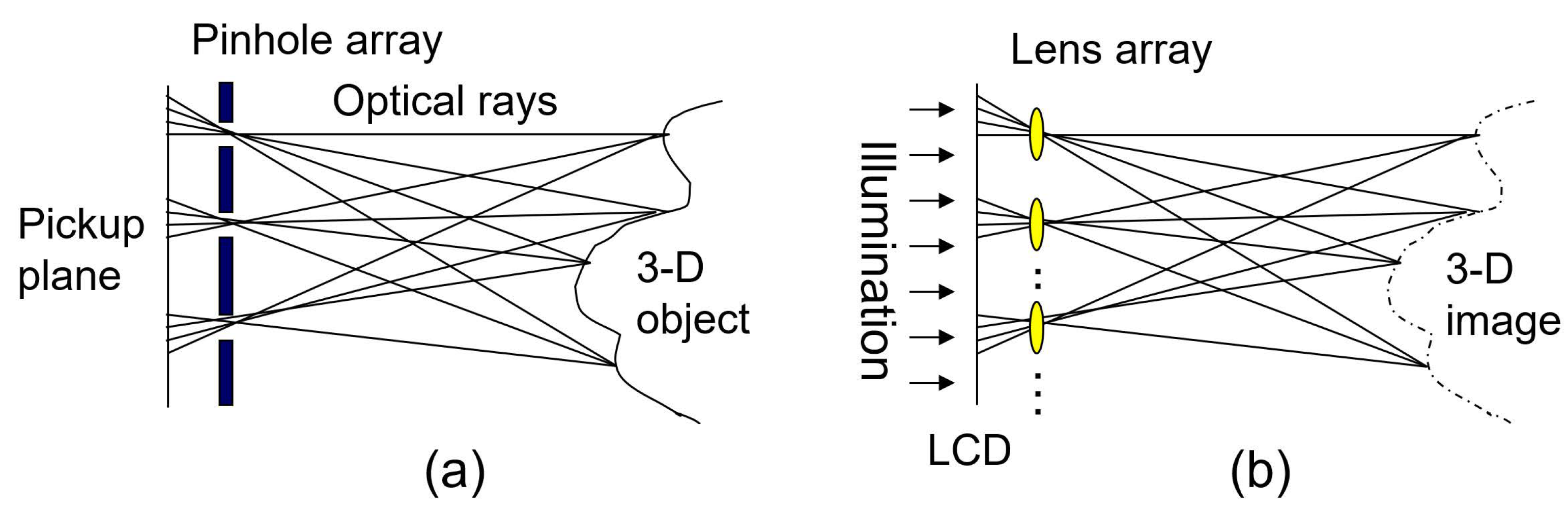
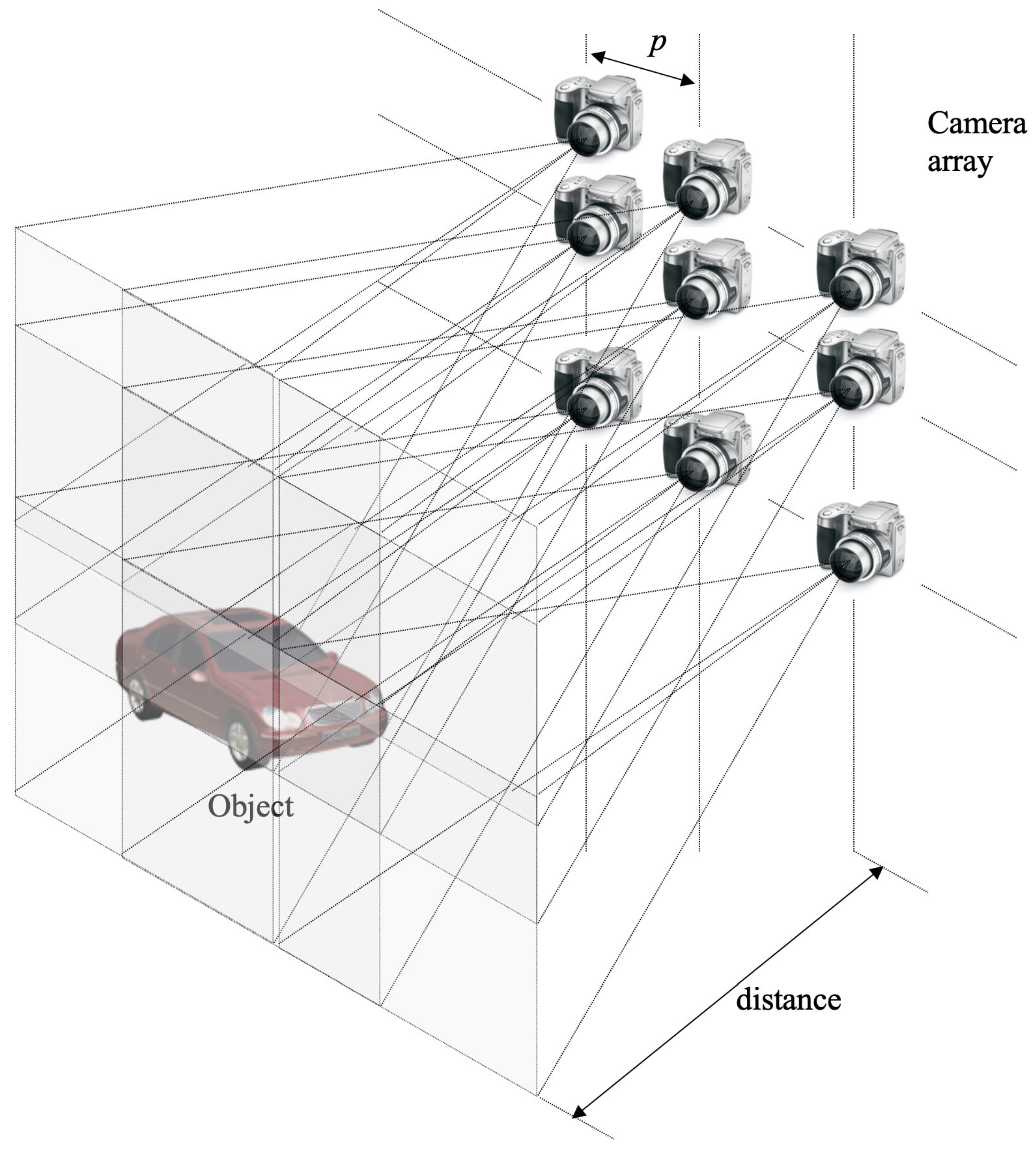
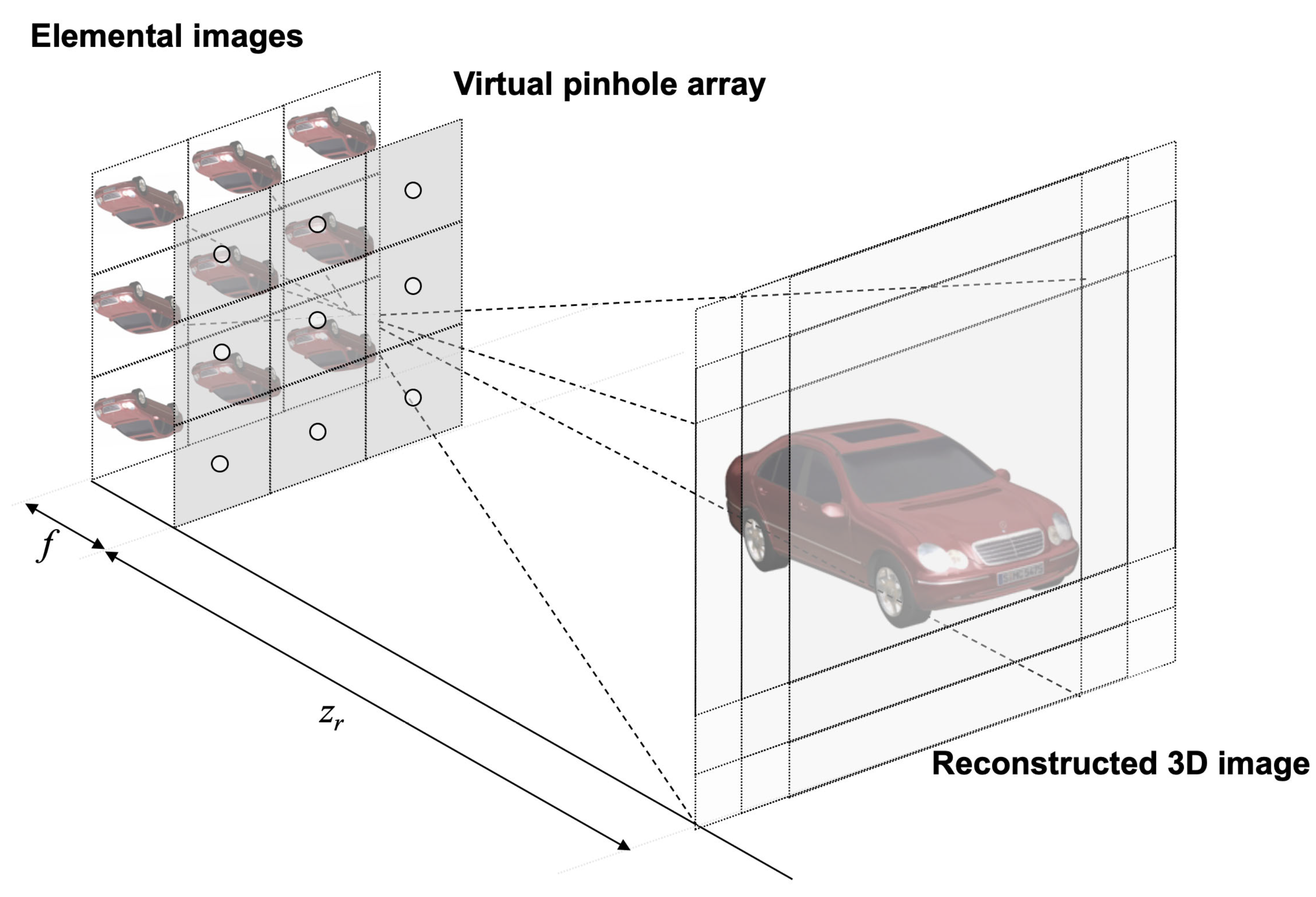
2.1. Integral Imaging
2.2. MIMO Technique
3. Wireless 3D Image Transmission System over MIMO Channel
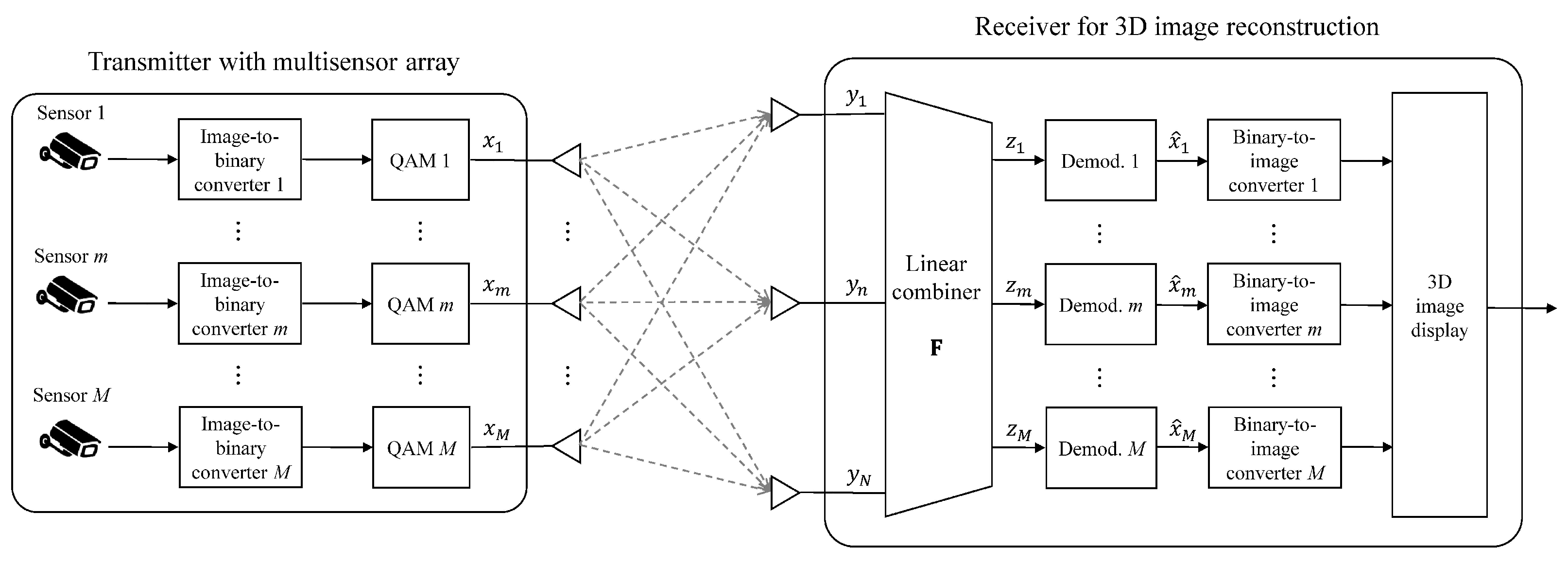
3.1. Wireless 3D Image Transmission System
3.2. Discussion on the Linear Combiners
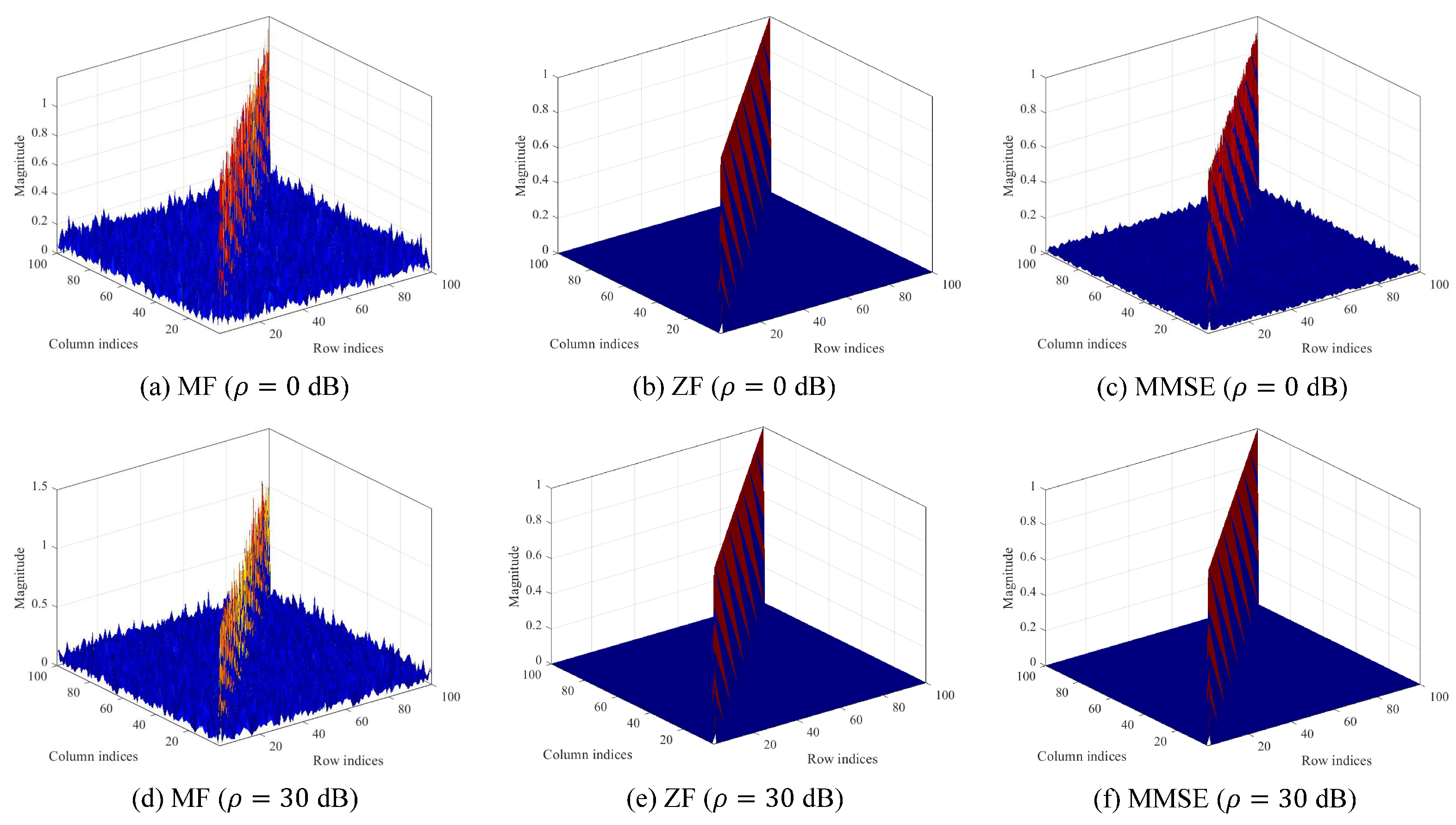
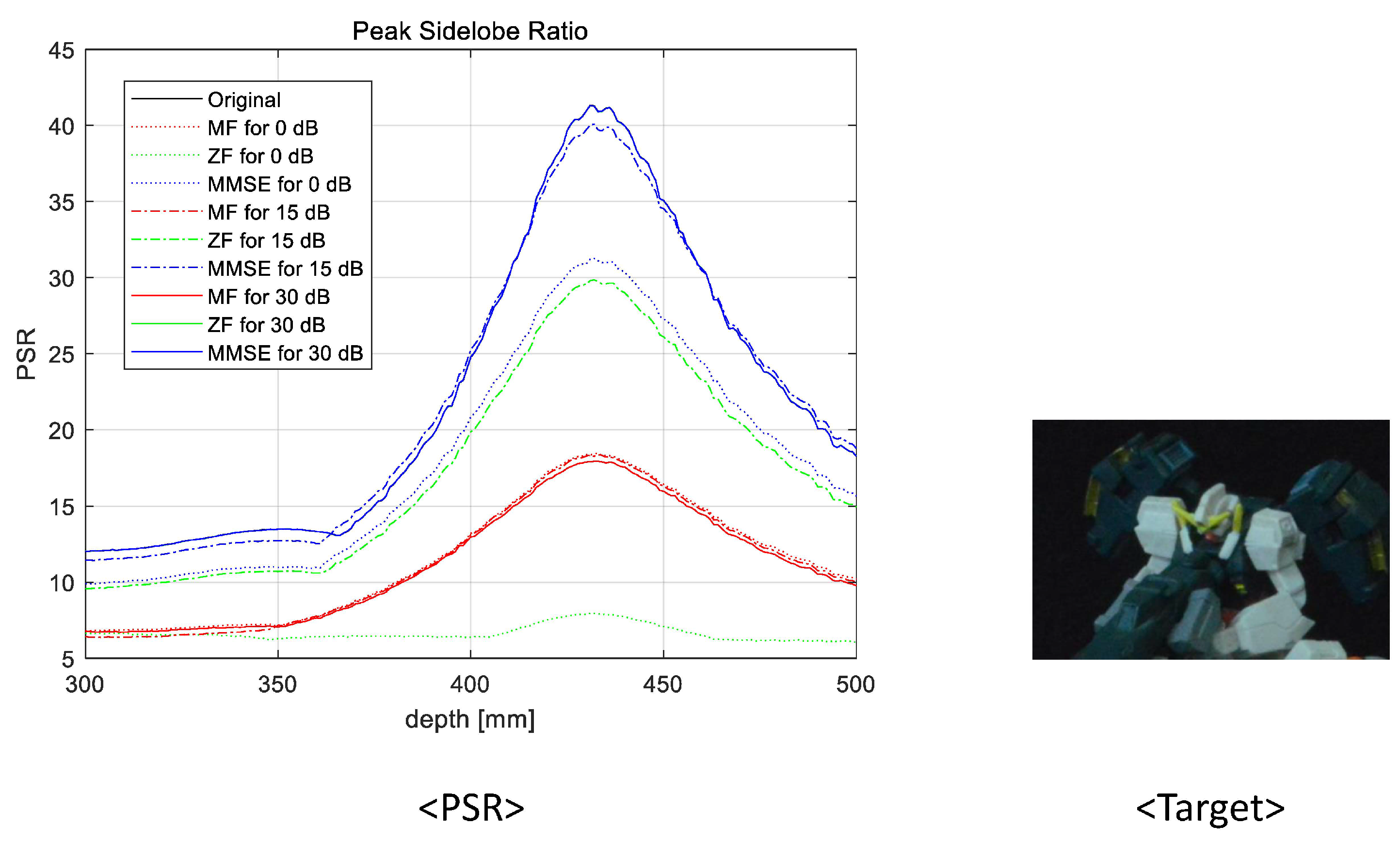
4. Experimental Results
4.1. Experimental Setup
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| AR | Augmented reality |
| AWGN | Additive white Gaussian noise |
| CSI | Channel state information |
| MALT | Moving array lenslet technique |
| MF | Matched filter |
| MIMO | Multiple-input multiple-output |
| ML | Maximum likelihood |
| MMSE | Minimum mean squared error |
| PSR | Peak sidelobe ratio |
| QAM | Quadrature amplitude modulation |
| SAII | Synthetic aperture integral imaging |
| SINR | Signal-to-interference-plus-noise ratio |
| SNR | Signal-to-noise ratio |
| V-BLAST | Vertical Bell Laboratories layered space–time |
| VCR | Volumetric computational reconstruction |
| VR | Virtual reality |
| ZF | Zero forcing |
References
- Lippmann, G. La Photographie Integrale. Comp. Rend. Acad. Sci. 1908, 146, 446–451. [Google Scholar]
- Arai, J.; Okano, F.; Hoshino, H.; Yuyama, I. Gradient index lens array method based on real time integral photography for three dimensional images. Appl. Opt. 1998, 37, 2034–2045. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Corral, M.; Javidi, B. Fundamentals of 3D imaging and displays: A tutorial on integral imaging, light-field, and plenoptic systems. Adv. Opt. Photon. 2018, 10, 512–566. [Google Scholar] [CrossRef]
- Xiao, X.; Daneshpanah, M.; Cho, M.; Javidi, B. 3D integral imaging using sparse sensors with unknown positions. IEEE J. Display Technol. 2010, 6, 614–619. [Google Scholar] [CrossRef]
- Cho, M.; Javidi, B. Optimization of 3D integral imaging system parameters. IEEE J. Disp. Technol. 2012, 8, 357–360. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Improved viewing resolution of three-dimensional integral imaging by use of nonstationary micro-optics. Opt. Lett. 2002, 27, 324–326. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Three-dimensional synthetic aperture integral imaging. Opt. Lett. 2002, 27, 1144–1146. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cho, M. Three-Dimensional Integral Imaging with Enhanced Lateral and Longitudinal Resolutions Using Multiple Pickup Positions. Sensors 2022, 22, 9199. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Improvement of viewing angle in integral imaging by use of moving lenslet arrays with low fill factor. Appl. Opt. 2003, 42, 1996–2002. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Large depth-of-focus time-multiplexed three-dimensional integral imaging by use of lenslets with nonuniform focal lengths and aperture sizes. Opt. Lett. 2003, 28, 1924–1926. [Google Scholar] [CrossRef]
- Cho, B.; Kopycki, P.; Martinez-Corral, M.; Cho, M. Computational volumetric reconstruction of integral imaging with improved depth resolution considering continuously non-uniform shifting pixels. Opt. Laser Eng. 2018, 111, 114–121. [Google Scholar] [CrossRef]
- Inoue, K.; Cho, M. Fourier focusing in integral imaging with optimum visualization pixels. Opt. Laser Eng. 2020, 127, 105952. [Google Scholar] [CrossRef]
- Bae, J.; Yoo, H. Image Enhancement for Computational Integral Imaging Reconstruction via Four-Dimensional Image Structure. Sensors 2020, 20, 4795. [Google Scholar] [CrossRef]
- Charfi, Y.; Wakamiya, N.; Murata, M. Challenging issues in visual sensor networks. IEEE Wireless Commun. 2009, 16, 44–49. [Google Scholar] [CrossRef]
- Yeo, C.; Ramchandran, K. Robust distributed multiview video compression for wireless camera networks. IEEE Trans. Image Process. 2010, 19, 995–1008. [Google Scholar] [PubMed]
- Ye, Y.; Ci, S.; Katsaggelos, A.K.; Liu, Y.; Qian, Y. Wireless video surveillance: A survey. IEEE Access 2013, 1, 646–660. [Google Scholar]
- Kodera, S.; Fujihashi, T.; Saruwatari, S.; Watanabe, T. Multi-view video streaming with mobile cameras. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 12 December 2014. [Google Scholar]
- Nu, T.T.; Fujihashi, T.; Watanabe, T. Power-efficient video uploading for crowdsourced multi-view video streaming. In Proceedings of the 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
- Foschini, G.J.; Gans, M.J. On limits of wireless communications in a fading environment when using multiple antennas. Wireless Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Telatar, E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjöland, H.; Tufvesson, F. 6G wireless systems: Vision, requirements, challenges, insights, and opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Wolniansky, P.W.; Foschini, G.J.; Golden, G.D.; Valenzuela, R.A. V-BLAST: An architecture for realizing very high data rates over the rich-scattering wireless channel. In Proceedings of the URSI International Symposium on Signals, Systems, and Electronics, Pisa, Italy, 2 October 1998. [Google Scholar]
- Verdú, S. Multiuser Detection; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Lupas, R.; Verdú, S. Linear multiuser detectors for synchronous code-division multiple-access channels. IEEE Trans. Inform. Theory 1989, 35, 123–136. [Google Scholar] [CrossRef]
- Madhow, U.; Honig, M.L. MMSE interference suppression for direct-sequence spread-spectrum CDMA. IEEE Trans. Commun. 1994, 42, 3178–3188. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Lim, Y.-G.; Chae, C.-B.; Caire, G. Performance Analysis of Massive MIMO for Cell-Boundary Users. IEEE Trans. Wireless Commun. 2015, 14, 6827–6842. [Google Scholar] [CrossRef]
- Javidi, B. Nonlinear joint power spectrum based optical correlation. Appl. Opt. 1989, 28, 2358–2367. [Google Scholar] [CrossRef]
- Cho, M.; Mahalanobis, A.; Javidi, B. 3D passive photon counting automatic target recognition using advanced correlation filters. Opt. Lett. 2011, 36, 861–863. [Google Scholar] [CrossRef] [PubMed]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, S.-C.; Cho, M. Three-Dimensional Image Transmission of Integral Imaging through Wireless MIMO Channel. Sensors 2023, 23, 6154. https://doi.org/10.3390/s23136154
Lim S-C, Cho M. Three-Dimensional Image Transmission of Integral Imaging through Wireless MIMO Channel. Sensors. 2023; 23(13):6154. https://doi.org/10.3390/s23136154
Chicago/Turabian StyleLim, Seung-Chan, and Myungjin Cho. 2023. "Three-Dimensional Image Transmission of Integral Imaging through Wireless MIMO Channel" Sensors 23, no. 13: 6154. https://doi.org/10.3390/s23136154
APA StyleLim, S.-C., & Cho, M. (2023). Three-Dimensional Image Transmission of Integral Imaging through Wireless MIMO Channel. Sensors, 23(13), 6154. https://doi.org/10.3390/s23136154





