Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site
Abstract
1. Introduction
2. Materials and Methods
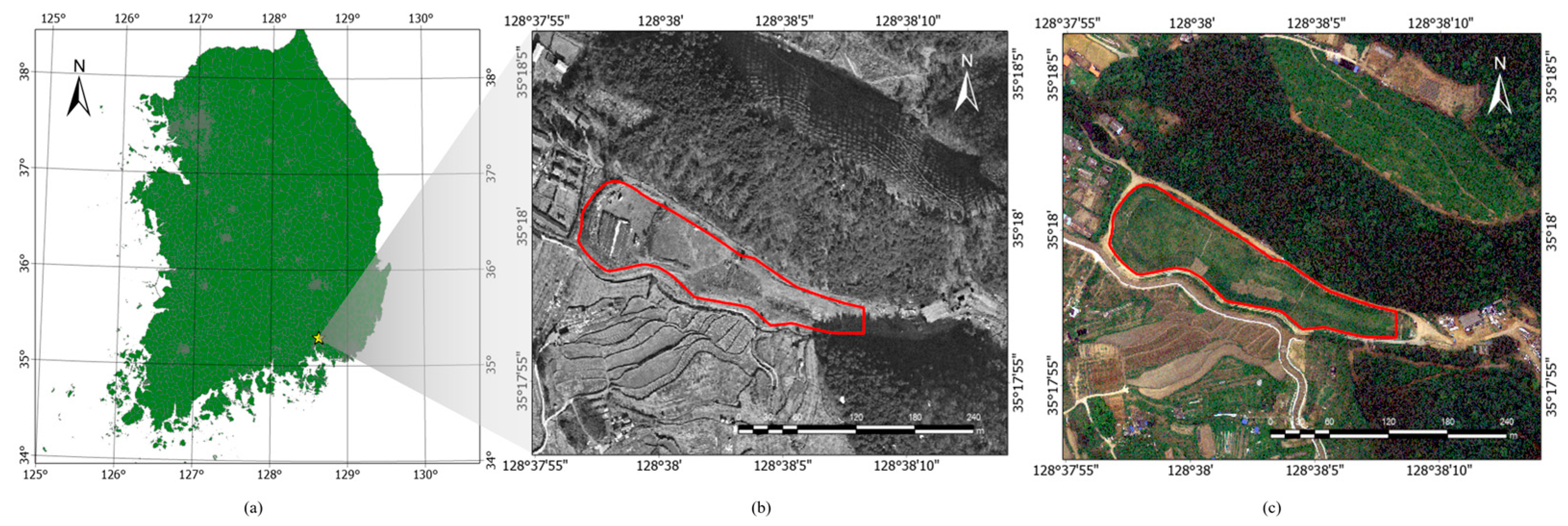
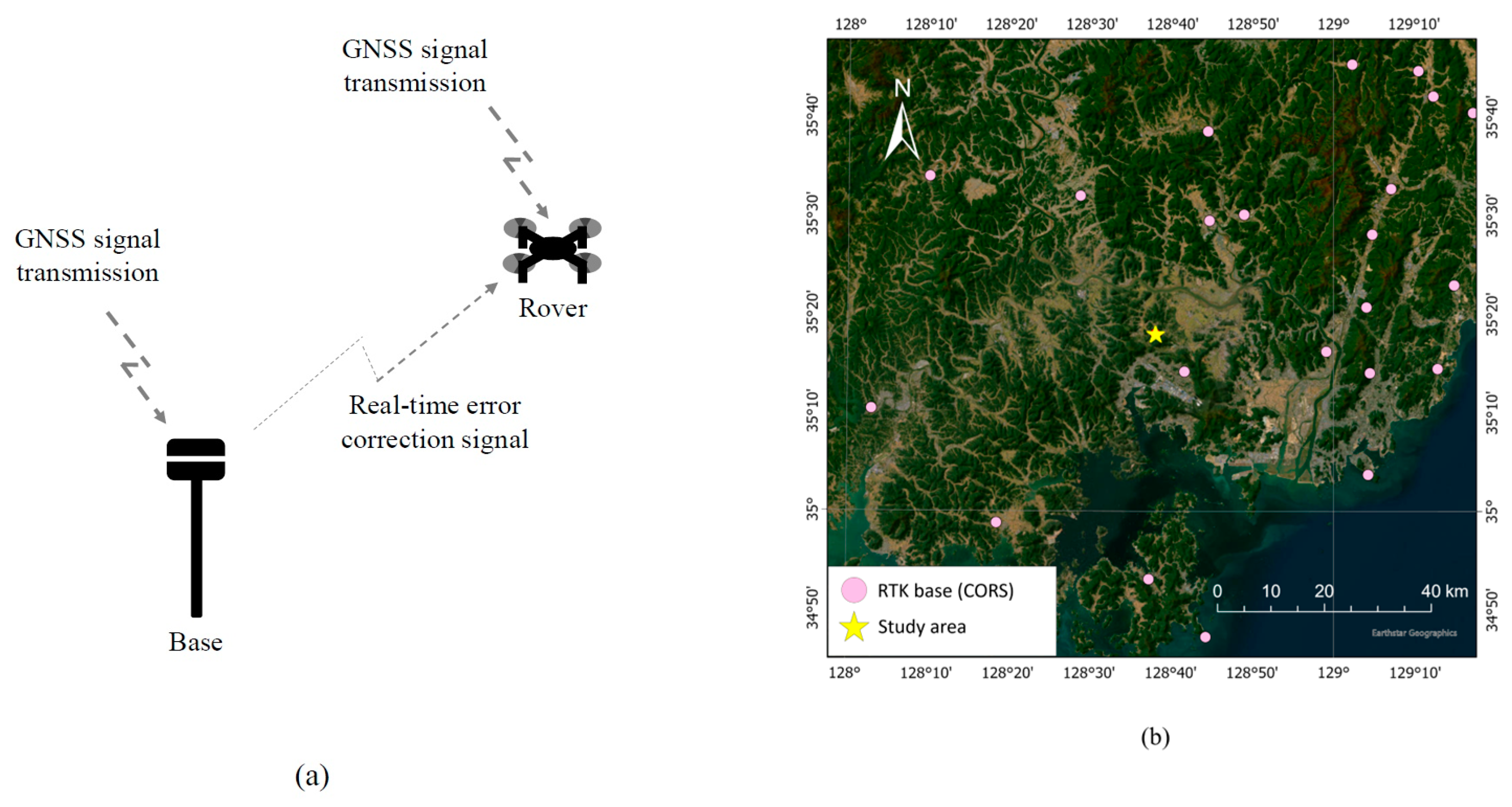
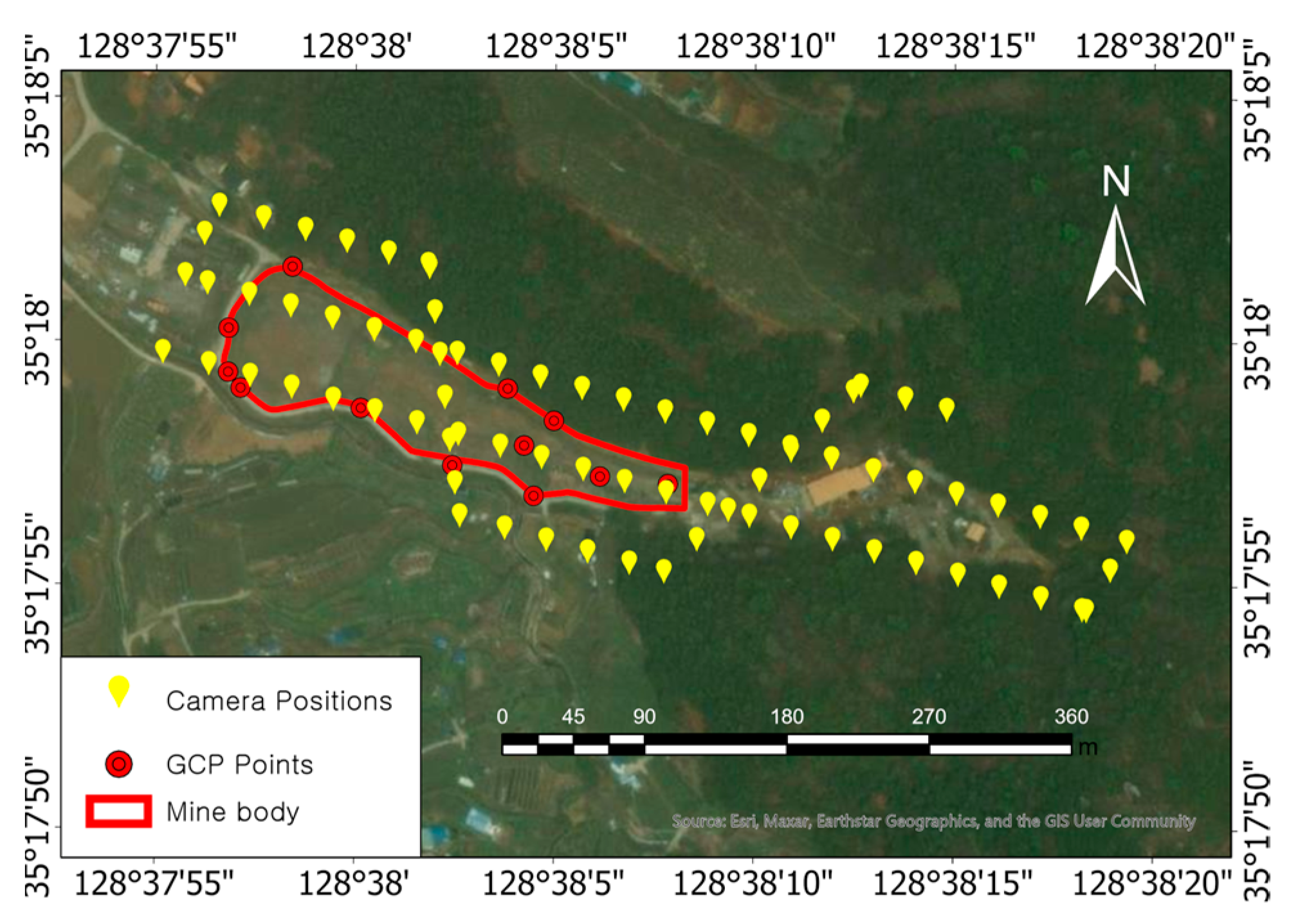
2.1. Study Area
2.2. Applied Positioning Method
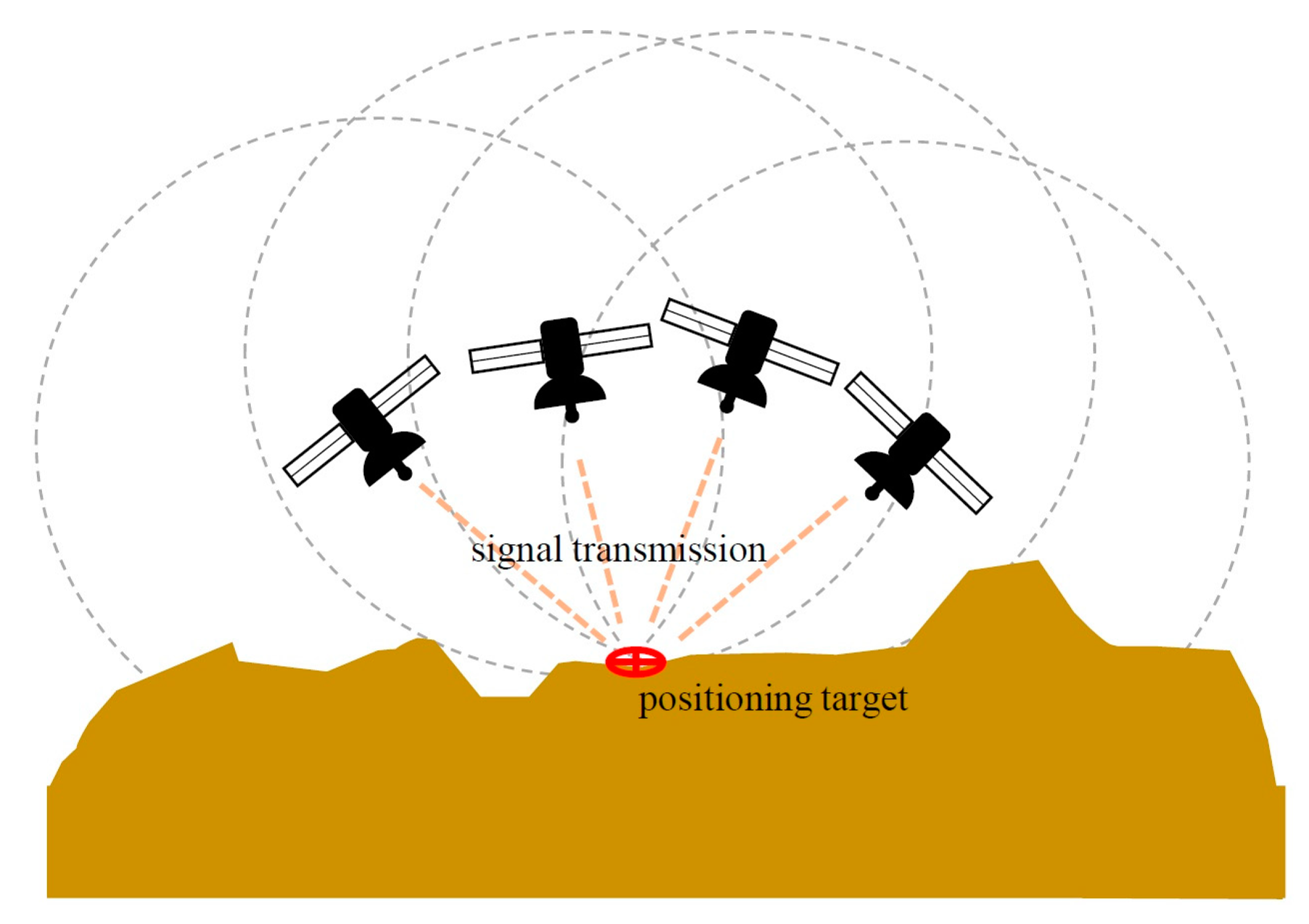
2.2.1. Standalone GNSS Positioning
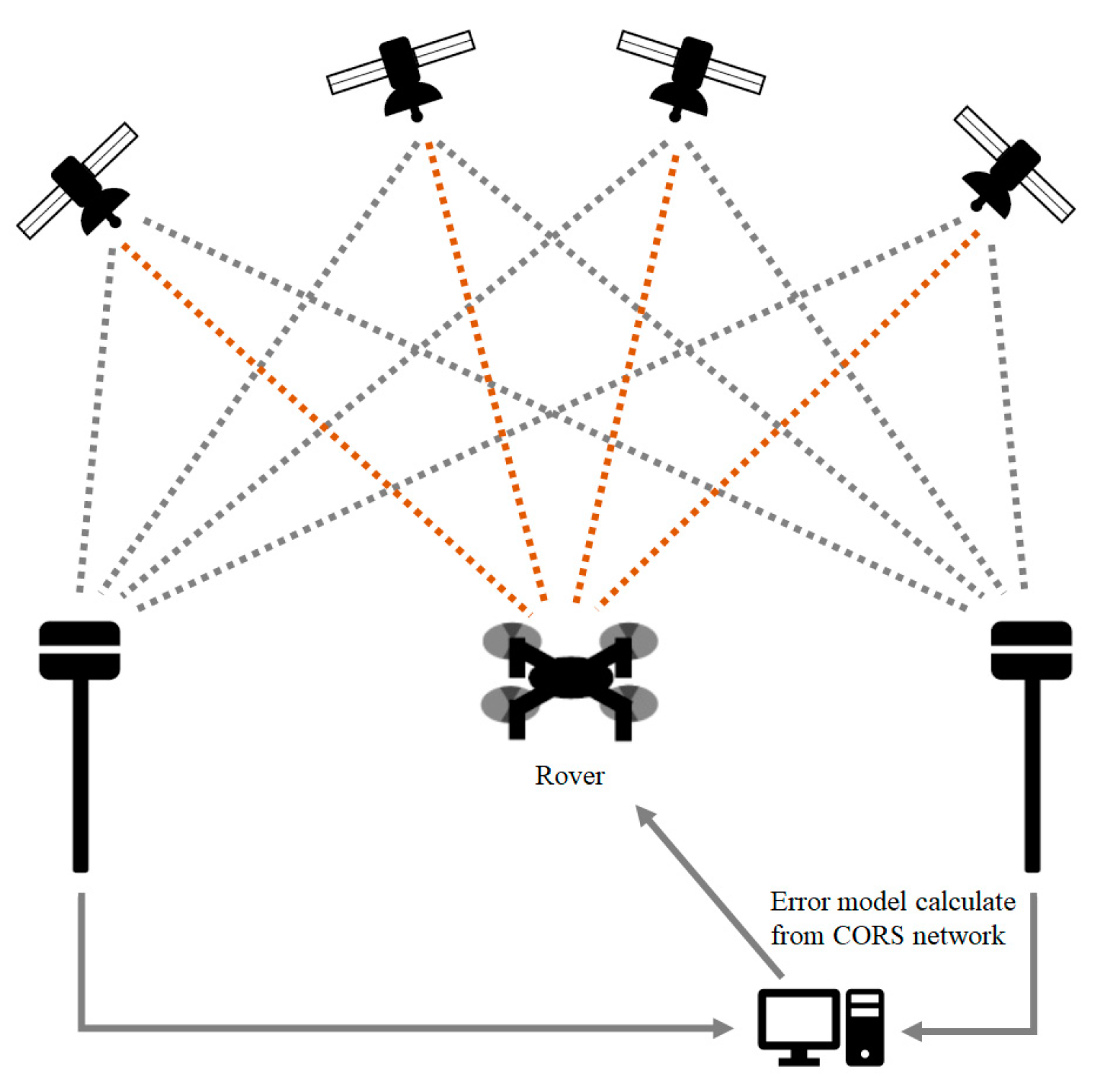
2.2.2. Differential (RTK) GNSS Positioning
2.2.3. Post-Mission PPP Processing
2.3. UAV Data Acquisition
2.4. UAV Image Processing
2.5. Ground Control Point Measurement
2.6. Accuracy Evaluation
2.6.1. Relative Camera Location Accuracy Assessment
2.6.2. GCP-Based Mapping Accuracy Assessment
2.6.3. Comparison of Areal and Volumetric Differences of Mine Tailings
3. Results
3.1. UAV Data Acquisition and Image Processing
3.2. GCP Measurement
3.3. Accuracy Assessment
3.3.1. Estimation of Relative Camera Location Error
3.3.2. Estimation of GCP-Based Image Mapping Error
3.3.3. Areal and Volumetric Differences of Mine Tailings Using Different GNSS Positioning Techniques
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Parkinson, B.W.; Stansell, T.; Beard, R.; Gromov, K. A history of satellite navigation. Navigation 1995, 42, 109–164. [Google Scholar] [CrossRef]
- Parkinson, B.W.; Enge, P.K.; Spilker, J. Differential GPS. Prog. Astronaut. Aeronaut. Glob. Position. Syst. Theory Appl. 1996, 2, 3–32. [Google Scholar]
- Park, K.W.; Park, J.-I.; Park, C. Efficient Methods of Utilizing Multi-SBAS Corrections in Multi-GNSS Positioning. Sensors 2020, 20, 256. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS Precise Point Positioning with a Difference. Natural Resources Canada, Geomatics Canada, Geodetic Survey Division Ottawa: Ottawa, ON, Canada, 1995. [Google Scholar]
- Shahmoradi, J.; Talebi, E.; Roghanchi, P.; Hassanalian, M. A comprehensive review of applications of drone technology in the mining industry. Drones 2020, 4, 34. [Google Scholar]
- Ren, H.; Zhao, Y.; Xiao, W.; Hu, Z. A review of UAV monitoring in mining areas: Current status and future perspectives. Int. J. Coal Sci. Technol. 2019, 6, 320–333. [Google Scholar] [CrossRef]
- Lee, I.-S.; Ge, L. The performance of RTK-GPS for surveying under challenging environmental conditions. Earth Planets Space 2006, 58, 515–522. [Google Scholar]
- Peppa, M.; Hall, J.; Goodyear, J.; Mills, J. Photogrammetric assessment and comparison of DJI Phantom 4 pro and phantom 4 RTK small unmanned aircraft systems. In Proceedings of the ISPRS Geospatial Week 2019, Enschede, The Netherlands, 10–14 June 2019. [Google Scholar]
- Czyża, S.; Szuniewicz, K.; Kowalczyk, K.; Dumalski, A.; Ogrodniczak, M.; Zieleniewicz, Ł. Assessment of Accuracy in Unmanned Aerial Vehicle (UAV) Pose Estimation with the REAL-Time Kinematic (RTK) Method on the Example of DJI Matrice 300 RTK. Sensors 2023, 23, 2092. [Google Scholar] [PubMed]
- Alkan, R.M.; Erol, S.; Ozulu, I.M.; Ilci, V. Accuracy comparison of post-processed PPP and real-time absolute positioning techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
- Qafisheh, M.; Martín, A.; Capilla, R.M.; Anquela, A.B. SVR and ARIMA models as machine learning solutions for solving the latency problem in real-time clock corrections. GPS Solut. 2022, 26, 85. [Google Scholar] [CrossRef]
- Ocalan, T.; Turk, T.; Tunalioglu, N.; Gurturk, M. Investigation of accuracy of PPP and PPP-AR methods for direct georeferencing in UAV photogrammetry. Earth Sci. Inform. 2022, 15, 2231–2238. [Google Scholar]
- Transportation Research Board. Available online: https://trid.trb.org/view/788289 (accessed on 11 March 2022).
- Moon, Y.; Song, Y.; Moon, H.-S. The potential acid-producing capacity and factors controlling oxidation tailings in the Guryong mine, Korea. Environ. Geol. 2008, 53, 1787–1797. [Google Scholar]
- Moon, Y.; Zhang, Y.-S.; Sonn, Y.-K.; Hyun, B.-K.; Song, Y.; Moon, H.-S. Mineralogical characterization related to physico-chemical conditions in the pyrite-rich tailings in Guryong Mine, Korea. Soil Sci. Plant Nutr. 2013, 59, 509–521. [Google Scholar] [CrossRef]
- Kim, J.; Koo, S.-Y.; Kim, J.-Y.; Lee, E.-H.; Lee, S.-D.; Ko, K.-S.; Ko, D.-C.; Cho, K.-S. Influence of acid mine drainage on microbial communities in stream and groundwater samples at Guryong Mine, South Korea. Environ. Geol. 2009, 58, 1567–1574. [Google Scholar] [CrossRef]
- Dawoud, S. GNSS Principles and Comparison; Potsdam University: Brandenburg, Germany, 2012. [Google Scholar]
- Jing, H.; Gao, Y.; Shahbeigi, S.; Dianati, M. Integrity monitoring of GNSS/INS based positioning systems for autonomous vehicles: State-of-the-art and open challenges. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14166–14187. [Google Scholar]
- De Angelis, G.; Baruffa, G.; Cacopardi, S. GNSS/cellular hybrid positioning system for mobile users in urban scenarios. IEEE Trans. Intell. Transp. Syst. 2012, 14, 313–321. [Google Scholar] [CrossRef]
- Karaim, M.; Elsheikh, M.; Noureldin, A. GNSS error sources. In Multifunctional Operation and Application of GPS; InTech: London, UK, 2018. [Google Scholar]
- European GNSS Agency. PPP-RTK Market and Technology Report; European GNSS Agency: Prague, Czech Republic, 2019. [Google Scholar]
- Zhao, S.; Cui, X.; Guan, F.; Lu, M. A Kalman filter-based short baseline RTK algorithm for single-frequency combination of GPS and BDS. Sensors 2014, 14, 15415–15433. [Google Scholar] [CrossRef]
- Schloderer, G.; Bingham, M.; Awange, J.L.; Fleming, K.M. Application of GNSS-RTK derived topographical maps for rapid environmental monitoring: A case study of Jack Finnery Lake (Perth, Australia). Environ. Monit. Assess. 2011, 180, 147–161. [Google Scholar] [CrossRef] [PubMed]
- Nugraha, W.; Parapat, A.D.; Arum, D.S.; Istighfarini, F. GNSS RTK application to determine coastline case study at northen area of Sulawesi and Gorontalo. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2019; p. 01016. [Google Scholar]
- Pirti, A. Evaluating the usage of RTK GPS Technique in the control of highway geometry. Geod. List 2008, 62, 237–248. [Google Scholar]
- Gerke, M.; Przybilla, H.-J. Accuracy analysis of photogrammetric UAV image blocks: Influence of onboard RTK-GNSS and cross flight patterns. Photogramm. Fernerkund. Geoinf. (PFG) 2016, 1, 17–30. [Google Scholar] [CrossRef]
- Hill, A.C.; Limp, F.; Casana, J.; Laugier, E.J.; Williamson, M. A new era in spatial data recording: Low-cost GNSS. Adv. Archaeol. Pract. 2019, 7, 169–177. [Google Scholar] [CrossRef]
- Hussain, A.; Ahmed, A.; Magsi, H.; Tiwari, R. Adaptive GNSS receiver design for highly dynamic multipath environments. IEEE Access 2020, 8, 172481–172497. [Google Scholar] [CrossRef]
- Real Time Kinematics. Available online: https://gssc.esa.int/navipedia/index.php/Real_Time_Kinematics (accessed on 14 July 2022).
- MakeItAccurate. Available online: https://www.makeitaccurate.com/ (accessed on 11 March 2022).
- Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 8, 893–904. [Google Scholar] [CrossRef]
- Wang, G. Millimeter-accuracy GPS landslide monitoring using Precise Point Positioning with Single Receiver Phase Ambiguity (PPP-SRPA) resolution: A case study in Puerto Rico. J. Geod. Sci. 2013, 3, 22–31. [Google Scholar] [CrossRef]
- Scopus. Available online: https://www.scopus.com/ (accessed on 6 January 2023).
- DJI. Available online: https://www.dji.com/phantom-4-rtk/info#specs/ (accessed on 1 July 2022).
- Agisoft, L. Agisoft Metashape User Manual: Professional Edition. Version 2019, 1, 138. [Google Scholar]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; Morra di Cella, U.; Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with on-board RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Elkhrachy, I. Accuracy assessment of low-cost unmanned aerial vehicle (UAV) photogrammetry. Alex. Eng. J. 2021, 60, 5579–5590. [Google Scholar]
- Emlid. Available online: https://emlid.com/reachrs2plus/ (accessed on 5 July 2022).
- Hyun, C.-U.; Kim, J.-H.; Han, H.; Kim, H.-C. Mosaicking Opportunistically Acquired very High-Resolution Helicopter-Borne Images over Drifting Sea Ice Using COTS Sensors. Sensors 2019, 19, 1251. [Google Scholar] [CrossRef]
- Yilmaz, V.; Konakoglu, B.; Serifoglu, C.; Gungor, O.; Gökalp, E. Image classification-based ground filtering of point clouds extracted from UAV-based aerial photos. Geocarto Int. 2018, 33, 310–320. [Google Scholar] [CrossRef]
- Karney, C. Transverse Mercator with an accuracy of a few nanometers. J. Geod. 2011, 85, 475–485. [Google Scholar] [CrossRef]
- Kwon, J. Korea Geodetic Framework for Sustainable Development. In Proceedings of the Nineteenth United Nations Regional Cartographic Conference for Asia and the Pacific, Bangkok, Thailand, 29 October–1 November 2012; United Nations: New York, NY, USA, 2012. [Google Scholar]
- Cracknell, M.J.; Nascimento, S.C.; Heng, W.X.; Parbhakar-Fox, A.; Schaap, T.A. Geophysical investigation of mine waste in the King River Delta, Macquarie Harbour, Tasmania. ASEG Ext. Abstr. 2019, 2019, 1–4. [Google Scholar] [CrossRef]
- Parviainen, A.; Soto, F.; Caraballo, M.A. Revalorization of Haveri Au-Cu mine tailings (SW Finland) for potential reprocessing. J. Geochem. Explor. 2020, 218, 106614. [Google Scholar]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS precise point positioning for UAV photogrammetry. Photogramm. Rec. 2018, 33, 427–447. [Google Scholar]
- Yeh, M.; Chou, Y.; Yang, L. The Evaluation of GPS techniques for UAV-based Photogrammetry in Urban Area. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016 XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016; Volume 41. [Google Scholar]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure-from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dyn. 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Xu, C.-H.; Wang, J.-L.; Gao, J.-X.; Jian, W.; Hong, H. Precise point positioning and its application in mining deformation monitoring. Trans. Nonferrous Met. Soc. China 2011, 21, s499–s505. [Google Scholar] [CrossRef]
- Fraser, R.H.; Pouliot, D.; van der Sluijs, J. UAV and high resolution satellite mapping of Forage Lichen (Cladonia spp.) in a Rocky Canadian Shield Landscape. Can. J. Remote Sens. 2022, 48, 5–18. [Google Scholar]




| Equipment | Category | Specifications |
|---|---|---|
| UAV | Model | DJI Phantom 4 RTK |
| Imaging sensor | 20 mega pixels | |
| GNSS positioning accuracy in RTK mode | Vertical 1.5 cm and 1 ppm (RMS), horizontal 1 cm and 1 ppm (RMS) |
| Equipment | Category | Specifications |
|---|---|---|
| Network RTK GNSS receiver | Model | Emlid Reach RS2 |
| Positioning accuracy in RTK mode | Vertical 1.4 cm and 1 ppm (RMS), Horizontal 0.7 cm and 1 ppm (RMS) |
| Category | Specifications |
|---|---|
| Number of UAV image datasets | Three flights using network RTK GNSS positionings (RTK1, RTK2, and RTK3), three flights using standalone GNSS positioning (GNSS1, GNSS2, and GNSS3), and three post-mission processing datasets using PPP positioning on images with standalone GNSS positioning (PPP1, PPP2, and PPP3) |
| Number of images acquired per flight | 77 |
| Flight height | 110 m above ground level at starting point of flights |
| Flight duration | 4 min, 57–59 s |
| Forward overlap | 75% |
| Side overlap | 70% |
| Number of images used for image mosaicking | 73 |
| Category | Specifications |
|---|---|
| Number of GCPs | 12 |
| Number of measurements for averaging | 5 |
| Case | X (cm) | Y (cm) | Z (cm) | XY Error (cm) | Total Error (cm) |
|---|---|---|---|---|---|
| RTK1 | 0.4 | 0.6 | 2.0 | 0.7 | 2.1 |
| RTK2 | 0.5 | 0.4 | 1.3 | 0.6 | 1.4 |
| RTK3 | 0.4 | 0.3 | 1.2 | 0.5 | 1.3 |
| GNSS1 | 20.0 | 25.0 | 117.7 | 32.0 | 122.0 |
| GNSS2 | 9.8 | 15.2 | 107.9 | 18.1 | 109.4 |
| GNSS3 | 15.2 | 21.2 | 101.6 | 26.0 | 104.9 |
| PPP1 | 3.1 | 3.1 | 26.2 | 4.4 | 26.6 |
| PPP2 | 4.1 | 2.3 | 26.8 | 4.8 | 27.2 |
| PPP3 | 13.4 | 8.0 | 49.9 | 15.6 | 52.2 |
| Case | X (cm) | Y (cm) | Z (cm) | XY Error (cm) | Total Error (cm) |
|---|---|---|---|---|---|
| RTK1 | 8.5 | 6.1 | 36.4 | 11.0 | 38.3 |
| RTK2 | 5.3 | 4.6 | 34.7 | 7.9 | 36.1 |
| RTK3 | 4.3 | 4.8 | 17.7 | 7.2 | 19.6 |
| GNSS1 | 149.3 | 28.3 | 396.0 | 155.1 | 434.9 |
| GNSS2 | 152.1 | 51.6 | 230.9 | 168.2 | 303.5 |
| GNSS3 | 137.1 | 82.4 | 133.3 | 169.0 | 227.0 |
| PPP1 | 81.7 | 35.1 | 155.6 | 89.4 | 181.3 |
| PPP2 | 64.5 | 10.0 | 73.7 | 65.5 | 102.0 |
| PPP3 | 102.0 | 14.6 | 32.2 | 103.5 | 109.8 |
| Case | 2D Area (m2) | Surface Area (m2) | Volume (m3) | Difference from RTK1 Volume (%) |
|---|---|---|---|---|
| RTK1 | 16,129.5 | 17,071.6 | 52,482.4 | - |
| RTK2 | 16,128.0 | 17,083.8 | 52,279.0 | −0.4 |
| RTK3 | 16,130.2 | 17,136.4 | 52,466.6 | 0.0 |
| GNSS1 | 16,129.4 | 17,063.0 | 71,291.4 | 35.8 |
| GNSS2 | 16,122.7 | 17,068.7 | 72,125.1 | 37.4 |
| GNSS3 | 16,131.7 | 17,120.0 | 68,582.1 | 30.7 |
| PPP1 | 16,125.6 | 17,041.6 | 57,540.4 | 9.6 |
| PPP2 | 16,125.6 | 17,058.4 | 58,542.2 | 11.6 |
| PPP3 | 16,128.9 | 17,114.2 | 65,139.2 | 24.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Hyun, C.-U.; Park, H.-D.; Cha, J. Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site. Sensors 2023, 23, 5858. https://doi.org/10.3390/s23135858
Kim H, Hyun C-U, Park H-D, Cha J. Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site. Sensors. 2023; 23(13):5858. https://doi.org/10.3390/s23135858
Chicago/Turabian StyleKim, Hanjin, Chang-Uk Hyun, Hyeong-Dong Park, and Jongmun Cha. 2023. "Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site" Sensors 23, no. 13: 5858. https://doi.org/10.3390/s23135858
APA StyleKim, H., Hyun, C.-U., Park, H.-D., & Cha, J. (2023). Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site. Sensors, 23(13), 5858. https://doi.org/10.3390/s23135858









