Metaheuristic for Optimal Dynamic K-Coloring Application on Band Sharing for Automotive Radars
Abstract
1. Introduction
2. State of the Art
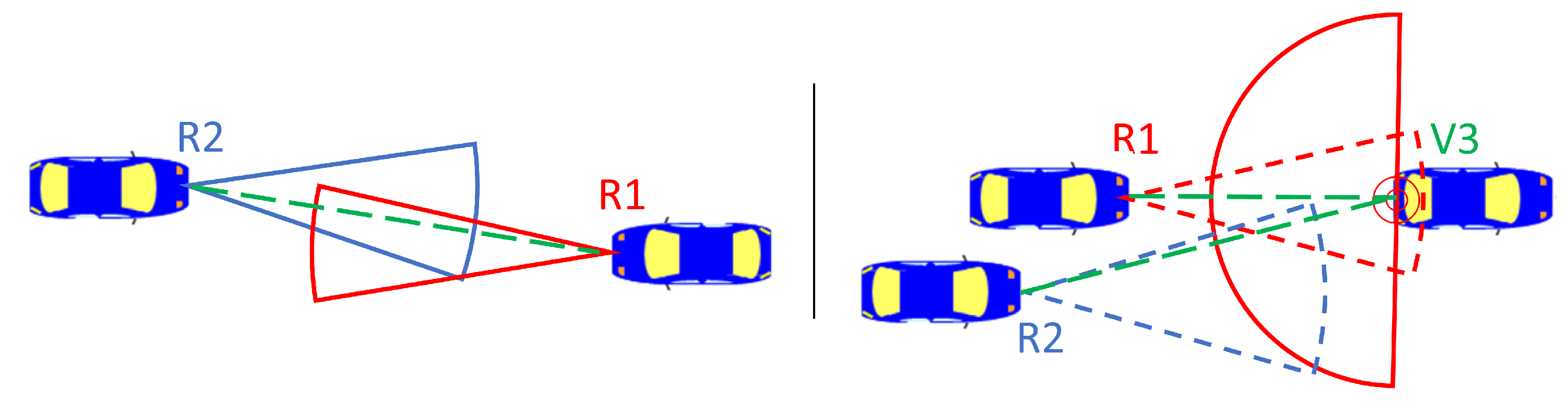
2.1. Automotive Radar Interference Mitigation
2.2. The Vertex Coloring Problem
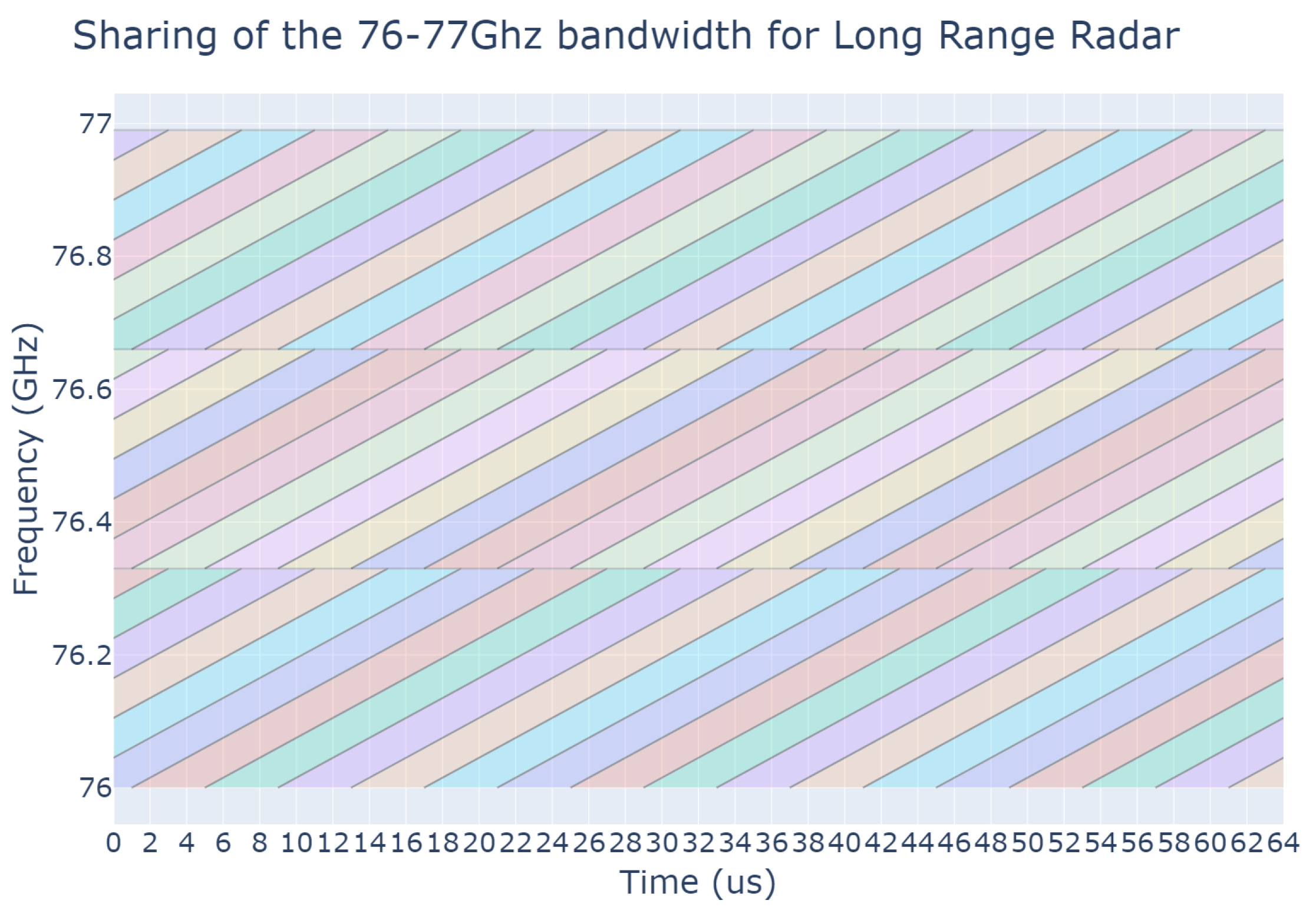
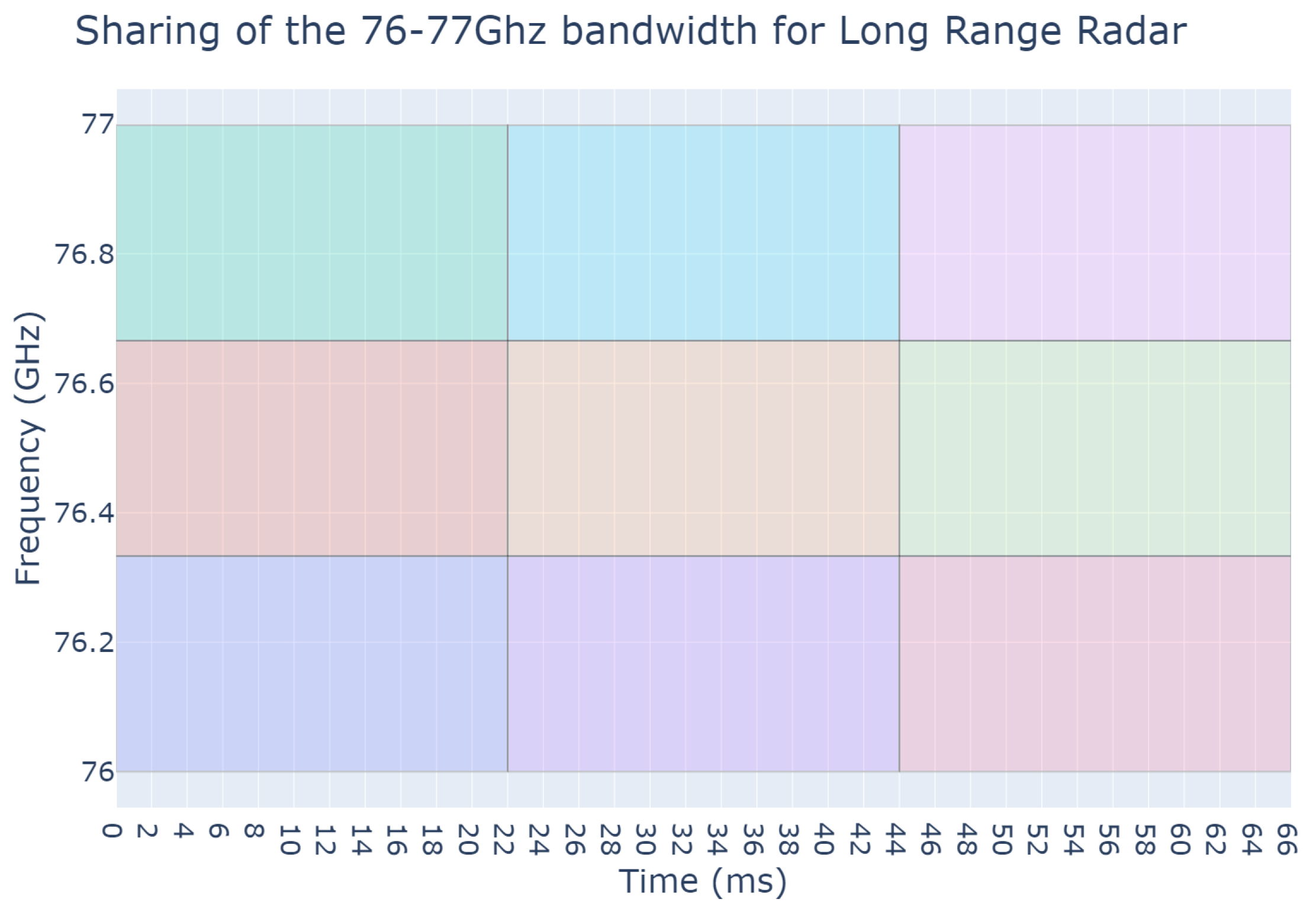
3. Simulation Environment
4. Mathematical Modeling
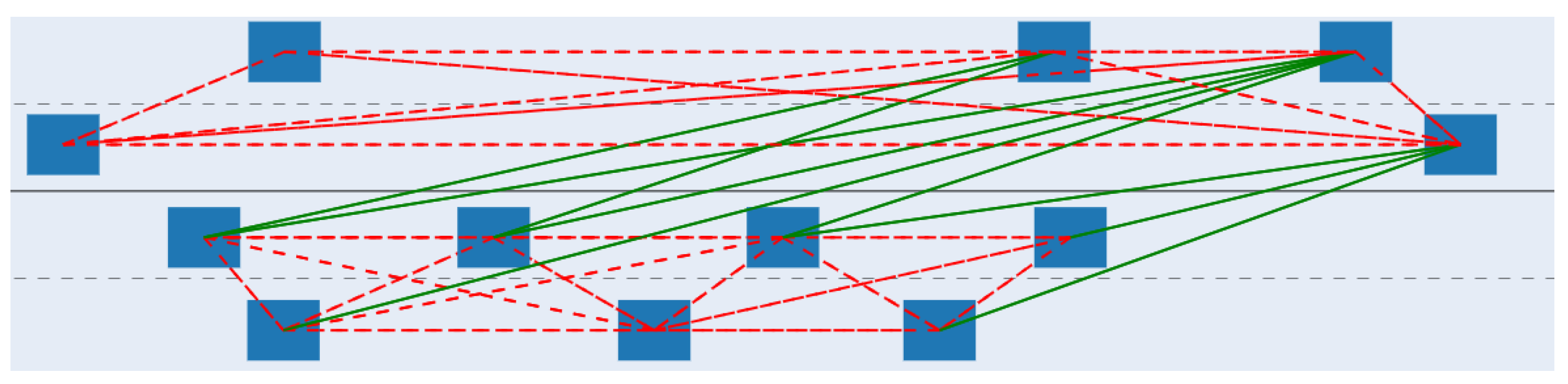
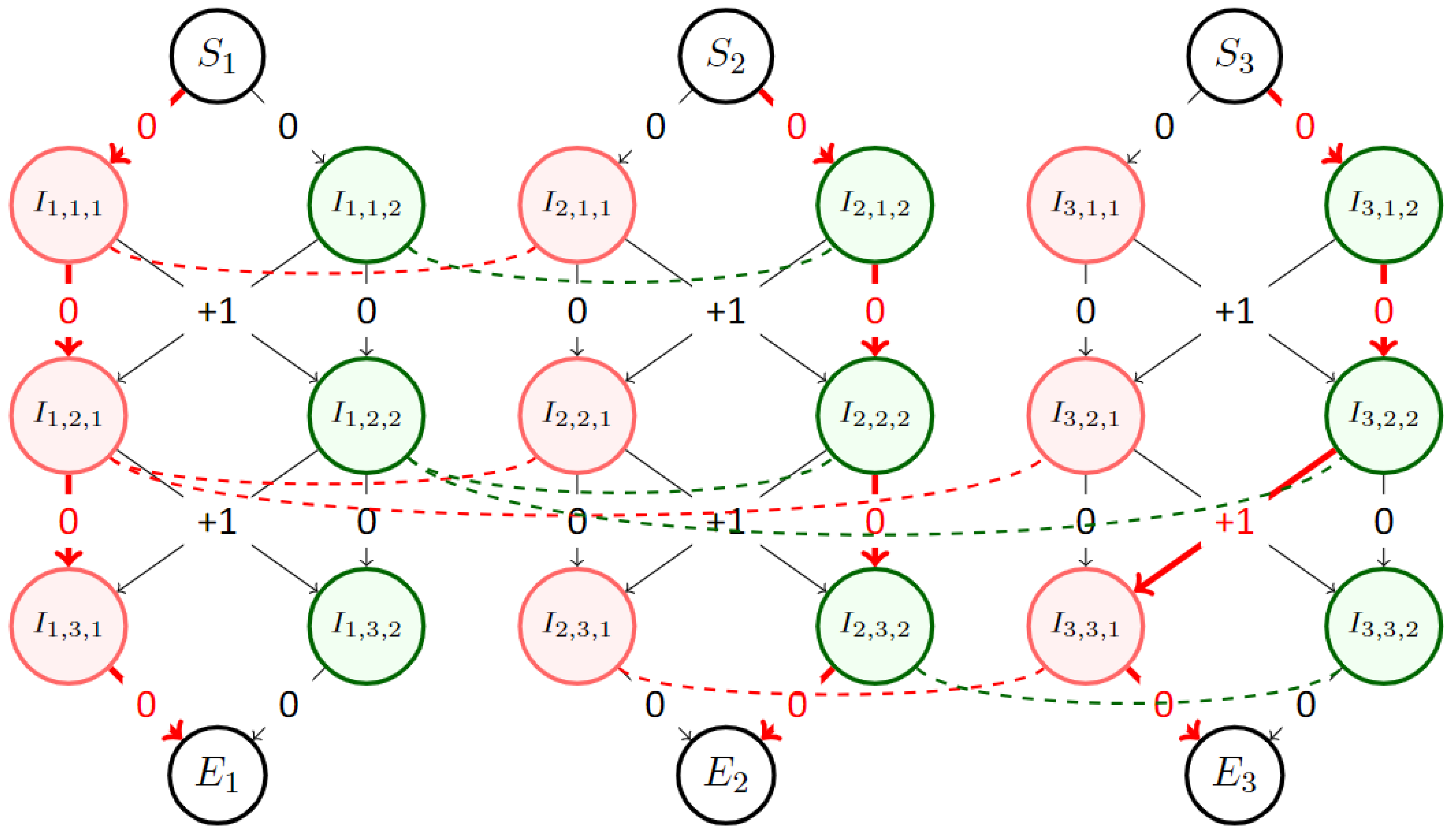
4.1. Dynamic Graph K-Coloring
4.2. Optimization Mathematical Model
- the individual starting state of each radar r. This state is not associated with any color. It corresponds to the start of the simulation where the first colors used by each radar are not determined yet.
- the individual ending state of each radar r. Like the starting state, it is not associated with any color and represents the end of the simulation.
- the set of intermediary possible states for each radar r other than starting and ending states. At timestep t, a radar r using color k will be in the state represented by the node .
5. Metaheuristic
5.1. Principle
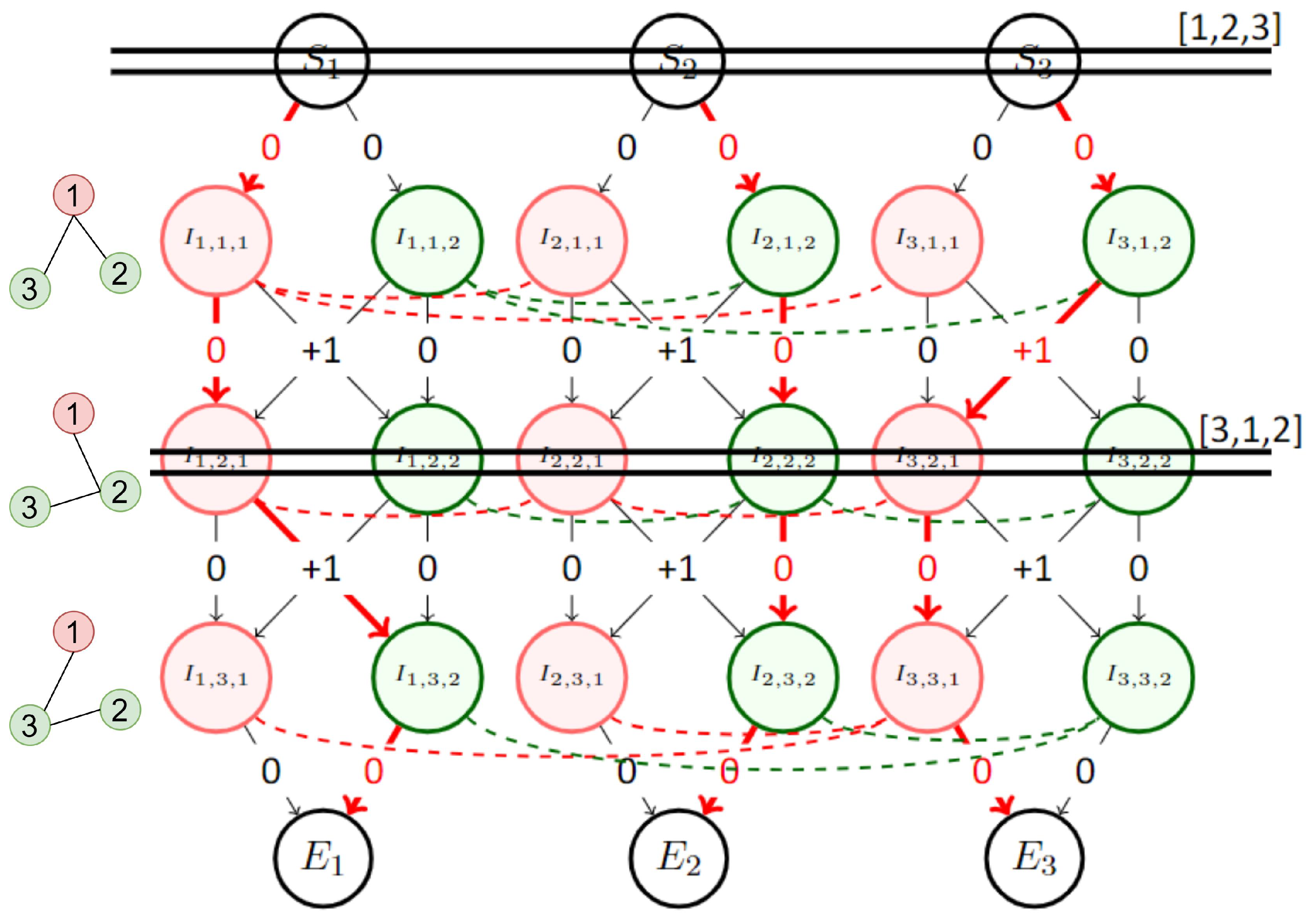
5.2. Sliding Window Adaptation
5.3. Simulated Annealing
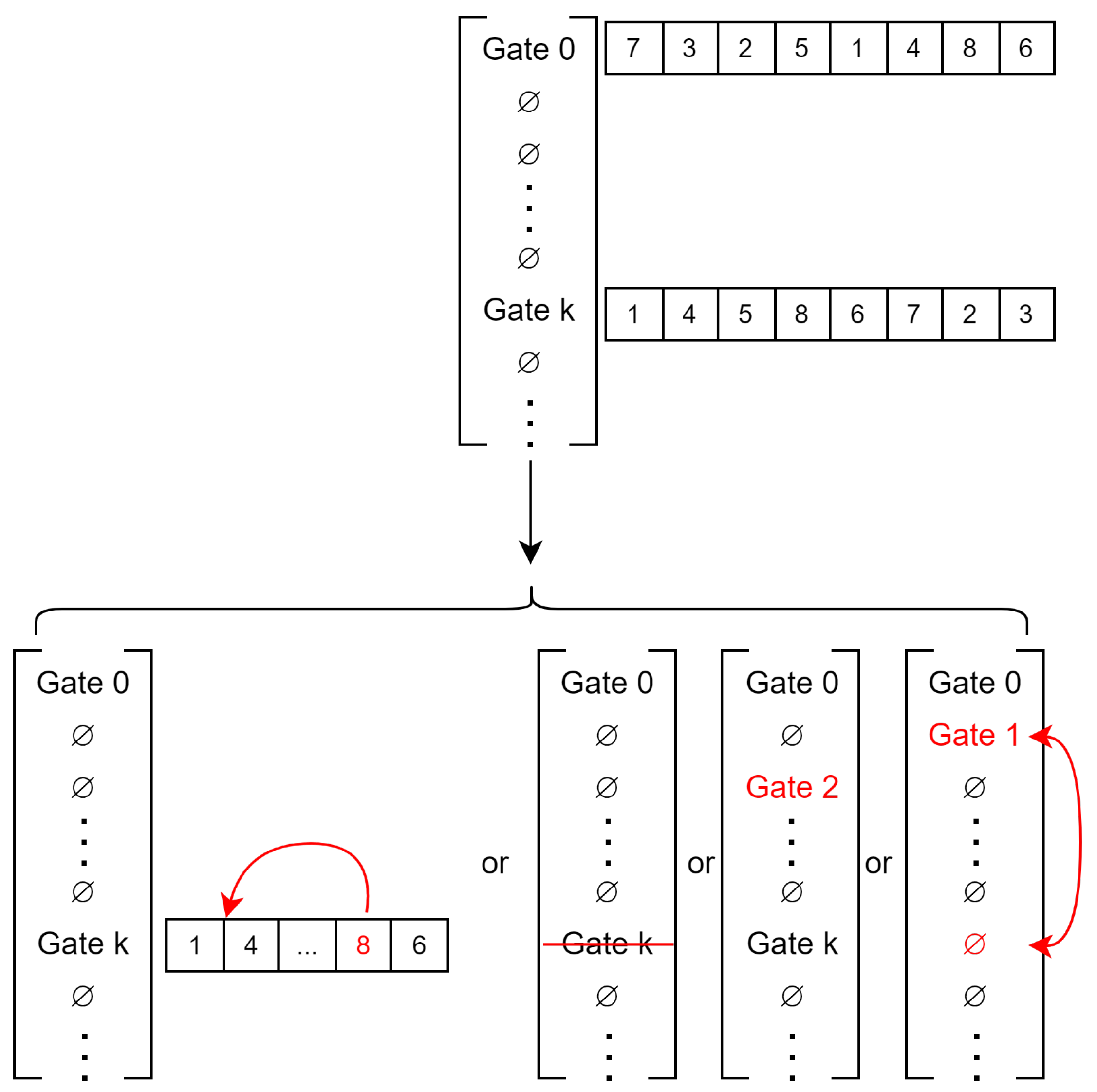
- Solution: a solution for our simulated annealing implementation is a list of size T containing or not a gate for each timestep as illustrated in Figure 7. Only the first timestep always has a gate that cannot be removed. As the Bellman–Ford algorithm is deterministic, the same list of gates will yield the same result (if the edge and conflict costs are the same).
- Evaluation: for each gate, the Bellman–Ford algorithm is applied to each sub-graph in the order of the gate to find the shortest path to the next gate (or to the end). The costs of conflicting nodes are updated once the shortest path is found for a sub-graph. The cost of a solution is the sum of the cost of all of the sub-graphs. As the cost of a conflict is changing, it is important to keep track of the number of conflicts of a solution so to not have to re-evaluate it entirely when the cost of a conflict is lowered. It allows one to fairly compare two solutions without being biased by the lower cost of a conflict for one of them.
- Neighborhood operator: to select a neighboring solution, multiple modifications can be carried out as illustrated in Figure 8. First, add or remove a random gate. This will remix completely the sub-graph running order. By extracting the cost of each timestep, it is possible to weight the random generation of the gate to focus more on high cost timesteps.Second, switch the position of two “gates”. This is achieved by selecting a gate at random (weighted by the timestep costs following it) and moving it to another timestep. If a gate is already present in this timestep, then both gates switch.Finally, change the order of a gate. This is achieved by selecting a sub-graph at random (weighted by its cost) and moving it earlier in the order. The earlier a sub-graph is in the permutation order, the fewer constraints it will have for its shortest-path. Since the node’s cost within a sub-graph depends on the path taken by other sub-graph before it, going early means that fewer sub-graphs have already chosen a path and thus have affected the nodes’ cost.
- Temperature and conflict cost: temperature is decreased by factor every iterations until the temperature reaches (usually ). At the same time temperature is lowered, the cost of a conflict increases by a factor . This factor is designed for conflict cost to reach near the end of the simulated annealing as is the maximum number of color changes possible (one color change by each radar at each timestep). When the cost of a conflict is equal to , a solution having fewer conflicts than another is ensured to achieve a lower cost whatever the number of color changes. Having a low cost for a conflict at the beginning of the simulated annealing favors the exploration of the solution space by avoiding local optima with a low number of conflicts and a high number of color changes. The conflict cost is then increased as the goal is to find a solution with the minimum number of color changes while still avoiding every conflict.
5.4. Genetic Algorithm
- Solution: A solution for our genetic algorithm is a permutation order for the first gate. Since this genetic algorithm is to be used on the sliding window coloring graph, it does not require the use of additional gates for the reason mentioned in Section 5.2.
- Evaluation: The evaluation of a solution is the same as for the simulated annealing version. Following the order of the starting gate, each small sub-graph computes its shortest path using the Bellman–Ford algorithm. The cost of the solution is the sum of the conflict cost and color change cost of each small sub-graph.
- Selection: The selection is achieved by a deterministic tournament of size 2 without replacement. Each solution is paired randomly, and the one with the lower cost is the winner.
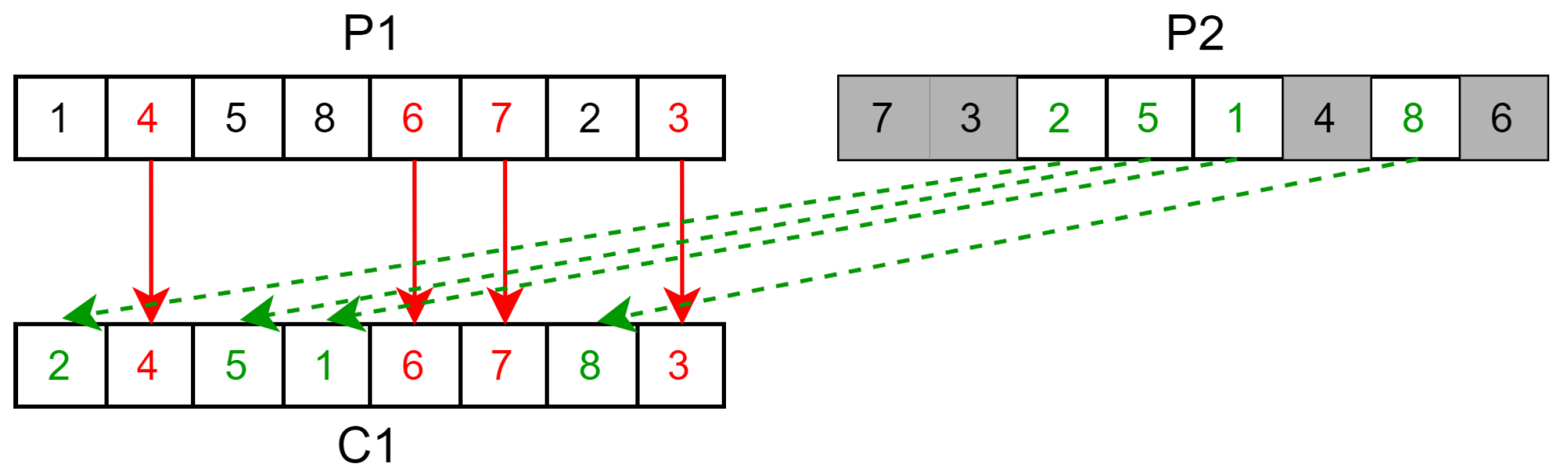
- Crossover: Crossover is carried out by using the position-based crossover operator (POS). It functions by randomly selecting a subset of the permutation order of the parent P1 and copying it into the child order. Then, the blanks in the child permutation order are filled in the order of the permutation of the second parent P2. This is described in Figure 9.This is then repeated again, but by copying from P2 first and filling the blank following the order of P1 to generate a second child solution.
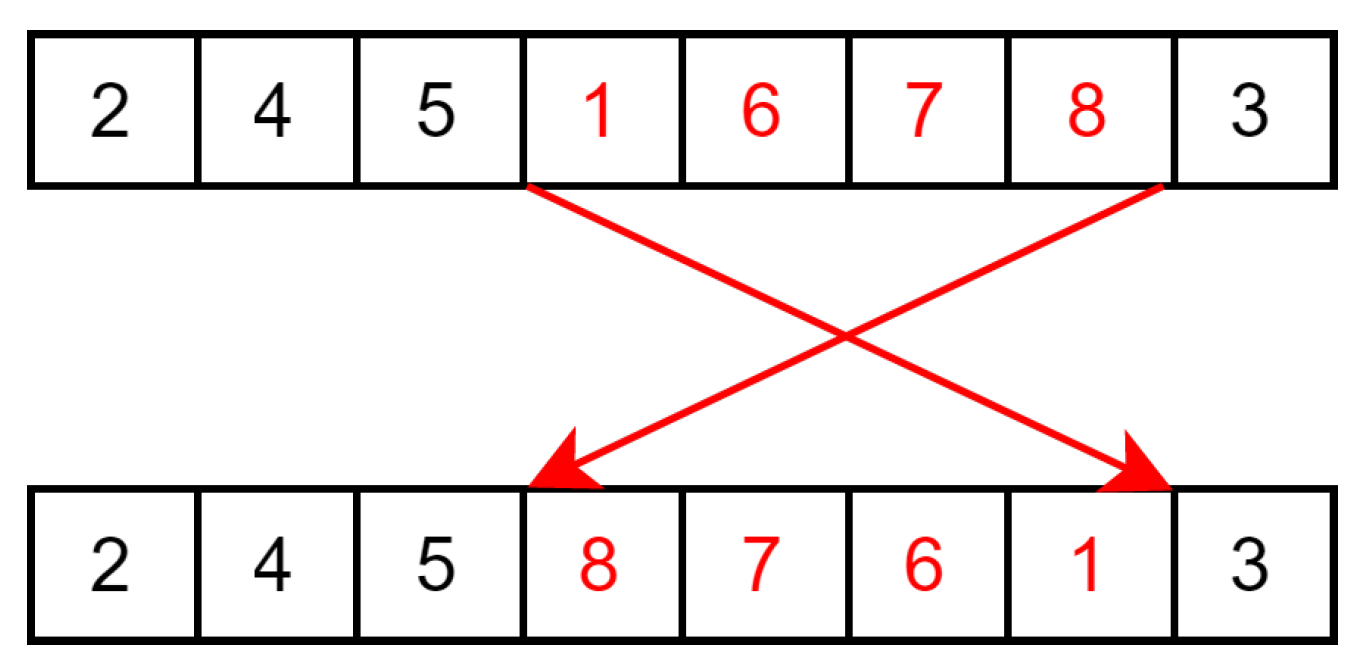
- Mutation: Each children solution has a probability to mutate to favor the exploration of the solution space. This mutation is implemented with the reverse sequence mutation (RSM) as it is a well performing mutation operator on the travelling salesman problem [37] (and the TSP uses the same solution formulation of a permutation order). This mutation takes a random section of the order and reverses it as illustrated in Figure 10.
- Conflict cost: The conflict cost is handled in the same way as for the the simulated annealing version. It starts low to avoid local optima that have a low number of conflicts, and then it gradually increases up to in order to find a solution that does not contain any conflict by the end of the metaheuristic. Compared to the non-windowed variant, the sliding window adaptation solves smaller graphs of a length W; thus, the maximum cost is instead of .
6. Results
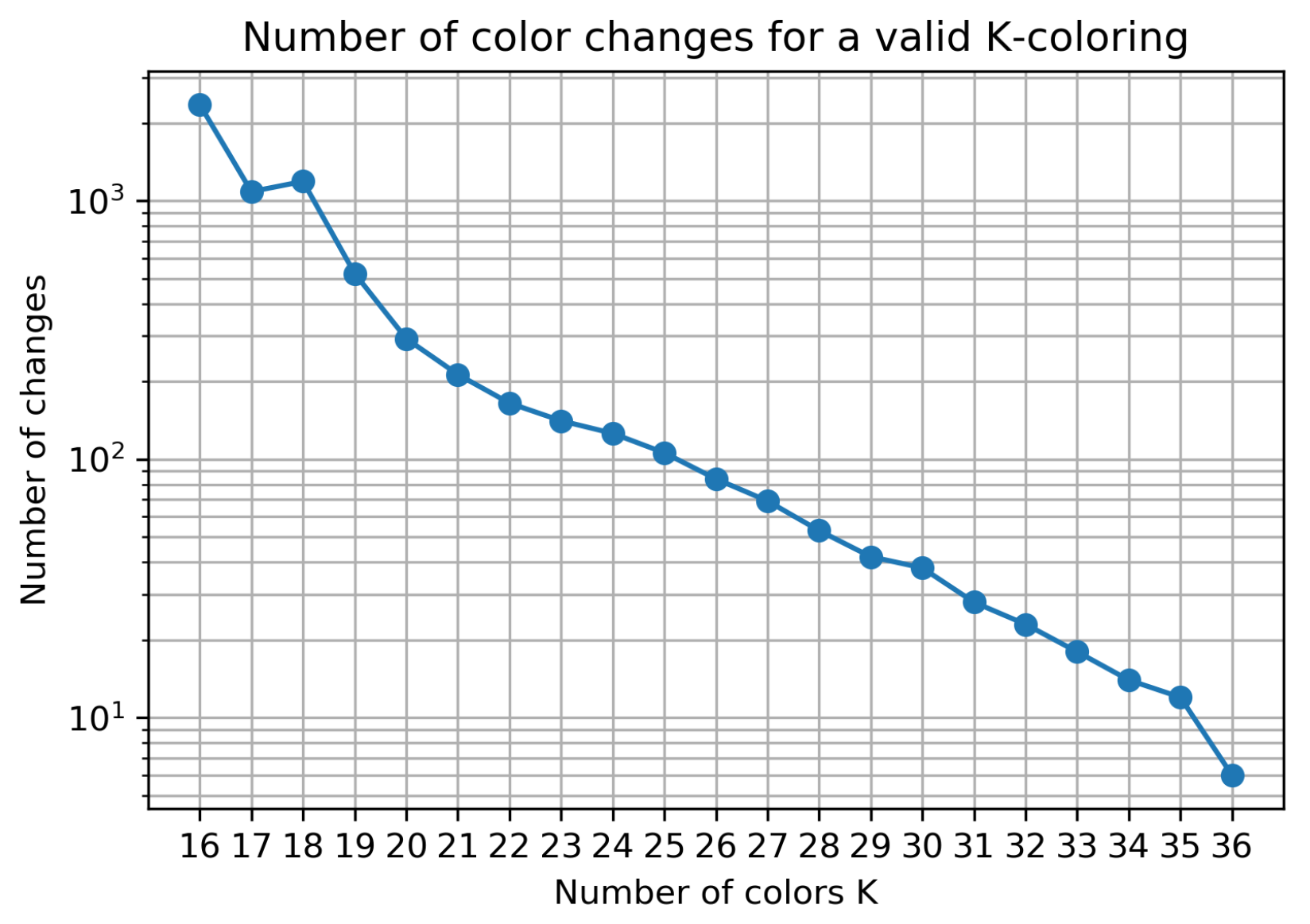
6.1. Color Changes Lower Bound
6.2. Metaheuristic Results
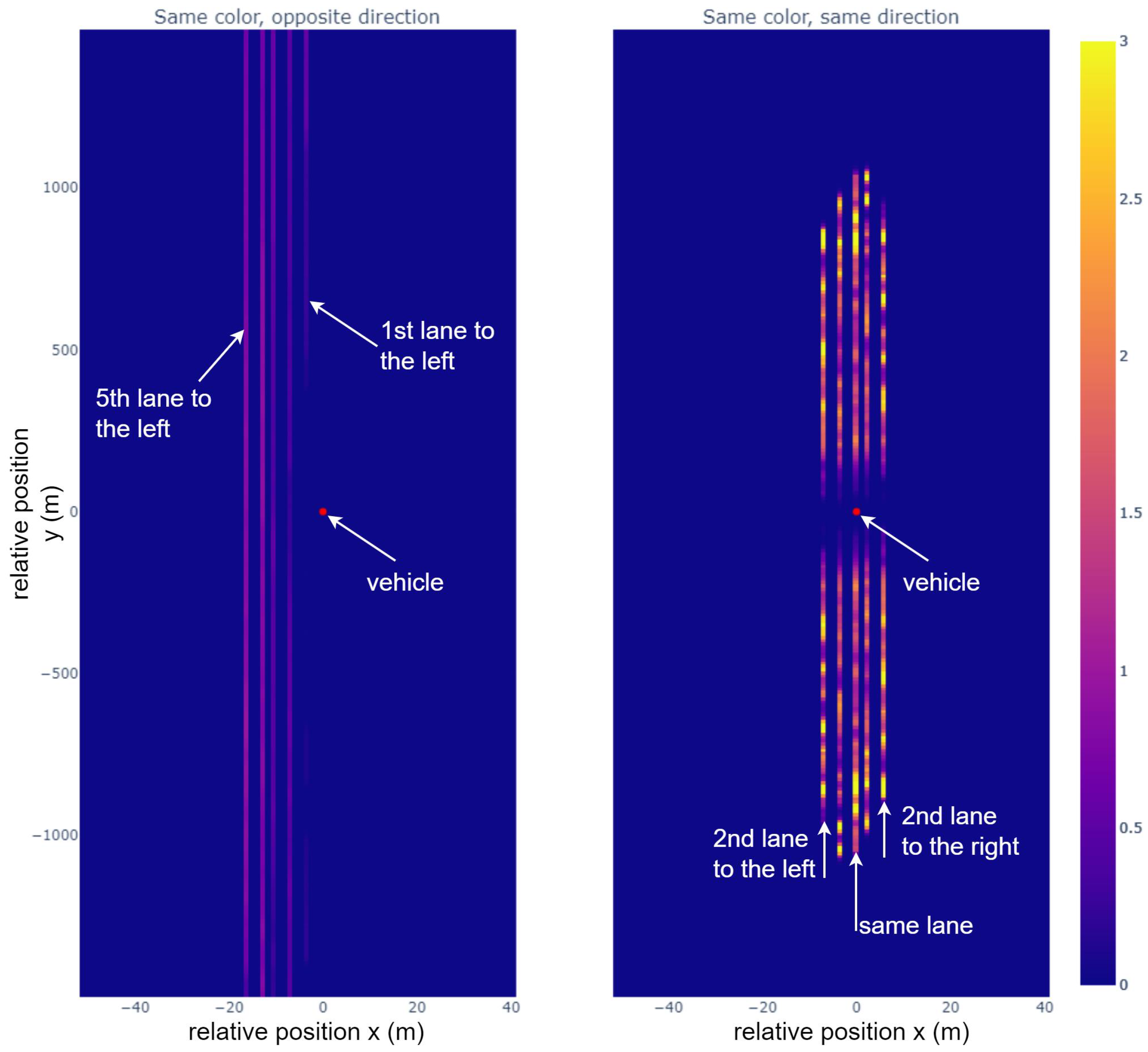
6.3. Example Data Extraction from Optimum
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Simulated Annealing Pseudo-Code
| Algorithm A1 Metaheuristic (Simulated Annealing) |
|
Appendix B. Genetic Algorithm Pseudo-Code
| Algorithm A2 Metaheuristic (Genetic Algorithm) |
|
References
- Automotive Radar Market Size, Share & Trends Analysis Report by Range (Long Range, Medium & Short Range), by Vehicle Type (Passenger Cars, Commercial Vehicles), by Application, by Frequency, by Region, and Segment Forecasts, 2018–2025; Technical Report; Grand View Research: San Francisco, CA, USA, 2017.
- Kunert, M.; Bosch, R. More Safety for All by Radar Interference Mitigation—Final Report. Technical Report, MOSARIM. 2012. Available online: https://cordis.europa.eu/docs/projects/cnect/1/248231/080/deliverables/001-D611finalreportfinal.pdf (accessed on 25 April 2023).
- Norouzian, F.; Pirkani, A.; Hoare, E.; Cherniakov, M.; Gashinova, M. Phenomenology of automotive radar interference. IET Radar Sonar Navig. 2021, 15, 1045–1060. [Google Scholar] [CrossRef]
- Borngräber, F.; John, A.; Sörgel, W.; Köber, R.; Vogler, T.; Miel, E.; Torres, F.; Kritzner, M.; Gölz, H.; Moss, J.; et al. IMIKO Radar—Minimizing Interference through Cooperation at Radar Sensors for Autonomous Electric Vehicles; Technical Report; German Federal Ministry of Education and Research: Bonn, Germany, 2022.
- Ramasubramanian, K.; Ramaiah, K.D. Moving from Legacy 24 GHz to State-of-the-Art 77-GHz Radar. ATZelektronik Worldw. 2018, 13, 46–49. [Google Scholar] [CrossRef]
- EN 303 883-1; Short Range Devices (SRD) and Ultra Wide Band (UWB); Part 1: Measurement Techniques for Transmitter Requirements. European Telecommunications Standards Institute: Sophia Antipolis, France, 2021.
- ETSI EN 301 091-1; Short Range Devices; Transport and Traffic Telematics (TTT); Radar Equipment Operating in the 76 GHz to 77 GHz Range; Harmonised Standard Covering the Essential Requirements of article 3.2 of Directive 2014/53/EU; Part 1: Ground Based Vehicular Radar. European Telecommunications Standards Institute: Sophia Antipolis, France, 2017.
- ETSI EN 302 264; Short Range Devices; Transport and Traffic Telematics (TTT); Short Range Radar Equipment Operating in the 77 GHz to 81 GHz Band; Harmonised Standard Covering the Essential Requirements of Article 3.2 of Directive 2014/53/EU. European Telecommunications Standards Institute: Sophia Antipolis, France, 2017.
- Filippi, A.; Martinez, V.; Vlot, M. Spectrum for Automotive Radar in the 140 GHz Band in Europe. In Proceedings of the 2022 19th European Radar Conference (EuRAD), Milan, Italy, 28–30 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Gu, H. The Importance of Imaging Radar. 2022. Available online: https://www.nxp.com/company/blog/the-importance-of-imaging-radar:BL-THE-IMPORTANCE-OF-IMAGING-RADAR#:~:text=In%20addition%20to%20measuring%20speed,cars%2C%20pedestrians%20and%20other%20objects. (accessed on 13 June 2023).
- Xu, Y.; Zhang, X.; Wei, S.; Shi, J.; Zhan, X.; Zhang, T. 3D Super-Resolution Imaging Method for Distributed Millimeter-Wave Automotive Radar System. 2022. Available online: http://xxx.lanl.gov/abs/2209.11037 (accessed on 1 June 2023).
- Gor, H. Orthogonal Frequency Division Multiplexing Multiple-Input Multiple-Output Automotive Radar with Novel Signal Processing Algorithms. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Gisder, T.; Meinecke, M.M.; Biebl, E. Synthetic Aperture Radar Towards Automotive Applications. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Li, J.; Xu, X.; Wang, B.; Zhan, X.; Xu, Y.; Ke, X.; Zeng, T.; Su, H.; et al. SAR Ship Detection Dataset (SSDD): Official Release and Comprehensive Data Analysis. Remote Sens. 2021, 13, 3690. [Google Scholar] [CrossRef]
- Roudiere, S.; Martinez, V.; Delahaye, D. A First Investigation of V2X communication for Radar Interference Mitigation. In Proceedings of the ITS World Congress 2021, Hamburg, Germany, 11–15 October 2021; Volume 27, pp. 1056–1070. [Google Scholar]
- Roudiere, S.; Martinez, V.; Delahaye, D. Orientation Based Bandwidth Sharing for Radar Interference Mitigation. In Proceedings of the IEEE Vehicular Technology Conference: VTC2023-Spring, Florence, Italy, 20–23 June 2023. [Google Scholar]
- Anwar, W.; Franchi, N.; Fettweis, G. Physical Layer Evaluation of V2X Communications Technologies: 5G NR-V2X, LTE-V2X, IEEE 802.11bd, and IEEE 802.11p. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ma, D.; Shlezinger, N.; Huang, T.; Liu, Y.; Eldar, Y.C. Joint Radar-Communication Strategies for Autonomous Vehicles: Combining Two Key Automotive Technologies. IEEE Signal Process. Mag. 2020, 37, 85–97. [Google Scholar] [CrossRef]
- Aydogdu, C.; Keskin, M.F.; Garcia, N.; Wymeersch, H.; Bliss, D.W. RadChat: Spectrum Sharing for Automotive Radar Interference Mitigation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 416–429. [Google Scholar] [CrossRef]
- Khoury, J.; Ramanathan, R.; McCloskey, D.; Smith, R.; Campbell, T. RadarMAC: Mitigating Radar Interference in Self-Driving Cars. In Proceedings of the 2016 13th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), London, UK, 27–30 June 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Leighton, F.T. A Graph Coloring Algorithm for Large Scheduling Problems. J. Res. Natl. Bur. Stand. 1979, 84, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Chow, F.C.; Hennessy, J.L. The Priority-Based Coloring Approach to Register Allocation. ACM Trans. Program. Lang. Syst. 1990, 12, 501–536. [Google Scholar] [CrossRef]
- Woo, T.K.; Su, S.; Newman-Wolfe, R. Resource allocation in a dynamically partitionable bus network using a graph coloring algorithm. IEEE Trans. Commun. 1991, 39, 1794–1801. [Google Scholar] [CrossRef]
- Gamst, A. Some lower bounds for a class of frequency assignment problems. IEEE Trans. Veh. Technol. 1986, 35, 8–14. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1990. [Google Scholar]
- Brélaz, D. New methods to color the vertices of a graph. Commun. ACM 1979, 22, 251–256. [Google Scholar] [CrossRef]
- Hertz, A.; Werra, D. Werra, D.: Using Tabu Search Techniques for Graph Coloring. Computing 1987, 39, 345–351. [Google Scholar] [CrossRef]
- Johnson, D.; Aragon, C.; McGeoch, L.; Schevon, C. Optimization by Simulated Annealing: An Experimental Evaluation; Part II, Graph Coloring and Number Partitioning. Oper. Res. 1991, 39, 378–406. [Google Scholar] [CrossRef]
- Davis, L. Handbook Of Genetic Algorithms; Thomson Publishing Group: Stamford, CT, USA, 1991. [Google Scholar]
- Solomon, S.; Wein, N. Improved Dynamic Graph Coloring. ACM Trans. Algorithms 2020, 16, 41. [Google Scholar] [CrossRef]
- Barba, L.; Cardinal, J.; Korman, M.; Langerman, S.; van Renssen, A.; Roeloffzen, M.; Verdonschot, S. Dynamic Graph Coloring. arXiv 2018, arXiv:1708.09080. [Google Scholar]
- Roudiere, S.; Martinez, V.; Delahaye, D. Importance of Synchronizing Radars with V2X communication for Radar Interference Mitigation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021. [Google Scholar]
- US Highway 101 Dataset. U.S. Department of Transportation: Federal Highway Administration. Available online: https://www.fhwa.dot.gov/publications/research/operations/07030/ (accessed on 1 June 2023).
- Xia, X.; Meng, Z.; Han, X.; Li, H.; Tsukiji, T.; Xu, R.; Zheng, Z.; Ma, J. An automated driving systems data acquisition and analytics platform. Transp. Res. Part C: Emerg. Technol. 2023, 151, e104120. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; Reidel, D., Ed.; Kluwer Academic: Berlin, Germany, 1987. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Otman, A.; Abouchabaka, J.; Tajani, C. Analyzing the Performance of Mutation Operators to Solve the Travelling Salesman Problem. arXiv 2012, arXiv:1203.3099. [Google Scholar]
- Arnold, E.; Dianati, M.; de Temple, R.; Fallah, S. Cooperative Perception for 3D Object Detection in Driving Scenarios Using Infrastructure Sensors. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1852–1864. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control Syst. Technol. 2023, 31, 179–192. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| 1 | |
| 1000 | |
| Metaheuristic Results | Benchmark Method | |||
|---|---|---|---|---|
| K | Conflicts | Changes | Conflicts | Changes |
| 36 | 0 | 6 | 179 | 159 |
| 35 | 0 | 12 | 190 | 166 |
| 34 | 0 | 14 | 203 | 177 |
| 33 | 0 | 18 | 214 | 184 |
| 32 | 0 | 23 | 226 | 196 |
| 31 | 0 | 28 | 245 | 208 |
| 30 | 0 | 38 | 263 | 219 |
| 29 | 0 | 42 | 288 | 241 |
| 28 | 0 | 53 | 307 | 252 |
| 27 | 0 | 69 | 333 | 266 |
| 26 | 0 | 84 | 368 | 292 |
| 25 | 0 | 106 | 405 | 317 |
| 24 | 0 | 126 | 449 | 352 |
| 23 | 0 | 141 | 491 | 373 |
| 22 | 0 | 165 | 554 | 416 |
| 21 | 0 | 213 | 655 | 477 |
| 20 | 0 | 293 | 767 | 536 |
| 19 | 0 | 524 | 916 | 610 |
| 18 | 0 | 1190 | 1148 | 707 |
| 17 | 10 | 1086 | 1709 | 898 |
| 16 | 22 | 2357 | 2664 | 1165 |
| K | Nb of Conflicts | Nb of Changes |
|---|---|---|
| 36 | 0 | 699 |
| 34 | 0 | 684 |
| 32 | 0 | 770 |
| 30 | 0 | 845 |
| 28 | 0 | 811 |
| 26 | 0 | 944 |
| 24 | 0 | 1123 |
| 22 | 0 | 1060 |
| 20 | 0 | 1287 |
| 18 | 123 | 1403 |
| 16 | 1773 | 1679 |
| Parameter | Value |
|---|---|
| W | 10 |
| 100 | |
| 1 | |
| 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roudiere, S.; Martinez, V.; Maréchal, P.; Delahaye, D. Metaheuristic for Optimal Dynamic K-Coloring Application on Band Sharing for Automotive Radars. Sensors 2023, 23, 5765. https://doi.org/10.3390/s23125765
Roudiere S, Martinez V, Maréchal P, Delahaye D. Metaheuristic for Optimal Dynamic K-Coloring Application on Band Sharing for Automotive Radars. Sensors. 2023; 23(12):5765. https://doi.org/10.3390/s23125765
Chicago/Turabian StyleRoudiere, Sylvain, Vincent Martinez, Pierre Maréchal, and Daniel Delahaye. 2023. "Metaheuristic for Optimal Dynamic K-Coloring Application on Band Sharing for Automotive Radars" Sensors 23, no. 12: 5765. https://doi.org/10.3390/s23125765
APA StyleRoudiere, S., Martinez, V., Maréchal, P., & Delahaye, D. (2023). Metaheuristic for Optimal Dynamic K-Coloring Application on Band Sharing for Automotive Radars. Sensors, 23(12), 5765. https://doi.org/10.3390/s23125765







