Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data
Abstract
1. Introduction
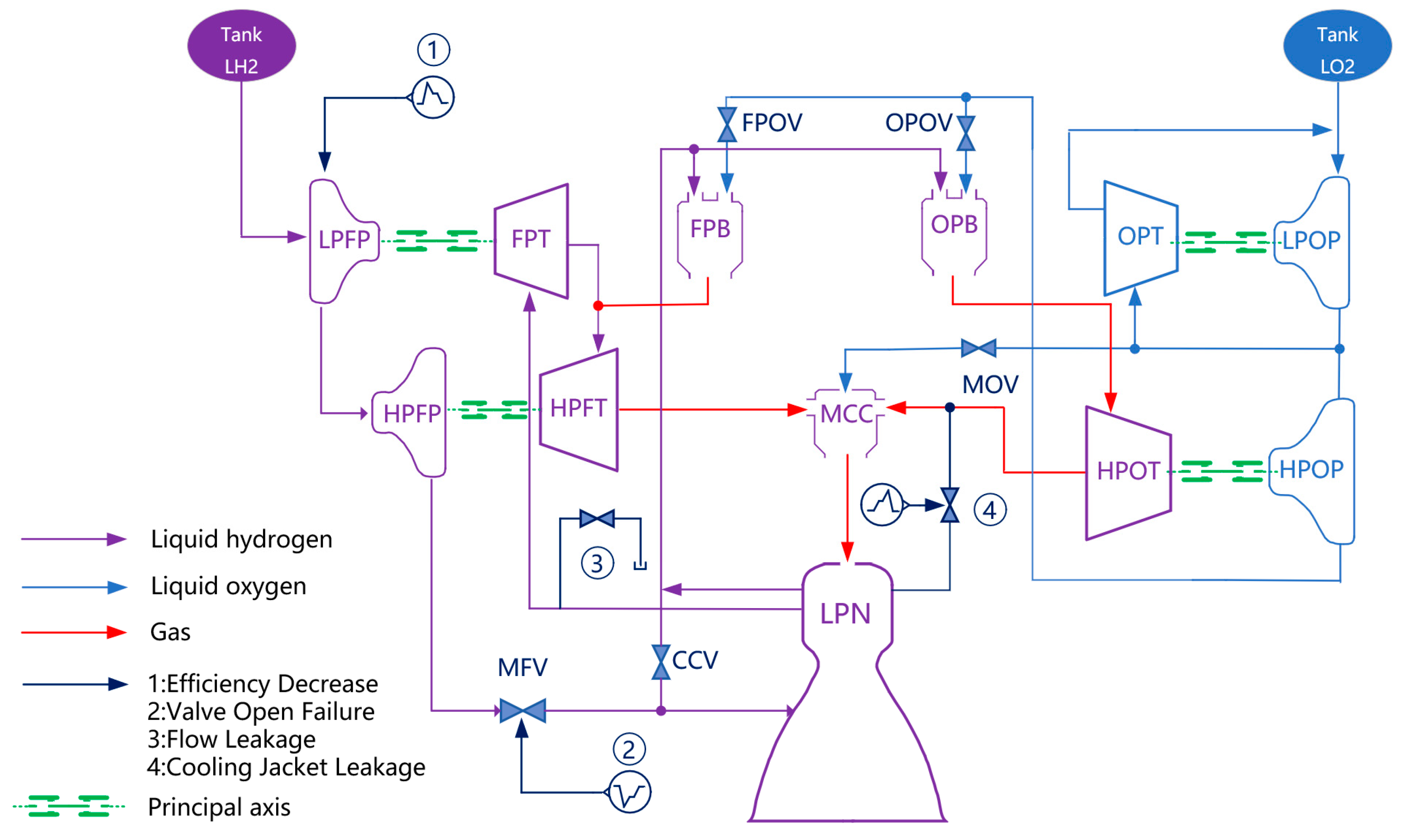
2. Simulation System Construction
2.1. System Simulation of LRE
2.2. Fault Simulation of LRE System
2.2.1. Valve Opening Failure
2.2.2. Hydrogen Turbine Leakage
2.2.3. Cooling Jacket Leakage
2.2.4. Turbine Component Efficiency Decrease
3. Methodology
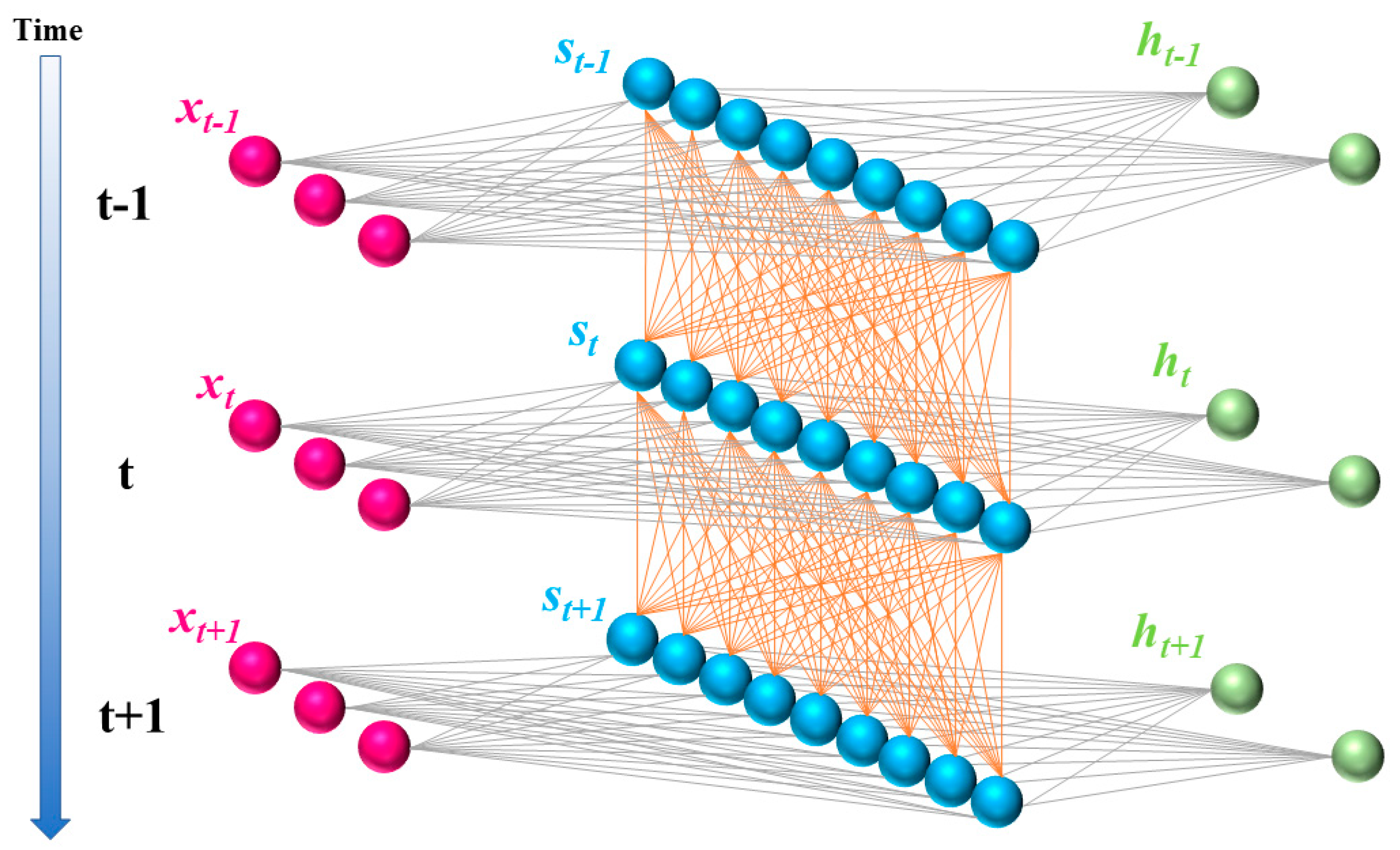
3.1. Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM)
- Forget gate: The forgetting gate decides what information to discard. The input is the calculation result of the previous neuron St−1 and the current input vector xt. After the two are joined and passed through the forgetting gate ( will decide what information to keep and what information to discard), a 0–1 vector (the dimension is the same as the output vector Ct−1 of the previous neuron) is generated (See Equation (5)). When the vector is dotted with Ct−1, the information retained by the previous neuron after calculation is obtained, which determines how much Ct−1 is kept in Ct.
- Input gate: Represents information to be saved or information to be updated. As shown in the Figure 3b, it is the connection vector between St−1 and xt. The result obtained after passing through the sigmoid function is the output result of the input gate, which determines how much information from xt can be used to calculate cell state Ct.The update status of a new cell is shown in Equation (7).
- Output gate: The output gate determines the hidden vector St of the current neurogenic cell output. Different from Ct, St is a little more complicated. It is the multiplication product of the computed with the computed result of the input gate, which is described by the formula as shown in Equation (8).
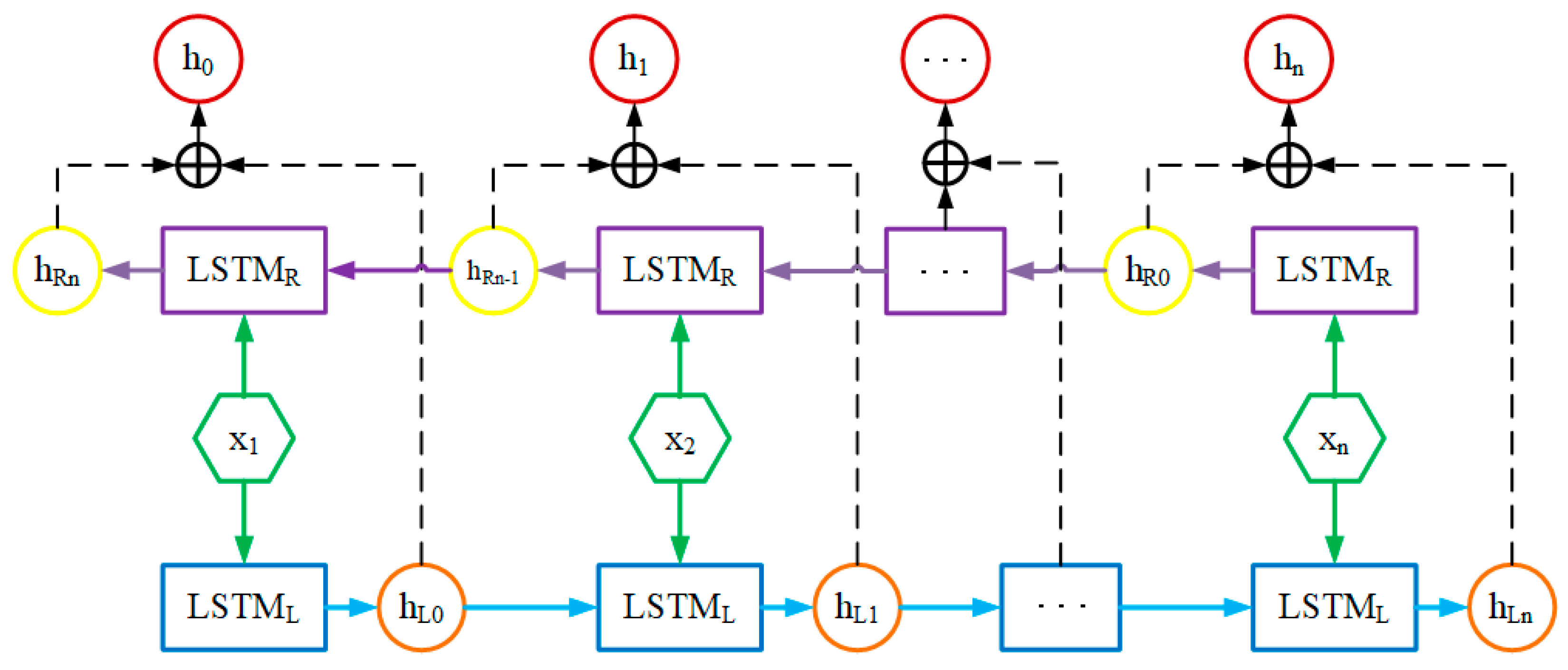
3.2. Bidirectional LSTM
- The forward LSTM reads the input sequence in chronological order and computes the hidden state vector for each time step.
- The backward LSTM reads the input sequence in the reverse order and computes the hidden state vector for each time step.
- The hidden state vectors of the forward and backward LSTMs are added element-wise to obtain the final hidden state vector for each time step.
3.3. Interpertable LSTM Based on Attention Mechanism
- The encoder encodes the input data to generate a set of feature vectors.
- Calculate the similarity between each feature vector and a specific “attention weight” vector to determine the importance of each feature vector.
- Multiply the attention weights with the feature vectors and add the results to obtain a weighted feature vector representation.
- Use the weighted feature vector as input to the next layer and repeat the above steps.
- Finally, add all the weighted feature vectors to obtain a comprehensive representation for the final prediction.
3.4. Spatial Attention Operation
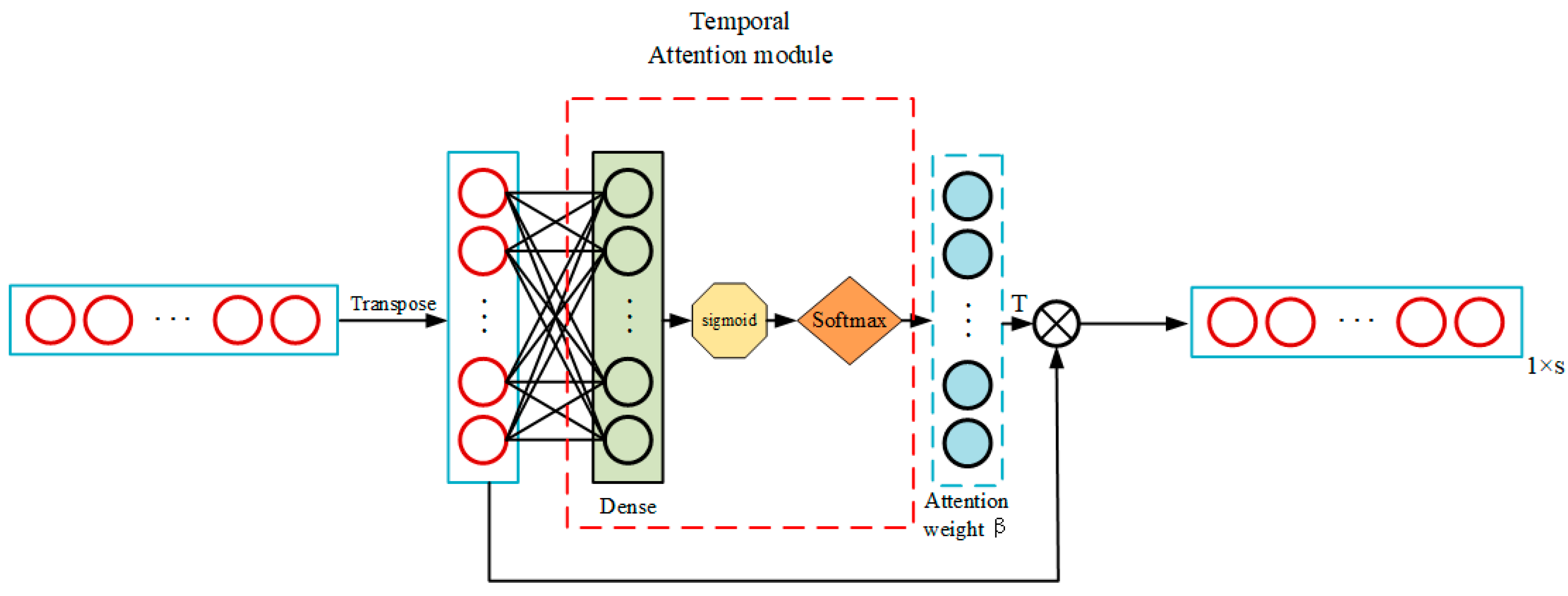
3.5. Temporal Attention Operation
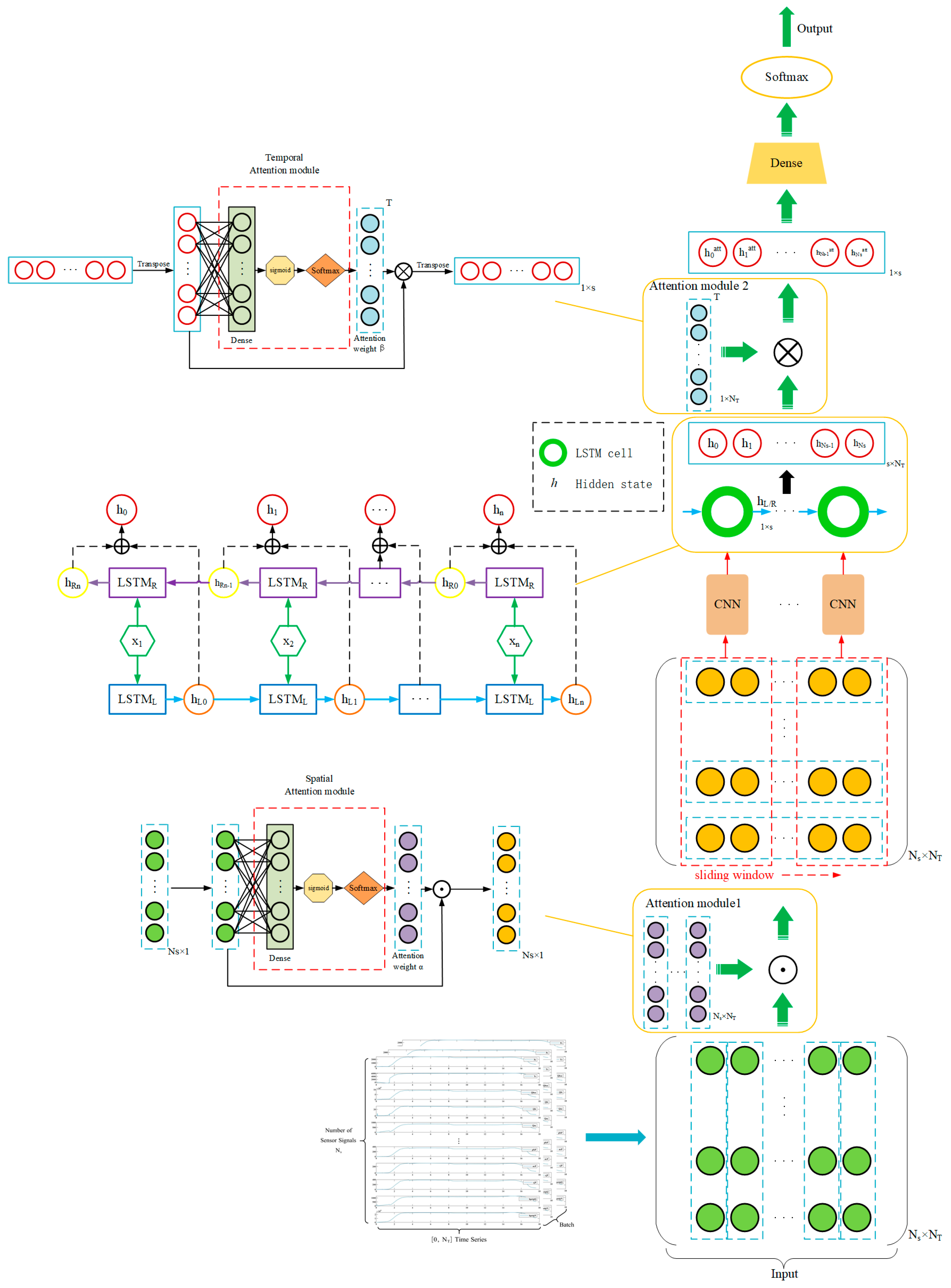
3.6. The Proposed Fault Detection Framework
4. Fault Diagnosis
4.1. Overall Model Analysis of Fault Diagnosis
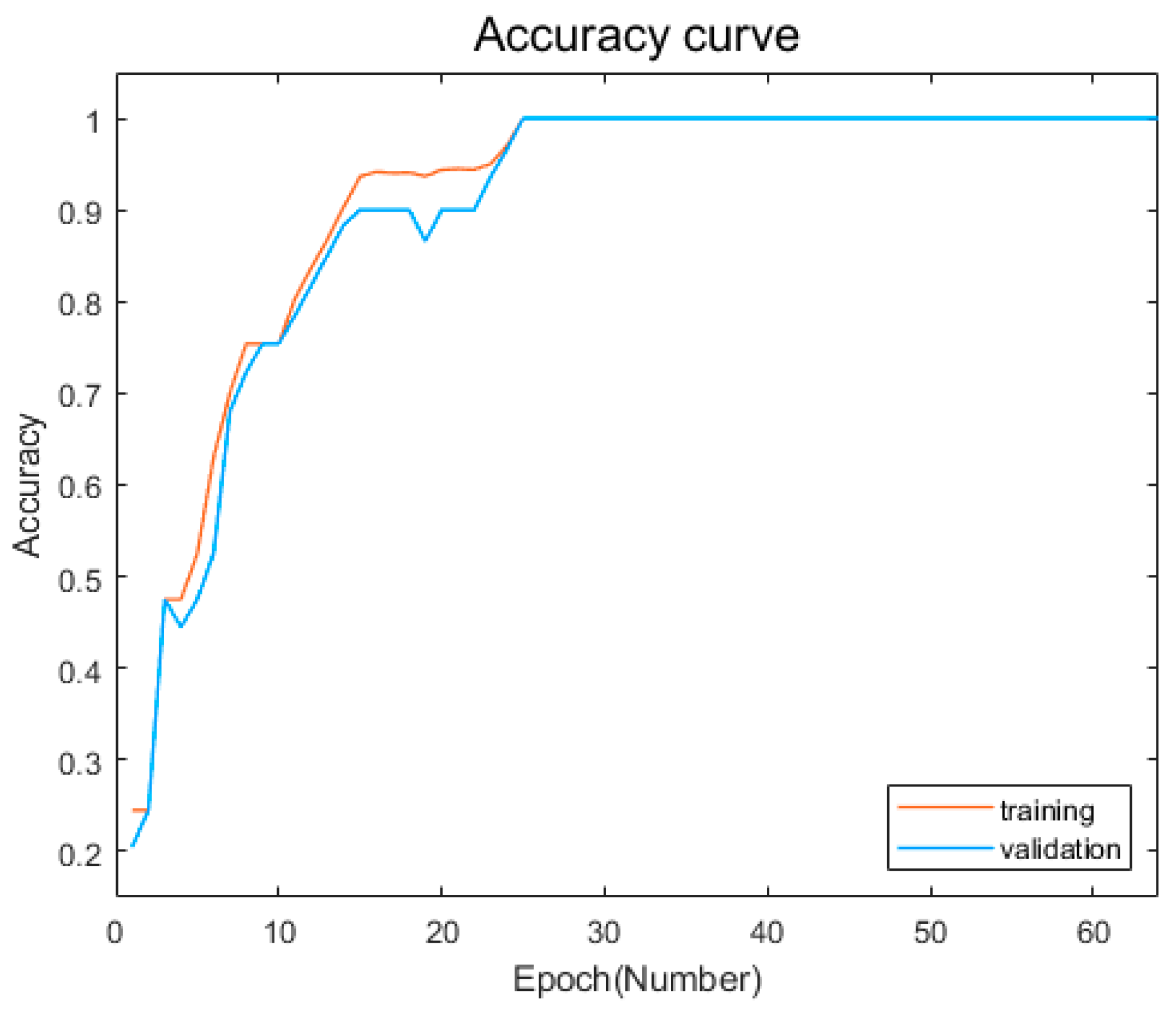
4.2. Result Analysis
4.3. Comparative Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iannetti, A.; Marzat, J.; Piet-Lahanier, H.; Sarotte, C.; Ordonneau, G.; de la Hunière, C. Promising HMS approaches for liquid rocket engines. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017; p. 417. [Google Scholar]
- Cikanek, H. Space shuttle main engine failure detection. IEEE Control Syst. Mag. 1986, 6, 13–18. [Google Scholar] [CrossRef]
- Cikanek, H.A., III. Characteristics of space shuttle main engine failures. In Proceedings of the 23rd Joint Propulsion Conference, San Diego, CA, USA, 29 June–2 July 1987. [Google Scholar]
- Jue, F.; Kuck, F. Space shuttle main engine (SSME) options for the future shuttle. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, Indiana, 7–10 July 2002. [Google Scholar]
- Davidson, M.; Stephens, J. Advanced health management system for the space shuttle main engine. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Liu, J.; Ding, X.; Wang, H.; Wang, B.; Liu, H.; Yang, Z.; Wang, Z. Fault Diagnosis of Liquid Rocket Engine Based on Hierarchical Bayesian Network Variational Inference. Trans. Beijing Inst. Technol. 2022, 42, 289–296. [Google Scholar] [CrossRef]
- D’Addabbo, A.; Refice, A.; Pasquariello, G.; Lovergine, F.P.; Capolongo, D.; Manfreda, S. A bayesian network for flood detection combining SAR imagery and ancillary data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3612–3625. [Google Scholar] [CrossRef]
- De Souza, D.L.; Granzotto, M.H.; de Almeida, G.M.; Oliveira-Lopes, L.C. Fault Detection and Diagnosis Using Support Vector Machines—A SVC and SVR Comparison. J. Saf. Eng. 2014, 3, 18–29. [Google Scholar] [CrossRef]
- Pule, M.; Matsebe, O.; Samikannu, R. Application of PCA and SVM in Fault Detection and Diagnosis of Bearings with Varying Speed. Math. Probl. Eng. 2022, 2022, 5266054. [Google Scholar] [CrossRef]
- Liu, H.G.; Wei, P.F.; Xie, T.F.; Huang, Q.; Wu, J.J. Research of Real-time Fault Detection Method for Liquid Propellant Rocket Engines in Ground Test. J. Astronaut. 2007, 28, 1660–1663. [Google Scholar]
- Flora, J.J.; Auxillia, D.J. Sensor Failure Management in Liquid Rocket Engine using Artificial Neural Network. J. Sci. Ind. Res. India 2020, 79, 1024–1027. [Google Scholar]
- Liu, Y.J.; Huang, Q.; Cheng, Y.Q.; Wu, J.J. Fault Diagnosis Method for Liquid-propellant Rocket Engines Based on the Dynamic Cloud-BP Neural Network. J. Aerosp. Power 2012, 27, 2842–2849. [Google Scholar]
- Li, N.; Xue, W.; Guo, X.; Xu, L.; Wu, Y.; Yao, Y. Fault Detection in Liquid-propellant Rocket Engines Based on Improved PSO-BP Neural Network. J. Softw. 2019, 14, 380–387. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Chen, X.; Ma, M.; Zhao, Z.; Zhai, Z.; Mao, Z. Physics-Informed Deep Neural Network for Bearing Prognosis with Multisensory Signals. J. Dyn. Monit. Diagn. 2022, 200–207. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R. Intelligent Fault Diagnosis for Planetary Gearbox Using Transferable Deep Q Network Under Variable Conditions with Small Training Data. J. Dyn. Monit. Diagn. 2023, 2, 30–41. [Google Scholar]
- Lee, K.; Cha, J.; Ko, S.; Park, S.Y.; Jung, E. Fault detection and diagnosis algorithms for an open-cycle liquid propellant rocket engine using the kalman filter and fault factor methods. Acta Astronaut. 2018, 150, 15–27. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Y.L.; Cheng, M.S. Modularization modeling and simulation for the transients of liquid propellant rocket engines. J. Propuls. Technol. 2003, 24, 401–405. [Google Scholar]
- Yan, Z.; Peng, X.H.; Cheng, Y.Q.; Wu, J.J. System Dynamic Characteristic Simulation of Spacecraft Propulsion System Based on AMESim. Adv. Mater. Res. 2013, 605–607, 679–683. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; Hu, J. Transient Characteristics of High-Thrust Oxygen/Hydrogen Rocket Engine. J. Propuls. Technol. 2021, 42, 1761–1769. [Google Scholar]
- Zhang, J.; Gong, Y.; Liu, Z.; Wang, W. Fault Simulation and Experimental Study on High-Thrust LOX/LH2 Rocket Engine. J. Deep. Space Explor. 2021, 8, 389–398. [Google Scholar]
- Cheng, Y.; Hu, R.; Wu, J. Pipeline fault simulation and control of a liquid rocket engine. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023. [Google Scholar] [CrossRef]
- Gao, M.; Hu, N.; Qin, G.; Xia, L. Modeling and fault simulation of propellant filling system based on Modelica/Dymola. In Proceedings of the ISSCAA 2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008; Volume 5, pp. 1–5. [Google Scholar]
- Whitacker, L.H.L.; Tomita, J.T.; Bringhenti, C. An evaluation of the tip clearance effects on turbine efficiency for space propulsion applications considering liquid rocket engine using turbopumps. Aerosp. Sci. Technol. 2017, 70, 55–65. [Google Scholar] [CrossRef]
- Lee, H.; Shin, J.H.; Choi, C.H. Experimental Investigation of the Turbine in a Turbopump for a Liquid Rocket Engine with a 75-ton Force Thrust. Trans. Korean Soc. Mech. Eng. B 2018, 42, 519–524. [Google Scholar] [CrossRef]
- Graves, A.; Jaitly, N.; Mohamed, A.R. Hybrid speech recognition with deep bidirectional LSTM. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2013; pp. 273–278. [Google Scholar]
- Zhao, R.; Yan, R.; Wang, J.; Mao, K. Learning to monitor machine health with convolutional bi-directional LSTM networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef]
- Chen, H.; Wu, G.; Li, J.; Wang, J.; Tao, H. Research advances on deep learning recommendation based on attention mechanism. Comput. Eng. Sci. 2021, 43, 370–380. [Google Scholar]
- Passricha, V.; Aggarwal, R. A Hybrid of Deep CNN and Bidirectional LSTM for Automatic Speech Recognition. J. Intell. Syst. 2020, 29, 1261–1274. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Ren, H.; Wang, X. Review of attention mechanism. J. Computer Appl. 2021, 41, 1–6. [Google Scholar]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Zhang, X.; He, C.; Lu, Y.; Chen, B.; Zhu, L.; Zhang, L. Fault diagnosis for small samples based on attention mechanism. Measurement 2022, 187, 110242. [Google Scholar] [CrossRef]
- Gonzalez-Jimenez, D.; del-Olmo, J.; Poza, J.; Garramiola, F.; Madina, P. Data-Driven Fault Diagnosis for Electric Drives: A Review. Sensors 2021, 21, 4024. [Google Scholar] [CrossRef]
- Pan, H.; He, X.; Tang, S.; Meng, F. An improved bearing fault diagnosis method using one-dimensional CNN and LSTM. J. Mech. Eng. 2018, 64, 443–452. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Gu, K.; Zhang, Y.; Liu, X.; Li, H.; Ren, M. DWT-LSTM-Based Fault Diagnosis of Rolling Bearings with Multi-Sensors. Electronics 2021, 10, 2076. [Google Scholar] [CrossRef]
- Wang, W.; Lei, Y.; Yan, T.; Li, N.; Nandi, A. Residual Convolution Long Short-Term Memory Network for Machines Remaining Useful Life Prediction and Uncertainty Quantification. J. Dyn. Monit. Diagn. 2021, 1, 2–8. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Ai, T. Long-range Dependencies Learning Based on Non-Local 1D-Convolutional Neural Network for Rolling Bearing Fault Diagnosis. J. Dyn. Monit. Diagn. 2022, 1, 148–159. [Google Scholar] [CrossRef]
- Park, S.-Y.; Ahn, J. Deep neural network approach for fault detection and diagnosis during startup transient of liquid-propellant rocket engine. Acta Astronaut. 2020, 177, 714–730. [Google Scholar] [CrossRef]
- Ordóñez, F.J.; Roggen, D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; pp. 1001–1003. [Google Scholar]
- Kingma, D.P.; Adam, J.B. A Method for Stochastic Optimization. arXiv 2015, arXiv:1508.01745. [Google Scholar]







| Components | Classification | Fault Mode | Fault Performance |
|---|---|---|---|
| Turbopump | Centrifugal Pump | (1) Impeller damage (2) Bearing wear or damage (3) Pump cavitation | Pump efficiency decrease |
| Turbine | (1) Blade detachment (2) Bearing wear or damage (3) Turbine blade erosion (4) Gas flow obstruction (5) Turbine inlet flow leakage | Turbine efficiency decrease | |
| Downstream flow rate decrease | |||
| Pipeline | Gas pipeline | (1) Pipeline blockage (2) Pipeline leakage | Increased flow resistance |
| Liquid pipeline | Downstream flow rate decrease | ||
| Thrust chamber | Combustion chamber | Combustion deterioration | Combustion efficiency decrease |
| Gas generator | Combustion deterioration | ||
| Cooling jacket | Cooling jacket blockage | Increased flow resistance | |
| Cooling jacket leakage | Downstream flow rate decrease | ||
| Nozzle | (1) Nozzle deformation (2) Large nozzle detachment | Nozzle efficiency decrease | |
| Others | Regulating valve | Stuck during switching | Reduced flow area |
| Cavitation tube | Cavitation tube blockage | Increased flow resistance | |
| Sonic nozzle | Sonic nozzle blockage |
| Diagnosis Method | CNN | 1DCNN-SVM | CNN-LSTM | 1DCNN-A-BiLSTM |
|---|---|---|---|---|
| Ten times average classification accuracy/% | 86.99 | 93.83 | 94.76 | 97.39 |
| Standard deviation/% | 2.3236 | 1.3798 | 0.6271 | 0.5832 |
| Time/s (Using CPU) | 6.8 | 9.4 | 11.3 | 8.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Hua, X.; Zhu, J.; Ma, M. Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data. Sensors 2023, 23, 5636. https://doi.org/10.3390/s23125636
Zhang X, Hua X, Zhu J, Ma M. Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data. Sensors. 2023; 23(12):5636. https://doi.org/10.3390/s23125636
Chicago/Turabian StyleZhang, Xiaoguang, Xuanhao Hua, Junjie Zhu, and Meng Ma. 2023. "Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data" Sensors 23, no. 12: 5636. https://doi.org/10.3390/s23125636
APA StyleZhang, X., Hua, X., Zhu, J., & Ma, M. (2023). Intelligent Fault Diagnosis of Liquid Rocket Engine via Interpretable LSTM with Multisensory Data. Sensors, 23(12), 5636. https://doi.org/10.3390/s23125636





