Subgraph Learning for Topological Geolocalization with Graph Neural Networks
Abstract
1. Introduction
- Introduce a novel motion trajectory-based topological geolocalization method using a graph neural network, which combines the benefits of vector-based navigation and the graph representation of a map.
- Design two different subgraph representations for motion trajectories: one is for the encoding direction and the other for encoding both direction and distance by inserting virtual nodes.
- Demonstrate an affordable data collection setup that is used to generate visual-inertial navigation dataset to demonstrate the effectiveness of the proposed method in a practical setting.
2. Related Work
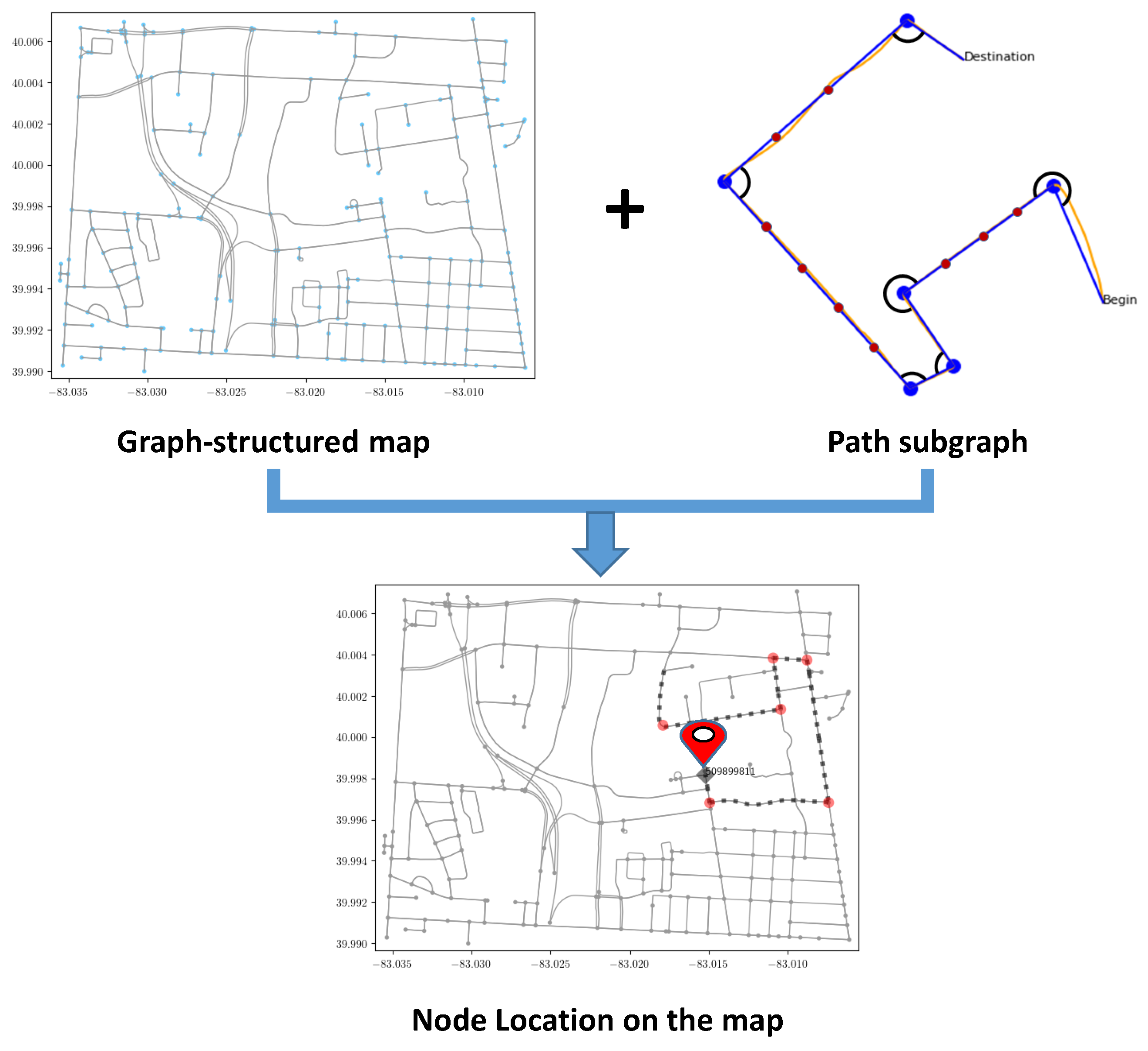
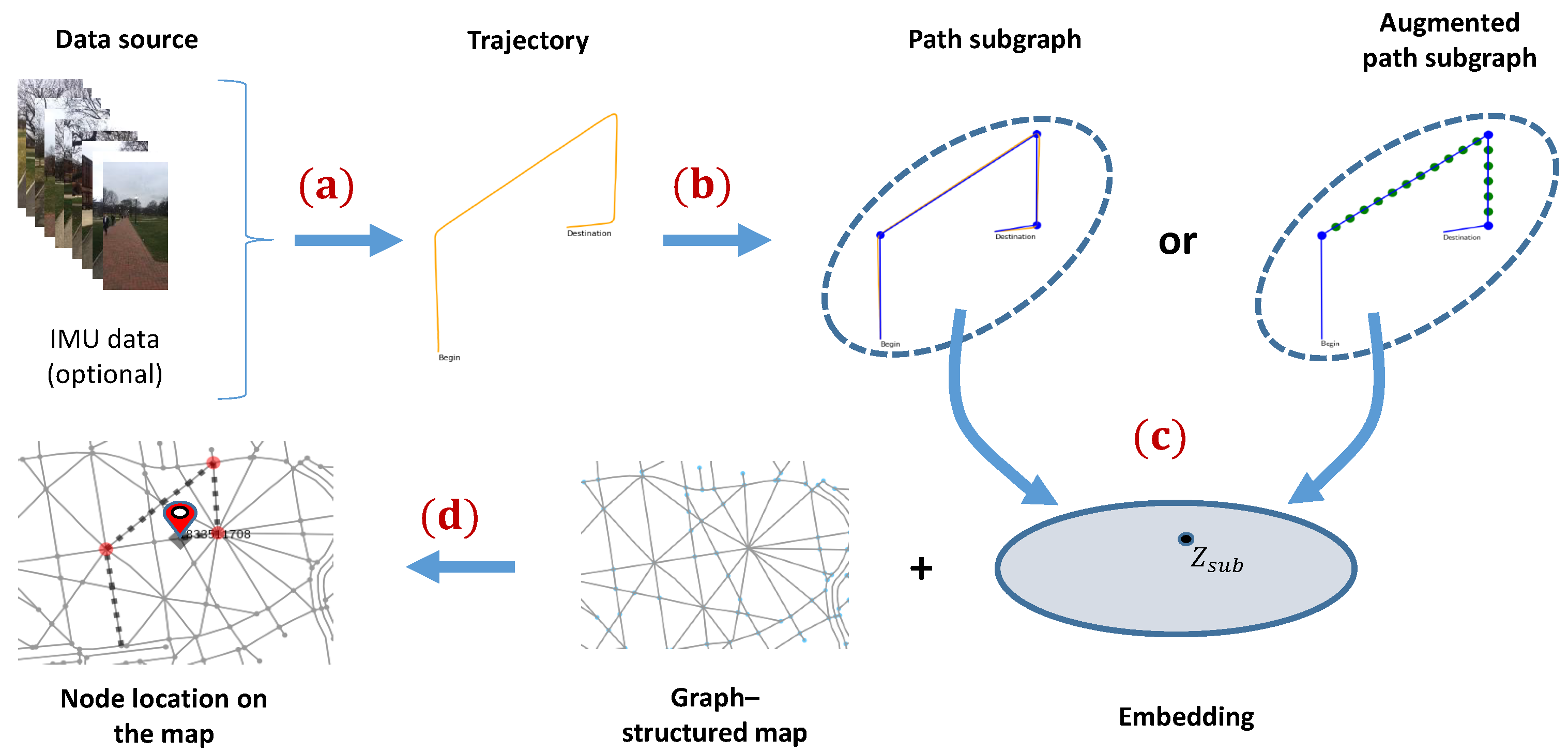
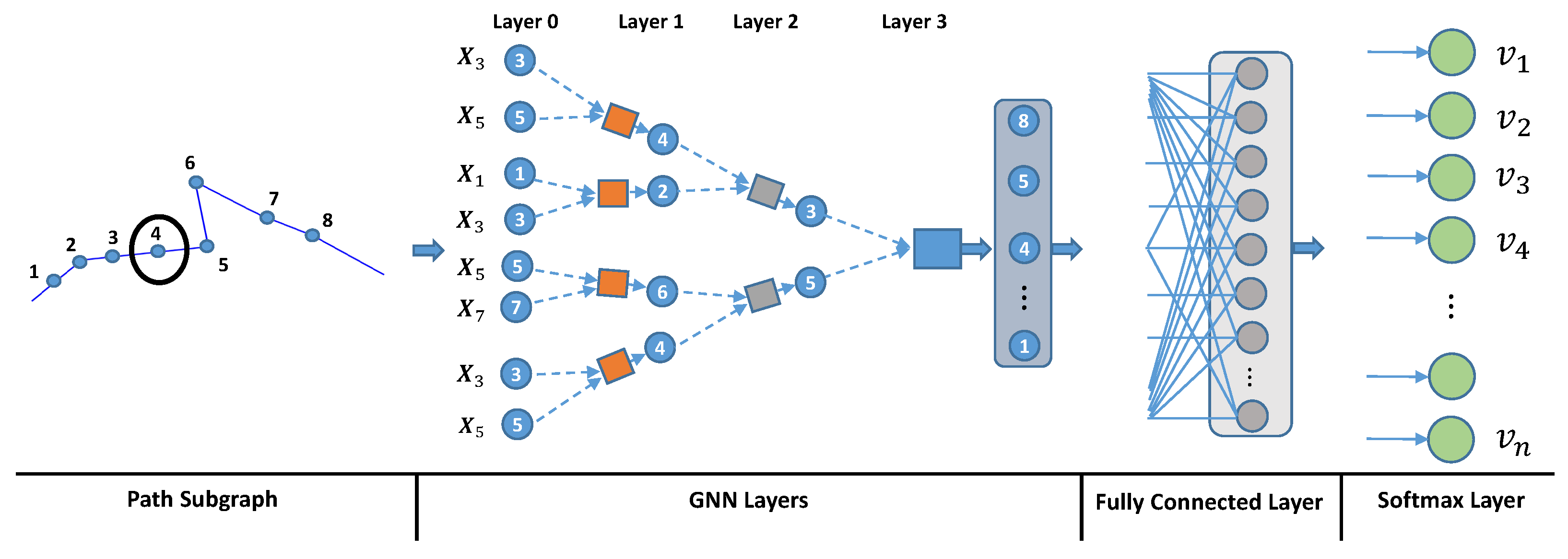
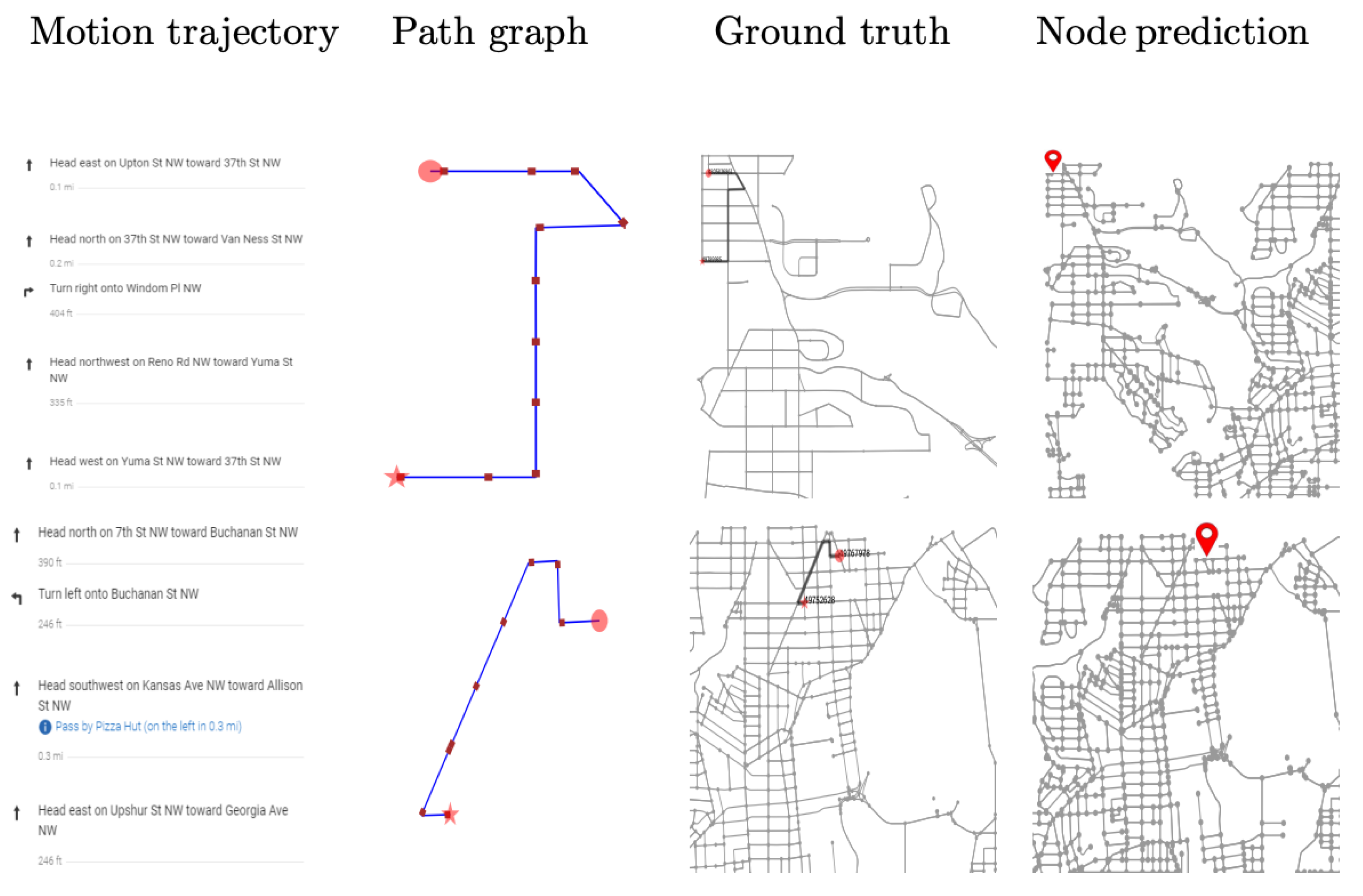
3. Proposed Method
3.1. Problem Formulation
- Input subgraph: , , where is the number of nodes of the subgraph and d is the dimension of node attribute;
- Embedding stage: is the embedding of subgraph obtained from graph neural network;
- Classification stage: the subgraph embedding is classified into label , through fully-connected neural network, where is the output label space and n is the number of nodes in the topological map;
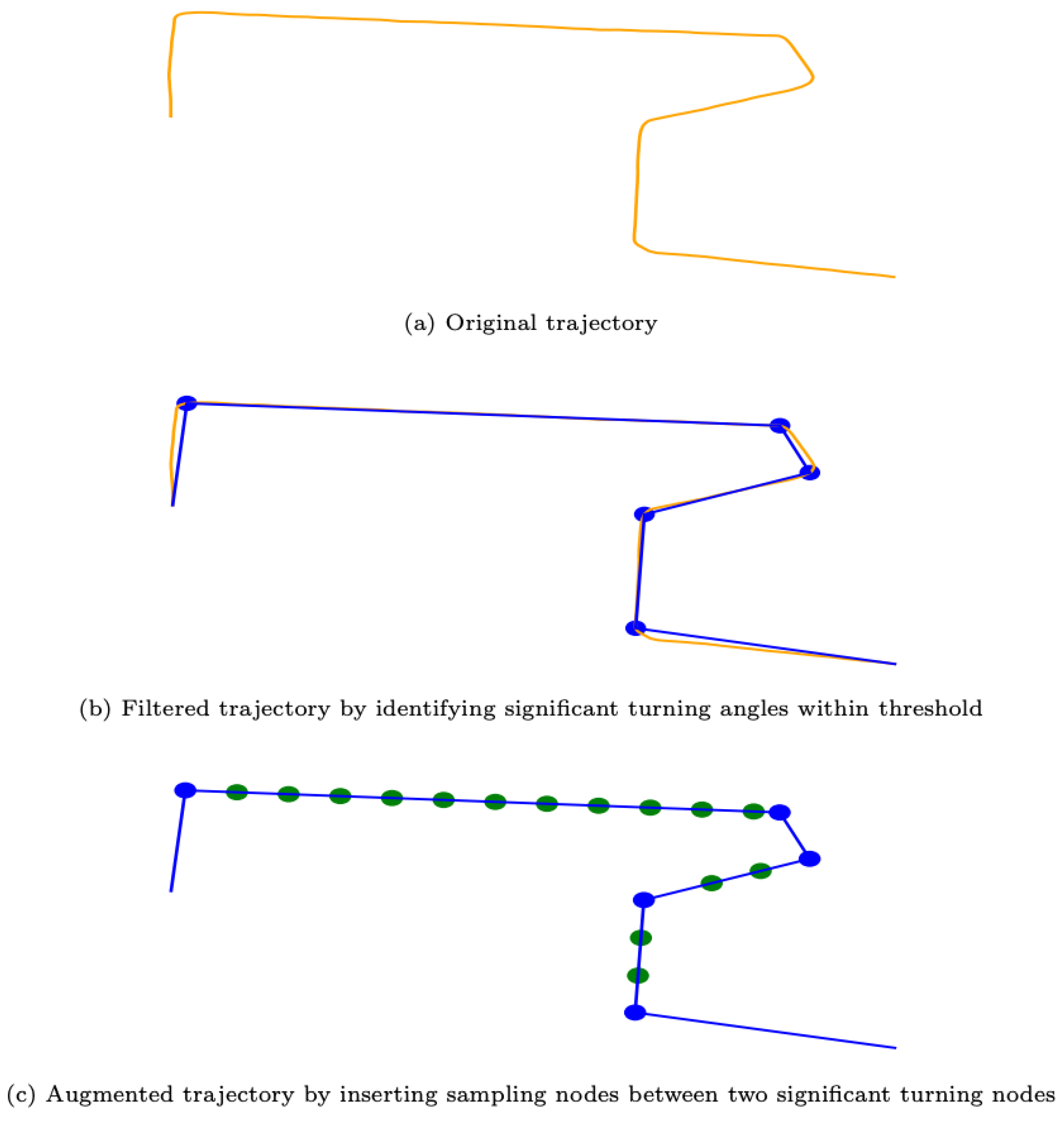
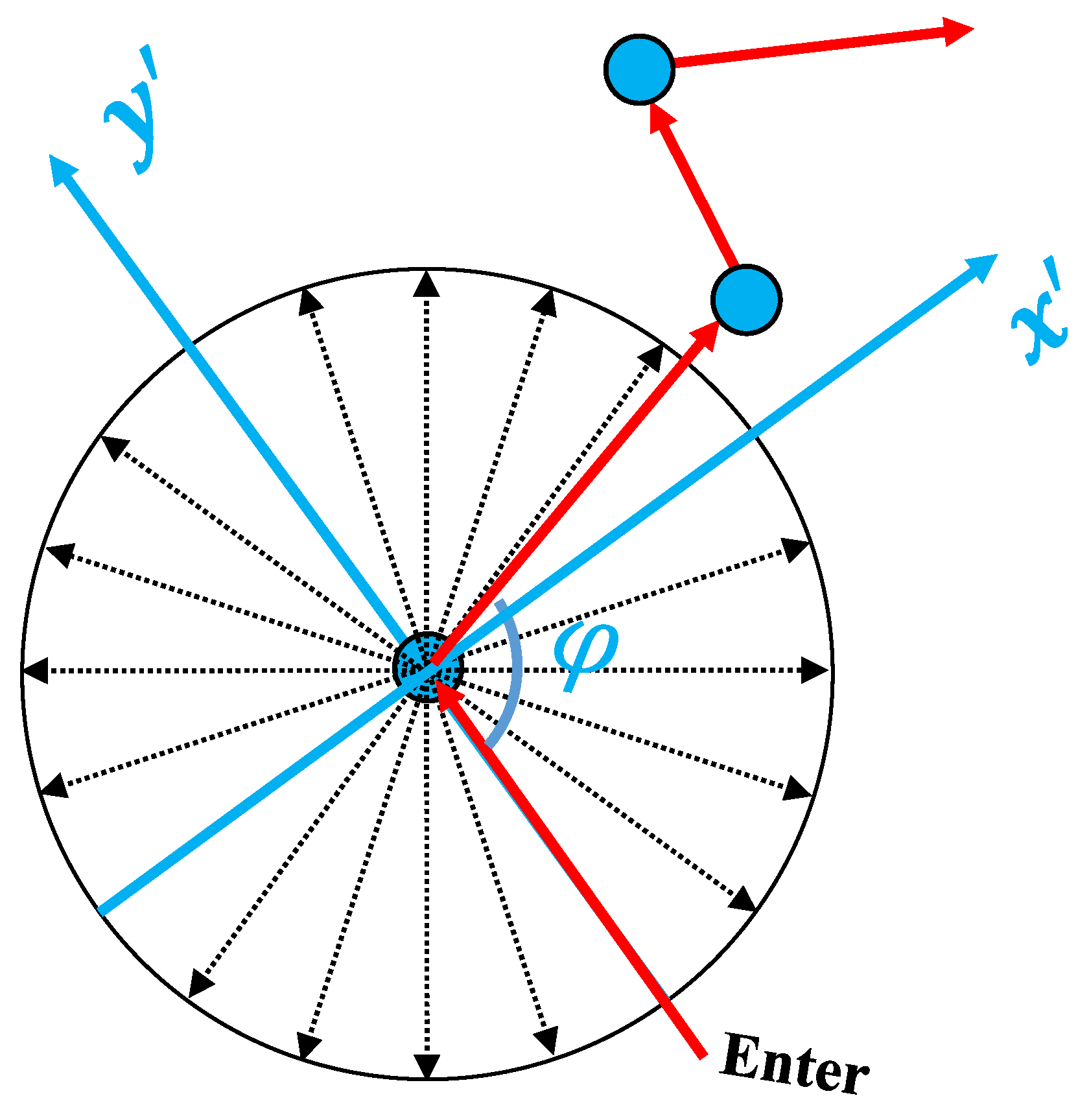
3.2. Subgraph Representation
3.3. Embedding Stage
3.4. Classification Stage
4. Experiments
4.1. Dataset
4.1.1. Map Generation
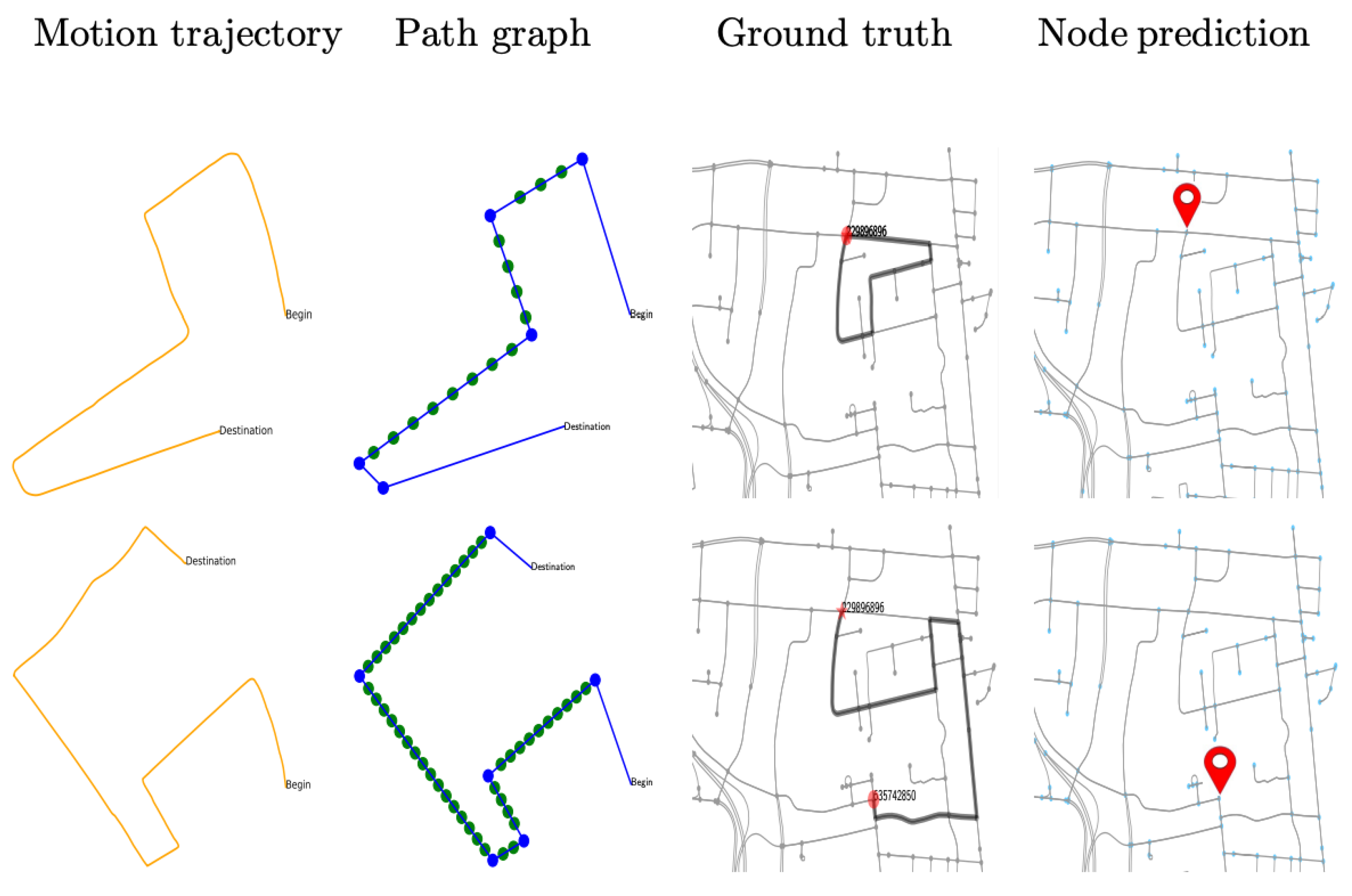
4.1.2. Map-Based Trajectory Generation
4.1.3. Generating Real Trajectory Data for Testing
4.2. Training Process
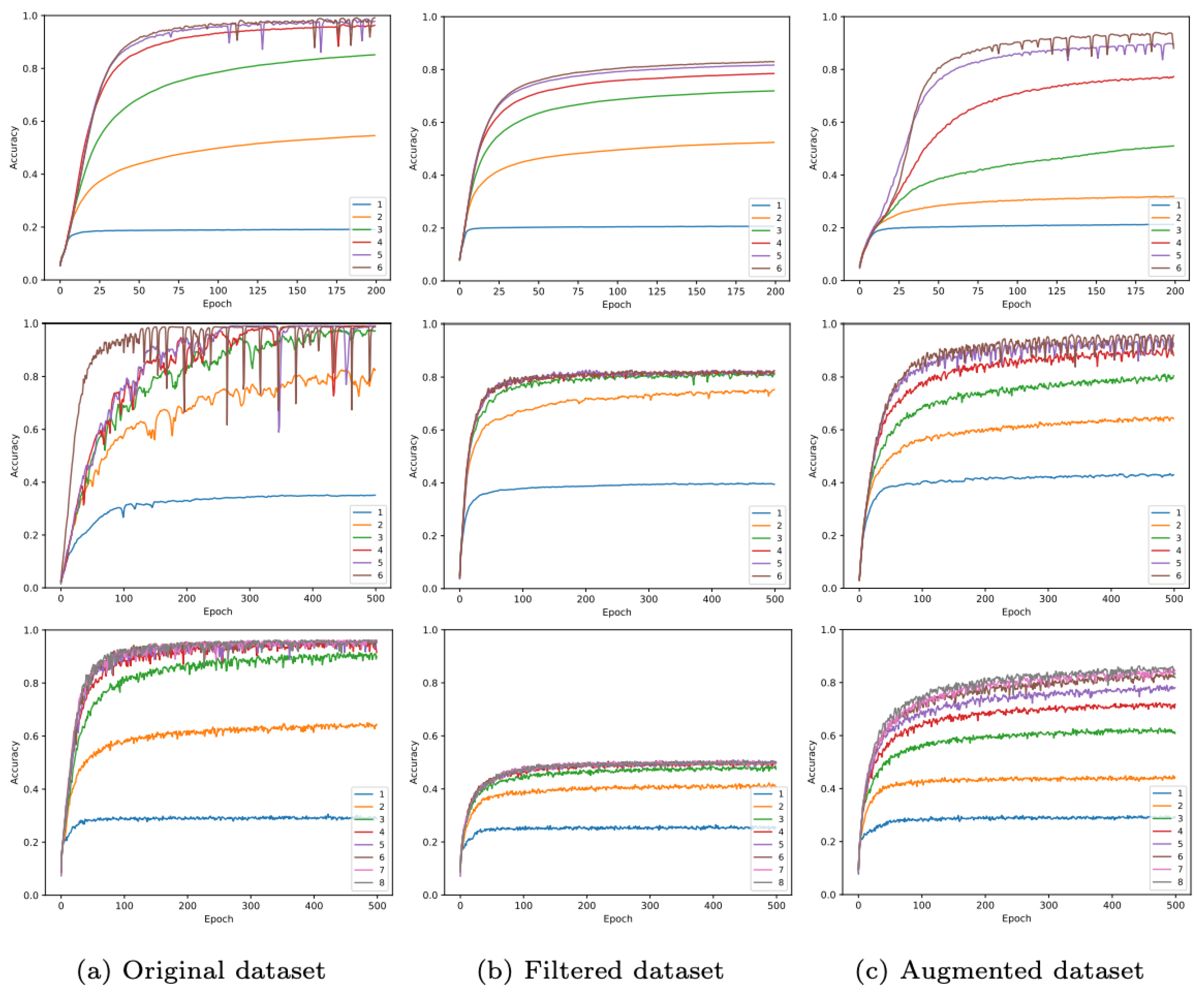
5. Results and Analyses
5.1. Comparisons with Existing Methods
5.2. Ablation Study
5.3. Discussions
5.3.1. Manhattan-World Ambiguity
5.3.2. Scalability
5.3.3. Image as Complementary Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- El-Rabbany, A. Introduction to GPS: The Global Positioning System; Artech House: New York, NY, USA, 2002. [Google Scholar]
- Tolman, E.C. Cognitive maps in rats and men. Psychol. Rev. 1948, 55, 189. [Google Scholar] [CrossRef] [PubMed]
- Erdem, U.M.; Hasselmo, M. A goal-directed spatial navigation model using forward trajectory planning based on grid cells. Eur. J. Neurosci. 2012, 35, 916–931. [Google Scholar] [CrossRef] [PubMed]
- Banino, A.; Barry, C.; Uria, B.; Blundell, C.; Lillicrap, T.; Mirowski, P.; Pritzel, A.; Chadwick, M.J.; Degris, T.; Modayil, J.; et al. Vector-based navigation using grid-like representations in artificial agents. Nature 2018, 557, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Edvardsen, V.; Bicanski, A.; Burgess, N. Navigating with grid and place cells in cluttered environments. Hippocampus 2020, 30, 220–232. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Chen, K.; de Vicente, J.P.; Sepulveda, G.; Xia, F.; Soto, A.; Vázquez, M.; Savarese, S. A Behavioral Approach to Visual Navigation with Graph Localization Networks. In Proceedings of the Robotics: Science and Systems, Breisgau, Germany, 22–26 June 2019. [Google Scholar] [CrossRef]
- Reid, T.G.; Chan, B.; Goel, A.; Gunning, K.; Manning, B.; Martin, J.; Neish, A.; Perkins, A.; Tarantino, P. Satellite navigation for the age of autonomy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, ON, USA, 20–23 April 2020; pp. 342–352. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- McNaughton, B.L.; Battaglia, F.P.; Jensen, O.; Moser, E.I.; Moser, M.B. Path integration and the neural basis of the ‘cognitive map’. Nat. Rev. Neurosci. 2006, 7, 663–678. [Google Scholar] [CrossRef]
- Bush, D.; Barry, C.; Manson, D.; Burgess, N. Using grid cells for navigation. Neuron 2015, 87, 507–520. [Google Scholar] [CrossRef]
- Hafting, T.; Fyhn, M.; Molden, S.; Moser, M.B.; Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. Nature 2005, 436, 801–806. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Shi, W.; Rajkumar, R. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1711–1719. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Kendall, A.; Cipolla, R. Geometric loss functions for camera pose regression with deep learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5974–5983. [Google Scholar]
- Sattler, T.; Leibe, B.; Kobbelt, L. Fast image-based localization using direct 2d-to-3d matching. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 667–674. [Google Scholar]
- Sattler, T.; Zhou, Q.; Pollefeys, M.; Leal-Taixe, L. Understanding the limitations of cnn-based absolute camera pose regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3302–3312. [Google Scholar]
- Weyand, T.; Kostrikov, I.; Philbin, J. Planet-photo geolocation with convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 37–55. [Google Scholar]
- Hays, J.; Efros, A.A. IM2GPS: Estimating geographic information from a single image. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, Alaska, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Walch, F.; Hazirbas, C.; Leal-Taixe, L.; Sattler, T.; Hilsenbeck, S.; Cremers, D. Image-based localization using lstms for structured feature correlation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 627–637. [Google Scholar]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Object retrieval with large vocabularies and fast spatial matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MI, USA, 18–23 June 2007; pp. 1–8. [Google Scholar]
- Perronnin, F.; Liu, Y.; Sánchez, J.; Poirier, H. Large-scale image retrieval with compressed fisher vectors. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3384–3391. [Google Scholar]
- Jégou, H.; Douze, M.; Schmid, C.; Pérez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3304–3311. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5297–5307. [Google Scholar]
- Lin, T.Y.; Cui, Y.; Belongie, S.; Hays, J. Learning deep representations for ground-to-aerial geolocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5007–5015. [Google Scholar]
- Oh, S.M.; Tariq, S.; Walker, B.N.; Dellaert, F. Map-based priors for localization. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2179–2184. [Google Scholar]
- Brubaker, M.A.; Geiger, A.; Urtasun, R. Map-based probabilistic visual self-localization. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 652–665. [Google Scholar] [CrossRef]
- Floros, G.; Van Der Zander, B.; Leibe, B. Openstreetslam: Global vehicle localization using openstreetmaps. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1054–1059. [Google Scholar]
- Gupta, A.; Chang, H.; Yilmaz, A. Gps-denied geo-localisation using visual odometry. In Proceedings of the ISPRS Annual Photogrammetry, Remote Sensing Spatial Information Science, Prague, Czech Republic, 12–19 July 2016; pp. 263–270. [Google Scholar]
- Gupta, A.; Yilmaz, A. Ubiquitous real-time geo-spatial localization. In Proceedings of the Eighth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Burlingame, CA, USA, 31 October 2016; pp. 1–10. [Google Scholar]
- Thrun, S. Probabilistic robotics. Commun. ACM 2002, 45, 52–57. [Google Scholar] [CrossRef]
- Costea, D.; Leordeanu, M. Aerial image geolocalization from recognition and matching of roads and intersections. arXiv 2016, arXiv:1605.08323. [Google Scholar]
- Panphattarasap, P.; Calway, A. Automated map reading: Image based localisation in 2-D maps using binary semantic descriptors. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6341–6348. [Google Scholar]
- Wei, J.; Koroglu, M.T.; Zha, B.; Yilmaz, A. Pedestrian localization on topological maps with neural machine translation network. In Proceedings of the 2019 IEEE Sensors, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Zha, B.; Koroglu, M.T.; Yilmaz, A. Trajectory Mining for Localization Using Recurrent Neural Network. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 1329–1332. [Google Scholar]
- Zha, B.; Yilmaz, A. Learning maps for object localization using visual-inertial odometry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 1, 343–350. [Google Scholar] [CrossRef]
- O’Keefe, J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976, 51, 78–109. [Google Scholar] [CrossRef]
- O’Keefe, J.; Dostrovsky, J. The hippocampus as a spatial map: Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971, 34, 171–175. [Google Scholar] [CrossRef]
- Fey, M.; Lenssen, J.E.; Weichert, F.; Müller, H. Splinecnn: Fast geometric deep learning with continuous b-spline kernels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 869–877. [Google Scholar]
- Henaff, M.; Bruna, J.; LeCun, Y. Deep convolutional networks on graph-structured data. arXiv 2015, arXiv:1506.05163. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- He, S.; Bastani, F.; Jagwani, S.; Park, E.; Abbar, S.; Alizadeh, M.; Balakrishnan, H.; Chawla, S.; Madden, S.; Sadeghi, M.A. RoadTagger: Robust road attribute inference with graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 10965–10972. [Google Scholar]
- Derrow-Pinion, A.; She, J.; Wong, D.; Lange, O.; Hester, T.; Perez, L.; Nunkesser, M.; Lee, S.; Guo, X.; Wiltshire, B.; et al. ETA Prediction with Graph Neural Networks in Google Maps. arXiv 2021, arXiv:2108.11482. [Google Scholar]
- Iddianozie, C.; McArdle, G. Improved Graph Neural Networks for Spatial Networks Using Structure-Aware Sampling. ISPRS Int. J. Geo-Inf. 2020, 9, 674. [Google Scholar] [CrossRef]
- Bahl, G.; Bahri, M.; Lafarge, F. Road extraction from overhead images with graph neural networks. arXiv 2021, arXiv:2112.05215. [Google Scholar]
- Rowland, D.C.; Roudi, Y.; Moser, M.B.; Moser, E.I. Ten years of grid cells. Annu. Rev. Neurosci. 2016, 39, 19–40. [Google Scholar] [CrossRef]
- Klatzky, R.; Freksa, C.; Habel, C.; Wender, K. Spatial Cognition: An Interdisciplinary Approach to Representing and Processing Spatial Knowledge; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Lou, Z.; You, J.; Wen, C.; Canedo, A.; Leskovec, J. Neural Subgraph Matching. arXiv 2020, arXiv:2007.03092. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sedgewick, R. Algorithms in C, Part 5: Graph Algorithms, 3rd ed.; Addison-Wesley Professional: Boston, MA, USA, 2001. [Google Scholar]
- Hua, J.; Zhang, Y.; Yilmaz, A. The Mobile AR Sensor Logger for Android and iOS Devices. In Proceedings of the 2019 IEEE Sensors, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Samano, N.; Zhou, M.; Calway, A. You are here: Geolocation by embedding maps and images. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 502–518. [Google Scholar]
- Vojir, T.; Budvytis, I.; Cipolla, R. Efficient Large-Scale Semantic Visual Localization in 2D Maps. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Amini, A.; Rosman, G.; Karaman, S.; Rus, D. Variational end-to-end navigation and localization. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8958–8964. [Google Scholar]
- Zha, B.; Yilmaz, A. Map-Based Temporally Consistent Geolocalization through Learning Motion Trajectories. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 31–36. [Google Scholar]
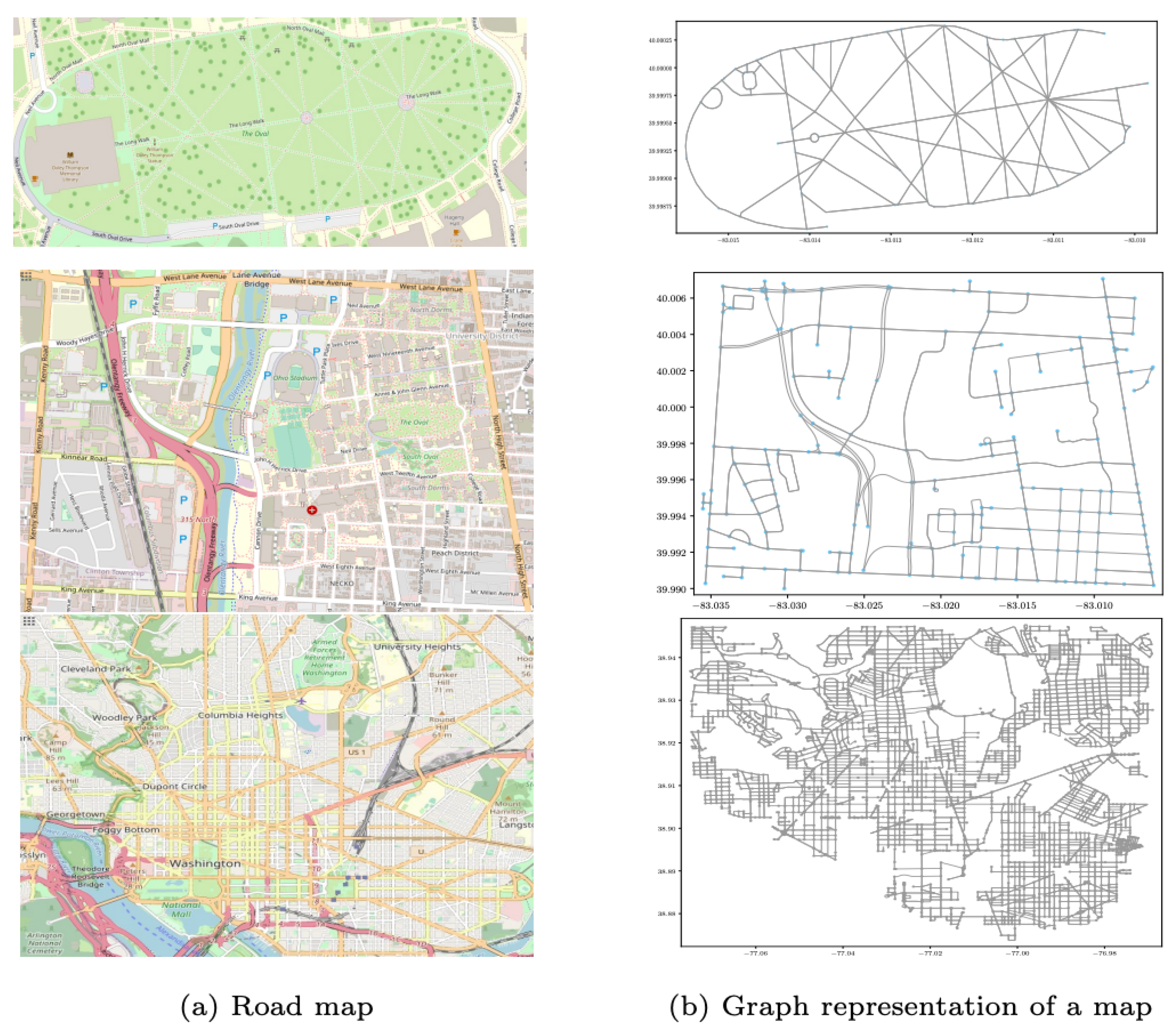


| Location | Node | Edge | Map Size | Avg. Centrality | |
|---|---|---|---|---|---|
| Small-sized map (S) | OSU Oval | 91 | 155 | 0.16 km ∗ 0.5 km | 3.5 |
| Medium-sized map (M) | OSU Campus | 115 | 147 | 2.5 km ∗ 2.5 km | 2.54 |
| large-sized map (L) | Washington DC | 3038 | 8211 | 10 km ∗ 10 km | 2.66 |
| Original | Filtered | Augmented | ||||
|---|---|---|---|---|---|---|
| Num. | Cls. | Num. | Cls. | Num. | Cls. | |
| S | 235,132 | 29 | 231,967 | 29 | 231,967 | 29 |
| M | 10,574 | 72 | 8551 | 72 | 8551 | 72 |
| L | 644,088 | 1000 | 644,088 | 1000 | 644,088 | 1000 |
| Filtered Case | Augmented Case | |
|---|---|---|
| S: 20 | 14 (70%) | 17 (85%) |
| M: 10 | 7 (70%) | 9 (90%) |
| L: 50 | 25 (50%) | 42 (84%) |
| Method | Model | Map | Localization | Initial Position | NN | Input | Accuracy |
|---|---|---|---|---|---|---|---|
| 2013 OpenStreetSLAM [35] | MCL | Graph | Metric | ✓ | ✗ | Image | ∼5 m |
| 2015 Brubaker et al. [34] | State-Space | Graph | Metric | ✓ | ✗ | Image | ∼4 m |
| 2017 Gupta et al. [36] | Graph Search | Graph | Metric | ✗ | ✗ | Image/IMU | ∼5 m |
| 2019 Amini et al. [63] | Variational NN | Tile | Metric | ✓ | ✓ | Image | − |
| 2019 Chen et al. [7] | CNN+GNN | Graph | Non-metric | ✓ | ✓ | RGBD | − |
| 2020 Wei et al. [41] | Seq2Seq | Graph | Non-metric | ✗ | ✓ | Motion | 95% |
| 2020 Zha et al. [43,64] | RNN | Graph | Non-metric | ✗ | ✓ | Motion | 93% |
| 2020 Samano et al. [61] | CNN | Tile | Non-metric | ✗ | ✓ | Image | 90% |
| Graph (S) | 93.61% | ||||||
| Ours | GNN | Graph (M) | Non-metric | ✗ | ✓ | Motion | 95.53% |
| Graph (L) | 87.56% |
| Nodes | S | M | L | |||
|---|---|---|---|---|---|---|
| Filtered | Augmented | Filtered | Augmented | Filtered | Augmented | |
| 4 | 47.18% | 66.71% | 55.56% | 81.48% | - | - |
| 5 | 46.56% | 67.72% | 69.71% | 88.24% | 2.40% | 10.70% |
| 6 | 53.15% | 72.82% | 78.95% | 89.65% | 6.40% | 24.70% |
| 7 | 58.05% | 77.05% | 85.28% | 91.48% | 13.01% | 40.12% |
| 8 | 68.52% | 89.47% | 86.57% | 93.20% | 21.90% | 58.42% |
| 10 | 83.54% | 93.61% | 88.61% | 95.33% | 51.00% | 87.50% |
| Model | S | M | L | |||
|---|---|---|---|---|---|---|
| Filtered | Augmented | Filtered | Augmented | Filtered | Augmented | |
| GNN-GCN | 75.31% | 86.56% | 82.04% | 85.42% | 49.91% | 78.72% |
| GNN-GAT | 71.39% | 86.81% | 82.63% | 87.44% | 49.85% | 79.22% |
| GNN-SAGE | 83.54% | 93.61% | 88.61% | 95.33% | 51.20% | 87.55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, B.; Yilmaz, A. Subgraph Learning for Topological Geolocalization with Graph Neural Networks. Sensors 2023, 23, 5098. https://doi.org/10.3390/s23115098
Zha B, Yilmaz A. Subgraph Learning for Topological Geolocalization with Graph Neural Networks. Sensors. 2023; 23(11):5098. https://doi.org/10.3390/s23115098
Chicago/Turabian StyleZha, Bing, and Alper Yilmaz. 2023. "Subgraph Learning for Topological Geolocalization with Graph Neural Networks" Sensors 23, no. 11: 5098. https://doi.org/10.3390/s23115098
APA StyleZha, B., & Yilmaz, A. (2023). Subgraph Learning for Topological Geolocalization with Graph Neural Networks. Sensors, 23(11), 5098. https://doi.org/10.3390/s23115098






