Adaptive Context Caching for IoT-Based Applications: A Reinforcement Learning Approach
Abstract
1. Introduction
1.1. Why Cache Context Information?
1.2. Problems with Caching Context Information
1.3. Research Problems
- maximizes the cost efficiency (i.e., minimizes the cost of responding to context queries) of the CMP;
- maximizes the performance efficiency of the CMP, enabling it to respond in a timely manner to time-critical context queries;
- achieves a quasi-Pareto optimal state between the cost and performance efficiencies, and;
- minimizes the additional overhead of adaptation to the CMP.
- develops mathematical models to compute costs for context caching and performance efficiently, cache-context adaptively;
- proposes a novel, scalable selective context-caching agent developed based on the TD3 algorithm in RL, different from adaptive data-caching approaches;
- proposes a cost and performance-efficient adaptive context-refreshing policy with refreshing-policy shifting;
- develops a time-aware context-management scheme to efficiently handle the context-management lifecycle costs;
- develops the ACOCA mechanism that encompasses the life cycle of context management. The mechanism is scalable and computationally less expensive compared to benchmarks that encounter the exploding cost of adaptive context management;
- verifies our theories and mathematical models using test results obtained from our experiments using a real-world-inspired synthetically generated large context-query load;
- compares the cost and performance efficiency of a CMP using ACOCA against several traditional data-caching policies and another RL-based context-aware data-caching policy for benchmarking.
2. Motivating Scenario—Autonomous Car Parking
3. Related Work
3.1. Traditional Data Versus Context Information Caching
- there are billions of context entity instances (and growing) that are not scalable to monitor individually; hence, suitable indexing and binning techniques for context need to be investigated;
- unforeseen novel context information can be inferred with respect to retrieved data and context queries at any time;
- the same context information can be requested in context queries using different structures and formats (e.g., a context entity such as a vehicle can be defined using two or more different ontologies such as schema.org (https://schema.org/Vehicle, accessed on 27 February 2023) and MobiVoc (http://schema.mobivoc.org/#http://schema.org/Vehicle, accessed on 27 February 2023) by many consumers), which would duplicate monitoring;
- semantically similar context queries can request similar context information which, through monitoring, only previously observed context information discreetly using identifiers (e.g., as in [27]) will be incorrectly missed in the cache memory.
3.2. Overhead of Adaptive Context Caching
3.3. Lack of Implemented Adaptive Context-Caching Mechanisms
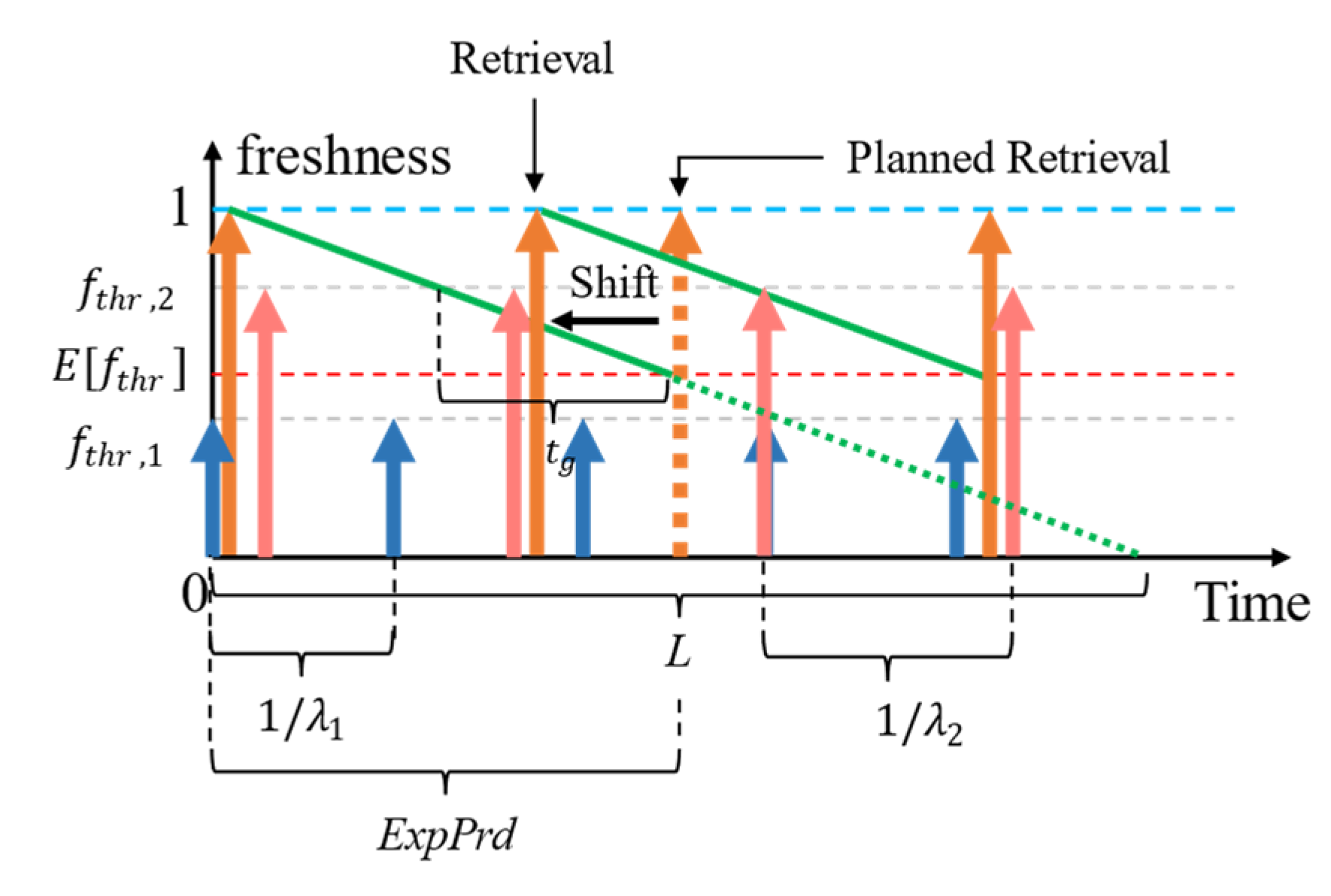
4. Adaptive Context Refreshing with Policy Shifting
4.1. Why Adaptive Refreshing with Policy Shifting?
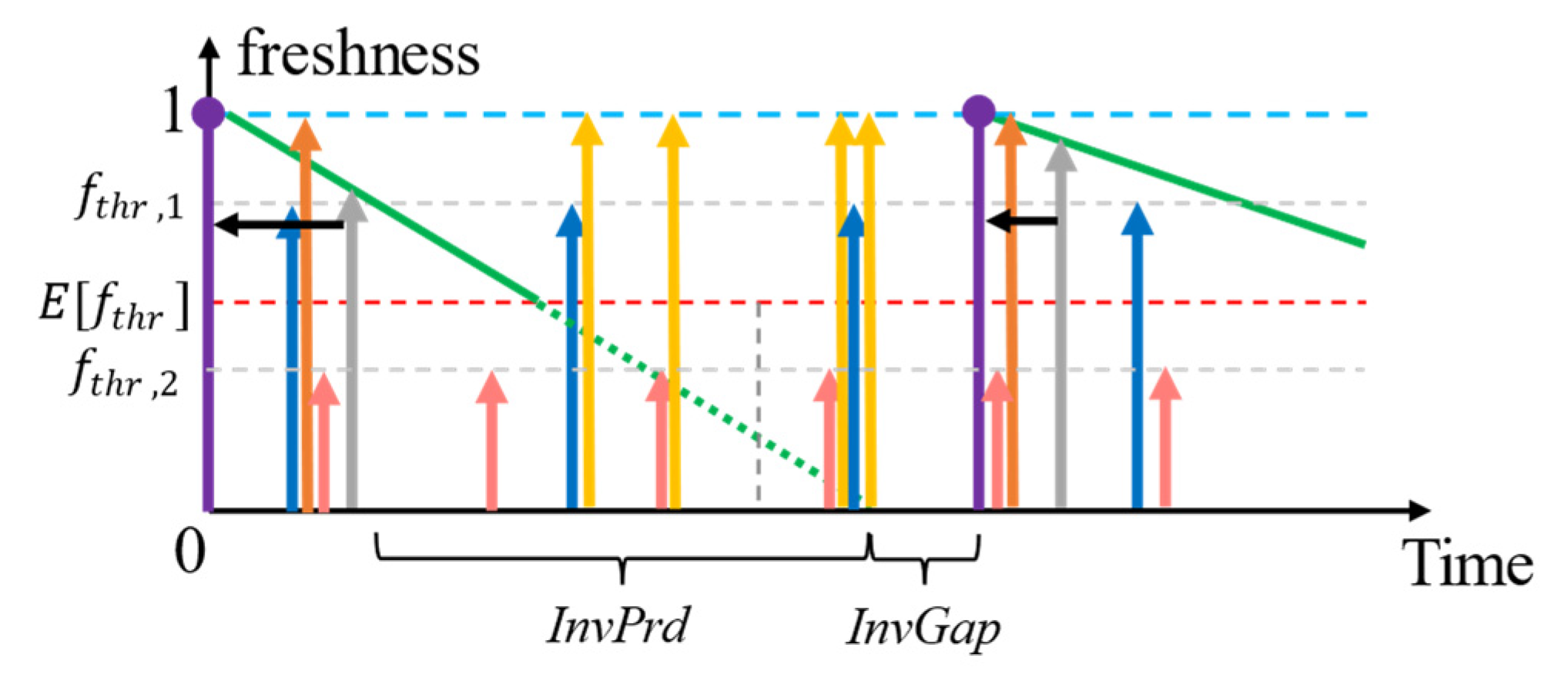
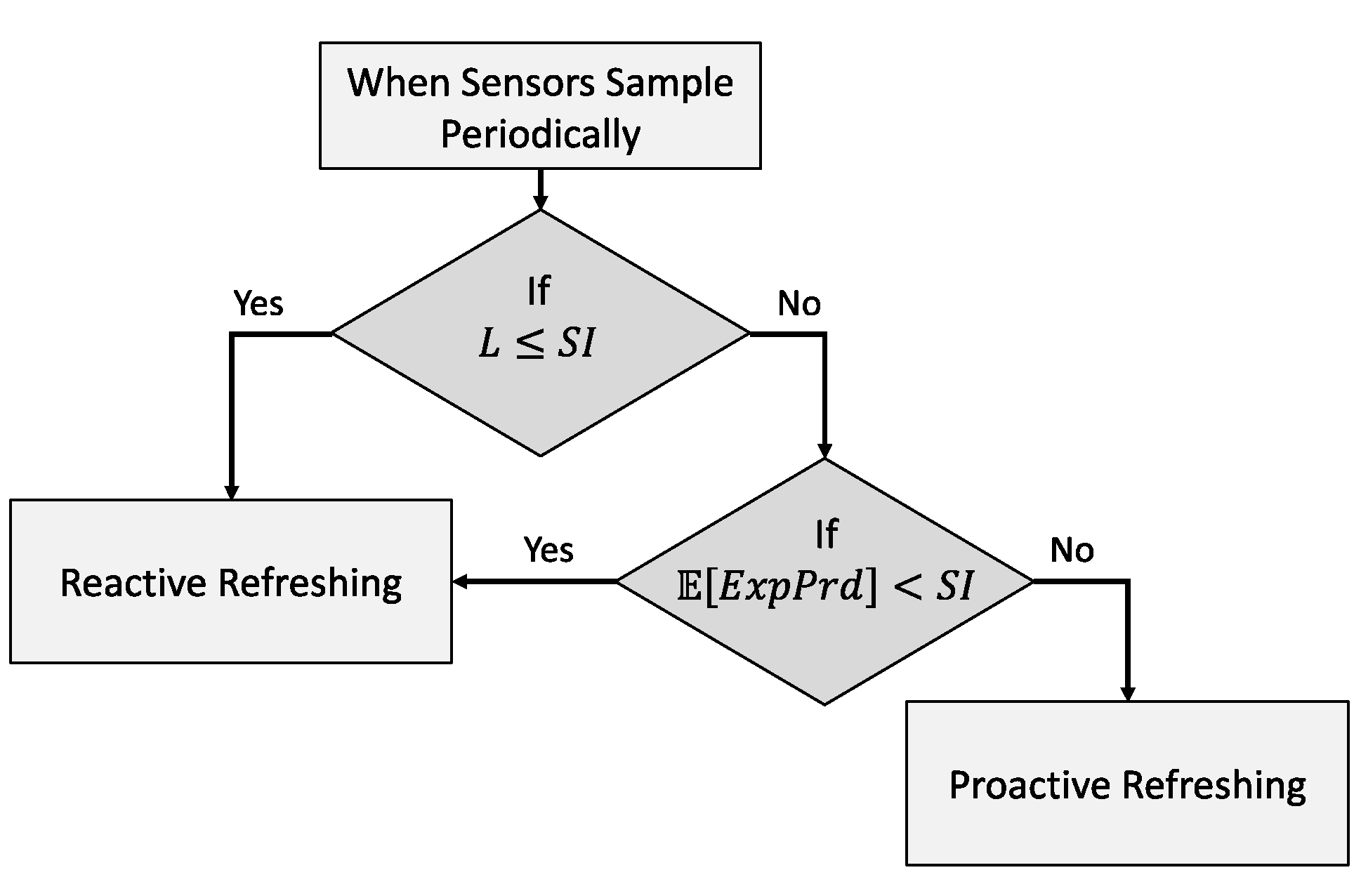
4.2. Adaptive Context Refresh Rate Setting
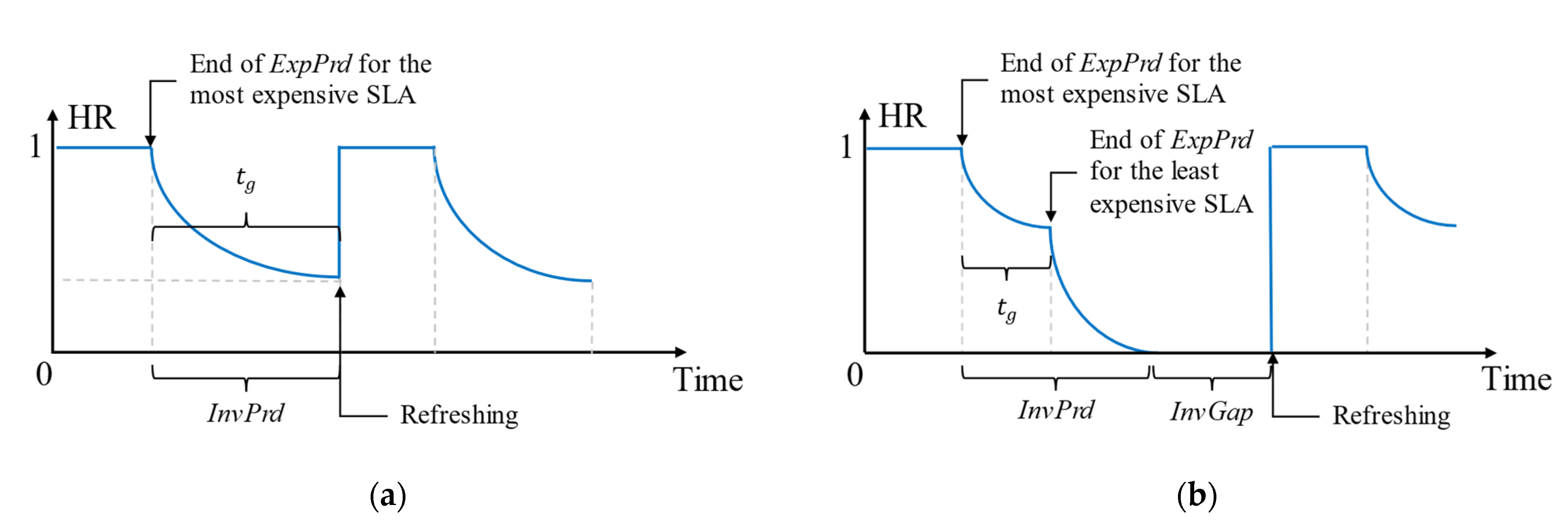
4.2.1. Handling the Different Context Lifetimes
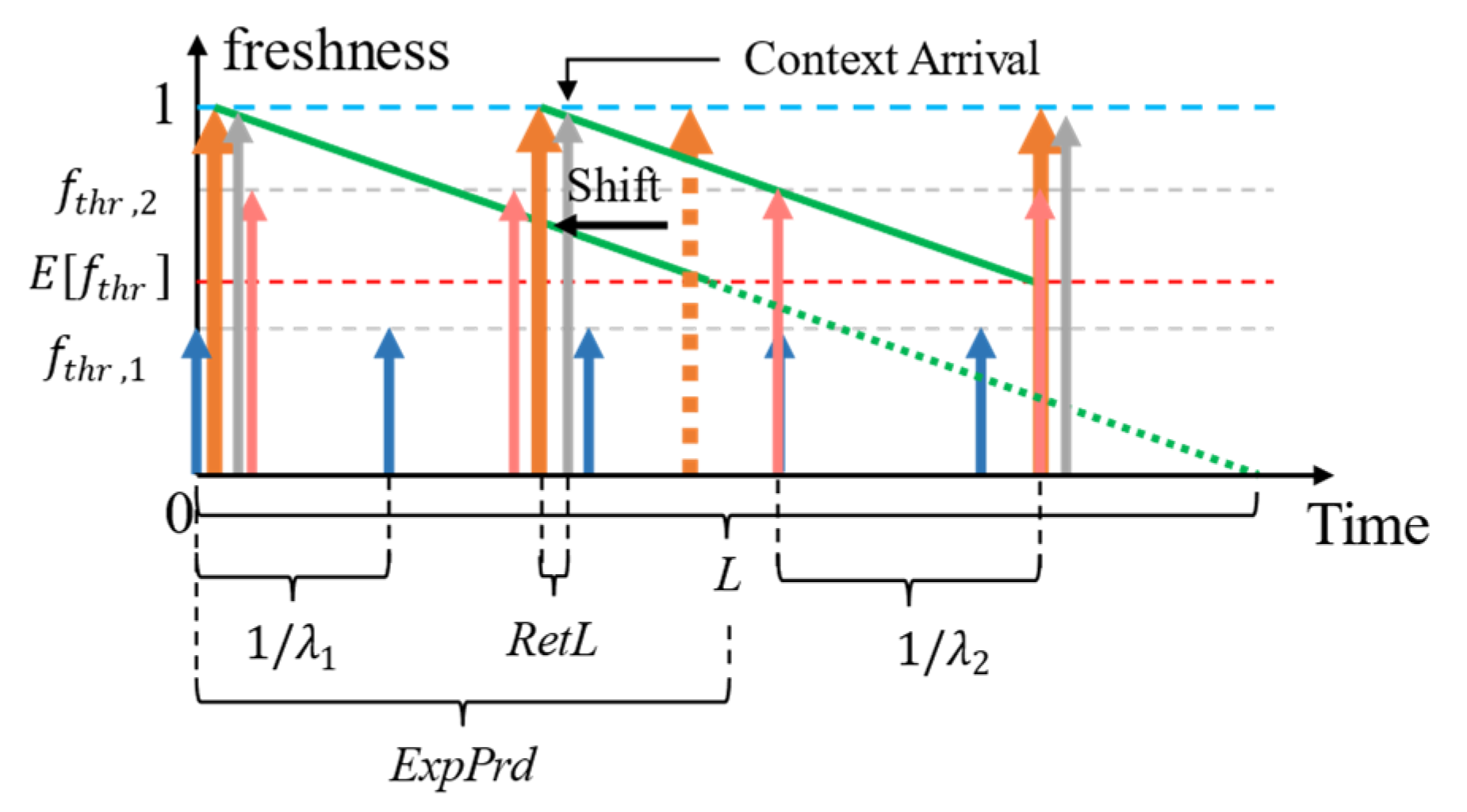
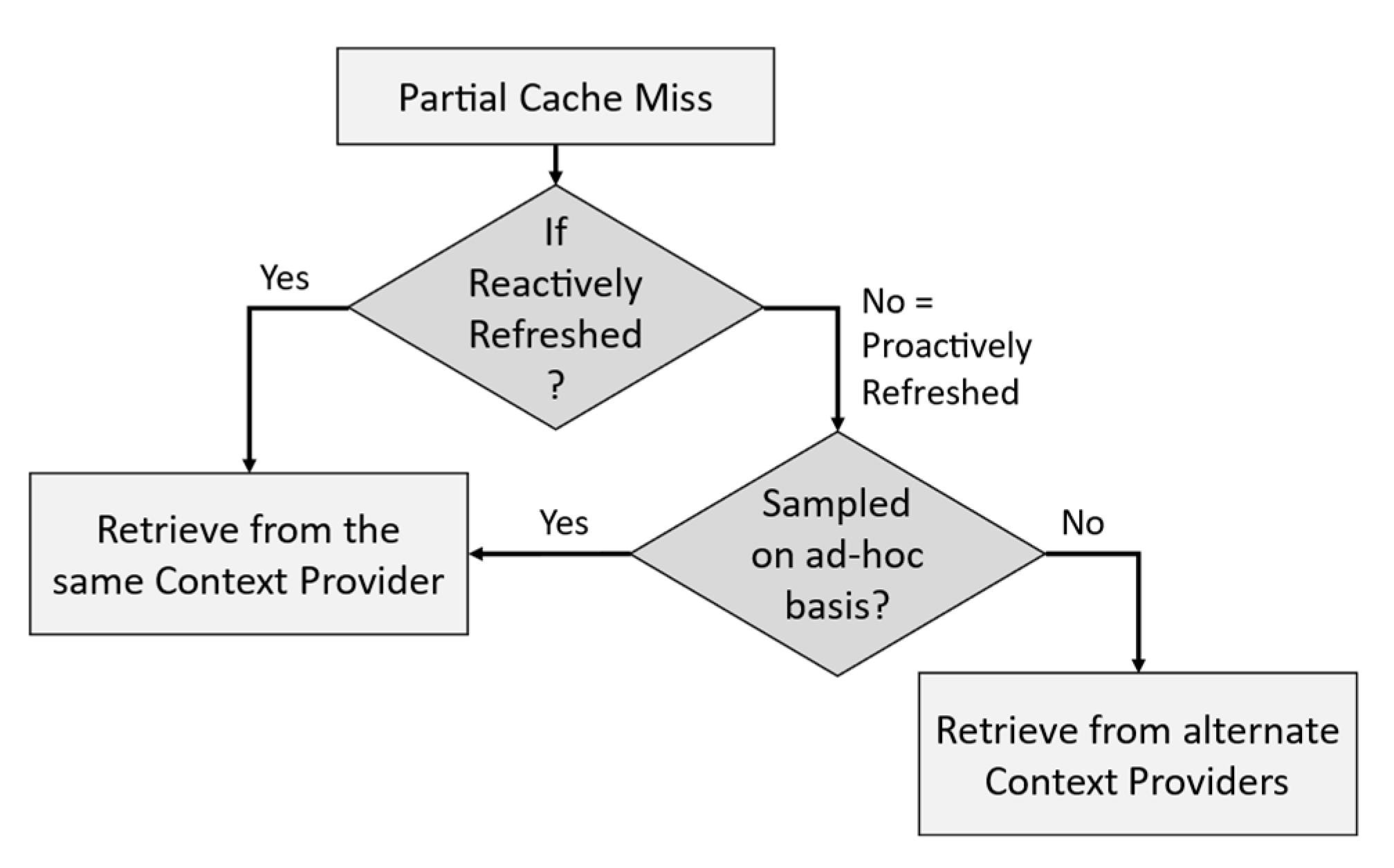
4.2.2. Synchronizing Context Refreshing to Maximize QoC and Using Alternate Context Retrievals
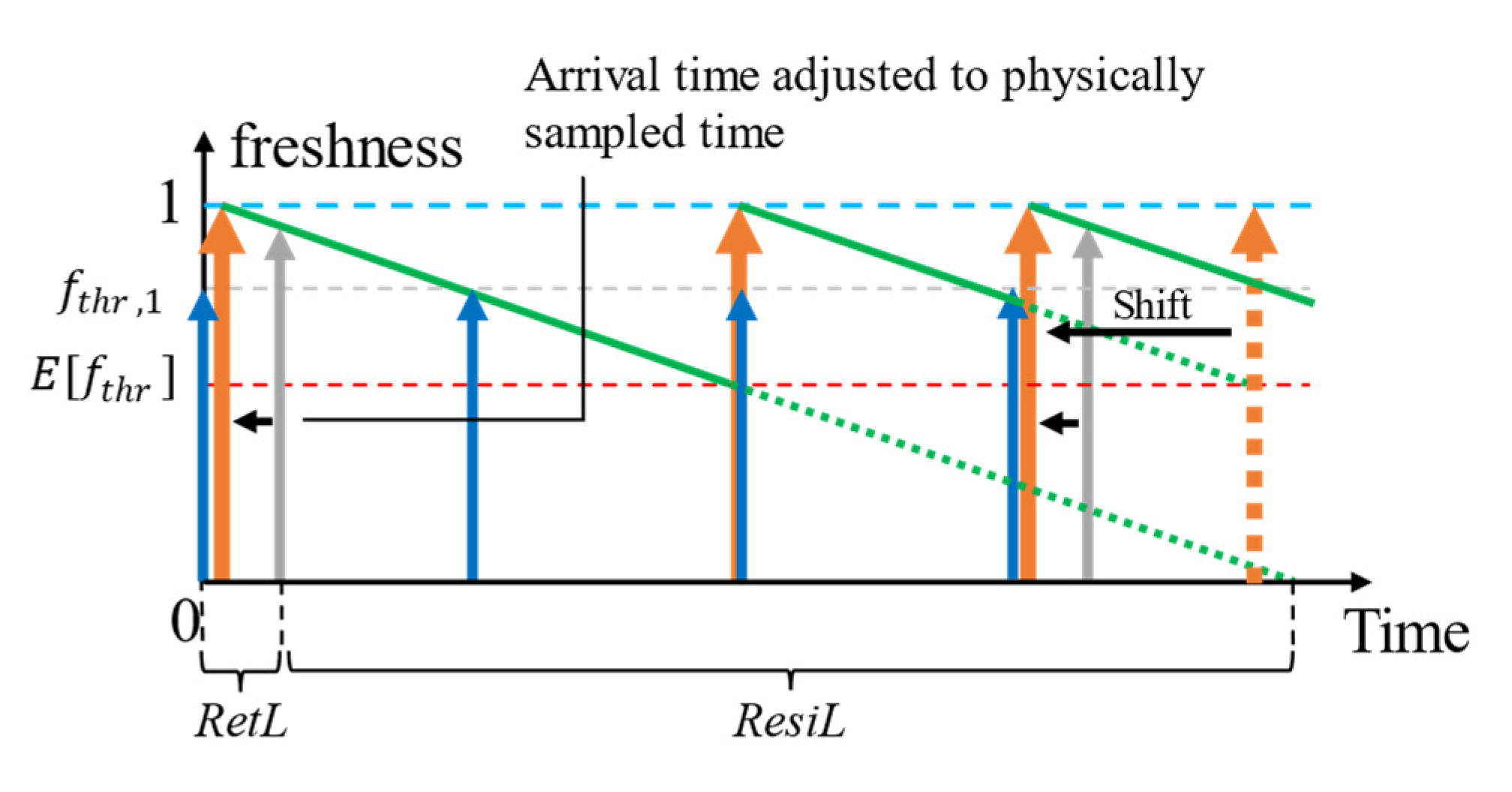
4.2.3. The Problem of Alternate Context Retrievals
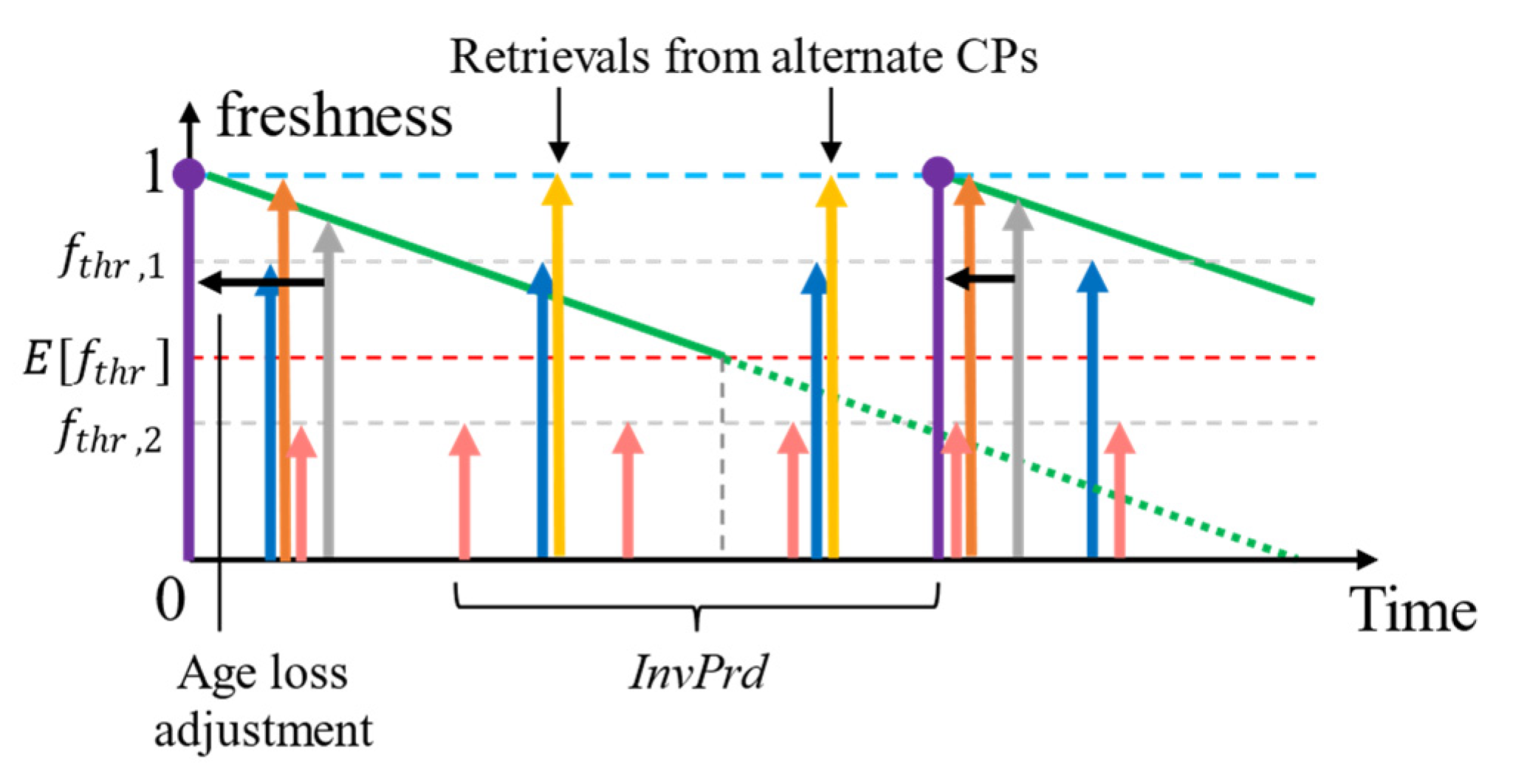
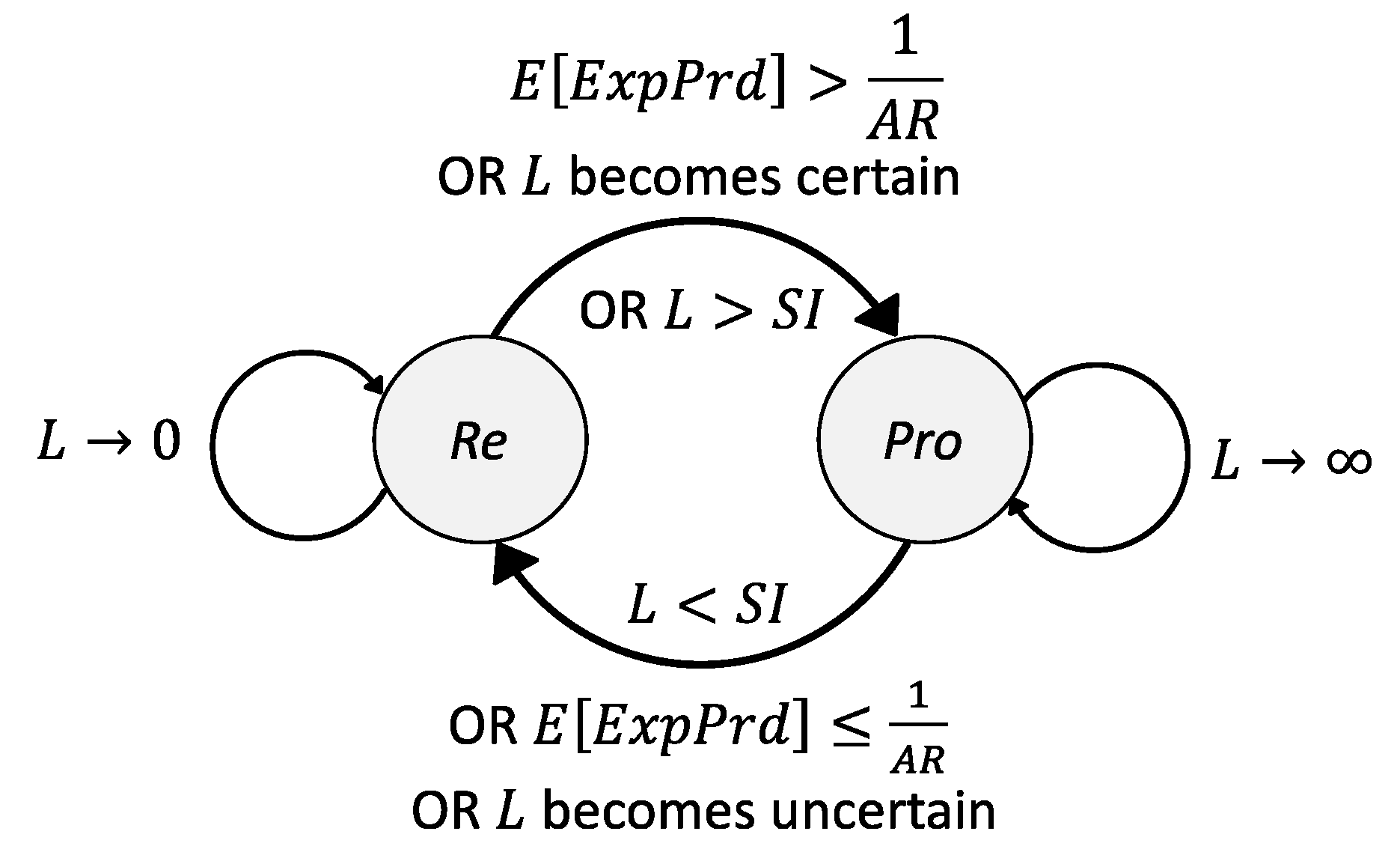
4.3. Adaptive Refresh Policy Shifting
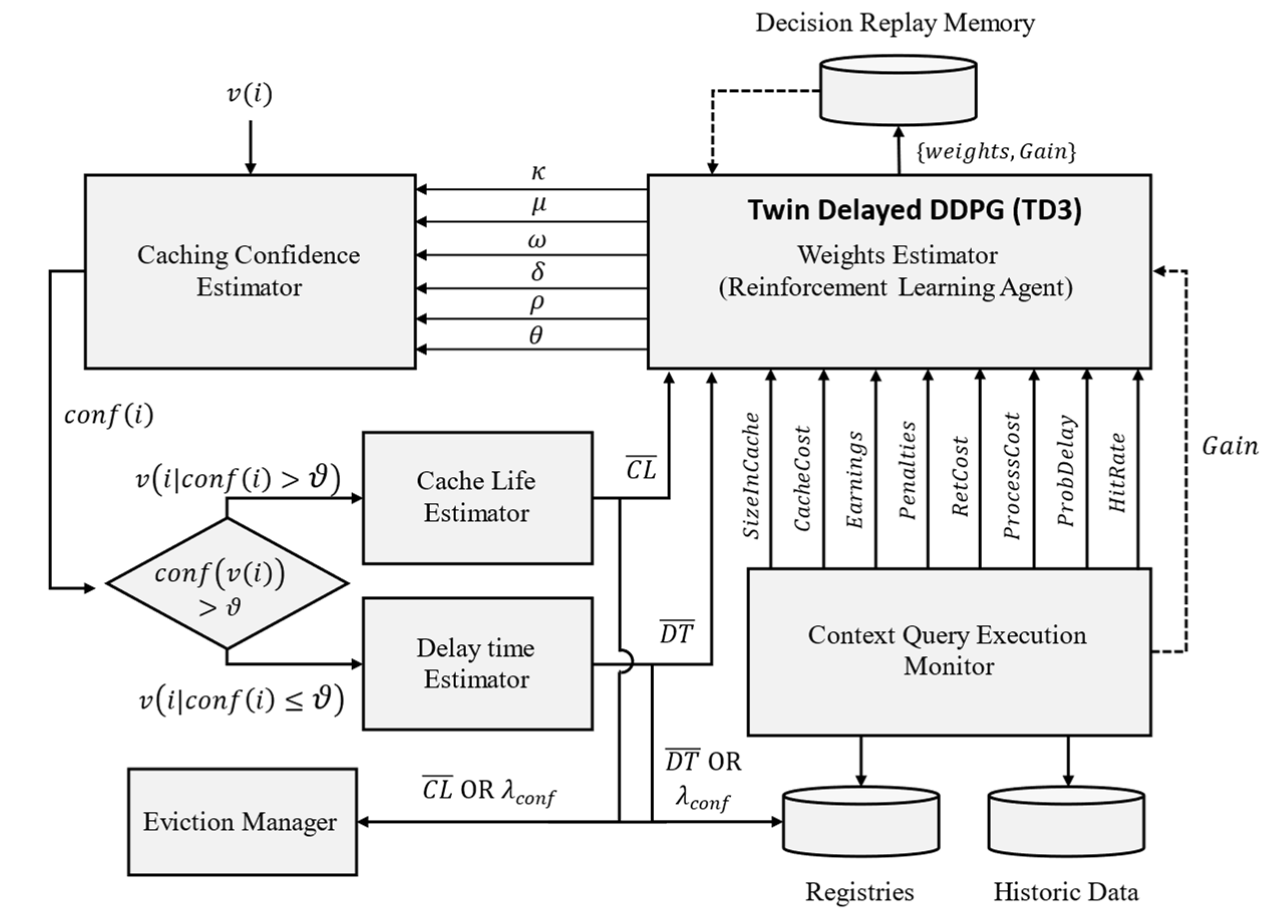
5. Reactive Context Cache Selection
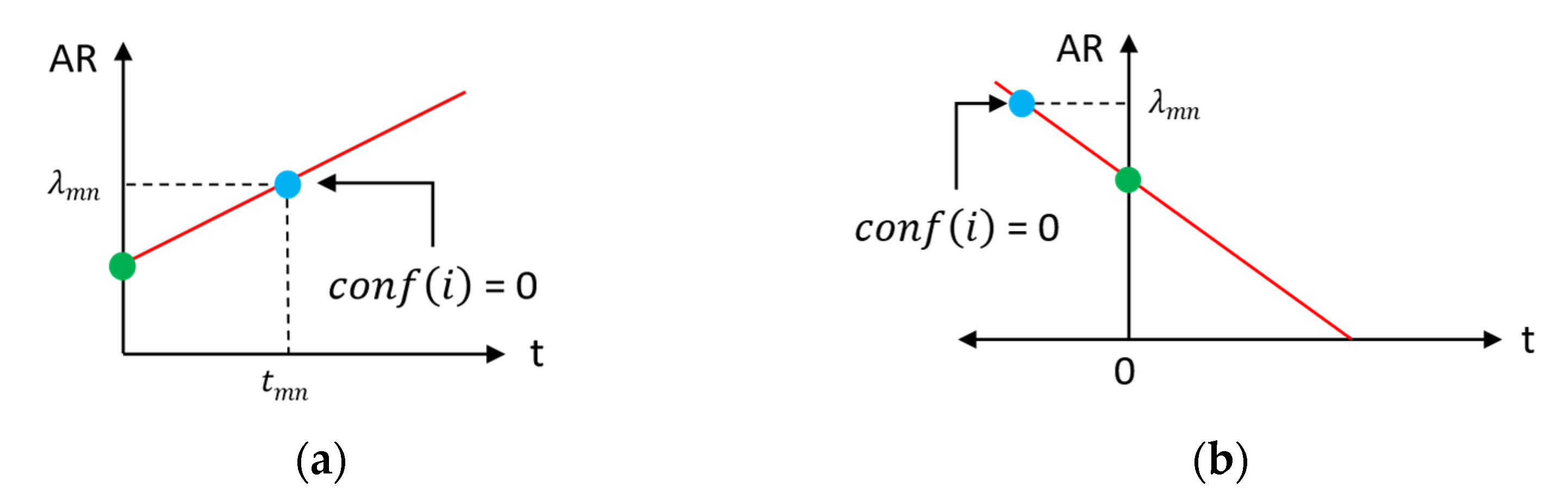
5.1. Confidence to Cache
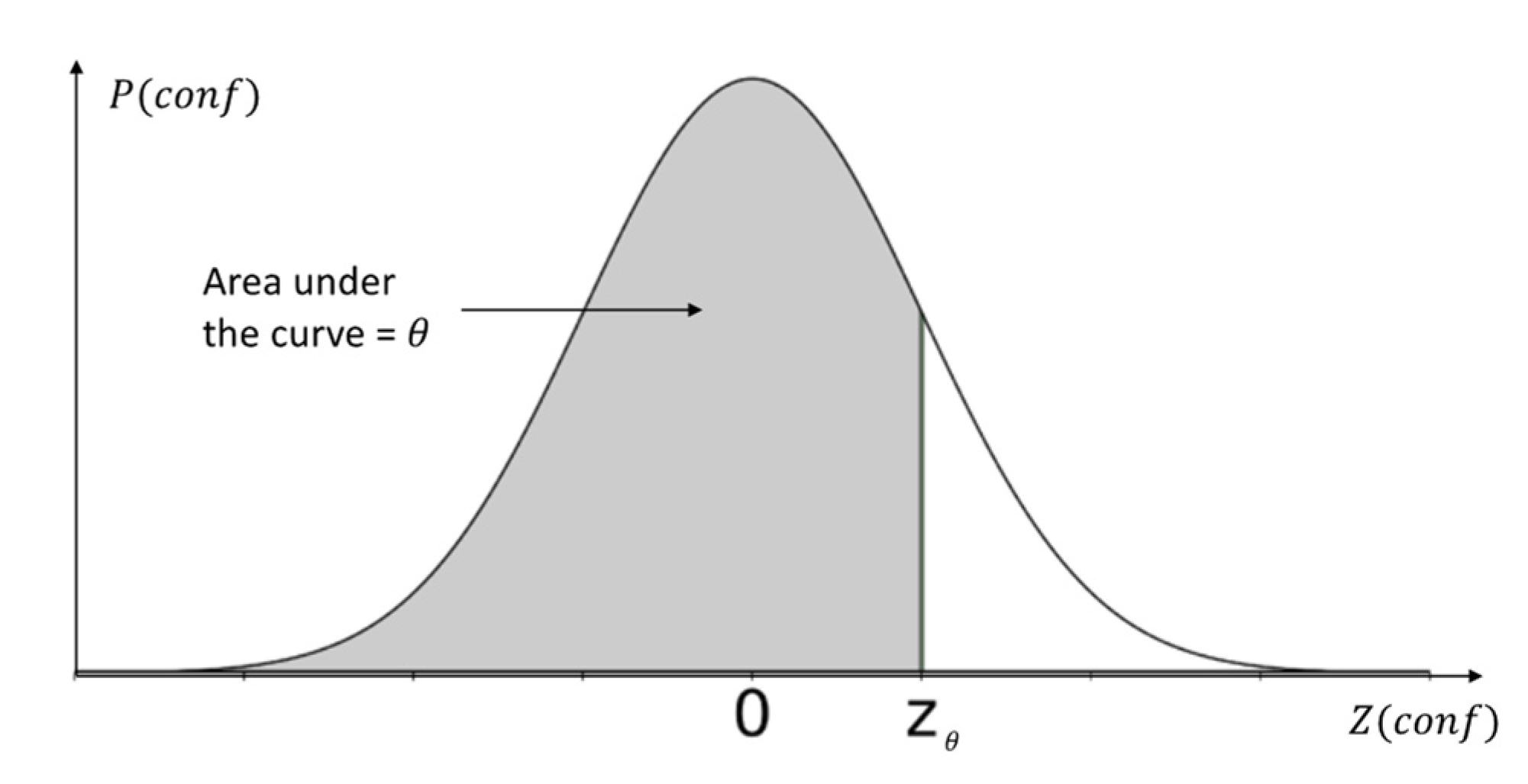
5.1.1. Deriving Confidence to Cache
5.1.2. Learning the Scalars and Optimizing the Selection Model
5.2. Access Trend
5.3. Cache Efficiency
5.4. Retrieval Efficiency
5.5. Un/Reliability of Retrieval
5.6. Expected Complexity of Context Queries That Use the Context to Respond to a Context Query
| prefix schema:http://schema.org pull (targetCarpark.*) define entity targetCarpark is from schema:ParkingFacility where targetCarpark.isOpen = true and targetCarpark.availableSlots > 0 and targetCarpark.price <= ${PRICE} |
| Query 1. Context query of low complexity (will refer to as the “Simple” query). |
| prefix schema:http://schema.org pull (targetCarpark.*) define entity targetLocation is from schema:Place where targetLocation.name=“${ADDRESS}”, entity consumerCar is from schema:Vehicle where consumerCar.vin=“${VIN}”, entity targetCarpark is from schema:ParkingFacility where distance(targetCarpark.location, targetLocation.location) < {“value”:${DISTANCE},”unit”:”m”} and targetCarpark.isOpen = true and targetCarpark.availableSlots > 0 and targetCarpark.rating >= ${RATING} and targetCarpark.price <= ${PRICE} and targetCarpark.maxHeight > consumerCar.height |
| Query 2. Context query of higher complexity to Query 1 (will refer to as the “Medium” query). |
| prefix schema:http://schema.org pull (targetCarpark.*) define entity targetLocation is from schema:Place where targetLocation.name=“${ADDRESS}”, entity consumerCar is from schema:Vehicle where consumerCar.vin=“${VIN}”, entity targetWeather is from schema:Thing where targetWeather.location=“Melbourne,Australia”, entity targetCarpark is from schema:ParkingFacility where ((distance(targetCarpark.location, targetLocation.location, “walking”) < {“value”:${DISTANCE},”unit”:”m”} and goodForWalking(targetWeather) >= 0.6) or goodForWalking(targetWeather) >= 0.9) and targetCarpark.isOpen = true and targetCarpark.availableSlots > 0 and targetCarpark.rating >= ${RATING} and targetCarpark.price <= ${PRICE} and targetCarpark.maxHeight > consumerCar.height |
| Query 3. Context query of higher complexity to Query 3 (will refer to as the “Complex” query). |
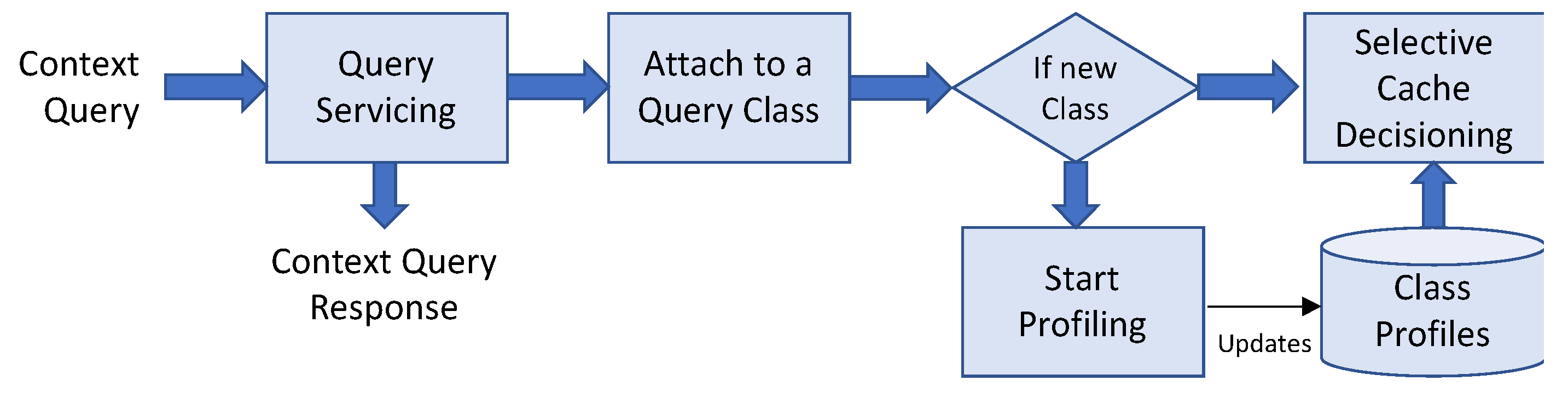
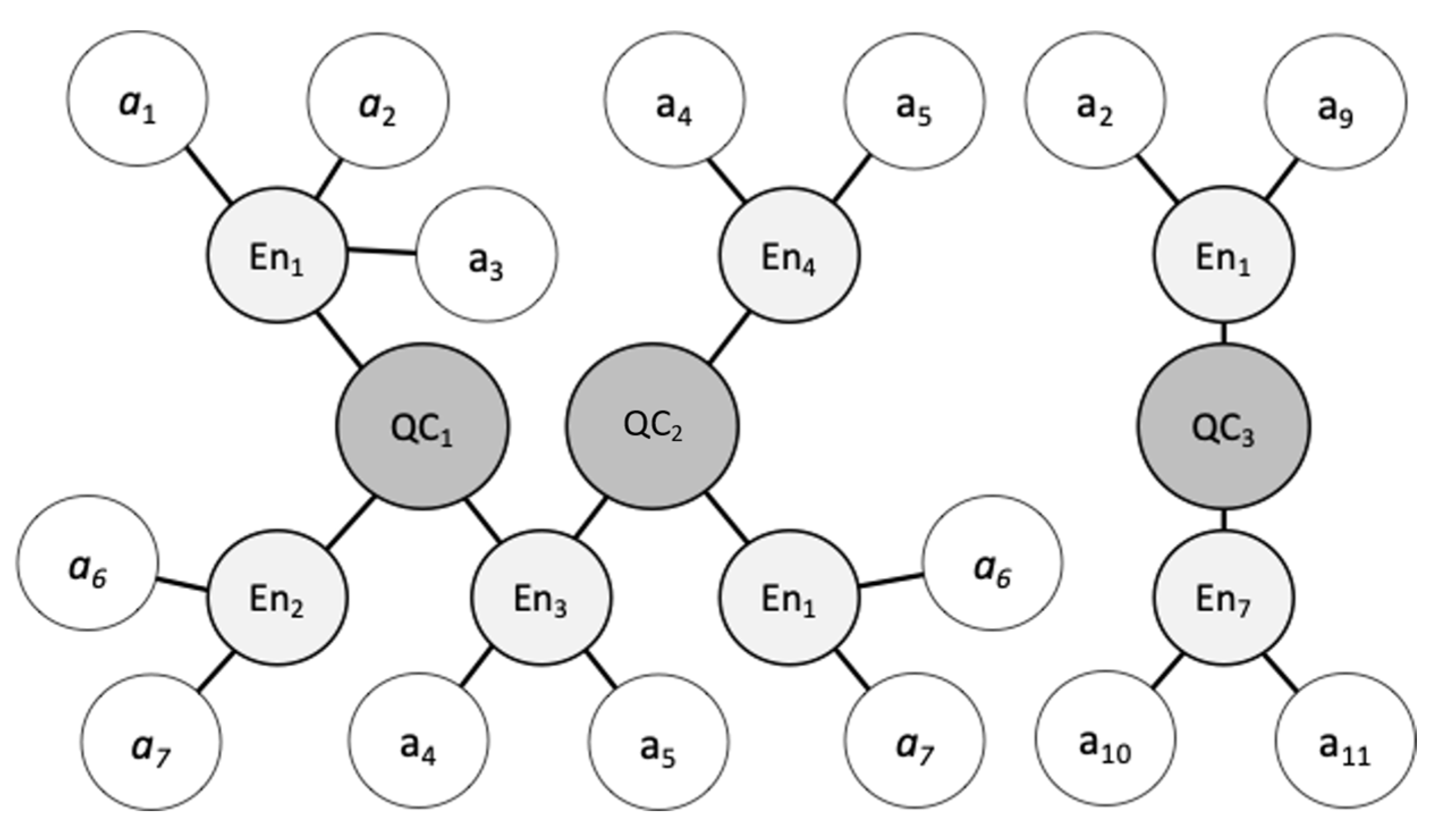
5.7. Context-Query Classes
- small-scale state and action space defined using low dimensions;
- time-aware context-cache residence (i.e., estimated cache lifetime-based eviction) and latent decision-making (i.e., using the estimated delay time);
- adaptively select and switch between refreshing policies to minimize the overhead of refreshing;
- identify and aggregate performance monitoring of context to minimize the overhead of monitoring individual context.
- a discretization technique also used to reduce the computational complexity of having to monitor, maintain records, and perform calculations individually for each independent piece of context information;
- generalize the performance data over a similar set of queries so that the learned model does not overfit;
- useful in collaborative filtering to cache novel context information that are not previously observed (and profiled) when making caching decisions based on similarity.
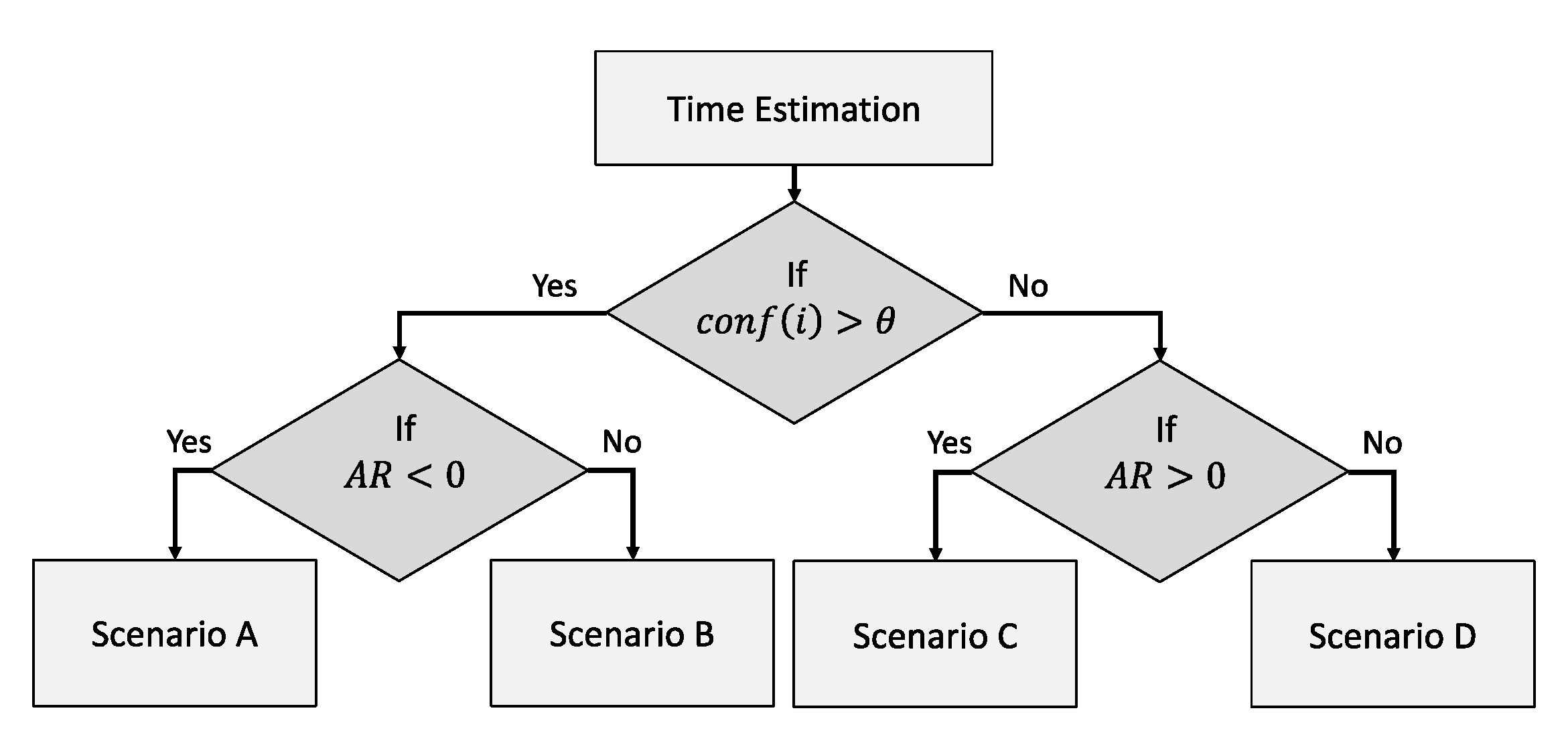
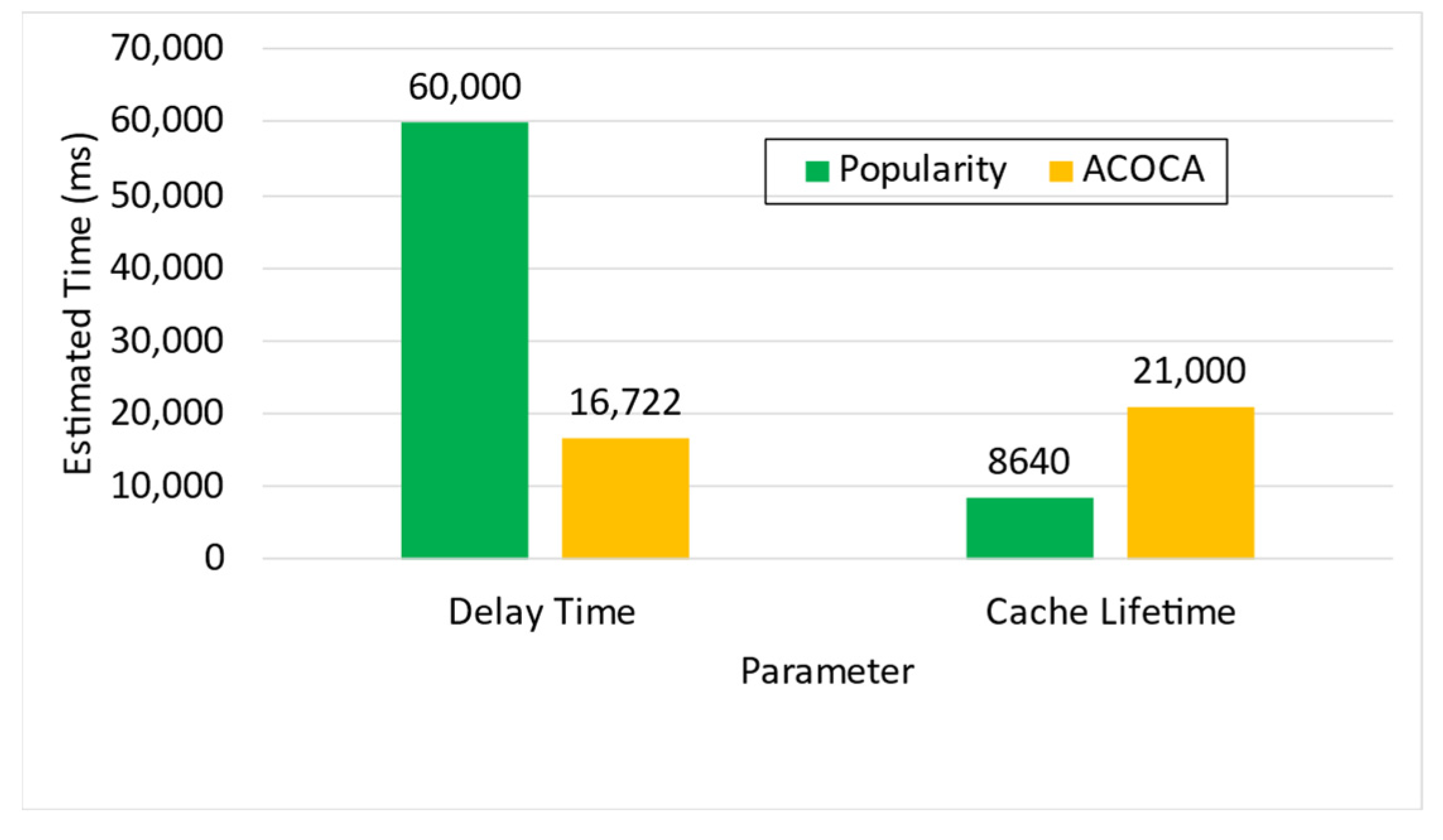
5.8. Estimating Cache Lifetime
5.9. Estimating Delay Time
5.10. Objective Function
- the optimization occurs continuously, subsequent to the warmup period ();
- there should exist at least one context information accessed from the CMP.
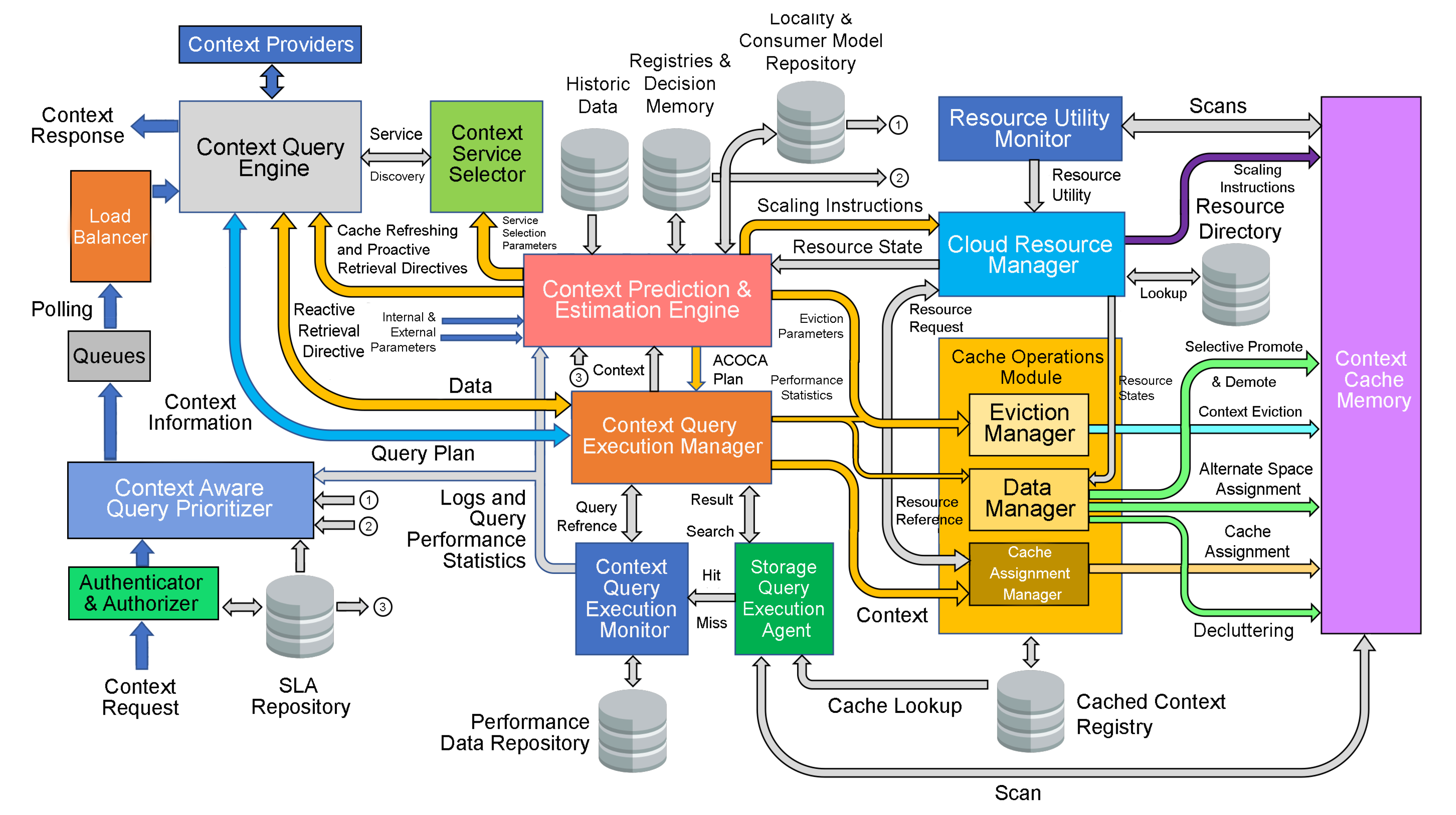
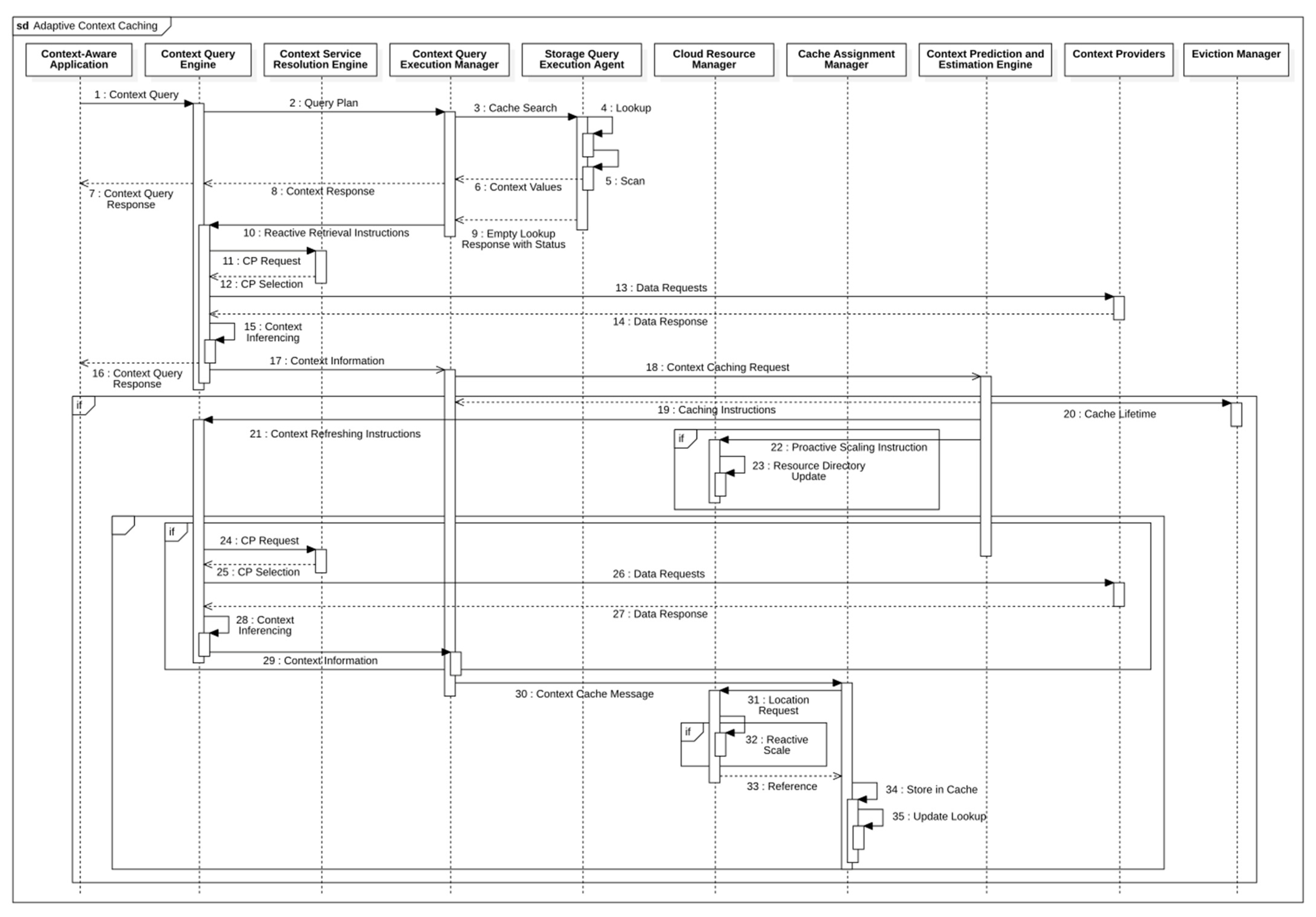
6. Evaluations
6.1. Experimental Setup
- RTmax = 2 s;
- Priceres = AUD 1.0/timely response;
- Pendelay= AUD 0.5/delayed response;
- fthr = 0.7.
6.2. Benchmarks
- traditional data caching policy;
- a context-aware (popularity of context information) caching policy.
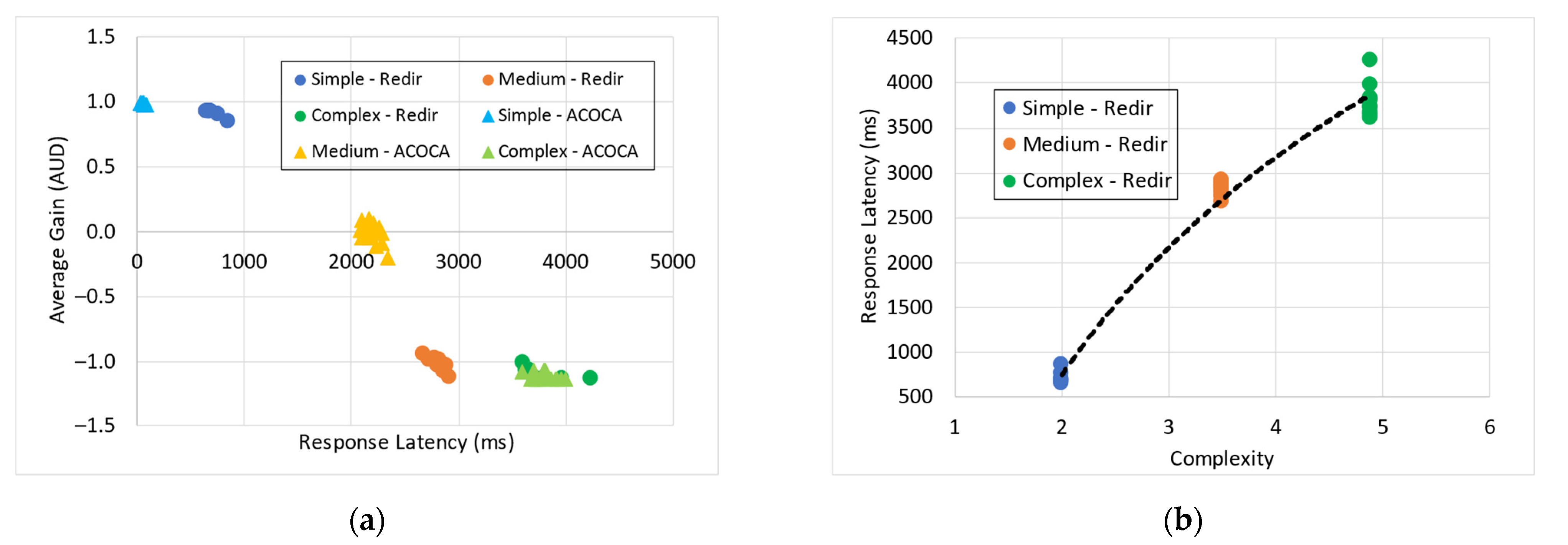
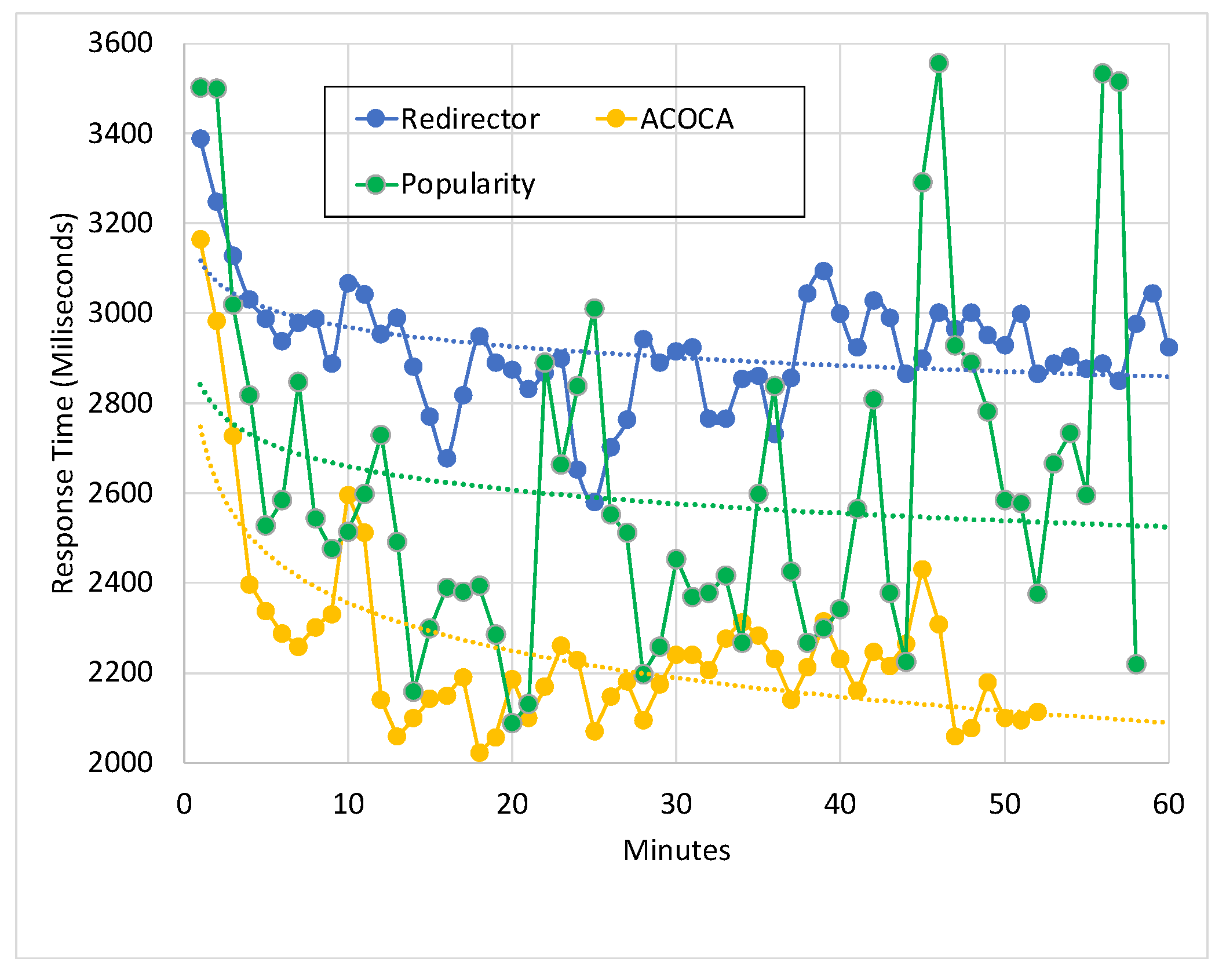
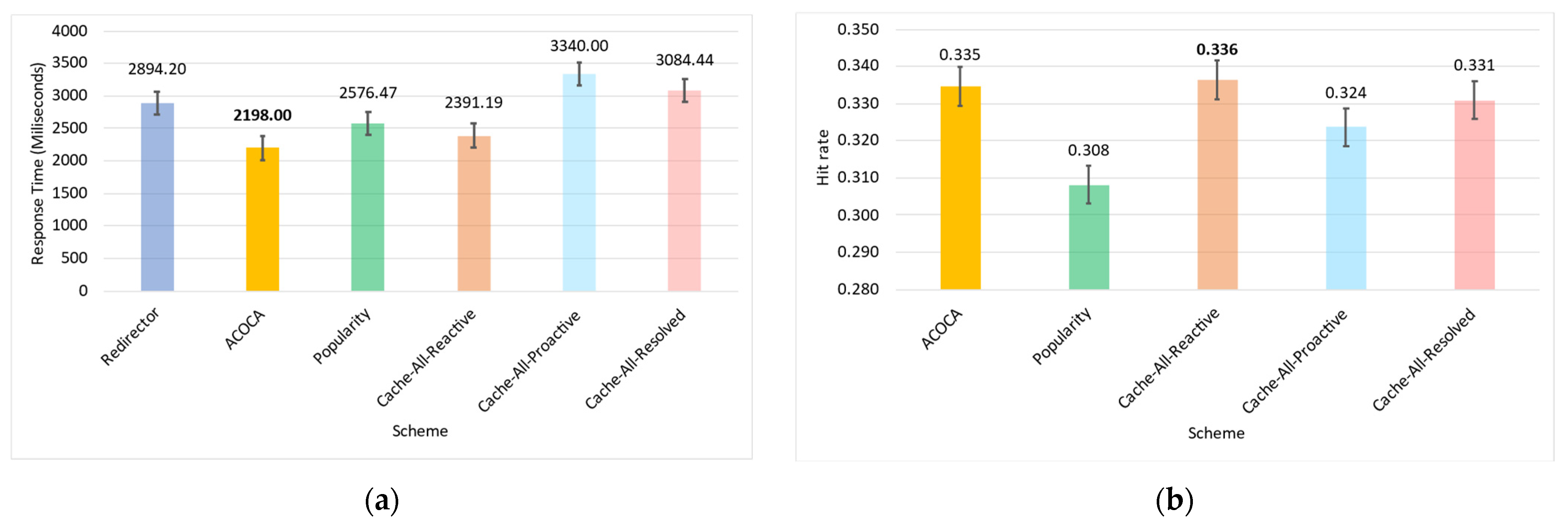
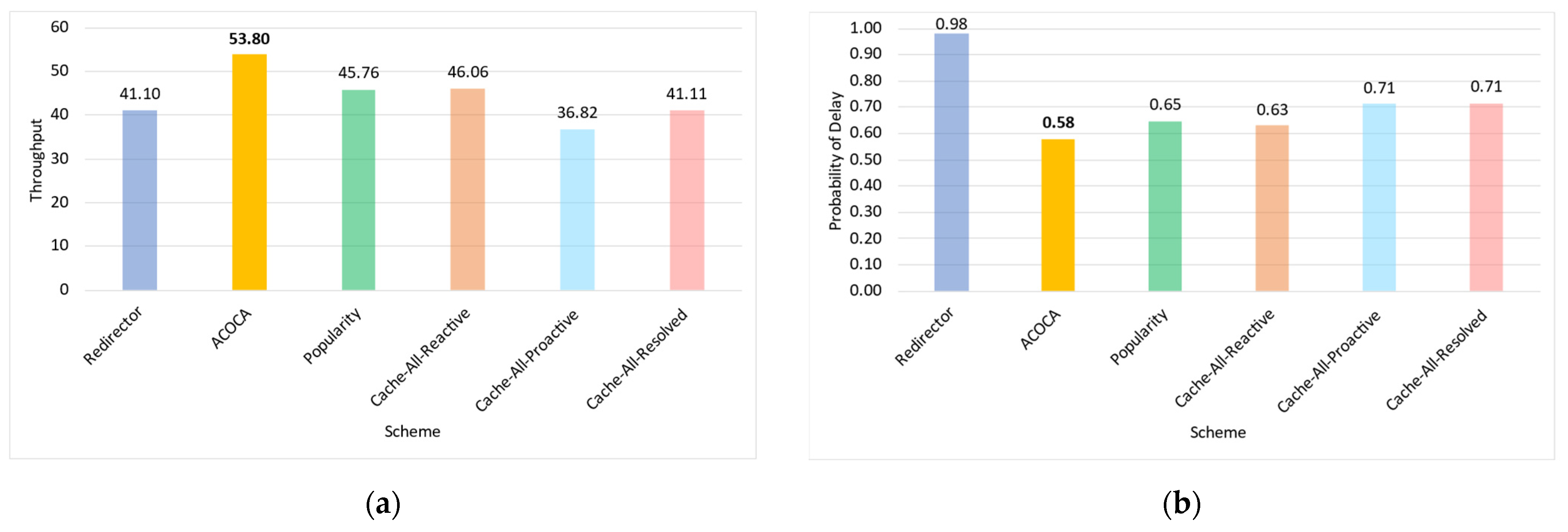
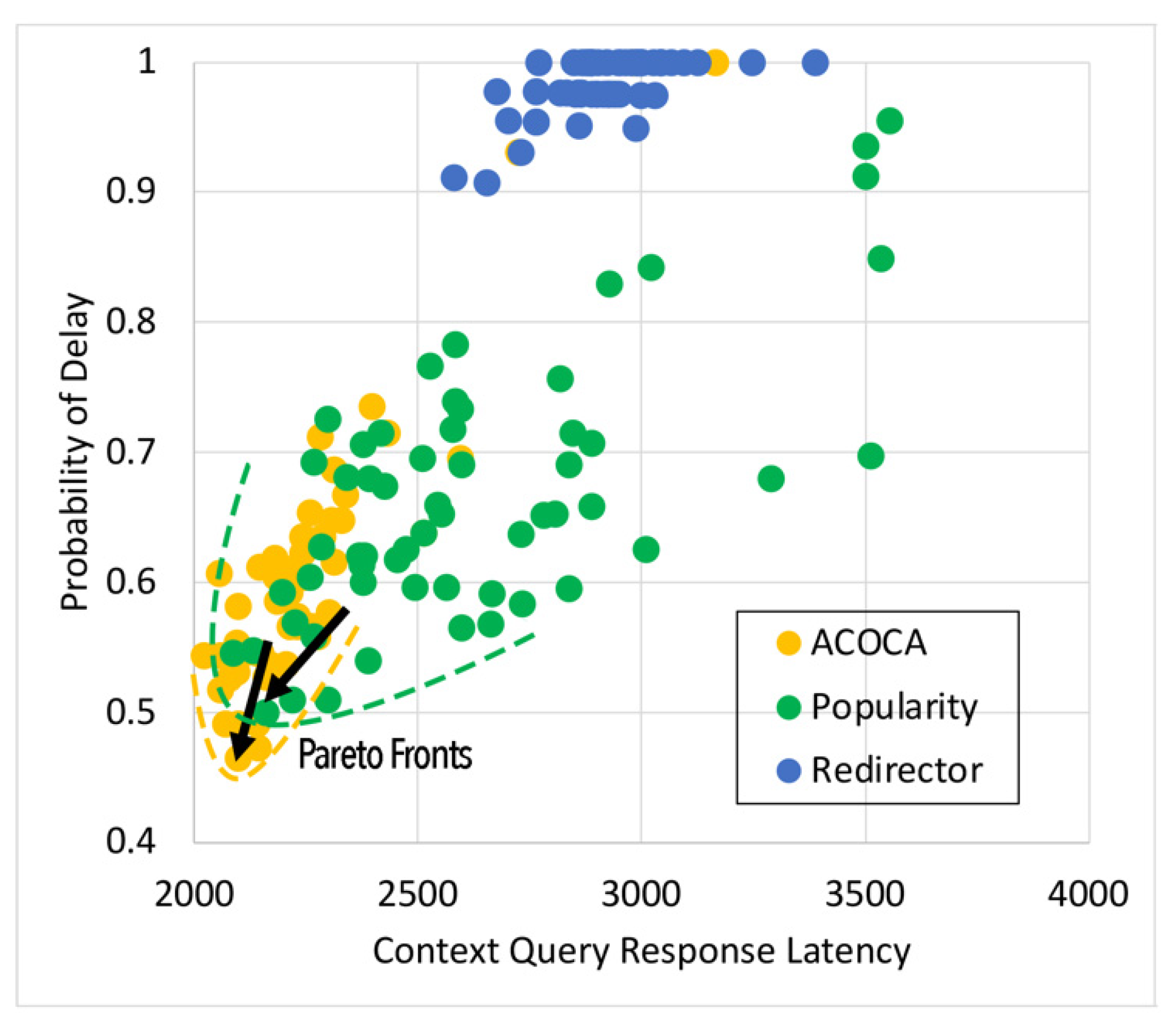
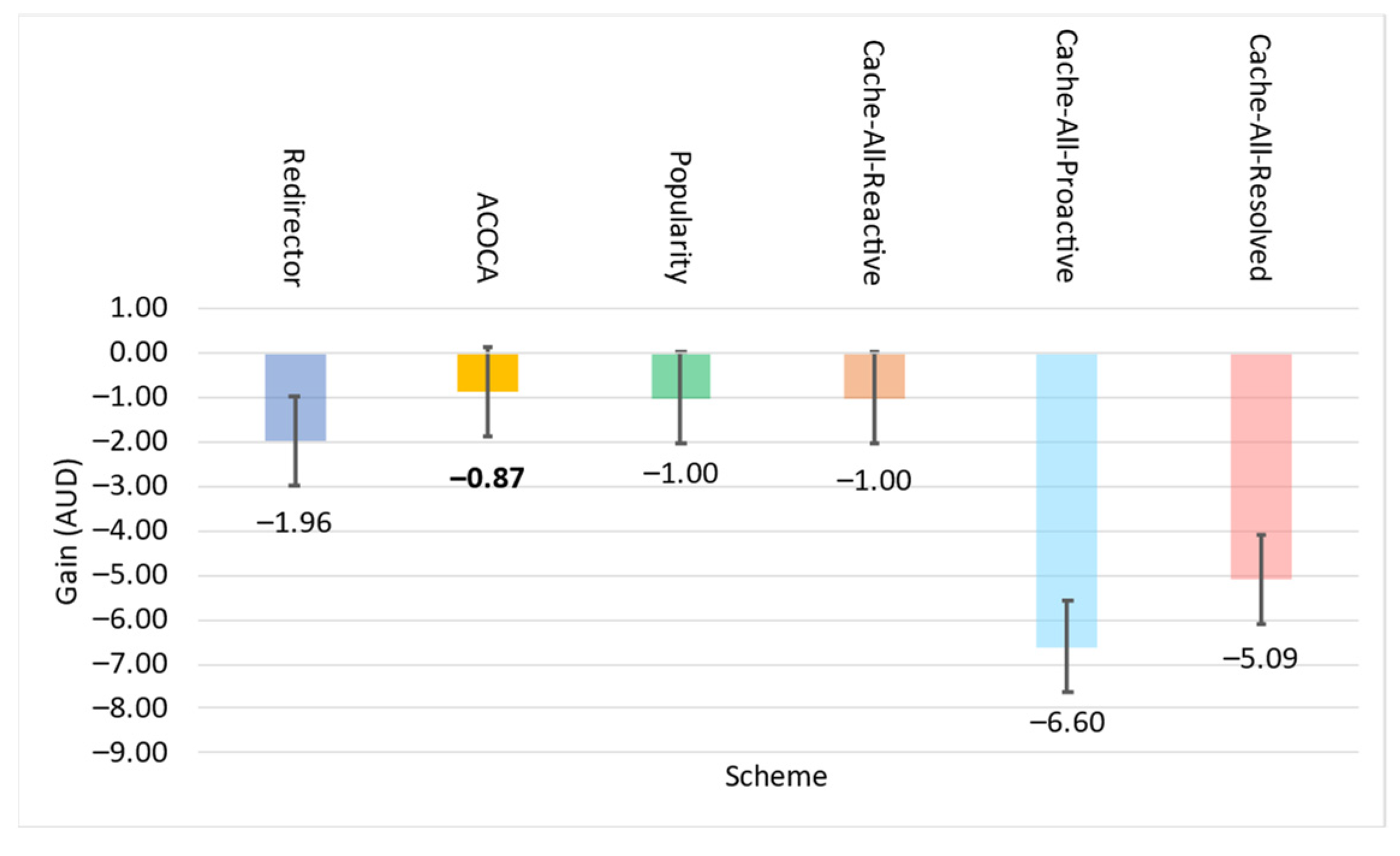
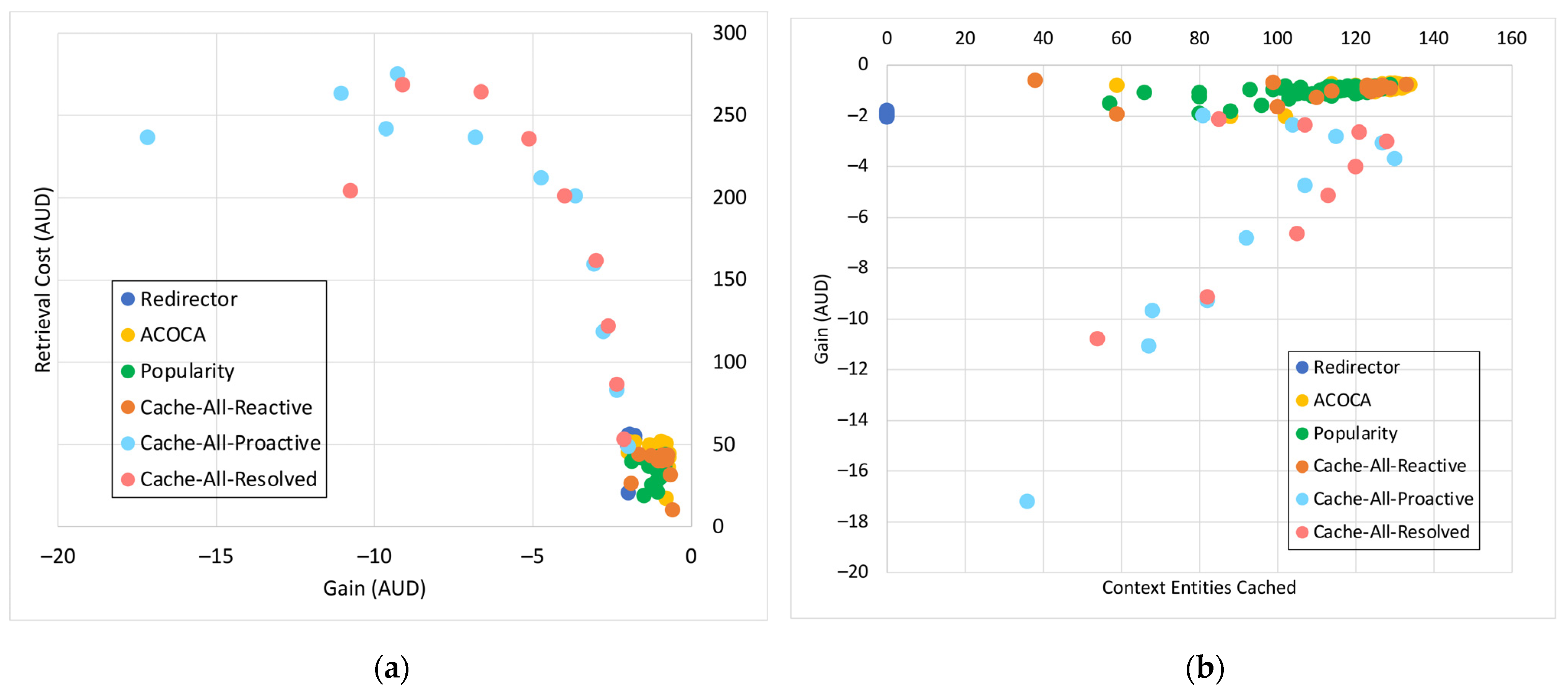
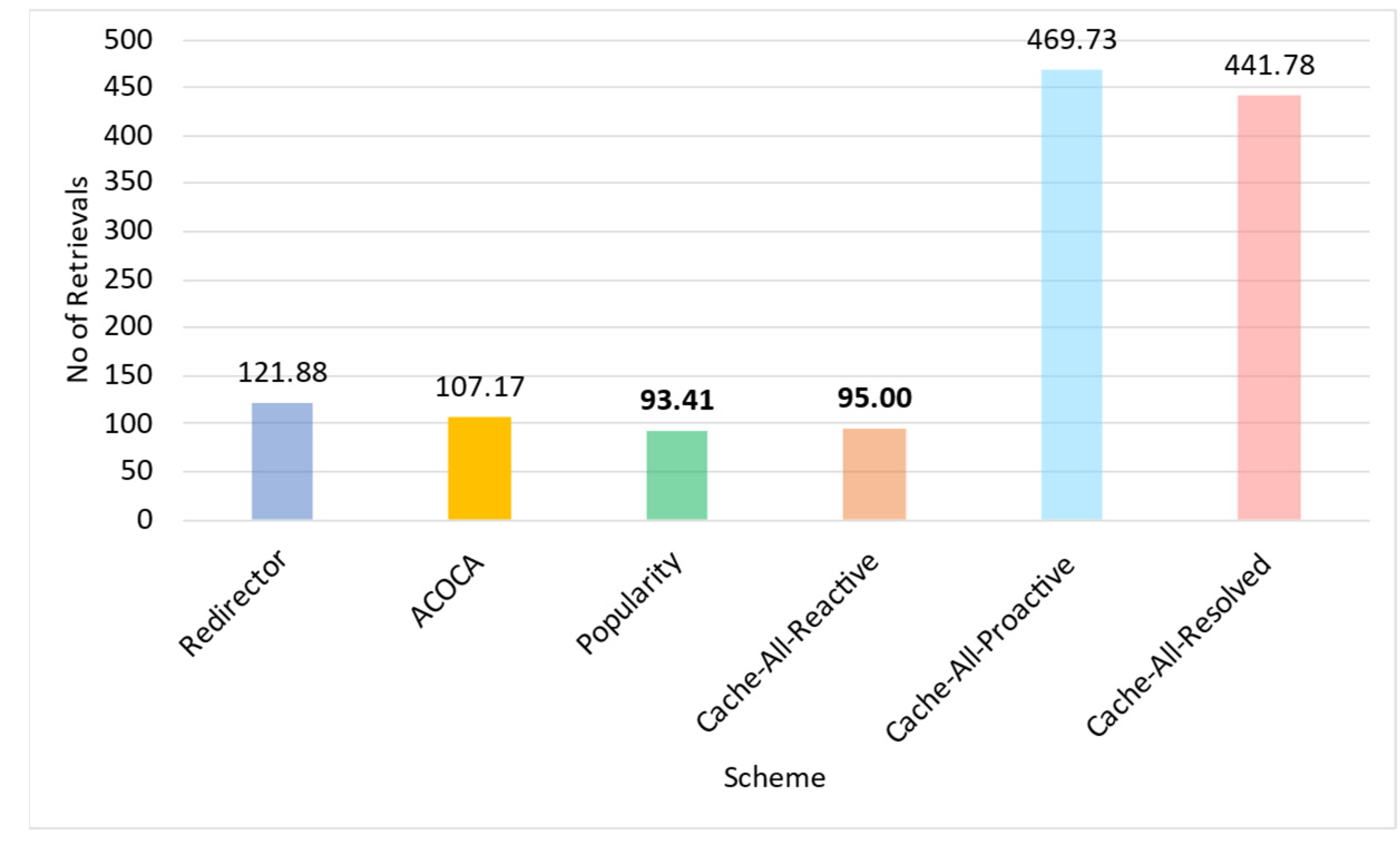
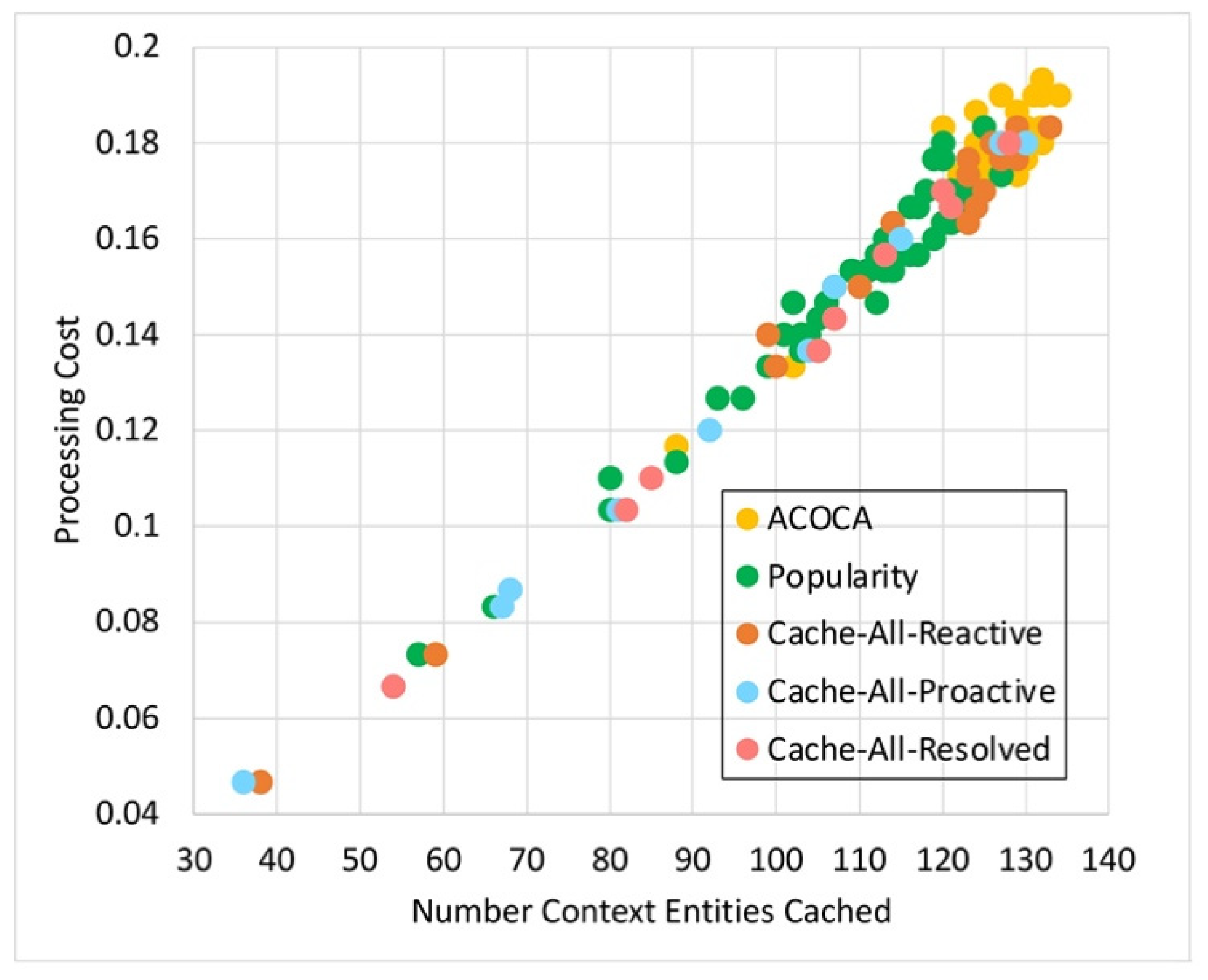
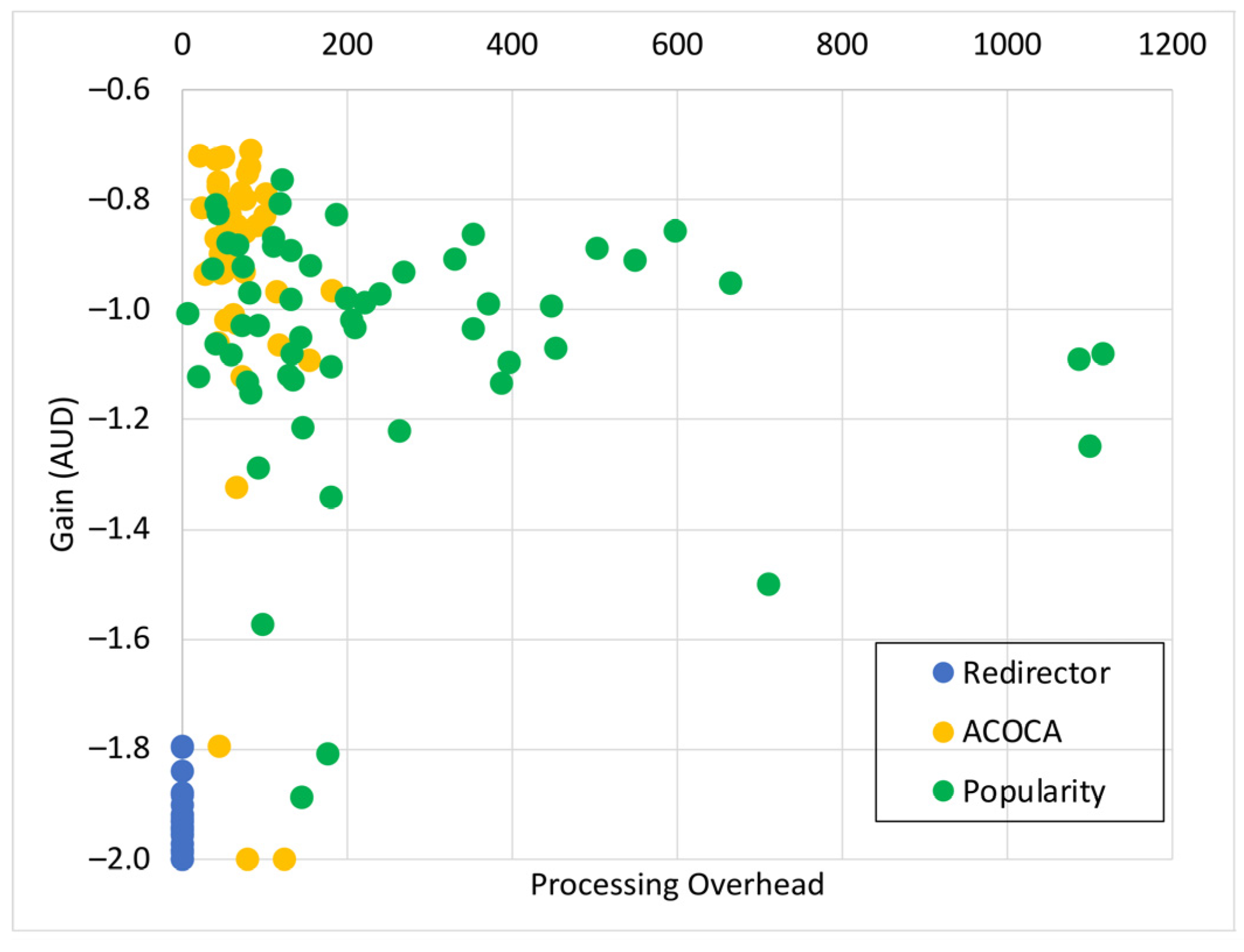
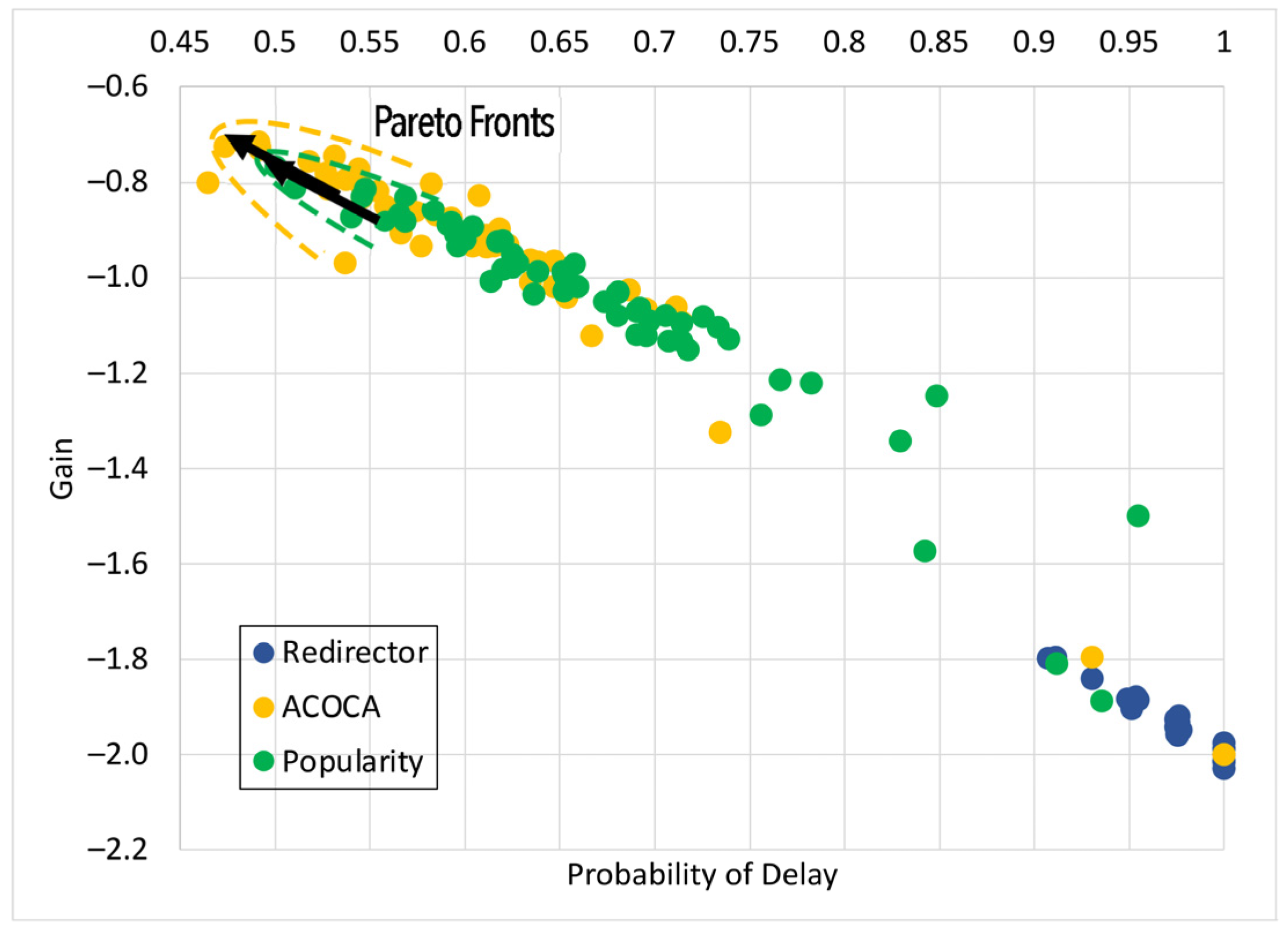
6.3. Results and Discussion
6.3.1. Case with Single IoT Application (1-SLA)
Testing the Improvement in Quality of Service
- ephemeral lifetimes of context information;
- network latency age of context problem;
- the difference in the physical and logical lifetime of context information causes an asynchrony in context refreshing;
- unreliability of context providers.
Testing the Improvement in Cost Efficiency
Testing the OVERHEAD of ACOCA to the CMP
Overall Outcomes for the 1-SLA Scenario
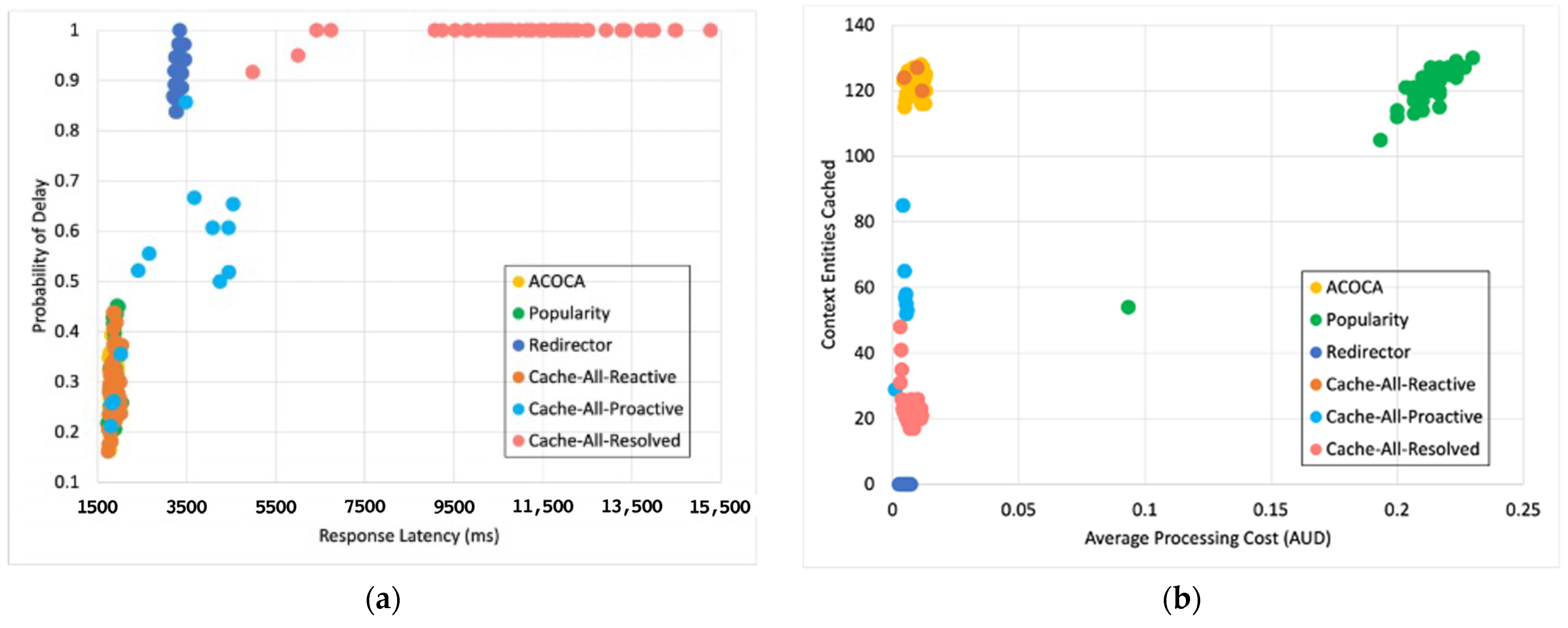
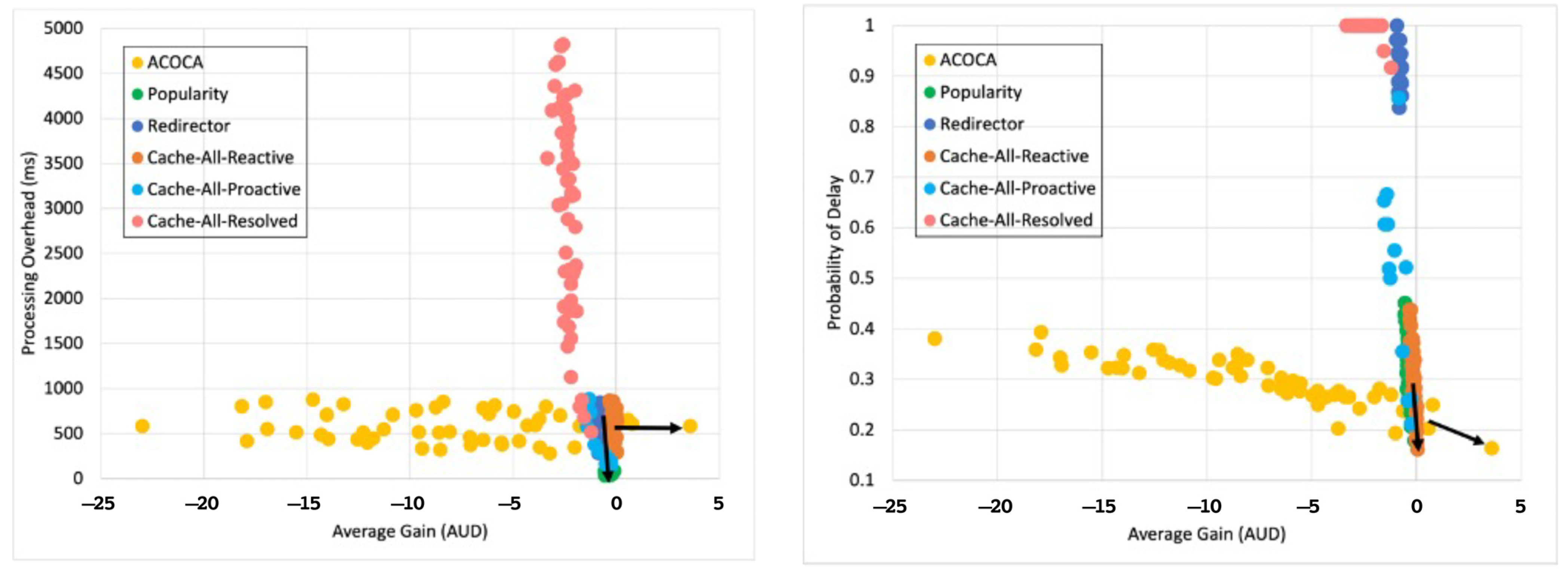
6.3.2. Case with Multiple IoT Applications (n-SLA)
7. Conclusions
- We developed a mathematical model for the ACOCA mechanism, focusing on each stage of the lifecycle;
- We developed and tested an ACOCA mechanism that maximized the cost and performance efficiencies of a CMP. The experimental results showed our mechanism reaches a quasi-optimal state that was better than any benchmarks;
- Our novel mechanism was aware of different heterogeneities (e.g., quality of context requirements of context consumers) and incorporated strategies either mathematically or algorithmically to handle them. Hence, ACOCA was tested for complex n-SLA scenarios using a heterogeneous query load. To the best of the authors’ knowledge, it was the first time such an experiment was performed on a context-caching mechanism.
- We proved the inapplicability of traditional caching techniques for caching context information. Traditional context-aware caching policies were shown to incur higher costs compared to ACOCA, proving our theory of the “exploding cost of adaptive context management”.
- We showed that the efficiency benefits of the ACOCA mechanism could be equally derived under dynamic homogeneous (e.g., 1-SLA scenario) or heterogeneous (e.g., n-SLA scenario) context-query loads.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perera, C.; Zaslavsky, A.; Christen, P.; Georgakopoulos, D. Context Aware Computing for The Internet of Things: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 414–454. [Google Scholar] [CrossRef]
- Abowd, G.D.; Dey, A.K.; Brown, P.J.; Davies, N.; Smith, M.; Steggles, P. Towards a Better Understanding of Context and Context-Awareness. In Handheld and Ubiquitous Computing; Gellersen, H.-W., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1707, pp. 304–307. ISBN 978-3-540-66550-2. [Google Scholar]
- Ruggeri, G.; Amadeo, M.; Campolo, C.; Molinaro, A.; Iera, A. Caching Popular Transient IoT Contents in an SDN-Based Edge Infrastructure. IEEE Trans. Netw. Serv. Manag. 2021, 18, 3432–3447. [Google Scholar] [CrossRef]
- Liu, X.; Derakhshani, M.; Lambotharan, S. Contextual Learning for Content Caching With Unknown Time-Varying Popularity Profiles via Incremental Clustering. IEEE Trans. Commun. 2021, 69, 3011–3024. [Google Scholar] [CrossRef]
- Peng, T.; Wang, H.; Liang, C.; Dong, P.; Wei, Y.; Yu, J.; Zhang, L. Value-aware Cache Replacement in Edge Networks for Internet of Things. Trans. Emerg. Telecommun. Technol. 2021, 32, e4261. [Google Scholar] [CrossRef]
- Jagarlamudi, K.S.; Zaslavsky, A.; Loke, S.W.; Hassani, A.; Medvedev, A. Quality and Cost Aware Service Selection in IoT-Context Management Platforms. In Proceedings of the 2021 IEEE International Conferences on Internet of Things (iThings) and IEEE Green Computing & Communications (GreenCom) and IEEE Cyber, Physical & Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Melbourne, Australia, 6–8 December 2021; pp. 89–98. [Google Scholar]
- Hassani, A.; Medvedev, A.; Haghighi, P.D.; Ling, S.; Indrawan-Santiago, M.; Zaslavsky, A.; Jayaraman, P.P. Context-as-a-Service Platform: Exchange and Share Context in an IoT Ecosystem. In Proceedings of the 2018 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Athens, Greece, 19–23 March 2018; pp. 385–390. [Google Scholar]
- Lehmann, O.; Bauer, M.; Becker, C.; Nicklas, D. From Home to World—Supporting Context-Aware Applications through World Models. In Proceedings of the Second IEEE Annual Conference on Pervasive Computing and Communications, Orlando, FL, USA, 14–17 March 2004; pp. 297–306. [Google Scholar]
- FIWARE-Orion. Available online: https://github.com/telefonicaid/fiware-orion (accessed on 14 March 2022).
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Medvedev, A.; Abken, A.; Hassani, A. Context Caching for IoT-based Applications: Opportunities and Challenges. IEEE Internet Things J. 2023. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Medvedev, A.; Abken, A. Estimating the Lifetime of Transient Context for Adaptive Caching in IoT Applications. In Proceedings of the ACM Symposium on Applied Computing, Brno, Czech Republic, 25–29 April 2022; p. 10. [Google Scholar]
- Medvedev, A. Performance and Cost Driven Data Storage and Processing for IoT Context Management Platforms. Doctoral Thesis, Monash University, Melbourne, Australia, 2020. [Google Scholar]
- Sheng, S.; Chen, P.; Chen, Z.; Wu, L.; Jiang, H. Edge Caching for IoT Transient Data Using Deep Reinforcement Learning. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18 October 2020; pp. 4477–4482. [Google Scholar]
- Zhang, Z.; Lung, C.-H.; Lambadaris, I.; St-Hilaire, M. IoT Data Lifetime-Based Cooperative Caching Scheme for ICN-IoT Networks. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–7. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Hassani, A.; Abken, A.; Medvedev, A. From Traditional Adaptive Data Caching to Adaptive Context Caching: A Survey. arXiv 2022, arXiv:2211.11259. [Google Scholar]
- Boytsov, A.; Zaslavsky, A. From Sensory Data to Situation Awareness: Enhanced Context Spaces Theory Approach. In Proceedings of the 2011 IEEE Ninth International Conference on Dependable, Autonomic and Secure Computing, Sydney, Australia, 12–14 December 2011; pp. 207–214. [Google Scholar]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.; Koksal, C.E.; Shroff, N.B. Update or Wait: How to Keep Your Data Fresh. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–15 April 2016; pp. 1–9. [Google Scholar]
- Schwefel, H.-P.; Hansen, M.B.; Olsen, R.L. Adaptive Caching Strategies for Context Management Systems. In Proceedings of the 2007 IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007; pp. 1–6. [Google Scholar]
- Zameel, A.; Najmuldeen, M.; Gormus, S. Context-Aware Caching in Wireless IoT Networks. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 712–717. [Google Scholar]
- Li, Q.; Shi, W.; Xiao, Y.; Ge, X.; Pandharipande, A. Content Size-Aware Edge Caching: A Size-Weighted Popularity-Based Approach. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 206–212. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Abken, A.; Hassani, A.; Medvedev, A. Adaptive Context Caching for Efficient Distributed Context Management Systems. In Proceedings of the ACM Symposium on Applied Computing, Tallinn, Estonia, 27–31 March 2023; p. 10. [Google Scholar]
- Cidon, A.; Eisenman, A.; Alizadeh, M.; Katti, S. Cliffhanger: Scaling Performance Cliffs in Web Memory Caches. In Proceedings of the NSDI’16: Proceedings of the 13th Usenix Conference on Networked Systems Design and Implementation, Santa Clara, CA, USA, 16–18 March 2016. [Google Scholar]
- Arcaini, P.; Riccobene, E.; Scandurra, P. Modeling and Analyzing MAPE-K Feedback Loops for Self-Adaptation. In Proceedings of the 2015 IEEE/ACM 10th International Symposium on Software Engineering for Adaptive and Self-Managing Systems, Florence, Italy, 18–19 May 2015; pp. 13–23. [Google Scholar]
- Fizza, K.; Banerjee, A.; Jayaraman, P.P.; Auluck, N.; Ranjan, R.; Mitra, K.; Georgakopoulos, D. A Survey on Evaluating the Quality of Autonomic Internet of Things Applications. IEEE Commun. Surv. Tutor. 2022, 25, 567–590. [Google Scholar] [CrossRef]
- Wang, Y.; He, S.; Fan, X.; Xu, C.; Sun, X.-H. On Cost-Driven Collaborative Data Caching: A New Model Approach. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 662–676. [Google Scholar] [CrossRef]
- Zhu, H.; Cao, Y.; Wei, X.; Wang, W.; Jiang, T.; Jin, S. Caching Transient Data for Internet of Things: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2019, 6, 2074–2083. [Google Scholar] [CrossRef]
- Khargharia, H.S.; Jayaraman, P.P.; Banerjee, A.; Zaslavsky, A.; Hassani, A.; Abken, A.; Kumar, A. Probabilistic Analysis of Context Caching in Internet of Things Applications. In Proceedings of the 2022 IEEE International Conference on Services Computing (SCC), Barcelona, Spain, 10–16 July 2022; pp. 93–103. [Google Scholar]
- Kiani, S.; Anjum, A.; Antonopoulos, N.; Munir, K.; McClatchey, R. Context Caches in the Clouds. J. Cloud Comput. Adv. Syst. Appl. 2012, 1, 7. [Google Scholar] [CrossRef]
- Wang, Y.; Friderikos, V. A Survey of Deep Learning for Data Caching in Edge Network. Informatics 2020, 7, 43. [Google Scholar] [CrossRef]
- Shuja, J.; Bilal, K.; Alasmary, W.; Sinky, H.; Alanazi, E. Applying Machine Learning Techniques for Caching in Next-Generation Edge Networks: A Comprehensive Survey. J. Netw. Comput. Appl. 2021, 181, 103005. [Google Scholar] [CrossRef]
- Guo, Y.; Lama, P.; Rao, J.; Zhou, X. V-Cache: Towards Flexible Resource Provisioning for Multi-Tier Applications in IaaS Clouds. In Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, Cambridge, MA, USA, 20–24 May 2013; pp. 88–99. [Google Scholar]
- Garetto, M.; Leonardi, E.; Martina, V. A Unified Approach to the Performance Analysis of Caching Systems. ACM Trans. Model. Perform. Eval. Comput. Syst. 2016, 1, 1–28. [Google Scholar] [CrossRef]
- Sadeghi, A.; Wang, G.; Giannakis, G.B. Deep Reinforcement Learning for Adaptive Caching in Hierarchical Content Delivery Networks. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 1024–1033. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Imran, M.; Vasilakos, A. Value-Based Caching in Information-Centric Wireless Body Area Networks. Sensors 2017, 17, 181. [Google Scholar] [CrossRef]
- Somuyiwa, S.O.; Gyorgy, A.; Gunduz, D. A Reinforcement-Learning Approach to Proactive Caching in Wireless Networks. IEEE J. Select. Areas Commun. 2018, 36, 1331–1344. [Google Scholar] [CrossRef]
- Nasehzadeh, A.; Wang, P. A Deep Reinforcement Learning-Based Caching Strategy for Internet of Things. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9 August 2020; pp. 969–974. [Google Scholar]
- Al-Turjman, F.M.; Al-Fagih, A.E.; Hassanein, H.S. A Value-Based Cache Replacement Approach for Information-Centric Networks. In Proceedings of the 38th Annual IEEE Conference on Local Computer Networks—Workshops, Sydney, Australia, 21–24 October 2013; pp. 874–881. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Abken, A.; Hassani, A. Reinforcement Learning Based Approaches to Adaptive Context Caching in Distributed Context Management Systems. arXiv 2022, arXiv:2212.11709. [Google Scholar]
- Medvedev, A.; Zaslavsky, A.; Indrawan-Santiago, M.; Haghighi, P.D.; Hassani, A. Storing and Indexing IoT Context for Smart City Applications. In Internet of Things, Smart Spaces, and Next Generation Networks and Systems; Galinina, O., Balandin, S., Koucheryavy, Y., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 9870, pp. 115–128. ISBN 978-3-319-46300-1. [Google Scholar]
- FIWARE-Orion Components. Available online: https://www.fiware.org/catalogue/ (accessed on 27 December 2022).
- Jung, J.; Berger, A.W. Hari Balakrishnan Modeling TTL-Based Internet Caches. In Proceedings of the IEEE INFOCOM 2003. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 1, pp. 417–426. [Google Scholar]
- Larson, R.C.; Odoni, A.R. Urban Operations Research; Dynamic Ideas: Belmont, MA, USA, 2007; ISBN 978-0-9759146-3-2. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Medvedev, A.; Abken, A. Estimating the Dynamic Lifetime of Transient Context in near Real-Time for Cost-Efficient Adaptive Caching. SIGAPP Appl. Comput. Rev. 2022, 22, 44–58. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2019, arXiv:1509.02971. [Google Scholar]
- Appendix to Adaptive Context Caching for IoT-Based Applications. Available online: https://bit.ly/3eEMJxc (accessed on 19 October 2022).
- Fujimoto, S. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80. [Google Scholar]
- Wu, X.; Li, X.; Li, J.; Ching, P.C.; Leung, V.C.M.; Poor, H.V. Caching Transient Content for IoT Sensing: Multi-Agent Soft Actor-Critic. IEEE Trans. Commun. 2021, 69, 5886–5901. [Google Scholar] [CrossRef]
- Hassani, A.; Medvedev, A.; Delir Haghighi, P.; Ling, S.; Zaslavsky, A.; Prakash Jayaraman, P. Context Definition and Query Language: Conceptual Specification, Implementation, and Evaluation. Sensors 2019, 19, 1478. [Google Scholar] [CrossRef] [PubMed]
- Kul, G.; Luong, D.T.A.; Xie, T.; Chandola, V.; Kennedy, O.; Upadhyaya, S. Similarity Metrics for SQL Query Clustering. IEEE Trans. Knowl. Data Eng. 2018, 30, 2408–2420. [Google Scholar] [CrossRef]
- Kul, G.; Luong, D.; Xie, T.; Coonan, P.; Chandola, V.; Kennedy, O.; Upadhyaya, S. Ettu: Analyzing Query Intents in Corporate Databases. In Proceedings of the 25th International Conference Companion on World Wide Web—WWW ’16 Companion, Montreal, QC, Canada, 11–15 April 2016; pp. 463–466. [Google Scholar]
- Yang, J.; McAuley, J.; Leskovec, J.; LePendu, P.; Shah, N. Finding Progression Stages in Time-Evolving Event Sequences. In Proceedings of the 23rd international conference on World wide web—WWW ’14, Seoul, Korea, 7–11 April 2014; pp. 783–794. [Google Scholar]
- Sheikh, R.; Kharbutli, M. Improving Cache Performance by Combining Cost-Sensitivity and Locality Principles in Cache Replacement Algorithms. In Proceedings of the 2010 IEEE International Conference on Computer Design, Amsterdam, The Netherlands, 3–6 October 2010; pp. 76–83. [Google Scholar]
- Weerasinghe, S.; Zaslavsky, A.; Hassani, A.; Loke, S.W.; Medvedev, A.; Abken, A. Context Query Simulation for Smart Carparking Scenarios in the Melbourne CDB. arXiv 2022, arXiv:2302.07190. [Google Scholar]
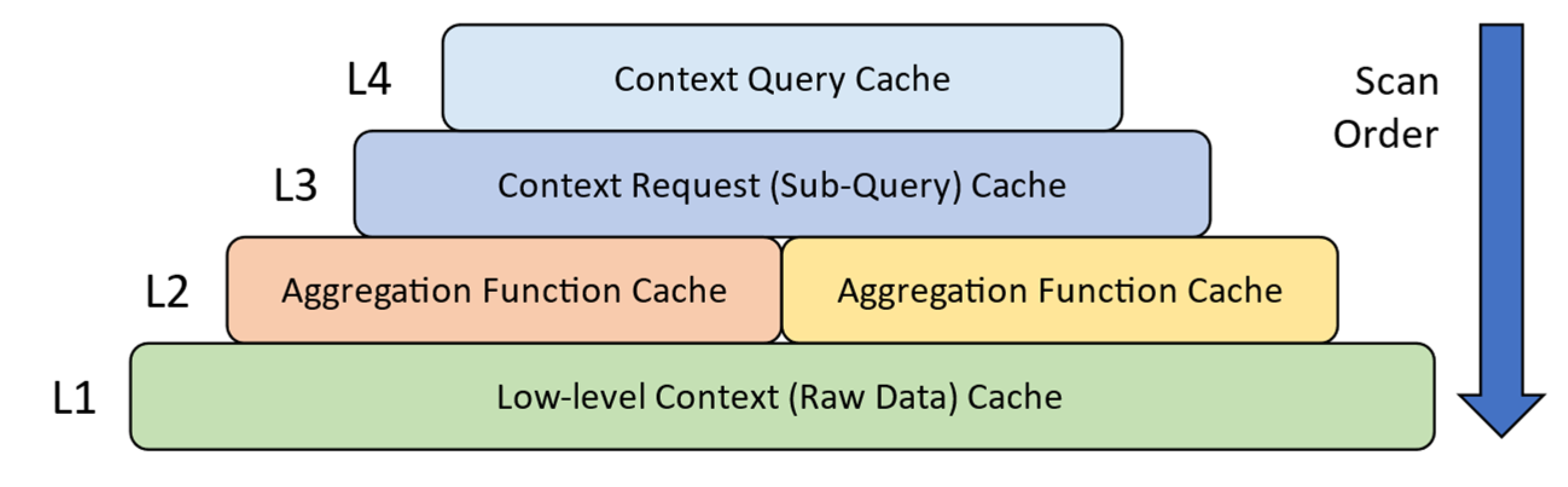
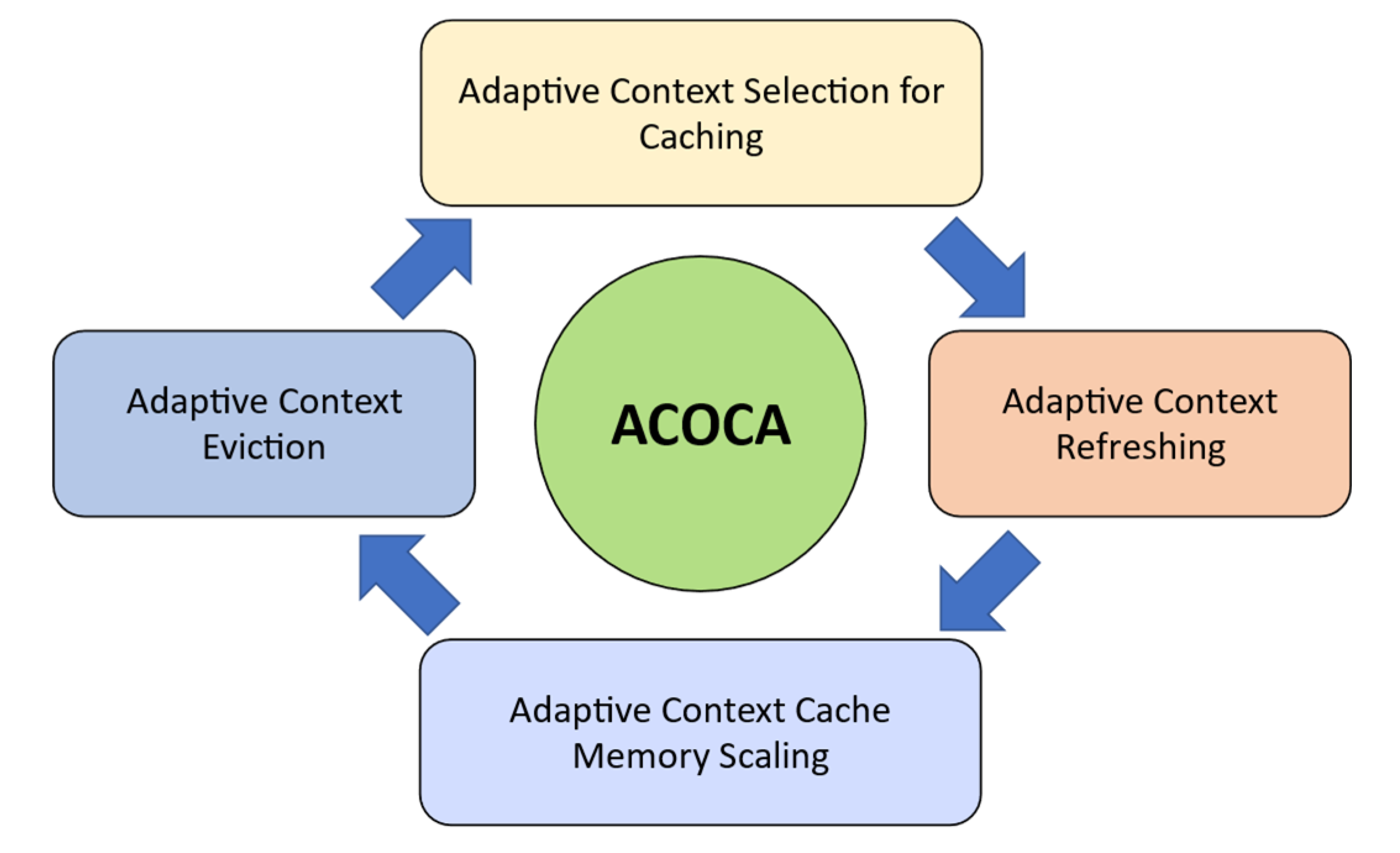
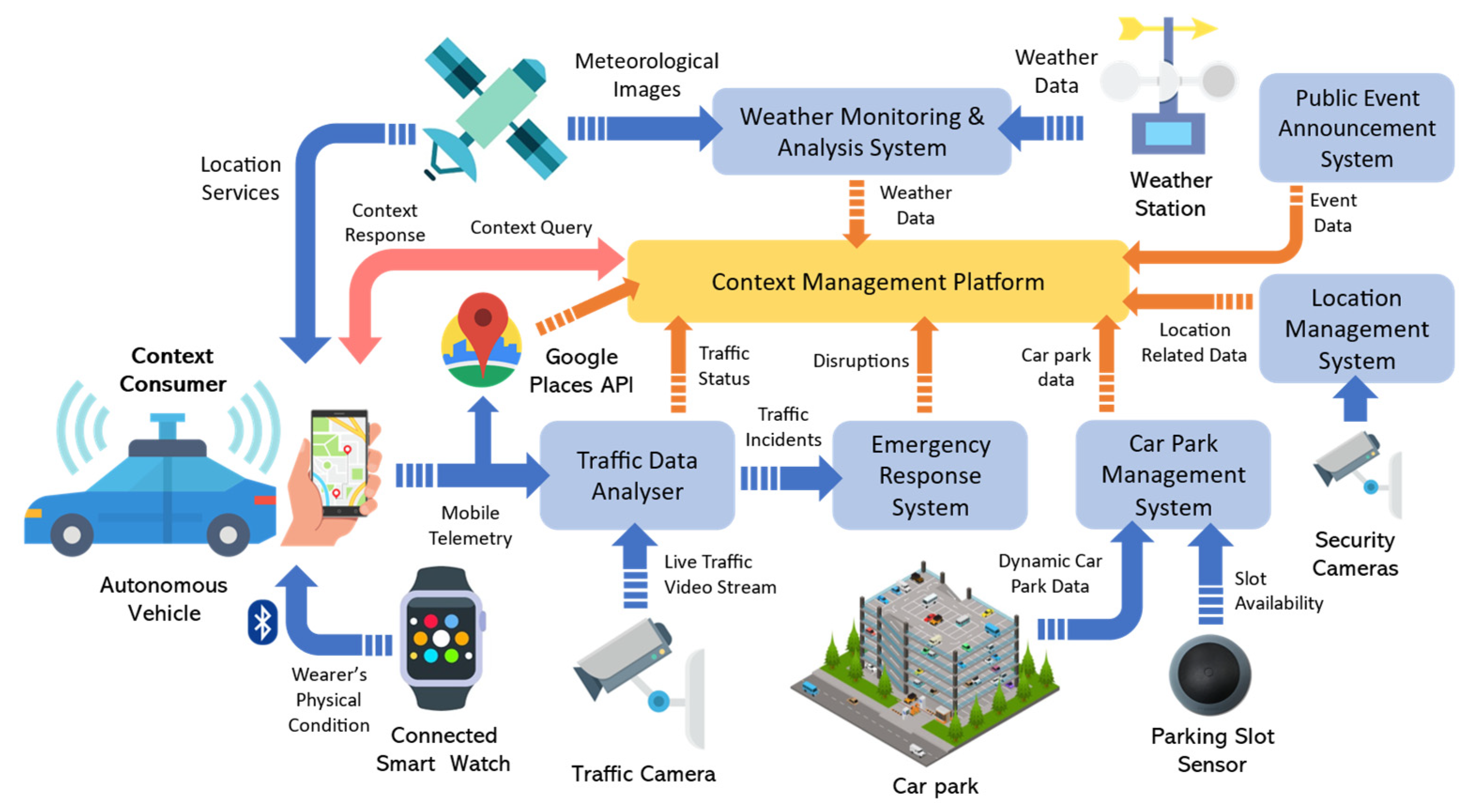
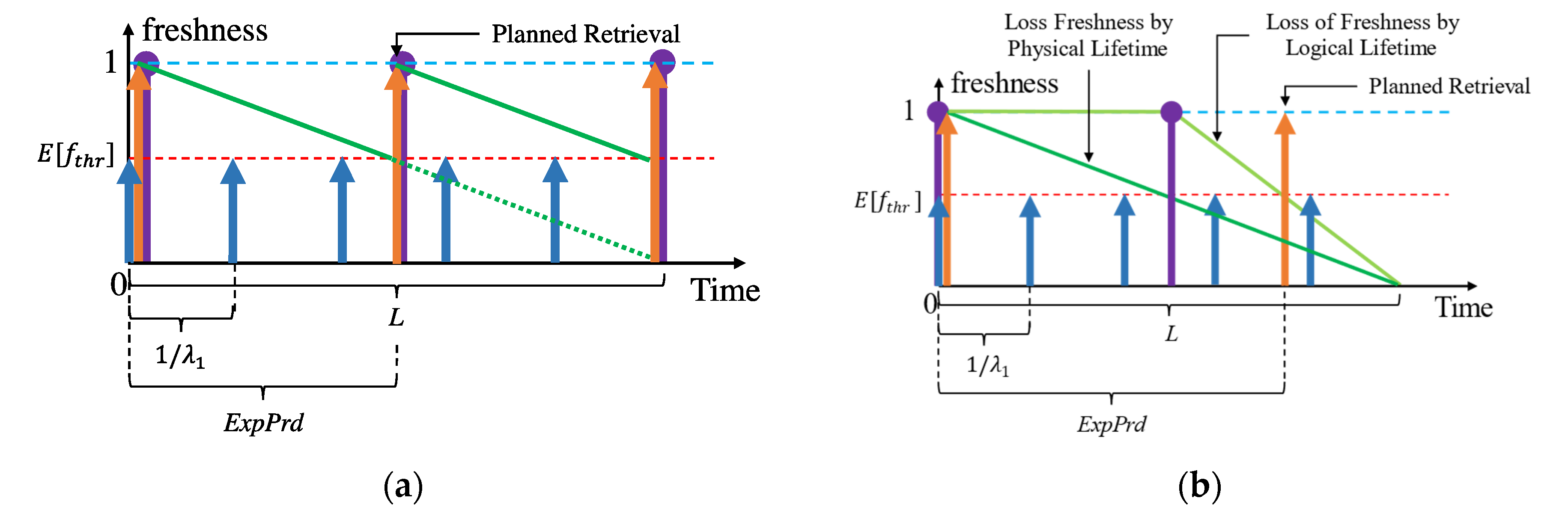
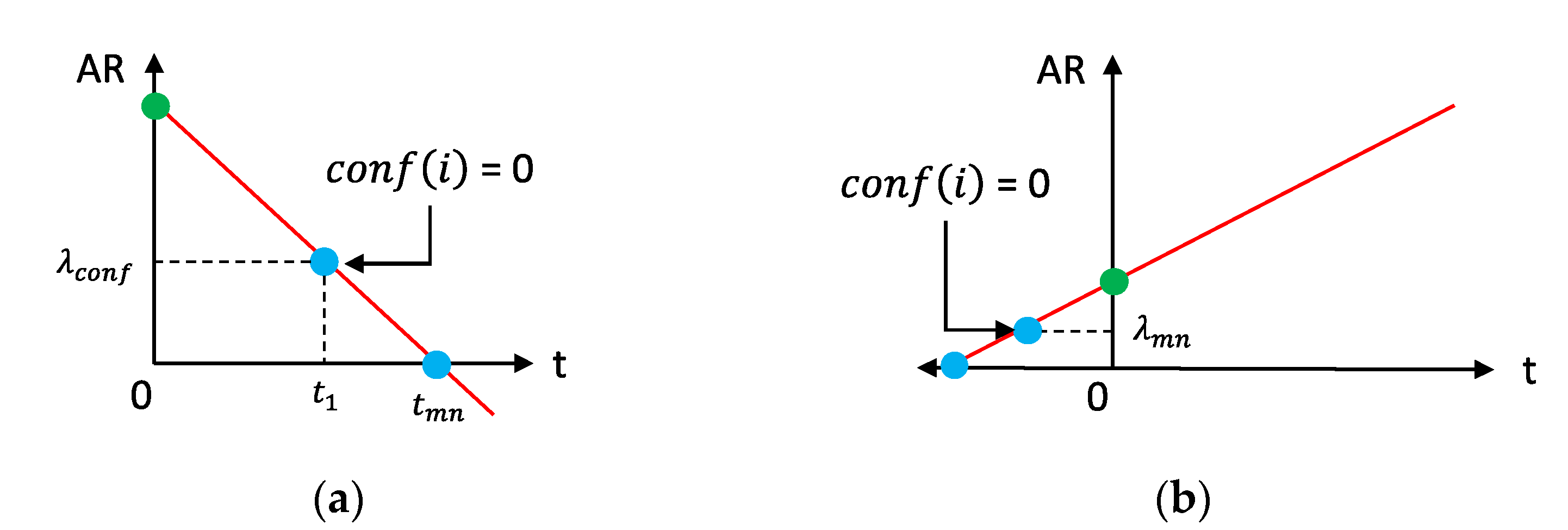
| Feature | Data Caching | Context Caching |
|---|---|---|
| Refreshing | Only for transient data. | Necessary. |
| Fault tolerance | Recoverable from the data provider. | Unrecoverable (need to re-interpret). |
| Prior knowledge of offline learning | Available (e.g., data libraries, transition probabilities). | Unavailable, uncertain, or limited. |
| Quality concerns about cached data | Limited (e.g., response latency, hit rate) | Multivariate and complicated. |
| Size of possible caching actions | Predefined and limited. often based on the number of distinct data. | Evolving and cannot be predefined at all. |
| Notation | Description | Notation | Description |
|---|---|---|---|
| i | i.e., i. | The monetary earnings received from responding to context queries while adhering to the quality parameters. | |
| n | i.e., n. | The cost of processing for the context. | |
| Number of context providers from which the data is retrieved to infer a piece of context information. | The cost incurred as penalties due to nonadherence to quality parameters when responding to context queries. | ||
| Number of related contexts of higher logical order. | The cost of storing the context in persistent storage. | ||
| HR | . | Total cost incurred to store in the cache. | |
| MR | . | or | Cost of retrieving a context data. |
| PD | [11]. | Cost of responding to context queries using the redirector mode. | |
| Request rate, e.g., 1 per second. | Cost of managing a context in cache. | ||
| Freshness threshold—the minimum freshness tolerated by a Context Consumer when requesting a piece of context information. | Cost of caching a physical unit in the cache, e.g., AUD 0.3 per Giga Byte. | ||
| AR | Access Rate, e.g., 0.8 per second. | Size of a window, e.g., 60 s. | |
| ExpPrd | Expiry Period—the time period during which a context is considered fresh enough to be used in responding to a context query [11,12]. | The cache-lookup overhead when a partial miss occurs. | |
| PP | Planning Period [12]. | The cache-lookup and retrieval overhead when a cache hit occurs. | |
| IR | [11]. | The cache-lookup overhead when a complete (i.e., full) miss occurs. | |
| InvGap | Invalid Gap [11]. | The cost of context retrieval for the CMP when using the redirector mode. | |
| InvPrd | The time until the subsequent retrieval from the point of time the freshness threshold is no longer met. | The cost of context retrieval from the CMP with context caching. | |
| AcsInt | The average time between two requests for the same context, which is equal to . | The cost to retrieve the context data. | |
| Average monetary gain from responding to any context query. | The cost to be incurred as penalties for not meeting the quality parameters set by the context consumer. | ||
| The gap time between the time a context is expired and refreshed. | The expected maximum accepted response latency for the context consumers. | ||
| The probability of fthr from the nth SLA being applied on an accessed context information. | RR | Refresh Rate, e.g., 0.5 per second. | |
| Variance of a distribution. | Context entity. | ||
| The number of expensive SLAs. | Context attribute. | ||
| Lifetime of a context. | CL | Estimated cache lifetime (i.e., residence time). | |
| SI | Sampling Interval of a sensor. | DT | Estimated delay time. |
| RetL | Context retrieval latency. | Cost of refreshing a context. | |
| ResiL | Residual Lifetime. | The sum of weighted parameters other than where . | |
| age | Age of context information. | Calculated z-value for the estimated . | |
| Cost of context retrieval. | Confidence to selectively cache i. | ||
| . | CE | Cache Efficiency. | |
| K | Number of gaps, where K < N-1. | RE | Retrieval Efficiency. |
| S | The number of successful retrievals. | AT | Access Trend. |
| R | The total number of context retrievals attempted. | Unreli | Unreliability of context retrieval for a piece of context, i.e., Unreli = 1–Reliability. |
| Confidence of the inferred lifetime. | Cmpx | The complexity of a context query. | |
| . | Average monetary gain per context query from responding to context queries. | Cmpx(i) | The probabilistic complexity of context queries that would access the context information i. |
| Average of the historical sample. | Weights that are assigned to each of the parameters in the formula. | ||
| The feature vector of a candidate context i to cache. | Caching decision threshold. | ||
| Set of all the weights. | Cache distribution bias, where | ||
| AUD | Australian Dollar. | The standard deviation of the sample of values. |
| Data Ingestion | CP Sampling | L < SI? | Refreshing Policy |
|---|---|---|---|
| Streamed | Periodic | False | Depends on ExpPrd |
| True | Reactive | ||
| Fetched | Aperiodic | False | Proactive |
| True | |||
| Periodic | False | Depends on ExpPrd | |
| True | Reactive |
| Parameter | Query 1 | Query 2 | Query 3 |
|---|---|---|---|
| 4 | 7 | 9 | |
| 6 | 16 | 23 | |
| 5 | 14 | 23 | |
| 6 | 16 | 25 | |
| Cmpx |
| Average | AUD 0.5198 | 0.74 | 2217 ms | AUD 0.6925 |
| Std Deviation | 0.3844 | 0.1071 | 618.8027 | 0.4347 |
| Minimum | AUD 0.0070 | 0.5 | 14400 ms | AUD 0.1000 |
| Maximum | AUD 1.4000 | 0.9 | 3600 ms | AUD 2.0000 |
| Parameter | |||
|---|---|---|---|
| ACOCA | |||
| Context Aware | |||
| CA Reactive | |||
| CA Proactive | |||
| CA Resolved | |||
| Redirector |
| Parameter | |||
|---|---|---|---|
| ACOCA | |||
| Context Aware | |||
| CA Reactive | |||
| CA Proactive | |||
| CA Resolved | |||
| Redirector |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weerasinghe, S.; Zaslavsky, A.; Loke, S.W.; Hassani, A.; Medvedev, A.; Abken, A. Adaptive Context Caching for IoT-Based Applications: A Reinforcement Learning Approach. Sensors 2023, 23, 4767. https://doi.org/10.3390/s23104767
Weerasinghe S, Zaslavsky A, Loke SW, Hassani A, Medvedev A, Abken A. Adaptive Context Caching for IoT-Based Applications: A Reinforcement Learning Approach. Sensors. 2023; 23(10):4767. https://doi.org/10.3390/s23104767
Chicago/Turabian StyleWeerasinghe, Shakthi, Arkady Zaslavsky, Seng Wai Loke, Alireza Hassani, Alexey Medvedev, and Amin Abken. 2023. "Adaptive Context Caching for IoT-Based Applications: A Reinforcement Learning Approach" Sensors 23, no. 10: 4767. https://doi.org/10.3390/s23104767
APA StyleWeerasinghe, S., Zaslavsky, A., Loke, S. W., Hassani, A., Medvedev, A., & Abken, A. (2023). Adaptive Context Caching for IoT-Based Applications: A Reinforcement Learning Approach. Sensors, 23(10), 4767. https://doi.org/10.3390/s23104767









