Multiple Physical Quantities Janus Metastructure Sensor Based on PSHE
Abstract
1. Introduction
2. The Theoretical Model
3. Analysis and Discussion of Performances
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Cao, L.; Merkel, A.; Fan, S.-W.; Vincent, B.; Assouar, B. Janus Acoustic Metascreen with Nonreciprocal and Reconfigurable Phase Modulations. Nat. Commun. 2021, 12, 7089. [Google Scholar] [CrossRef] [PubMed]
- De Gennes P, G. Mechanical properties of polymer interfaces. Butterworth-Heinemann Phys. Polym. Surf. Interfaces 1992, 1992, 55–71. [Google Scholar]
- Casagrande, C. Janus beads-realization and 1st observation of interfacial properties. Europhys. Lett. 1998, 306, 1423–1425. [Google Scholar]
- Walther, A.; Müller, A.H.E. Janus Particles. Soft Matter. 2008, 4, 663–668. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.-H.; Gao, X. Nanocomposites with Spatially Separated Functionalities for Combined Imaging and Magnetolytic Therapy. J. Am. Chem. Soc. 2010, 132, 7234–7237. [Google Scholar] [CrossRef]
- Wu, L.Y.; Ross, B.M.; Hong, S.; Lee, L.P. Bioinspired Nanocorals with Decoupled Cellular Targeting and Sensing Functionality. Small 2010, 6, 503–507. [Google Scholar] [CrossRef]
- Jiang, J.; Gu, H.; Shao, H.; Devlin, E.; Papaefthymiou, G.C.; Ying, J.Y. Bifunctional Fe3O4–Ag Heterodimer Nanoparticles for Two-Photon Fluorescence Imaging and Magnetic Manipulation. Adv. Mater. 2008, 20, 4403–4407. [Google Scholar] [CrossRef]
- Huck, C.; Vogt, J.; Sendner, M.; Hengstler, D.; Neubrech, F.; Pucci, A. Plasmonic Enhancement of Infrared Vibrational Signals: Nanoslits versus Nanorods. ACS Photonics 2015, 2, 1489–1497. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef]
- Cong, L.; Xu, N.; Han, J.; Zhang, W.; Singh, R. A Tunable Dispersion-Free Terahertz Metadevice with Pancharatnam–Berry-Phase-Enabled Modulation and Polarization Control. Adv. Mater. 2015, 27, 6630–6636. [Google Scholar] [CrossRef]
- Chen, M.L.N.; Jiang, L.J.; Sha, W.E.I. Artificial Perfect Electric Conductor-Perfect Magnetic Conductor Anisotropic Metasurface for Generating Orbital Angular Momentum of Microwave with Nearly Perfect Conversion Efficiency. J. Appl. Phys. 2016, 119, 064506. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Y.; Hu, H.; Xue, W.; Yvind, K.; Mork, J. Nonreciprocal Transmission in a Nonlinear Photonic-Crystal Fano Structure with Broken Symmetry. Laser Photonics Rev. 2015, 9, 241–247. [Google Scholar] [CrossRef]
- Chen, C.; Ye, X.; Sun, J.; Chen, Y.; Huang, C.; Xiao, X.; Song, W.; Zhu, S.; Li, T. Bifacial-Metasurface-Enabled Pancake Metalens with Polarized Space Folding. Optica 2022, 9, 1314–1322. [Google Scholar] [CrossRef]
- Yang, P.; He, J.; Ju, Y.; Zhang, Q.; Wu, Y.; Xia, Z.; Chen, L.; Tang, S. Dual-Mode Integrated Janus Films with Highly Efficient NaH2PO2-Enhanced Infrared Radiative Cooling and Solar Heating for Year-Round Thermal Management. Adv. Sci. 2023, 10, 2206176. [Google Scholar] [CrossRef] [PubMed]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef]
- Zhou, X.; Ling, X.; Luo, H.; Wen, S. Identifying Graphene Layers via Spin Hall Effect of Light. Appl. Phys. Lett. 2012, 101, 251602. [Google Scholar] [CrossRef]
- Hosten, O.; Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef]
- Dong, P.; Cheng, J.; Da, H.; Yan, X. Spin Hall Effect of Transmitted Light for Graphene–Silica Aerogel Photonic Crystal in Terahertz Region. Opt. Commun. 2021, 485, 126744. [Google Scholar] [CrossRef]
- Bing, P.; Sui, J.; Wu, G. Analysis of dual-channel simultaneous detection of photonic crystal fiber sensors. Plasmonics 2020, 15, 1071–1076. [Google Scholar] [CrossRef]
- Khansili, N.; Rattu, G.; Krishna, P.M. Label-Free Optical Biosensors for Food and Biological Sensor Applications. Sens. Actuators B Chem. 2018, 265, 35–49. [Google Scholar] [CrossRef]
- Lin, S.; Xu, X.; Hu, F.; Chen, Z.; Wang, Y.; Zhang, L.; Peng, Z.; Li, D.; Zeng, L.; Chen, Y.; et al. Using Antibody Modified Terahertz Metamaterial Biosensor to Detect Concentration of Carcinoembryonic Antigen. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–7. [Google Scholar] [CrossRef]
- Huang, T.-J.; Zhao, J.; Yin, L.-Z.; Liu, P.-K. Terahertz Subwavelength Edge Detection Based on Dispersion-Induced Plasmons. Opt. Lett. 2021, 46, 2746–2749. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Xiang, Y.; Xu, J.; Liu, S.; Dong, P. Highly Sensitive Refractive Index Sensing Based on Photonic Spin Hall Effect and Its Application on Cancer Detection. IEEE Sens. J. 2022, 22, 12754–12760. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, H.; Pan, J.; Zhang, S.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z. Black Phosphorus Terahertz Sensing Based on Photonic Spin Hall Effect. Opt. Express 2020, 28, 25869–25878. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Sharma, A.K.; Prajapati, Y.K. Graphene-Based Plasmonic Sensor at THz Frequency with Photonic Spin Hall Effect Assisted by Magneto-Optic Phenomenon. Plasmonics 2022, 17, 957–963. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yin, X.; Zhao, H. Dual-Function Photonic Spin Hall Effect Sensor for High-Precision Refractive Index Sensing and Graphene Layer Detection. Opt. Express 2022, 30, 31925–31936. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Hu, C.; Zhang, H. Ultra-Wide Unidirectional Infrared Absorber Based on 1D Gyromagnetic Photonic Crystals Concatenated with General Fibonacci Quasi-Periodic Structure in Transverse Magnetization. J. Opt. 2020, 22, 105101. [Google Scholar] [CrossRef]
- Lewin, L. Electr. Engineers—Part III: Radio and Communic. Engineer 1947, 94, 65. [Google Scholar]
- Liu, X.; Zhao, Q.; Lan, C.; Zhou, J. Isotropic Mie Resonance-Based Metamaterial Perfect Absorber. Appl. Phys. Lett. 2013, 103, 031910. [Google Scholar] [CrossRef]
- Herzberger, M.; Salzberg, C.D. Refractive Indices of Infrared Optical Materials and Color Correction of Infrared Lenses. J. Opt. Soc. Am. 1962, 52, 420–427. [Google Scholar] [CrossRef]
- Andryieuski, A.; Lavrinenko, A.V. Graphene Metamaterials Based Tunable Terahertz Absorber: Effective Surface Conductivity Approach. Opt. Express 2013, 21, 9144–9155. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Yang, Z.; Lan, F.; Gao, X.; Shi, Z. Properties of Obliquely Incident Electromagnetic Wave in One-Dimensional Magnetized Plasma Photonic Crystals. Phys. Plasmas 2010, 17, 042501. [Google Scholar] [CrossRef]
- Fenton, E.W. Absence of Proximity Effect between S-Wave and p-Wave Superconductors. Solid State Commun. 1980, 34, 917–922. [Google Scholar] [CrossRef]
- Gao, C.; Guo, B. Enhancement and Tuning of Spin Hall Effect of Light in Plasma Metamaterial Waveguide. Phys. Plasmas 2017, 24, 093520. [Google Scholar] [CrossRef]
- Qi, L.; Liu, C.; Ali Shah, S.M. A Broad Dual-Band Switchable Graphene-Based Terahertz Metamaterial Absorber. Carbon 2019, 153, 179–188. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Xiang, Y.-T.; Wan, B.-F.; Zhang, H.-F. Multiscale and Multiple Physical Quantities Sensor Based on Nonreciprocal Evanescent Wave in the One-Dimensional Photonic Crystals. IEEE Sens. J. 2021, 21, 19984–19992. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Jia, P.; Zhai, C.; An, G.; Liu, L.; Zhu, F.; Su, J. High-Sensitivity Refractive Index Sensor with Cascaded Dual-Core Photonic Crystal Fiber Based on Vernier Effect. Optik 2022, 256, 168488. [Google Scholar] [CrossRef]
- Shi, X.; Han, Z. Enhanced Terahertz Fingerprint Detection with Ultrahigh Sensitivity Using the Cavity Defect Modes. Sci. Rep. 2017, 7, 13147. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Cai, L. A Reflective Intensity Modulated Fiber Tilt Angle Sensor Based on an All-Photonic Crystal Fiber Interferometer. Sens. Actuators A Phys. 2016, 244, 106–111. [Google Scholar] [CrossRef]
- Wan, B.-F.; Zhou, Z.-W.; Xu, Y.; Zhang, H.-F. A Theoretical Proposal for a Refractive Index and Angle Sensor Based on One-Dimensional Photonic Crystals. IEEE Sens. J. 2021, 21, 331–338. [Google Scholar] [CrossRef]



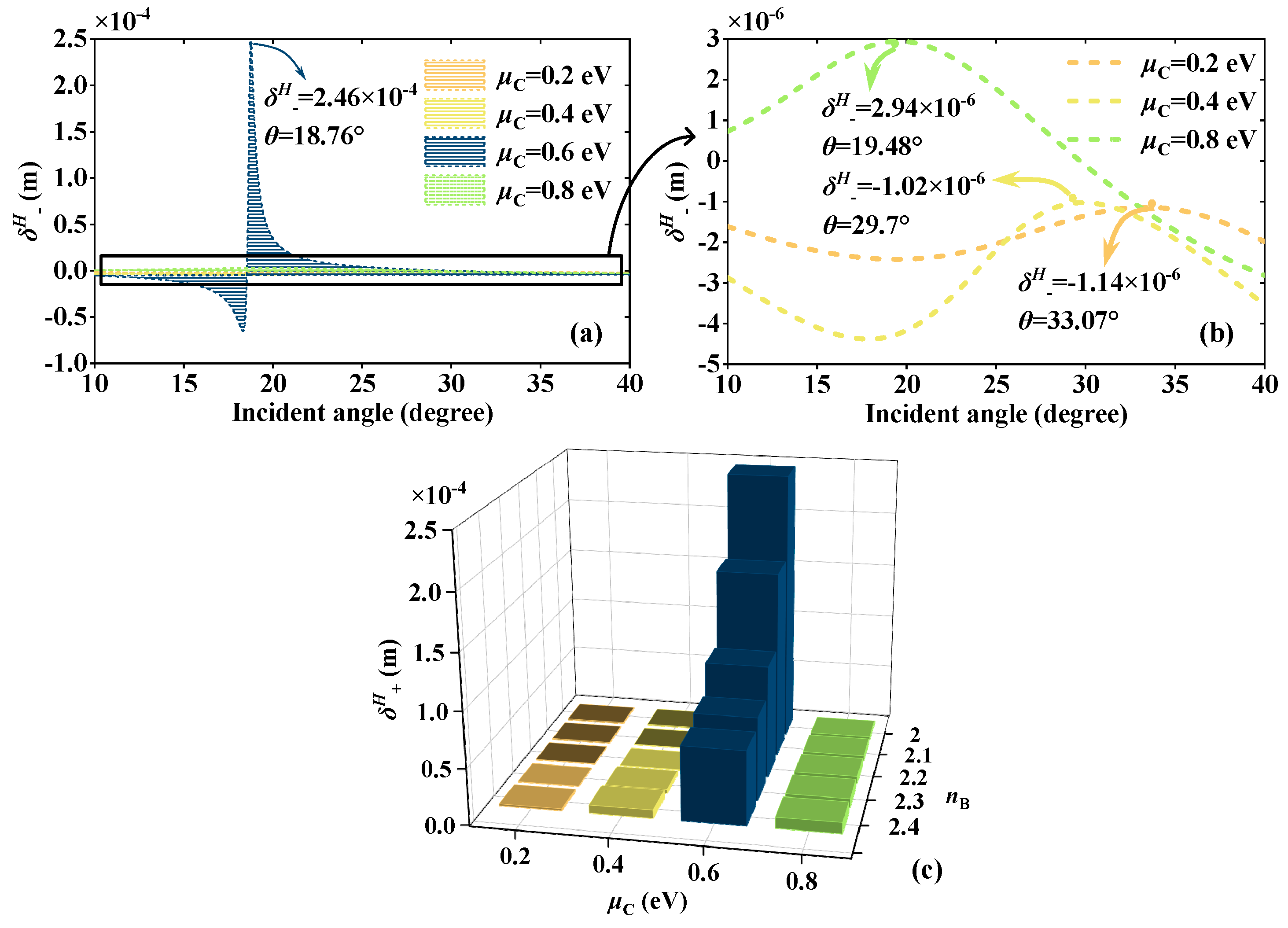
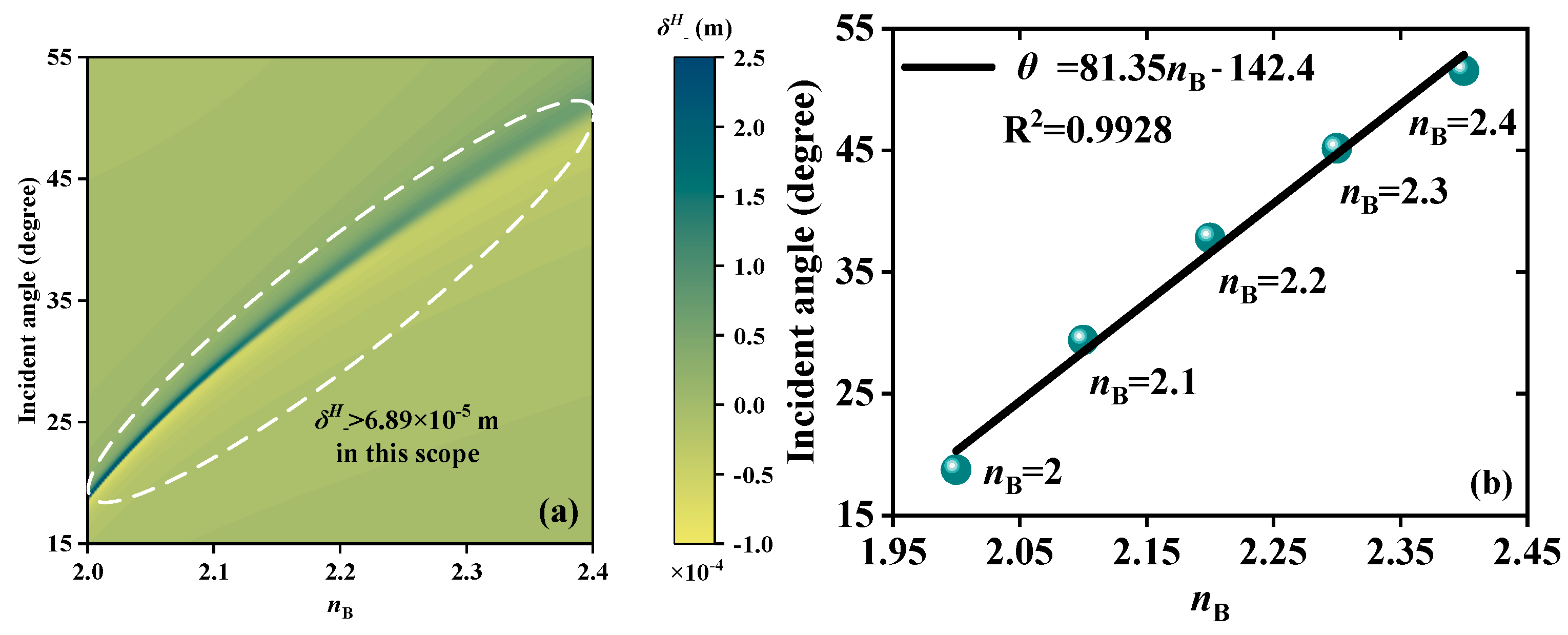
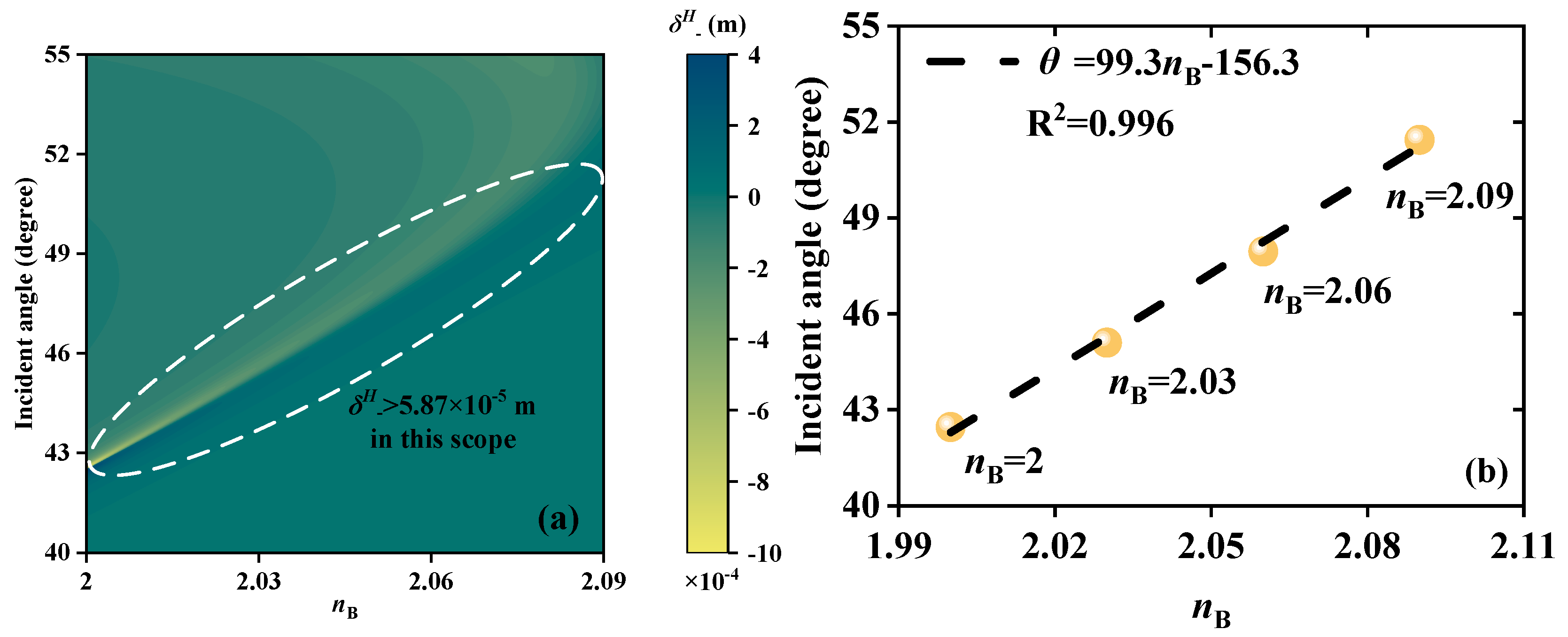
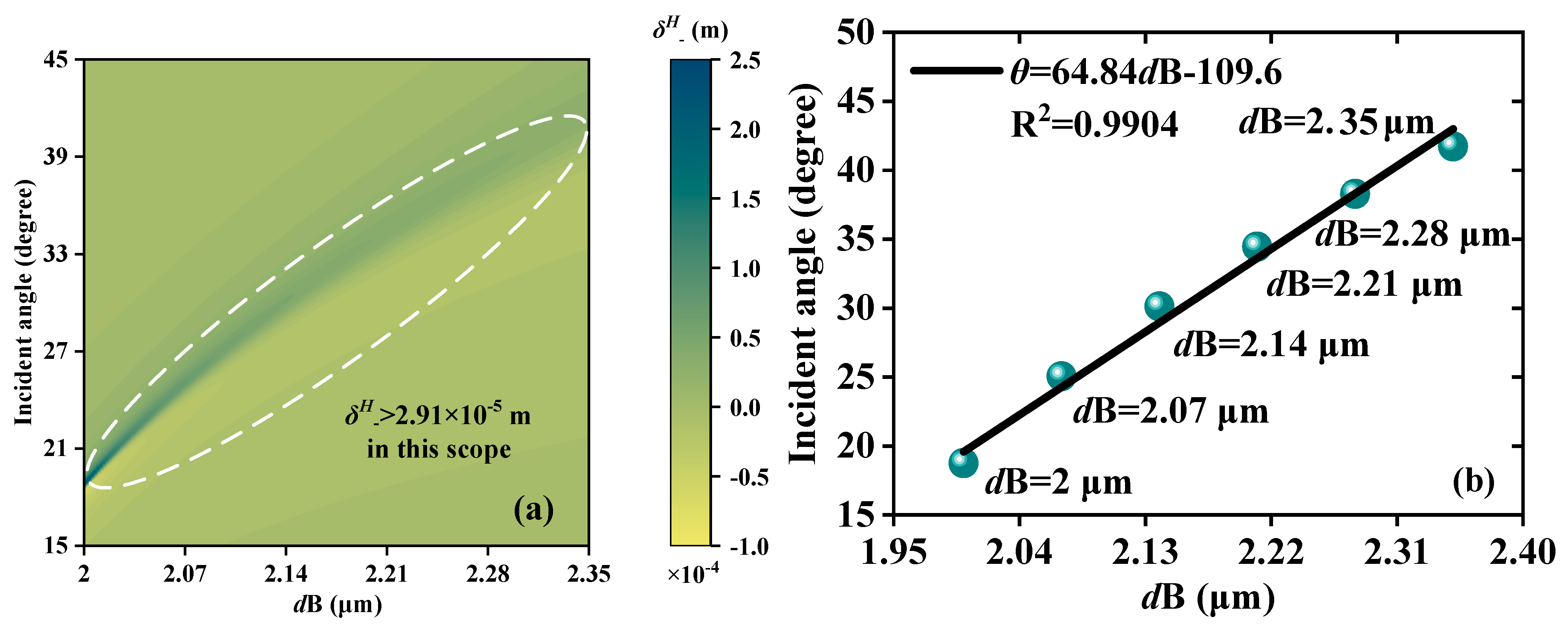


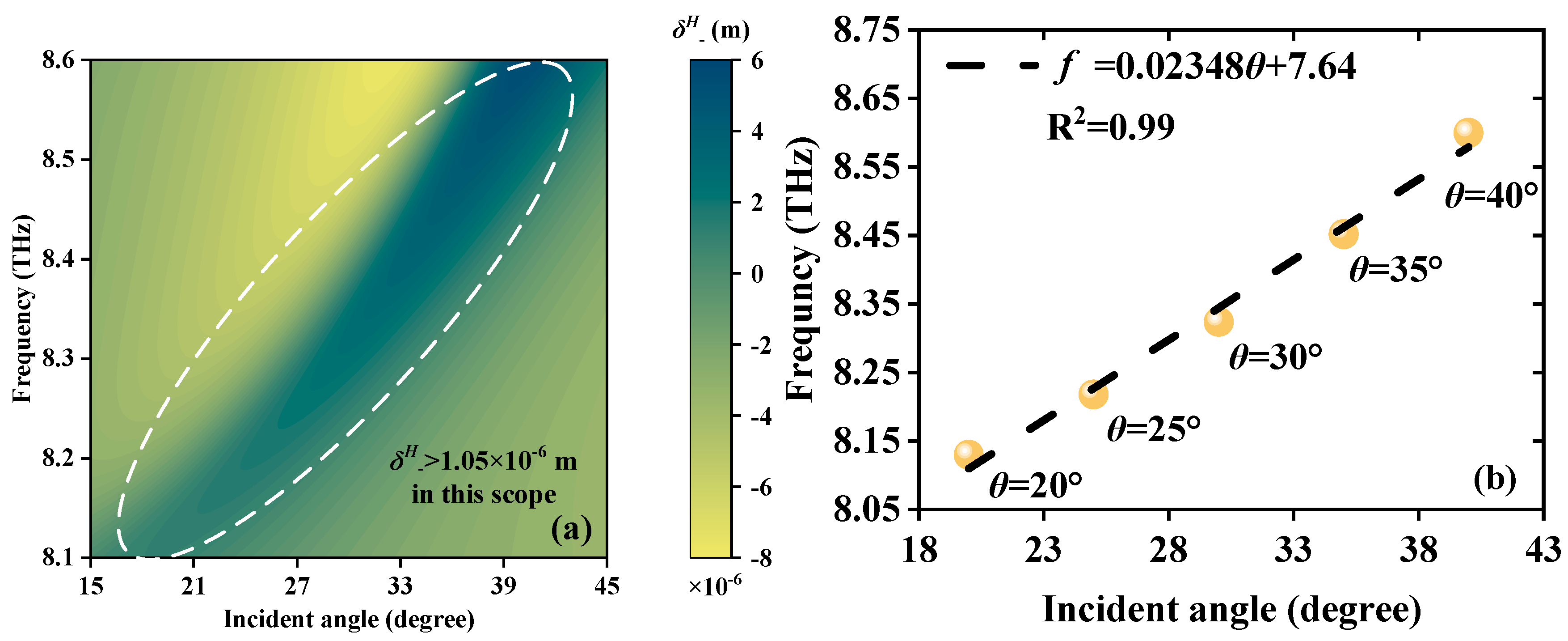
| RI | Thickness (μm) | Angle (°) | ||
|---|---|---|---|---|
| Forward | Range | 2~2.4 | 2~2.35 | 27~47 |
| S | 81.35 °/RIU | 64.84 °/μm | 0.02238 THz/° | |
| Backward | Range | 2~2.09 | 1.85~2.02 | 20~40 |
| S | 99.3 °/RIU | 70.07 °/μm | 0.02348 THz/° |
| Refs. | Janus | Multifunction | Physical Quantities Detection | |||
|---|---|---|---|---|---|---|
| [38] | No | No | RI | Range | 1.362~1.366 | |
| S | 303,376 nm/RIU | |||||
| [39] | No | No | Thickness | Range | 0~0.5 μm | |
| S | / | |||||
| [40] | No | No | Angle | Range | 0~45 | |
| S | 55.67 pm/° | |||||
| [37] | Yes | No | RI | Forward | Range | 1.35~2.09 |
| S | 132 MHz/RIU | |||||
| Backward | Range | 1~1.57 | ||||
| S | 40.7 MHz/RIU | |||||
| [41] | No | Yes | RI | Range | 2~2.7 | |
| S | 32.3 THz/RIU | |||||
| Angle | Range | 25°~70° | ||||
| S | 0.5 THz/° | |||||
| This work | Yes | Yes | RI | Forward | Range | 2~2.4 |
| S | 81.35°/RIU | |||||
| Backward | Range | 2~2.09 | ||||
| S | 99.3°/RIU | |||||
| Thickness | Indicated in the article | |||||
| Angle | Indicated in the article | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, J.; Xu, J.; Liang, A.; Zou, J.; Wu, C.; Zhang, T.; Zhang, H. Multiple Physical Quantities Janus Metastructure Sensor Based on PSHE. Sensors 2023, 23, 4747. https://doi.org/10.3390/s23104747
Sui J, Xu J, Liang A, Zou J, Wu C, Zhang T, Zhang H. Multiple Physical Quantities Janus Metastructure Sensor Based on PSHE. Sensors. 2023; 23(10):4747. https://doi.org/10.3390/s23104747
Chicago/Turabian StyleSui, Junyang, Jie Xu, Aowei Liang, Jiahao Zou, Chuanqi Wu, Tinghao Zhang, and Haifeng Zhang. 2023. "Multiple Physical Quantities Janus Metastructure Sensor Based on PSHE" Sensors 23, no. 10: 4747. https://doi.org/10.3390/s23104747
APA StyleSui, J., Xu, J., Liang, A., Zou, J., Wu, C., Zhang, T., & Zhang, H. (2023). Multiple Physical Quantities Janus Metastructure Sensor Based on PSHE. Sensors, 23(10), 4747. https://doi.org/10.3390/s23104747







