Dynamic Resource Optimization for Energy-Efficient 6G-IoT Ecosystems
Abstract
1. Introduction
- We design an energy-efficient resource allocation framework and formulate a non-convex MINLP problem for joint optimization of user selection, subchannel allocation, user selection, power allocation, and the number of activated RRUs in order to enhance the energy efficiency in dynamic large-scale 6G-IoT ecosystems.
- In order to decompose the problems of non-convex optimization into small segments, we leverage the fractional programming property. We propose the Lagrangian decomposition method to optimize power allocation and the KM algorithm to dynamically allocate resources to IoT users to obtain optimal solutions. This can significantly reduce the computational complexity and make the optimization process more scalable in dynamic large-scale IoT systems.
- The effectiveness of the proposed algorithm compared to the leading-edge approaches in the form of energy efficiency gain is verified through extensive simulations.
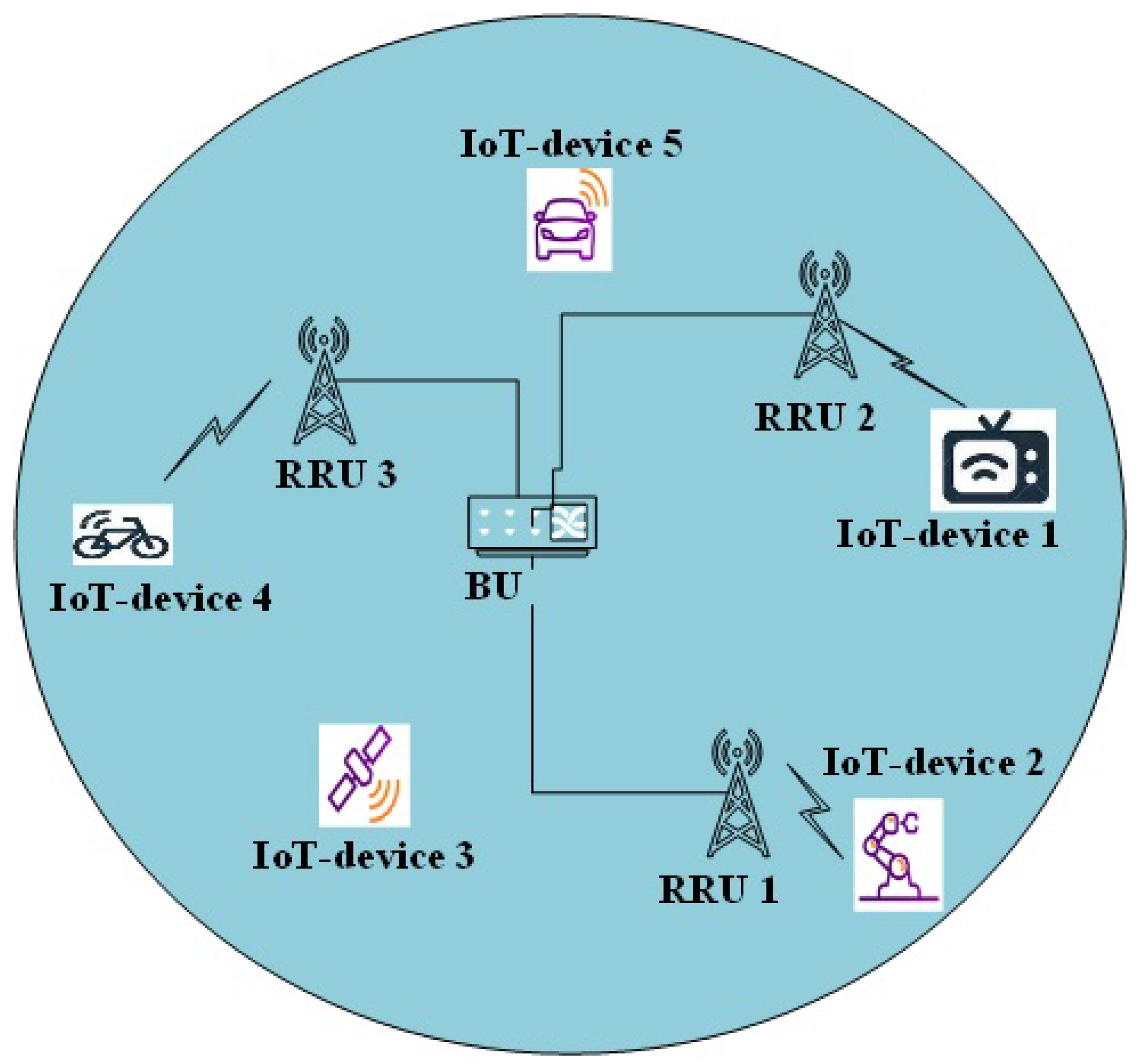
2. IoT Network Model
2.1. Channel Model and Estimation
2.2. Data Transmission Model
2.3. The Power Consumption Model
3. Resource Allocation and Optimization Problem
3.1. Energy Efficiency Optimization
3.2. Formulation of Optimization Problem
3.3. Novel Dynamic Resource Allocation Design
Transformation of Energy Efficiency Optimization
4. Proposed Joint Optimal Iterative Method
4.1. Relaxed Problem Formulation
4.2. Dual Decomposition Problem
4.3. Inner Loop Method
4.3.1. Optimal Power Allocation
4.3.2. Optimal Number of Activated RRUs Allocation
4.3.3. Optimal Subchannel Allocation
4.4. Outer Loop: Master Subproblem Solution
4.5. Optimal User Selection
- Initialize perfect matching M and feasible labelling ℓ in .
- Set .
- If ℜ denotes an optimal matching of complete bipartite graph G, the Equation (29) can be optimally solved.
- Otherwise, select vertex .
- If and , then set .
- Update the feasible labels aswhere the new feasible label can be expressed asiff and .
- If , set , and go to step 2.
4.6. Proposed Joint Resource Allocation Algorithm
| Algorithm 1: Proposed JEERA Algorithm to Maximize Energy Efficiency |
 |
4.7. Computational Complexity and Feasibility
5. Performance Evaluation and Discussion
5.1. Numerical Results and Discussion
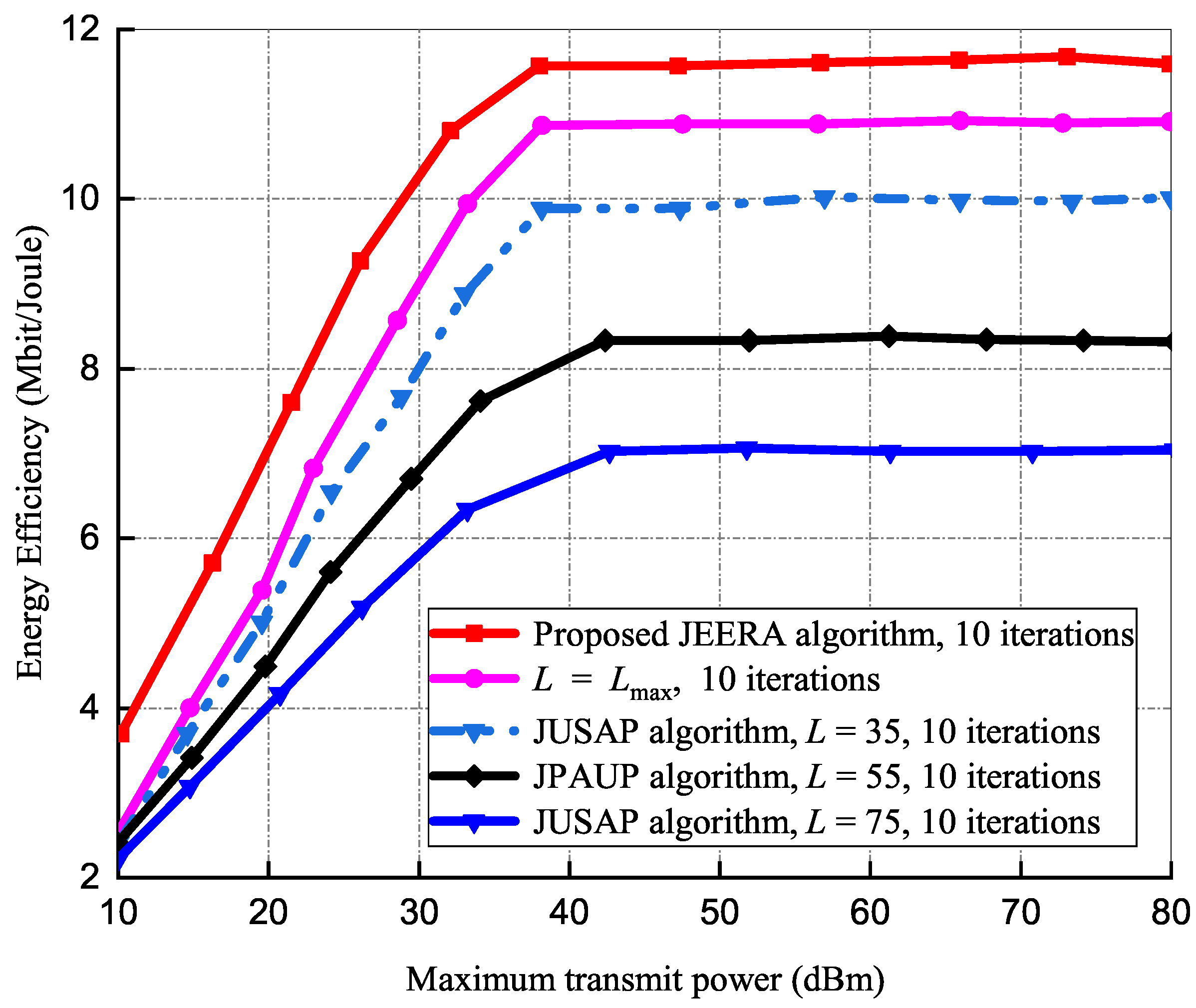
5.1.1. Effects of Transmission Power on Energy Efficiency
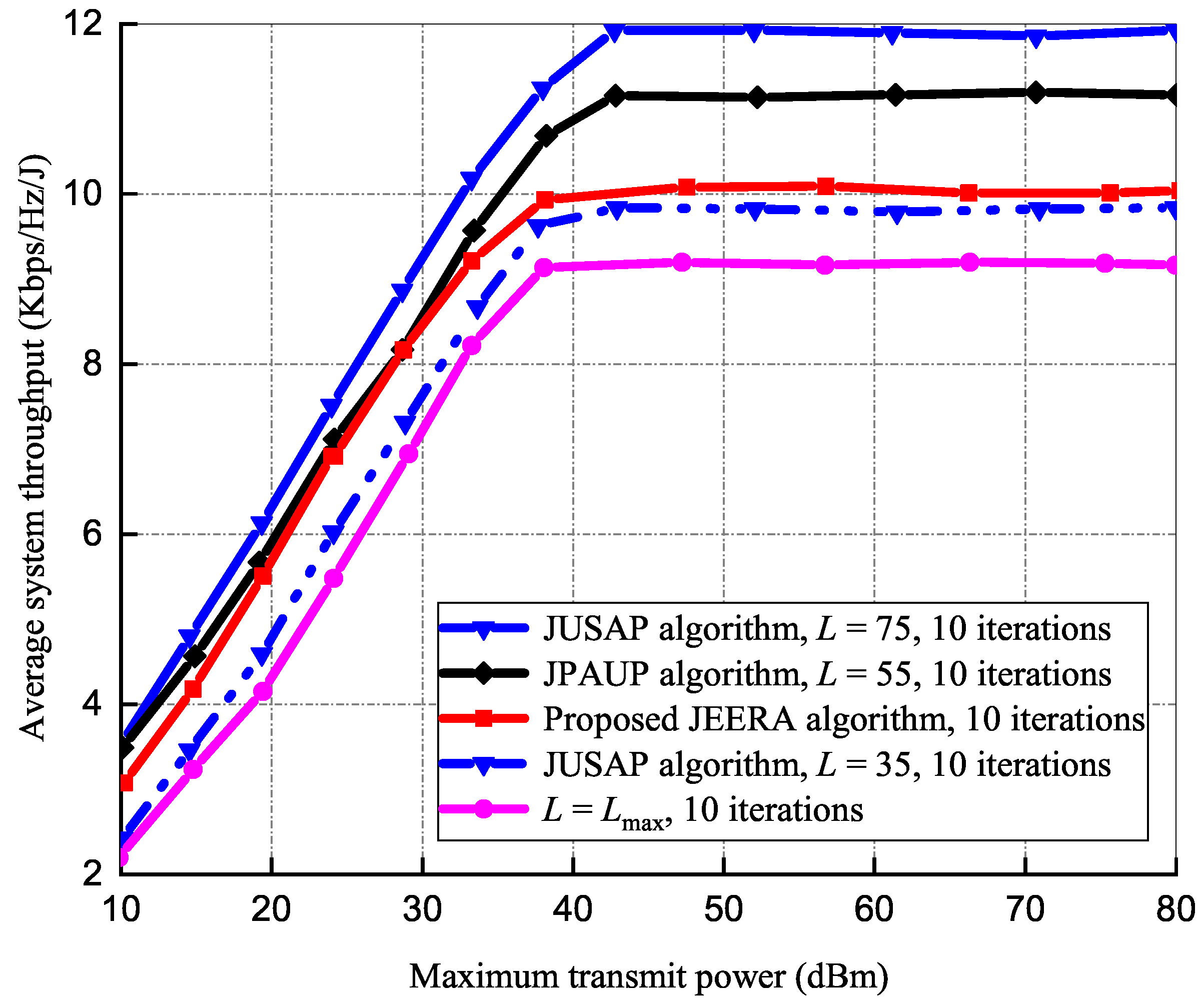
5.1.2. Impact of Transmit Power on Average System Throughput
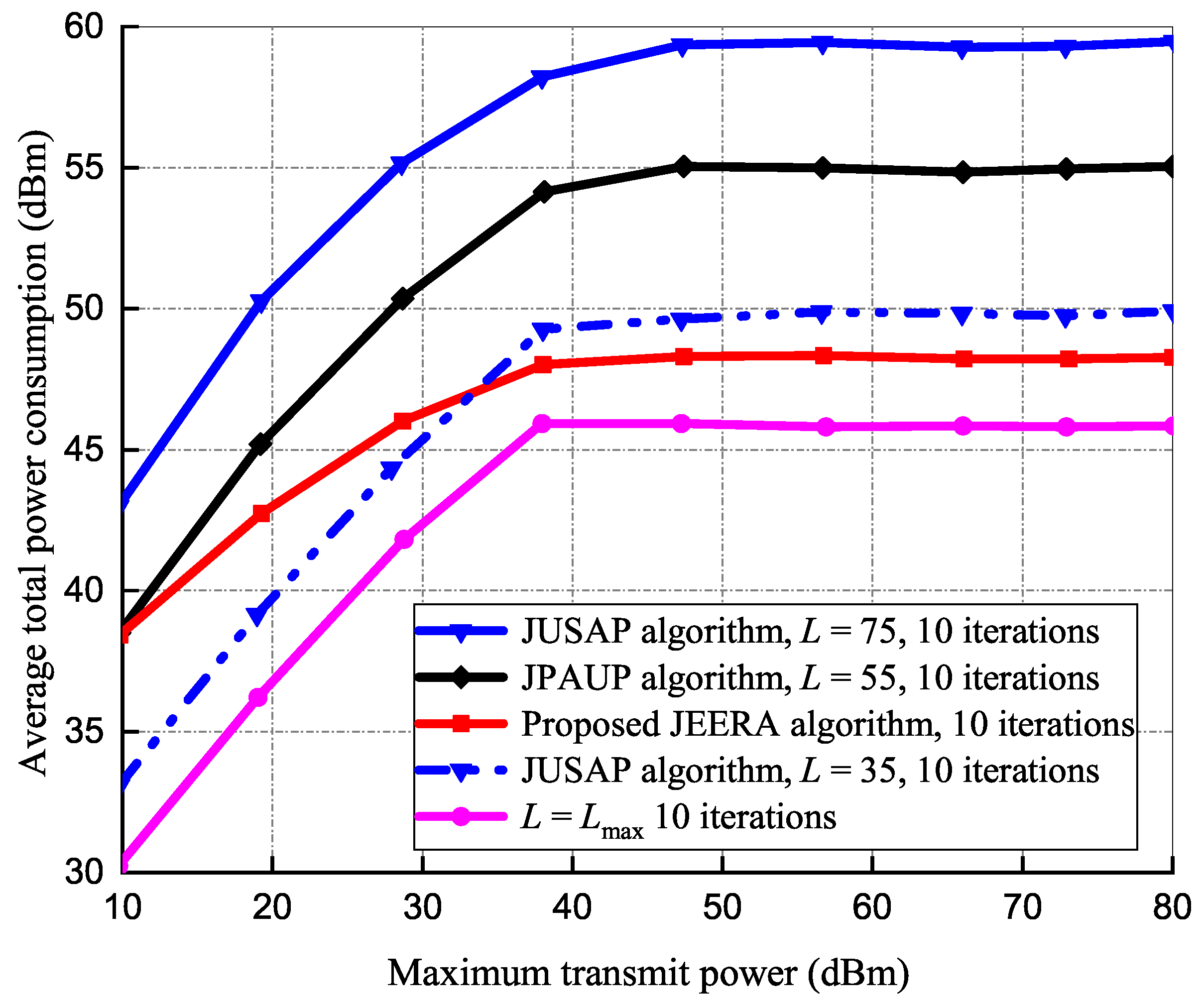
5.1.3. Effects of Transmit Power on Total Power Consumption
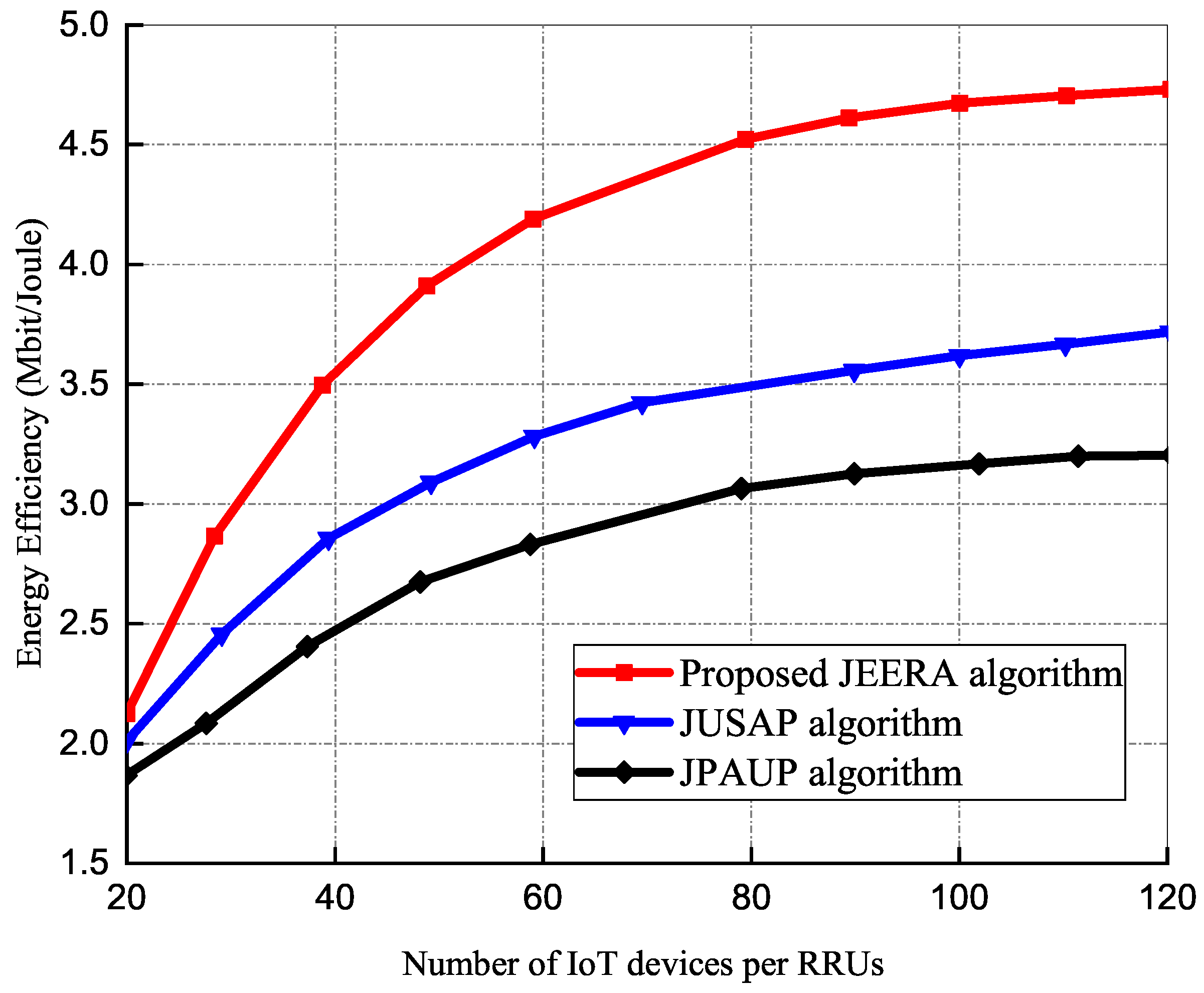
5.1.4. Effect of IoT Devices on Energy Efficiency
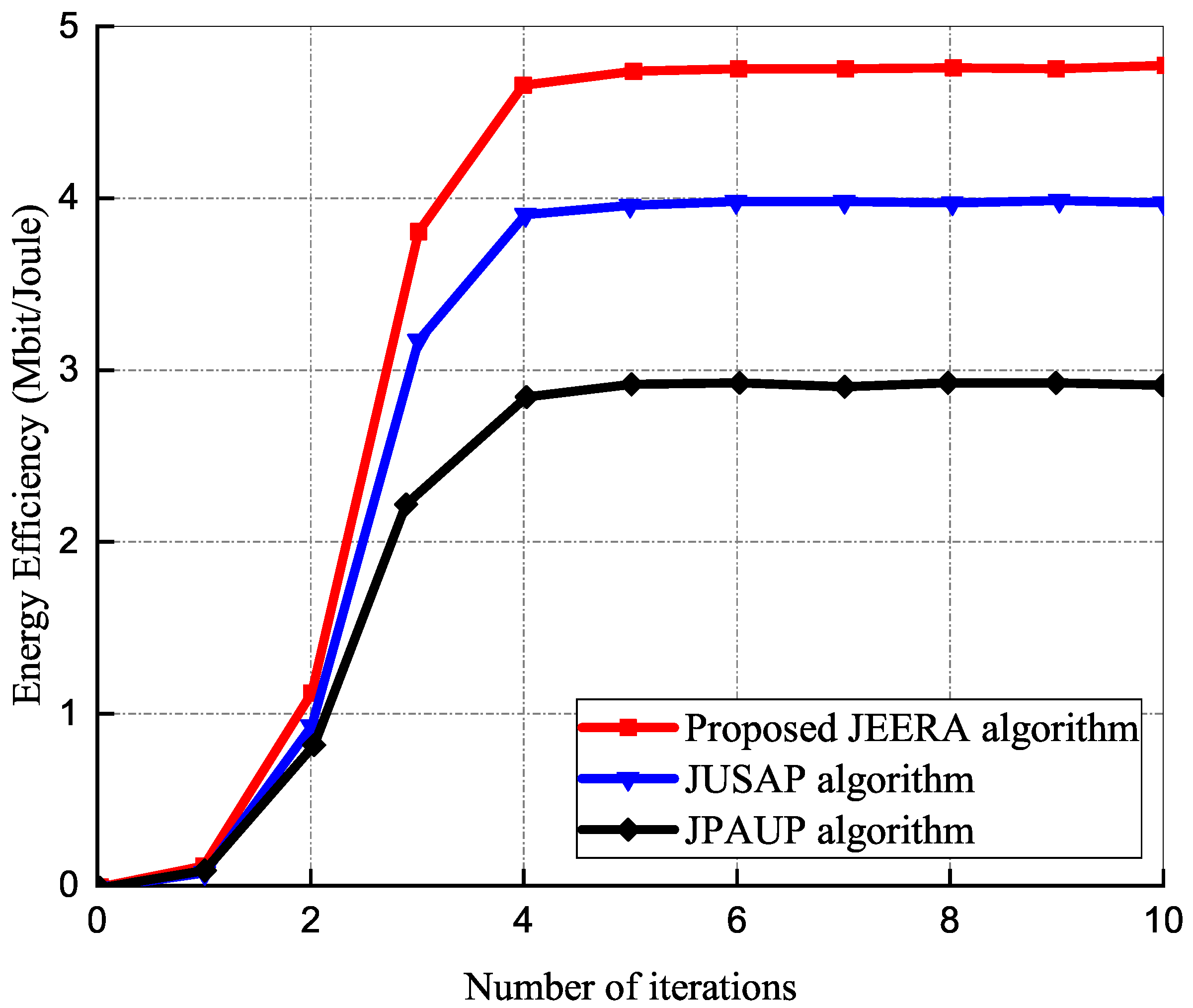
5.1.5. The Convergence of Proposed Iterative Algorithm
5.1.6. Impact of SINR Constraints on the Performance of Energy Efficiency
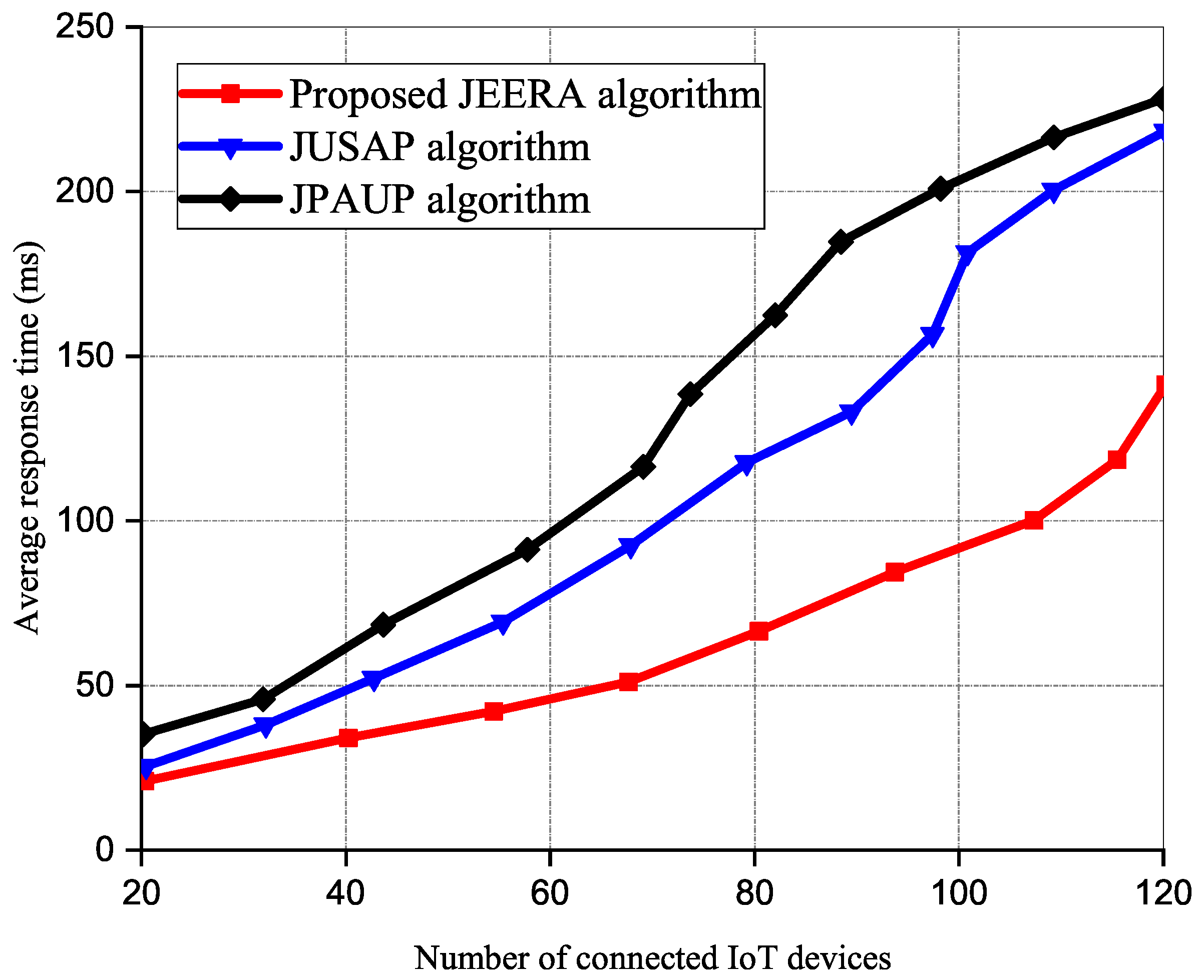
5.1.7. Effects of Activated RRUs on Transmission Power
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gyamfi, E.; Ansere, J.A.; Xu, L. ECC based lightweight cybersecurity solution for IoT networks utilising multi-access mobile edge computing. In Proceedings of the 2019 Fourth International Conference on Fog and Mobile Edge Computing (FMEC), Rome, Italy, 10–13 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 149–154. [Google Scholar]
- Kamal, M.; Tariq, M.; Srivastava, G.; Malina, L. Optimized security algorithms for intelligent and autonomous vehicular transportation systems. IEEE Trans. Intell. Transp. Syst. 2021, 24, 2038–2044. [Google Scholar] [CrossRef]
- Peisa, J.; Persson, P.; Parkvall, S.; Dahlman, E.; Grøvlen, A.; Hoymann, C.; Gerstenberger, D. 5G evolution: 3GPP releases 16 & 17 overview. Ericsson Technol. Rev. 2020, 2020, 2–13. [Google Scholar]
- Wu, J.; Rangan, S.; Zhang, H. Green Communications: Theoretical Fundamentals, Algorithms, and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Gandotra, P.; Jha, R.K.; Jain, S. Prolonging user battery lifetime using green communication in spectrum sharing networks. IEEE Commun. Lett. 2018, 22, 1490–1493. [Google Scholar] [CrossRef]
- Ansere, J.A.; Kamal, M.; Gyamfi, E.; Sam, F.; Tariq, M.; Mohammed, A. Energy efficient resource optimization in cooperative Internet of Things networks. Internet Things 2020, 12, 100302. [Google Scholar] [CrossRef]
- Peng, M.; Zhang, K.; Jiang, J.; Wang, J.; Wang, W. Energy-efficient resource assignment and power allocation in heterogeneous cloud radio access networks. IEEE Trans. Veh. Technol. 2014, 64, 5275–5287. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A comprehensive survey. IEEE Internet Things J. 2021, 9, 359–383. [Google Scholar] [CrossRef]
- Guo, F.; Yu, F.R.; Zhang, H.; Li, X.; Ji, H.; Leung, V.C. Enabling massive IoT toward 6G: A comprehensive survey. IEEE Internet Things J. 2021, 8, 11891–11915. [Google Scholar] [CrossRef]
- Ansere, J.A.; Han, G.; Wang, H.; Choi, C.; Wu, C. A reliable energy efficient dynamic spectrum sensing for cognitive radio IoT networks. IEEE Internet Things J. 2019, 6, 6748–6759. [Google Scholar] [CrossRef]
- Yassein, M.B.; Al-smadi, L.; Mrayan, L. A Survey of Mobile Health Applications in Context of Internet of Things. In Proceedings of the 2019 7th International Conference on Future Internet of Things and Cloud (FiCloud), Istanbul, Turkey, 26–28 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 351–357. [Google Scholar]
- Gyamfi, E.; Ansere, J.A.; Kamal, M.; Tariq, M.; Jurcut, A. An adaptive network security system for iot-enabled maritime transportation. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2538–2547. [Google Scholar] [CrossRef]
- Kurt, A.; Dolu, U.; Kaya, B.; Poyrazoglu, G. Design of the circuitry, battery management system, and wireless communication of an electric vehicle. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 12–15 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 233–237. [Google Scholar]
- Bhat, R.V.; Motani, M.; Murthy, C.R.; Vaze, R. Energy harvesting communications with batteries having cycle constraints. IEEE Trans. Green Commun. Netw. 2019, 4, 263–276. [Google Scholar] [CrossRef]
- Han, F.; Bandarkar, A.W.; Sozer, Y. Energy harvesting from moving vehicles on highways. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 12 September–3 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 974–978. [Google Scholar]
- Liu, X.; Ansari, N. Green relay assisted D2D communications with dual batteries in heterogeneous cellular networks for IoT. IEEE Internet Things J. 2017, 4, 1707–1715. [Google Scholar] [CrossRef]
- Jahid, A.; Hossain, M.S.; Monju, M.K.H.; Rahman, M.F.; Hossain, M.F. Techno-economic and energy efficiency analysis of optimal power supply solutions for green cellular base stations. IEEE Access 2020, 8, 43776–43795. [Google Scholar] [CrossRef]
- Kaur, N.; Sood, S.K. An energy-efficient architecture for the Internet of Things (IoT). IEEE Syst. J. 2015, 11, 796–805. [Google Scholar] [CrossRef]
- He, C.; Li, G.Y.; Zheng, F.C.; You, X. Power allocation criteria for distributed antenna systems. IEEE Trans. Veh. Technol. 2014, 64, 5083–5090. [Google Scholar] [CrossRef]
- Castaneda, E.; Silva, A.; Gameiro, A.; Kountouris, M. An overview on resource allocation techniques for multi-user MIMO systems. IEEE Commun. Surv. Tutor. 2016, 19, 239–284. [Google Scholar] [CrossRef]
- Fang, F.; Cheng, J.; Ding, Z. Joint energy efficient subchannel and power optimization for a downlink NOMA heterogeneous network. IEEE Trans. Veh. Technol. 2018, 68, 1351–1364. [Google Scholar] [CrossRef]
- Wang, F.; Chen, W.; Tang, H.; Wu, Q. Joint optimization of user association, subchannel allocation, and power allocation in multi-cell multi-association OFDMA heterogeneous networks. IEEE Trans. Commun. 2017, 65, 2672–2684. [Google Scholar] [CrossRef]
- Iwendi, C.; Ansere, J.A.; Nkurunziza, P.; Anajemba, J.H.; Yixuan, Z. An ACO-KMT energy efficient routing scheme for sensed-IoT network. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3841–3846. [Google Scholar]
- Shen, X.; Liao, W.; Yin, Q. A Novel Wireless Resource Management for the 6G-Enabled High-Density Internet of Things. IEEE Wirel. Commun. 2022, 29, 32–39. [Google Scholar] [CrossRef]
- Janjua, M.B.; Arslan, H. A Survey of Symbiotic Radio: Methodologies, Applications, and Future Directions. Sensors 2023, 23, 2511. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Practical Algorithm Development; Pearson Education: London, UK, 2013; Volume 3. [Google Scholar]
- Abrardo, A.; Fodor, G.; Moretti, M.; Telek, M. MMSE receiver design and SINR calculation in MU-MIMO systems with imperfect CSI. IEEE Wirel. Commun. Lett. 2018, 8, 269–272. [Google Scholar] [CrossRef]
- Ansere, J.A.; Han, G.; Liu, L.; Peng, Y.; Kamal, M. Optimal resource allocation in energy-efficient Internet-of-Things networks with imperfect CSI. IEEE Internet Things J. 2020, 7, 5401–5411. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Ha, V.N.; Le, L.B. Resource allocation optimization in multi-user multi-cell massive MIMO networks considering pilot contamination. IEEE Access 2015, 3, 1272–1287. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lee, I.; Oh, S. System-level Data Rate Evaluation for IMT-2020 Urban Micro Channel Model. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 17–19 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 876–879. [Google Scholar]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-efficient resource allocation in OFDMA systems with hybrid energy harvesting base station. IEEE Trans. Wirel. Commun. 2013, 12, 3412–3427. [Google Scholar] [CrossRef]


| Parameter | Values |
|---|---|
| Operating frequency | 3.8 GHz |
| Total channel bandwidth | 8 MHz |
| Transmitting antenna gain | 12 dB |
| Path-loss exponent | 4 |
| Constant back-off factor | 0.3 |
| Noise power per subchannel | −167 dBm |
| Power amplifier efficiency | 0.2 |
| Number of subchannels | 32 |
| Power consumption | 50 dBm |
| Minimum data rate | 4.2 Mbps |
| SINR threshold | 2.0 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansere, J.A.; Kamal, M.; Khan, I.A.; Aman, M.N. Dynamic Resource Optimization for Energy-Efficient 6G-IoT Ecosystems. Sensors 2023, 23, 4711. https://doi.org/10.3390/s23104711
Ansere JA, Kamal M, Khan IA, Aman MN. Dynamic Resource Optimization for Energy-Efficient 6G-IoT Ecosystems. Sensors. 2023; 23(10):4711. https://doi.org/10.3390/s23104711
Chicago/Turabian StyleAnsere, James Adu, Mohsin Kamal, Izaz Ahmad Khan, and Muhammad Naveed Aman. 2023. "Dynamic Resource Optimization for Energy-Efficient 6G-IoT Ecosystems" Sensors 23, no. 10: 4711. https://doi.org/10.3390/s23104711
APA StyleAnsere, J. A., Kamal, M., Khan, I. A., & Aman, M. N. (2023). Dynamic Resource Optimization for Energy-Efficient 6G-IoT Ecosystems. Sensors, 23(10), 4711. https://doi.org/10.3390/s23104711






