Comparison of Common Algorithms for Single-Pixel Imaging via Compressed Sensing
Abstract
1. Introduction
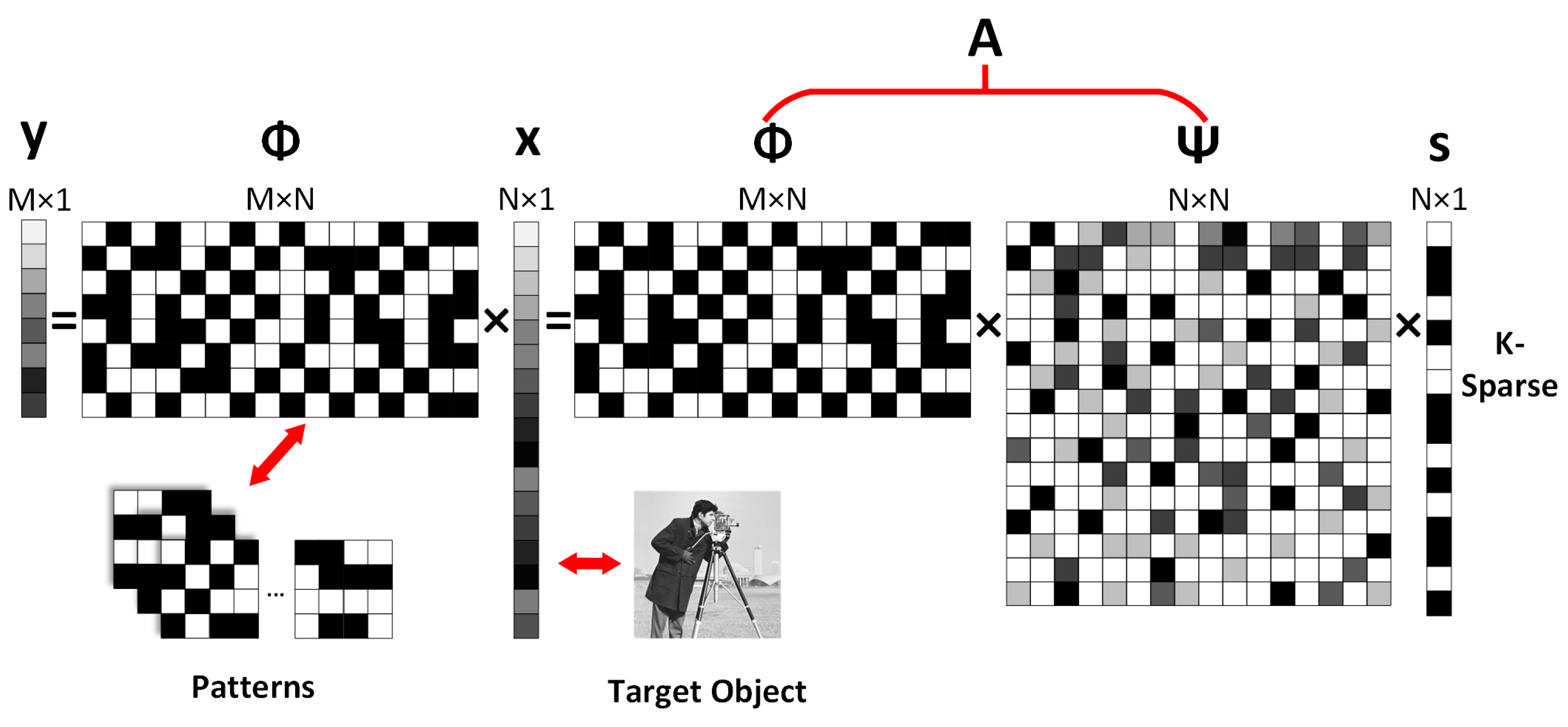
2. Compressed Sensing SPI
3. Selection of Measurement Matrix
3.1. Random Measurement Matrix
3.1.1. Gaussian Random Measurement Matrix
3.1.2. Bernoulli Random Measurement Matrix
3.2. Partial Orthogonal Measurement Matrix
3.2.1. Partial Hadamard Matrix
3.2.2. Partial Fourier Matrix
3.3. Semi-Deterministic Random Measurement Matrix
3.3.1. Toeplitz and Circulant Matrix
3.3.2. Sparse Random Matrix
4. Selection of the Reconstruction Algorithm
4.1. Convex Optimization Algorithms
4.1.1. Basis Pursuit
4.1.2. Basis Pursuit Denoising/Least Absolute Shrinkage and Selection Operator
4.1.3. Decoding by Linear Programming
4.1.4. Dantzig Selector
4.2. Greedy Algorithms
4.2.1. Orthogonal Matching Pursuit
4.2.2. Compressive Sampling Matching Pursuit/Subspace Pursuit
4.2.3. Iterative Hard Thresholding
4.3. Non-Convex Optimization Algorithms
4.3.1. Iterative Reweighted Least Square Algorithm
4.3.2. Bayesian Compressed Sensing Algorithm
4.4. Bregman Distance Minimization Algorithms
4.5. Total Variation Minimization Algorithms
4.5.1. Min-TV with Equality Constraints
4.5.2. Min-TV with Quadratic Constraints
4.5.3. TV Dantzig Selector
4.5.4. Total Variation Augmented Lagrangian Alternating Direction Algorithm
4.6. Other Algorithms
5. Simulation
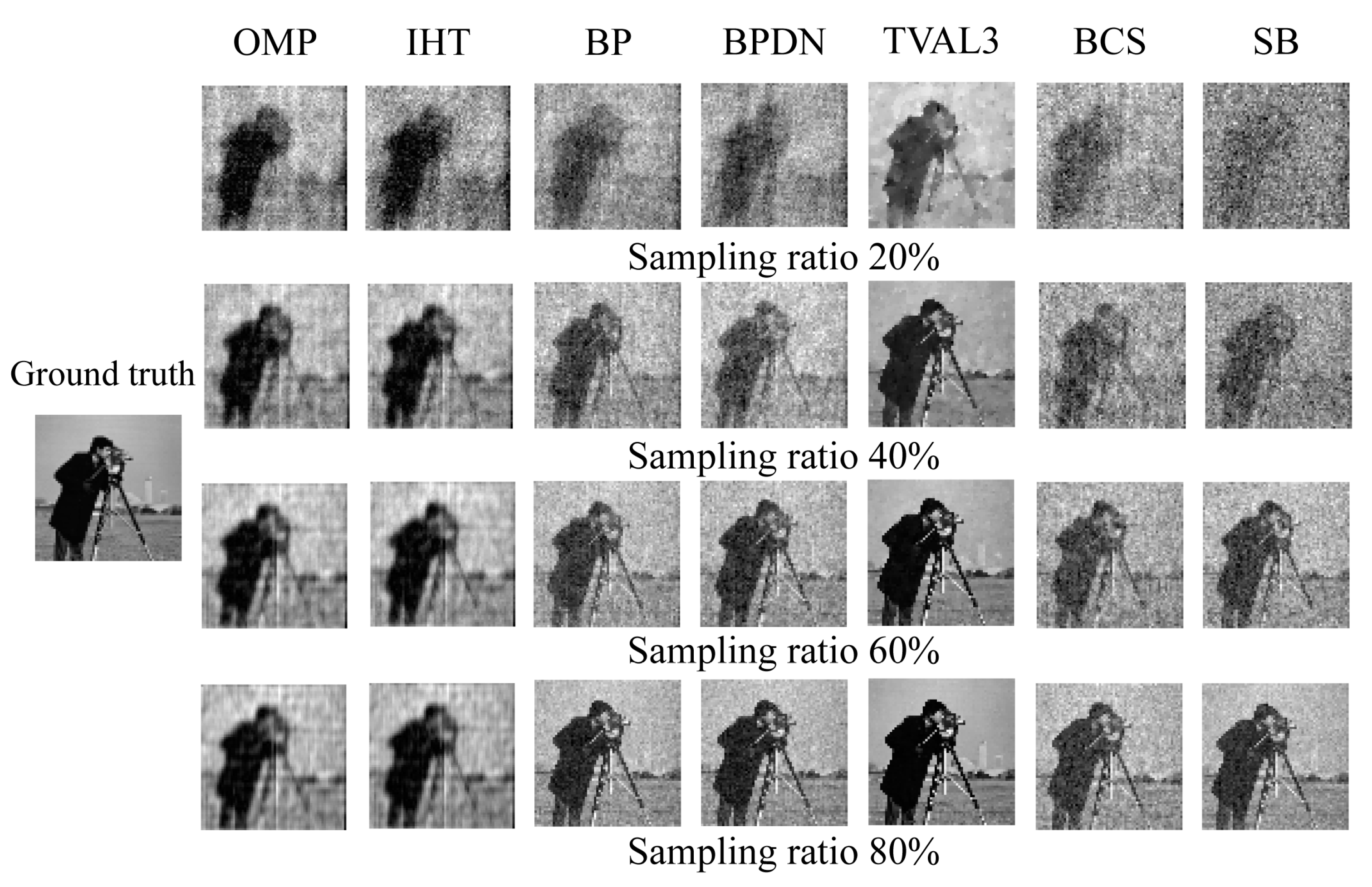
5.1. Comparison of Measurement Matrix Performance
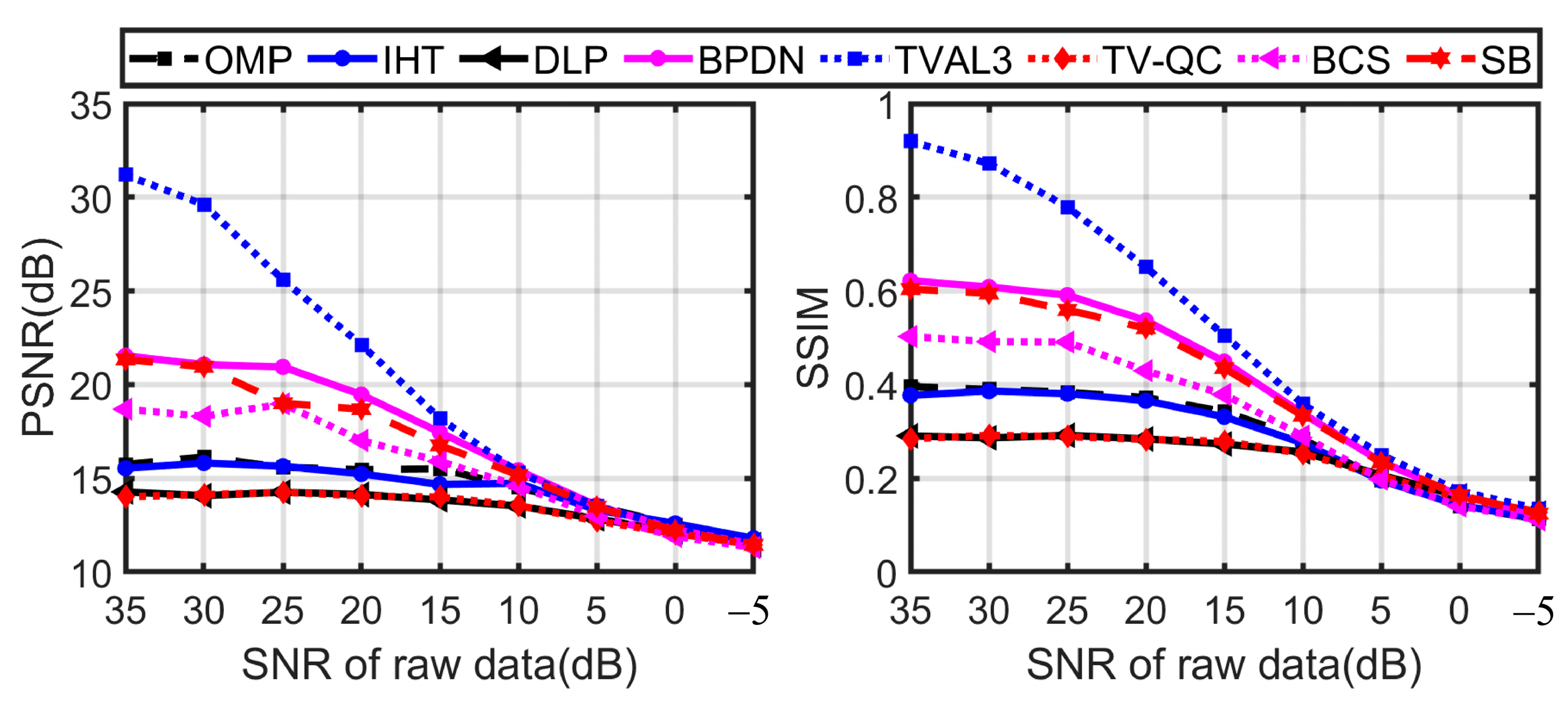
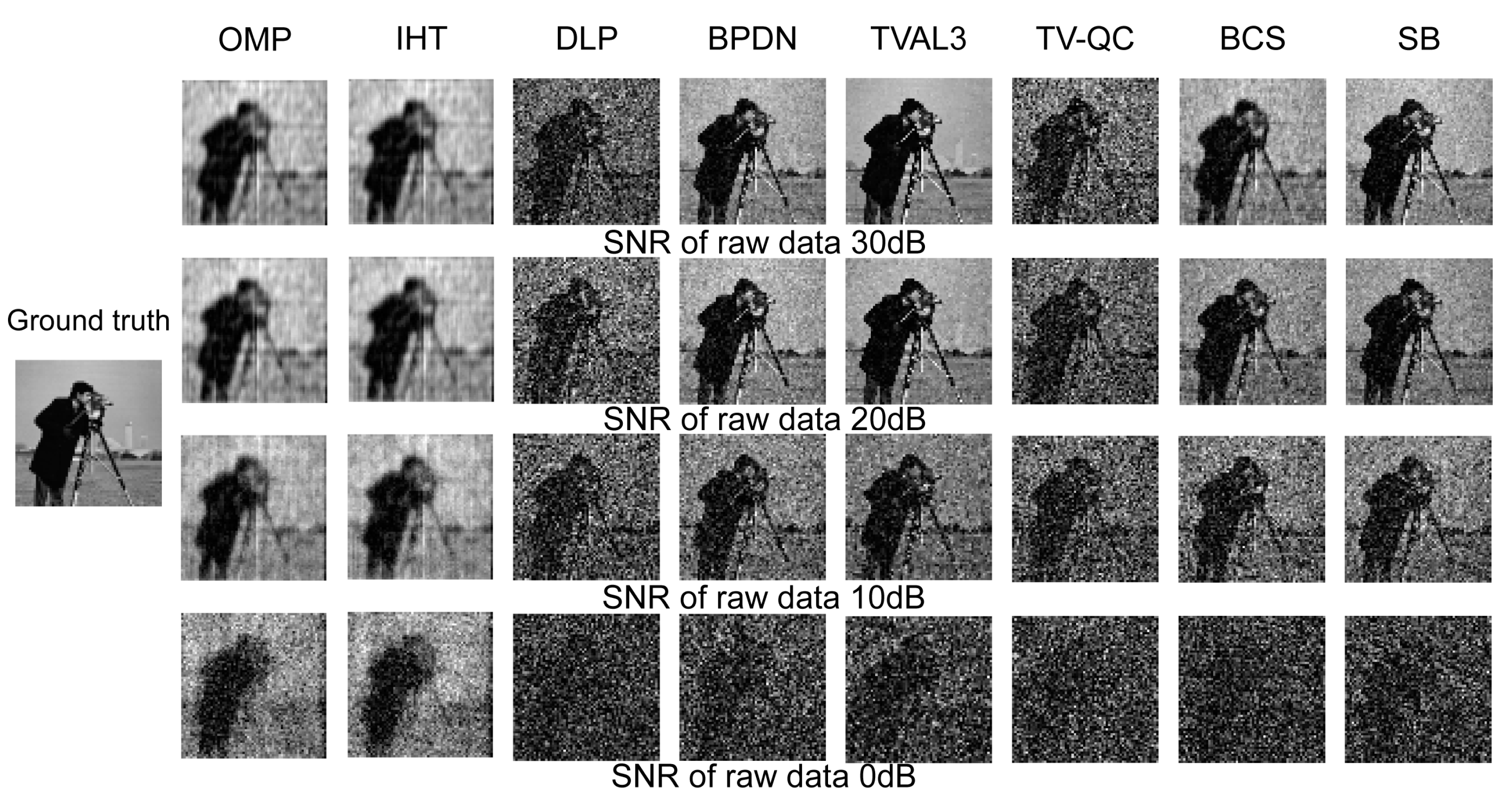
5.2. Comparison of Reconstruction Algorithm Performance
6. Experiment
7. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




References
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Sen, P.; Chen, B.; Garg, G.; Marschner, S.R.; Horowitz, M.; Levoy, M.; Lensch, H.P. Dual photography. In ACM SIGGRAPH 2005 Papers; Association for Computing Machinery: New York, NY, USA, 2005; pp. 745–755. [Google Scholar]
- Bian, L.; Suo, J.; Situ, G.; Li, Z.; Fan, J.; Chen, F.; Dai, Q. Multispectral imaging using a single bucket detector. Sci. Rep. 2016, 6, 24752. [Google Scholar] [CrossRef]
- Rousset, F.; Ducros, N.; Peyrin, F.; Valentini, G.; D’andrea, C.; Farina, A. Time-resolved multispectral imaging based on an adaptive single-pixel camera. Opt. Express 2018, 26, 10550–10558. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Qi, H.; Zhang, S.; Zhao, Z.; Han, J.; Bai, L. A super-resolution fusion video imaging spectrometer based on single-pixel camera. Opt. Commun. 2022, 520, 128464. [Google Scholar] [CrossRef]
- Tao, C.; Zhu, H.; Wang, X.; Zheng, S.; Xie, Q.; Wang, C.; Wu, R.; Zheng, Z. Compressive single-pixel hyperspectral imaging using RGB sensors. Opt. Express 2021, 29, 11207–11220. [Google Scholar] [CrossRef]
- Liu, A.; Gao, L.; Zou, W.; Huang, J.; Wu, Q.; Cao, Y.; Chang, Z.; Peng, C.; Zhu, T. High speed surface defects detection of mirrors based on ultrafast single-pixel imaging. Opt. Express 2022, 30, 15037–15048. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, K.; Fang, J.; Yan, M.; Wu, E.; Zeng, H. Mid-infrared single-pixel imaging at the single-photon level. Nat. Commun. 2023, 14, 1073. [Google Scholar] [CrossRef]
- Watts, C.M.; Shrekenhamer, D.; Montoya, J.; Lipworth, G.; Hunt, J.; Sleasman, T.; Krishna, S.; Smith, D.R.; Padilla, W.J. Terahertz compressive imaging with metamaterial spatial light modulators. Nat. Photonics 2014, 8, 605–609. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, X.K.; Sun, W.F.; Feng, S.F.; Ye, J.S.; Han, P.; Zhang, Y. Reflective single-pixel terahertz imaging based on compressed sensing. IEEE Trans. Terahertz Sci. Technol. 2020, 10, 495–501. [Google Scholar] [CrossRef]
- Li, W.; Hu, X.; Wu, J.; Fan, K.; Chen, B.; Zhang, C.; Hu, W.; Cao, X.; Jin, B.; Lu, Y. Dual-color terahertz spatial light modulator for single-pixel imaging. Light Sci. Appl. 2022, 11, 191. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.M.; Sun, B.; Edgar, M.P.; Phillips, D.B.; Hempler, N.; Maker, G.T.; Malcolm, G.P.A.; Padgett, M.J. Real-time imaging of methane gas leaks using a single-pixel camera. Opt. Express 2017, 25, 2998–3005. [Google Scholar] [CrossRef] [PubMed]
- Studer, V.; Bobin, J.; Chahid, M.; Mousavi, H.S.; Candes, E.; Dahan, M. Compressive fluorescence microscopy for biological and hyperspectral imaging. Proc. Natl. Acad. Sci. USA 2012, 109, E1679–E1687. [Google Scholar] [CrossRef] [PubMed]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- Mostafavi, S.M.; Amjadian, M.; Kavehvash, Z.; Shabany, M. Fourier photoacoustic microscope improved resolution on single-pixel imaging. Appl. Opt. 2022, 61, 1219–1228. [Google Scholar] [CrossRef]
- Durán, V.; Soldevila, F.; Irles, E.; Clemente, P.; Tajahuerce, E.; Andrés, P.; Lancis, J. Compressive imaging in scattering media. Opt. Express 2015, 23, 14424–14433. [Google Scholar] [CrossRef]
- Deng, H.; Wang, G.; Li, Q.; Sun, Q.; Ma, M.; Zhong, X. Transmissive single-pixel microscopic imaging through scattering media. Sensors 2021, 21, 2721. [Google Scholar] [CrossRef]
- Guo, Y.; Li, B.; Yin, X. Dual-compressed photoacoustic single-pixel imaging. Natl. Sci. Rev. 2023, 10, nwac058. [Google Scholar] [CrossRef]
- Radwell, N.; Johnson, S.D.; Edgar, M.P.; Higham, C.F.; Murray-Smith, R.; Padgett, M.J. Deep learning optimized single-pixel LiDAR. Appl. Phys. Lett. 2019, 115, 231101. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Shi, D.; Chen, Y.; Yuan, K.; Hu, S.; Wang, Y. Scanning single-pixel imaging lidar. Opt. Express 2022, 30, 37484–37492. [Google Scholar] [CrossRef] [PubMed]
- Sefi, O.; Klein, Y.; Strizhevsky, E.; Dolbnya, I.P.; Shwartz, S. X-ray imaging of fast dynamics with single-pixel detector. Opt. Express 2020, 28, 24568–24576. [Google Scholar] [CrossRef] [PubMed]
- He, Y.H.; Zhang, A.X.; Li, M.F.; Huang, Y.Y.; Quan, B.G.; Li, D.Z.; Wu, L.A.; Chen, L.M. High-resolution sub-sampling incoherent x-ray imaging with a single-pixel detector. APL Photonics 2020, 5, 056102. [Google Scholar] [CrossRef]
- Salvador-Balaguer, E.; Latorre-Carmona, P.; Chabert, C.; Pla, F.; Lancis, J.; Tajahuerce, E. Low-cost single-pixel 3D imaging by using an LED array. Opt. Express 2018, 26, 15623–15631. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, W.; Zhai, A.; Wang, D. OAM-basis wavefront single-pixel imaging via compressed sensing. J. Light. Technol. 2023, 41, 2131–2137. [Google Scholar]
- Gong, W. Performance comparison of computational ghost imaging versus single-pixel camera in light disturbance environment. Opt. Laser Technol. 2022, 152, 108140. [Google Scholar] [CrossRef]
- Padgett, M.J.; Boyd, R.W. An introduction to ghost imaging: Quantum and classical. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160233. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, X.R.; Zhao, Q.; Liu, S.; Liu, X.F.; Wang, C.; Zhai, G.J. Single-pixel compressive imaging based on the transformation of discrete orthogonal Krawtchouk moments. Opt. Express 2019, 27, 29838–29853. [Google Scholar] [CrossRef]
- Su, J.; Zhai, A.; Zhao, W.; Han, Q.; Wang, D. Hadamard Single-pixel Imaging Using Adaptive Oblique Zigzag Sampling. Acta Photonica Sin. 2021, 50, 311003. [Google Scholar]
- Wang, Z.; Zhao, W.; Zhai, A.; He, P.; Wang, D. DQN based single-pixel imaging. Opt. Express 2021, 29, 15463–15477. [Google Scholar] [CrossRef]
- Xu, C.; Zhai, A.; Zhao, W.; He, P.; Wang, D. Orthogonal single-pixel imaging using an adaptive under-Nyquist sampling method. Opt. Commun. 2021, 500, 127326. [Google Scholar] [CrossRef]
- Kallepalli, A.; Innes, J.; Padgett, M.J. Compressed sensing in the far-field of the spatial light modulator in high noise conditions. Sci. Rep. 2021, 11, 17460. [Google Scholar] [CrossRef] [PubMed]
- Shin, Z.; Chai, T.Y.; Pua, C.H.; Wang, X.; Chua, S.Y. Efficient spatially-variant single-pixel imaging using block-based compressed sensing. J. Signal Process. Syst. 2021, 93, 1323–1337. [Google Scholar] [CrossRef]
- Sun, M.J.; Meng, L.T.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef]
- Shin, J.; Bosworth, B.T.; Foster, M.A. Single-pixel imaging using compressed sensing and wavelength-dependent scattering. Opt. Lett. 2016, 41, 886–889. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Wang, L.H.; Zhang, W.; Guan, M.H.; Jiang, S.Y.; Fan, M.H.; Abu, P.A.R.; Chen, C.A.; Chen, S.L. A Low-Power High-Data-Transmission Multi-Lead ECG Acquisition Sensor System. Sensors 2019, 19, 4996. [Google Scholar] [CrossRef]
- Gibson, G.M.; Johnson, S.D.; Padgett, M.J. Single-pixel imaging 12 years on: A review. Optics Express 2020, 28, 28190. [Google Scholar] [CrossRef]
- Qaisar, S.; Bilal, R.M.; Iqbal, W.; Naureen, M.; Lee, S. Compressive sensing: From theory to applications, a survey. J. Commun. Netw. 2013, 15, 443–456. [Google Scholar] [CrossRef]
- Rani, M.; Dhok, S.B.; Deshmukh, R.B. A systematic review of compressive sensing: Concepts, implementations and applications. IEEE Access 2018, 6, 4875–4894. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N.; El Ghazi, H.; Tamtaoui, A. A performance comparison of measurement matrices in compressive sensing. Int. J. Commun. Syst. 2018, 31, e3576. [Google Scholar] [CrossRef]
- Abo-Zahhad, M.M.; Hussein, A.I.; Mohamed, A.M. Compressive sensing algorithms for signal processing applications: A survey. Int. J. Commun. Netw. Syst. Sci. 2015, 8, 197–216. [Google Scholar]
- Gunasheela, S.K.; Prasantha, H.S. Compressed Sensing for Image Compression: Survey of Algorithms. In Emerging Research in Computing, Information, Communication and Applications; Springer: Singapore, 2019; pp. 507–517. [Google Scholar]
- Marques, E.C.; Maciel, N.; Naviner, L.; Cai, H.; Yang, J. A review of sparse recovery algorithms. IEEE Access 2018, 7, 1300–1322. [Google Scholar] [CrossRef]
- Bian, L.; Suo, J.; Dai, Q.; Chen, F. Experimental comparison of single-pixel imaging algorithms. J. Opt. Soc. Am. A 2018, 35, 78–87. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, Z.; Zhong, J. Comprehensive comparison of single-pixel imaging methods. Opt. Lasers Eng. 2020, 134, 106301. [Google Scholar]
- Arjoune, Y.; Kaabouch, N.; El Ghazi, H.; Tamtaoui, A. Compressive sensing: Performance comparison of sparse recovery algorithms. In Proceedings of the 2017 IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 9–11 January 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Candès, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; Volume 3, pp. 1433–1452. [Google Scholar]
- Baraniuk, R.; Davenport, M.A.; Duarte, M.F.; Hegde, C. An introduction to compressive sensing. Connex. e-Textb. 2011. [Google Scholar]
- Donoho, D.; Tanner, J. Counting faces of randomly projected polytopes when the projection radically lowers dimension. J. Am. Math. Soc. 2009, 22, 1–53. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Kovacevic, J.; Chebira, A. Life beyond bases: The advent of frames (Part I). IEEE Signal Process. Mag. 2007, 24, 86–104. [Google Scholar] [CrossRef]
- Kovacevic, J.; Chebira, A. Life beyond bases: The advent of frames (Part II). IEEE Signal Process. Mag. 2007, 24, 115–125. [Google Scholar] [CrossRef]
- Rubinstein, R.; Bruckstein, A.M.; Elad, M. Dictionaries for sparse representation modeling. Proc. IEEE 2010, 98, 1045–1057. [Google Scholar] [CrossRef]
- Gribonval, R.; Nielsen, M. Sparse representations in unions of bases. IEEE Trans. Inf. Theory 2003, 49, 3320–3325. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y. Fast Solution of ℓ0-Norm Minimization Problems When the Solution May Be Sparse. IEEE Trans. Inf. Theory 2008, 54, 4789–4812. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969–985. [Google Scholar] [CrossRef]
- Chen, Z.; Dongarra, J.J. Condition numbers of Gaussian random matrices. SIAM J. Matrix Anal. Appl. 2005, 27, 603–620. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, S.; Xu, X.; Wang, L. Compressed sensing and reconstruction with bernoulli matrices. In Proceedings of the The 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 455–460. [Google Scholar]
- Duarte, M.F.; Eldar, Y.C. Structured compressed sensing: From theory to applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Tsaig, Y.; Donoho, D.L. Extensions of compressed sensing. Signal Process. 2006, 86, 549–571. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, S.; Xu, X. Compressed sensing and reconstruction with semi-hadamard matrices. In Proceedings of the 2010 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 July 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 1, pp. 194–197. [Google Scholar]
- Yin, W.; Morgan, S.; Yang, J.; Zhang, Y. Practical compressive sensing with Toeplitz and circulant matrices. In Proceedings of the Visual Communications and Image Processing, Huangshan, China, 14 July 2010; Volume 7744, p. 77440K. [Google Scholar]
- Do, T.T.; Tran, T.D.; Gan, L. Fast compressive sampling with structurally random matrices. 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 30 March–4 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3369–3372. [Google Scholar]
- Do, T.T.; Gan, L.; Nguyen, N.H.; Tran, T.D. Fast and efficient compressive sensing using structurally random matrices. IEEE Trans. Signal Process. 2011, 60, 139–154. [Google Scholar] [CrossRef]
- Sarvotham, S.; Baron, D.; Baraniuk, R.G. Compressed sensing reconstruction via belief propagation. Preprint 2006, 14. [Google Scholar]
- Akçakaya, M.; Park, J.; Tarokh, V. Compressive sensing using low density frames. arXiv 2009, arXiv:0903.0650. [Google Scholar]
- Gilbert, A.; Indyk, P. Sparse recovery using sparse matrices. Proc. IEEE 2010, 98, 937–947. [Google Scholar] [CrossRef]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian compressive sensing via belief propagation. IEEE Trans. Signal Process. 2009, 58, 269–280. [Google Scholar] [CrossRef]
- Akçakaya, M.; Park, J.; Tarokh, V. A coding theory approach to noisy compressive sensing using low density frames. IEEE Trans. Signal Process. 2011, 59, 5369–5379. [Google Scholar] [CrossRef]
- Baron, D.; Duarte, M.F.; Wakin, M.B.; Sarvotham, S.; Baraniuk, R.G. Distributed compressive sensing. arXiv 2009, arXiv:0901.3403. [Google Scholar]
- Park, J.Y.; Yap, H.L.; Rozell, C.J.; Wakin, M.B. Concentration of measure for block diagonal matrices with applications to compressive signal processing. IEEE Trans. Signal Process. 2011, 59, 5859–5875. [Google Scholar] [CrossRef]
- Li, S.; Gao, F.; Ge, G.; Zhang, S. Deterministic construction of compressed sensing matrices via algebraic curves. IEEE Trans. Inf. Theory 2012, 58, 5035–5041. [Google Scholar] [CrossRef]
- Berinde, R.; Gilbert, A.C.; Indyk, P.; Karloff, H.; Strauss, M.J. Combining geometry and combinatorics: A unified approach to sparse signal recovery. In Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 23–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 798–805. [Google Scholar]
- Calderbank, R.; Howard, S.; Jafarpour, S. Construction of a large class of deterministic sensing matrices that satisfy a statistical isometry property. IEEE J. Sel. Top. Signal Process. 2010, 4, 358–374. [Google Scholar] [CrossRef]
- DeVore, R.A. Deterministic constructions of compressed sensing matrices. J. Complex. 2007, 23, 918–925. [Google Scholar] [CrossRef]
- Nguyen, T.L.N.; Shin, Y. Deterministic sensing matrices in compressive sensing: A survey. Sci. World J. 2013, 2013, 192795. [Google Scholar] [CrossRef]
- Amini, A.; Montazerhodjat, V.; Marvasti, F. Matrices with small coherence using p-ary block codes. IEEE Trans. Signal Process. 2011, 60, 172–181. [Google Scholar] [CrossRef]
- Khajehnejad, M.A.; Dimakis, A.G.; Xu, W.; Hassibi, B. Sparse recovery of nonnegative signals with minimal expansion. IEEE Trans. Signal Process. 2010, 59, 196–208. [Google Scholar] [CrossRef]
- Elad, M. Optimized projections for compressed sensing. IEEE Trans. Signal Process. 2007, 55, 5695–5702. [Google Scholar] [CrossRef]
- Nhat, V.D.M.; Vo, D.; Challa, S.; Lee, S. Efficient projection for compressed sensing. In Proceedings of the Seventh IEEE/ACIS International Conference on Computer and Information Science (icis 2008), Portland, OR, USA, 14–16 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 322–327. [Google Scholar]
- Wu, S.; Dimakis, A.; Sanghavi, S.; Yu, F.; Holtmann-Rice, D.; Storcheus, D.; Rostamizadeh, A.; Kumar, S. Learning a compressed sensing measurement matrix via gradient unrolling. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2019; pp. 6828–6839. [Google Scholar]
- Wu, Y.; Rosca, M.; Lillicrap, T. Deep compressed sensing. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2019; pp. 6850–6860. [Google Scholar]
- Islam, S.R.; Maity, S.P.; Ray, A.K.; Mandal, M. Deep learning on compressed sensing measurements in pneumonia detection. Int. J. Imaging Syst. Technol. 2022, 32, 41–54. [Google Scholar] [CrossRef]
- Ahmed, I.; Khan, A. Genetic algorithm based framework for optimized sensing matrix design in compressed sensing. Multimed. Tools Appl. 2022, 81, 39077–39102. [Google Scholar] [CrossRef]
- Pope, G. Compressive Sensing: A Summary of Reconstruction Algorithms. Master’s Thesis, ETH, Swiss Federal Institute of Technology Zurich, Department of Computer Science, Zürich, Switzerland, 2009. [Google Scholar]
- Siddamal, K.V.; Bhat, S.P.; Saroja, V.S. A survey on compressive sensing. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 639–643. [Google Scholar]
- Carmi, A.Y.; Mihaylova, L.; Godsill, S.J. Compressed Sensing & Sparse Filtering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hameed, M.A. Comparative Analysis of Orthogonal Matching Pursuit and Least Angle Regression; Michigan State University, Electrical Engineering: East Lansing, MI, USA, 2012. [Google Scholar]
- Santosa, F.; Symes, W.W. Linear inversion of band-limited reflection seismograms. SIAM J. Sci. Stat. Comput. 1986, 7, 1307–1330. [Google Scholar] [CrossRef]
- Donoho, D.L.; Stark, P.B. Uncertainty principles and signal recovery. SIAM J. Appl. Math. 1989, 49, 906–931. [Google Scholar] [CrossRef]
- Donoho, D.L.; Logan, B.F. Signal recovery and the large sieve. SIAM J. Appl. Math. 1992, 52, 577–591. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Bruckstein, A.M. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Trans. Inf. Theory 2002, 48, 2558–2567. [Google Scholar] [CrossRef]
- Zhang, Y. Theory of compressive sensing via ℓ1-minimization: A non-rip analysis and extensions. J. Oper. Res. Soc. China 2013, 1, 79–105. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Huggins, P.S.; Zucker, S.W. Greedy basis pursuit. IEEE Trans. Signal Process. 2007, 55, 3760–3772. [Google Scholar] [CrossRef]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fu, W.J. Penalized regressions: The bridge versus the lasso. J. Comput. Graph. Stat. 1998, 7, 397–416. [Google Scholar]
- Maleki, A.; Anitori, L.; Yang, Z.; Baraniuk, R.G. Asymptotic analysis of complex LASSO via complex approximate message passing (CAMP). IEEE Trans. Inf. Theory 2013, 59, 4290–4308. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J. l1-Magic: Recovery of Sparse Signals Via Convex Programming. Available online: www.acm.caltech.edu/l1magic/downloads/l1magic.pdf (accessed on 14 April 2005).
- Candes, E.; Tao, T. The Dantzig selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Meenakshi, S.B. A survey of compressive sensing based greedy pursuit reconstruction algorithms. Int. J. Image Graph. Signal Process. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Akhila, T.; Divya, R. A survey on greedy reconstruction algorithms in compressive sensing. Int. J. Res. Comput. Commun. Technol. 2016, 5, 126–129. [Google Scholar]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 40–44. [Google Scholar]
- DeVore, R.A.; Temlyakov, V.N. Some remarks on greedy algorithms. Adv. Comput. Math. 1996, 5, 173–187. [Google Scholar] [CrossRef]
- Wen, J.; Zhou, Z.; Wang, J.; Tang, X.; Mo, Q. A sharp condition for exact support recovery with orthogonal matching pursuit. IEEE Trans. Signal Process. 2016, 65, 1370–1382. [Google Scholar] [CrossRef]
- Wang, J. Support recovery with orthogonal matching pursuit in the presence of noise: A new analysis. arXiv 2015, arXiv:1501.04817. [Google Scholar]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative thresholding for sparse approximations. J. Fourier Anal. Appl. 2008, 14, 629–654. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Normalized iterative hard thresholding: Guaranteed stability and performance. IEEE J. Sel. Top. Signal Process. 2010, 4, 298–309. [Google Scholar] [CrossRef]
- Chartrand, R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Wen, J.; Li, D.; Zhu, F. Stable recovery of sparse signals via lp-minimization. Appl. Comput. Harmon. Anal. 2015, 38, 161–176. [Google Scholar] [CrossRef]
- Kanevsky, D.; Carmi, A.; Horesh, L.; Gurfil, P.; Ramabhadran, B.; Sainath, T.N. Kalman filtering for compressed sensing. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Chartrand, R.; Staneva, V. Restricted isometry properties and nonconvex compressive sensing. Inverse Probl. 2008, 24, 035020. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NA, USA, 30 March –4 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3869–3872. [Google Scholar]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Ji, S.; Carin, L. Bayesian compressive sensing and projection optimization. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 377–384. [Google Scholar]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for ℓ1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Cai, J.F.; Osher, S.; Shen, Z. Linearized Bregman iterations for compressed sensing. Math. Comput. 2009, 78, 1515–1536. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for ℓ1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Yang, J.; Zhang, Y.; Yin, W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise. SIAM J. Sci. Comput. 2009, 31, 2842–2865. [Google Scholar] [CrossRef]
- Geman, D.; Yang, C. Nonlinear image recovery with half-quadratic regularization. IEEE Trans. Image Process. 1995, 4, 932–946. [Google Scholar] [CrossRef]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing; Rice University: Houston, TX, USA, 2010. [Google Scholar]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Rangan, S. Generalized approximate message passing for estimation with random linear mixing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2168–2172. [Google Scholar]
- Khajehnejad, M.A.; Xu, W.; Avestimehr, A.S.; Hassibi, B. Weighted ℓ1 minimization for sparse recovery with prior information. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Republic of Korea, 28 June–3 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 483–487. [Google Scholar]
- De Paiva, N.M.; Marques, E.C.; de Barros Naviner, L.A. Sparsity analysis using a mixed approach with greedy and LS algorithms on channel estimation. In Proceedings of the 2017 3rd International Conference on Frontiers of Signal Processing (ICFSP), Paris, France, 6–8 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 91–95. [Google Scholar]
- Kwon, S.; Wang, J.; Shim, B. Multipath matching pursuit. IEEE Trans. Inf. Theory 2014, 60, 2986–3001. [Google Scholar] [CrossRef]
- Wen, J.; Zhou, Z.; Li, D.; Tang, X. A novel sufficient condition for generalized orthogonal matching pursuit. IEEE Commun. Lett. 2016, 21, 805–808. [Google Scholar] [CrossRef]
- Sun, H.; Ni, L. Compressed sensing data reconstruction using adaptive generalized orthogonal matching pursuit algorithm. In Proceedings of the 2013 3rd International Conference on Computer Science and Network Technology, Dalian, China, 12–13 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1102–1106. [Google Scholar]
- Huang, H.; Makur, A. Backtracking-based matching pursuit method for sparse signal reconstruction. IEEE Signal Process. Lett. 2011, 18, 391–394. [Google Scholar] [CrossRef]
- Gilbert, A.C.; Strauss, M.J.; Tropp, J.A.; Vershynin, R. Algorithmic linear dimension reduction in the l_1 norm for sparse vectors. arXiv 2006, arXiv:cs/0608079. [Google Scholar]
- Blanchard, J.D.; Tanner, J.; Wei, K. CGIHT: Conjugate gradient iterative hard thresholding for compressed sensing and matrix completion. Inf. Inference A J. IMA 2015, 4, 289–327. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, L.; Dai, W.; Wang, Z.; Moonen, M. Tracking a dynamic sparse channel via differential orthogonal matching pursuit. In Proceedings of the MILCOM 2015–2015 IEEE Military Communications Conference, Tampa, FL, USA, 26–28 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 792–797. [Google Scholar]
- Karahanoglu, N.B.; Erdogan, H. Compressed sensing signal recovery via forward–backward pursuit. Digit. Signal Process. 2013, 23, 1539–1548. [Google Scholar] [CrossRef]
- Gilbert, A.C.; Muthukrishnan, S.; Strauss, M. Improved time bounds for near-optimal sparse Fourier representations. In Wavelets XI; International Society for Optics and Photonics: Washington, DC, USA, 2005; Volume 5914, p. 59141A. [Google Scholar]
- Foucart, S. Hard thresholding pursuit: An algorithm for compressive sensing. SIAM J. Numer. Anal. 2011, 49, 2543–2563. [Google Scholar] [CrossRef]
- Gilbert, A.C.; Strauss, M.J.; Tropp, J.A.; Vershynin, R. One sketch for all: Fast algorithms for compressed sensing. In Proceedings of the Thirty-Ninth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 11–13 June 2007; pp. 237–246. [Google Scholar]
- Tanner, J.; Wei, K. Normalized iterative hard thresholding for matrix completion. SIAM J. Sci. Comput. 2013, 35, S104–S125. [Google Scholar] [CrossRef]
- Mileounis, G.; Babadi, B.; Kalouptsidis, N.; Tarokh, V. An adaptive greedy algorithm with application to nonlinear communications. IEEE Trans. Signal Process. 2010, 58, 2998–3007. [Google Scholar] [CrossRef]
- Lee, J.; Choi, J.W.; Shim, B. Sparse signal recovery via tree search matching pursuit. J. Commun. Netw. 2016, 18, 699–712. [Google Scholar] [CrossRef]
- Rangan, S.; Schniter, P.; Fletcher, A.K. Vector approximate message passing. IEEE Trans. Inf. Theory 2019, 65, 6664–6684. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef] [PubMed]
- Montanari, A.; Eldar, Y.C.; Kutyniok, G. Graphical models concepts in compressed sensing. Compress. Sens. 2012, 394–438. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Gorodnitsky, I.F.; Rao, B.D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans. Signal Process. 1997, 45, 600–616. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, SYSTEMS and computers, Pacific Grove, CA, USA, 26–29 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 581–587. [Google Scholar]
- Blumensath, T.; Davies, M.E. Gradient pursuits. IEEE Trans. Signal Process. 2008, 56, 2370–2382. [Google Scholar] [CrossRef]
- Gu, H.; Yaman, B.; Moeller, S.; Ellermann, J.; Ugurbil, K.; Akçakaya, M. Revisiting ℓ1-wavelet compressed-sensing MRI in the era of deep learning. Proc. Natl. Acad. Sci. USA 2022, 119, e2201062119. [Google Scholar]
- Adler, A.; Boublil, D.; Elad, M.; Zibulevsky, M. A deep learning approach to block-based compressed sensing of images. arXiv 2016, arXiv:1606.01519. [Google Scholar]
- Xie, Y.; Li, Q. A review of deep learning methods for compressed sensing image reconstruction and its medical applications. Electronics 2022, 11, 586. [Google Scholar] [CrossRef]
- Zonzini, F.; Carbone, A.; Romano, F.; Zauli, M.; De Marchi, L. Machine learning meets compressed sensing in vibration-based monitoring. Sensors 2022, 22, 2229. [Google Scholar] [CrossRef] [PubMed]






| Works | Content |
|---|---|
| Our works | -Reviews the concept of CSSPI. -Summarizes the main measurement matrices in CSSPI. -Summarizes the main reconstruction algorithms in CSSPI. -The performance of measurement matrices and reconstruction algorithms in CSSPI is discussed in detail through simulations and experiments. -The advantages and disadvantages of mainstream measurement matrices and reconstruction algorithms in CSSPI are summarized. |
| Existing works | Refs. [40,41]: Review the development of CS. |
| Refs. [42,43]: Review the main measurement matrices in CS. | |
| Refs. [44,45,46]: Review the reconstruction algorithms in CS. | |
| Refs. [2,47]: Review the development of SPI. | |
| Refs. [48,49]: Review the algorithms of SPI. For CS, only the TVAL3 algorithm is involved. |
| Type of Measurement Matrix | Definition | Advantages | Disadvantages | References | |
|---|---|---|---|---|---|
| Random Matrix | Gaussian | -Each coefficient obeys a random distribution separately. | -The RIP property is satisfied with high probability. -Fewer measurements and noise robustness. | -Large storage space. -Difficult to implement in hardware. -No explicit constructions. | [62] |
| Bernoulli | [63] | ||||
| Semi-deterministic random matrix | Toeplitz and Circulant | -Each coefficient is generated in a particular way. | -Easy hardware implementation and robustness. -Sparse random matrix retains the advantage of an unstructured random matrix. | -High uncertainty. -More measurements. -For a particular type of signal. | [67,68] |
| Sparse random | [70,71,72,73] | ||||
| Partial orthogonal matrix | Partial Fourier | -Some rows are randomly selected from the orthogonal matrix. | -It is fast to generate and easy to save. -Easy hardware implementation and robustness. | -Fourier matrix needs more recovery time and measurement times. -The dimension limit of the Hadamard matrix. | [47] |
| Partial Hadamard | [65,66] | ||||
| Algorithm | Advantages | Disadvantages | References | |
|---|---|---|---|---|
| Convex | Dantzig | -Fewer measurements. -Noise robustness. | -High computational complexity. -Slower, not suitable for large-scale problems. | [109] |
| BPDN | [101,104,105,106] | |||
| BP | [101,102] | |||
| DLP | [107,108] | |||
| Greedy | OMP | -Easier to implement and faster. -IHT and CoSaMP can add/discard entries per iteration. - Noise robustness. | -A priori knowledge of signal sparsity is required. -The sparsity of the solution cannot be guaranteed. -More measurements. | [113,114,115,116,117] |
| CoSaMP | [120] | |||
| IHT | [122,123,124] | |||
| SP | [121] | |||
| TV | TVAL3 | -Preserves the sharp edges and prevents blurring. -Noise robustness. -TVAL3 and TV-Qc are faster. | -Not linear. -Not differentiable. -Dantzig selector is slower. | [142] |
| TV-DS | [109] | |||
| TV-QC | [108] | |||
| Non-Convex | BCS | -More sparse solution. -Faster, suitable for large-scale problems. | -Rely more on the prior knowledge of the signal. -High computational complexity. | [130,131,132,133] |
| IRLS | -Fewer measurements than the convex algorithm. -Can be implemented under weaker RIP. | -High computational complexity. -Slower, not suitable for large-scale problems. | [128,129] | |
| Bregman | SB | -Faster, noise robustness. -Small memory footprint. | -More measurements than the convex algorithm. | [137] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Gao, L.; Zhai, A.; Wang, D. Comparison of Common Algorithms for Single-Pixel Imaging via Compressed Sensing. Sensors 2023, 23, 4678. https://doi.org/10.3390/s23104678
Zhao W, Gao L, Zhai A, Wang D. Comparison of Common Algorithms for Single-Pixel Imaging via Compressed Sensing. Sensors. 2023; 23(10):4678. https://doi.org/10.3390/s23104678
Chicago/Turabian StyleZhao, Wenjing, Lei Gao, Aiping Zhai, and Dong Wang. 2023. "Comparison of Common Algorithms for Single-Pixel Imaging via Compressed Sensing" Sensors 23, no. 10: 4678. https://doi.org/10.3390/s23104678
APA StyleZhao, W., Gao, L., Zhai, A., & Wang, D. (2023). Comparison of Common Algorithms for Single-Pixel Imaging via Compressed Sensing. Sensors, 23(10), 4678. https://doi.org/10.3390/s23104678






