An Evidence Theory Based Embedding Model for the Management of Smart Water Environments
Abstract
1. Introduction
- An uncertainty-aware modeling of the smart water environment that quantifies and incorporates uncertainty factors into the water information network (WIN);
- An uncertain embedding of the WIN combining probabilistic and network representation learning (NRL) models to ensure the learning and classification of representations of water information entities under uncertainty of the monitored data;
- An uncertainty-aware decision mechanism that applies the evidence theory, and that consists of querying the uncertain WIN to select the suitable management actions for each class of affected water zones.
2. Related Works
2.1. Smart Water Management: Recent Related Studies
- Lack of standardization and resource constraints: There is a lack of standardization in the methods used for monitoring and managing water environments, making it difficult to compare data from different sources or develop consistent models for decision-making. Furthermore, the resources available for monitoring and managing water environments may be limited, affecting the quality and quantity of collected data and the ability to make decisions based on that data. To provide a standard method to model, monitor, and manage water environments and solve problems related to resource limitations in terms of water quality and quantity management, we represent the water environment as a knowledge graph, which identifies the elements involved, such as water entities, sensors, water issues, observed data, water management processes, and so on. This multi-relational and semantic structure serves as a dictionary, including all water-related information. In addition, we exploit network embedding to progressively acquire semantics and rich representations of water entities and transfer them into a low-dimensional vector space based on their related characteristics, behaviors, and variations. This stage aids in the classification of impacted water entities as well as the efficient selection and execution of relevant corrective actions.
- Uncertainty of water environments: Current solutions failed to represent correctly and model uncertainty factors and sources, as they assume sensors correctly capture the monitored data. However, water environments are ever-changing by nature, and their sensor infrastructure is often subject to unstable behavior, leading to inaccurate or incompleteness of collected data. We solve this issue by modeling and quantifying uncertainty at different levels of the water information network, including the water entities level and the management policies level.
- Water network complexity: As complex water information networks are processed in a real-time and continuous way, such a graph-like structure coupled with uncertainty sources is expected to add a new complexity factor. To solve this issue, we extend our previous incremental embedding model [24] by incorporating confidence scores into the factual relations between the nodes (water entities, events, management policies).
- Decision making granularity: Current approaches to water management, including smart solutions, perform management operations at a high granularity level and in an isolated manner. However, in the water network, several entities may feature similar deviations (e.g., pressure loss) and require compatible management policies (e.g., specific discharge level to the canal). To ensure efficient handling of water zone issues, we precede the decision process by classifying those entities while considering the confidence of their related knowledge and the monitoring step’s output.
2.2. Our Previous Work
2.2.1. Water Information Network Modeling and Embedding
2.2.2. Classification-Based Water Management
2.3. Motivations
- NRL captures complex relationships: NRL can capture complex relationships between nodes in a water network, which can be difficult to model using traditional techniques. By representing the network as a vectorized form, NRL can preserve the structural information of the network, including its topology, connectivity, and node attributes.
- NRL handles changing network structure: Water networks are constantly changing due to changes in water demand, pipe breaks, and other factors. NRL effectively handles these changes by updating the network representation as the structure evolves. This ensures that the learned representations remain up-to-date and accurate.
- NRL handles large-scale networks: Water networks can be vast, consisting of thousands or even millions of nodes. NRL can efficiently handle large-scale networks by leveraging artificial-intelligence-based techniques, which can scale up to large graphs while preserving the structural information of the network.
- NRL is used for various downstream tasks. This makes it a versatile technique for analyzing, modeling, and processing water networks.
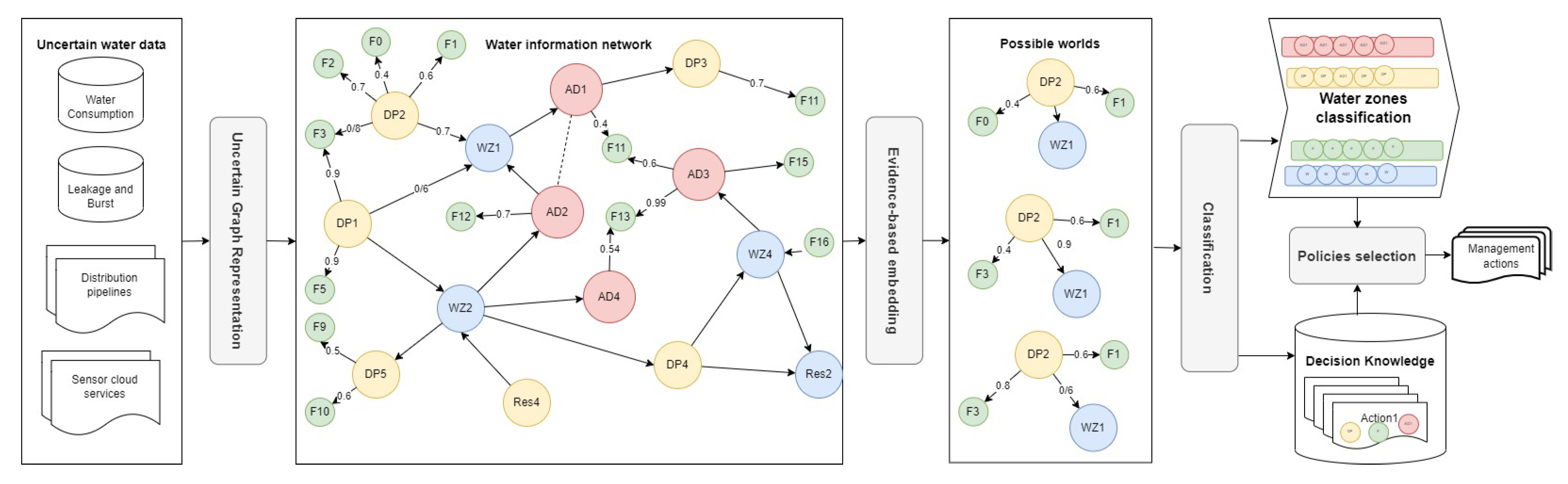
3. Uncertainty Handling in Water Environments
3.1. Modeling of Uncertain Embedding of the Water Information Network
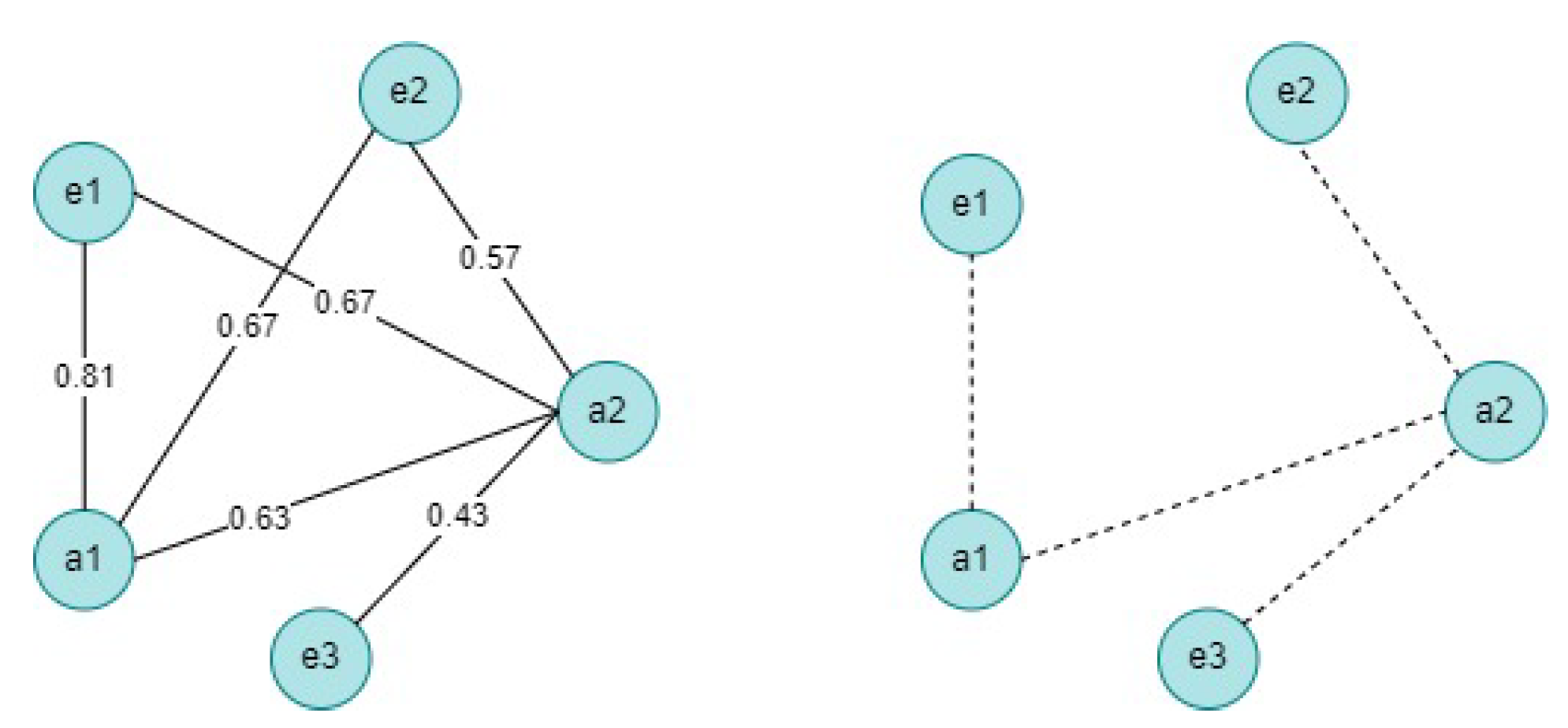
3.1.1. Uncertainty Quantification
3.1.2. Water Network Modeling
3.2. Uncertain Embedding of the Water Network
- Firstly, it can help in quantifying the degree of uncertainty associated with the data collected from various sensors in the network. This can enable decision makers to have a more accurate understanding of the reliability of the data and, consequently, make more informed decisions.
- Secondly, probabilistic techniques can enable the representation of complex dependencies and correlations between the different factors that contribute to the uncertainty in the water zone data. This can help in building more accurate models that can better capture the underlying dynamics of the system and, in turn, improve the decision-making process.
- Finally, probabilistic techniques can provide a principled way of combining different sources of information, including historical data and expert knowledge, to arrive at a more comprehensive and robust assessment of the uncertainties in the water zones. This can lead to better-informed decisions that take into account a wide range of factors and sources of uncertainty.
| Algorithm 1: Uncertain knowledge graph embedding for water quality management |
|
3.3. Uncertainty-Aware Decision Making for Water Management
| Algorithm 2: Smart water decision making |
|
4. Experiments
4.1. Dataset and Experimental Protocol
- Temperature: The temperature of water samples can affect various physical and chemical properties, such as the density, viscosity, and solubility of different substances.
- pH: The pH level of water samples indicates their acidity or alkalinity, which can affect the chemical reactions and the behavior of different substances in water. The pH scale ranges from 0 to 14, with 7 being considered neutral, below 7 acidic, and above 7 alkaline or basic.
- Conductivity: Conductivity is a measure of the ability of water to conduct electric current, which is influenced by the presence of dissolved ions or salts.
- Dissolved oxygen (DO): DO is the amount of oxygen dissolved in water, which is critical for the survival of aquatic organisms and the health of aquatic ecosystems.
- Biological oxygen demand (BOD): The amount of oxygen required by microorganisms to break down organic matter in the water sample, measured in milligrams per liter (mg/L).
- Nitrate (NI): The concentration of nitrate ions in the water sample, usually measured in milligrams per liter (mg/L).
- Fecal coliforms (FC): The presence or concentration of fecal coliform bacteria in the water sample, often used to indicate fecal contamination and potential health risks.
- Total coliforms (TC): The presence or concentration of total coliform bacteria in the water sample, including fecal and non-fecal coliforms.
4.2. Experimental Results
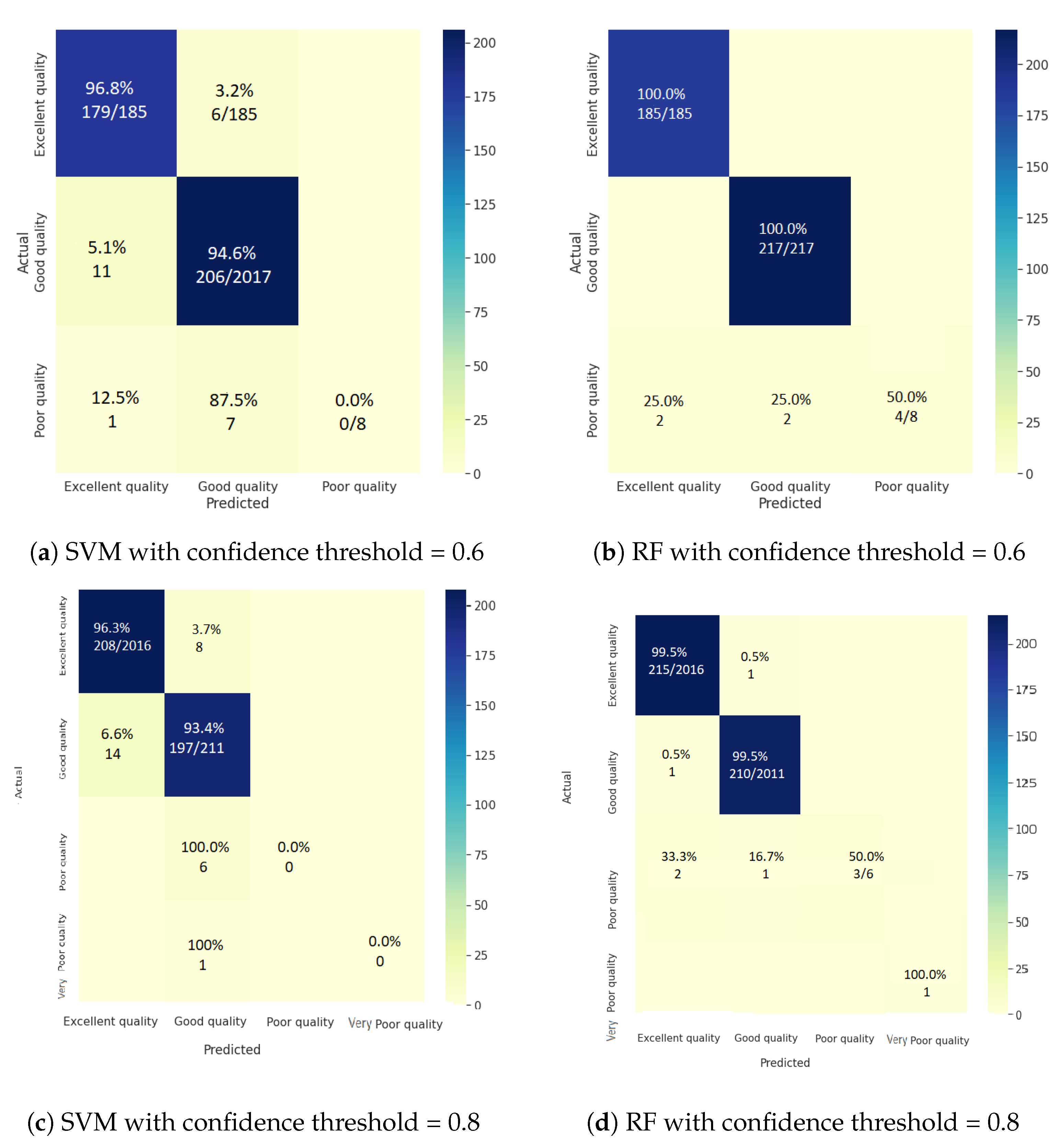
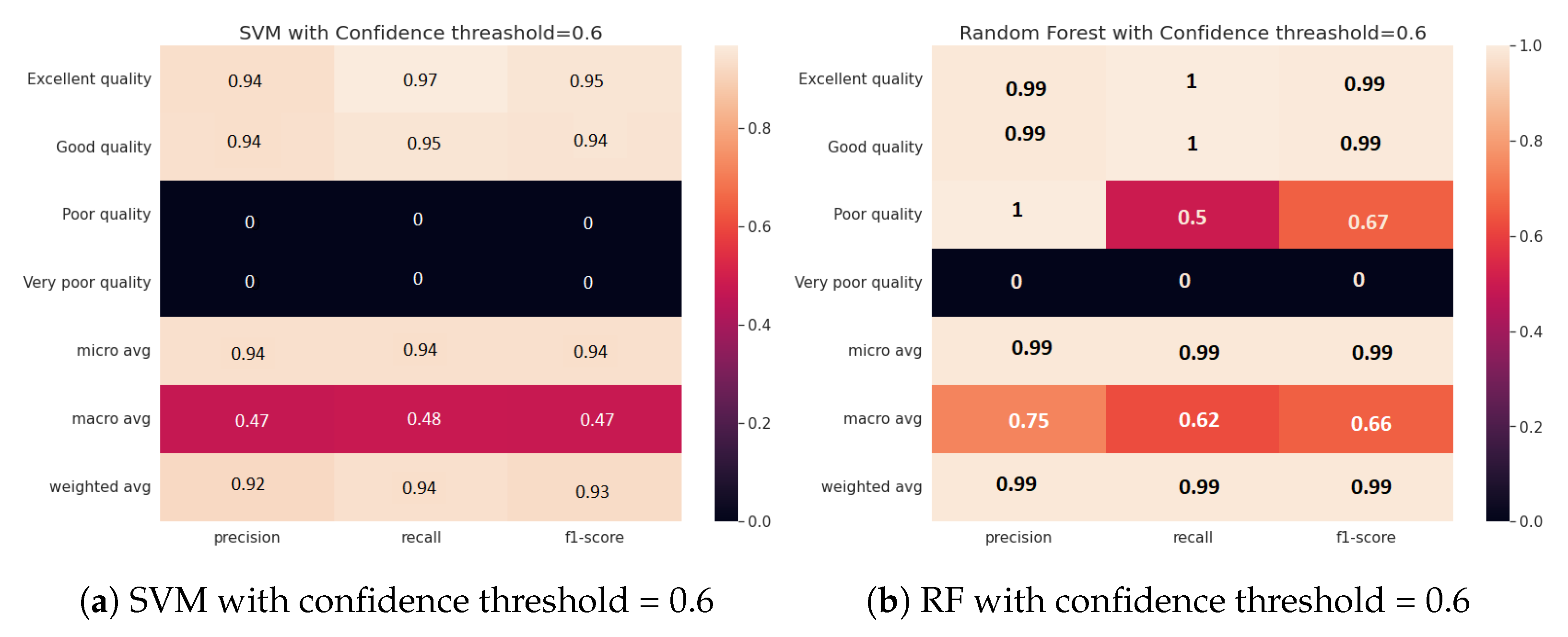
4.2.1. Impact of Confidence on the Accuracy of Water Zones’ Classification
4.2.2. Water Zones Embedding Visualization
- Handling different types of uncertainty: The use of other techniques for modeling uncertainty, such as fuzzy logic systems and possibility-based theory, can help handle uncertainty in water environments, which is crucial for making accurate and reliable decisions.
- Improving network representation learning: While knowledge graph embedding is a powerful technique, there are other network representation learning techniques, such as graph convolutional networks and attention-based models, that can potentially provide more accurate and informative embeddings of water entities.
- Distributed learning: The application of the distributed learning concept to water networks can enable collaborative, scalable, and privacy-preserved analytics of water data in larger-scale and more complex smart water networks, leading to better decision making and resource management.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreno-Pizani, M.A. Water management in agricultural production, the economy, and Venezuelan society. Front. Sustain. Food Syst. 2021, 4, 624066. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Sitzenfrei, R. Rethinking the framework of smart water system: A review. Water 2020, 12, 412. [Google Scholar] [CrossRef]
- Ullo, S.L.; Sinha, G. Advances in smart environment monitoring systems using IoT and sensors. Sensors 2020, 20, 3113. [Google Scholar] [CrossRef]
- Singh, M.; Ahmed, S. IoT based smart water management systems: A systematic review. Mater. Today Proc. 2020, 46, 5211–5218. [Google Scholar] [CrossRef]
- Jan, F.; Min-Allah, N.; Düştegör, D. Iot based smart water quality monitoring: Recent techniques, trends and challenges for domestic applications. Water 2021, 13, 1729. [Google Scholar] [CrossRef]
- Hasan, D.; Driss, M. SUBLμME: Secure Blockchain as a Service and Microservices-based Framework for IoT Environments. In Proceedings of the 2021 IEEE/ACS 18th International Conference on Computer Systems and Applications (AICCSA), Tangier, Morocco, 30 November–3 December 2021; pp. 1–9. [Google Scholar]
- Driss, M.; Hasan, D.; Boulila, W.; Ahmad, J. Microservices in IoT security: Current solutions, research challenges, and future directions. Procedia Comput. Sci. 2021, 192, 2385–2395. [Google Scholar] [CrossRef]
- Atitallah, S.B.; Driss, M.; Ghzela, H.B. Microservices for Data Analytics in IoT Applications: Current Solutions, Open Challenges, and Future Research Directions. Procedia Comput. Sci. 2022, 207, 3938–3947. [Google Scholar] [CrossRef]
- Beck, M.B. Water quality modeling: A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef]
- McMillan, H.K.; Westerberg, I.K.; Krueger, T. Hydrological data uncertainty and its implications. Wiley Interdiscip. Rev. Water 2018, 5, e1319. [Google Scholar] [CrossRef]
- Loga, M.; Przeździecki, K. Uncertainty of chemical status in surface waters. Sci. Rep. 2021, 11, 13644. [Google Scholar] [CrossRef]
- Li, B.; Pi, D. Network representation learning: A systematic literature review. Neural Comput. Appl. 2020, 32, 16647–16679. [Google Scholar] [CrossRef]
- Ranjithkumar, M.; Robert, L. Machine Learning Techniques and Cloud Computing to Estimate River Water Quality—Survey. In Inventive Communication and Computational Technologies; Springer: Singapore, 2021; pp. 387–396. [Google Scholar]
- Driss, M.; Atitallah, S.B.; Albalawi, A.; Boulila, W. Req-WSComposer: A novel platform for requirements-driven composition of semantic web services. J. Ambient. Intell. Humaniz. Comput. 2021, 13, 849–865. [Google Scholar] [CrossRef]
- Goel, D.; Chaudhury, S.; Ghosh, H. Smart water management: An ontology-driven context-aware IoT application. In International Conference on Pattern Recognition and Machine Intelligence; Springer: Cham, Switzerland, 2017; pp. 639–646. [Google Scholar]
- Wybrands, M.; Frohmann, F.; Andree, M.; Gómez, J.M. WISdoM: An Information System for Water Management. In Advances and New Trends in Environmental Informatics; Springer: Cham, Switzerland, 2021; pp. 131–146. [Google Scholar]
- Salam, A. Internet of Things for Sustainable Community Development; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Prasad, A.; Mamun, K.A.; Islam, F.; Haqva, H. Smart water quality monitoring system. In Proceedings of the 2015 2nd Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Nadi, Fiji, 2–4 December 2015; pp. 1–6. [Google Scholar]
- Shahanas, K.M.; Sivakumar, P.B. Framework for a smart water management system in the context of smart city initiatives in India. Procedia Comput. Sci. 2016, 92, 142–147. [Google Scholar] [CrossRef]
- Simmhan, Y.; Ravindra, P.; Chaturvedi, S.; Hegde, M.; Ballamajalu, R. Towards a data-driven IoT software architecture for smart city utilities. Softw. Pract. Exp. 2018, 48, 1390–1416. [Google Scholar] [CrossRef]
- Wang, X.; Wei, H.; Chen, N.; He, X.; Tian, Z. An Observational Process Ontology-Based Modeling Approach for Water Quality Monitoring. Water 2020, 12, 715. [Google Scholar] [CrossRef]
- Bretreger, D.; Yeo, I.Y.; Hancock, G. Quantifying irrigation water use with remote sensing: Soil water deficit modelling with uncertain soil parameters. Agric. Water Manag. 2022, 260, 107299. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Diganta, M.T.M.; Rahman, A.; Olbert, A.I. Robust machine learning algorithms for predicting coastal water quality index. J. Environ. Manag. 2022, 321, 115923. [Google Scholar] [CrossRef]
- Mezni, H.; Driss, M.; Boulila, W.; Atitallah, S.B.; Sellami, M.; Alharbi, N. SmartWater: A Service-Oriented and Sensor Cloud-Based Framework for Smart Monitoring of Water Environments. Remote Sens. 2022, 14, 922. [Google Scholar] [CrossRef]
- Chen, X.; Jia, S.; Xiang, Y. A review: Knowledge reasoning over knowledge graph. Expert Syst. Appl. 2019, 141, 112948. [Google Scholar] [CrossRef]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar]
- Zhang, D.; Yin, J.; Zhu, X.; Zhang, C. Network representation learning: A survey. IEEE Trans. Big Data 2018, 6, 3–28. [Google Scholar] [CrossRef]
- Chen, X.; Chen, M.; Shi, W.; Sun, Y.; Zaniolo, C. Embedding uncertain knowledge graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3363–3370. [Google Scholar]
- Kim, D.; Xie, L.; Ong, C.S. Probabilistic knowledge graph construction: Compositional and incremental approaches. In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; pp. 2257–2262. [Google Scholar]
- Jiang, T.; Liu, T.; Ge, T.; Sha, L.; Chang, B.; Li, S.; Sui, Z. Towards time-aware knowledge graph completion. In Proceedings of the COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, Osaka, Japan, 11–16 December 2016; pp. 1715–1724. [Google Scholar]
- Wang, Y.; Tseng, M.M. Customized products recommendation based on probabilistic relevance model. J. Intell. Manuf. 2013, 24, 951–960. [Google Scholar] [CrossRef]
- Sitkrongwong, P.; Maneeroj, S.; Takasu, A. Latent probabilistic model for context-aware recommendations. In Proceedings of the 2013 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Atlanta, GA, USA, 17–20 November 2013; IEEE Computer Society: Washington, DC, USA, 2013; Volume 01, pp. 95–100. [Google Scholar]
- Sitkrongwong, P.; Maneeroj, S.; Samatthiyadikun, P.; Takasu, A. Bayesian probabilistic model for context-aware recommendations. In Proceedings of the 17th International Conference on Information Integration and Web-Based Applications & Services, Brussels, Belgium, 11–13 December 2015; pp. 1–10. [Google Scholar]
- Ren, X.; Song, M.; Haihong, E.; Song, J. Context-aware probabilistic matrix factorization modeling for point-of-interest recommendation. Neurocomputing 2017, 241, 38–55. [Google Scholar] [CrossRef]
- Colombo-Mendoza, L.O.; Valencia-García, R.; Rodríguez-González, A.; Colomo-Palacios, R.; Alor-Hernández, G. Towards a knowledge-based probabilistic and context-aware social recommender system. J. Inf. Sci. 2018, 44, 464–490. [Google Scholar] [CrossRef]
- Ferchichi, A.; Boulila, W.; Farah, I.R. Propagating aleatory and epistemic uncertainty in land cover change prediction process. Ecol. Inform. 2017, 37, 24–37. [Google Scholar] [CrossRef]
- Boulila, W.; Ayadi, Z.; Farah, I.R. Sensitivity analysis approach to model epistemic and aleatory imperfection: Application to Land Cover Change prediction model. J. Comput. Sci. 2017, 23, 58–70. [Google Scholar] [CrossRef]
- Agarwal, H.; Renaud, J.E.; Preston, E.L.; Padmanabhan, D. Uncertainty quantification using evidence theory in multidisciplinary design optimization. Reliab. Eng. Syst. Saf. 2004, 85, 281–294. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Zhao, B.; Cheng, J.; Zhao, X.; Duan, Z. Knowledge graph completion: A review. IEEE Access 2020, 8, 192435–192456. [Google Scholar] [CrossRef]
- Create Production-Grade Machine Learning Models with TensorFlow. Available online: https://www.tensorflow.org/ (accessed on 27 April 2023).
- scikit-learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/ (accessed on 27 April 2023).
- Van Der Maaten, L. Accelerating t-SNE using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Indian Water Quality Data. Available online: https://www.kaggle.com/datasets/anbarivan/indian-water-quality-data (accessed on 19 January 2023).
- Aldhyani, T.H.; Al-Yaari, M.; Alkahtani, H.; Maashi, M. Water quality prediction using artificial intelligence algorithms. Appl. Bionics Biomech. 2020, 2020, 6659314. [Google Scholar] [CrossRef]
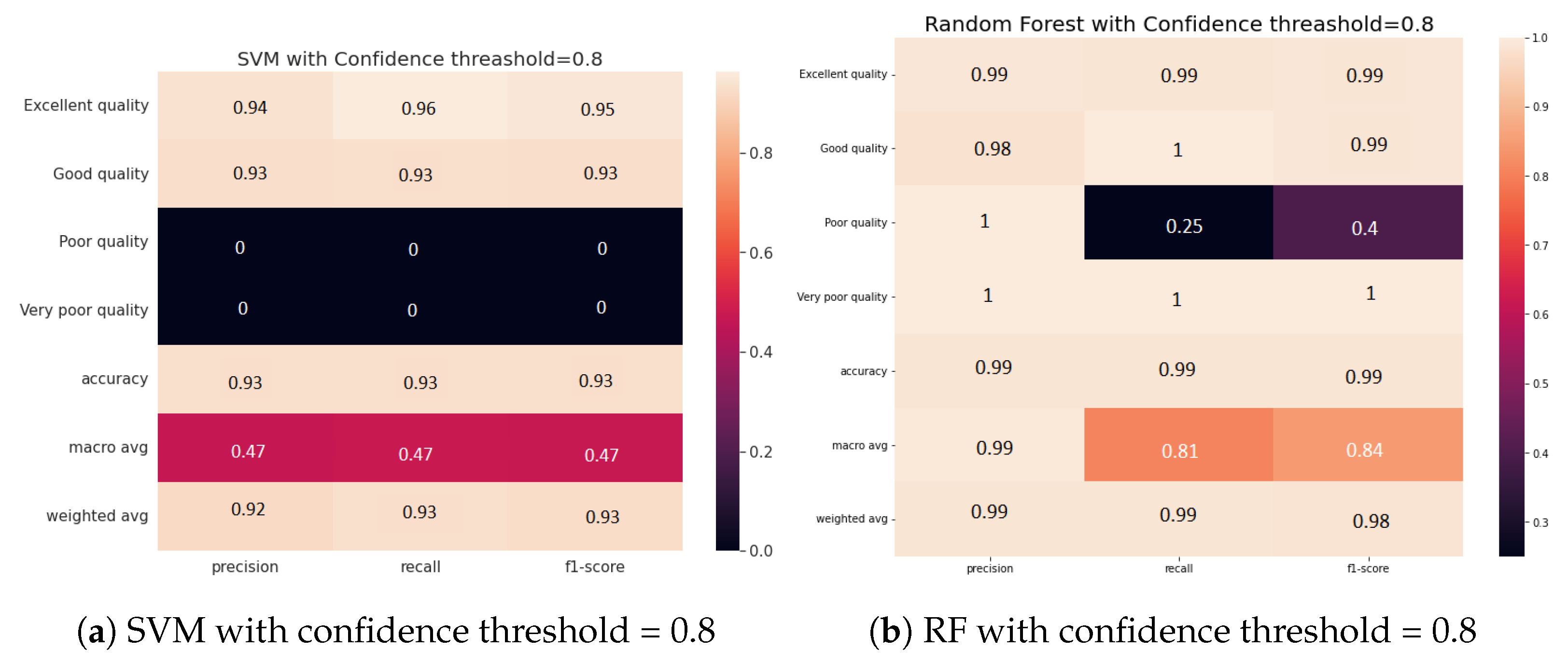
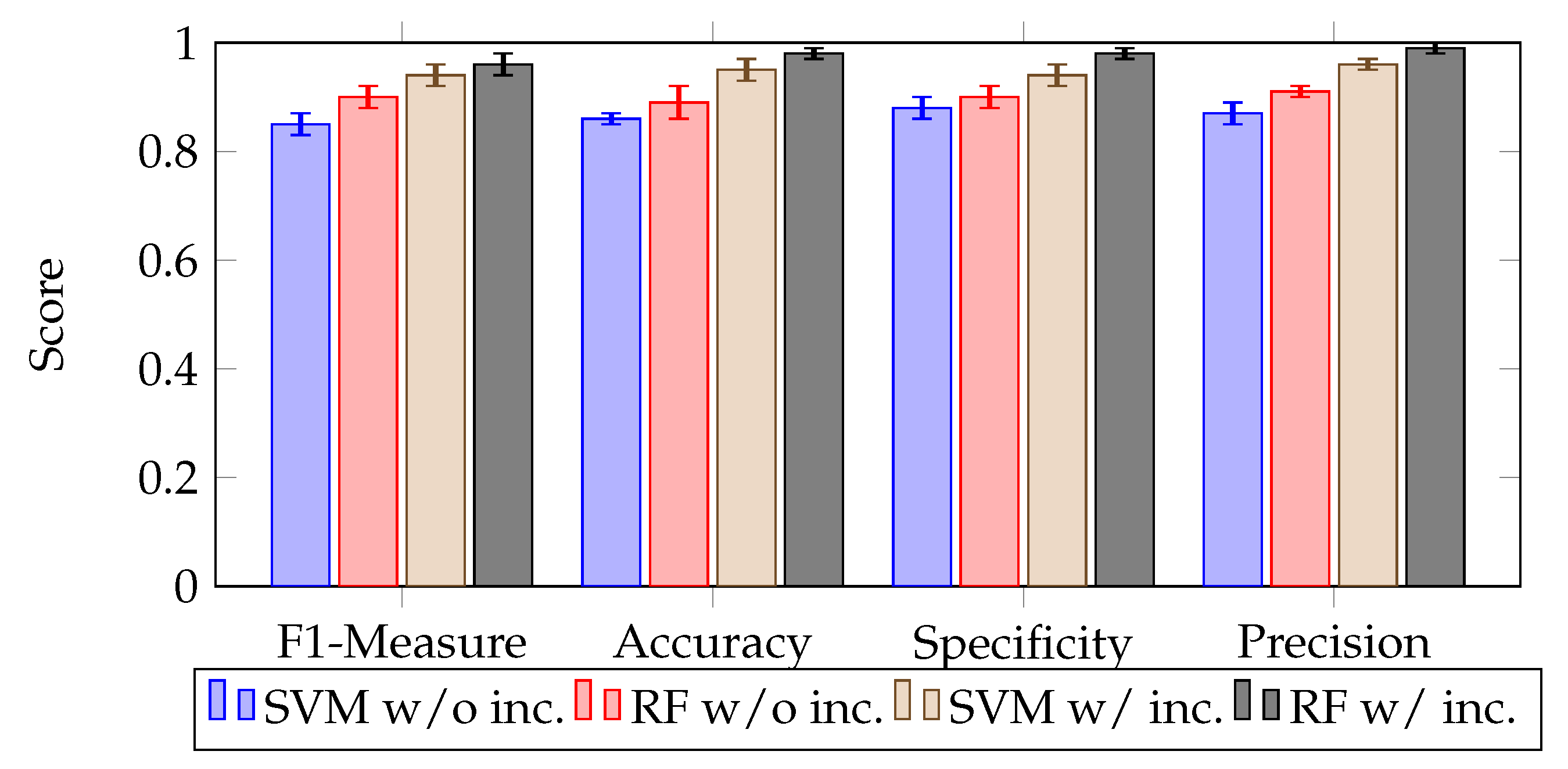
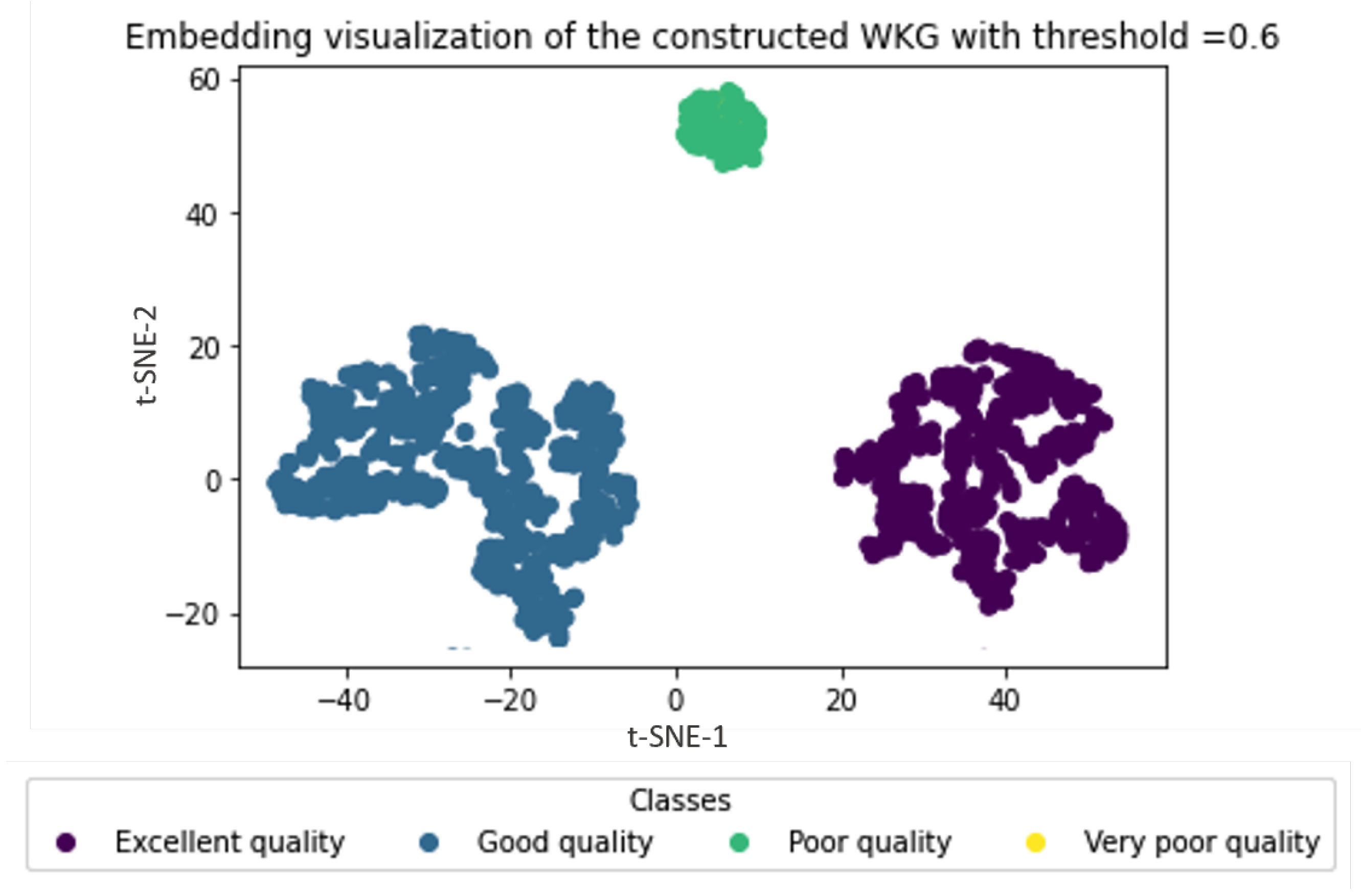
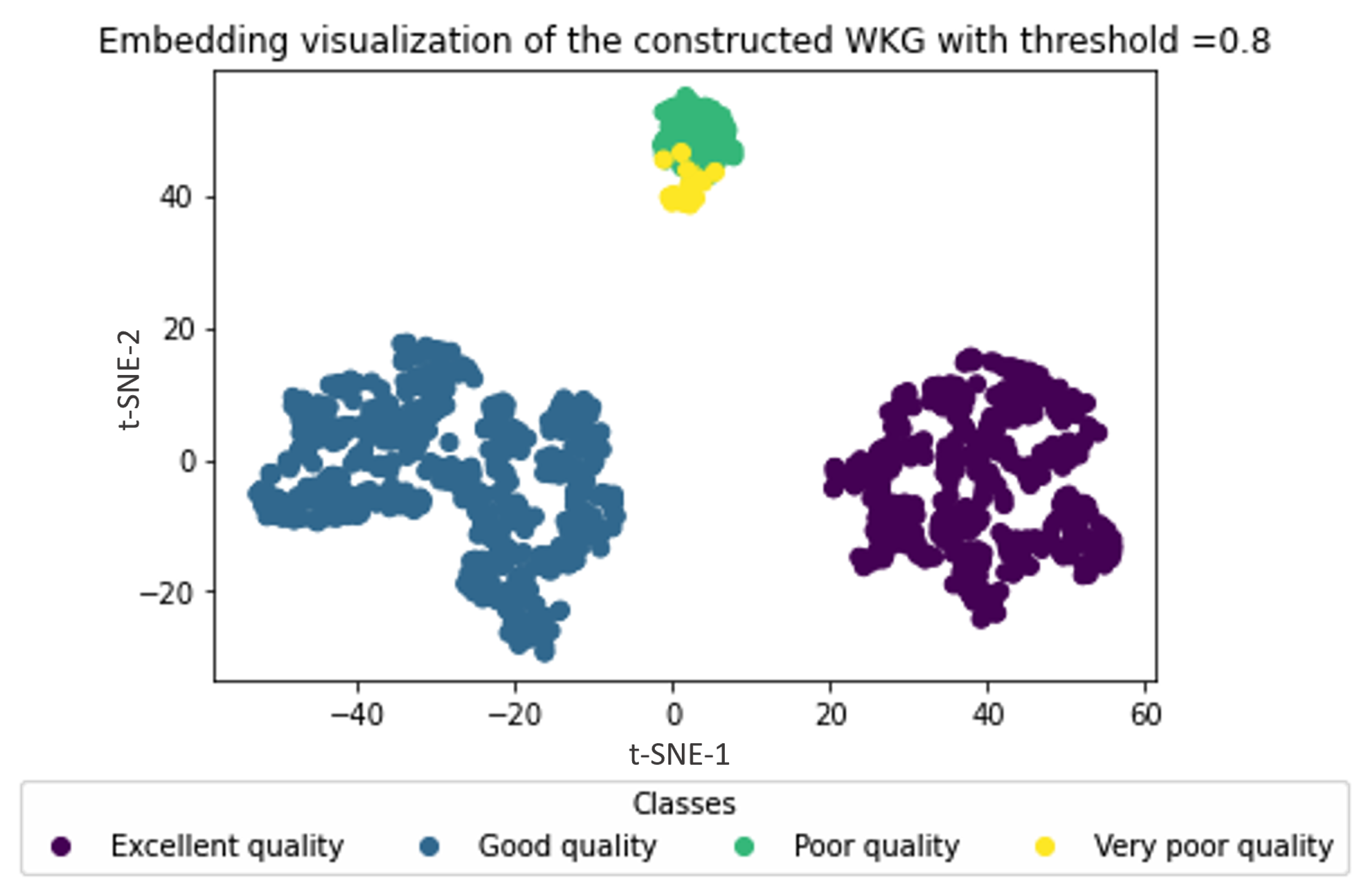
| Comparison Criteria | Existing Approaches | Our Approach |
|---|---|---|
| Management granularity | Entity level | Class level |
| Uncertainty handling | No | Yes |
| Monitoring data | Static | Dynamic |
| Monitoring space | Not specified | Heterogeneous water zones |
| Others | ⊖ Data impreciseness ⊖ No uncertainty quantification ⊖ Decision complexity ⊖ No unified representation ⊖ No corrective actions ⊖ No consideration of temporal variations | ⊕ Low number of management policies ⊕ Reduced decision time ⊕ Fewer policy conflicts ⊕ Accurate decision ⊕ Improved capabilities for corrective action suggestions ⊕ Improved capabilities for temporal variation consideration |
| Symbol | Definition |
|---|---|
| Uncertain Water Information Network (UWIN) | |
| A snapshot, i.e., possible world of the water network, given the monitored data | |
| Set of connections between UWIN entities | |
| Set of valid relations in the Water Information Network | |
| An uncertain fact in | |
| A valid fact in | |
| ,, | Embeddings of water entities, management policies, and feature entities, respectively, |
| d | The dimension of embeddings |
| d-dimensional continuous vector space | |
| , , , | Vector representations of entities (w,p,f) and relations (r) in the UWIN. |
| , | Sets of positive and negative triples |
| A function denoting the objective loss function for the uncertain embedding |
| Event | Corrective Measure | Confidence |
|---|---|---|
| Turbidity [>1 NTU] | Settling and decanting | 0.78 |
| Pressure loss [<20 psi] | Flushing | 0.91 |
| Pressure loss [<20 psi] OR Pumps fail | Disinfection | 0.83 |
| Pollution | Sediment removal | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Driss, M.; Boulila, W.; Mezni, H.; Sellami, M.; Ben Atitallah, S.; Alharbi, N. An Evidence Theory Based Embedding Model for the Management of Smart Water Environments. Sensors 2023, 23, 4672. https://doi.org/10.3390/s23104672
Driss M, Boulila W, Mezni H, Sellami M, Ben Atitallah S, Alharbi N. An Evidence Theory Based Embedding Model for the Management of Smart Water Environments. Sensors. 2023; 23(10):4672. https://doi.org/10.3390/s23104672
Chicago/Turabian StyleDriss, Maha, Wadii Boulila, Haithem Mezni, Mokhtar Sellami, Safa Ben Atitallah, and Nouf Alharbi. 2023. "An Evidence Theory Based Embedding Model for the Management of Smart Water Environments" Sensors 23, no. 10: 4672. https://doi.org/10.3390/s23104672
APA StyleDriss, M., Boulila, W., Mezni, H., Sellami, M., Ben Atitallah, S., & Alharbi, N. (2023). An Evidence Theory Based Embedding Model for the Management of Smart Water Environments. Sensors, 23(10), 4672. https://doi.org/10.3390/s23104672







