Robust Mesh Segmentation Using Feature-Aware Region Fusion †
Abstract
1. Introduction
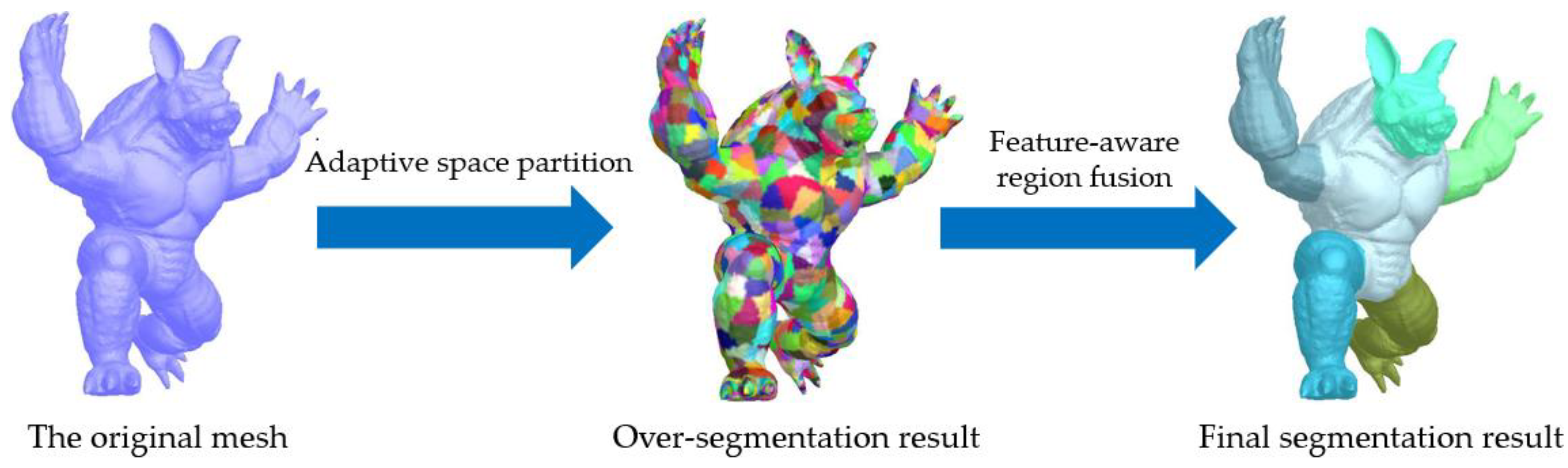
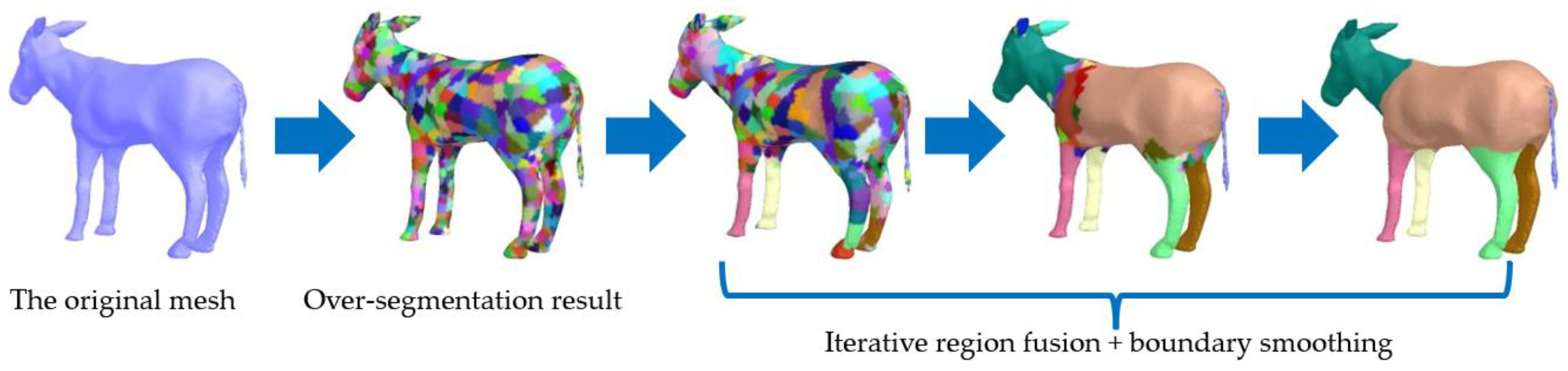
- An efficient over-segmentation method is introduced via adaptive space partition.
- By defining a new intra-region difference, inter-region difference, and fusion condition, a simple but powerful feature-aware region fusion algorithm is proposed that can robustly achieve mesh segmentation.
2. Related Work
3. Feature-Aware Mesh Segmentation Algorithm
3.1. Efficient Adaptive Space Partition
3.2. New Feature-Aware Region Fusion
3.2.1. Feature Description
3.2.2. Region Fusion
3.2.3. Boundary Smoothing
4. Experiments and Discussions
4.1. Results and Analysis
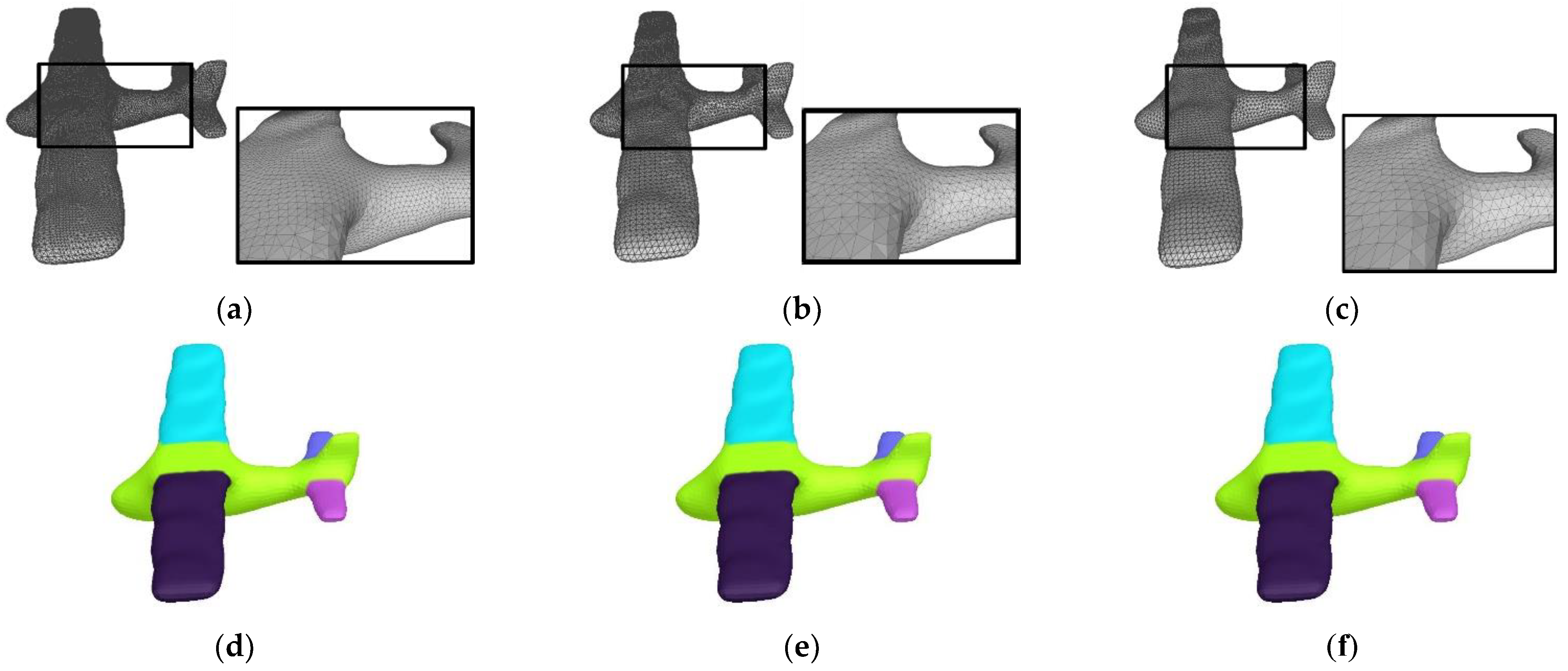
4.2. Robustness Evaluations
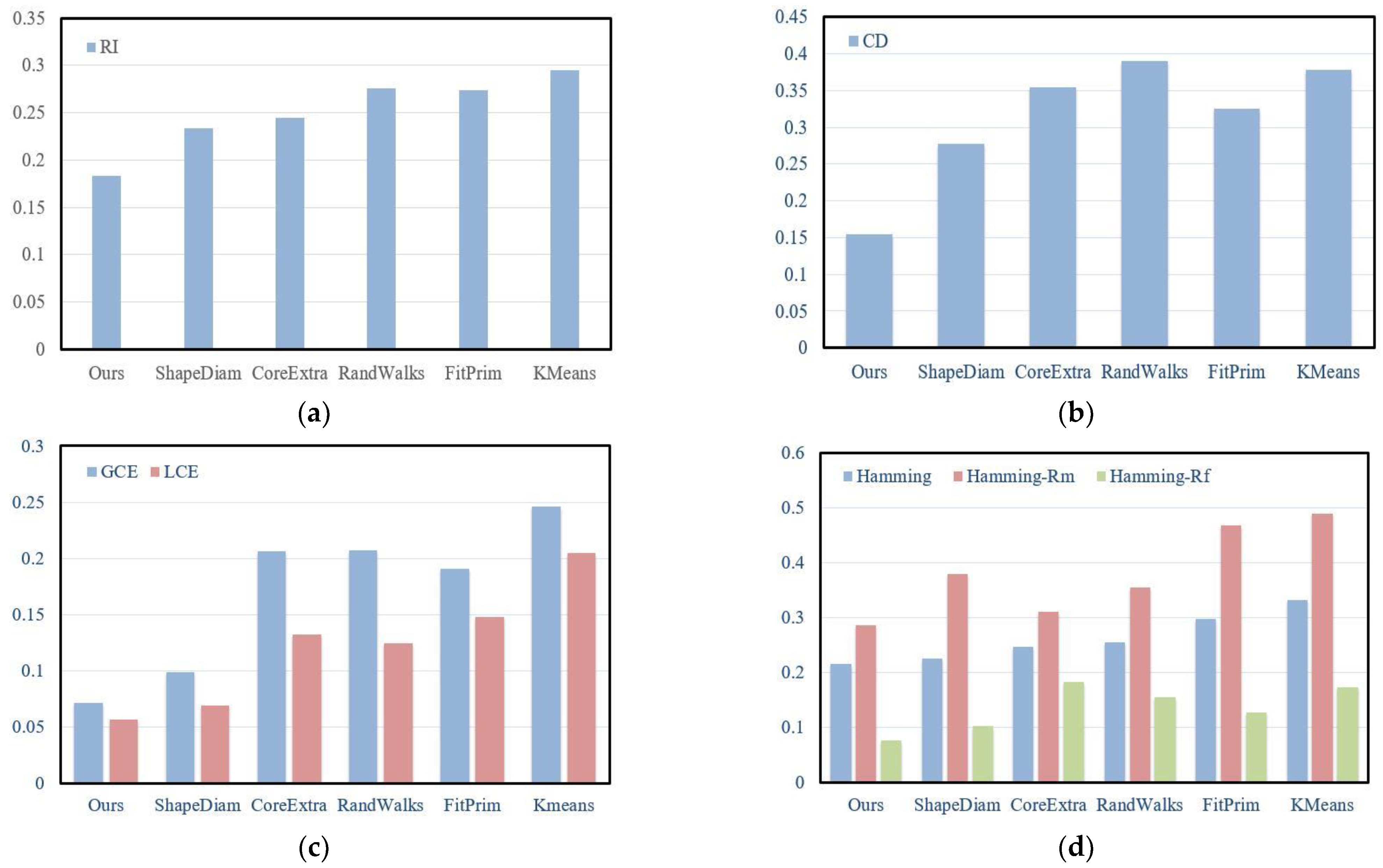
4.3. Qualitative and Quantitative Comparisons
4.4. Further Discussions and Time Performance
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katz, S.; Tal, A. Hierarchical mesh decomposition using fuzzy clustering and cuts. ACM Trans. Graph. 2003, 22, 954–961. [Google Scholar] [CrossRef]
- Au, O.K.; Zheng, Y.; Chen, M.; Xu, P.; Tai, C. Mesh segmentation with concavity-aware fields. IEEE Trans. Vis. Comput. Graph. 2011, 18, 1125–1134. [Google Scholar]
- Tong, W.; Yang, X.; Pan, M.; Chen, F. Spectral mesh segmentation via L0 gradient minimization. IEEE Trans. Vis. Comput. Graph. 2020, 26, 1807–1820. [Google Scholar]
- Ji, Z.; Liu, L.; Chen, Z.; Wang, G. Easy mesh cutting. Comput. Graph. Forum 2006, 25, 283–291. [Google Scholar] [CrossRef]
- Zheng, Y.; Tai, C.; Au, O.K. Dot scissor: A single-click interface for mesh segmentation. IEEE Trans. Vis. Comput. Graph. 2011, 18, 1304–1312. [Google Scholar] [CrossRef]
- Kalogerakis, E.; Hertzmann, A.; Singh, K. Learning 3D mesh segmentation and labeling. ACM Trans. Graph. 2010, 29, 102. [Google Scholar] [CrossRef]
- Benhabiles, H.; Lavoué, G.; Vandeborre, J.; Daoudi, M. Learning boundary edges for 3D-mesh segmentation. Comput. Graph. Forum 2011, 30, 2170–2182. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, M.; Wang, T.; Cohen-Or, D.; Zhang, H.; Chen, B. Projective analysis for 3D shape segmentation. ACM Trans. Graph. 2013, 32, 192. [Google Scholar] [CrossRef]
- Guo, K.; Zou, D.; Chen, X. 3D mesh labeling via deep convolutional neural networks. ACM Trans. Graph. 2015, 35, 3. [Google Scholar] [CrossRef]
- Kalogerakis, E.; Averkiou, M.; Maji, S.; Chaudhuri, S. 3D shape segmentation with projective convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6630–6639. [Google Scholar]
- Xu, H.; Dong, M.; Zhong, Z. Directionally convolutional networks for 3D shape segmentation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2717–2726. [Google Scholar]
- George, D.; Xie, X.; Tam, G.K. 3D mesh segmentation via multi-branch 1D convolutional neural networks. Graph. Model. 2018, 96, 1–10. [Google Scholar] [CrossRef]
- Meyer, M.; Desbrun, M.; Schroder, P.; Barr, A.H. Discrete differential-geometry operators for triangulated 2-manifolds. In Proceedings of the 3rd International Workshop Visualization and Mathematics (VisMath), Berlin, Germany, 22–25 May 2002; pp. 35–57. [Google Scholar]
- Shapira, L.; Shamir, A.; Cohen-Or, D. Consistent mesh partitioning and skeletonisation using the shape diameter function. Vis. Comput. 2008, 24, 249–259. [Google Scholar] [CrossRef]
- Hilaga, M.; Shinagawa, Y.; Komura, T.; Kunii, T.L. Topology matching for fully automatic similarity estimation of 3D shapes. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH), New York, NY, USA, 12–17 August 2001; pp. 203–212. [Google Scholar]
- Ben-Chen, M.; Gotsman, C. Characterizing shape using conformal factors. In Proceedings of the 1st Eurographics Workshop on 3D Object Retrieval (3DOR@Eurographis), Hersonissos, Greece, 15 April 2008; pp. 1–8. [Google Scholar]
- Sun, J.; Ovsjanikov, M.; Guibas, L.J. A concise and provably informative multi-scale signature based on heat diffusion. Comput. Graph. Forum 2009, 28, 1383–1392. [Google Scholar] [CrossRef]
- Chazelle, B.; Dobkin, D.P.; Shouraboura, N.; Tal, A. Strategies for polyhedral surface decomposition: An experimental study. Comput. Geom. 1997, 7, 327–342. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Z. Decomposing polygon meshes by means of critical points. In Proceedings of the 10th International Multimedia Modeling Conference (MMM), Brisbane, QLD, Australia, 5–7 January 2004; pp. 187–195. [Google Scholar]
- Lavoué, G.; Wolf, C. Markov random fields for improving 3D mesh analysis and segmentation. In Proceedings of the 1st Eurographics Workshop on 3D Object Retrieval (3DOR@Eurographis), Crete, Greece, 15 April 2008; pp. 25–32. [Google Scholar]
- Golovinskiy, A.; Funkhouser, T.A. Randomized cuts for 3D mesh analysis. ACM Trans. Graph. 2008, 27, 145. [Google Scholar] [CrossRef]
- Chen, X.; Golovinskiy, A.; Funkhouser, T. A benchmark for 3D mesh segmentation. ACM Trans. Graph. 2009, 28, 13. [Google Scholar] [CrossRef]
- Theologou, P.; Pratikakis, I.; Theoharis, T. Unsupervised spectral mesh segmentation driven by heterogeneous graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 397–410. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, C.; Deng, J.; Liu, Z.; Yang, Y. A new two-stage mesh surface segmentation method. Vis. Comput. 2018, 34, 1597–1615. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.; Xiao, J.; Zhang, X.; Yan, D. Blending surface segmentation and editing for 3D models. IEEE Trans. Vis. Comput. Graph. 2022, 28, 2879–2894. [Google Scholar] [CrossRef]
- Lin, C.; Liu, L.; Li, C.; Kobbelt, L.; Wang, B.; Xin, S.; Wang, W. SEG-MAT: 3D shape segmentation using medial axis transform. IEEE Trans. Vis. Comput. Graph. 2022, 28, 2430–2444. [Google Scholar] [CrossRef]
- Zheng, Y.; Tai, C. Mesh decomposition with cross-boundary brushes. Comput. Graph. Forum 2010, 29, 527–535. [Google Scholar] [CrossRef]
- Fan, L.; Liu, L.; Liu, K. Paint mesh cutting. Comput. Graph. Forum 2011, 30, 603–612. [Google Scholar] [CrossRef]
- Hou, Y.; Zhao, Y.; Shan, X. 3D mesh segmentation via L0-constrained random walks. Multim. Tools Appl. 2021, 80, 24885–24899. [Google Scholar] [CrossRef]
- Shu, Z.; Qi, C.; Xin, S.; Hu, C.; Wang, L.; Zhang, Y.; Liu, L. Unsupervised 3D shape segmentation and co-segmentation via deep learning. Comput. Aided Geom. Des. 2016, 43, 39–52. [Google Scholar] [CrossRef]
- Yi, L.; Su, H.; Guo, X.; Guibas, L.J. SyncSpecCNN: Synchronized spectral CNN for 3D shape segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6584–6592. [Google Scholar]
- Wang, Z.; Lu, F. VoxSegNet: Volumetric CNNs for semantic part segmentation of 3D shapes. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2919–2930. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Bai, X.; Shang, J.; Zhang, R.; Dong, J.; Wang, X.; Sun, G.; Fu, H.; Tai, C. Voxel-mesh network for geodesic-aware 3D semantic segmentation of indoor scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef]
- Shu, Z.; Shen, X.; Xin, S.; Chang, Q.; Feng, J.; Kavan, L.; Liu, L. Scribble-based 3D shape segmentation via weakly-supervised learning. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2671–2682. [Google Scholar] [CrossRef]
- Shu, Z.; Yang, S.; Wu, H.; Xin, S.; Pang, C.; Kavan, L.; Liu, L. 3D shape segmentation using soft density peak clustering and semi-Supervised learning. Comput. Aided Des. 2022, 145, 103181. [Google Scholar] [CrossRef]
- Xu, X.; Liu, C.; Zheng, Y. 3D tooth segmentation and labeling using deep convolutional neural networks. IEEE Trans. Vis. Comput. Graph. 2019, 25, 2336–2348. [Google Scholar] [CrossRef]
- Lawonn, K.; Meuschke, M.; Wickenhöfer, R.; Preim, B.; Hildebrandt, K. A geometric optimization approach for the detection and segmentation of multiple aneurysms. Comput. Graph. Forum. 2019, 38, 413–425. [Google Scholar] [CrossRef]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. SGPN: Similarity group proposal network for 3D point cloud instance segmentation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2569–2578. [Google Scholar]
- Hoang, L.; Lee, S.-H.; Kwon, K.-R. A deep learning method for 3D object classification and retrieval using the global point signature plus and deep wide residual network. Sensors 2021, 21, 2644. [Google Scholar] [CrossRef]
- Liu, B.; Wang, W.; Zhou, J.; Li, B.; Liu, X. Detail-preserving shape unfolding. Sensors 2021, 21, 1187. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Xiao, X.; Zhong, S.; Wang, W.; Li, Y.; Zhang, L.; Xie, Z. A feature-preserving framework for point cloud denoising. Comput. Aided Des. 2020, 127, 102857. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Wang, W.; Liu, L.; Chen, R. Mesh total generalized variation for denoising. IEEE Trans. Vis. Comput. Graph. 2022, 28, 4418–4433. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Zhao, Y. A robust segmentation algorithm for 3D complex meshes. In Proceedings of the 7th International Conference on Computer-Aided Design, Manufacturing, Modeling and Simulation (CDMMS), Busan, Republic of Korea, 14–15 November 2020; p. 032045. [Google Scholar]
- Jones, R.T.; Durand, F.; Desbrun, M. Non-iterative, feature-preserving mesh smoothing. ACM Trans. Graph. 2003, 22, 943–949. [Google Scholar] [CrossRef]
- Zheng, Y.; Fu, H.; Kin-Chung Au, O.; Tai, C. Bilateral normal filtering for mesh denoising. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1521–1530. [Google Scholar] [CrossRef]
- Pauly, M.; Gross, M.H.; Kobbelt, L. Efficient simplification of point-sampled surfaces. In Proceedings of the 13th IEEE Visualization Conference (IEEE Vis), Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of Min-Cut/Max-Flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef]
- Katz, S.; Leifman, G.; Tal, A. Mesh segmentation using feature point and core extraction. Vis. Comput. 2005, 21, 649–658. [Google Scholar] [CrossRef]
- Lai, Y.; Hu, S.; Martin, R.R.; Rosin, P.L. Fast mesh segmentation using random walks. In Proceedings of the 2008 ACM Symposium on Solid and Physical Modeling, New York, NY, USA, 2–4 June 2008; pp. 183–191. [Google Scholar]
- Attene, M.; Falcidieno, B.; Spagnuolo, M. Hierarchical mesh segmentation based on fitting primitives. Vis. Comput. 2006, 22, 181–193. [Google Scholar] [CrossRef]
- Chen, L.; Georganas, N.D. An efficient and robust algorithm for 3D mesh segmentation. Multim. Tools Appl. 2006, 29, 109–125. [Google Scholar] [CrossRef]










| Ours | Shapeboost [6] | TOG15 [9] | ShapePFCN [10] | 1DCNN [12] |
|---|---|---|---|---|
| 0.9587 | 0.9371 | 0.9024 | 0.9398 | 0.9362 |
| Mesh | Number of Vertices | Number of Facets | Number of Superfacets | Time |
|---|---|---|---|---|
| Airplane | 5400 | 10,796 | 389 | 0.0844 |
| Armadillo | 25,273 | 50,542 | 1311 | 1.1754 |
| Bird | 7849 | 15,694 | 587 | 0.1507 |
| Cup | 15,198 | 30,396 | 1307 | 0.2736 |
| Hand | 7112 | 14,220 | 536 | 0.1298 |
| Horse | 48,485 | 96,966 | 1218 | 1.5426 |
| Octopus | 5944 | 11,888 | 412 | 0.1013 |
| Teddy | 11,090 | 22,176 | 329 | 0.0964 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Hou, Y.; Xu, J.; Zhao, Y. Robust Mesh Segmentation Using Feature-Aware Region Fusion. Sensors 2023, 23, 416. https://doi.org/10.3390/s23010416
Wu L, Hou Y, Xu J, Zhao Y. Robust Mesh Segmentation Using Feature-Aware Region Fusion. Sensors. 2023; 23(1):416. https://doi.org/10.3390/s23010416
Chicago/Turabian StyleWu, Lulu, Yu Hou, Junli Xu, and Yong Zhao. 2023. "Robust Mesh Segmentation Using Feature-Aware Region Fusion" Sensors 23, no. 1: 416. https://doi.org/10.3390/s23010416
APA StyleWu, L., Hou, Y., Xu, J., & Zhao, Y. (2023). Robust Mesh Segmentation Using Feature-Aware Region Fusion. Sensors, 23(1), 416. https://doi.org/10.3390/s23010416





