Constant Tension Control System of High-Voltage Coil Winding Machine Based on Smith Predictor-Optimized Active Disturbance Rejection Control Algorithm
Abstract
1. Introduction
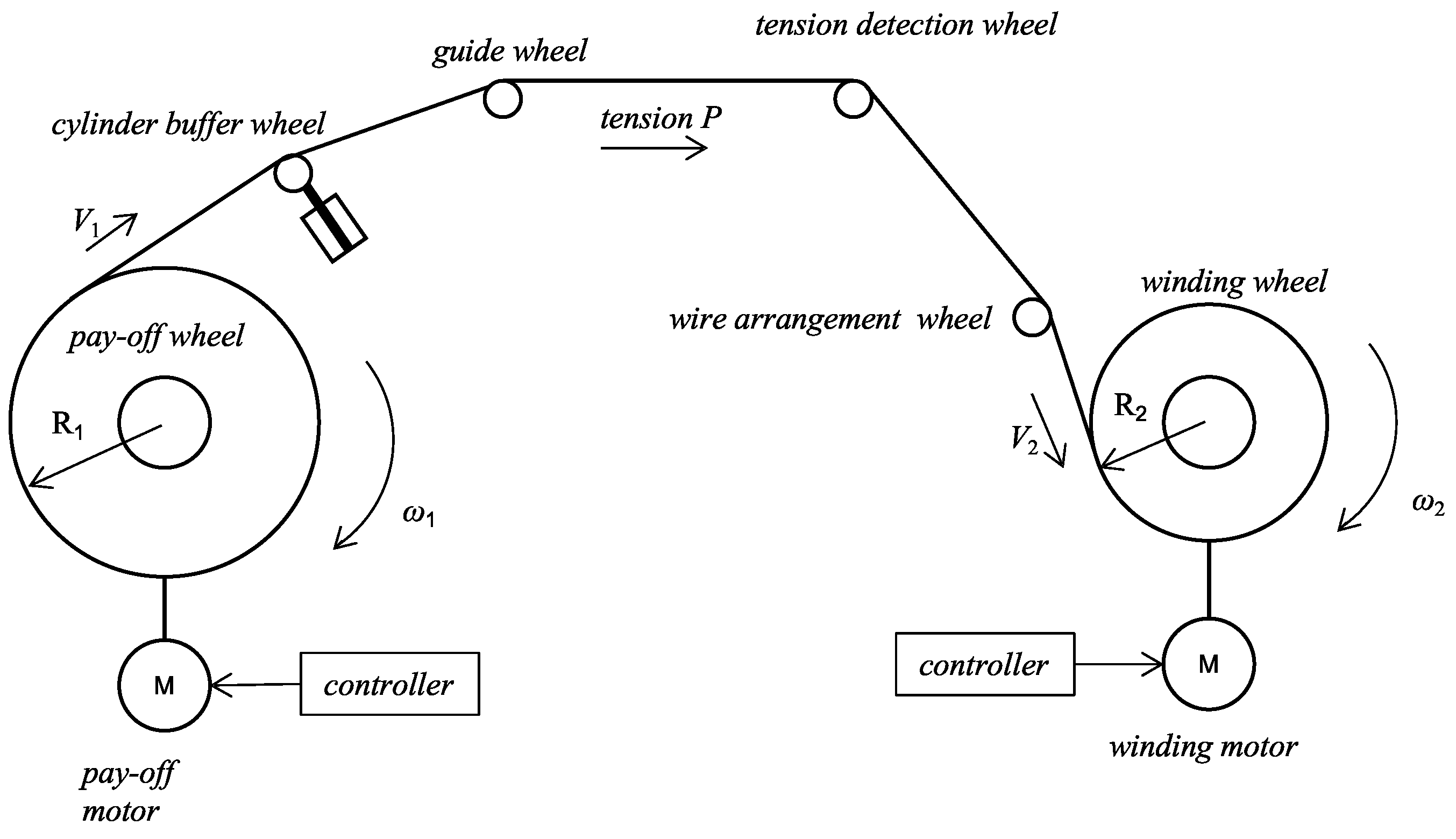
2. Tension Control Model of Winding System
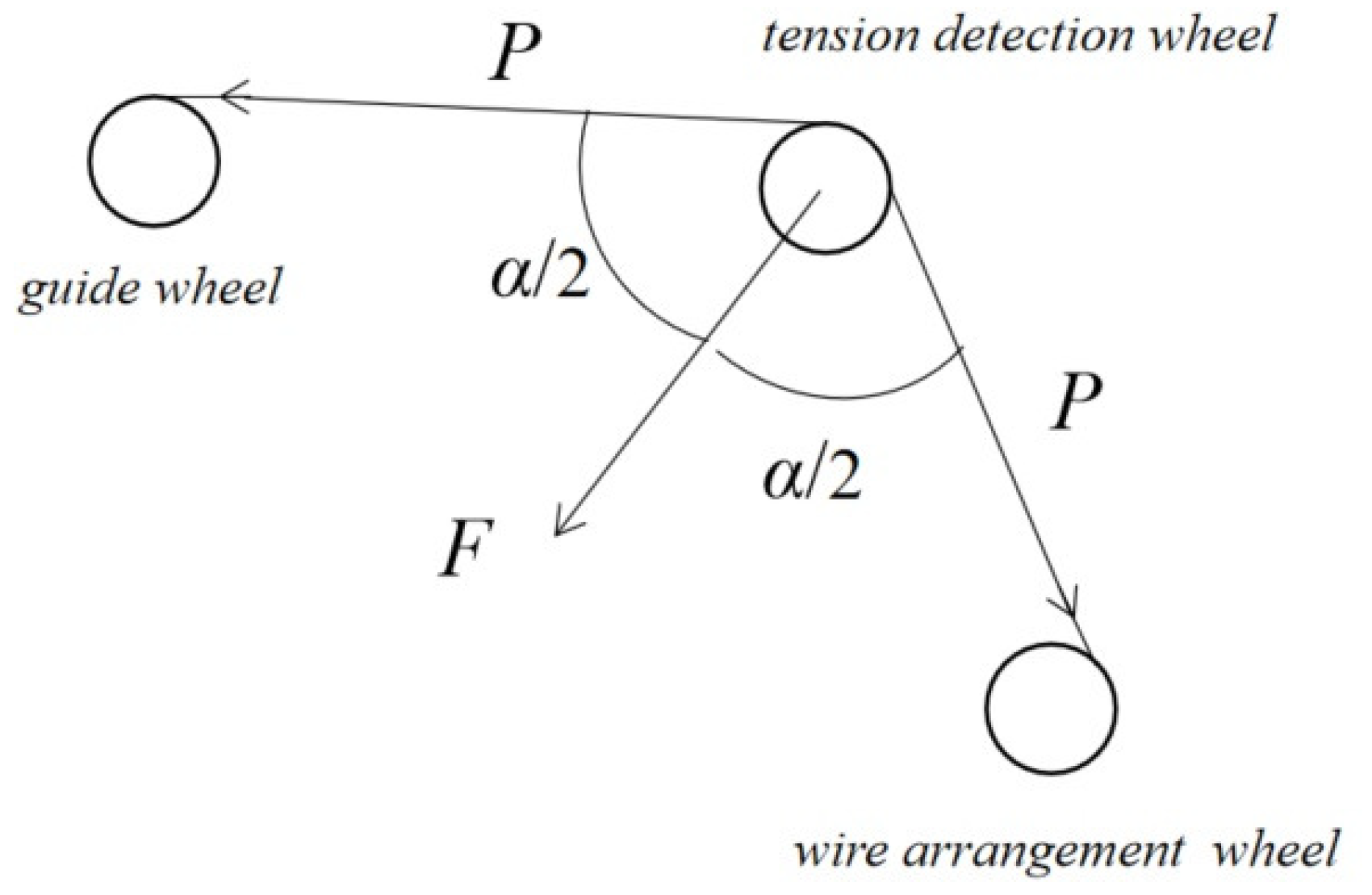
2.1. Tension Detection Principle
2.2. Mathematical Analysis of Winding System
2.3. The Design of the Tension Control System
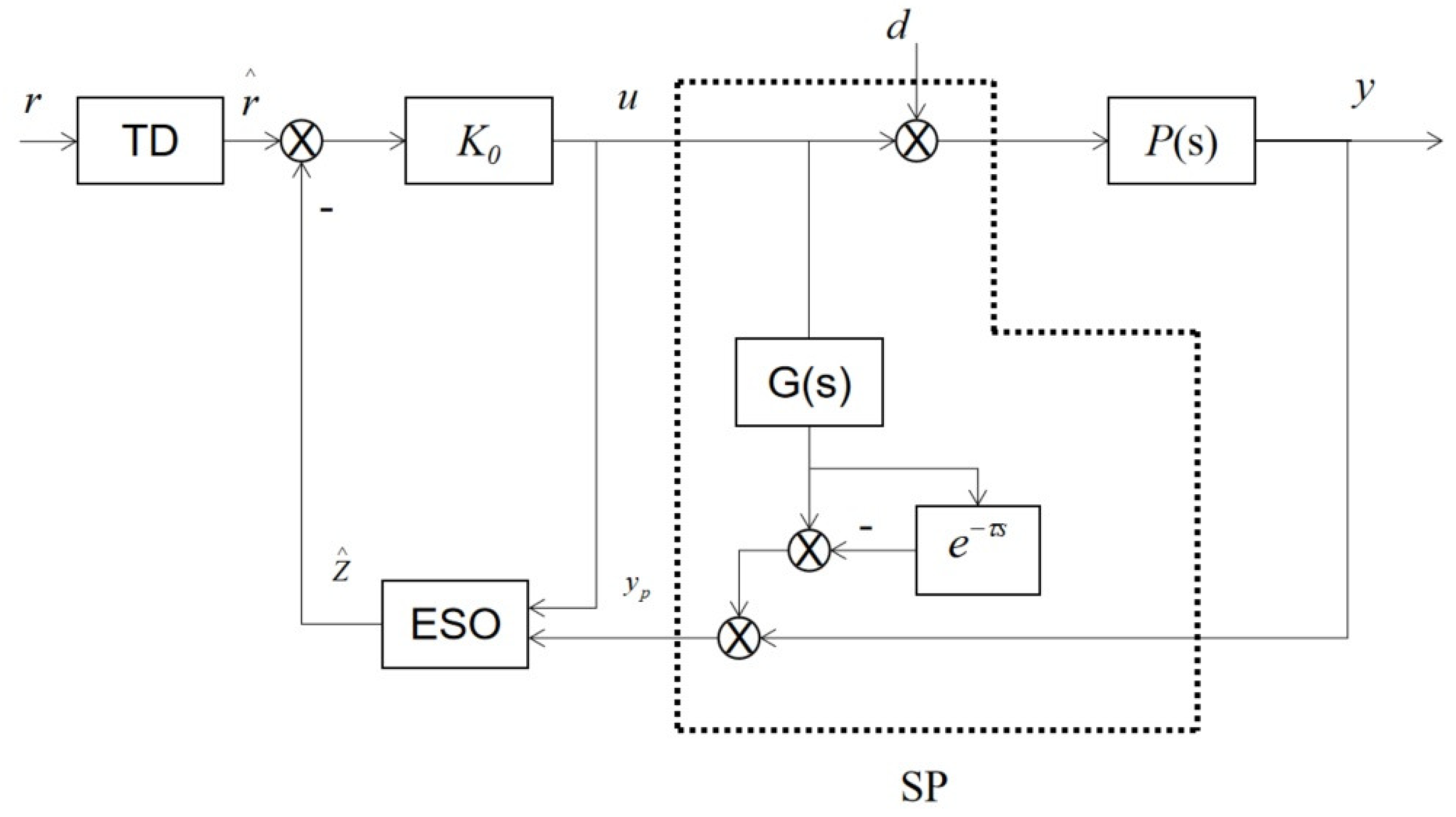
3. Controller Design for SP-ADRC
4. Results
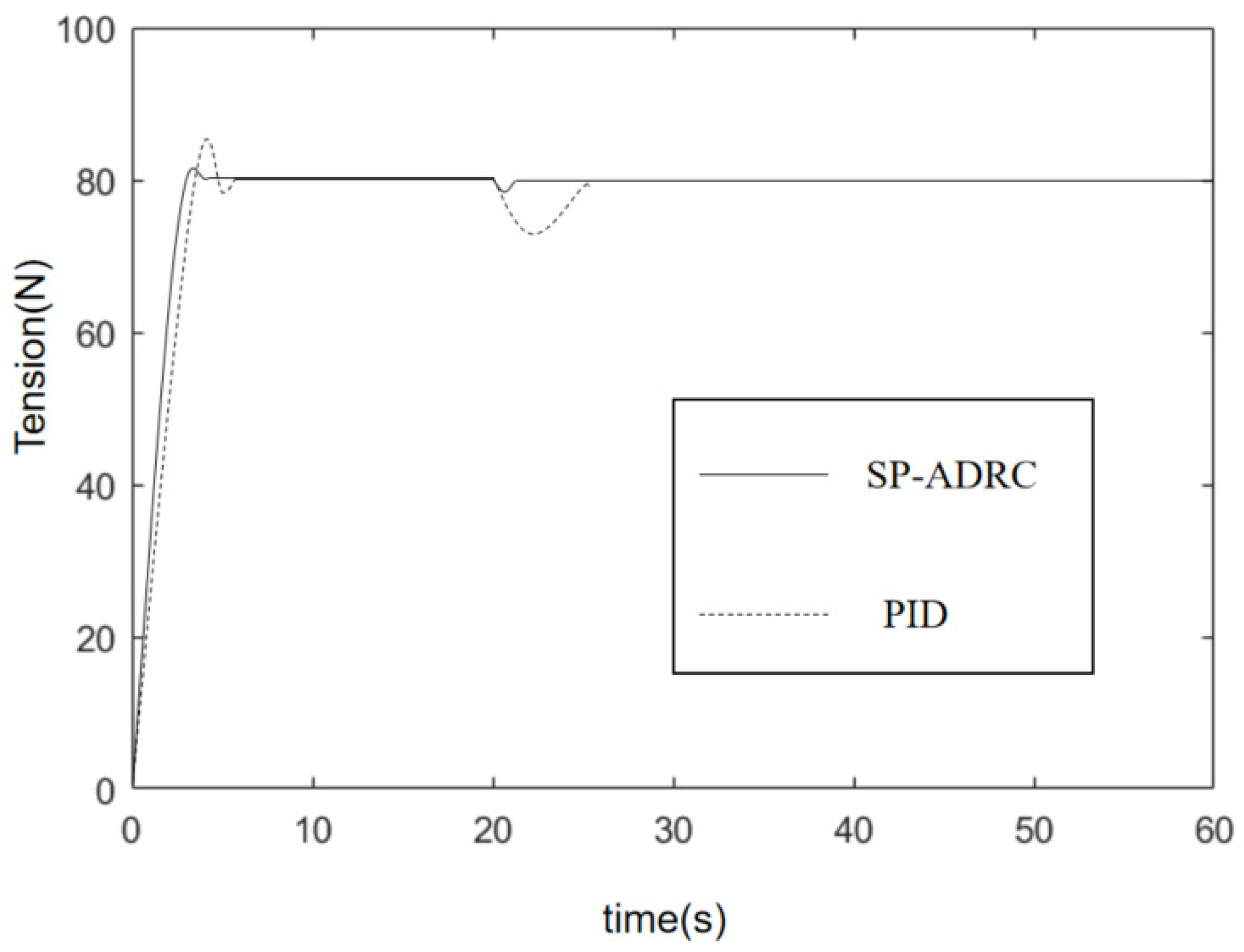
4.1. Simulation Analysis
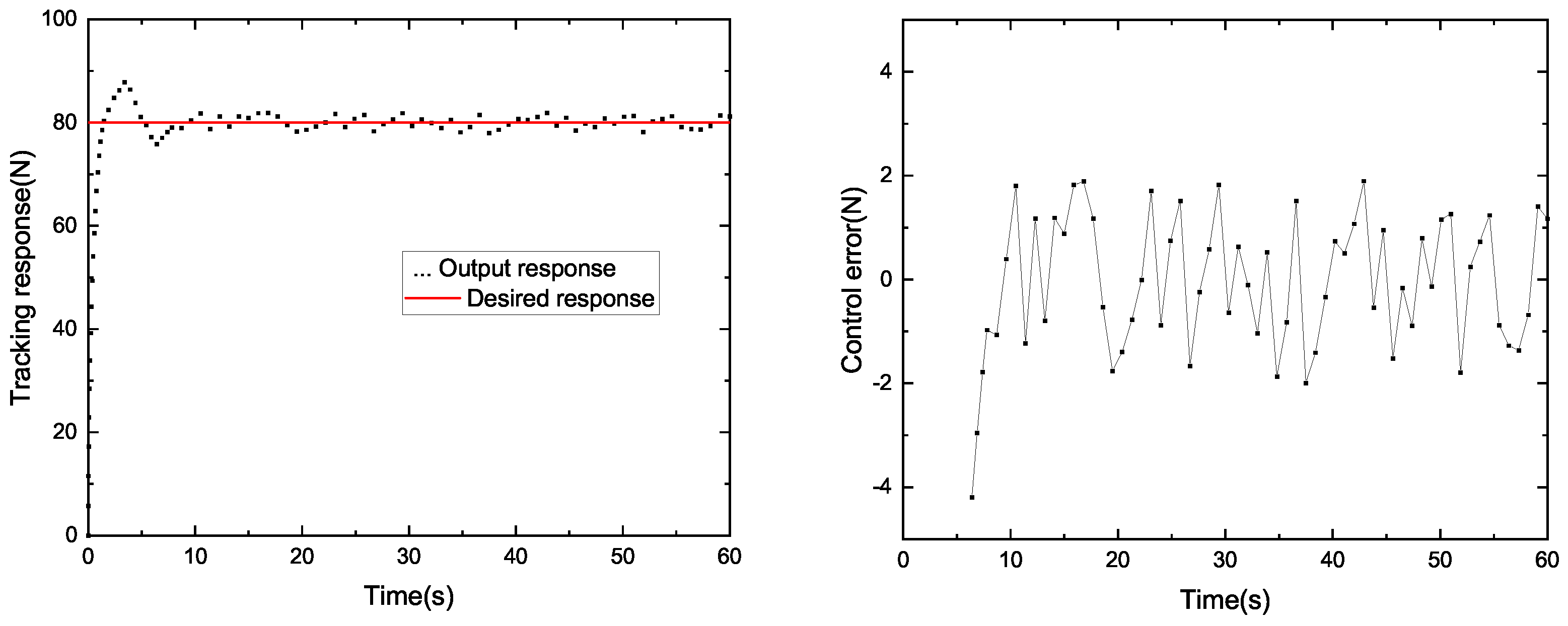
4.2. Constant Tension Control Test
4.3. Analysis of Static Difference Rate
4.4. Disturbance Suppression Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SP | Smith Predictor |
| ADRC | Active Disturbance Rejection Control |
| PID | Proportion Integral Derivative |
References
- Moradnouri, A.; Ardeshiri, A.; Vakilian, M.; Hekmati, A.; Fardmanesh, M. Survey on High-Temperature Superconducting Transformer Windings Design. J. Supercond. Nov. Magn. 2020, 33, 2581–2599. [Google Scholar] [CrossRef]
- Trkulja, B.; Drandic, A.; Milardic, V.; Zupan, T.; Ziger, I.; Filipovic-Grcic, D. Lightning impulse voltage distribution over voltage transformer windings — Simulation and measurement. Electr. Power Syst. Res. 2017, 147, 185–191. [Google Scholar] [CrossRef]
- Zhou, H.; Hong, K.; Huang, H.; Zhou, J. Transformer winding fault detection by vibration analysis methods. Appl. Acoust. 2016, 114, 136–146. [Google Scholar] [CrossRef]
- Gutten, M.; Korenciak, D.; Kucera, M.; Janura, R.; Glowacz, A.; Kantoch, E. Frequency and time fault diagnosis methods of power transformers. Meas. Sci. Rev. 2018, 18, 162–167. [Google Scholar] [CrossRef]
- Venikar, P.A.; Ballal, M.S.; Umre, B.S.; Suryawanshi, H.M. Search Coil based Online Diagnostics of Transformer Internal Faults. IEEE Trans. Power Deliv. 2017, 32, 2520–2529. [Google Scholar] [CrossRef]
- Tapiawala, G.; Mishra, R.K. Comprehensive modeling of dry type foil winding transformer to analyse inter turn insulation under lightning impulse voltage. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–5. [Google Scholar]
- Mytnikov, A.; Lavrinovich, A.; Strugov, V.; Saqib, M. Development of impulse method for transformer winding condition control technology. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1019, 12–24. [Google Scholar] [CrossRef]
- Hashemnia, N.; Abu-Siada, A.; Islam, S. Improved power transformer winding fault detection using FRA diagnostics—Part 1: Axial displacement simulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 556–563. [Google Scholar] [CrossRef]
- Dawood, K.; Komurgoz, G. Effect of the Tap Winding Configurations on the Leakage Reactance of the Concentric Transformer Coils. In Proceedings of the 2019 1st Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkey, 12–15 June 2019; pp. 200–205. [Google Scholar]
- Abbasi, A.R.; Mahmoudi, M.R.; Arefi, M.M. Transformer Winding Faults Detection Based on Time Series Analysis. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Ni, J.; Zhao, Z.; Tan, S.; Chen, Y.; Yao, C.; Tang, C. The actual measurement and analysis of transformer winding deformation fault degrees by FRA using mathematical indicators. Electr. Power Syst. Res. 2020, 184, 106324. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Mohammadi-Ivatloo, B.; Gharehpetian, B.G.; Aguiar, A.P. Turn-to-Turn Short Circuit Fault Localization in Transformer Winding via Image Processing and Deep Learning Method. IEEE Trans. Ind. Inform. 2021, 18, 4417–4426. [Google Scholar] [CrossRef]
- Abbasi, A.R.; Mahmoudi, M.R. Application of Statistical Control Charts to Discriminate Transformer Winding Defects. Electr. Power Syst. Res. 2021, 191, 106890. [Google Scholar] [CrossRef]
- Li, Q.; Bai, J.; Fan, Y.; Zhang, Z. Study of wire tension control system based on closed loop PID control in HS-WEDM. Int. J. Adv. Manuf. Technol. 2015, 82, 1089–1097. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, G.; Yan, H. A high-precision constant wire tension control system for improving workpiece surface quality and geometric accuracy in WEDM. Precis. Eng. 2018, 54, 51–59. [Google Scholar] [CrossRef]
- Hong, Q.; Shi, Y.; Chen, Z. Dynamics Modeling and Tension Control of Composites Winding System Based on ASMC. IEEE Access 2020, 8, 102795–102810. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, H.; Shao, C.; Yan, R.; Zhang, C.; Yang, G. Control Strategy for Smooth Wire Sending and Constant Tension in Multi-Wire Slicer. IEEE Trans. Ind. Inform. 2018, 15, 1668–1677. [Google Scholar] [CrossRef]
- Wei, D.; Chen, L.; Wang, J.S.; Yao, X. Design of Automatic Control System for Constant Tension and Linear Speed of Rewinder Machine. Eng. Lett. 2021, 29, 1–10. [Google Scholar]
- He, F.; Wang, S.; Wang, C. Inhibition of Tension Vibration for Winding Tension Control System. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; Volume 1, pp. 3725–3730. [Google Scholar]
- Huang, H.; Xu, J.; Sun, K.; Deng, L.; Huang, C. Design and Analysis of Tension Control System for Transformer Insulation Layer Winding. IEEE Access 2020, 8, 95068–95081. [Google Scholar] [CrossRef]
- Li, X.; Gao, Z. The invariance principle in disturbance rejection control. Control Theory Appl. 2020, 3, 236–244. [Google Scholar]
- Sira-Ramírez, H.; Zurita-Bustamante, E.W.; Huang, C. Equivalence among flat filters, dirty derivative-based PID controllers, ADRC, and integral reconstructor-based sliding mode control. IEEE Trans. Control Syst. Technol. 2019, 28, 1696–1710. [Google Scholar] [CrossRef]
- Zhang, B.; Tan, W.; Li, J. Tuning of Smith predictor based generalized ADRC for time-delayed processes via IMC. ISA Trans. 2020, 99, 159–166. [Google Scholar] [CrossRef]
- Ba, D.; Chen, G.; Li, P.; An, K.; Liu, X. Fuzzy Smith predictor–based active disturbance rejection controller for time-delay systems with application to drilling stick–slip vibration control. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2022, 09596518221134136. [Google Scholar] [CrossRef]
- Chen, S.; Xue, W.; Zhong, S.; Huang, Y. On comparison of modified ADRCs for nonlinear uncertain systems with time delay. Sci. China Inf. Sci. 2018, 61, 1–15. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, Z.; Li, D.; Chen, Y.; Liu, Y. On transitioning from PID to ADRC in thermal power plants. Control Theory Technol. 2021, 19, 3–18. [Google Scholar] [CrossRef]
- Safiullah, S.; Rahman, A.; Aftab, M.A.; Hussain, S.S. Performance study of ADRC and PID for concurrent Frequency-Voltage Control of Electric Vehicle Incorporated Hybrid Power System. In Proceedings of the IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy, Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar]
- Wang, Z.; Yun, Z.; Wang, L.; Wang, J. The Temperature Control of Blackbody Radiation Source Based on ADRC. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation, Changchun, China, 5–8 August 2018; pp. 77–82. [Google Scholar]
- Elameen, M.H.E.; Li, J.; Zhang, B.; Tan, W. Active disturbance rejection control design and analysis for first-order plus time delay systems. In Proceedings of the 2019 Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 71–75. [Google Scholar]
- Gao, Y.; Wu, W.; Zhang, Y. High-order LTD Based Predictive LADRC for Uncertain Systems with Time Delay. In Proceedings of the 2019 Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 318–323. [Google Scholar]
- Zhang, Y.; Li, D.; Gao, Z.; Zheng, Q. On oscillation reduction in feedback control for processes with an uncertain dead time and internal–external disturbances. ISA Trans. 2015, 59, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Tan, W. Analysis and tuning of reduced-order active disturbance rejection control. J. Frankl. Inst. 2021, 358, 339–362. [Google Scholar] [CrossRef]




| Status | Enactment Tension/N | ||
|---|---|---|---|
| PID control | 4.23 | 1.13 | 1.77 |
| SP-ADRC control | 2.21 | 0.57 | 0.48 |
| Status | Enactment Tension/N | |||||
|---|---|---|---|---|---|---|
| PID control | 80 | 81.89 | 78.00 | 3.89 | 79.61 | 4.89 |
| SP-ADRC control | 80 | 80.44 | 79.01 | 1.43 | 80.10 | 1.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, Y.; Yu, B.; Zhang, Y.; Xu, W.; Lu, T. Constant Tension Control System of High-Voltage Coil Winding Machine Based on Smith Predictor-Optimized Active Disturbance Rejection Control Algorithm. Sensors 2023, 23, 140. https://doi.org/10.3390/s23010140
Ai Y, Yu B, Zhang Y, Xu W, Lu T. Constant Tension Control System of High-Voltage Coil Winding Machine Based on Smith Predictor-Optimized Active Disturbance Rejection Control Algorithm. Sensors. 2023; 23(1):140. https://doi.org/10.3390/s23010140
Chicago/Turabian StyleAi, Yuming, Baocheng Yu, Yanduo Zhang, Wenxia Xu, and Tao Lu. 2023. "Constant Tension Control System of High-Voltage Coil Winding Machine Based on Smith Predictor-Optimized Active Disturbance Rejection Control Algorithm" Sensors 23, no. 1: 140. https://doi.org/10.3390/s23010140
APA StyleAi, Y., Yu, B., Zhang, Y., Xu, W., & Lu, T. (2023). Constant Tension Control System of High-Voltage Coil Winding Machine Based on Smith Predictor-Optimized Active Disturbance Rejection Control Algorithm. Sensors, 23(1), 140. https://doi.org/10.3390/s23010140






