CFD Model of a Mechanical Oscillator Flowmeter
Abstract
:1. Introduction
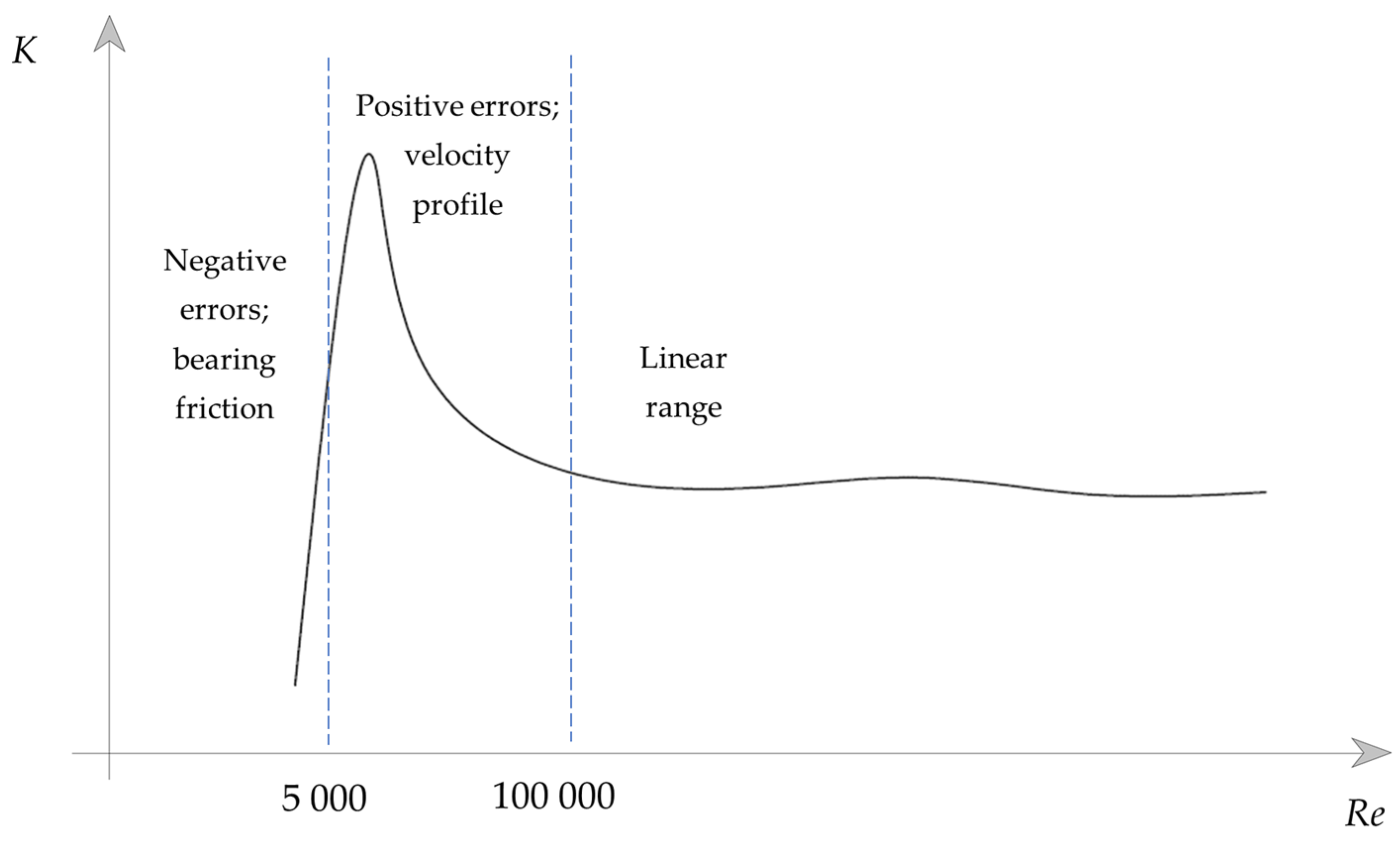
- The determination of factors affecting the linearity of the error curve. Only preliminary studies on this issue exist.
- Study on the influence of the energy of oscillations on the metrological and operational parameters of the flowmeter.
- Study of the influence of inlet profile disturbances on the flowmeter’s performance. Existing studies require extension.
- Study of the influence of pipe surface roughness on measurement characteristics. No such study has been conducted before.
- Verification of equations describing the influence of fluid properties on the characteristics. Existing studies are limited to water and liquid sulfur.
2. Materials and Methods
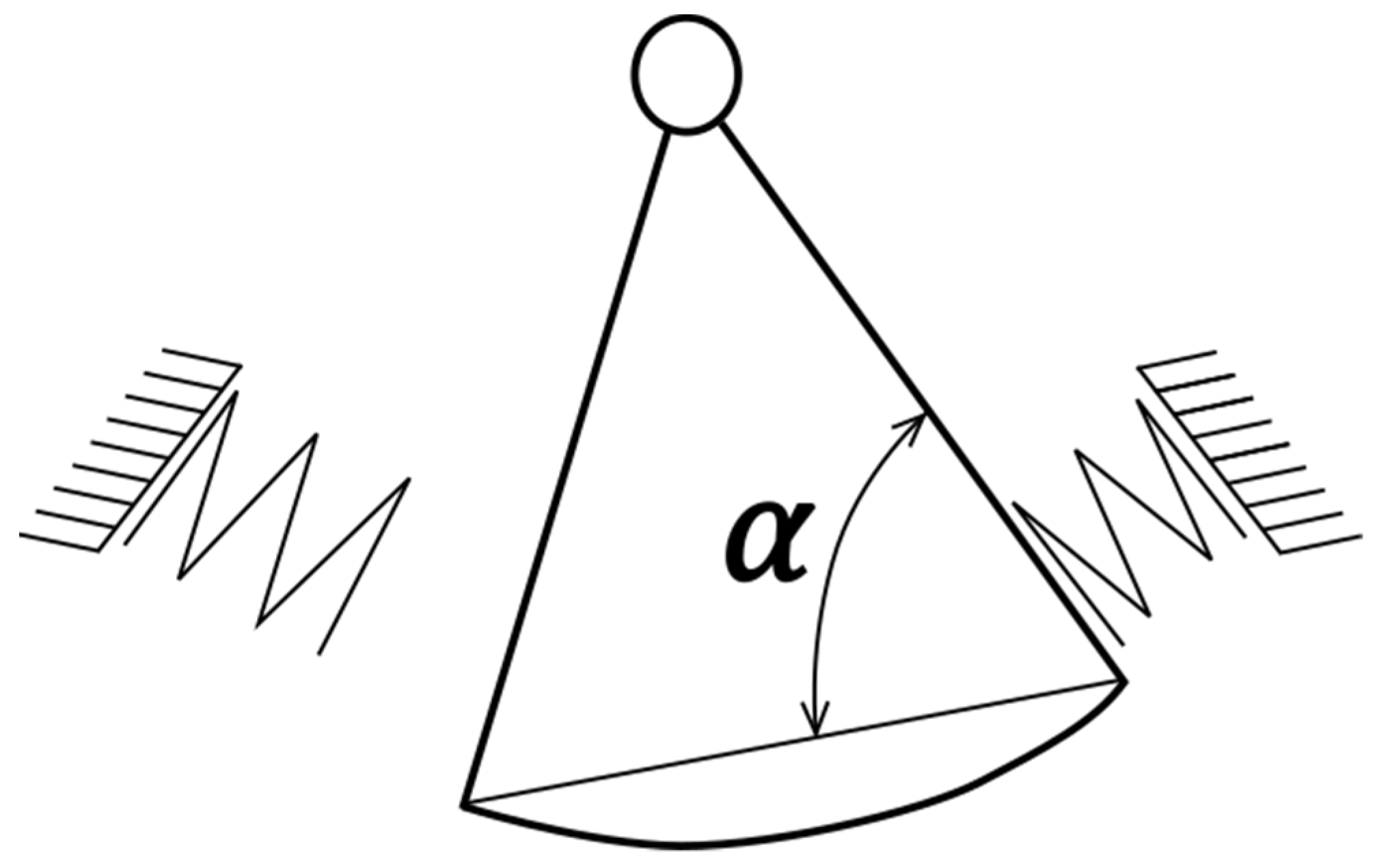
2.1. Principle of Operation of a Mechanical Oscillator Flowmeter
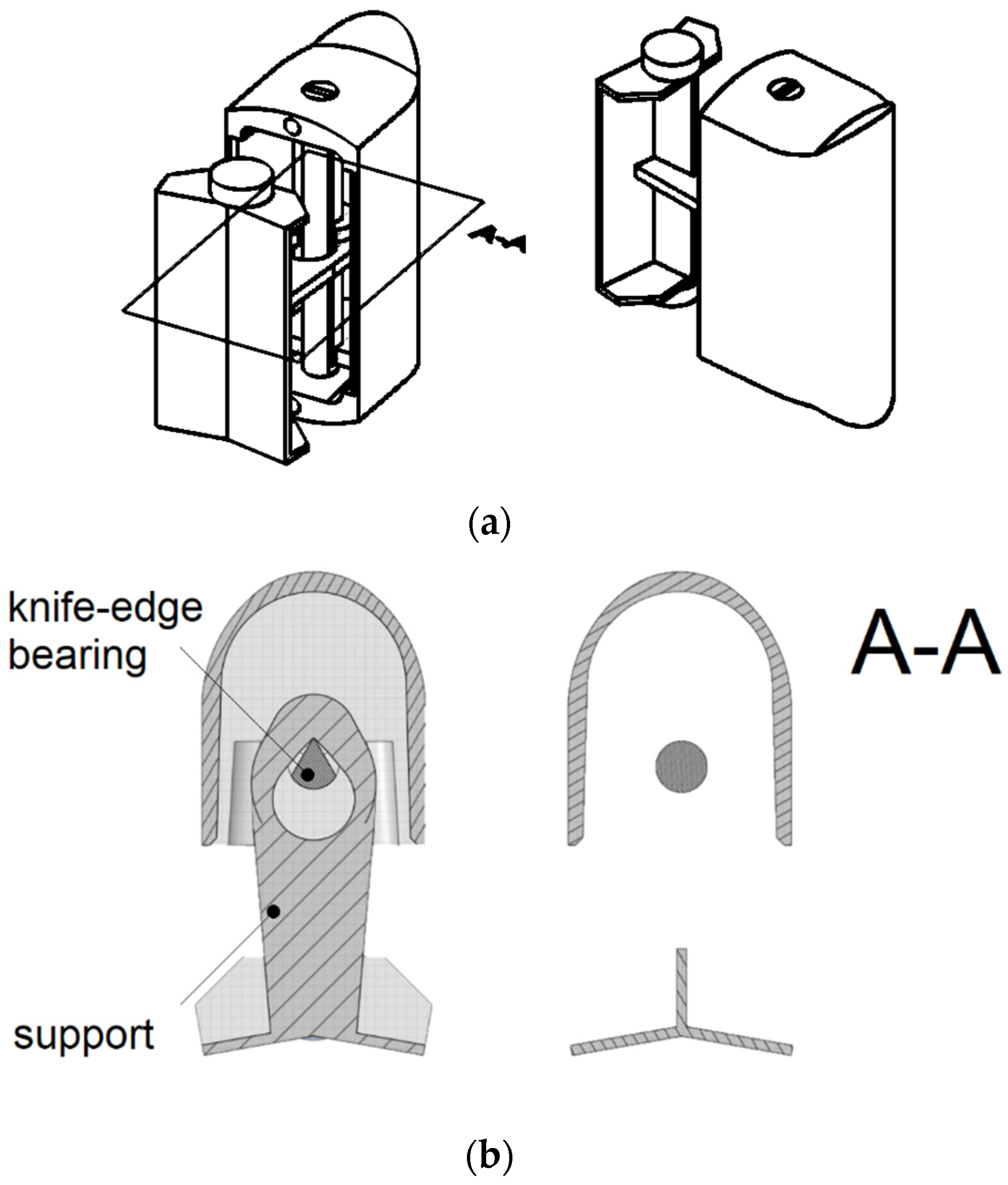
2.2. Experimental Setup
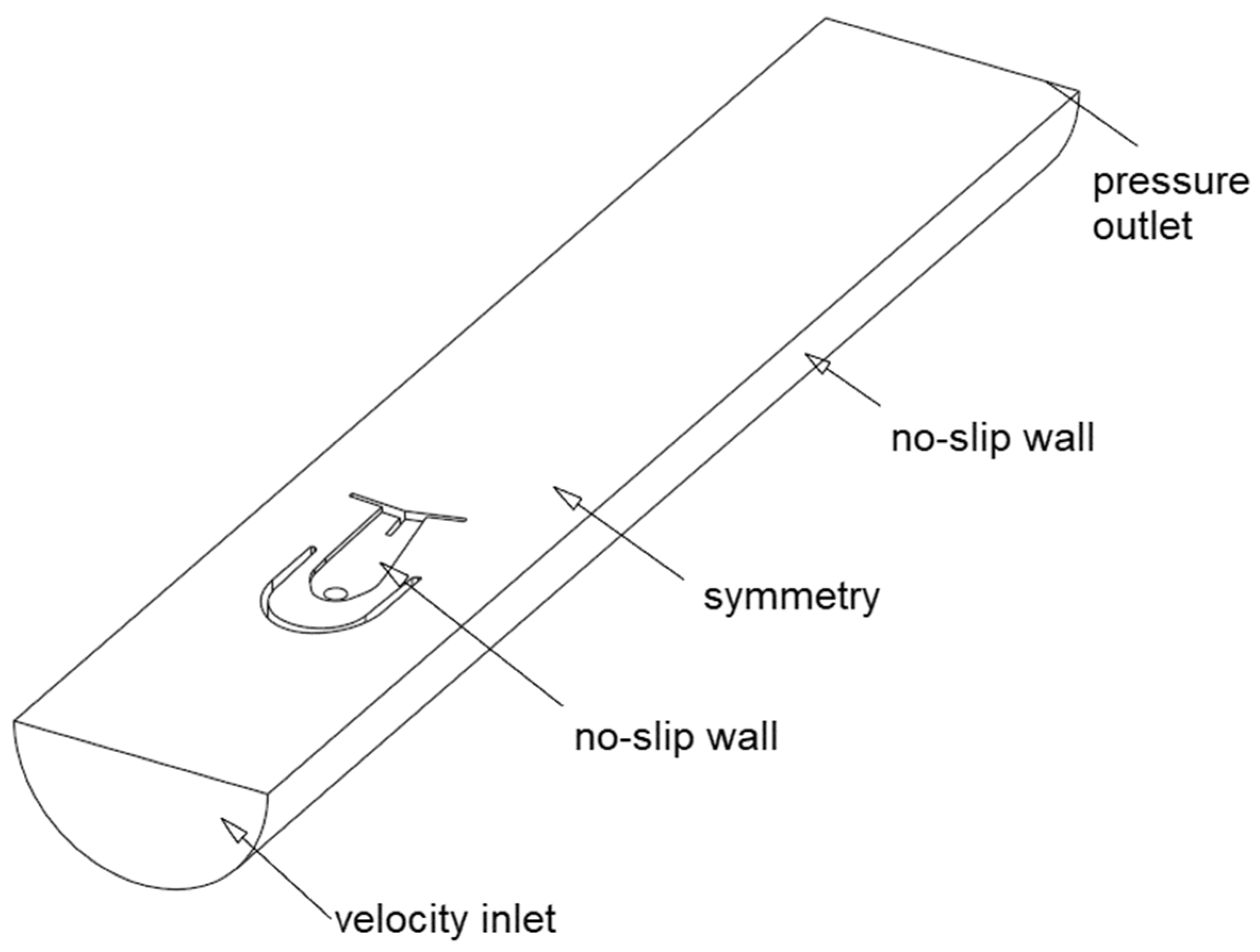
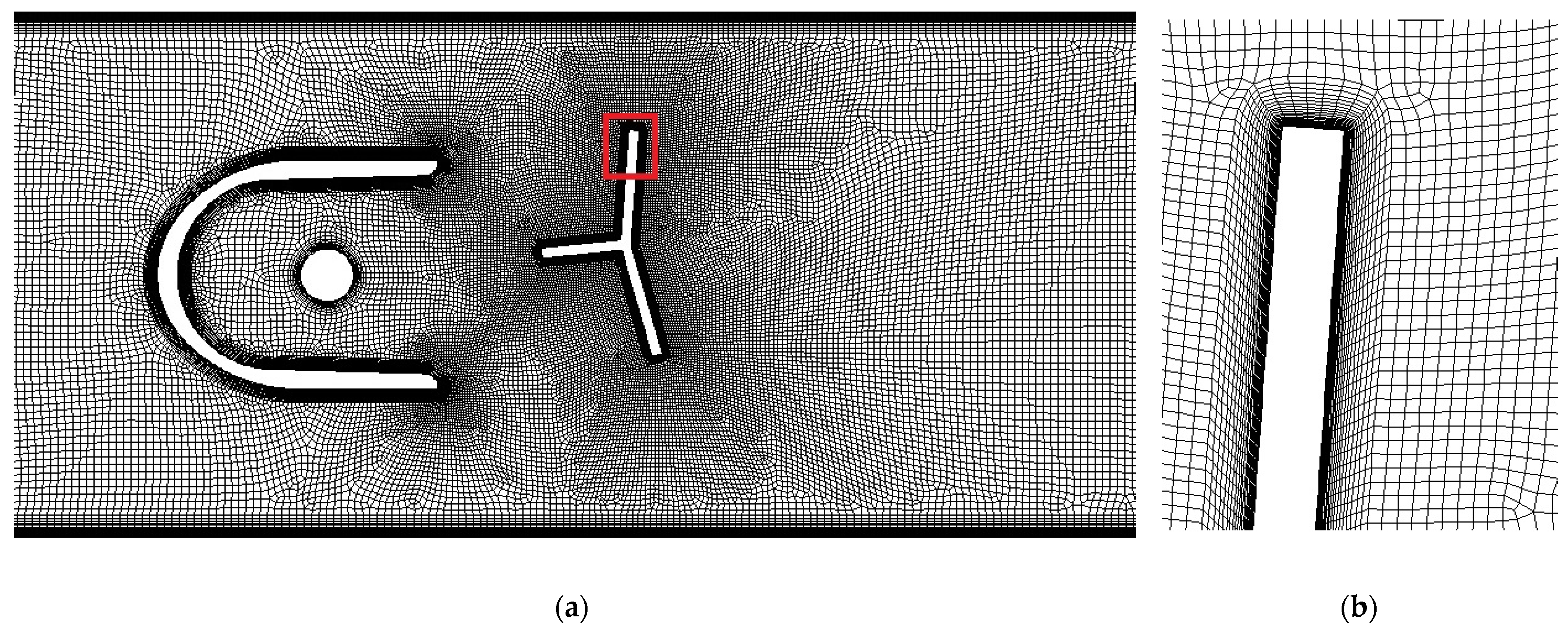
2.3. Numerical Model
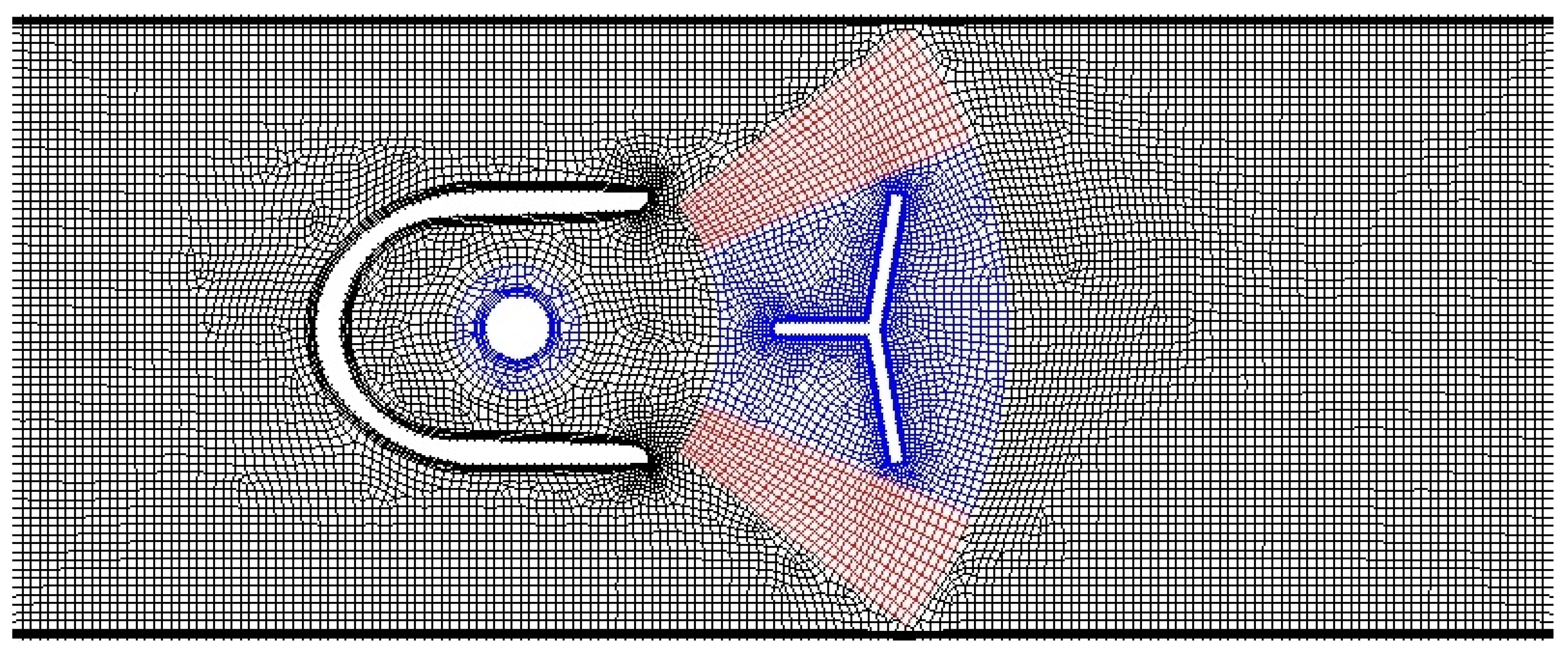
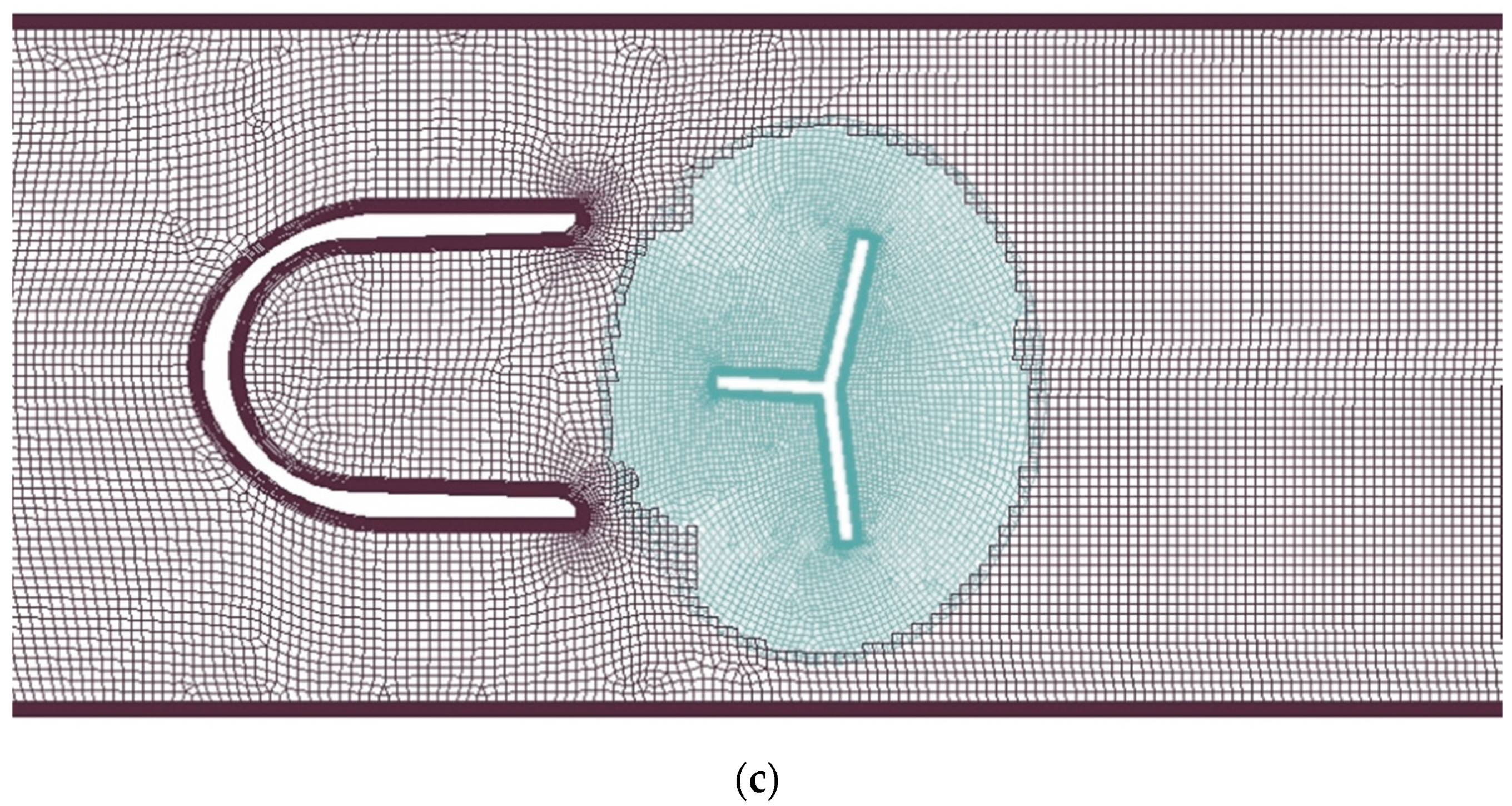
- Smoothing and remeshing—computational mesh stretches or shrinks in a spring-like manner. If the deformation causes a decrease in mesh quality below acceptable levels, local remeshing is activated. The main disadvantages are variable mesh quality and computational time.
- Layering—computational mesh collapses or is generated layer by layer. This method is the fastest and it is advantageous because of mesh quality, but the requirement of a hexahedral grid limits applications to simple geometries and motions (pure rotation, pure translation).
- Overset mesh [33]—multiple grids, related to background and moving components, are superimposed on each other. Overset interfaces connect fluid zones by interpolating cell data in the overlapping regions. The advantage is that a moving body mesh and a background mesh can be generated independently, with higher quality and fewer constraints than if the system was meshed all at once. However, the interpolation between grids is not conservative, so results should be examined carefully.
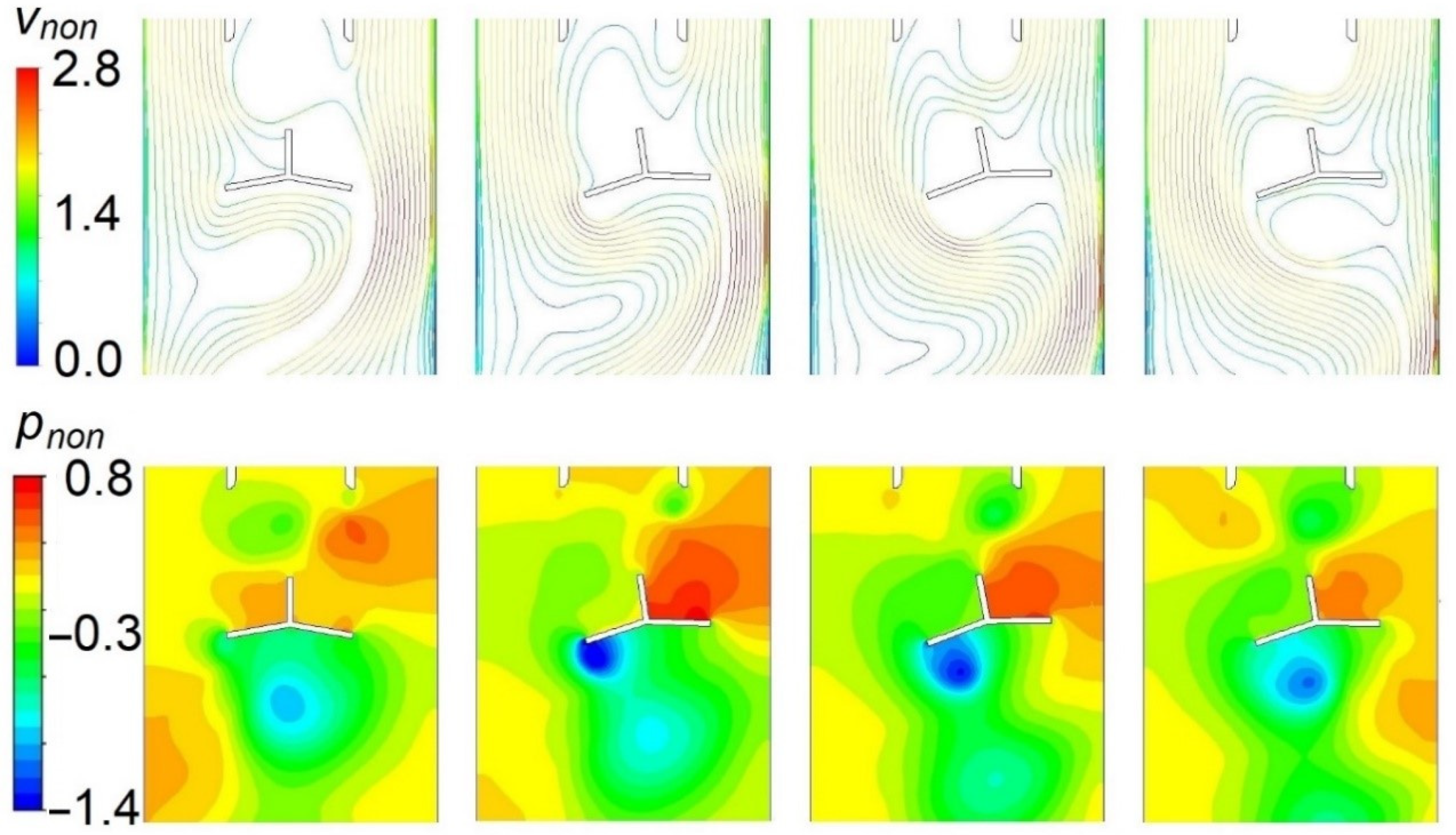
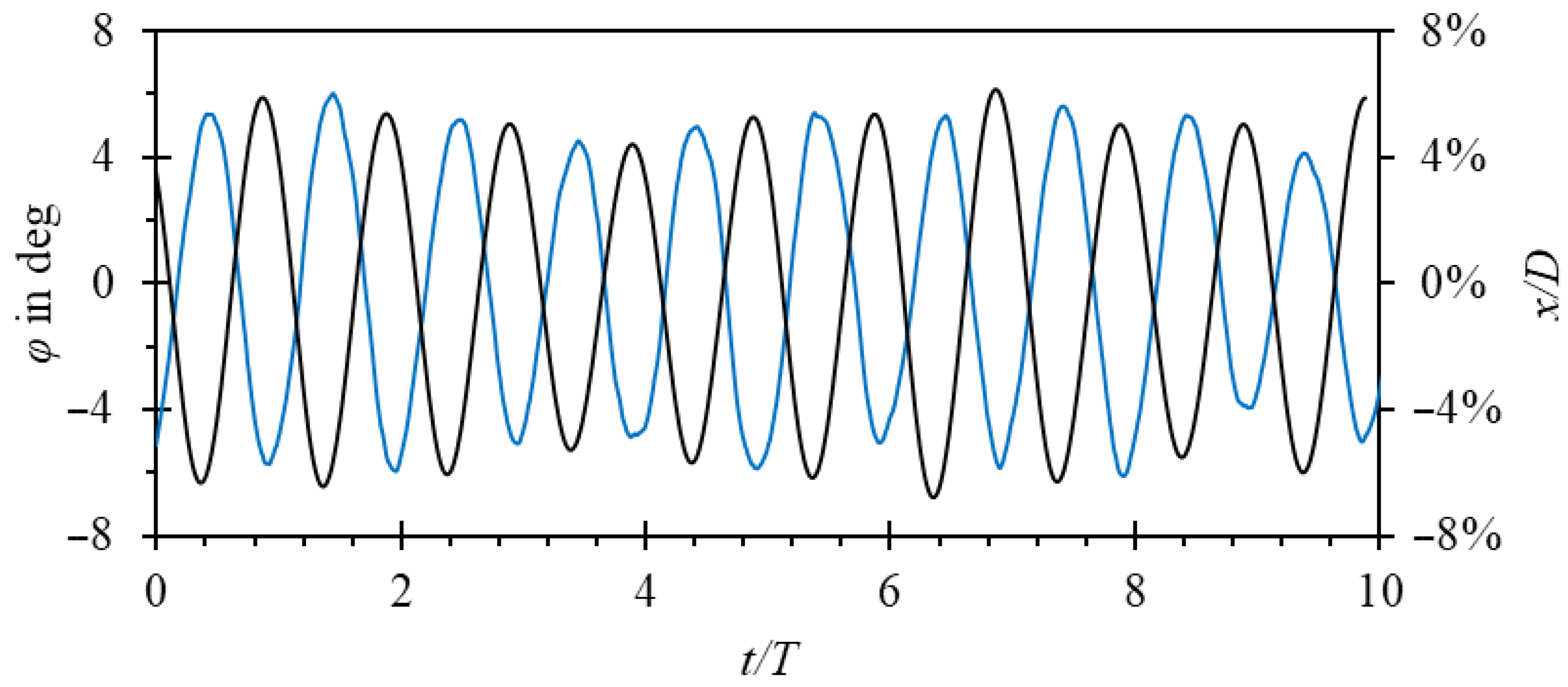
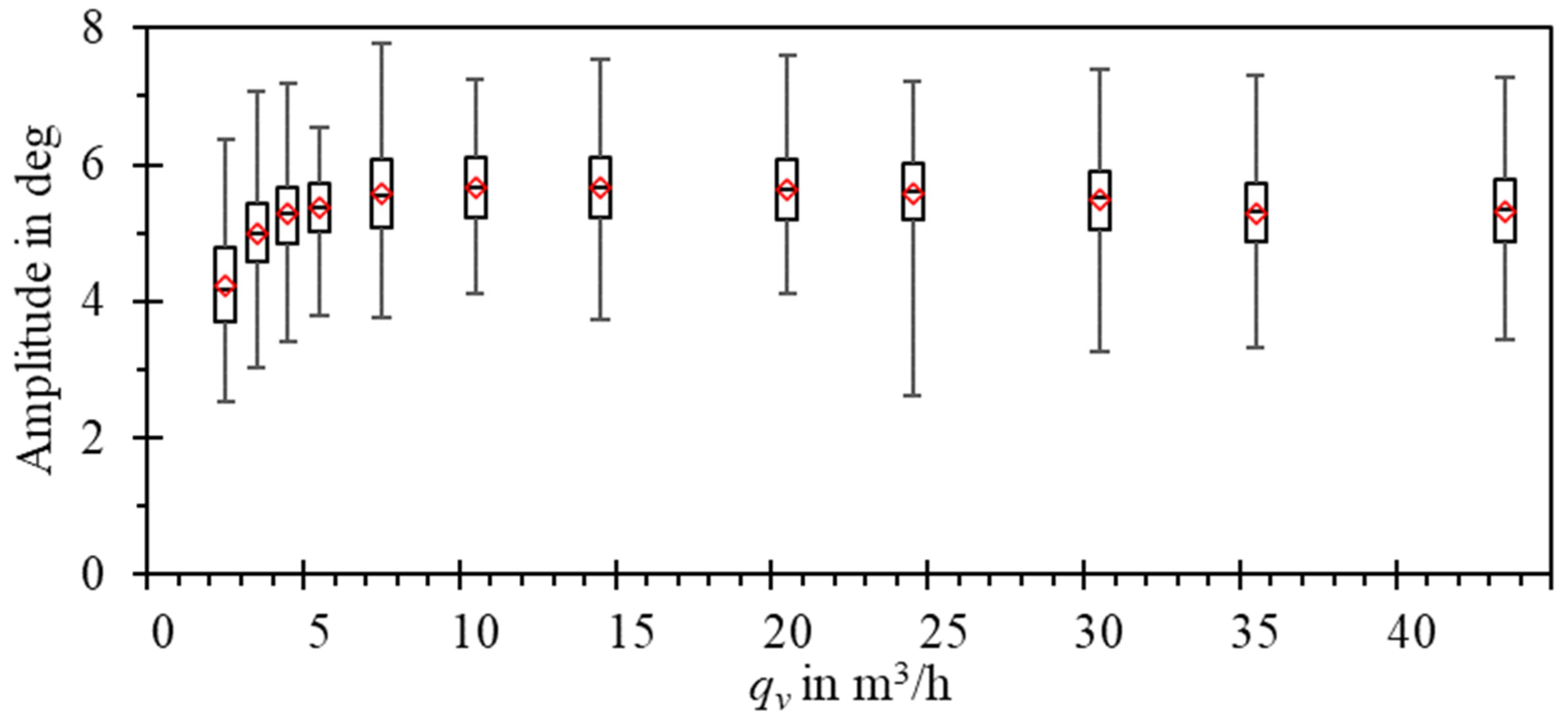
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spitzer, D.W. (Ed.) Flow Measurement: Practical Guides for Measurement and Control, 2nd ed.; Practical Guide Series; ISA: Research Triangle Park, NC, USA, 2001; ISBN 978-1-55617-736-1. [Google Scholar]
- Jiang, Z.; Li, A.; Xu, K.-J.; Xiong, W. Anti-Strong Pipeline Vibration Method Combining Frequency Variance and Amplitude Feature for Vortex Flowmeter. Measurement 2020, 166, 108193. [Google Scholar] [CrossRef]
- Sun, H.; Yang, P.; Wang, C.; Yin, W. Anti-Vibration Design and Research of Four-Wire Type Vortex Flow Meter. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Takahashi, S.; Itoh, I. Intelligent Vortex Flowmeter. In Proceedings of the International Conference of Flow Measurement FLOMEKO, Seoul, Republic of Korea, 25–29 October 1993; pp. 107–113. [Google Scholar]
- Wehrs, D.; Johnson, A. Applying Vortex Flow Metering Technology in Demanding Process Applications. In Proceedings of the International Conference on Flow Measurement, Glasgow, Scotland, May 2001. Paper 4.4. [Google Scholar]
- Miau, J.J.; Hu, C.C.; Chou, J.H. Response of a Vortex Flowmeter to Impulsive Vibrations. Flow Meas. Instrum. 2000, 11, 41–49. [Google Scholar] [CrossRef]
- Lagasse, F. Means for Measuring the Velocity and Volume of Fluids. U.S. Patent 2453376A, 9 November 1948. [Google Scholar]
- Shimomura, T. Flow Rate Measuring Instrument. U.S. Patent 12497080A, 6 March 1980. [Google Scholar]
- Waugh, C. Oscillating Vane Flowmeter. U.S. Patent US3273389A, 20 September 1966. [Google Scholar]
- Bahrton, P.S. Oscillating Vane Flowmeter. U.S. Patent 4409851A, 18 October 1983. [Google Scholar]
- Badger Meter. Europe LS-8904-HPV Catalog; Badger Meter: Stuttgart, Germany, 1985. [Google Scholar]
- DeCarlo, J.P. Oscillating Wing Flowmeter. U.S. Patent 4092859A, 6 June 1978. [Google Scholar]
- DeCarlo, J.P. Oscillating Wing Flowmeter: A New Concept in Large Line Size Gas Flow Measurement. ISA Trans. 1982, 21, 2. [Google Scholar]
- Bohac, Z. Flowmeter for Liquids. CS Patent 201360B1, 28 November 1980. [Google Scholar]
- Boszniak, L.L.; Słowskij, W.M. Raschodomier Dla Żikdostiej i Gazow. SU Patent 523282A1, 30 July 1976. [Google Scholar]
- Mahulikar, S.P.; Sane, S. Theoretical Analysis of Experimentally Observed Perplexing Calibration Characteristics of Ball-in-Vortex. J. Fluids Eng. 2005, 127, 1021–1028. [Google Scholar] [CrossRef]
- Lutz, K. Der Neuartige Schwingkörper—Durchflußmesser Rotaflux. CZ-Chem.-Tech. 1973, 7, 286–289. [Google Scholar]
- Heckle, M. Ein Neues Durchflussmessverfahren Mit Frequenzausgang. Messtechnik 1971, 9, 207–214. [Google Scholar]
- Heckle, M. Ein Neues Digitales Verfahren Zur Durchflußmessung. Chem. Ing. Tech. 1973, 45, 402–407. [Google Scholar] [CrossRef]
- Heckle, M. Method and Apparatus for Measuring the Flow Rate of Fluids Such as Gases or Liquids. U.S. Patent 3824855A, 23 July 1974. [Google Scholar]
- Turkowski, M. Progress towards the Optimisation of a Mechanical Oscillator Flowmeter. Flow Meas. Instrum. 2003, 14, 13–21. [Google Scholar] [CrossRef]
- Turkowski, M. Influence of Fluid Properties on the Characteristics of a Mechanical Oscillator Flowmeter. Measurement 2004, 35, 11–18. [Google Scholar] [CrossRef]
- Szudarek, M.; Turkowski, M. Experimental Study of a Lock-in Phenomenon in the Case of a Mechanical Oscillator Flowmeter. Mechanik 2020, 93, 13–15. [Google Scholar] [CrossRef]
- Szudarek, M.; Turkowski, M.; Twaróg, G. Test Stand for Studying Flow. In Mechatronics 2019: Recent Advances Towards Industry 4.0; Szewczyk, R., Krejsa, J., Nowicki, M., Ostaszewska-Liżewska, A., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2020; Volume 1044, pp. 157–163. ISBN 978-3-030-29992-7. [Google Scholar]
- Turkowski, M. Simple Installation for Measurement of Two-Phase Gas–Liquid Flow by Means of Conventional Single-Phase Flowmeters. Flow Meas. Instrum. 2004, 15, 295–299. [Google Scholar] [CrossRef]
- Baker, R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications, 2nd ed.; Cambridge University Press: New York, NY, USA, 2016; ISBN 978-1-107-04586-6. [Google Scholar]
- ISO 5167-1:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 1: General Principles and Requirements. International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 5167-2:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 2: Orifice Plates. International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 5167-3:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 3: Nozzles and Venturi Nozzles. International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 5167-4:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 4: Venturi Tubes. International Organization for Standardization: Geneva, Switzerland, 2003.
- Golijanek-Jędrzejczyk, A.; Mrowiec, A.; Kleszcz, S.; Hanus, R.; Zych, M.; Jaszczur, M. A Numerical and Experimental Analysis of Multi-Hole Orifice in Turbulent Flow. Measurement 2022, 193, 110910. [Google Scholar] [CrossRef]
- Turkowski, M. Optymalizacja Właściwości Metrologicznych Oraz Rozwiązań Konstrukcyjno-Technologicznych Przepływomierzy z Oscylatorem Mechanicznym; OWPW: Warszawa, Poland, 2003; ISBN 0137-2335. [Google Scholar]
- Steger, J.L.; Dougherty, F.C.; Benek, J.A. A Chimera Grid Scheme. [Multiple Overset Body-Conforming Mesh System for Finite Difference Adaptation to Complex Aircraft Configurations]. In Advances in Grid Generation, Proceedings of the Applied Mechanics, Bioengineering, and Fluids Engineering Conference, Houston, TX, USA, 20–22 June 1983; American Society of Mechanical Engineers: New York, NY, USA, 1983; pp. 59–69. [Google Scholar]

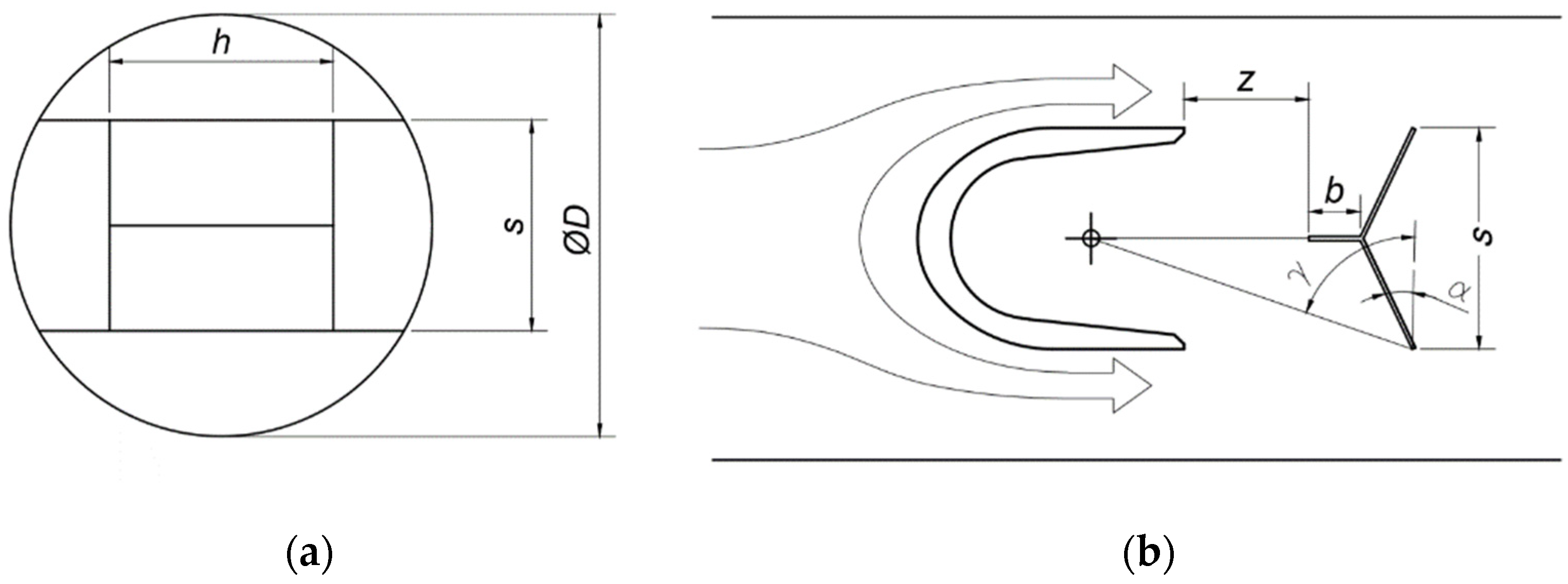









| Geometry | Mass Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| D | s/D | α | γ | b/D | z/D | h/D | Material | Mass m | Moment of Inertia Io |
| 50 mm | 43.3% | 10° | 70.1° | 15% | 20% | 78% | austenitic steel | 17,352 g | 1.06 × 10−5 kg·m2 |
| Quantity | Unit | Value xi | u(xi) | Probability Distribution | Sensitivity Coefficient c(xi) | c(xi)·u(xi) in Pulse/dm3 | % of Total |
|---|---|---|---|---|---|---|---|
| n | pulse | 10,060 | 0.41 | triangular | 0.001 | 0.00041 | 3% |
| V | dm3 | 1000 | 0.25 | normal | −0.01 | −0.0025 | 97% |
| K | pulse/dm3 | 10,060 | 0.0025 | 100% |
| Domain Size Downstream in Nominal Diameters | Shift in Oscillation Frequency Related to the Largest Domain |
|---|---|
| 0.5 | 1.60% |
| 1 | −0.13% |
| 2 | 0.06% |
| 3 | 0.00% |
| 6 | reference |
| Grid Number | Representative Cell Size in mm | Element Count 2D Model | Element Count 3D Model |
|---|---|---|---|
| G1 | 1.2 | - | 3.8·106 |
| G2 | 0.9 | 3.3·104 | 5.9·106 |
| G3 | 0.7 | 4.7·104 | 8.0·106 |
| G4 | 0.5 | 8.0·104 | 1.1·107 |
| G5 | 0.4 | 1.2·105 | - |
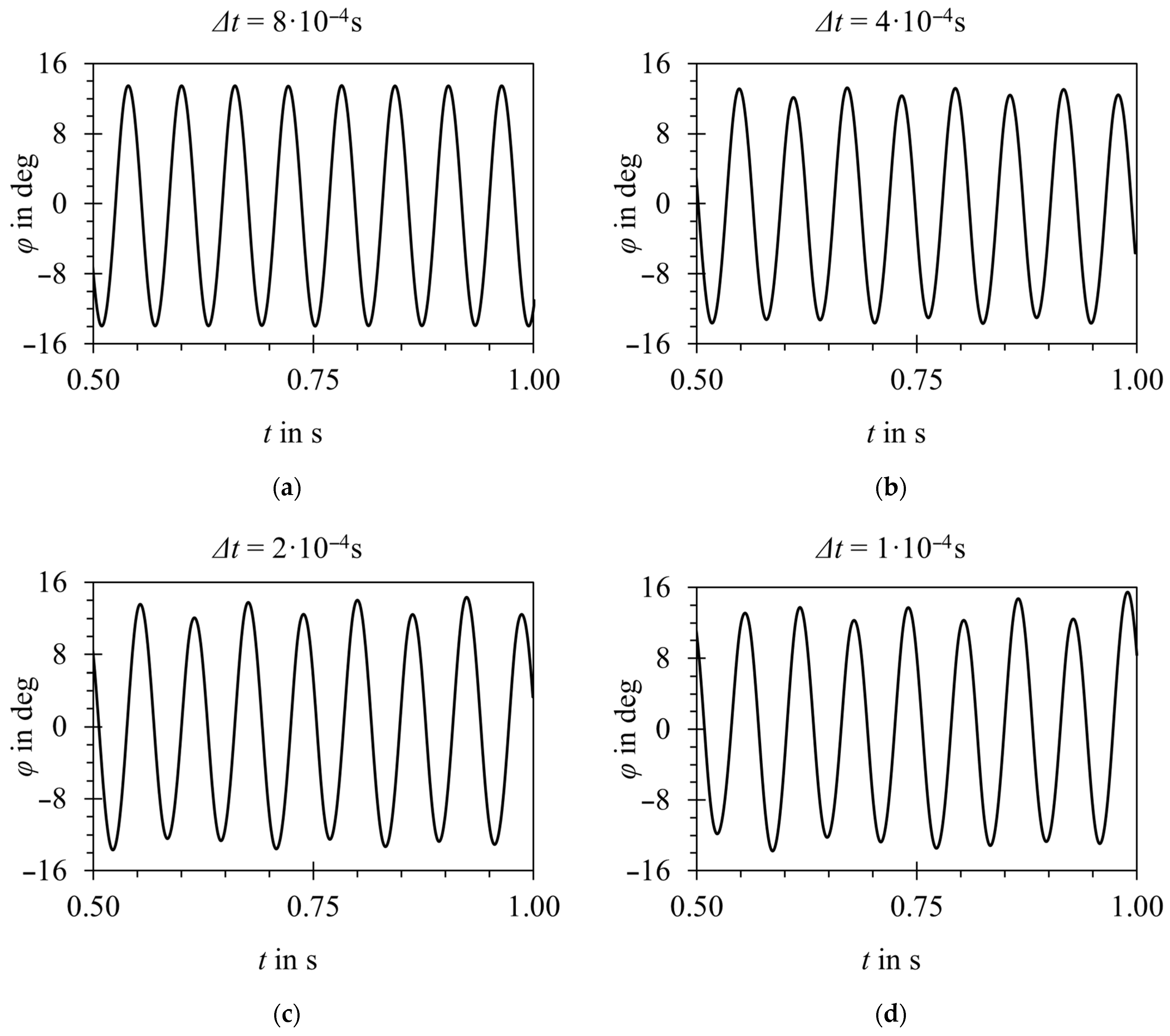
| Overset Mesh, 1st Order Time Discretization | Layering, 1st Order Time Discretization | Layering, 2nd Order Time Discretization | ||||||
|---|---|---|---|---|---|---|---|---|
| Δt in s | Time Steps per Oscillation Cycle | Mean CFL | in deg | f in Hz | in deg | f in Hz | in deg | f in Hz |
| 8 × 10−4 | 75 | 2.4 | 13.7 | 16.63 | - | - | - | - |
| 4 × 10−4 | 153 | 1.2 | 13.0 | 16.38 | 12.9 | 16.25 | 13.6 | 16.26 |
| 2 × 10−4 | 308 | 0.6 | 12.9 | 16.24 | 13.6 | 16.26 | 12.7 | 16.24 |
| 1 × 10−4 | 617 | 0.3 | 13.1 | 16.22 | 12.9 | 16.26 | 12.9 | 16.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szudarek, M.; Turkowski, M.; Piechna, A. CFD Model of a Mechanical Oscillator Flowmeter. Sensors 2023, 23, 116. https://doi.org/10.3390/s23010116
Szudarek M, Turkowski M, Piechna A. CFD Model of a Mechanical Oscillator Flowmeter. Sensors. 2023; 23(1):116. https://doi.org/10.3390/s23010116
Chicago/Turabian StyleSzudarek, Maciej, Mateusz Turkowski, and Adam Piechna. 2023. "CFD Model of a Mechanical Oscillator Flowmeter" Sensors 23, no. 1: 116. https://doi.org/10.3390/s23010116
APA StyleSzudarek, M., Turkowski, M., & Piechna, A. (2023). CFD Model of a Mechanical Oscillator Flowmeter. Sensors, 23(1), 116. https://doi.org/10.3390/s23010116







