Evaluation of Full-Duplex SWIPT Cooperative NOMA-Based IoT Relay Networks over Nakagami-m Fading Channels
Abstract
:1. Introduction
- First, we propose an FD SWIPT cooperative NOMA-based IoT relay system with pSIC and iSIC, where one master IoT node acts as an FD DF relay to enhance a cell-edge user’s performance. Specifically, to help a source node simultaneously communicate with a cell-edge user, the relay performs pairing of the received signal of a cell-edge user with an IoT user via the NOMA protocol. At the cell-edge user, a selection combining (SC) (the SC technique has been widely used for cell-edge users in the literature for improving wireless system performance. This is because it has the lowest implementation compared to maximal ratio combing (MRC) and equal-gain combining (EGC), which are required for full knowledge of the channel state information [33,34]) technique is employed to improve performance. We also consider two scenarios with a direct and a non-direct link between the source node and cell-edge user.
- Secondly, we analyze the performance analysis of the proposed system in terms of the OP, system throughput, EE, and ergodic capacity. Exact closed-form analytical expressions and approximate expressions for the OP, system throughput, EE, and ergodic capacity are derived accordingly. To reveal useful insights into the proposed system, the asymptotic expression for the system throughput is also given.
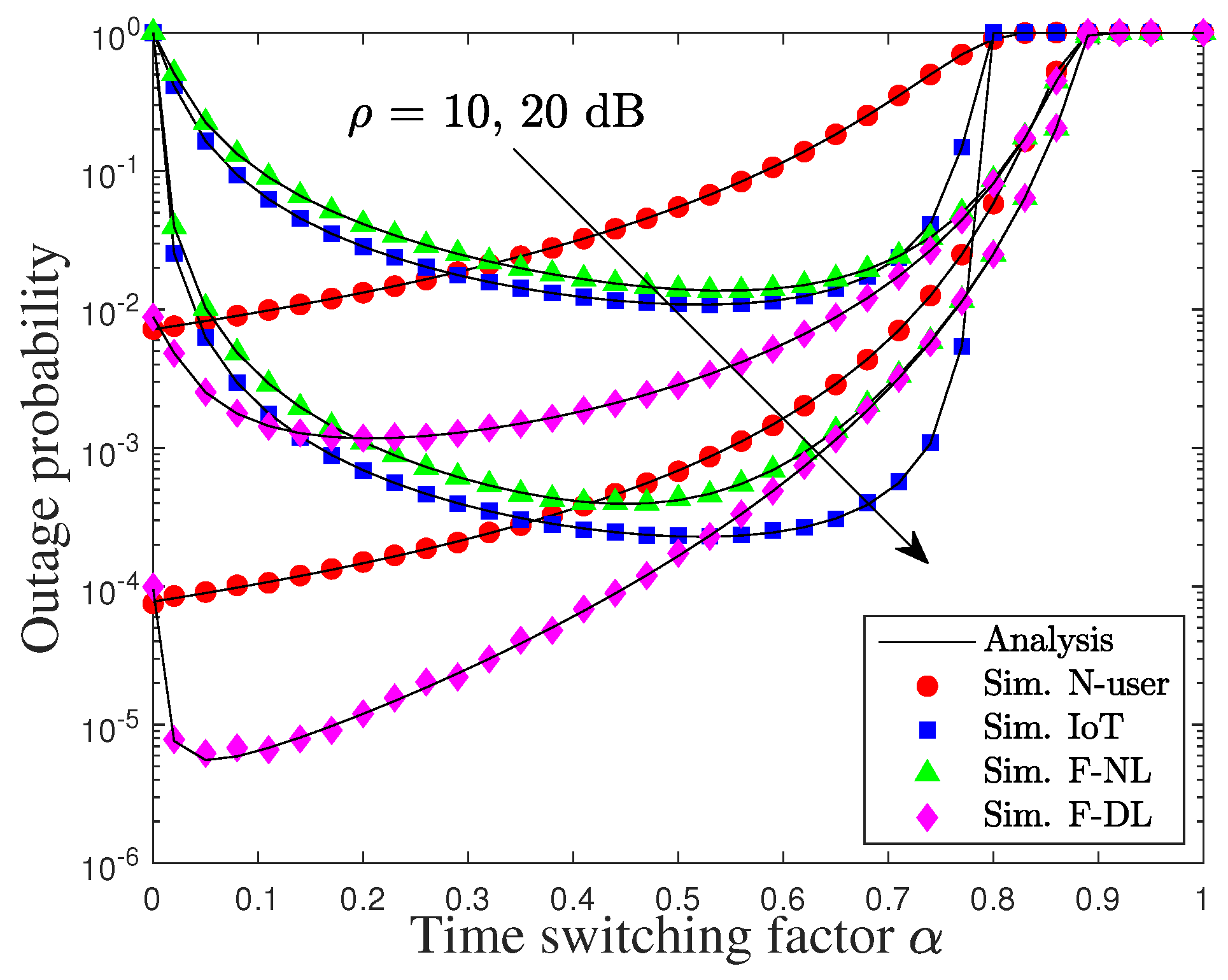
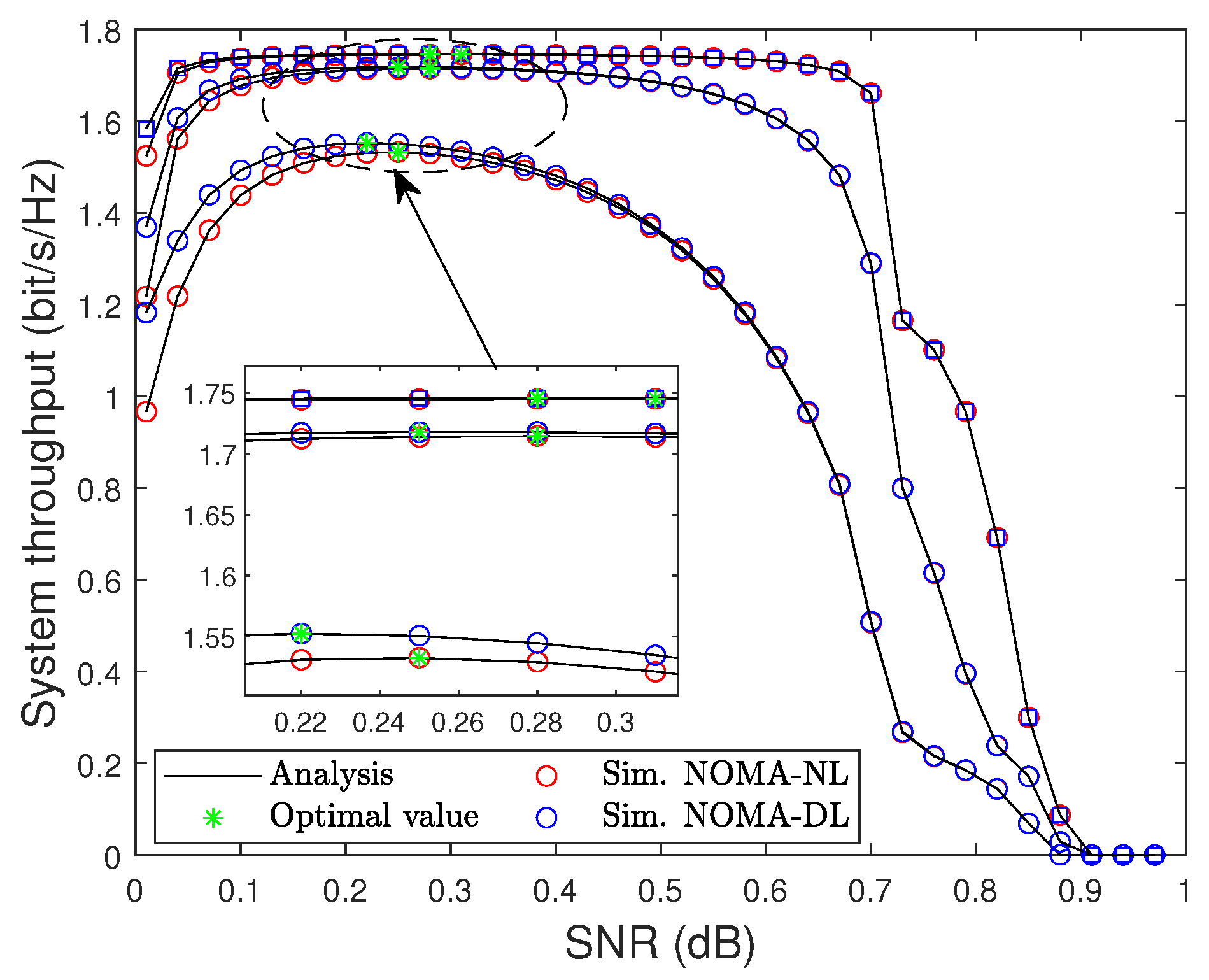
- Thirdly, we propose a low complexity algorithm to find the optimal TS factor that guarantees maximal system throughput. By performing our proposed algorithm, the system throughput can be vastly improved.
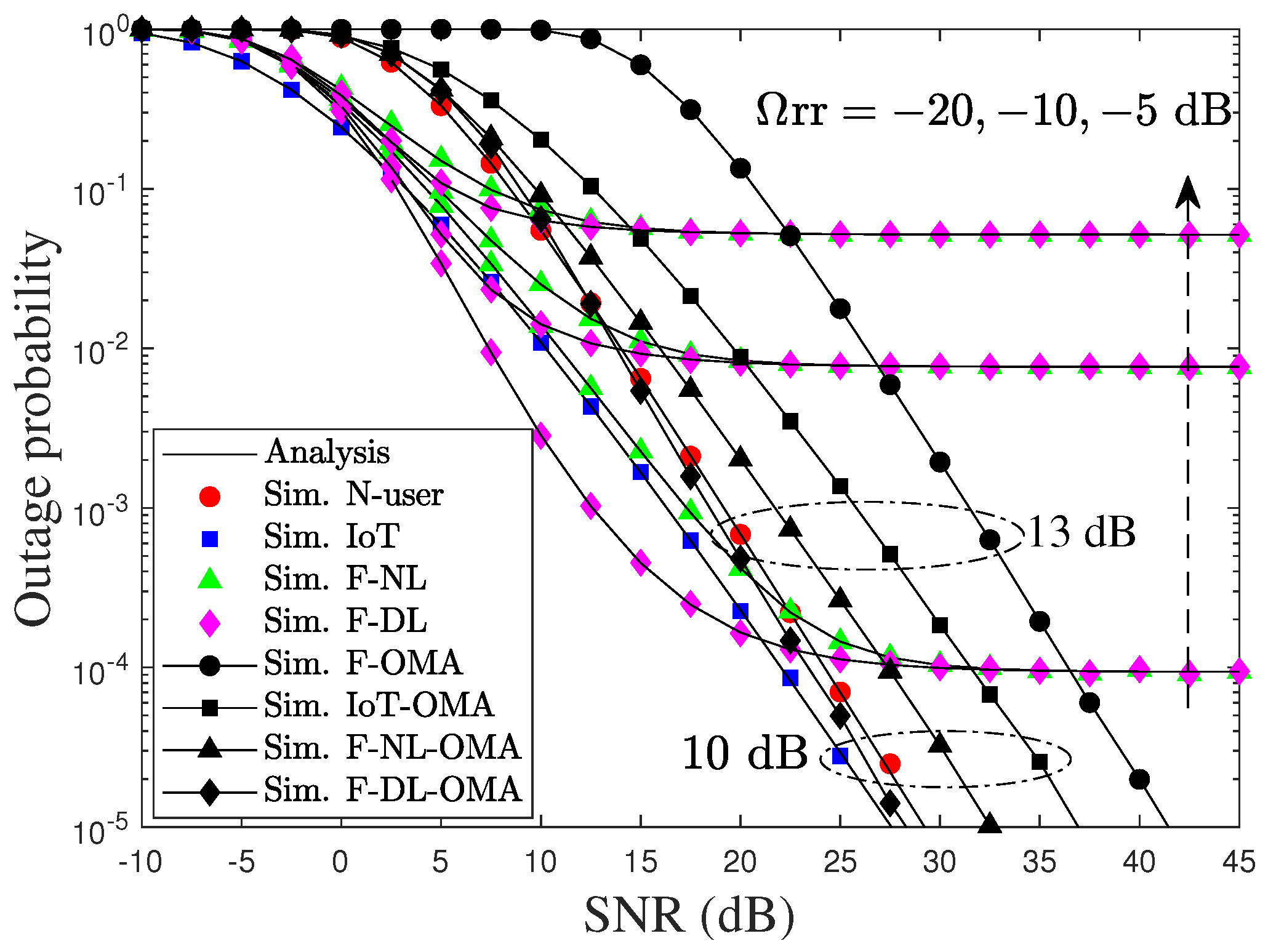
- Finally, we show through numerical results that our proposed system always outperforms its orthogonal multiple access (OMA) counterpart in terms of the OP, system throughput, and ergodic sum capacity under pSIC and achieves better performance for a low to medium signal-to-noise ratio (SNR). Furthermore, the system performance of the cell-edge user is significantly enhanced in the direct link scenario using SC compared to the non-direct link scenario when the residual SI caused by the iSIC process increases to larger than 40%.
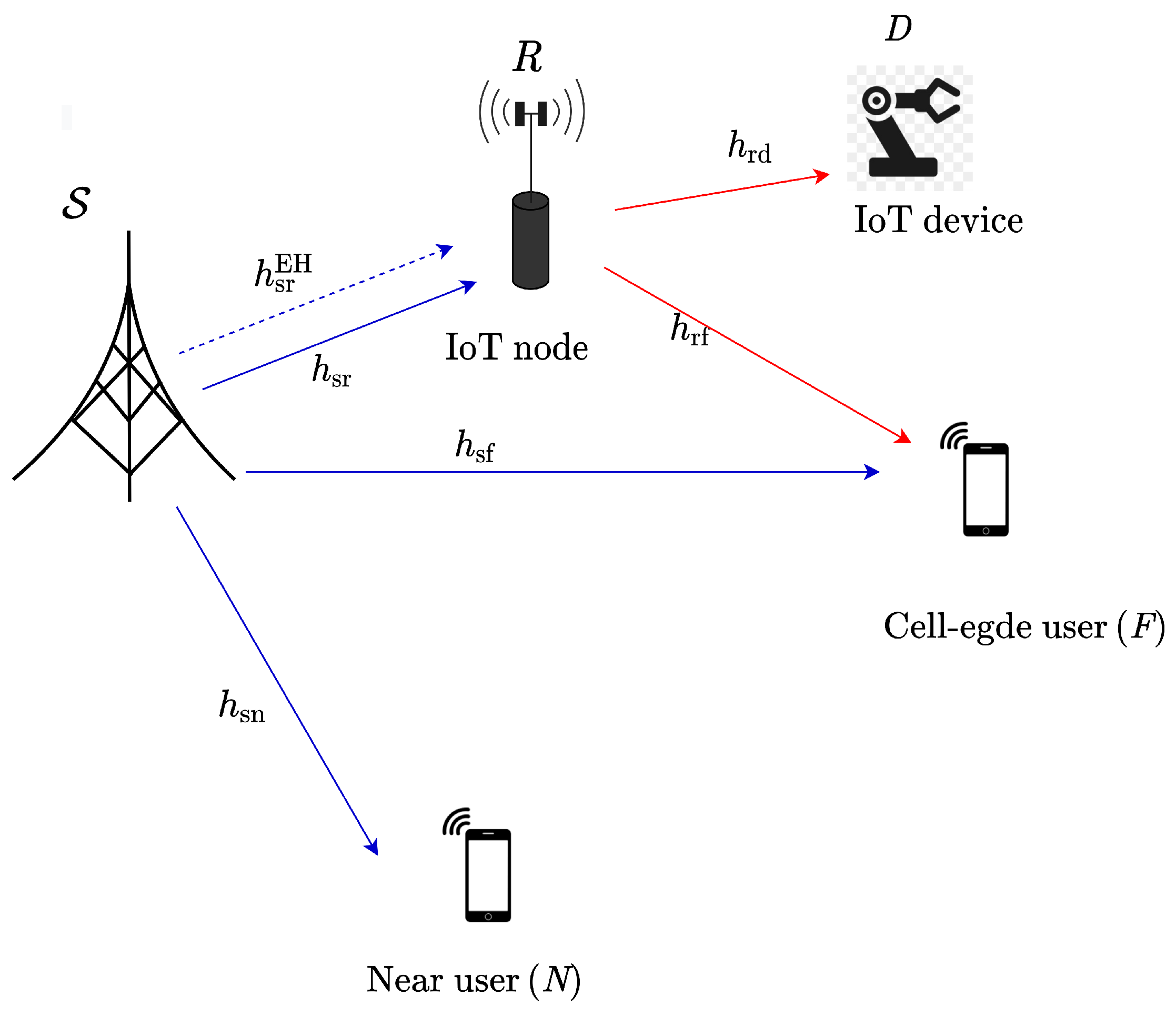
2. System Model
2.1. Channel Model
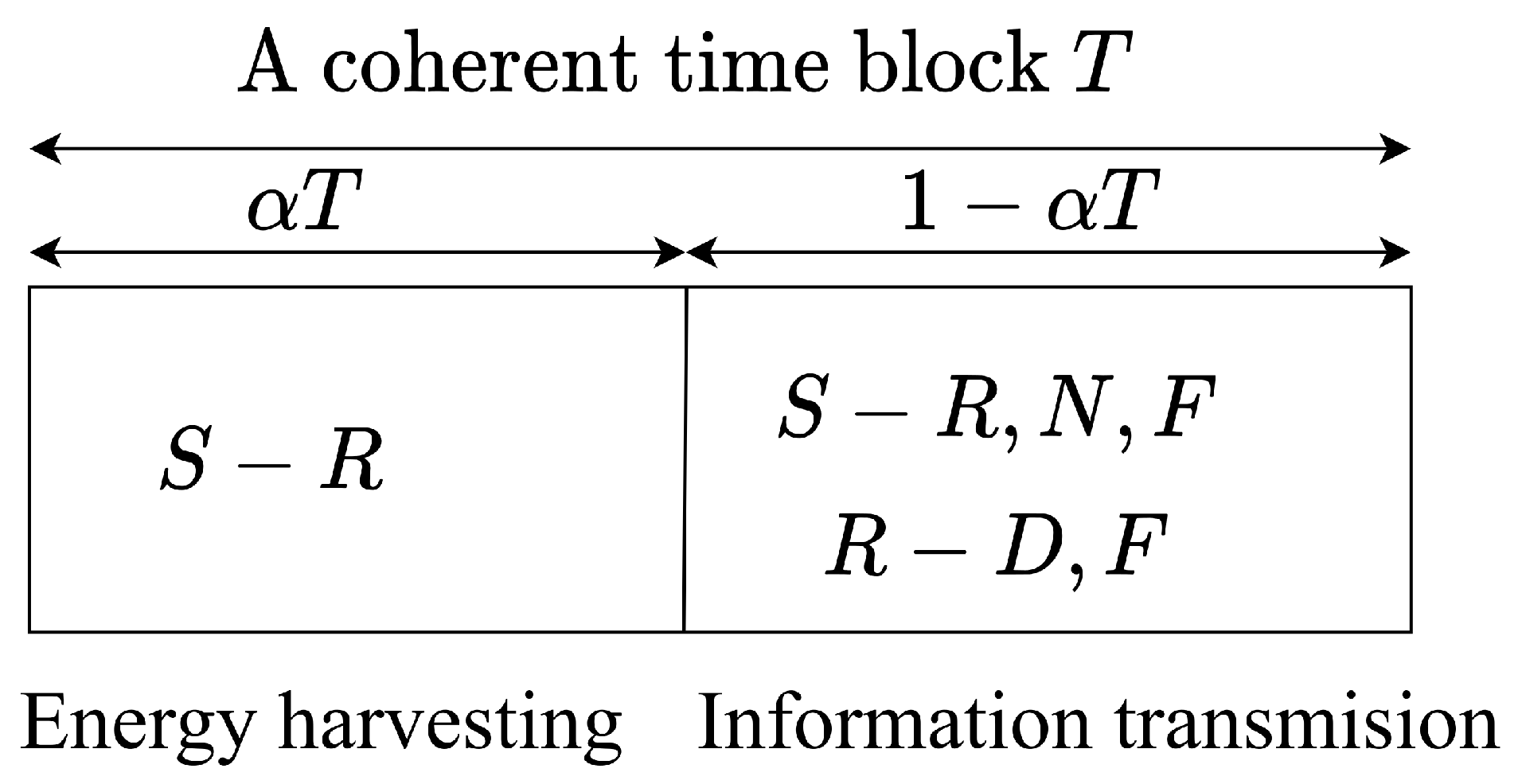
2.2. Energy Harvesting (EH) and Data Transmission Processes
3. Performance Analysis
3.1. Outage Probability (OP)
3.1.1. OP of Cell-Center User
3.1.2. OP of IoT User
3.1.3. OP of Cell-Edge User
3.2. System Throughput
3.3. Average Energy Efficiency (EE)
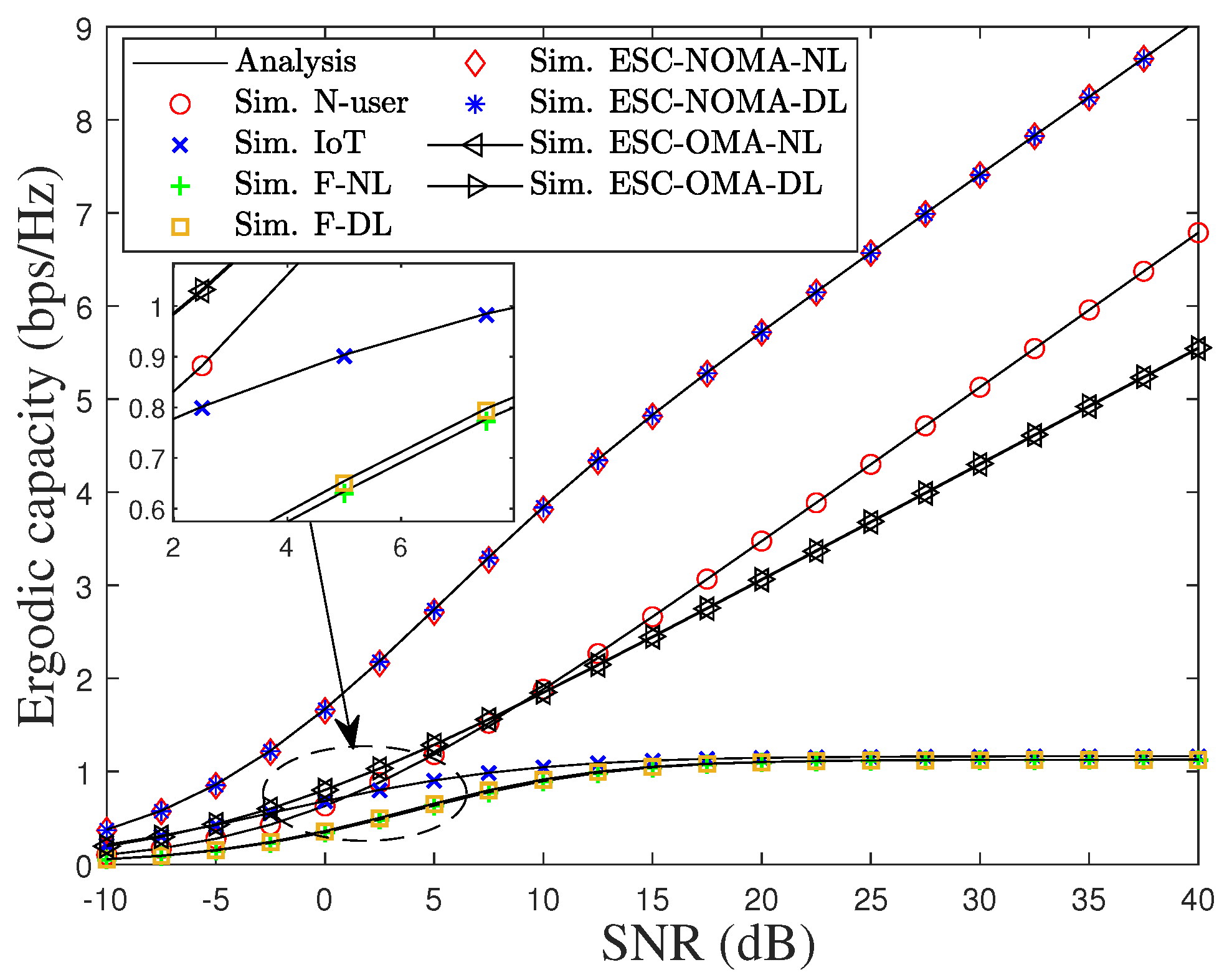
3.4. Ergodic Sum Capacity (ESC)
3.4.1. EC of Cell-Center User
3.4.2. EC of IoT User
3.4.3. EC of Cell-Edge User
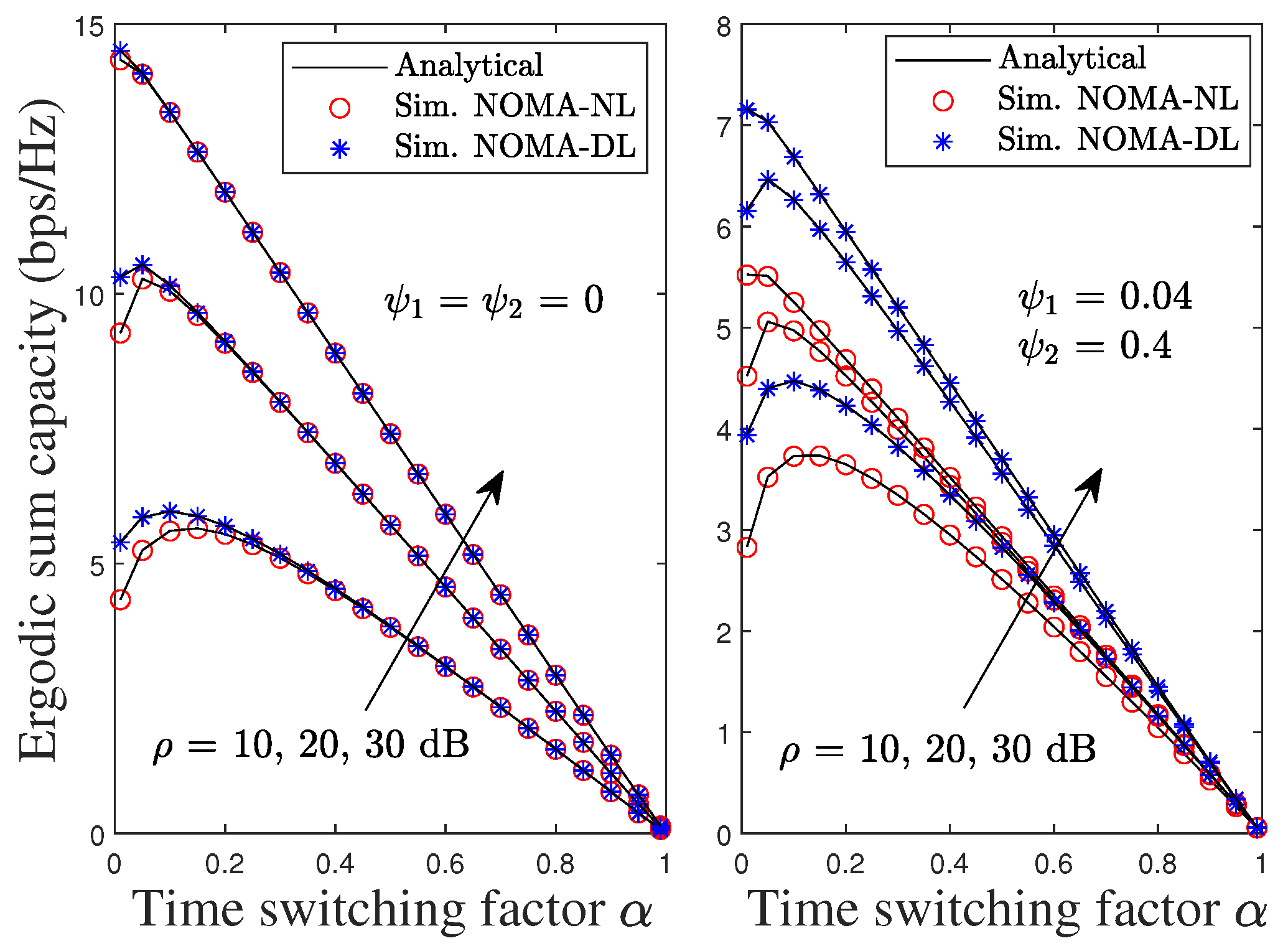
3.5. Optimal Solution for the Time-Switching Factor
| Algorithm 1 Optimal TS factor to maximize the system throughput. |
|
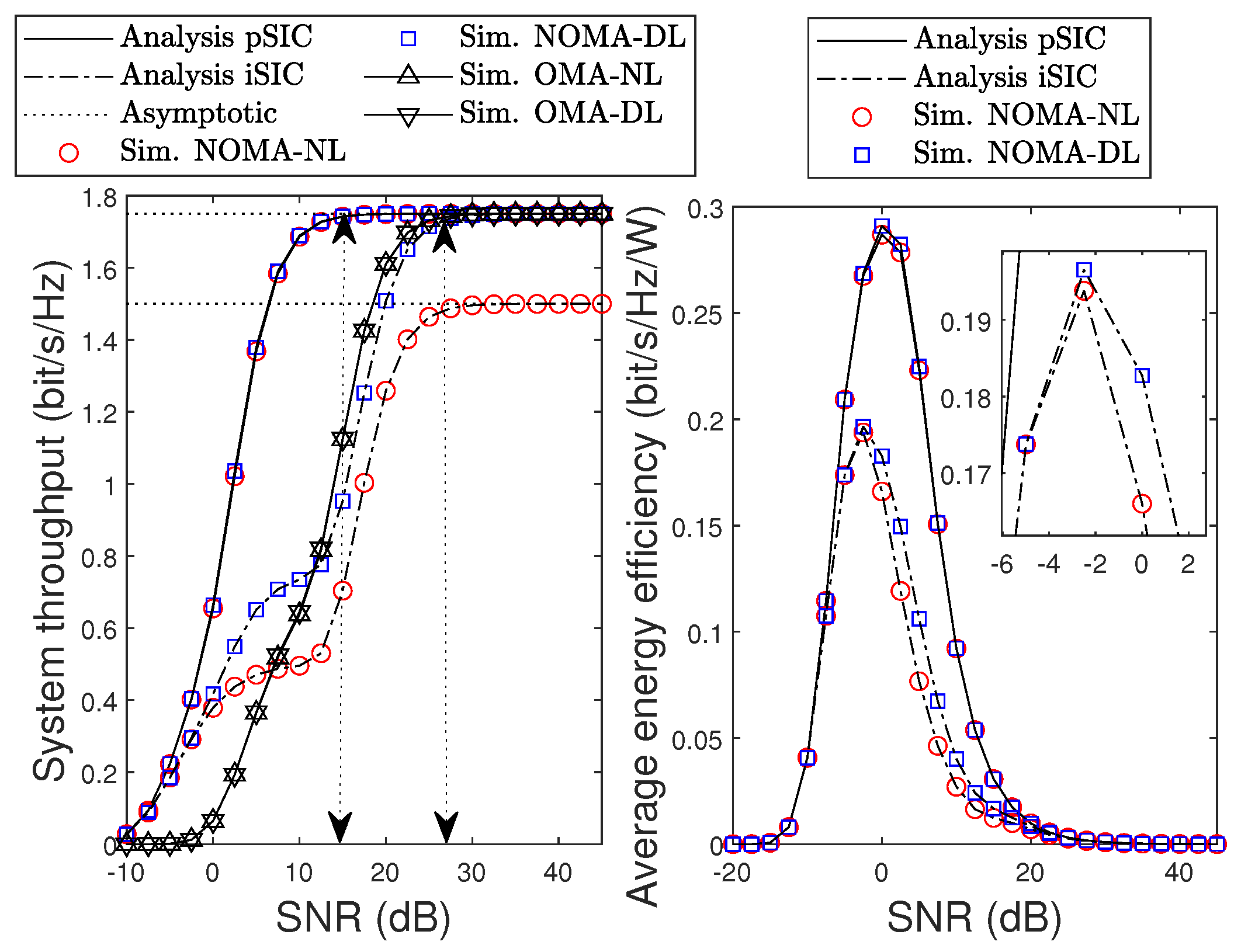
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of (27)
Appendix B. Proof of (29) and (31)
Appendix C. Proof of (39) and (40)
References
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE Internet Things J. 2020, 7, 16–32. [Google Scholar] [CrossRef]
- de Almeida, I.B.F.; Mendes, L.L.; Rodrigues, J.J.P.C.; da Cruz, M.A.A. 5G waveforms for IoT applications. IEEE Commun. Surv. Tutor. 2019, 21, 2554–2567. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; de Cola, T.; Wang, J.B.; Zhu, W.P.; Cheng, J. Supporting IoT with Rate-Splitting Multiple Access in Satellite and Aerial-Integrated Networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A survey of non-orthogonal multiple access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.T.; Nguyen, V.D.; Lee, J.H.; Kim, Y.H. Sum Rate Maximization for Multi-User Wireless Powered IoT Network with Non-Linear Energy Harvester: Time and Power Allocation. IEEE Access 2019, 7, 149698–149710. [Google Scholar] [CrossRef]
- Zhai, D.; Zhang, R.; Du, J.; Ding, Z.; Yu, F.R. Simultaneous Wireless Information and Power Transfer at 5G New Frequencies: Channel Measurement and Network Design. IEEE J. Sel. Areas Commun. 2019, 37, 171–186. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pham, Q.V.; Nguyen, V.D.; Lee, J.H.; Kim, Y.H. Resource Allocation for Energy Efficiency in OFDMA-Enabled WPCN. IEEE Wirel. Commun. Lett. 2020, 9, 2049–2053. [Google Scholar] [CrossRef]
- Pang, L.; Zhao, H.; Zhang, Y.; Chen, Y.; Lu, Z.; Wang, A.; Li, J. Energy-Efficient Resource Optimization for Hybrid Energy Harvesting Massive MIMO Systems. IEEE Syst. J. 2021. Early Access. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Zhu, W.P.; Wang, J.B.; Cheng, J. Robust Secure Beamforming for Wireless Powered Cognitive Satellite-Terrestrial Networks. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 567–580. [Google Scholar] [CrossRef]
- Cui, J.; Khan, M.B.; Deng, Y.; Ding, Z.; NaIlanathan, A. Unsupervised Learning Approaches for User Clustering in NOMA enabled Aerial SWIPT Networks. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, R.; Xiong, K.; Yang, H.C.; Cao, J.; Zhong, Z.; Ai, B. Coverage Performance of UAV-Assisted SWIPT Networks with Directional Antennas. IEEE Internet Things J. 2021. Early Access. [Google Scholar] [CrossRef]
- Niu, H.; Chu, Z.; Zhou, F.; Zhu, Z.; Zhen, L.; Wong, K.K. Robust Design for Intelligent Reflecting Surface Assisted Secrecy SWIPT Network. IEEE Trans. Wirel. Commun. 2021. Early Access. [Google Scholar] [CrossRef]
- Van Nguyen, B.; Vu, Q.D.; Kim, K. Analysis and optimization for weighted sum rate in energy harvesting cooperative NOMA systems. IEEE Trans. Veh. Technol. 2018, 67, 12379–12383. [Google Scholar] [CrossRef]
- Zaidi, S.K.; Hasan, S.F.; Gui, X. Evaluating the Ergodic Rate in SWIPT-Aided Hybrid NOMA. IEEE Commun. Lett. 2018, 22, 1870–1873. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Nguyen, V.D.; da Costa, D.B.; An, B. Hybrid User Pairing for Spectral and Energy Efficiencies in Multiuser MISO-NOMA Networks with SWIPT. IEEE Trans. Commun. 2020, 68, 4874–4890. [Google Scholar] [CrossRef]
- Rauniyar, A.; Engelstad, P.E.; Østerbø, O.N. On the Performance of Bidirectional NOMA-SWIPT Enabled IoT Relay Networks. IEEE Sens. J. 2021, 21, 2299–2315. [Google Scholar] [CrossRef]
- Qi, Q.; Chen, X. Wireless Powered Massive Access for Cellular Internet of Things with Imperfect SIC and Nonlinear EH. IEEE Internet Things J. 2019, 6, 3110–3120. [Google Scholar] [CrossRef]
- Li, G.; Mishra, D.; Hu, Y.; Atapattu, S. Optimal Designs for Relay-Assisted NOMA Networks with Hybrid SWIPT Scheme. IEEE Trans. Commun. 2020, 68, 3588–3601. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.V.; Vu, T.H.; da Costa, D.B.; Ho, C.D. IoT-Based Coordinated Direct and Relay Transmission with Non-Orthogonal Multiple Access. IEEE Wirel. Commun. Lett. 2021, 10, 503–507. [Google Scholar] [CrossRef]
- Rauniyar, A.; Engelstad, P.E.; Østerbø, O.N. Performance Analysis of RF Energy Harvesting and Information Transmission Based on NOMA with Interfering Signal for IoT Relay Systems. IEEE Sens. J. 2019, 19, 7668–7682. [Google Scholar] [CrossRef] [Green Version]
- Salem, A.; Musavian, L. NOMA in Cooperative Communication Systems with Energy-Harvesting Nodes and Wireless Secure Transmission. IEEE Trans. Wirel. Commun. 2021, 20, 1023–1037. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-Duplex Device-to-Device-Aided Cooperative Non-orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2017, 66, 4467–4471. [Google Scholar] [CrossRef]
- Xu, B.; Xiang, Z.; Ren, P.; Guo, X. Outage Performance of Downlink Full-Duplex Network-Coded Cooperative NOMA. IEEE Wirel. Commun. Lett. 2021, 10, 26–29. [Google Scholar] [CrossRef]
- Guo, C.; Zhao, L.; Feng, C.; Ding, Z.; Chen, H. Energy Harvesting Enabled NOMA Systems with Full-Duplex Relaying. IEEE Trans. Veh. Technol. 2019, 68, 7179–7183. [Google Scholar] [CrossRef] [Green Version]
- Alsaba, Y.; Leow, C.Y.; Rahim, S.K.A. Full-Duplex Cooperative Non-Orthogonal Multiple Access with Beamforming and Energy Harvesting. IEEE Access 2018, 6, 19726–19738. [Google Scholar] [CrossRef]
- Hakimi, A.; Mohammadi, M.; Mobini, Z.; Ding, Z. Full-Duplex Non-Orthogonal Multiple Access Cooperative Spectrum-Sharing Networks with Non-Linear Energy Harvesting. IEEE Trans. Veh. Technol. 2020, 69, 10925–10936. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, K.; Lu, Y.; Fan, P.; Zhong, Z.; Letaief, K.B. SWIPT-Enabled Full-Duplex NOMA Networks with Full and Partial CSI. IEEE Trans. Green Commun. Netw. 2020, 4, 804–818. [Google Scholar] [CrossRef]
- Agrawal, K.; Flanagan, M.F.; Prakriya, S. NOMA with Battery-Assisted Energy Harvesting Full-Duplex Relay. IEEE Trans. Veh. Technol. 2020, 69, 13952–13957. [Google Scholar] [CrossRef]
- Kurup, R.R.; Babu, A.V. Power Adaptation for Improving the Performance of Time Switching SWIPT-Based Full-Duplex Cooperative NOMA Network. IEEE Commun. Lett. 2020, 24, 2956–2960. [Google Scholar] [CrossRef]
- Aswathi, V.; Babu, A.V. Outage and Throughput Analysis of Full-Duplex Cooperative NOMA System with Energy Harvesting. IEEE Trans. Veh. Technol. 2021, 70, 11648–11664. [Google Scholar] [CrossRef]
- Men, J.; Ge, J.; Zhang, C. Performance Analysis for Downlink Relaying Aided Non-Orthogonal Multiple Access Networks with Imperfect CSI Over Nakagami-m Fading. IEEE Access 2017, 5, 998–1004. [Google Scholar] [CrossRef]
- Zanella, A.; Bazzi, A.; Masini, B.M. Relay Selection Analysis for an Opportunistic Two-Hop Multi-User System in a Poisson Field of Nodes. IEEE Trans. Wirel. Commun. 2017, 16, 1281–1293. [Google Scholar] [CrossRef]
- Bao, V.N.Q.; Kong, H.Y. Performance analysis of multi-hop decode-and-forward relaying with selection combining. J. Commun. Netw. 2010, 12, 616–623. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Selection Combining Scheme over Non-identically Distributed Fisher-Snedecor F Fading Channels. IEEE Wirel. Commun. Lett. 2021, 10, 840–843. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Do, D.T.; Nguyen, M.S.V.; Nguyen, T.N.; Li, X.; Choi, K. Enabling Multiple Power Beacons for Uplink of NOMA-Enabled Mobile Edge Computing in Wirelessly Powered IoT. IEEE Access 2020, 8, 148892–148905. [Google Scholar] [CrossRef]
- Nguyen, T.; An, B. Cognitive Multihop Wireless Powered Relaying Networks Over Nakagami-m Fading Channels. IEEE Access 2019, 7, 154600–154616. [Google Scholar] [CrossRef]
- Bharadia, D.; McMilin, E.; Katti, S. Full duplex radios. In Proceedings of the ACM SIGCOMM 2013 Conference on SIGCOMM (SIGCOMM’13), Hong Kong, China, 12–16 August 2013; pp. 375–386. [Google Scholar]
- Khafagy, M.G.; Ismail, A.; Alouini, M.; Aïssa, S. Efficient Cooperative Protocols for Full-Duplex Relaying Over Nakagami-m Fading Channels. IEEE Trans. Wirel. Commun. 2015, 14, 3456–3470. [Google Scholar] [CrossRef] [Green Version]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Bao, V.N.Q.; Van, N.T. Incremental relaying networks with energy harvesting relay selection: Performance analysis. Trans. Emerg. Telecommun. Technol. 2018, 29, e3483. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1972. [Google Scholar]






| Bandwidth | 1 MHz |
| Antenna noise power density, | −90 dBm |
| Fix target data rate, | 1 Bit/s/Hz |
| Fix target data rate of | 0.25 Bit/s/Hz |
| Fix target data rate of | 0.5 Bit/s/Hz |
| Normalized distance of | 0.5 unit |
| Normalized distance of | 1.4 unit |
| Normalized distance of | 0.8 unit |
| Normalized distance of | 0.6 unit |
| Normalized distance of | 0.5 unit |
| Path-loss exponent, | 3 |
| Path-loss at reference distance, ( = 1 M) | −30 dB |
| Fixed time switching factor, | 0.5 |
| Fixed energy conversion efficiency, | 0.8 |
| Fixed total static power consumed by circuit, | 0.5 mW |
| Power allocation factors, | 0.8 |
| Power allocation factors, | 0.8 |
| Trial number | |
| Fixed number of terms in the GCQ, N | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-T.; Nguyen, S.Q.; Nguyen, P.X.; Kim, Y.-H. Evaluation of Full-Duplex SWIPT Cooperative NOMA-Based IoT Relay Networks over Nakagami-m Fading Channels. Sensors 2022, 22, 1974. https://doi.org/10.3390/s22051974
Nguyen T-T, Nguyen SQ, Nguyen PX, Kim Y-H. Evaluation of Full-Duplex SWIPT Cooperative NOMA-Based IoT Relay Networks over Nakagami-m Fading Channels. Sensors. 2022; 22(5):1974. https://doi.org/10.3390/s22051974
Chicago/Turabian StyleNguyen, Tien-Tung, Sang Quang Nguyen, Phu X. Nguyen, and Yong-Hwa Kim. 2022. "Evaluation of Full-Duplex SWIPT Cooperative NOMA-Based IoT Relay Networks over Nakagami-m Fading Channels" Sensors 22, no. 5: 1974. https://doi.org/10.3390/s22051974
APA StyleNguyen, T.-T., Nguyen, S. Q., Nguyen, P. X., & Kim, Y.-H. (2022). Evaluation of Full-Duplex SWIPT Cooperative NOMA-Based IoT Relay Networks over Nakagami-m Fading Channels. Sensors, 22(5), 1974. https://doi.org/10.3390/s22051974






