LSO-FastSLAM: A New Algorithm to Improve the Accuracy of Localization and Mapping for Rescue Robots
Abstract
:1. Introduction
- This paper designs and implements a new scheme to optimise the FastSLAM algorithm by means of the Lion Swarm algorithm.
- In the process of optimizing the FastSLAM algorithm through the lion swarm algorithm, the distribution of the particle set after important sampling in the FastSLAM algorithm is achieved through the division of labour between different individuals in the lion swarm optimisation algorithm, so that the particles are distributed in the high likelihood region, and solving the particle weight degradation problem. In addition, to ensure particle diversity, a genetic algorithm is used instead of the lioness movement process in the lion swarm to further increase the particle diversity.
- In this paper, the innovative FastSLAM algorithm is applied to a rescue robot by optimizing the Lion Swarm algorithm, aiming to improve the localization and mapping accuracy of the rescue robot.
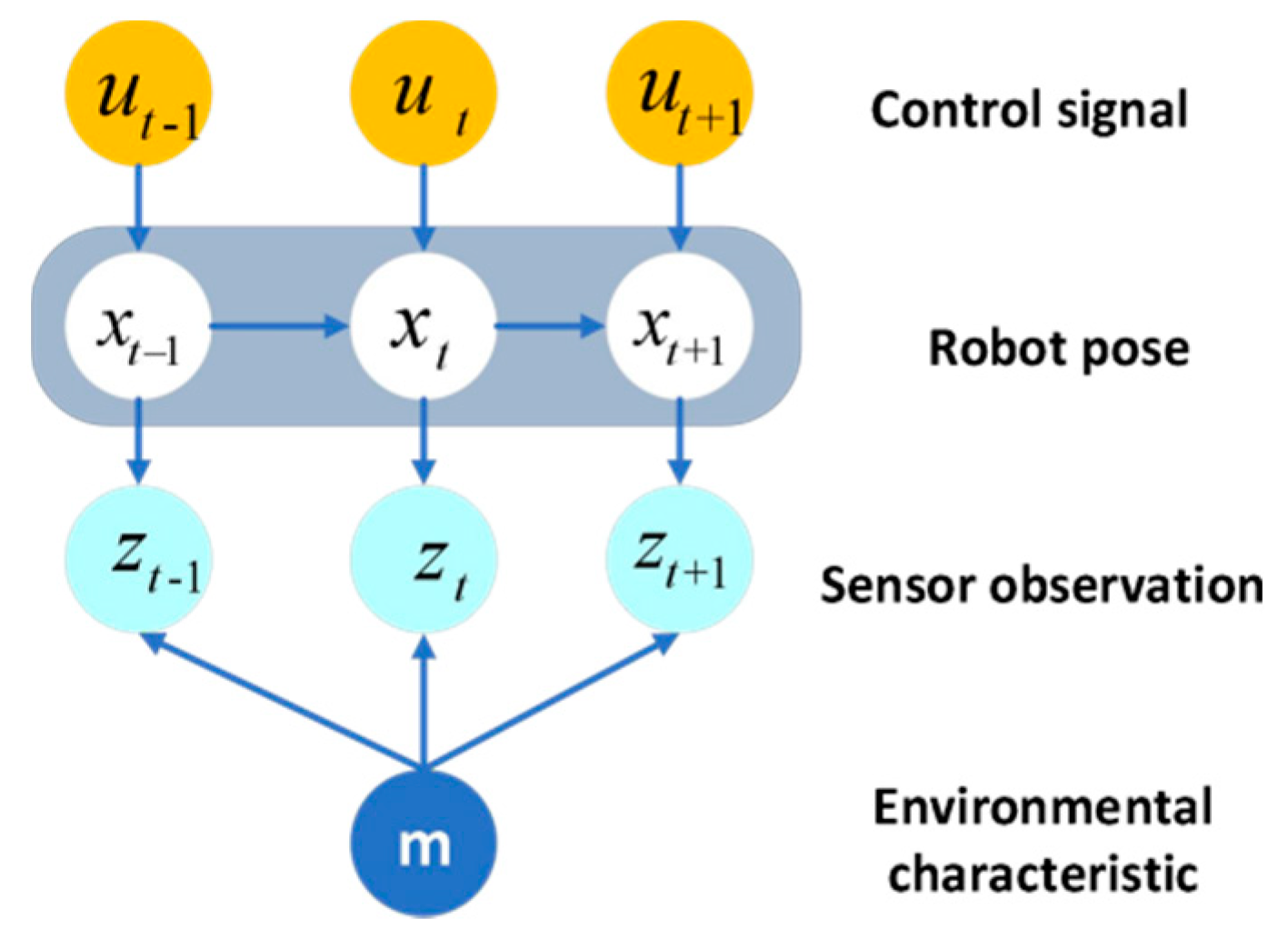
2. Background of the FastSLAM
- (1)
- Sampling the pose
- (2)
- EKF updates the observed landmark estimates.
- (3)
- Importance weight calculation:
- (4)
- Re-sampling.
- (5)
- Unknown data associations.
- (6)
- Feature management.
3. Lion Swarm Optimization Algorithm
4. Lion Swarm Optimization Algorithm Improves FastSLAM
- A.
- Improved Lion position update strategy
- B.
- Reset the Lioness Hunting Method
- C.
- Cub Follow Formula Selection
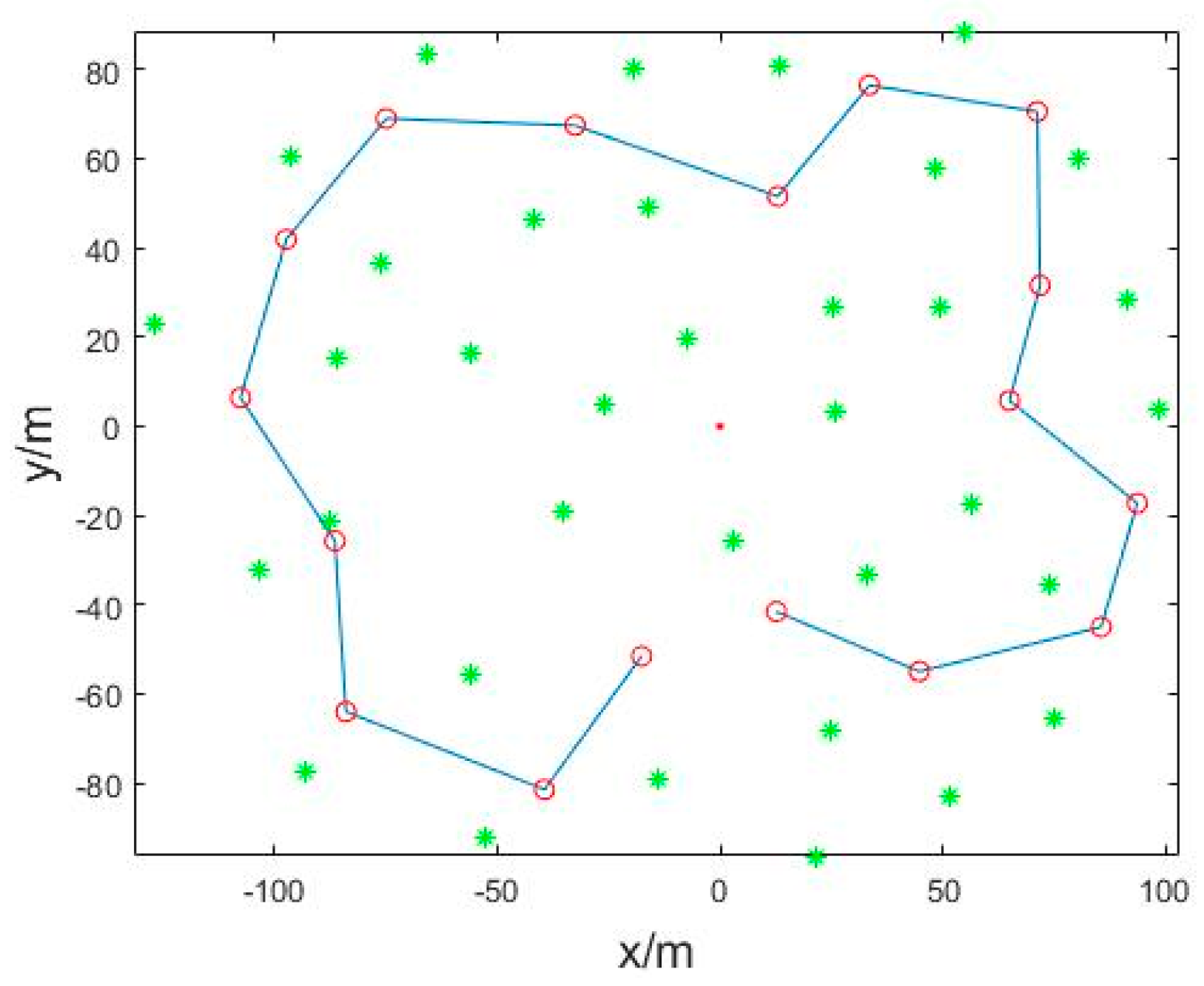
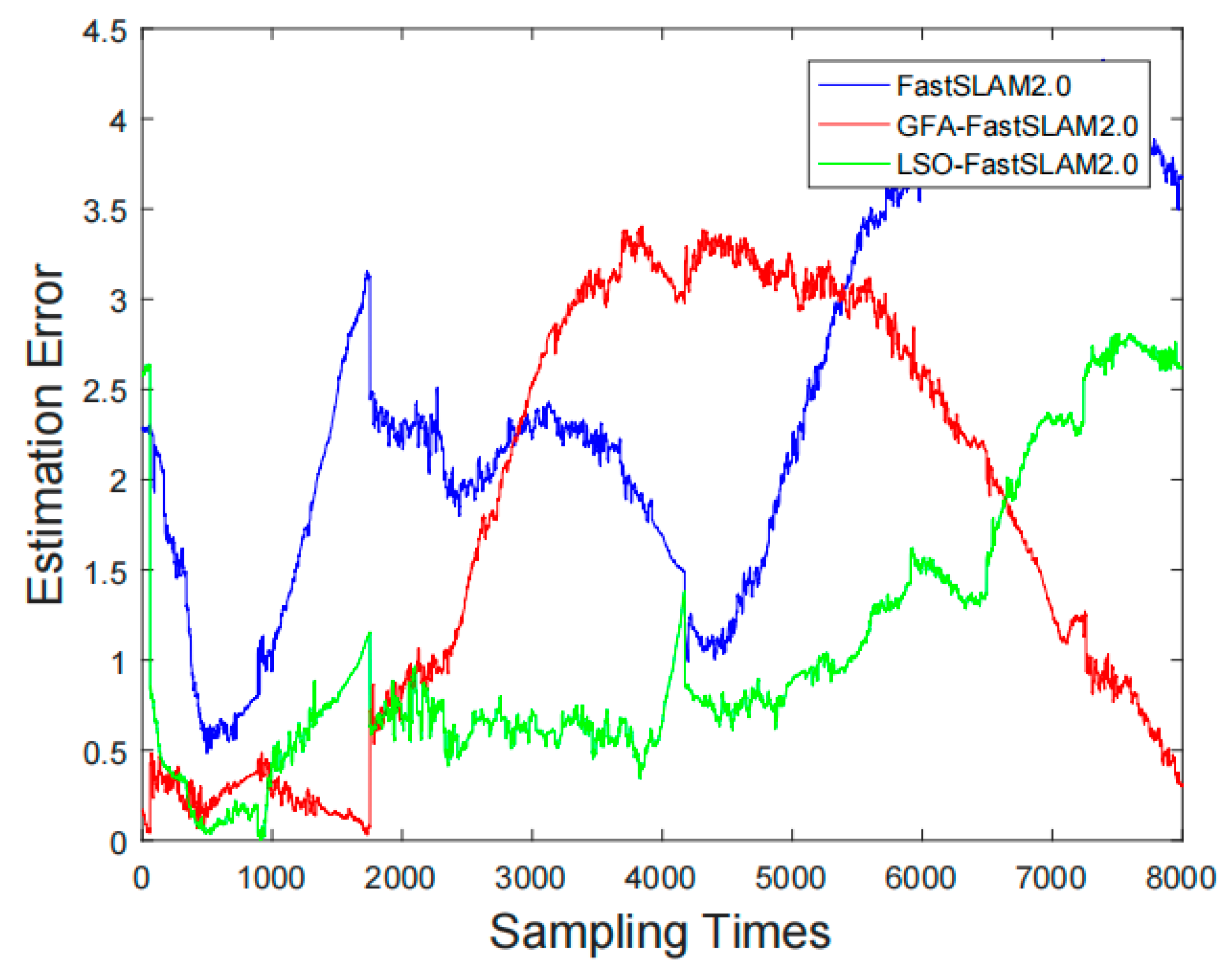
5. Performance Analysis
Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hua, Z.; Shaoze, Y. Research and experiment of a new type of coal mine rescue robot. J. China Coal Soc. 2020, 45, 2170–2181. [Google Scholar]
- Qian, S.-H.; Ge, S.-R.; Wang, Y.-S.; Wang, Y.; Liu, C.-Q. Research status of the disaster rescue robot and its applications to the mine rescue. Robot 2006, 28, 350–354. [Google Scholar]
- Ge, S.; Hu, E.; Pei, W. Classification system and key technology of coal mine robot. J. China Coal Soc. 2020, 45, 455–463. [Google Scholar]
- Durrant, W.; Hugh, F.; Bailey, T. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Guivant, J.E.; Nebot, E.M. Optimization of the simultaneous localization and map-building algorithm for real-time implementation. IEEE Trans. Robot. Autom. 2002, 17, 242–257. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, S.; Shree, V.; Chakravorty, S. RFM-SLAM: Exploiting relative feature measurements to separate orientation and position estimation in SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Chen, H.; Yu, P. Application of Laser SLAM Technology in Backpack Indoor Mobile Measurement System. IOP Conf. Ser. Earth Environ. Sci. 2019, 237, 032026. [Google Scholar] [CrossRef]
- Nemra, A.; Aouf, N. Robust cooperative UAV Visual SLAM. In Proceedings of the IEEE International Conference on Cybernetic Intelligent Systems, Hangzhou, China, 26–27 August 2011. [Google Scholar]
- Lina, M.; Tardos, J.D.; Neira, J. Divide and Conquer: EKF SLAM in 0(n). IEEE Trans. Robot. 2008, 24, 1107–1120. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: A Factored Solution to Simultaneous Mapping and Localization. In Proceedings of the National Conference on Artificial Intelligence, Bellevue, WA, USA, 14–18 July 2013. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Havangi, R. Improved FastSLAM2.0 using ANFIS and PSO. Automatika 2016, 57, 996–1006. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.F.; Luo, Y. SLAM algorithm with Gaussian distributed resampling Rao-Blackwellized particle filter. Control Decis. 2016, 31, 2299–2304. [Google Scholar]
- Roy, S.S.; Pratihar, D.K. Dynamic modeling, stability and energy consumption analysis of a realistic six-legged walking robot. Robot. Comput. -Integr. Manuf. 2013, 29, 400–416. [Google Scholar] [CrossRef]
- Lv, T.; Feng, M. A FastSLAM 2.0 algorithm based on FC&ASD-PSO. Robotica 2016, 35, 1–21. [Google Scholar]
- Ankişhan, H.; Ari, F.; Tartan, E.Ö.; Pafkfiliz, A.G. Square root central difference-based FastSLAM approach improved by differential evolution. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 994–1013. [Google Scholar] [CrossRef]
- Kim, C.; Sakthivel, R.; Chung, W.K. Unscented FastSLAM: A Robust and Efficient Solution to the SLAM Problem. IEEE Trans. Robot. 2008, 24, 808–820. [Google Scholar] [CrossRef]
- He, B.; Ying, L.; Shang, S.; Feng, X.; Yan, T.; Nian, R.; Shen, Y. Autonomous navigation based on unscented-FastSLAM using particle swarm optimization for autonomous underwater vehicles. Measurement 2015, 71, 89–101. [Google Scholar] [CrossRef]
- Kurt-Yavuz, Z.; Yavuz, S. A comparison of EKF, UKF, FastSLAM2.0, and UKF-based FastSLAM Algorithms. In Proceedings of the IEEE International Conference on Intelligent Engineering Systems, Lisbon, Portugal, 13–15 June 2012. [Google Scholar]
- Darwish, S.M. Combining firefly algorithm and Bayesian classifier: New direction for automatic multilabel image annotation. IET Image Process. 2016, 10, 763–772. [Google Scholar] [CrossRef]
- Do, K.D. Stability in probability and inverse optimal control of evolution systems driven by Levy processes. IEEE/CAA J. Autom. Sin. 2020, 7, 405–419. [Google Scholar] [CrossRef]
- Anwar, N.; Deng, H. Ant Colony Optimization based multicast routing algorithm for mobile ad hoc networks. In Proceedings of the Advances in Wireless & Optical Communications, Riga, Latvia, 5–6 November 2015. [Google Scholar]
- Kharwar, P.K.; Verma, R.K. Exploration of nature inspired grey wolf algorithm and grey theory in machining of multiwall carbon nanotube/polymer nanocomposites. Eng. Comput. 2020, 1–22. [Google Scholar] [CrossRef]
- Sengupta, S.; Das, S.; Nasir, M.; Vasilakos, A.V.; Pedrycz, W. Energy-Efficient Differentiated Coverage of Dynamic Objects Using an Improved Evolutionary Multi-Objective Optimization Algorithm with Fuzzy-Dominance. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012. [Google Scholar]
- Lee, H.-C.; Park, S.-K.; Choi, J.-S.; Lee, B.-H. PSO-FastSLAM: An Improved FastSLAM Framework Using Particle Swarm Optimization. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009. [Google Scholar]
- Haydar, A.; Tartan, E.Ö.; Arı, F. Square Root Unscented Based FastSlam Optimized by Particle Swarm Optimization Passive Congregation. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013. [Google Scholar]
- Lv, T.-Z.; Zhao, C.-X.; Zhang, H.-F. An Improved FastSLAM Algorithm Based on Revised Genetic Resampling and SR-UPF. Int. J. Autom. Comput. 2018, 15, 325–334. [Google Scholar] [CrossRef]
- Cui, J.; Feng, D.; Li, Y.; Tian, Q. Research on simultaneous localization and mapping for AUV by an improved method: Variance reduction FastSLAM with simulated annealing. Def. Technol. 2019, 16, 651–661. [Google Scholar] [CrossRef]
- Tian, M.-C.; Bo, Y.-M.; Chen, Z.-M.; Yue, C.; Wang, H. Novel target tracking method based on firefly algorithm optimized particle filter. Control Decis. 2017, 32, 1758–1766. [Google Scholar]
- Zhang, Q.-M.; Liu, L.-Q.; Ma, L.-Q. New Swarm Intelligent Algorithms: Lions Algorithm. Comput. Sci. 2018, 45, 114–116. [Google Scholar]
- Montemerlo, M.S.; Thrun, S.B.; Roller, D.; Wegbreit, B. FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. Proc. Int. Conf. Artif. Intell. 2003, 133, 1151–1156. [Google Scholar]
- Yang, X.; Jiao, Q.; Liu, X. Research on GRNN-based Particle Filter Algorithm. In Proceedings of the Information Technology, Networking, Electronic and Automation Control Conference, Chengdu, China, 15–17 March 2019. [Google Scholar]
- Chen, S.-M.; Liu, J.-K.; Xiao, J. Unscented Fast SLAM2.0 algorithm based on gravitational field optimization. Control Theory Appl. 2018, 35, 1186–1193. [Google Scholar]



| Parameter | Numerical Value | Noise Parameters | Numerical Value |
|---|---|---|---|
| Robot speed | 3 m/s | Motion noise | 0.3 m/s 1.5° |
| Max steering angle | 10° | ||
| Maxi steering angular speed | 15°/s | Observation noise | 0.1 m/s 1° |
| Wheel spacing | 4 m | ||
| Sampling time interval | 0.025 s |
| Number of Particles | Algorithm | Mean Localization Accuracy Error/M | RMSE of Road Sign Estimation (m) |
|---|---|---|---|
| 20 | FastSLAM2.0 | 3.0535 | 4.1399 |
| GFA-FastSLAM2.0 | 2.9060 | 3.3545 | |
| LSO-FastSLAM2.0 | 2.3025 | 2.2837 | |
| 50 | FastSLAM2.0 | 2.7718 | 3.2106 |
| GFA-FastSLAM2.0 | 2.3629 | 2.5990 | |
| LSO-FastSLAM2.0 | 2.0470 | 2.2837 | |
| 80 | FastSLAM2.0 | 2.6843 | 2.9199 |
| GFA-FastSLAM2.0 | 1.7504 | 1.9072 | |
| LSO-FastSLAM2.0 | 1.2745 | 1.3762 | |
| 100 | FastSLAM2.0 | 2.5907 | 2.8538 |
| GFA-FastSLAM2.0 | 1.3693 | 1.6422 | |
| LSO-FastSLAM2.0 | 1.1745 | 1.3279 |
| Algorithm | Mean Localization Accuracy Error/m | Variance of Localization Accuracy Error |
|---|---|---|
| FastSLAM2.0 | 2.7718 | 1.6403 |
| GFA-FastSLAM2.0 | 1.4036 | 0.9059 |
| LSO-FastSLAM2.0 | 1.1867 | 0.2519 |
| Algorithm | RMSE of x-Axis (m) | RMSE of y-Axis (m) | RMSE of Road Sign Estimation (m) |
|---|---|---|---|
| FastSLAM2.0 | 2.0447 | 2.2676 | 2.9871 |
| GFA-FastSLAM2.0 | 1.6015 | 1.1018 | 1.5841 |
| LSO-FastSLAM2.0 | 0.6932 | 1.0518 | 1.3383 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Ma, Y.; Wang, M.; Yang, J.; Yin, Y.; Liu, S. LSO-FastSLAM: A New Algorithm to Improve the Accuracy of Localization and Mapping for Rescue Robots. Sensors 2022, 22, 1297. https://doi.org/10.3390/s22031297
Zhu D, Ma Y, Wang M, Yang J, Yin Y, Liu S. LSO-FastSLAM: A New Algorithm to Improve the Accuracy of Localization and Mapping for Rescue Robots. Sensors. 2022; 22(3):1297. https://doi.org/10.3390/s22031297
Chicago/Turabian StyleZhu, Daixian, Yinan Ma, Mingbo Wang, Jing Yang, Yichen Yin, and Shulin Liu. 2022. "LSO-FastSLAM: A New Algorithm to Improve the Accuracy of Localization and Mapping for Rescue Robots" Sensors 22, no. 3: 1297. https://doi.org/10.3390/s22031297
APA StyleZhu, D., Ma, Y., Wang, M., Yang, J., Yin, Y., & Liu, S. (2022). LSO-FastSLAM: A New Algorithm to Improve the Accuracy of Localization and Mapping for Rescue Robots. Sensors, 22(3), 1297. https://doi.org/10.3390/s22031297






