Visible Particle Series Search Algorithm and Its Application in Structural Damage Identification
Abstract
:1. Introduction
2. Problem Formulation
3. Visible Particle Series Search Algorithm
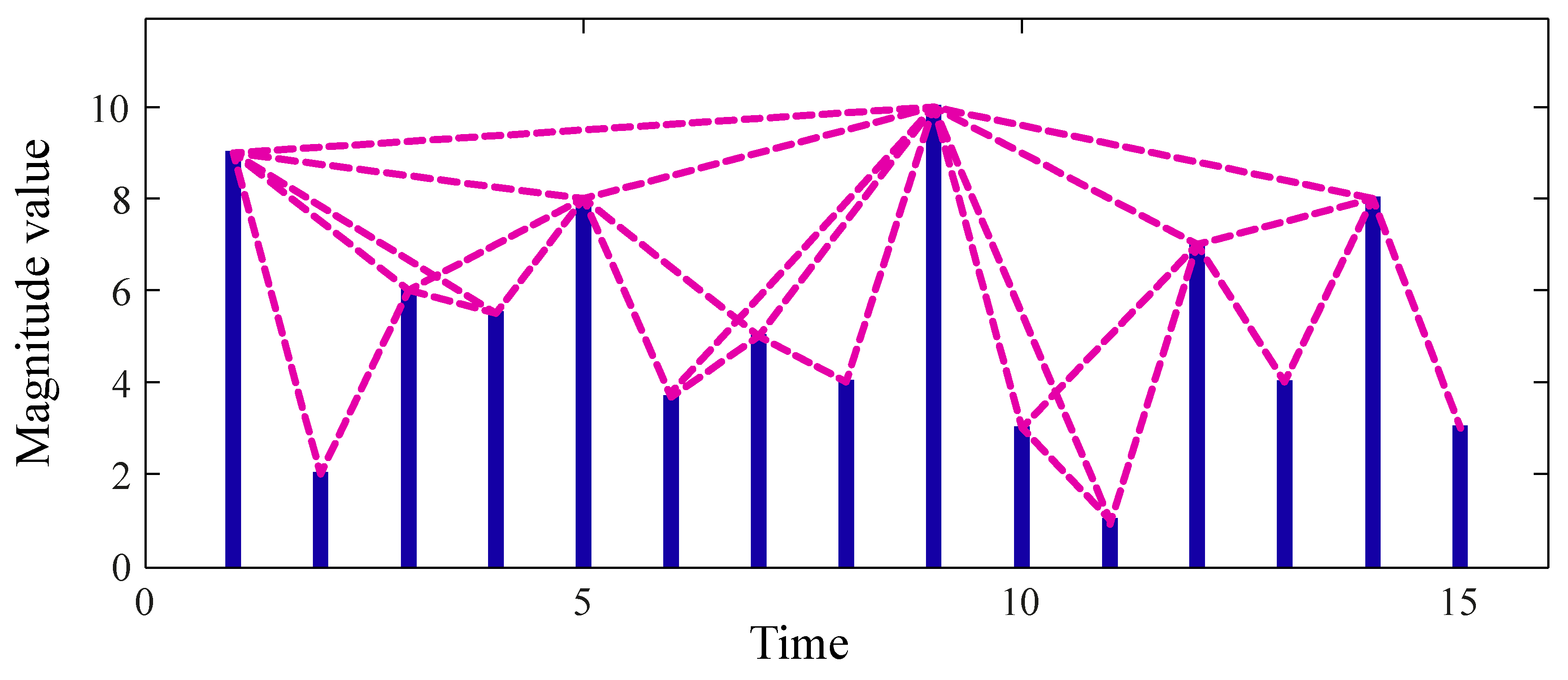
3.1. Background of the Visibility Graph Technique
3.2. The VPSS Algorithm
3.2.1. Step 1: Initialization
3.2.2. Step 2: Particle Series Construction
3.2.3. Step 3: Visibility Criterion Assessment
3.2.4. Step 4: Generation of New Solutions
3.2.5. Step 5: Fitness Function Evaluation
3.2.6. Step 6: Selection
3.2.7. Step 7: Termination
| Algorithm 1. Visible particle series search algorithm |
| Begin |
| 1. Set the population size and maximum number of iterations . |
| 2. Initialize a random population using Equation (7). |
| 3. Evaluate the fitness function value of each solution . |
| 4. Set the current iteration number . |
| 5. while () do |
| 6. Consider the population as a particle series with random arrangement; |
| 7. Obtain the visible particles associated with each particle using Equation (8); |
| 8. for do |
| 9. Select a random number from ; |
| 10. if then |
| 11. Generate a new solution using Equation (9); |
| 12. else |
| 13. Generate a new solution using Equation (10); |
| 14. end if |
| 15. Evaluate the fitness value of the new solution ; |
| 16. if then |
| 17. |
| 18. else |
| 19. |
| 20. end if |
| 21. end for |
| 22. ; |
| 23. end while |
| 24. Return the best solution achieved; |
| End |
4. Validation of VPSS on Mathematical Benchmark Functions
5. Application of VPSS in Structural Damage Identification
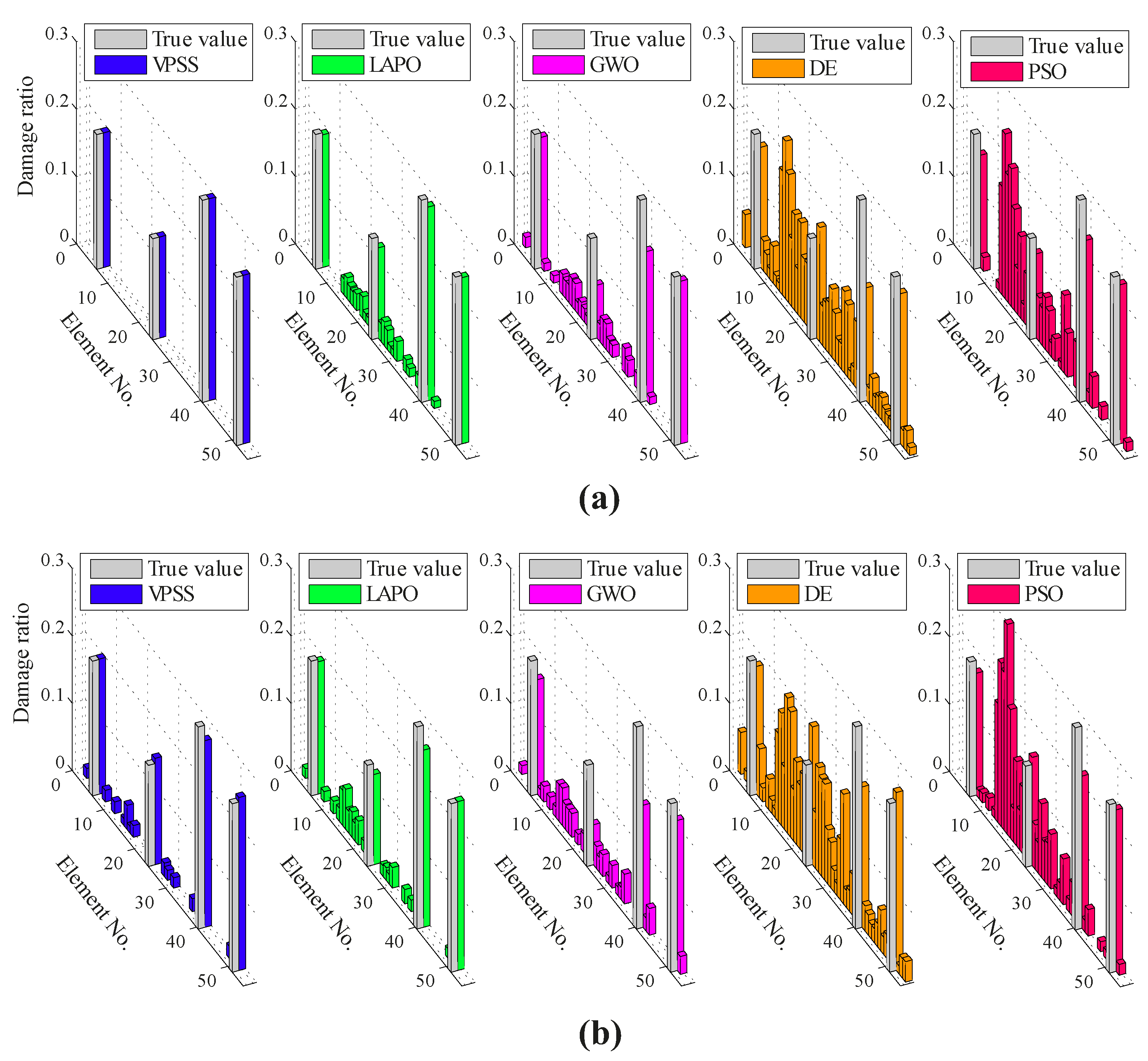
5.1. A 47-Bar Planar Truss
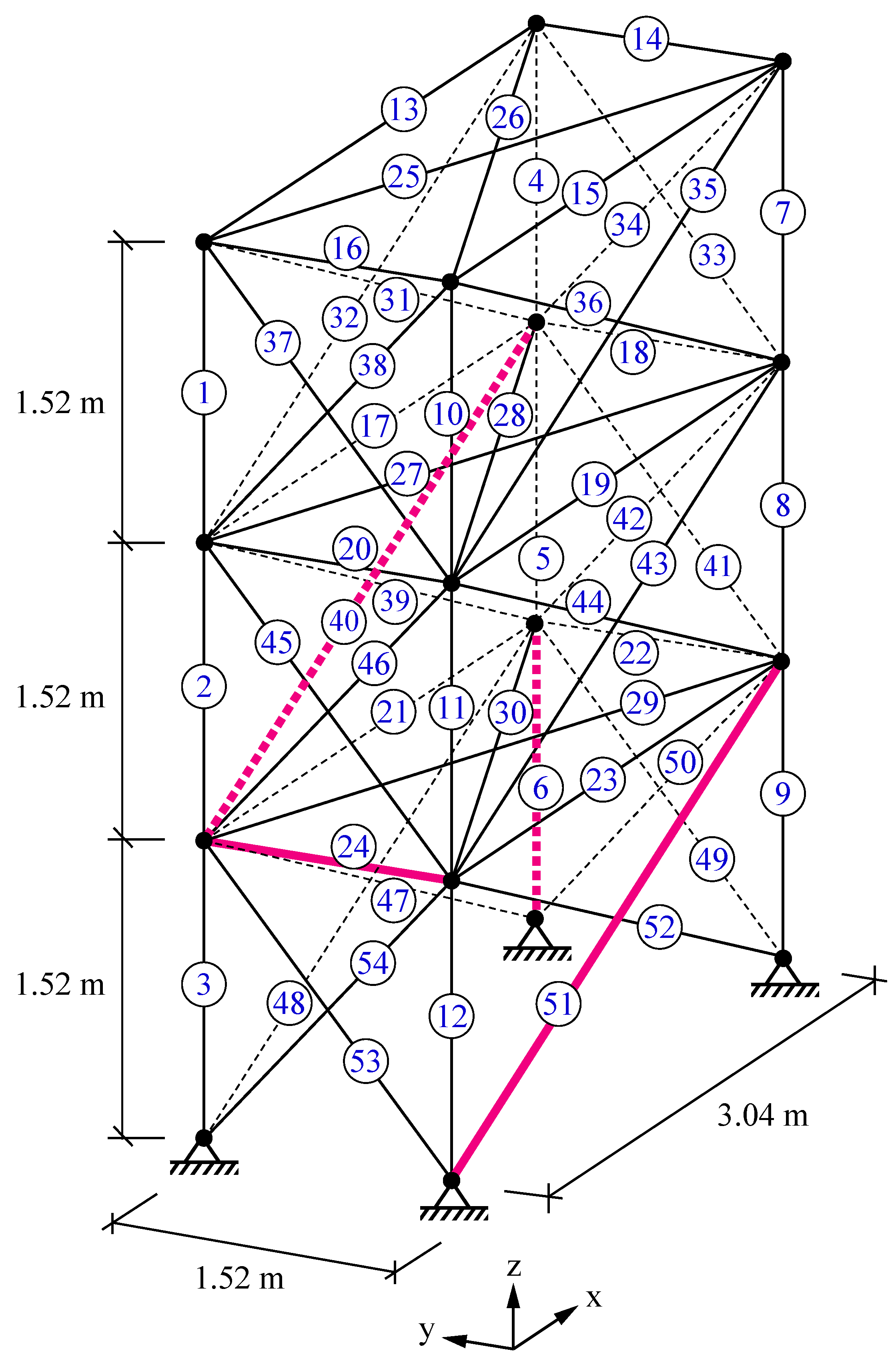
5.2. A 54-Bar Space Truss
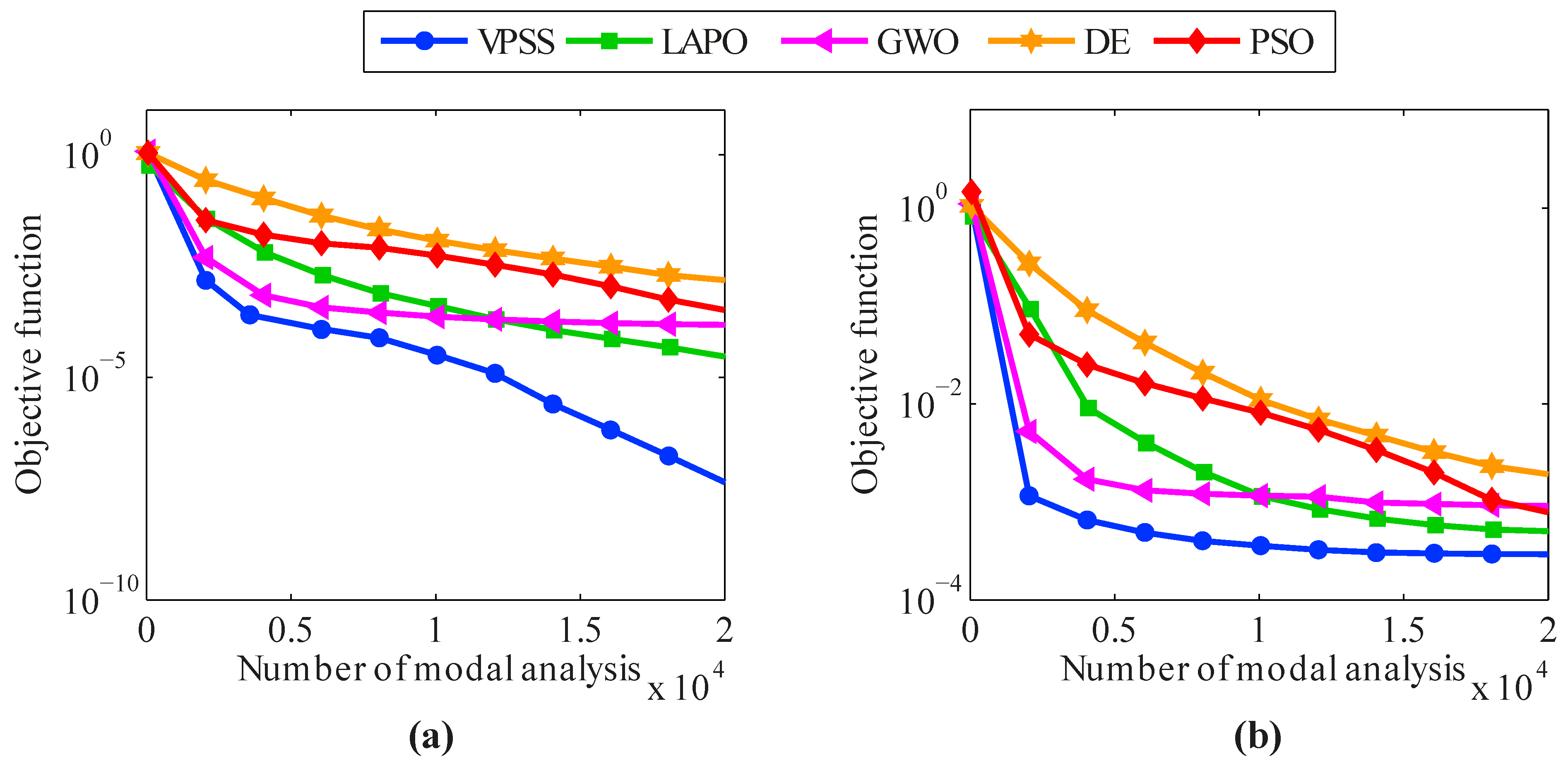
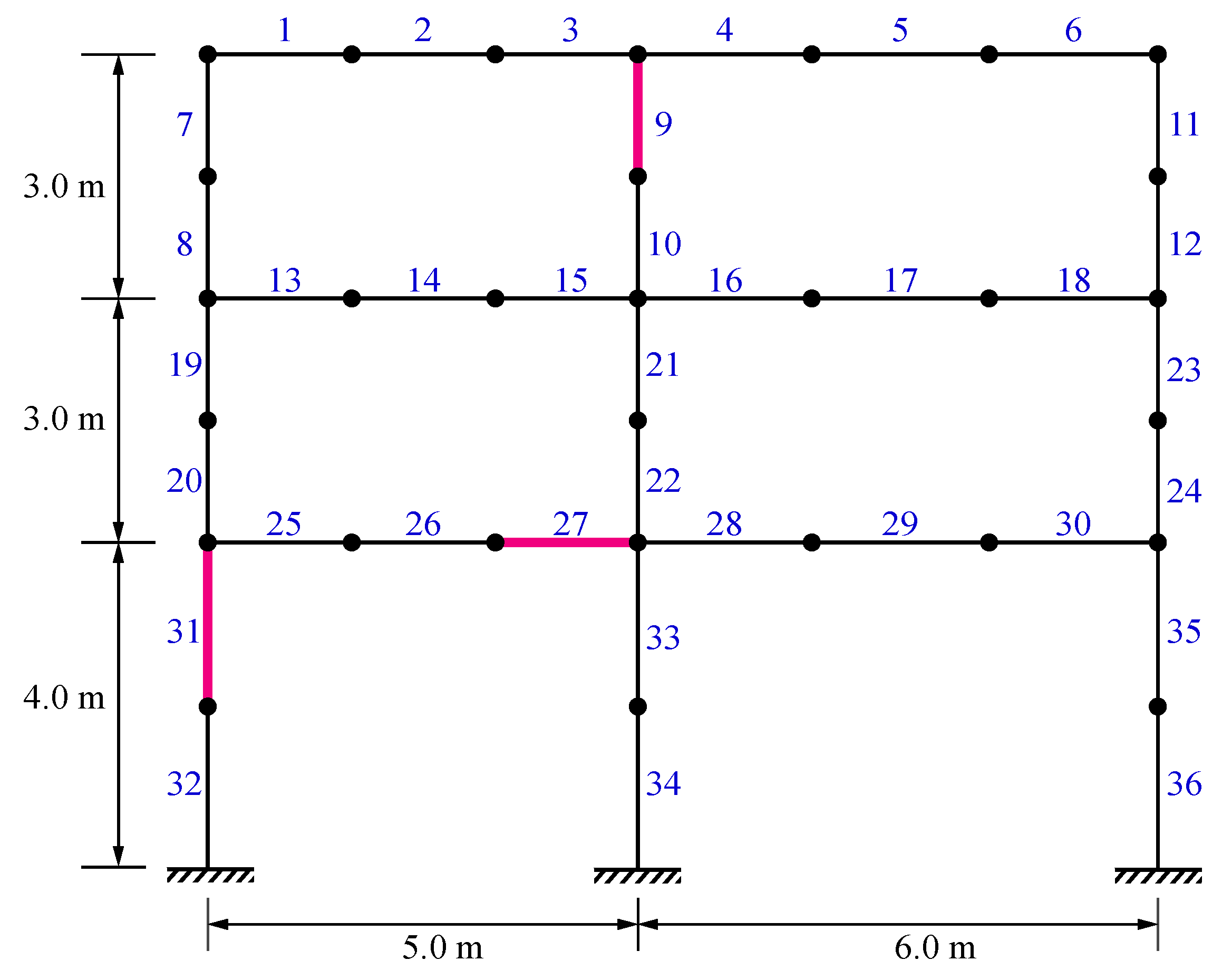
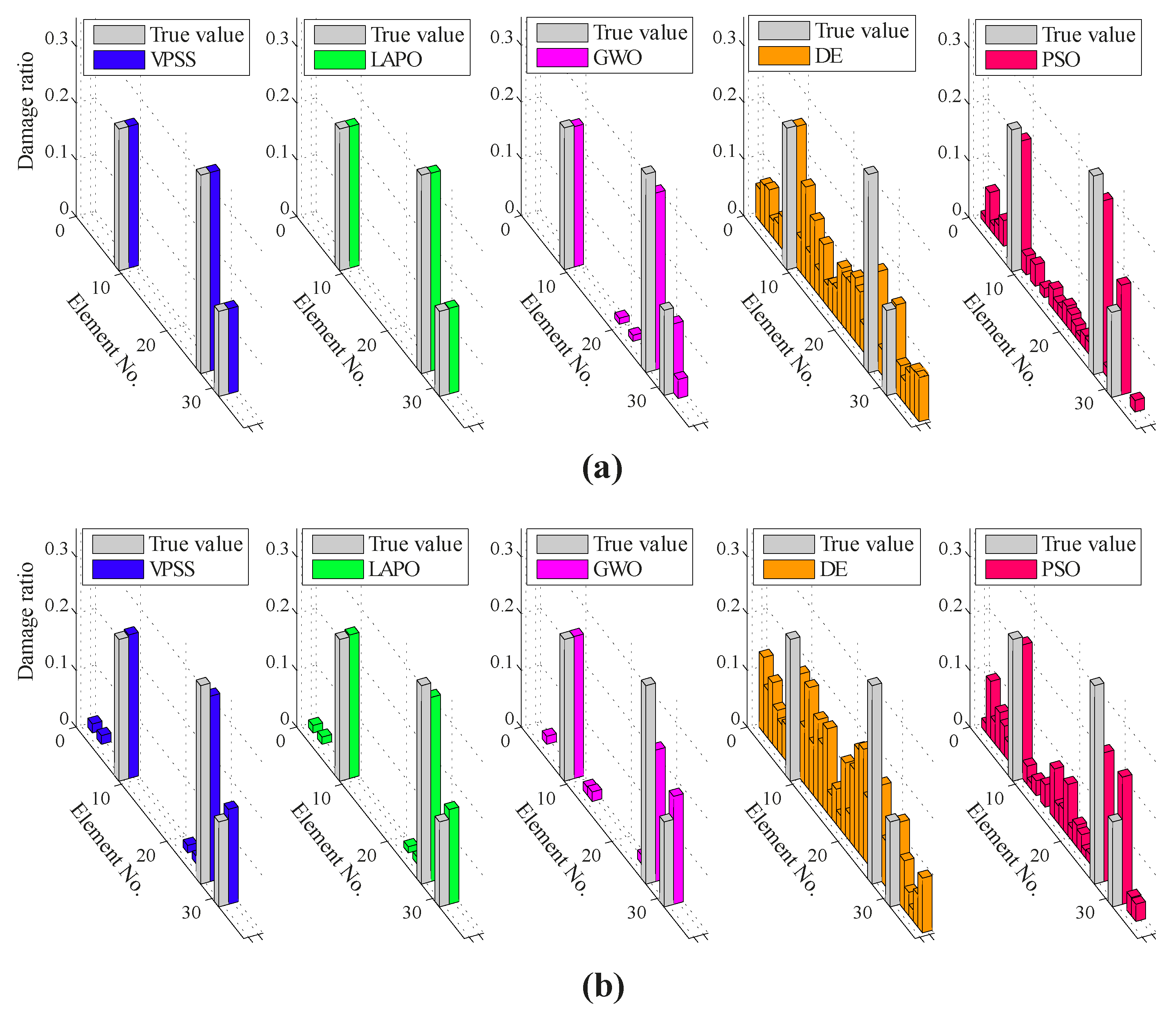
5.3. A Two-Bay Three-Story Frame
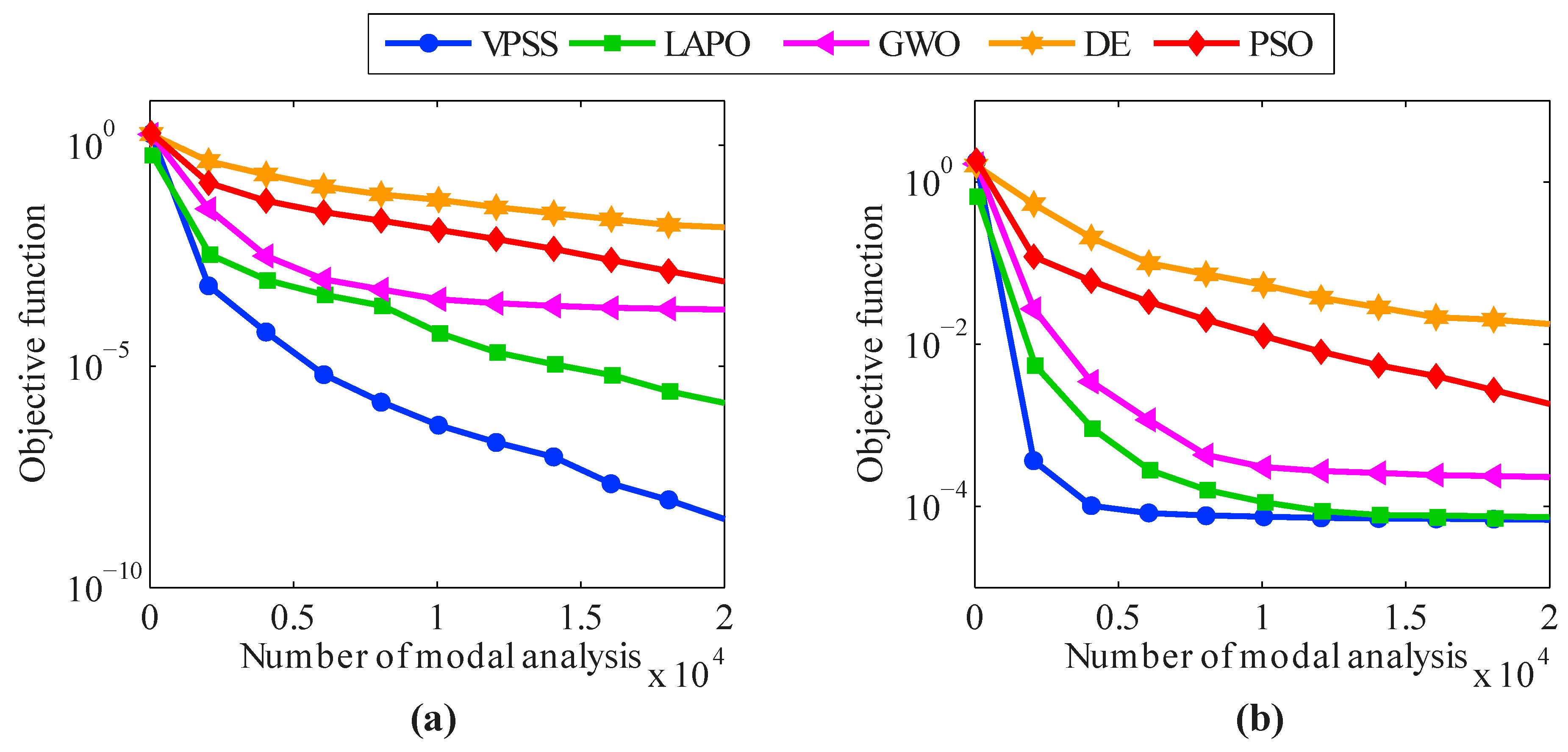
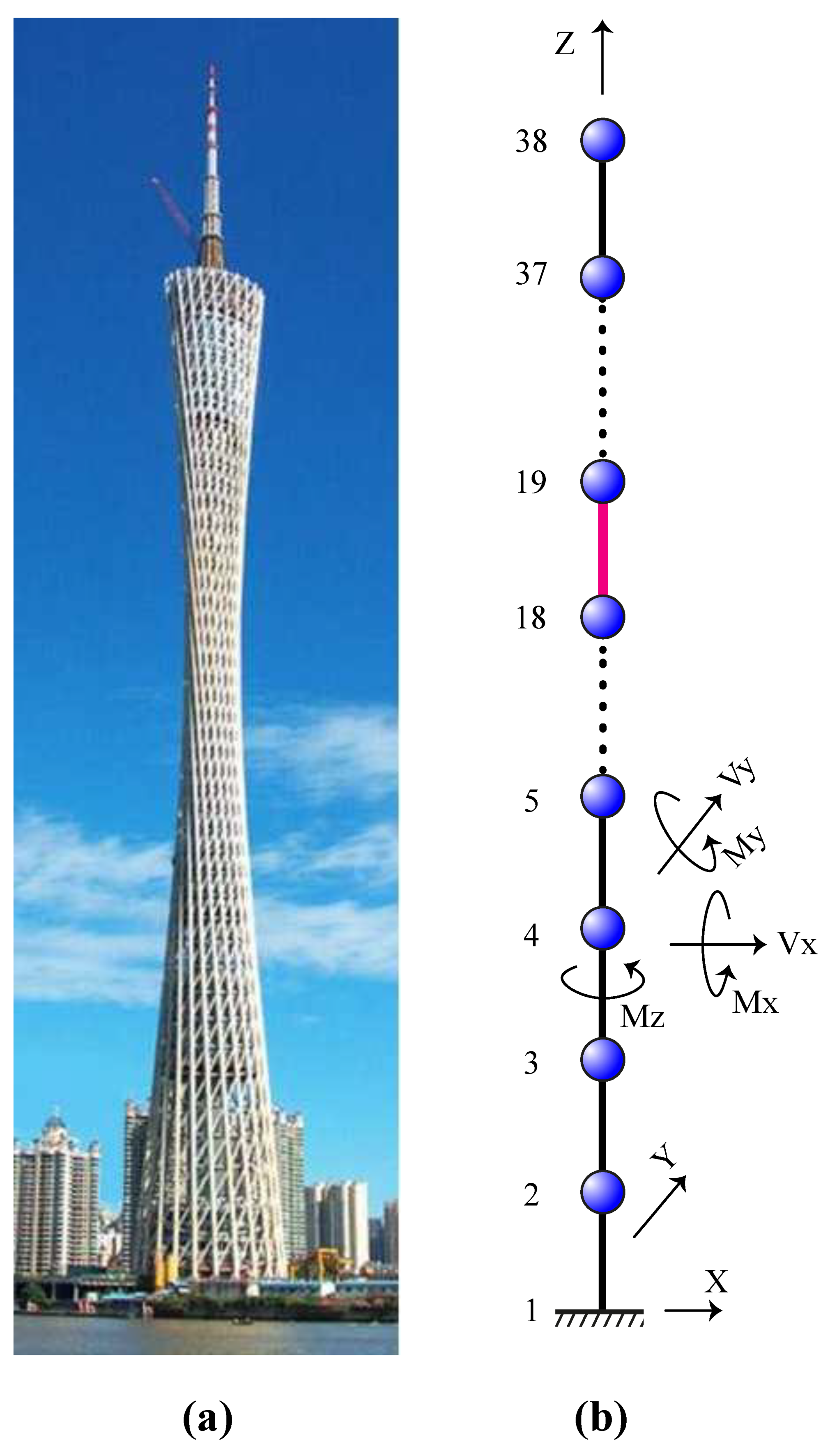
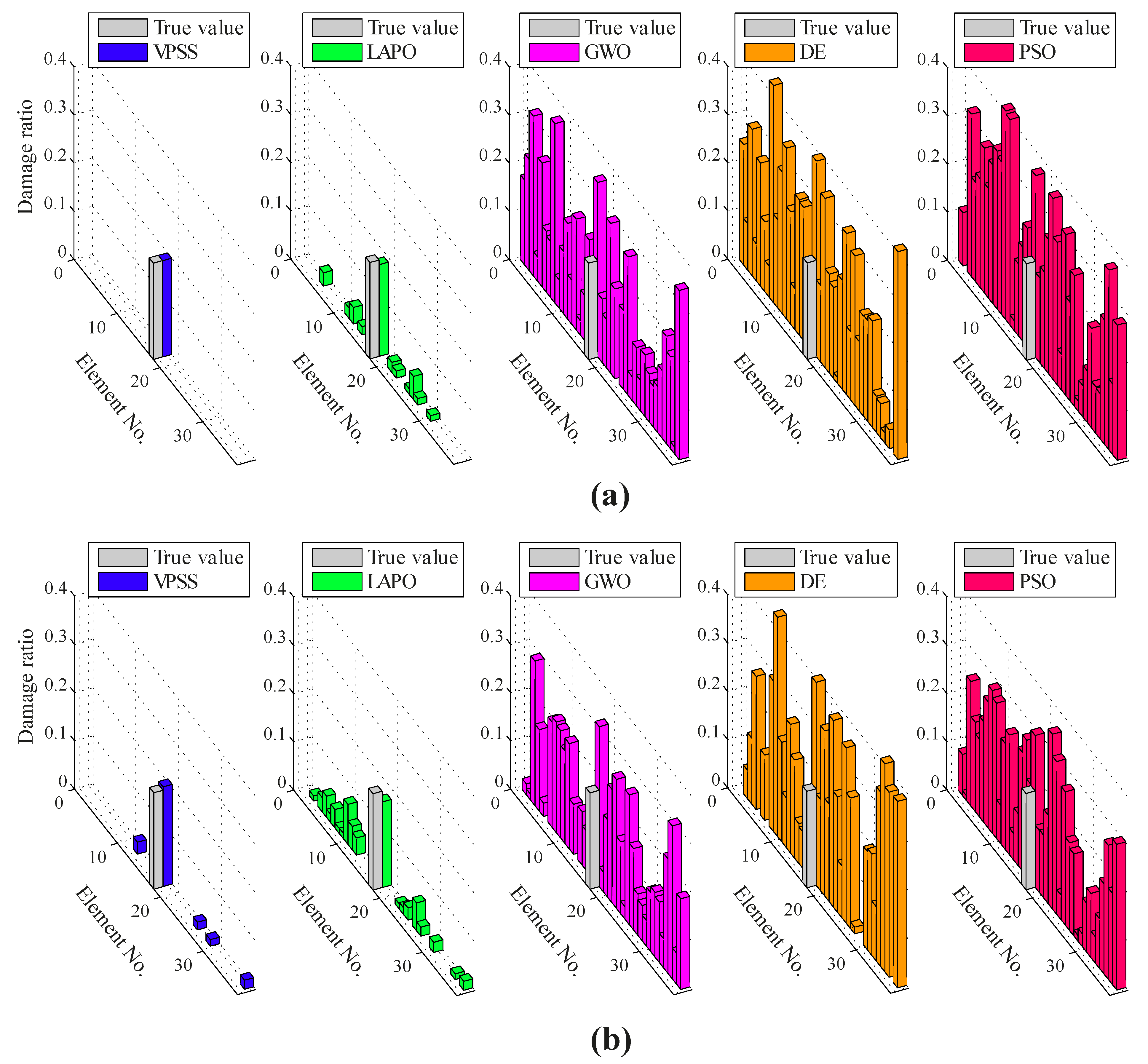
5.4. The Canton Tower
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Truong, T.T.; Dinh-Cong, D.; Lee, J.; Nguyen-Thoi, T. An effective deep feedforward neural networks (DFNN) method for damage identification of truss structures using noisy incomplete modal data. J. Build. Eng. 2020, 30, 101244. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Hao, H.; Lu, Z.R. Structural damage identification with uncertain modelling error and measurement noise by clustering based tree seeds algorithm. Eng. Struct. 2019, 185, 301–314. [Google Scholar] [CrossRef]
- Seyedpoor, S.M.; Ahmadi, A.; Pahnabi, N. Structural damage detection using time domain responses and an optimization method. Inverse Probl. Sci. Eng. 2019, 27, 669–688. [Google Scholar] [CrossRef]
- Silik, A.; Noori, M.; Altabey, W.; Dang, J.; Ghiasi, R.; Wu, Z. Optimum wavelet selection for nonparametric analysis toward structural health monitoring for processing big data from sensor network: A comparative study. Struct. Health Monit. 2021, in press. [CrossRef]
- Silik, A.; Noori, M.; Altabey, W.A.; Ghiasi, R. Selecting optimum levels of wavelet multi-resolution analysis for time-varying signals in structural health monitoring. Struct. Control. Health Monit. 2021, 28, e2762. [Google Scholar] [CrossRef]
- Ghiasi, R.; Noori, M.; Altabey, W.A.; Silik, A.; Wang, T.; Wu, Z. Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach. Appl. Sci. 2021, 11, 770. [Google Scholar] [CrossRef]
- Altabey, W.A.; Noori, M.; Alarjani, A.; Zhao, Y. Tensile creep monitoring of basalt fiber-reinforced polymer plates via electrical po-tential change and artificial neural network. Sci. Iran. Int. J. Sci. Technol. Trans. Mech. Eng. B 2020, 27, 1995–2008. [Google Scholar] [CrossRef]
- Altabey, W.A.; Noori, M.; Alarjani, A.; Zhao, Y. Nano-Delamination Monitoring of BFRP Nano-Pipes of Electrical Potential Change with ANNs. Adv. Nano Res. 2020, 9, 1–13. [Google Scholar] [CrossRef]
- Wang, T.; Altabey, W.A.; Noori, M.; Ghiasi, R. A Deep Learning Based Approach for Response Prediction of Beam-Like Structures. Struct. Durab. Health Monit. 2020, 14, 315–388. [Google Scholar] [CrossRef]
- Altabey, W.A. Applying deep learning and wavelet transform for predicting the vibration behavior in variable thickness skew composite plates with intermediate elastic support. J. Vibroeng. 2021, 23, 770–783. [Google Scholar] [CrossRef]
- Altabey, W.A.; Noori, M.; Wang, T.; Ghiasi, R.; Kuok, S.-C.; Wu, Z. Deep learning-based crack identification for steel pipelines by extracting features from 3d shadow modeling. Appl. Sci. 2021, 11, 6063. [Google Scholar] [CrossRef]
- Ni, F.; Zhang, J.; Noori, M. Deep Learning for Data Anomaly Detection and Data Compression of a Long-span Suspension Bridge. Comput. Aided Civ. Infrastruct. Eng. 2020, 35, 685–700. [Google Scholar] [CrossRef]
- Zhao, Y.; Noori, M.; Altabey, W.A.; Awad, T. A Comparison of Three Different Methods for the Identification of Hysterically Degrading Structures Using BWBN Model. Front. Built Environ. 2019, 4, 80. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Noori, M.; Altabey, W.A. Damage detection for a beam under transient excitation via three different algorithms. Struct. Eng. Mech. 2017, 63, 803–817. [Google Scholar] [CrossRef]
- Wang, T.; Noori, M.; Altabey, W.A. Identification of cracks in an Euler–Bernoulli beam using Bayesian inference and closed-form solution of vibration modes. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 421–438. [Google Scholar] [CrossRef]
- Aval, S.B.B.; Mohebian, P. A Novel Optimization Algorithm Based on Modal Force Information for Structural Damage Identification. Int. J. Struct. Stab. Dyn. 2021, 21, 50100. [Google Scholar] [CrossRef]
- Barontini, A.; Perera, R.; Masciotta, M.G.; Amado-Mendes, P.; Ramos, L.; Lourenço, P. Deterministically generated negative selection algorithm for damage detection in civil engineering systems. Eng. Struct. 2019, 197, 109444. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Das, S.; Saha, P.; Patro, S.K. Vibration-based damage detection techniques used for health monitoring of structures: A review. J. Civ. Struct. Health Monit. 2016, 6, 477–507. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Kong, X.; Cai, C.S.; Hu., J. The state-of-the-art on framework of vibration-based structural damage identification for decision making. Appl. Sci. 2017, 7, 497. [Google Scholar] [CrossRef] [Green Version]
- Silik, A.; Noori, M.; Altabey, W.A.; Ghiasi, R.; Wu, Z. Comparative Analysis of Wavelet Transform for Time-Frequency Analysis and Transient Localization in Structural Health Monitoring. Struct. Durab. Health Monit. 2021, 15, 1–22. [Google Scholar] [CrossRef]
- Noori, M.; Haifegn, W.; Altabey, W.A.; Silik, A.I.H. A Modified Wavelet Energy Rate Based Damage Identification Method for Steel Bridges. Sci. Iran. Int. J. Sci. Technol. Trans. Mech. Eng. B 2018, 25, 3210–3230. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Noori, M.; Altabey, W.A.; Beheshti-Aval, S.B. Mode shape-based damage identification for a reinforced concrete beam using wavelet coefficient differences and multiresolution analysis. Struct. Control. Health Monit. 2017, 25, e2041. [Google Scholar] [CrossRef]
- Silik, A.; Noori, M.; Altabey, W.A. Analytic Wavelet Selection for Time—Frequency Analysis of Big Data Form Civil Structure Monitoring. In Civil Structural Health Monitoring, Proceedings of CSHM-8 Workshop 2021, Online, 29–31 March 2021; Rainieri, C., Fabbrocino, G., Caterino, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Chapter 29. [Google Scholar] [CrossRef]
- Kumar, R.; Ismail, M.; Zhao, W.; Noori, M.; Yadav, A.R.; Chen, S.; Singh, V.; Altabey, W.A.; Silik, A.I.H.; Kumar, G.; et al. Damage detection of wind turbine system based on signal processing approach: A critical review. Clean Technol. Environ. Policy 2021, 23, 561–580. [Google Scholar] [CrossRef]
- Xu, H.J.; Liu, J.K.; Lu, Z.R. Structural damage identification based on cuckoo search algorithm. Adv. Struct. Eng. 2016, 19, 849–859. [Google Scholar] [CrossRef]
- Dinh-Cong, D.; Pham-Toan, T.; Nguyen-Thai, D.; Nguyen-Thoi, T. Structural damage assessment with incomplete and noisy modal data using model reduction technique and LAPO algorithm. Struct. Infrastruct. Eng. 2019, 15, 1436–1449. [Google Scholar] [CrossRef]
- Li, Z.; Noori, M.; Zhao, Y.; Wan, C.; Feng, D.; Altabey, W.A. A multi-objective optimization algorithm for Bouc–Wen–Baber–Noori model to identify re-inforced concrete columns failing in different modes. Proc. Instit. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 2165–2182. [Google Scholar] [CrossRef]
- Zhao, Y.; Noori, M.; Altabey, W.A. Reaching Law Based Sliding Mode Control for a Frame Structure under Seismic Load. Earthq. Eng. Eng. Vib. 2021, 20, 727–745. [Google Scholar] [CrossRef]
- Nobahari, M.; Ghasemi, M.R.; Shabakhty, N. A fast and robust method for damage detection of truss structures. Appl. Math. Model. 2019, 68, 368–382. [Google Scholar] [CrossRef]
- Ghiasi, R.; Torkzadeh, P.; Noori, M. A machine-learning approach for structural damage detection using least square support vector machine based on a new combinational kernel function. J. Struct. Health Monit. 2016, 15, 302–316. [Google Scholar] [CrossRef]
- Hao, H.; Xia, Y. Vibration-based damage detection of structures by genetic algorithm. J. Comput. Civ. Eng. 2002, 16, 222–229. [Google Scholar] [CrossRef]
- Mohan, S.C.; Maiti, D.K.; Maity, D. Structural damage assessment using FRF employing particle swarm optimization. Appl. Math. Comput. 2013, 219, 10387–10400. [Google Scholar] [CrossRef]
- Majumdar, A.; Maiti, D.K.; Maity, D. Damage assessment of truss structures from changes in natural frequencies using ant colony optimization. Appl. Math. Comput. 2012, 218, 9759–9772. [Google Scholar] [CrossRef]
- Torkzadeh, P.; Ghiasi, R.; Noori, M. Structural Damage Detection Using Artificial Neural Networks and Least Square Support Vector Machine with Particle Swarm Harmony Search Algorithm. Int. J. Sustain. Mater. Struct. Syst. 2014, 1, 303–320. [Google Scholar]
- Ding, Z.H.; Huang, M.; Lu, Z.R. Structural damage detection using artificial bee colony algorithm with hybrid search strategy. Swarm Evol. Comput. 2016, 28, 1–3. [Google Scholar] [CrossRef]
- Seyedpoor, S.M.; Shahbandeh, S.; Yazdanpanah, O. An efficient method for structural damage detection using a differential evolution algorithm-based optimisation approach. Civ. Eng. Environ. Syst. 2015, 32, 230–250. [Google Scholar] [CrossRef]
- Wang, T.; Noori, M.; Altabey, W.A.; Farrokh, M.; Ghiasi, R. Parameter Identification and Dynamic Response Analysis of a Modified Prandtl-Ishlinskii Asymmetric Hysteresis Model via Least-Mean Square algorithm and Particle Swarm Optimization. Proc. IMechE Part L J. Mater. Des. Appl. 2021, 235, 2639–2653. [Google Scholar] [CrossRef]
- Kaveh, A.; Zolghadr, A. An improved CSS for damage detection of truss structures using changes in natural frequencies and mode shapes. Adv. Eng. Softw. 2015, 80, 93–100. [Google Scholar] [CrossRef]
- Zhu, J.J.; Huang, M.; Lu, Z.R. Bird mating optimizer for structural damage detection using a hybrid objective function. Swarm Evol. Comput. 2017, 35, 41–52. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S.; Noori, N.; Altabey, W.A. Structural Damage Detection and Severity Identification Using Mode Shape Expansion and Grey Wolf Optimizer. Adv. Struct. Eng. 2020, 23, 2850–2865. [Google Scholar] [CrossRef]
- Nobahari, M.; Ghasemi, M.R.; Shabakhty, N. A novel heuristic search algorithm for optimization with application to structural damage identification. Smart Struct Syst. 2017, 19, 449–461. [Google Scholar] [CrossRef]
- Fallah, N.; Vaez, S.R.; Mohammadzadeh, A. Multi-damage identification of large-scale truss structures using a two-step approach. J. Build. Eng. 2018, 19, 494–505. [Google Scholar] [CrossRef]
- Fathi, H.; Vaez, S.H.; Zhang, Q.; Alavi, A.H. A new approach for crack detection in plate structures using an integrated extended finite element and enhanced vibrating particles system optimization methods. Structures 2021, 29, 638–651. [Google Scholar] [CrossRef]
- Du, D.C.; Vinh, H.H.; Trung, V.D.; Hong Quyen, N.T.; Trung, N.T. Efficiency of Jaya algorithm for solving the optimization-based structural damage identification problem based on a hybrid objective function. Eng. Optim. 2018, 50, 1233–1251. [Google Scholar] [CrossRef]
- Dinh-Cong, D.; Nguyen-Thoi, T.; Nguyen, D.T. A FE model updating technique based on SAP2000-OAPI and enhanced SOS algorithm for damage assessment of full-scale structures. Appl. Soft Comput. 2020, 89, 106100. [Google Scholar] [CrossRef]
- Mishra, M.; Barman, S.K.; Maity, D.; Maiti, D.K. Ant lion optimisation algorithm for structural damage detection using vibration data. J. Civ. Struct. Health Monit. 2019, 9, 117–136. [Google Scholar] [CrossRef]
- Mishra, M.; Barman, S.K.; Maity, D.; Maiti, D.K. Performance studies of 10 metaheuristic techniques in determination of damages for large-scale spatial trusses from changes in vibration responses. J. Comput. Civ. Eng. 2020, 34, 04019052. [Google Scholar] [CrossRef]
- Aval, S.B.B.; Mohebian, P. Combined joint and member damage identification of skeletal structures by an improved biology migration algorithm. J. Civ. Struct. Health Monit. 2020, 10, 357–375. [Google Scholar] [CrossRef]
- Chen, C.; Yu, L. A hybrid ant lion optimizer with improved Nelder–Mead algorithm for structural damage detection by improving weighted trace lasso regularization. Adv. Struct. Eng. 2020, 23, 468–484. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Hao, H. Non-probabilistic method to consider uncertainties in structural damage identification based on Hybrid Jaya and Tree Seeds Algorithm. Eng. Struct. 2020, 220, 110925. [Google Scholar] [CrossRef]
- Aval, S.B.B.; Mohebian, P. Joint Damage Identification in Frame Structures by Integrating a New Damage Index with Equilibrium Optimizer Algorithm. Int. J. Struct. Stab. Dyn. 2022, in press. [CrossRef]
- Tiachacht, S.; Khatir, S.; Le Thanh, C.; Rao, R.V.; Mirjalili, S.; Wahab, M.A. Inverse problem for dynamic structural health monitoring based on slime mould algorithm. Eng. Comput. 2021, 26, 1–24. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S. Multiverse optimizer for structural damage detection: Numerical study and experimental validation. Struct. Des. Tall Spec. Build. 2020, 29, e1777. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evolut. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Nematollahi, A.F.; Rahiminejad, A.; Vahidi, B. A novel physical based meta-heuristic optimization method known as Lightning Attachment Procedure Optimization. Appl. Soft Comput. 2017, 59, 596–621. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, J.; Lu, Z. Structural damage detection using improved particle swarm optimization. Inverse Probl. Sci. Eng. 2018, 26, 792–810. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Lacasa, L.; Just, W. Visibility graphs and symbolic dynamics. Phys. D Nonlinear Phenom. 2018, 374, 35–44. [Google Scholar] [CrossRef] [Green Version]
- Long, Y. Visibility graph network analysis of gold price time series. Phys. A Stat. Mech. Appl. 2013, 392, 3374–3384. [Google Scholar] [CrossRef]
- Zhang, R.; Zou, Y.; Zhou, J.; Gao, Z.K.; Guan, S. Visibility graph analysis for re-sampled time series from auto-regressive stochastic processes. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 396–403. [Google Scholar] [CrossRef]
- Iacobello, G.; Scarsoglio, S.; Ridolfi, L. Visibility graph analysis of wall turbulence time-series. Phys. Lett. A 2018, 382, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimization problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Huang, H.; Huang, C.; Han, B. An improved TLBO with logarithmic spiral and triangular mutation for global optimization. Neural Comput. Appl. 2019, 31, 4435–4450. [Google Scholar] [CrossRef]
- Kim, N.I.; Kim, S.; Lee, J. Vibration-based damage detection of planar and space trusses using differential evolution algorithm. Appl. Acoust. 2019, 148, 308–321. [Google Scholar] [CrossRef]
- Kaveh, A.; Vaez, S.H.; Hosseini, P.; Fathali, M.A. A new two-phase method for damage detection in skeletal structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 49–65. [Google Scholar] [CrossRef]
- Chen, W.H.; Lu, Z.R.; Lin, W.; Chen, S.H.; Ni, Y.Q.; Xia, Y.; Liao, W.Y. Theoretical and experimental modal analysis of the Guangzhou New TV Tower. Eng. Struct. 2011, 33, 3628–3646. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Xia, Y.; Lin, W.; Chen, W.H.; Ko, J.M. SHM benchmark for high-rise structures: A reduced-order finite element model and field measurement data. Smart Struct. Syst. 2012, 10, 411–426. [Google Scholar] [CrossRef] [Green Version]

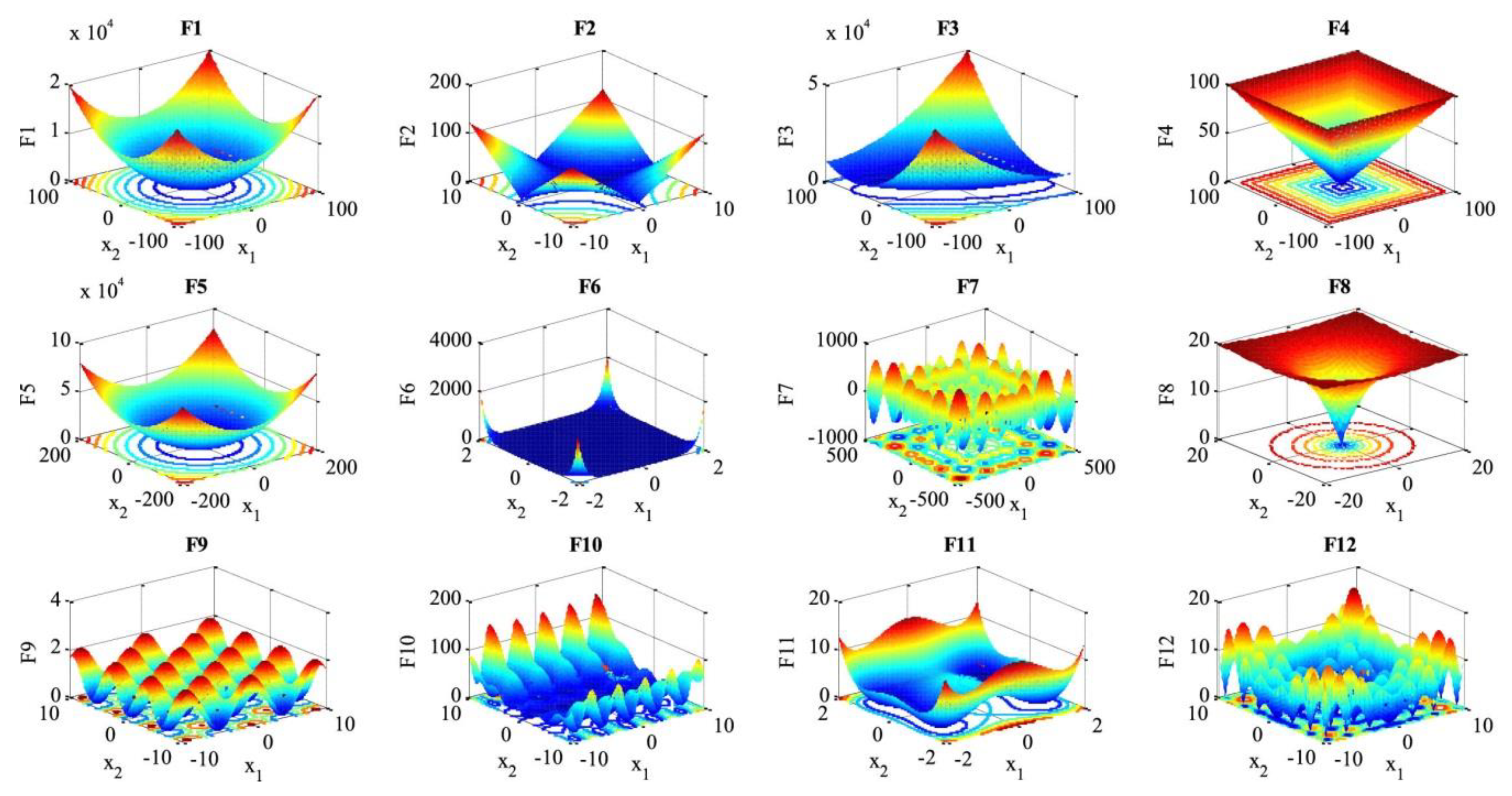





| No. | Name | Formula | Dim | Range |
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | ||
| Schwefel 2.22 | 30 | [−10, 10] | ||
| Schwefel 1.2 | 30 | [−100, 100] | ||
| Schwefel 2.21 | 30 | [−100, 100] | ||
| Step 2 | 30 | [−100, 100] | ||
| Brown | 30 | [−1, 4] | ||
| Schwefel 2.26 | 30 | [−500, 500] | ||
| Ackley | 30 | [−32, 32] | ||
| Griewank | 30 | [−600, 600] | ||
| Penalized | 30 | [−50, 50] | ||
| Qing | 30 | [−500, 500] | ||
| Alpine 1 | 30 | [−100, 100] |
| No. | VPSS | LAPO | GWO | DE | PSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.1 × 10−60 | 2.1 × 10−60 | 8.3 × 10−7 | 8.1 × 10−7 | 3.7 × 10−28 | 5.2 × 10−28 | 2.6 × 10−4 | 9.8 × 10−5 | 7.1 × 10−5 | 6.8 × 10−5 |
| F2 | 2.2 × 10−31 | 1.8 × 10−31 | 2.9 × 10−4 | 2.9 × 10−4 | 9.7 × 10−17 | 3.9 × 10−17 | 3.9 × 10−3 | 1.0 × 10−3 | 4.5 × 10−4 | 2.4 × 10−4 |
| F3 | 8.1 × 10−24 | 1.9 × 10−23 | 2.9 × 10−2 | 4.2 × 10−2 | 3.9 × 10−6 | 7.2 × 10−6 | 37450 | 5799.2 | 427.34 | 191.25 |
| F4 | 3.4 × 10−26 | 2.4 × 10−26 | 8.5 × 10−4 | 4.7 × 10−4 | 5.7 × 10−7 | 5.1 × 10−7 | 9.4889 | 2.0314 | 3.2985 | 7.6 × 10−1 |
| F5 | 4.8 × 10−6 | 7.2 × 10−6 | 1.0 × 10−1 | 1.2 × 10−1 | 8.6 × 10−1 | 4.6 × 10−1 | 3.4 × 10−4 | 1.3 × 10−4 | 3.6 × 10−5 | 5.8 × 10−5 |
| F6 | 1.6 × 10−62 | 3.2 × 10−62 | 3.1 × 10−8 | 4.0 × 10−8 | 1.3 × 10−30 | 1.5 × 10−30 | 5.6 × 10−7 | 2.5 × 10−7 | 3.2 × 10−7 | 6.0 × 10−7 |
| F7 | −7508.4 | 1262.5 | −4639.1 | 312.88 | −5822.0 | 995.73 | −6706.5 | 420.66 | −6272.1 | 543.41 |
| F8 | 4.4 × 10−15 | 0.0000 | 1.4 × 10−4 | 1.4 × 10−4 | 1.0 × 10−13 | 9.5 × 10−15 | 5.1 × 10−3 | 2.2 × 10−3 | 1.3 × 10−1 | 4.2 × 10−1 |
| F9 | 0.0000 | 0.0000 | 6.3 × 10−3 | 1.3 × 10−2 | 5.7 × 10−3 | 1.3 × 10−2 | 1.8 × 10−2 | 5.4 × 10−2 | 1.2 × 10−2 | 1.3 × 10−2 |
| F10 | 1.9 × 10−7 | 1.8 × 10−7 | 1.1 × 10−2 | 3.2 × 10−2 | 4.1 × 10−2 | 2.1 × 10−2 | 5.9 × 10−4 | 6.2 × 10−4 | 1.0 × 10−2 | 3.2 × 10-02 |
| F11 | 1.6 × 10−1 | 2.9 × 10−1 | 359.96 | 723.34 | 1.5 × 10+03 | 534.71 | 1320.8 | 222.23 | 2.6347 | 4.6566 |
| F12 | 3.5 × 10−30 | 5.5 × 10−30 | 2.1 × 10−4 | 2.0 × 10−4 | 1.9 × 10−3 | 1.5 × 10−3 | 20.253 | 3.3790 | 3.4 × 10−1 | 4.1 × 10−1 |
| Condition | Method | Damage Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Sdt. | Avg. | Sdt. | Avg. | Sdt. | Avg. | Sdt. | ||||
| Noise-free | VPSS | 0.300 | 3.7 × 10−4 | 0.200 | 5.1 × 10−4 | 0.350 | 2.7 × 10−4 | 0.150 | 8.7 × 10−5 | 0.000 | 1.0 × 10−8 |
| LAPO | 0.293 | 5.1 × 10−3 | 0.159 | 5.4 × 10−2 | 0.350 | 1.6 × 10−3 | 0.148 | 2.3 × 10−3 | 0.074 | 1.3 × 10−5 | |
| GWO | 0.256 | 8.9 × 10−2 | 0.139 | 8.9 × 10−2 | 0.309 | 1.1 × 10−1 | 0.116 | 6.1 × 10−2 | 0.081 | 2.2 × 10−4 | |
| DE | 0.260 | 2.7 × 10−2 | 0.142 | 8.5 × 10−2 | 0.332 | 3.2 × 10−2 | 0.106 | 2.8 × 10−2 | 0.301 | 4.2 × 10−4 | |
| PSO | 0.216 | 5.3 × 10−2 | 0.181 | 6.0 × 10−2 | 0.315 | 2.4 × 10−2 | 0.127 | 1.4 × 10−2 | 0.420 | 3.1 × 10−4 | |
| Noisy | VPSS | 0.300 | 2.0 × 10−3 | 0.176 | 1.8 × 10−3 | 0.345 | 1.6 × 10−3 | 0.115 | 1.7 × 10−3 | 0.049 | 1.1 × 10−4 |
| LAPO | 0.294 | 5.9 × 10−3 | 0.141 | 7.1 × 10−2 | 0.345 | 3.6 × 10−3 | 0.114 | 1.9 × 10−3 | 0.112 | 1.7 × 10−4 | |
| GWO | 0.295 | 9.4 × 10−3 | 0.158 | 6.2 × 10−2 | 0.310 | 1.1 × 10−1 | 0.083 | 5.5 × 10−2 | 0.101 | 2.9 × 10−4 | |
| DE | 0.232 | 2.9 × 10−2 | 0.093 | 7.4 × 10−2 | 0.331 | 4.3 × 10−2 | 0.083 | 2.4 × 10−2 | 0.560 | 5.1 × 10−4 | |
| PSO | 0.198 | 4.6 × 10−2 | 0.171 | 6.9 × 10−2 | 0.306 | 2.7 × 10−2 | 0.087 | 2.7 × 10−2 | 0.610 | 6.8 × 10−4 | |
| Condition | Method | Damage Variables | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x6 | x24 | x40 | x51 | ||||||||
| Avg. | Sdt. | Avg. | Sdt. | Avg. | Sdt. | Avg. | Sdt. | ||||
| Noise-free | VPSS | 0.200 | 2.4 × 10−4 | 0.150 | 5.4 × 10−4 | 0.300 | 5.8 × 10−4 | 0.250 | 1.9 × 10−4 | 0.000 | 4.3 × 10−8 |
| LAPO | 0.197 | 5.5 × 10−3 | 0.134 | 1.7 × 10−2 | 0.287 | 1.0 × 10−2 | 0.246 | 4.0 × 10−3 | 0.035 | 2.9 × 10−5 | |
| GWO | 0.193 | 6.9 × 10−3 | 0.078 | 6.4 × 10−2 | 0.221 | 1.2 × 10−1 | 0.240 | 5.4 × 10−3 | 0.041 | 1.5 × 10−4 | |
| DE | 0.178 | 1.9 × 10−2 | 0.094 | 1.0 × 10−1 | 0.168 | 7.9 × 10−2 | 0.223 | 1.7 × 10−2 | 0.233 | 1.5 × 10−3 | |
| PSO | 0.167 | 1.1 × 10−2 | 0.125 | 1.9 × 10−2 | 0.238 | 3.2 × 10−2 | 0.236 | 8.2 × 10−3 | 0.246 | 2.4 × 10−4 | |
| Noisy | VPSS | 0.200 | 1.1 × 10−3 | 0.158 | 9.6 × 10−3 | 0.277 | 1.8 × 10−3 | 0.256 | 4.0 × 10−3 | 0.035 | 2.9 × 10−4 |
| LAPO | 0.196 | 5.2 × 10−3 | 0.134 | 4.5 × 10−2 | 0.263 | 2.2 × 10−2 | 0.250 | 9.4 × 10−3 | 0.059 | 5.0 × 10−4 | |
| GWO | 0.170 | 6.2 × 10−2 | 0.059 | 8.1 × 10−2 | 0.181 | 1.2 × 10−1 | 0.223 | 7.8 × 10−2 | 0.054 | 9.1 × 10−4 | |
| DE | 0.189 | 2.8 × 10−2 | 0.204 | 9.9 × 10−2 | 0.208 | 8.1 × 10−2 | 0.264 | 3.1 × 10−2 | 0.200 | 1.9 × 10−3 | |
| PSO | 0.181 | 1.2 × 10−2 | 0.160 | 1.9 × 10−2 | 0.226 | 3.5 × 10−2 | 0.240 | 1.2 × 10−2 | 0.320 | 8.6 × 10−4 | |
| Condition | Method | Damage Variables | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg | Std | Avg | Std | Avg | Std | ||||
| Noise-free | VPSS | 0.250 | 7.1 × 10−5 | 0.350 | 8.3 × 10−5 | 0.150 | 1.1 × 10−4 | 0.000 | 3.5 × 10−9 |
| LAPO | 0.249 | 7.0 × 10−4 | 0.349 | 1.6 × 10−3 | 0.151 | 1.4 × 10−3 | 0.000 | 1.5 × 10−6 | |
| GWO | 0.247 | 6.2 × 10−3 | 0.312 | 1.4 × 10−1 | 0.121 | 9.0 × 10−2 | 0.033 | 1.9 × 10−4 | |
| DE | 0.248 | 9.6 × 10−2 | 0.174 | 1.8 × 10−1 | 0.155 | 1.3 × 10−1 | 0.161 | 1.3 × 10−2 | |
| PSO | 0.226 | 2.1 × 10−2 | 0.302 | 3.2 × 10−2 | 0.193 | 2.8 × 10−2 | 0.064 | 8.2 × 10−4 | |
| Noisy | VPSS | 0.253 | 1.2 × 10−3 | 0.327 | 3.9 × 10−3 | 0.168 | 1.6 × 10−3 | 0.012 | 6.8 × 10−5 |
| LAPO | 0.253 | 3.6 × 10−3 | 0.325 | 5.5 × 10−3 | 0.167 | 6.7 × 10−3 | 0.015 | 7.0 × 10−5 | |
| GWO | 0.250 | 4.4 × 10−3 | 0.232 | 1.5 × 10−1 | 0.190 | 3.9 × 10−2 | 0.016 | 2.3 × 10−4 | |
| DE | 0.184 | 1.2 × 10−1 | 0.170 | 1.2 × 10−1 | 0.145 | 1.1 × 10−1 | 0.180 | 1.7 × 10−2 | |
| PSO | 0.236 | 8.9 × 10−3 | 0.227 | 5.9 × 10−2 | 0.224 | 3.0 × 10−2 | 0.100 | 1.8 × 10−3 | |
| Condition | Method | Damage Variables | |||
|---|---|---|---|---|---|
| x18 | |||||
| Avg. | Sdt. | ||||
| Noise-free | VPSS | 0.200 | 8.1 × 10−4 | 0.000 | 1.7 × 10−8 |
| LAPO | 0.190 | 5.3 × 10−3 | 0.047 | 7.2 × 10−6 | |
| GWO | 0.362 | 5.8 × 10−2 | 0.372 | 4.3 × 10−3 | |
| DE | 0.406 | 2.0 × 10−2 | 0425 | 1.1 × 10−2 | |
| PSO | 0.378 | 9.7 × 10−3 | 0.410 | 5.4 × 10−4 | |
| Noisy | VPSS | 0.207 | 7.3 × 10−3 | 0.024 | 4.1 × 10−5 |
| LAPO | 0.178 | 9.9 × 10−3 | 0.082 | 8.7 × 10−5 | |
| GWO | 0.332 | 7.9 × 10−2 | 0.300 | 1.6 × 10−3 | |
| DE | 0.421 | 4.9 × 10−2 | 0.430 | 9.8 × 10−3 | |
| PSO | 0.315 | 3.7 × 10−2 | 0.362 | 5.7 × 10−4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohebian, P.; Aval, S.B.B.; Noori, M.; Lu, N.; Altabey, W.A. Visible Particle Series Search Algorithm and Its Application in Structural Damage Identification. Sensors 2022, 22, 1275. https://doi.org/10.3390/s22031275
Mohebian P, Aval SBB, Noori M, Lu N, Altabey WA. Visible Particle Series Search Algorithm and Its Application in Structural Damage Identification. Sensors. 2022; 22(3):1275. https://doi.org/10.3390/s22031275
Chicago/Turabian StyleMohebian, Pooya, Seyed Bahram Beheshti Aval, Mohammad Noori, Naiwei Lu, and Wael A. Altabey. 2022. "Visible Particle Series Search Algorithm and Its Application in Structural Damage Identification" Sensors 22, no. 3: 1275. https://doi.org/10.3390/s22031275
APA StyleMohebian, P., Aval, S. B. B., Noori, M., Lu, N., & Altabey, W. A. (2022). Visible Particle Series Search Algorithm and Its Application in Structural Damage Identification. Sensors, 22(3), 1275. https://doi.org/10.3390/s22031275









