Fabrication and Underwater Testing of a Vector Hydrophone Comprising a Triaxial Piezoelectric Accelerometer and Spherical Hydrophone
Abstract
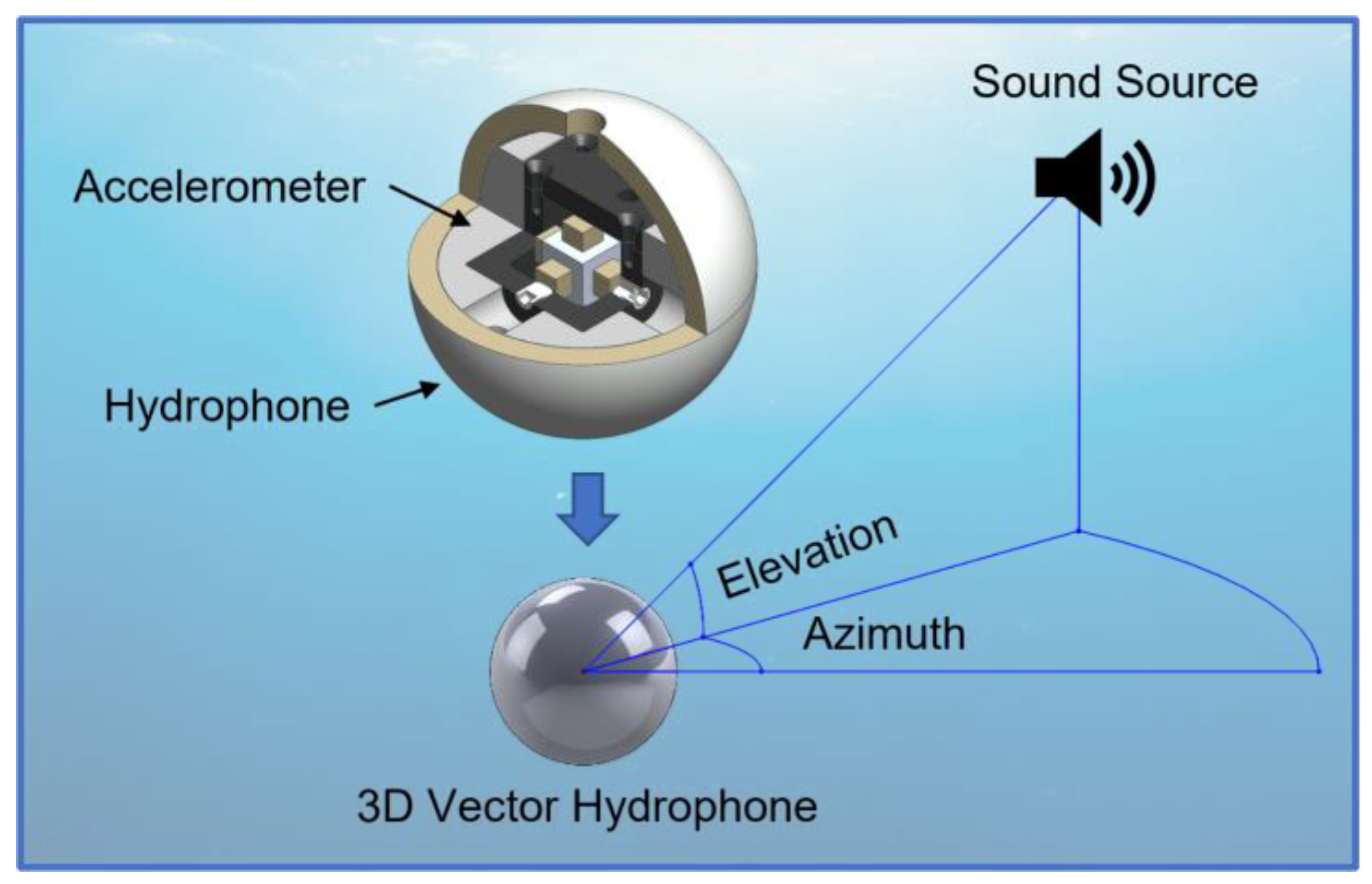
1. Introduction
2. Design and Fabrication
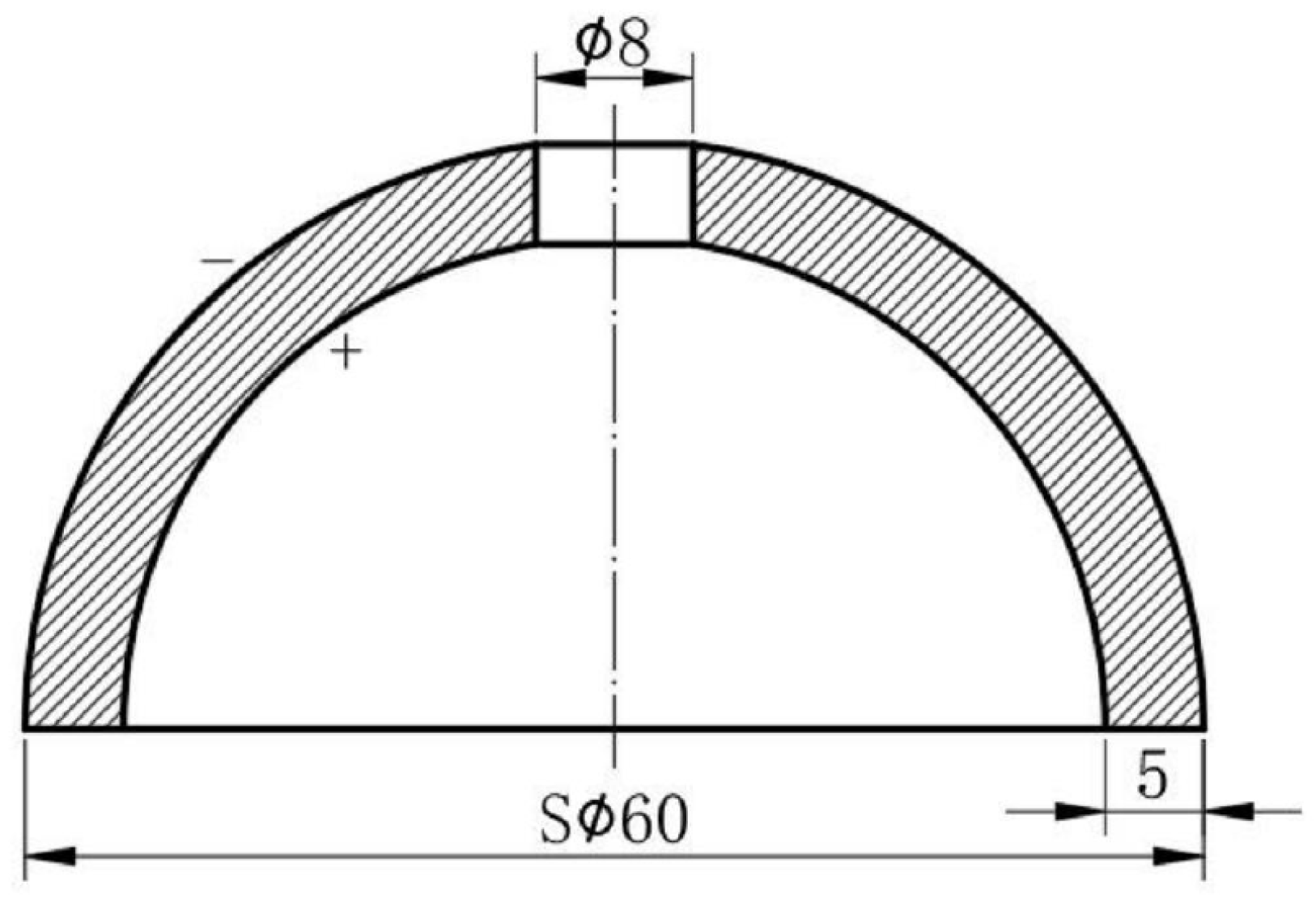
2.1. Spherical Hydrophone
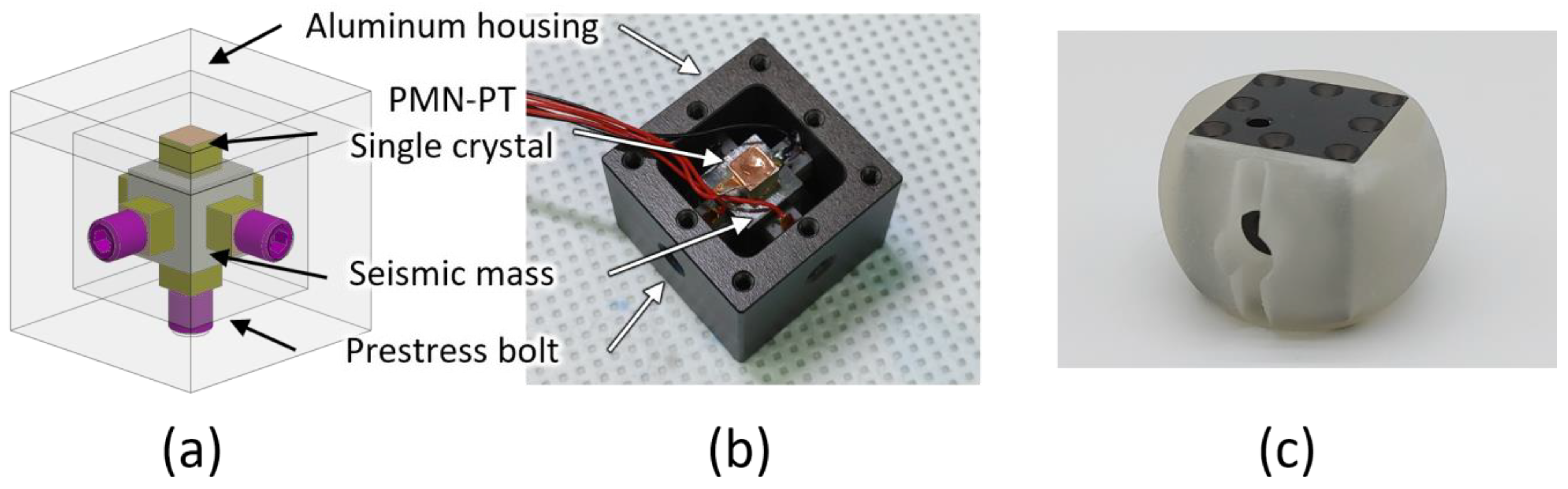
2.2. Triaxial Piezoelectric Accelerometer
2.3. Assembly of the 3D Vector Hydrophone
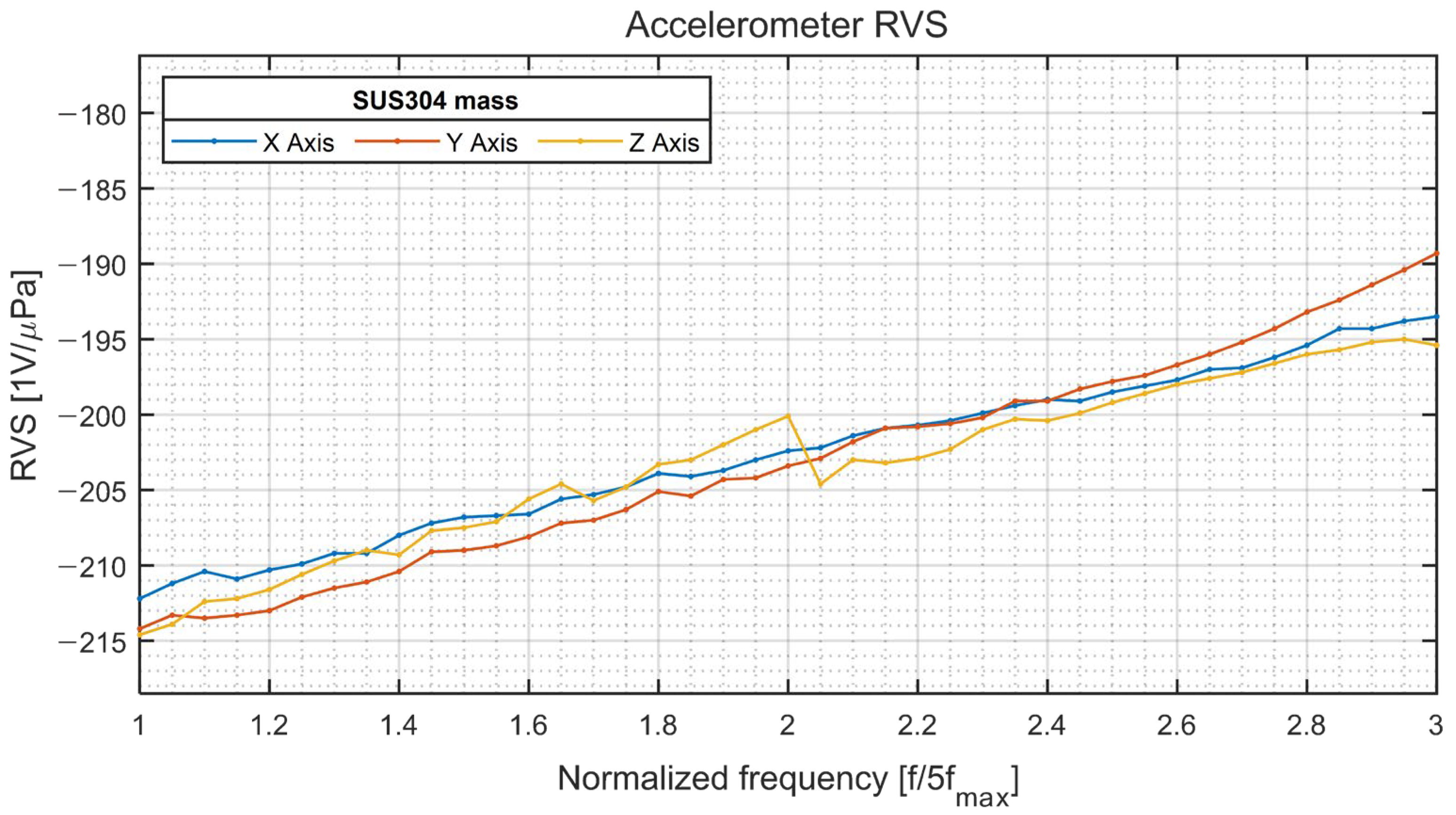
3. Characterization of the Accelerometer
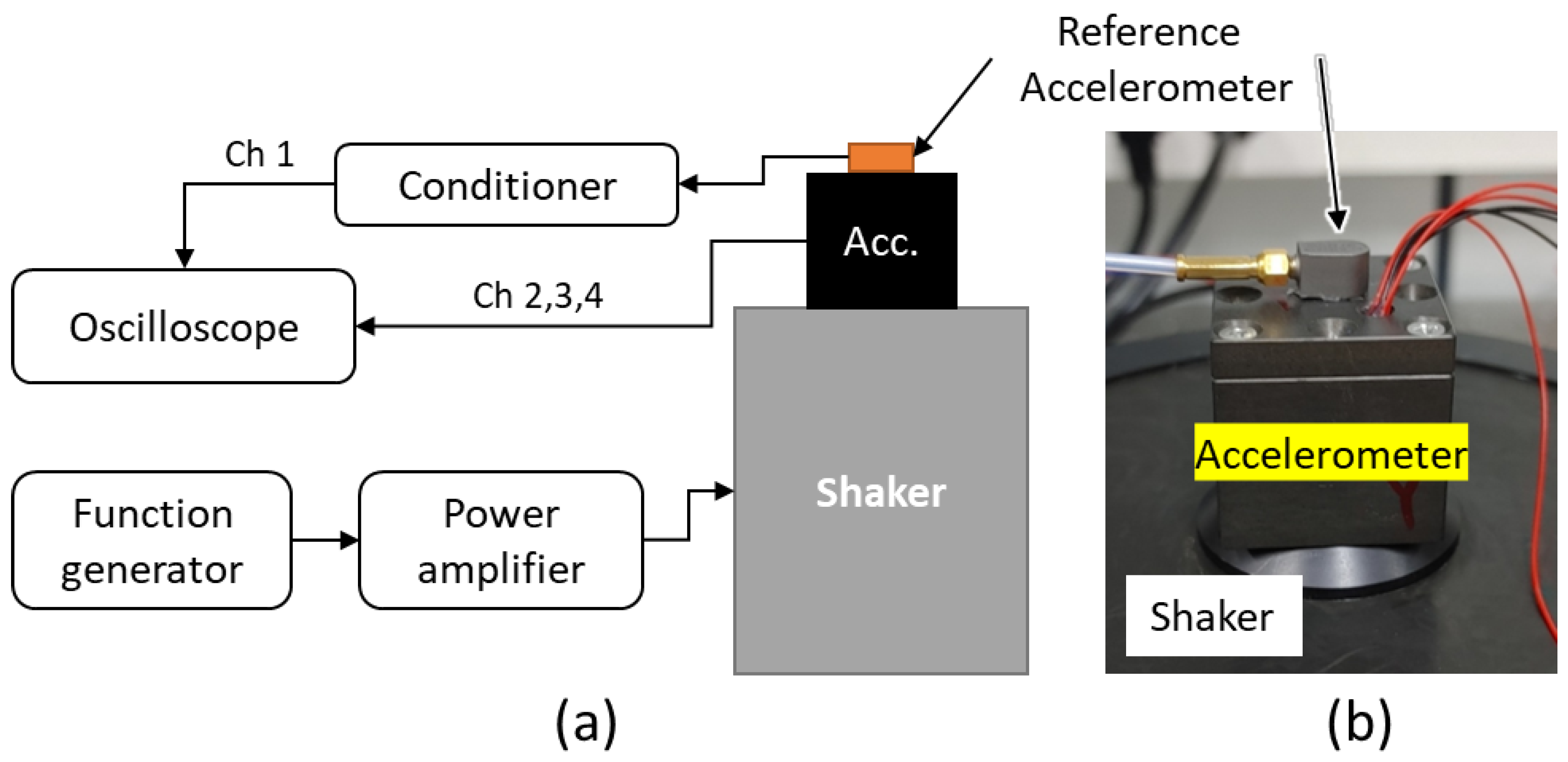
3.1. Sensitivity Measurement in Air
3.2. Directivity Measurement in Air
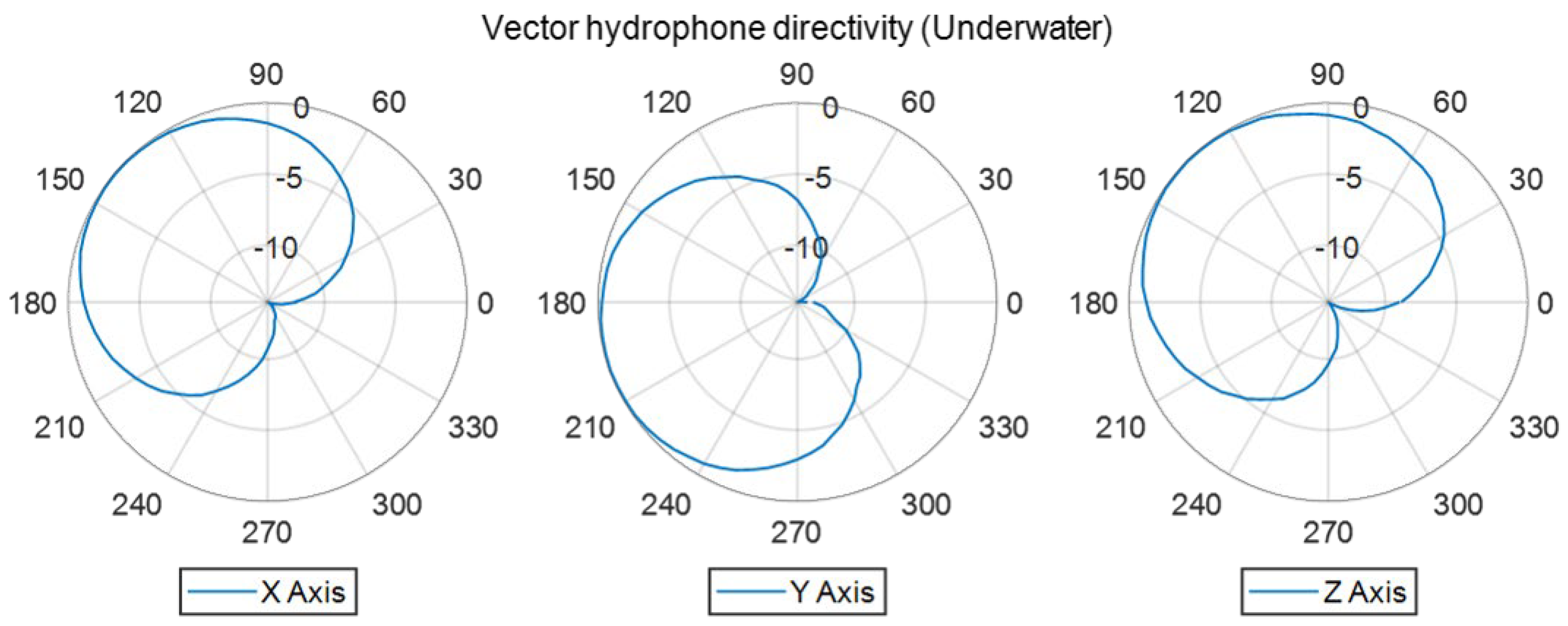
4. Underwater Characterization of the 3D Vector Hydrophone
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guojun, Z.; Panpan, W.; Linggang, G.; Jijun, X.; Wendong, Z. Improvement of the Mems Bionic Vector Hydrophone. Microelectron. Eng. 2011, 42, 815–819. [Google Scholar] [CrossRef]
- Agarwal, A.; Kumar, A.; Aggarwal, M.; Bahl, R. Design and Experimentation with Acoustic Vector Sensors. In Proceedings of the 2009 International Symposium on Ocean Electronics (SYMPOL 2009), Cochin, India, 18–20 November 2009; pp. 139–146. [Google Scholar]
- Holler, R.A. The Evolution of the Sonobuoy from World War II to the Cold War; ADA597432; Defense Technical Information Center: Alexandria, VA, USA, 2014. [Google Scholar]
- Nair, B.M.; Kumar, A.; Bahl, R. Left-Right Ambiguity Resolution Methods for Closely Spaced Arrays. IEEE J. Ocean. Eng. 2022, 47, 445–456. [Google Scholar] [CrossRef]
- Brinkmann, K.; Hurka, J. Broadband Passive Sonar Tracking. In Proceedings of the GI Jahrestagung, Como, Italy, 18–20 May 2004; pp. 2397–2404. [Google Scholar]
- Newhall, B.K.; Jenkins, J.W.; Dietz, J.E.G. Improved Estimation of the Shape of Towed Sonar Arrays. In Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference, Como, Italy, 18–20 May 2004; pp. 873–876. [Google Scholar]
- Leslie, C.B.; Kendall, J.M.; Jones, J.L. Hydrophone for Measuring Particle Velocity. J. Acoust. Soc. Am. 1956, 28, 711–715. [Google Scholar] [CrossRef]
- Silvia, M.T.; Richards, R.T. A Theoretical and Experimental Investigation of Low-Frequency Acoustic Vector Sensors. In Proceedings of the OCEANS ‘02 MTS/IEEE, Biloxi, MI, USA, 29–31 October 2002; Volume 1883, pp. 1886–1897. [Google Scholar]
- Saheban, H.; Kordrostami, Z. Hydrophones, Fundamental Features, Design Considerations, and Various Structures: A Review. Sens. Actuators A 2021, 329, 112790. [Google Scholar] [CrossRef]
- Shipps, J.C.; Deng, K. A Miniature Vector Sensor for Line Array Applications. In Proceedings of the Oceans 2003, San Diego, CA, USA, 22–26 September 2003; pp. 2367–2370. [Google Scholar]
- Wilcoxon, W.C. Vector Sensor Device and Calibration Method. U.S. Patent 7,026,826, 11 April 2006. [Google Scholar]
- Xue, C.Y.; Chen, S.; Zhang, W.D.; Zhang, B.Z.; Zhang, G.J.; Qiao, H. Design, Fabrication, and Preliminary Characterization of a Novel Mems Bionic Vector Hydrophone. Microelectron. J. 2007, 38, 1021–1026. [Google Scholar] [CrossRef]
- Xu, Q.D.; Zhang, G.J.; Ding, J.W.; Wang, R.X.; Pei, Y.; Ren, Z.M.; Shang, Z.Z.; Xue, C.Y.; Zhang, W.D. Design and Implementation of Two-Component Cilia Cylinder Mems Vector Hydrophone. Sens. Actuators A 2018, 277, 142–149. [Google Scholar] [CrossRef]
- Yeon, A.; Yeo, H.G.; Roh, Y.; Kim, K.; Seo, H.S.; Choi, H. A Piezoelectric Micro-Electro-Mechanical System Vector Sensor with a Mushroom-Shaped Proof Mass for a Dipole Beam Pattern. Sens. Actuators A 2021, 332, 113129. [Google Scholar] [CrossRef]
- Lim, Y.; Joh, C.; Seo, H.; Kim, J.; Roh, Y. Design and Fabrication of a Multimode Ring Vector Hydrophone. Jpn. J. Appl. Phys. 2014, 53, 07KD07. [Google Scholar] [CrossRef]
- Lim, Y.; Lee, J.; Joh, C.; Seo, H.; Roh, Y. Design of a Multimode Piezoelectric Spherical Vector Sensor for a Cardioid Beam Pattern. J. Acoust. Soc. Kr. 2013, 32, 32–42. [Google Scholar] [CrossRef][Green Version]
- Zhou, H.; Hong, L.; Sun, X.; Liu, W. An Inertial-Type Acoustic Vector Sensor Used in Airborne Sonobuoy. Instrum. Exp. Tech. 2021, 64, 153–156. [Google Scholar] [CrossRef]
- Cho, Y.H.; Je, Y.; Jeong, W.B. A Miniaturized Acoustic Vector Sensor with PIN-PMN-PT Single Crystal Cantilever Beam Accelerometers. Acta Acust. 2020, 4, 17. [Google Scholar] [CrossRef]
- Khadidos, A.O.; Shitharth, S.; Manoharan, H.; Yafoz, A.; Khadidos, A.O.; Alyoubi, K.H. An Intelligent Security Framework Based on Collaborative Mutual Authentication Model for Smart City Networks. IEEE Access 2022, 10, 85289–85304. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater Acoustic Sensor Networks: Research Challenges. Ad Hoc Networks. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- El-Rabaie, S.; Nabil, D.; Mahmoud, R.; Alsharqawy, M.A. Underwater Wireless Sensor Networks (Uwsn), Architecture, Routing Protocols, Simulation and Modeling Tools, Localization, Security Issues and Some Novel Trends. Netw. Commun. Eng. 2015, 7, 335–354. [Google Scholar]
- Mudiyala, J.; Shim, H.; Kim, D.; Roh, Y. Development of a Dual-Layer Structure for Cymbal Transducer Arrays to Achieve a Wider Bandwidth. Sensors 2022, 22, 6614. [Google Scholar] [CrossRef] [PubMed]
- Yeo, H.G.; Choi, J.; Jin, C.; Pyo, S.; Roh, Y.; Choi, H. The Design and Optimization of a Compressive-Type Vector Sensor Utilizing a PMN-28PT Piezoelectric Single-Crystal. Sensors 2019, 19, 5155. [Google Scholar] [CrossRef] [PubMed]
- Sherman, C.; Butler, J. Transducers and Arrays for Underwater Sound; The Underwater Acoustics Series; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33139-3. [Google Scholar]
- iBULe PHOTONICS. Piezoelectric Single Crystal Material. Available online: http://www.ibule.com/product/product1.php (accessed on 25 September 2022).







| Parameter | Unit | Value |
|---|---|---|
| Resonant frequency (Fr) | kHz | 36.5 ± 2.5 |
| Bandwidth ( | kHz | 3.8 |
| Capacitance (C) | pf | 11,700 ± 15% |
| Electromechanical coupling coefficient | kp | 0.58 | Piezoelectric charge constant (10−12 m/V) | d31 | −138 |
| k31 | 0.34 | d33 | 300 | ||
| k33 | 0.68 | Piezoelectric voltage constant (10−3 Vm/N) | g31 | 11 | |
| kt | 0.48 | g33 | 24 | ||
| Free dielectric constant | 1420 | Sound wave velocity (m/s) | 3360 | ||
| Dielectric dissipation factor | tanδ | 0.5 | 3200 | ||
| Elastic compliance constant | 13.2 | 3750 | |||
| Mechanical quality factor | 600 | 4150 | |||
| Young’s modulus (109 N/m2) | 76 | Curie temperature (°C) | 320 | ||
| Density (g/m3) | 7500 | Poisson’s ratio | 0.30 |
| Parameter | Symbol | Units | [001] Poled | |
|---|---|---|---|---|
| Low PT | High PT | |||
| Relative dielectric constant | - | 4842 | 7000 | |
| Piezoelectric constant | ×10−12 C/N | = 1282 | = 1620 | |
| Elastic compliance | ×10−12 m2/N | = 47 | = 56 | |
| Curie temperature | °C | 95 | 85 | |
| Coercive field | kV/cm | 2 | 2.5 | |
| Density | kg/m3 | 8080 | ||
| Parameter | Symbol | Units | |
|---|---|---|---|
| Dimensions | – | mm | 5 × 5 × 4 |
| Capacitance | nF | 0.249–0.278 | |
| Dielectric dissipation factor | % | 0.11–0.31 | |
| Resonance frequency | kHz | 155.50–163.00 | |
| Antiresonance frequency | kHz | 237.25–243.00 | |
| Free dielectric constant | – | 4506–5030 |
| Parameter | Units | Material | |
|---|---|---|---|
| Tungsten Alloy | Stainless Steel | ||
| Dimensions | mm | 9.5 × 9.5 × 9.5 | |
| Density | g/cm3 | 19.25 | 7.93 |
| Mass (measured) | g | 19.68 | 6.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roh, T.; Yeo, H.G.; Joh, C.; Roh, Y.; Kim, K.; Seo, H.-s.; Choi, H. Fabrication and Underwater Testing of a Vector Hydrophone Comprising a Triaxial Piezoelectric Accelerometer and Spherical Hydrophone. Sensors 2022, 22, 9796. https://doi.org/10.3390/s22249796
Roh T, Yeo HG, Joh C, Roh Y, Kim K, Seo H-s, Choi H. Fabrication and Underwater Testing of a Vector Hydrophone Comprising a Triaxial Piezoelectric Accelerometer and Spherical Hydrophone. Sensors. 2022; 22(24):9796. https://doi.org/10.3390/s22249796
Chicago/Turabian StyleRoh, Taehoun, Hong Goo Yeo, Cheeyoung Joh, Yongrae Roh, Kyungseop Kim, Hee-seon Seo, and Hongsoo Choi. 2022. "Fabrication and Underwater Testing of a Vector Hydrophone Comprising a Triaxial Piezoelectric Accelerometer and Spherical Hydrophone" Sensors 22, no. 24: 9796. https://doi.org/10.3390/s22249796
APA StyleRoh, T., Yeo, H. G., Joh, C., Roh, Y., Kim, K., Seo, H.-s., & Choi, H. (2022). Fabrication and Underwater Testing of a Vector Hydrophone Comprising a Triaxial Piezoelectric Accelerometer and Spherical Hydrophone. Sensors, 22(24), 9796. https://doi.org/10.3390/s22249796







