An Indoor UWB 3D Positioning Method for Coplanar Base Stations
Abstract
1. Introduction
- (1)
- Initial value selection scheme: For an indoor positioning scenario with coplanar deployment of base stations, we analyzed the influence of base-station deployment on the iterative calculation. We present a method for avoiding the computational difficulties caused by initial value selection;
- (2)
- Convergence control: Since there may be multiple extreme points in the nonconvex function, we applied a convergence control method to ensure convergence to the correct solution;
- (3)
- Theoretical analysis: The accuracy of the positioning results was theoretically calculated based on the least-squares method. The influence of base-station coplanar deployment on the calculation of the positioning equation was analyzed. In addition, the effect of a near-coplanar base-station equation on the results was derived.
2. Related Work
2.1. Traditional Distance-Based Indoor Position Method
| Algorithm The Newton’s method of solving the position algorithm |
| Step = 0; Iteration initial value = ; , ; Maximum number of iterative calculations = k; |
| While () and iterations < k ; ; ; ; ; End Return |
2.2. Advanced Research
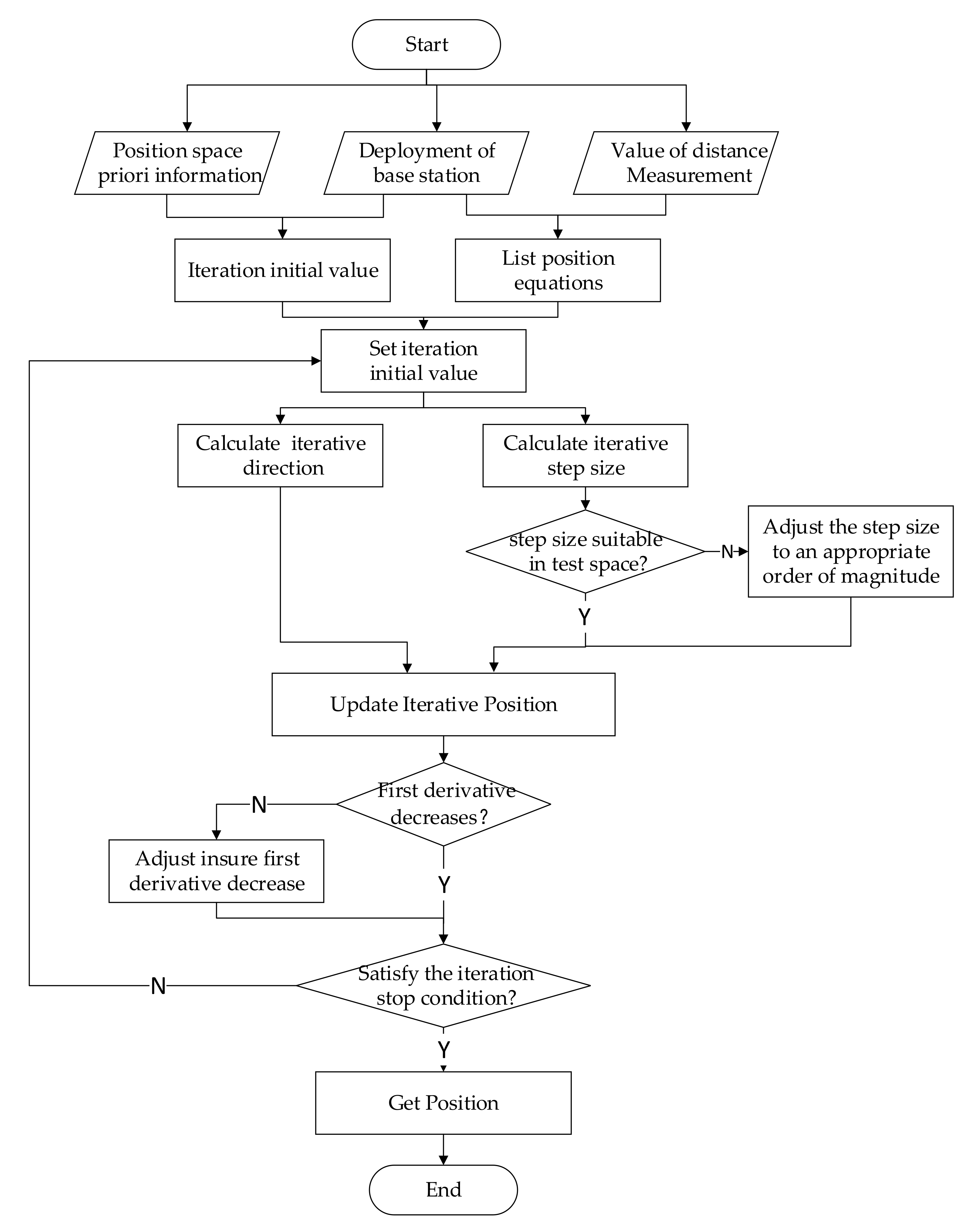
3. A Proposed Method for Base-Station Coplanar Iterations
3.1. Iterative Initial Value Selection
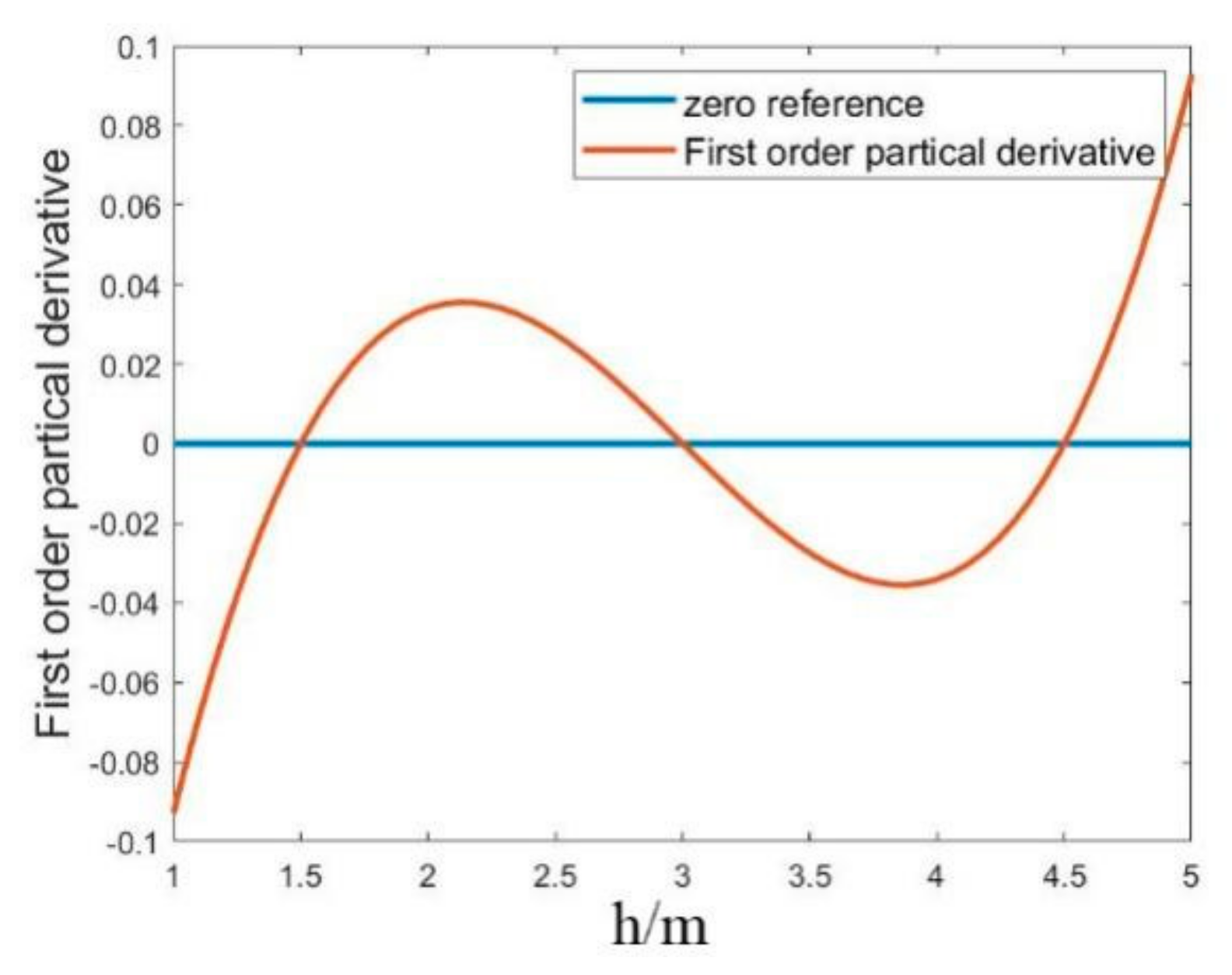
3.2. Iterative Process Controls
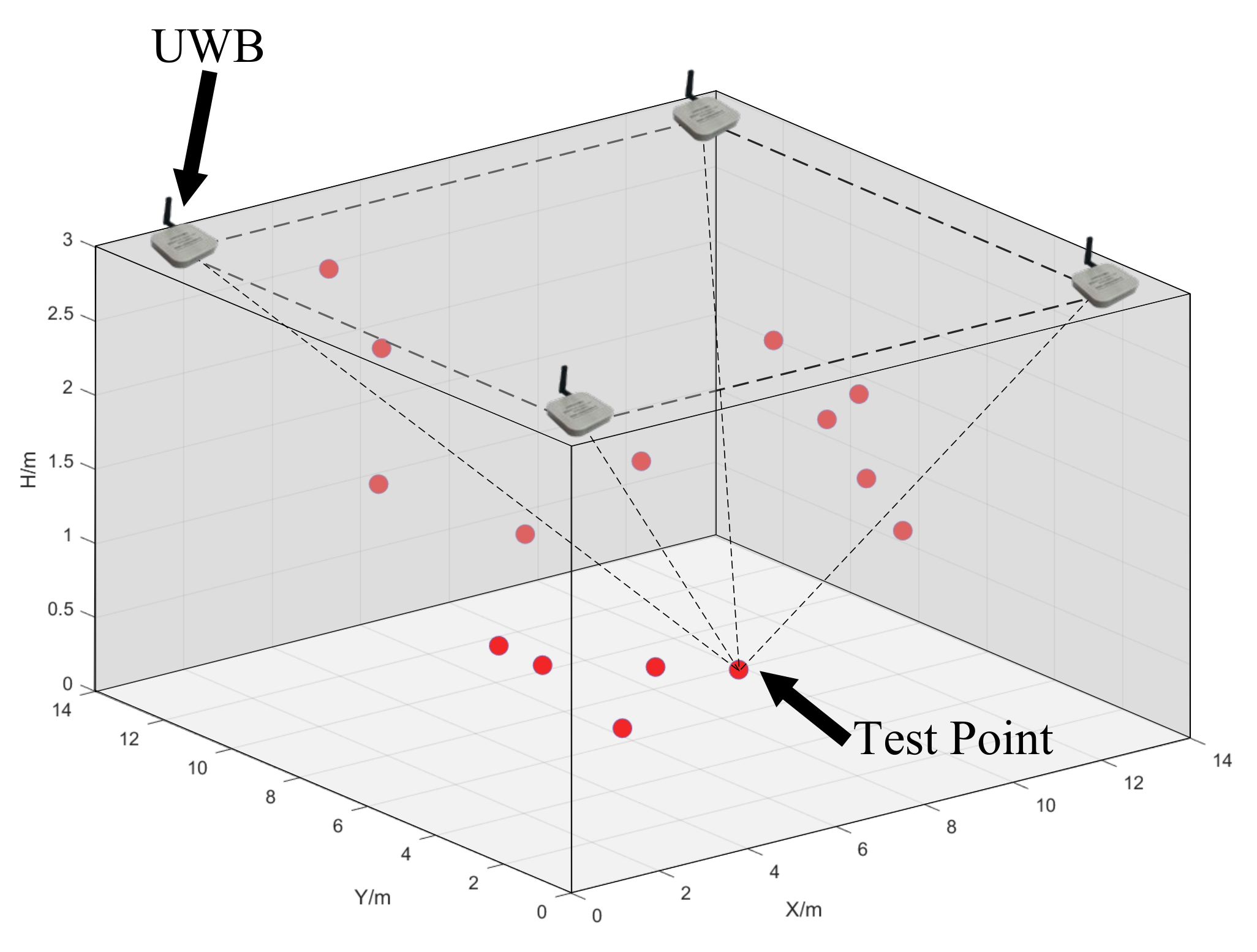
4. Experiment
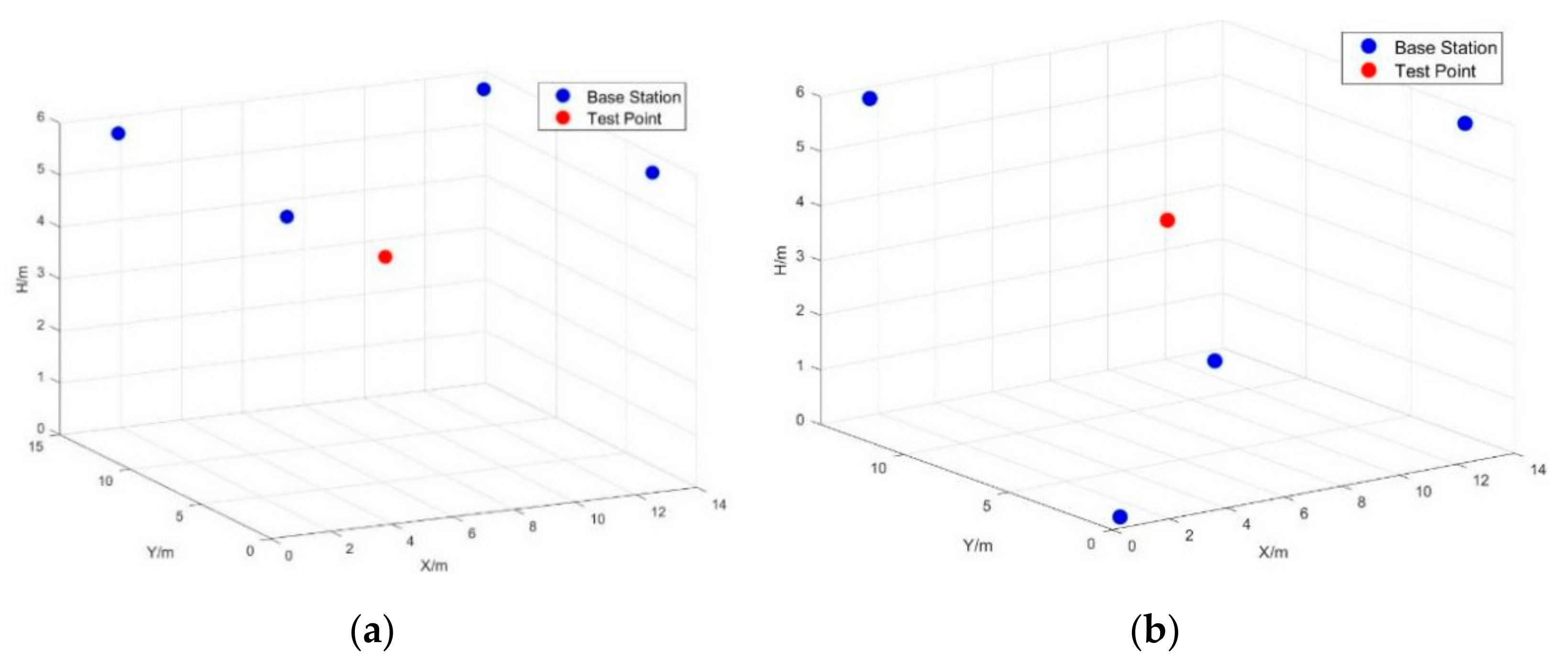
4.1. Multitest Point-Positioning Simulation
4.1.1. Internal Compliance Accuracy
4.1.2. External Compliance Accuracy
4.2. Simulation and Estimation of Different Ranging Error Positions
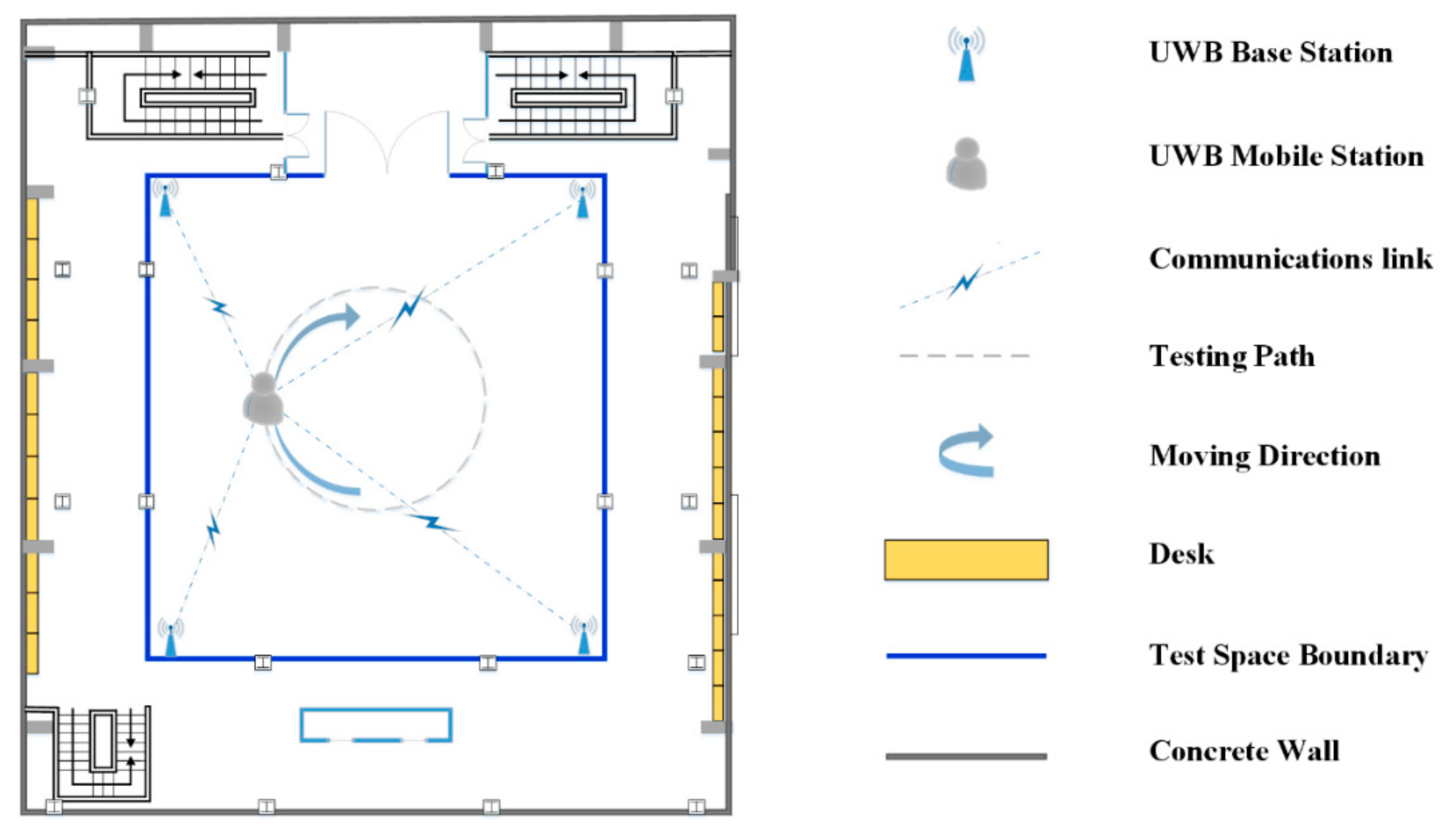
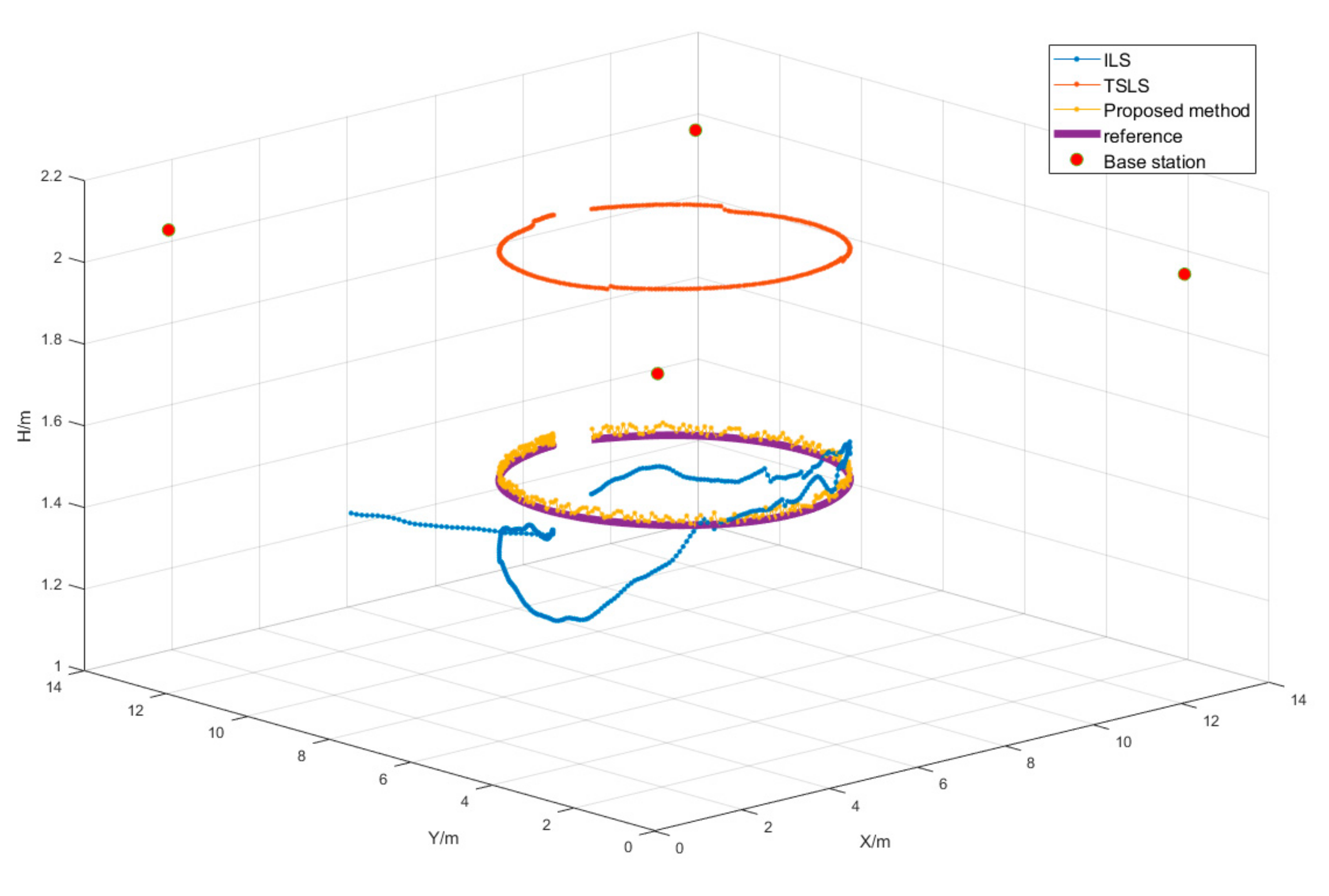
4.3. Dynamic Position Experimental Campaign
5. Performance Analysis
5.1. Least-Squares Algorithm Positioning Accuracy Analysis
5.2. Impact of the Iterative Method on Base-Station Coplanarity
5.3. Simulation Results for Different Base Station Layouts
6. Conclusions
- (1)
- Based on the observation equation, the influence of the initial value on the convergence result during calculation was analyzed, and a method for selecting the initial value under a coplanar base-station condition was proposed to facilitate the correct convergence of the iterative results;
- (2)
- Considering the observation conditions and positioning accuracy requirements, this paper proposed an iterative convergence control method. The iterative step length was adjusted to avoid iterative scattering; the intermediate value of iteration was determined to control the direction of iteration and ensure that the result converged to the correct solution;
- (3)
- The mathematical derivation of the localization accuracy of the least-squares criterion settlement method was carried out. Experiments were conducted for different base-station deployment scenarios. The results showed that the new method improved the convergence performance by about 15% in the uniform scenario and about 30% in the coplanar base-station scenario.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, G. Accurate TOA-Based UWB Localization System in Coal Mine Based on WSN. Phys. Procedia 2012, 24, 534–540. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.; Al-Khalifa, H. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Saad, M.M.; Bleakley, C.J.; Walsh, M.; Ye, T. High accuracy location estimation for a Mobile Tag using one-way UWB signaling. In Proceedings of the 2012 Ubiquitous Positioning, Indoor Navigation, and Location Based Service (UPINLBS), Helsinki, Finland, 3–4 October 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Barua, B.; Kandil, N.; Hakem, N. On performance study of TWR UWB ranging in underground mine. In Proceedings of the 2018 Sixth International Conference on Digital Information, Networking, and Wireless Communications (DINWC), Beirut, Lebanon, 25–27 April 2018; pp. 28–31. [Google Scholar] [CrossRef]
- Chehri, A.; Fortier, P.; Tardif, P.M. UWB-based sensor networks for localization in mining environments. Ad. Hoc. Netw. 2009, 7, 987–1000. [Google Scholar] [CrossRef]
- Yan, J. Algorithms for Indoor Positioning Systems Using Ultra-Wideband Signals. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Yu, K.; Sharp, I.; Guo, Y.J. Ground-Based Wireless Positioning, 1st ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Ma, C.; Jiang, L. Some research on Levenberg–Marquardt method for the nonlinear equations. Appl. Math. Comput. 2007, 184, 1032–1040. [Google Scholar] [CrossRef]
- Yuan, Y.-X. A Modified BFGS Algorithm for Unconstrained Optimization. IMA J. Numer. Anal. 1991, 11, 325–332. [Google Scholar] [CrossRef]
- Simoes, W.C.S.S.; Silva, W.A.E.; Lucena, M.M.D.; Jazdi, N.; Lucena, V.F.D. A Hybrid Indoor Positioning System Using a Linear Weighted Policy Learner and Iterative PDR. IEEE Access 2020, 8, 43630–43656. [Google Scholar] [CrossRef]
- Kumari, J.; Kumar, P.; Singh, S.K. Localization in three-dimensional wireless sensor networks: A survey. J. Supercomput. 2019, 75, 5040–5083. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, F.; Liu, Q.; Li, W. A UWB 3D Localization Algorithm Based on Residual Weighting. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; pp. 309–313. [Google Scholar] [CrossRef]
- Chu, Y.; Ganz, A. A UWB-based 3D location system for indoor environments. In Proceedings of the 2nd International Conference on Broadband Networks, Boston, MA, USA, 7 October 2005; pp. 224–232. [Google Scholar] [CrossRef]
- Department of Electronics and Multimedia Communications; Kocur, D.; Švecová, M.; Kažimír, P. Department of Mathematics and Theoretical Informatics Determining the Position of the Moving Personsin 3D Space by UWB Sensors using Taylor Series Based Localization Method. Acta Polytech. Hung. 2019, 16, 45–63. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y. Underground Personnel Positioning System Based on ZigBee. In Proceedings of the 2011 Fourth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–30 October 2011; pp. 298–300. [Google Scholar] [CrossRef]
- Wang, C.; Ning, Y.; Wang, J.; Yao, G.; Zhang, L.; Yang, H. Performance Analysis of Parameter Estimator Based on Closed-Form Newton Method for Ultrawideband Positioning. Math. Probl. Eng. 2020, 2020, 9762924. [Google Scholar] [CrossRef]
- Pan, H.; Qi, X.; Liu, M.; Liu, L. An UWB-based indoor coplanar localization and anchor placement optimization method. Neural Comput. Appl. 2022, 34, 16845–16860. [Google Scholar] [CrossRef]
- Shaffer, G.K.; Stentz, A.; Whittaker, W.L.; Fitzpatrick, K.W. Position estimator for underground mine equipment. IEEE Trans. Ind. Appl. 1992, 28, 1131–1140. [Google Scholar] [CrossRef]
- Ji, Y.; Xu, Z.; Feng, Q.; Sang, Y. Concurrent collision probability of RFID tags in underground mine personnel position systems. Min. Sci. Technol. China 2010, 20, 734–737. [Google Scholar] [CrossRef]
- Abrudan, T.E.; Xiao, Z.; Markham, A.; Trigoni, N. Underground Incrementally Deployed Magneto-Inductive 3-D Positioning Network. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4376–4391. [Google Scholar] [CrossRef]
- Xu, P. A hybrid global optimization method: The multi-dimensional case. J. Comput. Appl. Math. 2003, 155, 423–446. [Google Scholar] [CrossRef]
- Fan, L.; Chen, S.; Wan, S.; Zhu, S. Design and Completion of the Indoor Positioning System Based-on Taylor Iterative. In Proceedings of the 2015 3rd International Conference on Machinery, Materials and Information Technology Applications, Qingdao, China, 28–29 November 2015. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, Z.; Piao, A.; Zhang, S. Indoor localization algorithm based on iterative grid clustering and AP scoring. In Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 1997–2001. [Google Scholar] [CrossRef]
- Poulose, A.; Emersic, Z.; Steven Eyobu, O.; Seog Han, D. An Accurate Indoor User Position Estimator For Multiple Anchor UWB Localization. In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 21–23 October 2020; pp. 478–482. [Google Scholar] [CrossRef]
- Yan, J.; Tiberius, C.; Bellusci, G.; Janssen, G. Feasibility of Gauss-Newton method for indoor positioning. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 660–670. [Google Scholar] [CrossRef]

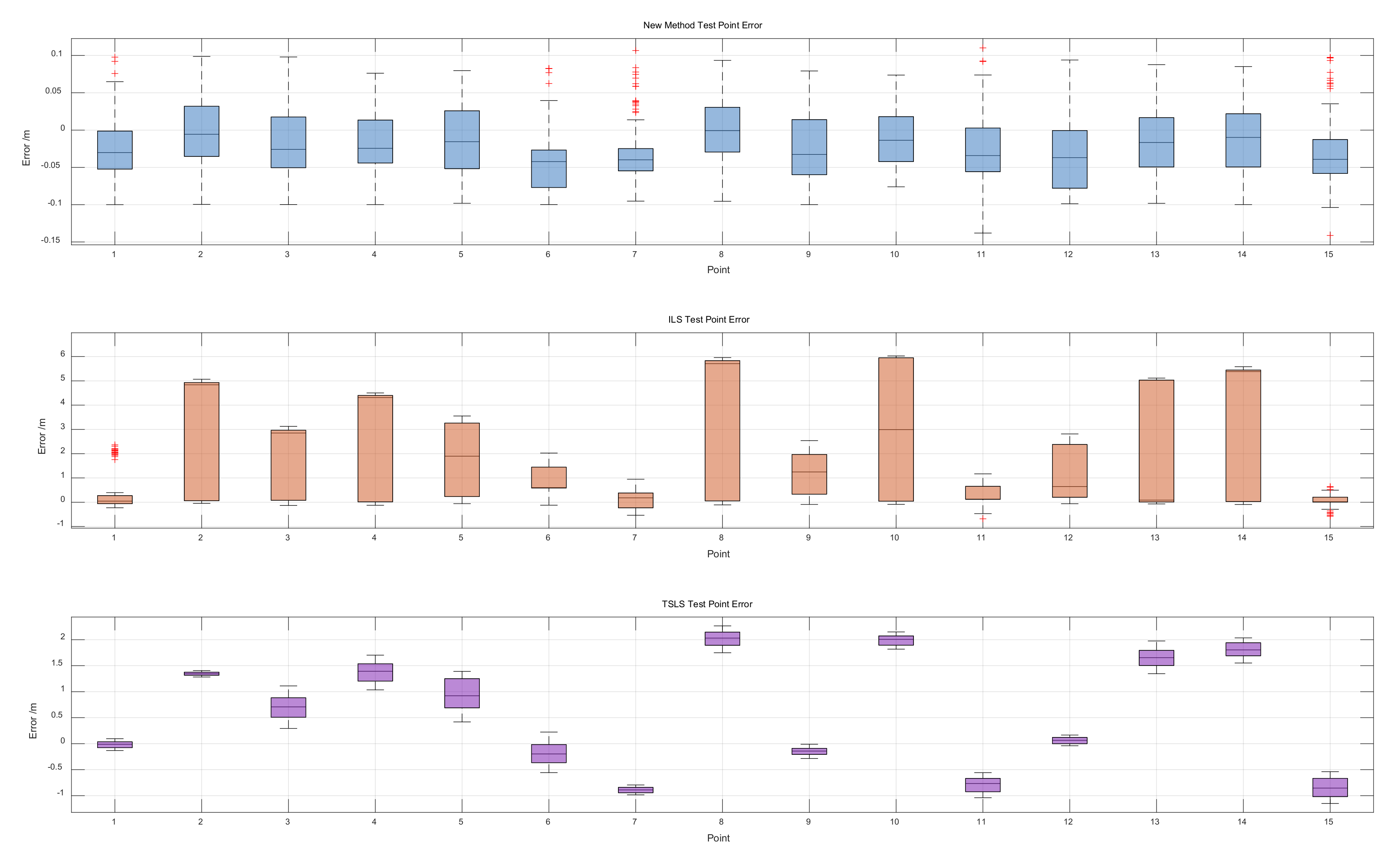




| Test Point | Maximum Error in Position/m | Standard Deviation/m | ||||
|---|---|---|---|---|---|---|
| Proposed Method | TSLS | ILS | Proposed Method | TSLS | ILS | |
| 1 | 0.098 | 0.129 | 2.364 | 0.045 | 0.088 | 0.868 |
| 2 | 0.099 | 1.285 | 5.066 | 0.048 | 0.051 | 2.449 |
| 3 | 0.098 | 0.286 | 3.124 | 0.049 | 0.072 | 1.448 |
| 4 | 0.076 | 1.034 | 4.501 | 0.043 | 0.052 | 2.200 |
| 5 | 0.08 | 0.400 | 3.553 | 0.048 | 0.058 | 1.541 |
| 6 | 0.083 | 0.566 | 2.025 | 0.044 | 0.064 | 0.596 |
| 7 | 0.083 | 0.983 | 0.947 | 0.06 | 0.215 | 0.362 |
| 8 | 0.093 | 1.749 | 5.96 | 0.039 | 0.045 | 2.905 |
| 9 | 0.079 | 0.289 | 2.538 | 0.047 | 0.092 | 0.837 |
| 10 | 0.074 | 1.808 | 6.026 | 0.036 | 0.037 | 2.967 |
| 11 | 0.093 | 1.048 | 1.169 | 0.058 | 0.202 | 0.375 |
| 12 | 0.094 | 0.039 | 2.812 | 0.052 | 0.064 | 1.098 |
| 13 | 0.088 | 1.343 | 5.112 | 0.043 | 0.045 | 2.499 |
| 14 | 0.085 | 1.553 | 5.582 | 0.045 | 0.051 | 2.668 |
| 15 | 0.073 | 1.150 | 0.646 | 0.052 | 0.154 | 0.250 |
| Test Point | Reference | ILS | TSLS | Proposed Method |
|---|---|---|---|---|
| 1 | (1.248, 7.284, 1.96) | 0.466 | −0.132 | −0.050 |
| 2 | (6.038, 5.374, 0.553) | 2.543 | 1.281 | −0.003 |
| 3 | (7.783, 8.064, 1.551) | 1.683 | 0.282 | −0.025 |
| 4 | (7.308, 10.866, 0.821) | 2.291 | 1.032 | −0.021 |
| 5 | (9.722, 2.896, 1.44) | 1.763 | 0.397 | −0.011 |
| 6 | (8.932, 3.157, 2.396) | 0.908 | −0.570 | −0.068 |
| 7 | (1.621, 7.683, 2.811) | 0.119 | −0.986 | −0.077 |
| 8 | (5.778, 6.012, 0.097) | 3.047 | 1.747 | −0.001 |
| 9 | (7.579, 1.174, 2.12) | 1.204 | −0.292 | −0.049 |
| 10 | (9.638, 7.617, 0.048) | 2.993 | 1.806 | −0.012 |
| 11 | (7.165, 3.367, 2.869) | 0.329 | −1.052 | −0.049 |
| 12 | (10.194, 5.744, 1.879) | 1.272 | −0.041 | −0.039 |
| 13 | (4.781, 8.351, 0.501) | 2.224 | 1.340 | −0.016 |
| 14 | (5.774, 8.356, 0.295) | 3.266 | 1.549 | −0.010 |
| 15 | (2.698, 10.638, 2.979) | 0.059 | −1.153 | −0.105 |
| Test Point | ILS MSE/m | TSLS MSE/m | Proposed Method MSE/m | Improvement over ILS | Improvement over TSLS |
|---|---|---|---|---|---|
| 1 | 0.088 | 0.868 | 0.001 | 36.29% | 99.89% |
| 2 | 0.051 | 2.449 | 0.002 | 76.68% | 99.91% |
| 3 | 0.072 | 1.448 | 0.001 | 76.71% | 99.92% |
| 4 | 0.052 | 2.200 | 0.001 | 40.43% | 99.97% |
| 5 | 0.058 | 1.541 | 0.001 | 78.30% | 99.91% |
| 6 | 0.064 | 0.596 | 0.002 | 77.26% | 99.74% |
| 7 | 0.215 | 0.362 | 0.002 | 82.64% | 99.45% |
| 8 | 0.045 | 2.905 | 0.001 | 29.47% | 99.96% |
| 9 | 0.092 | 0.837 | 0.002 | 71.12% | 99.82% |
| 10 | 0.037 | 2.967 | 0.001 | 88.55% | 99.97% |
| 11 | 0.202 | 0.375 | 0.002 | 64.79% | 99.50% |
| 12 | 0.064 | 1.098 | 0.001 | 65.76% | 99.90% |
| 13 | 0.045 | 2.499 | 0.001 | 77.05% | 99.96% |
| 14 | 0.051 | 2.668 | 0.001 | 34.95% | 99.96% |
| 15 | 0.154 | 0.250 | 0.001 | 80.05% | 99.52% |
| Method | Mean Error/m | Max Error/m | Min Error/m |
|---|---|---|---|
| ILS | 0.354 | 0.638 | 0.228 |
| TSLS | 0.565 | 0.579 | 0.553 |
| Proposed method | 0.024 | 0.054 | 0.002 |
| Mean Error/m | Max Error/m | Min Error/m | ||
|---|---|---|---|---|
| Multi-Point Simulation | Proposed Method | 0.0759 | 0.123 | 0.018 |
| ILS | 0.253 | 0.456 | 0.084 | |
| Single-Height Experiment | Proposed Method | 0.024 | 0.054 | 0.002 |
| ILS | 1.354 | 4.638 | 0.228 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, N.; Si, M.; Li, D.; Seow, C.K.; Mi, J. An Indoor UWB 3D Positioning Method for Coplanar Base Stations. Sensors 2022, 22, 9634. https://doi.org/10.3390/s22249634
Zhou N, Si M, Li D, Seow CK, Mi J. An Indoor UWB 3D Positioning Method for Coplanar Base Stations. Sensors. 2022; 22(24):9634. https://doi.org/10.3390/s22249634
Chicago/Turabian StyleZhou, Ning, Minghao Si, Dehai Li, Chee Kiat Seow, and Jinzhong Mi. 2022. "An Indoor UWB 3D Positioning Method for Coplanar Base Stations" Sensors 22, no. 24: 9634. https://doi.org/10.3390/s22249634
APA StyleZhou, N., Si, M., Li, D., Seow, C. K., & Mi, J. (2022). An Indoor UWB 3D Positioning Method for Coplanar Base Stations. Sensors, 22(24), 9634. https://doi.org/10.3390/s22249634






