Cervical Tissue Hydration Level Monitoring by a Resonant Microwave Coaxial Probe
Abstract
1. Introduction
2. Probe Design and Characterization
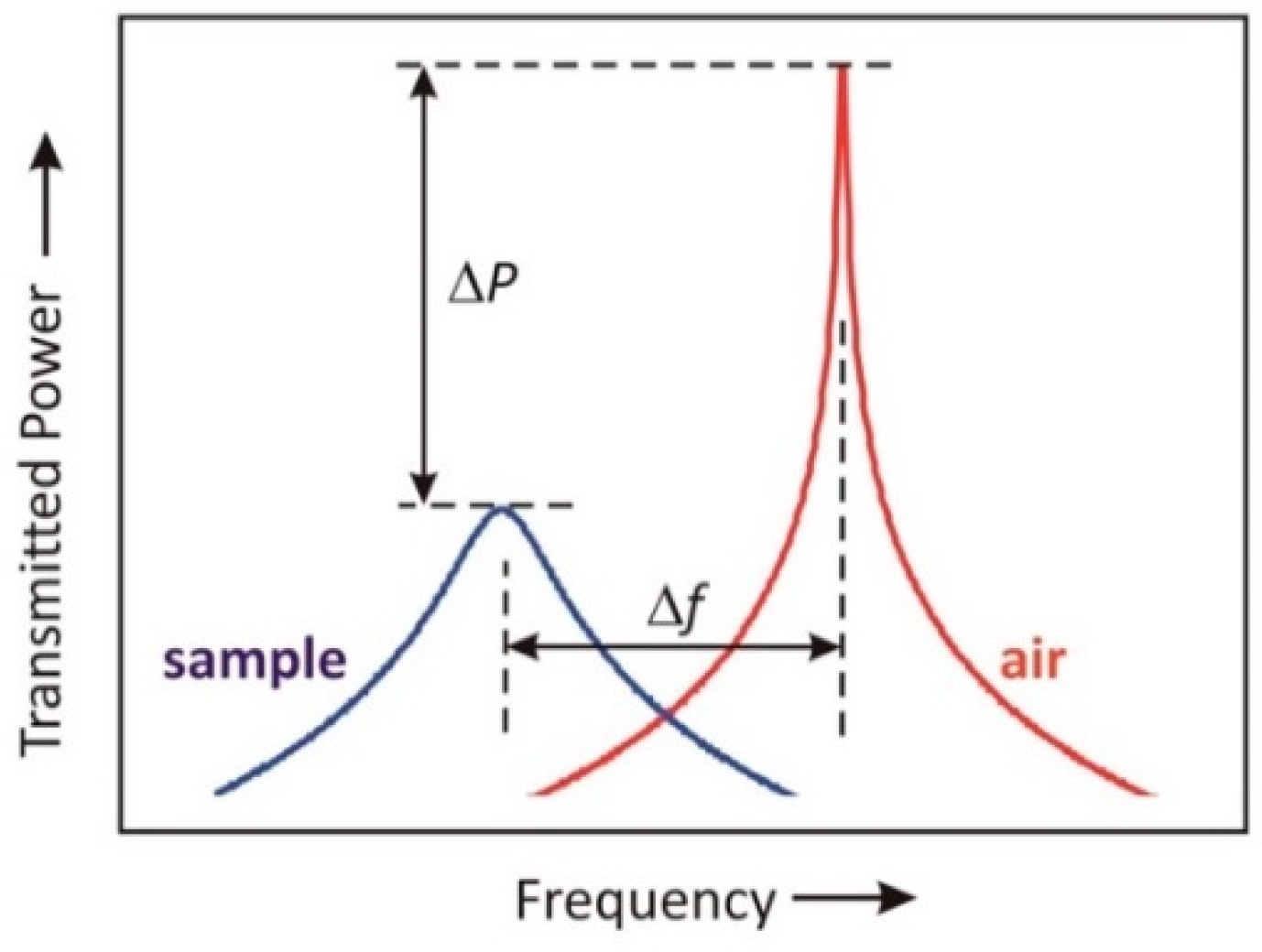
2.1. Advantages of Two-Port Transmission Measurement
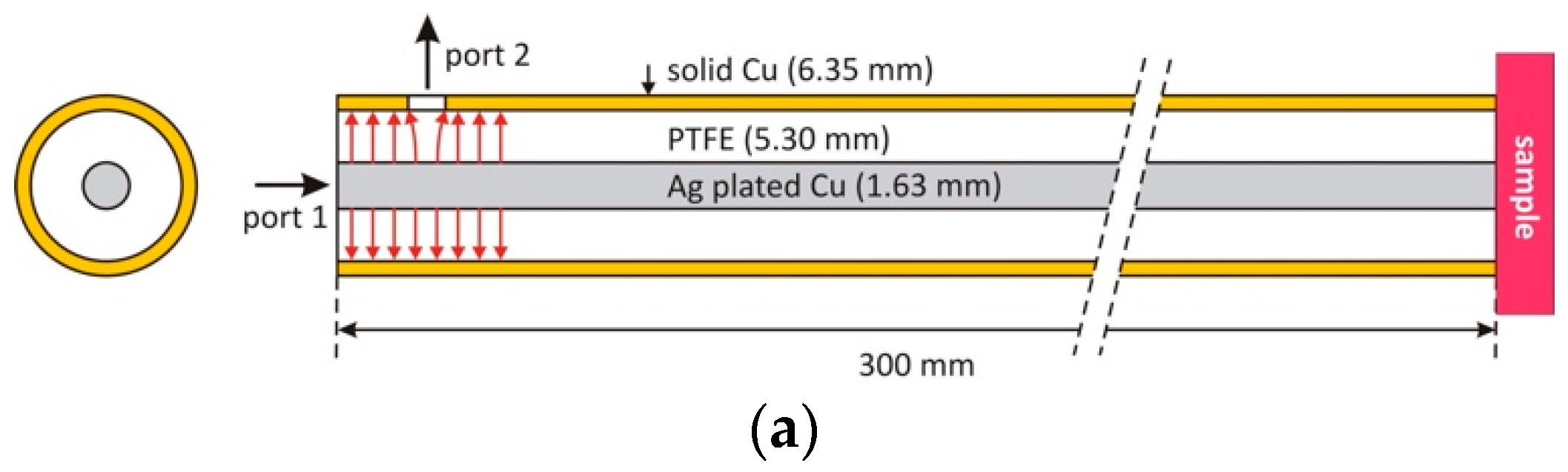
2.2. Two-Port Harmonic Resonance Coaxial Probe Design
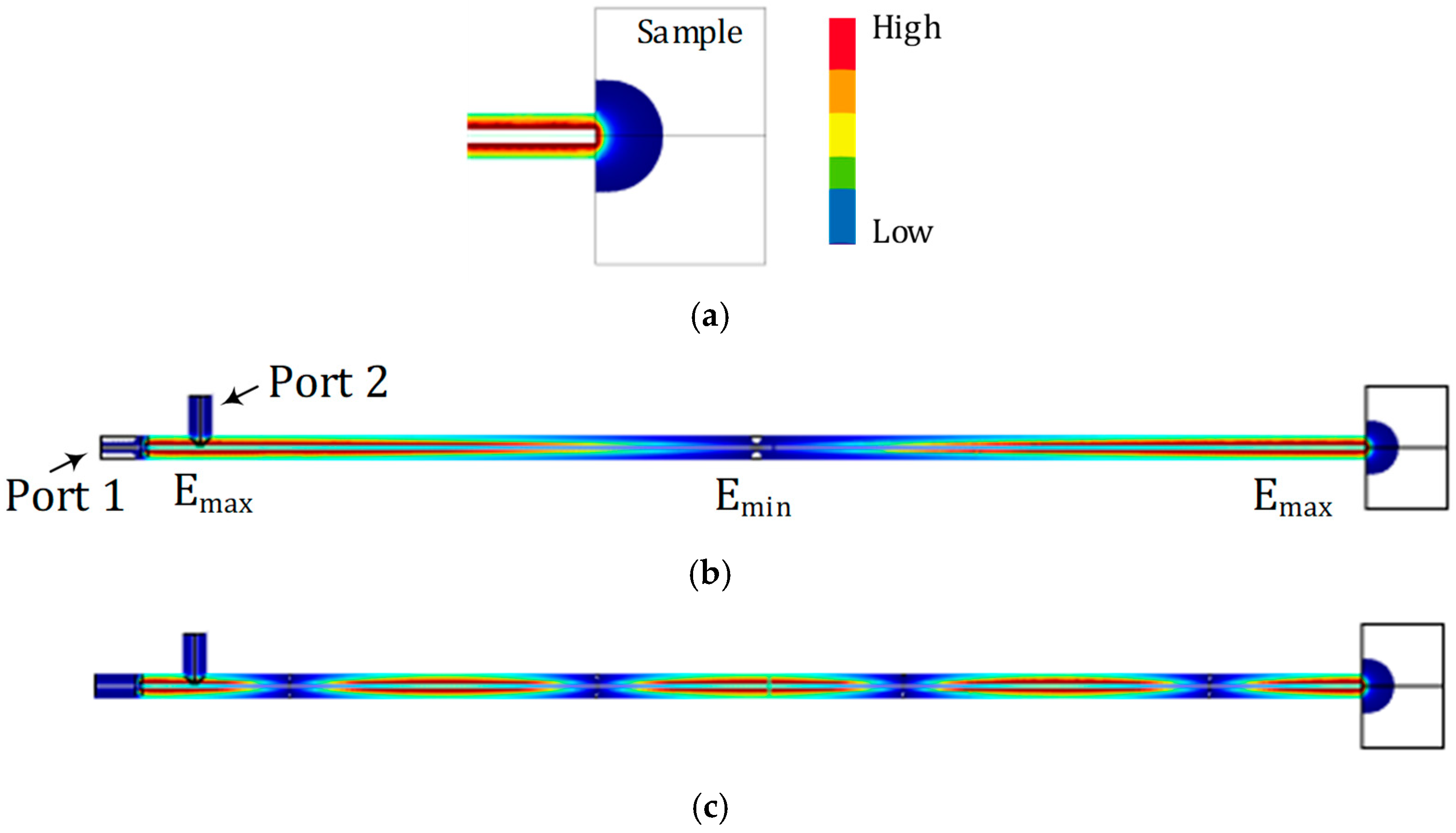
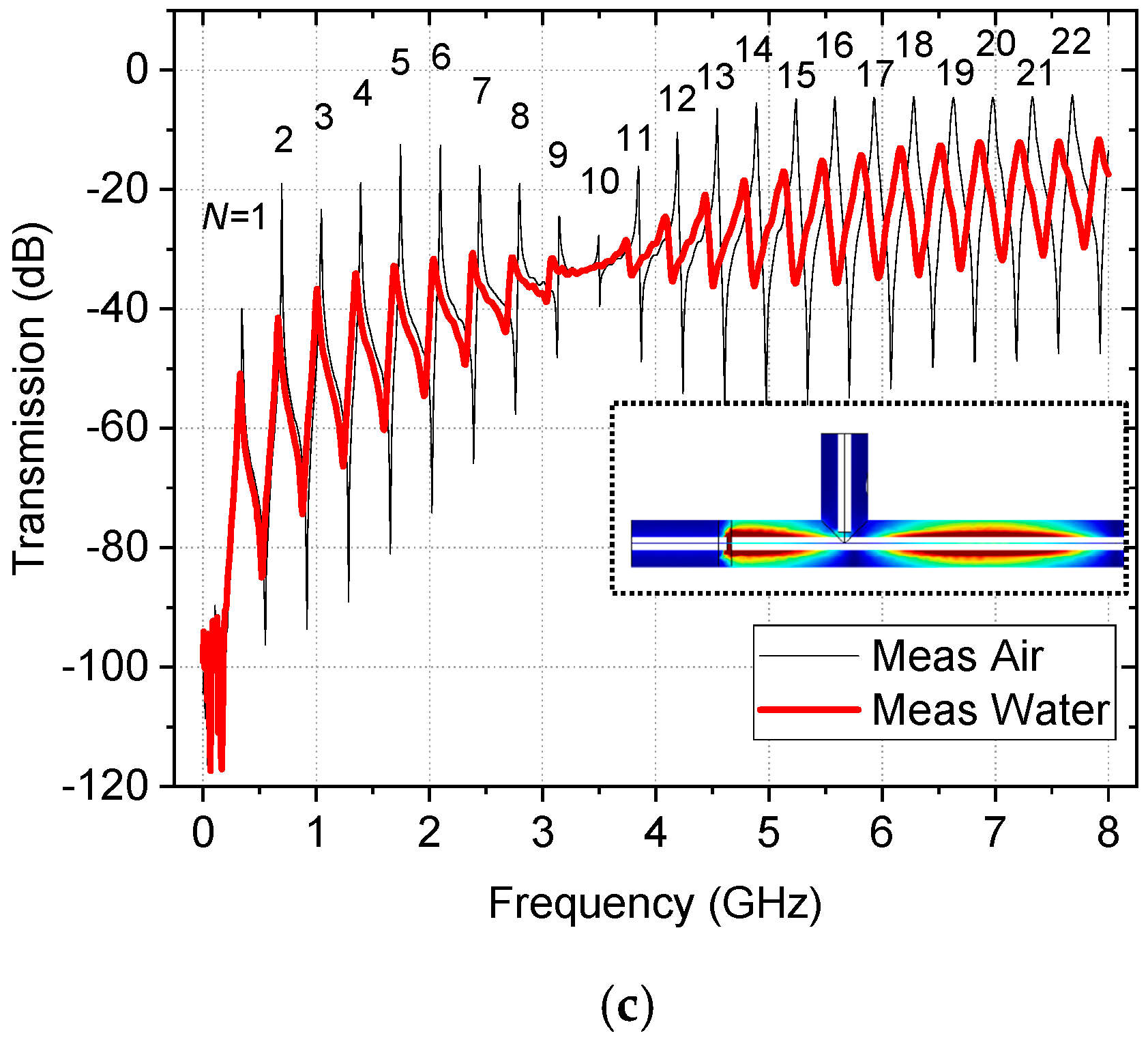
2.3. Simulation and Characterization
3. Experimental Section
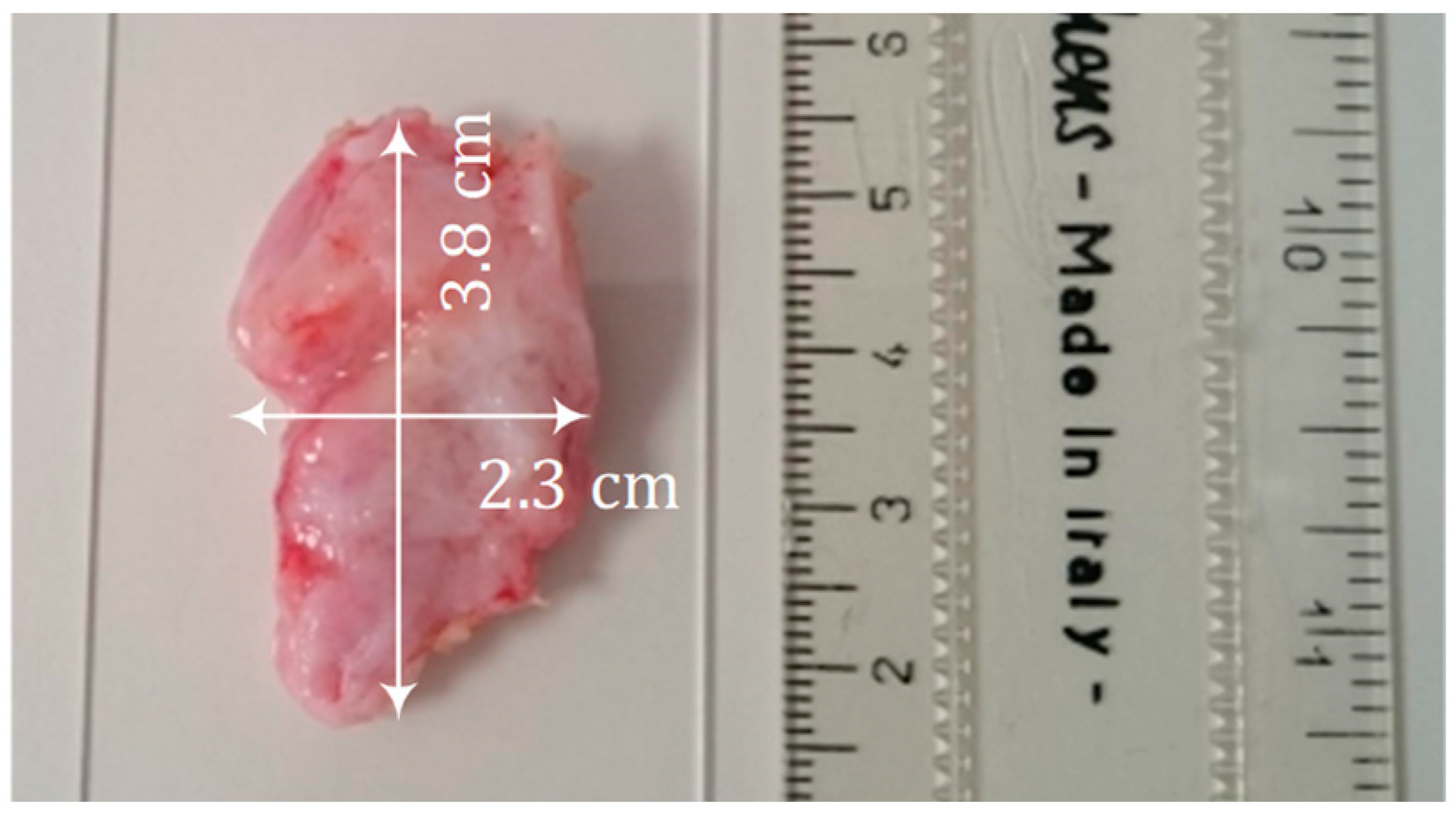
3.1. Sample Collection and Preparation
3.2. Experimental Setup and Test Procedure
3.3. Potential Confounders and Mitigation
3.3.1. Temperature and Humidity
3.3.2. Quality of Probe-Sample Contact
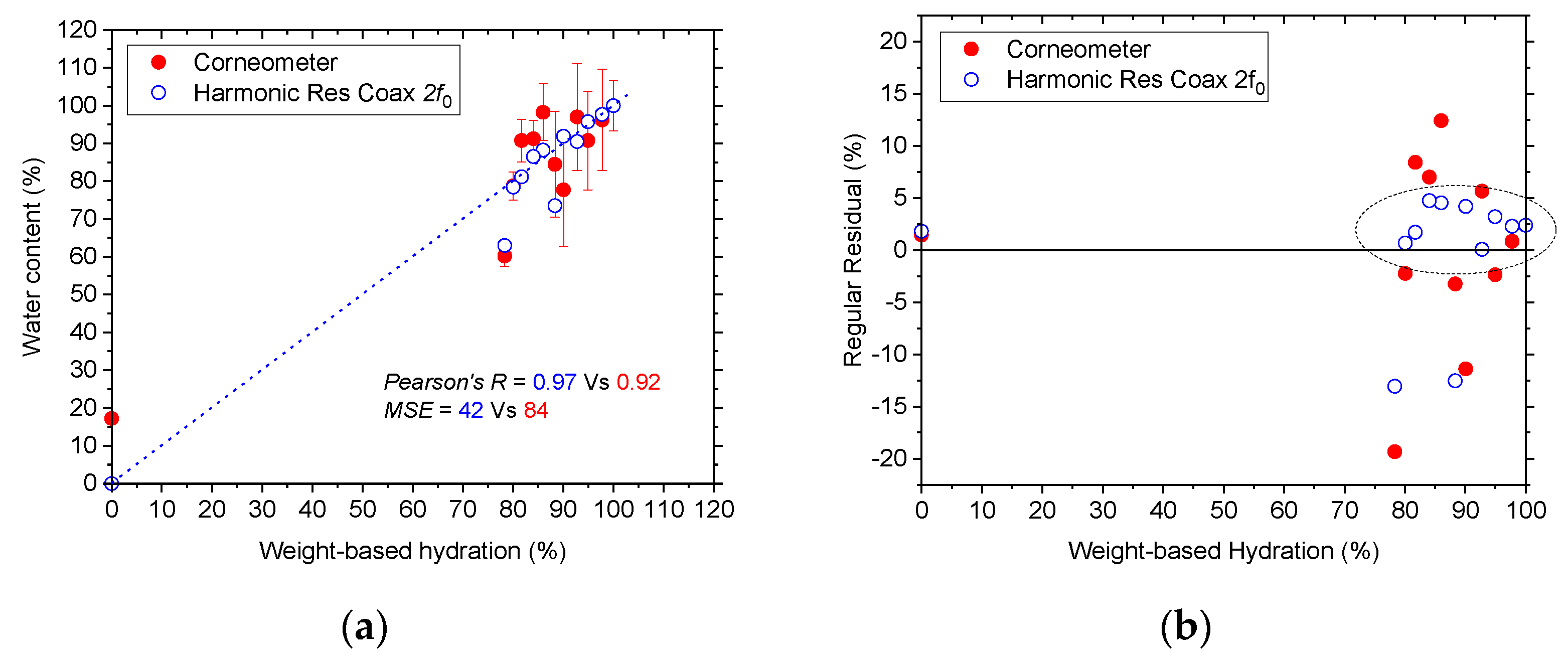
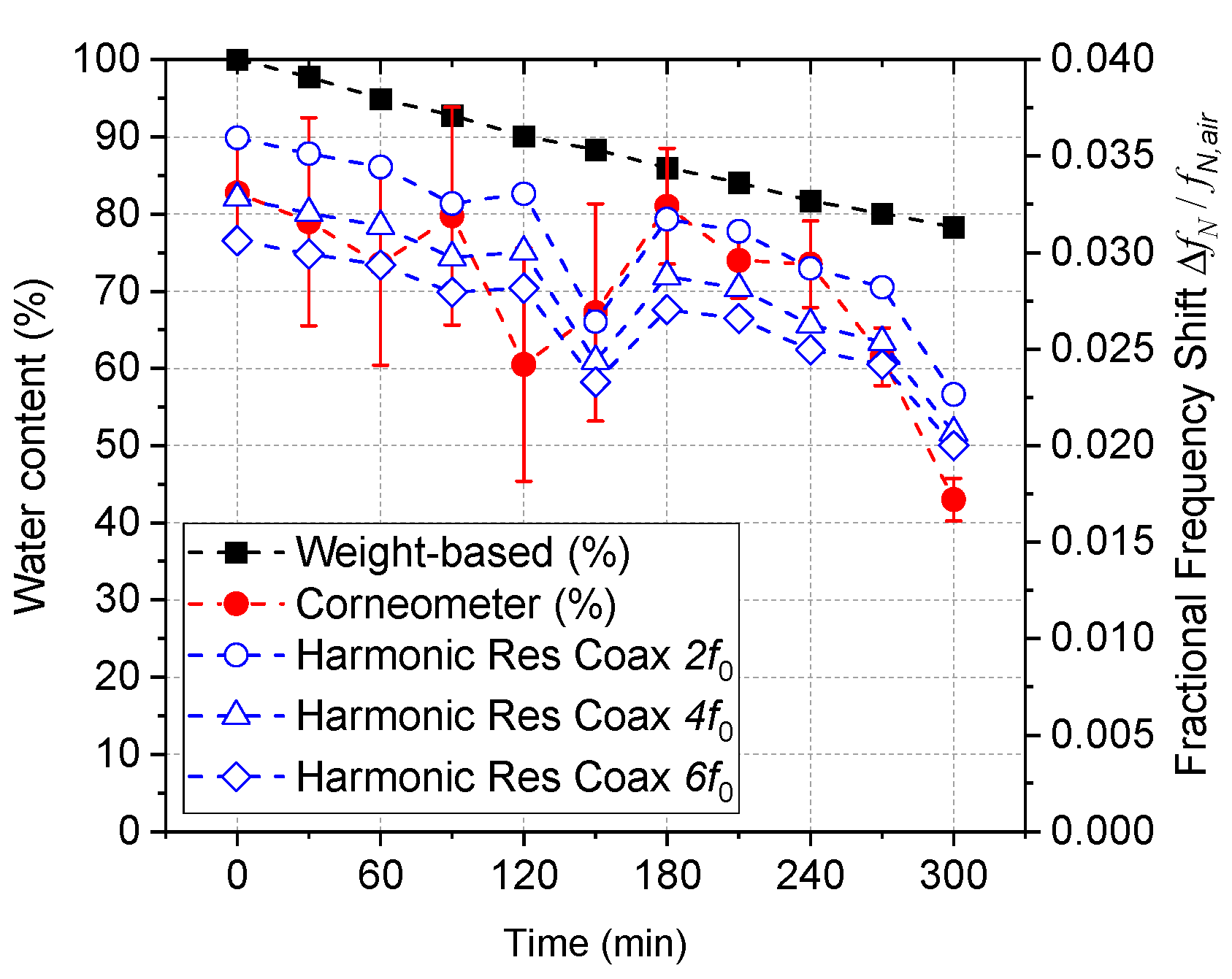
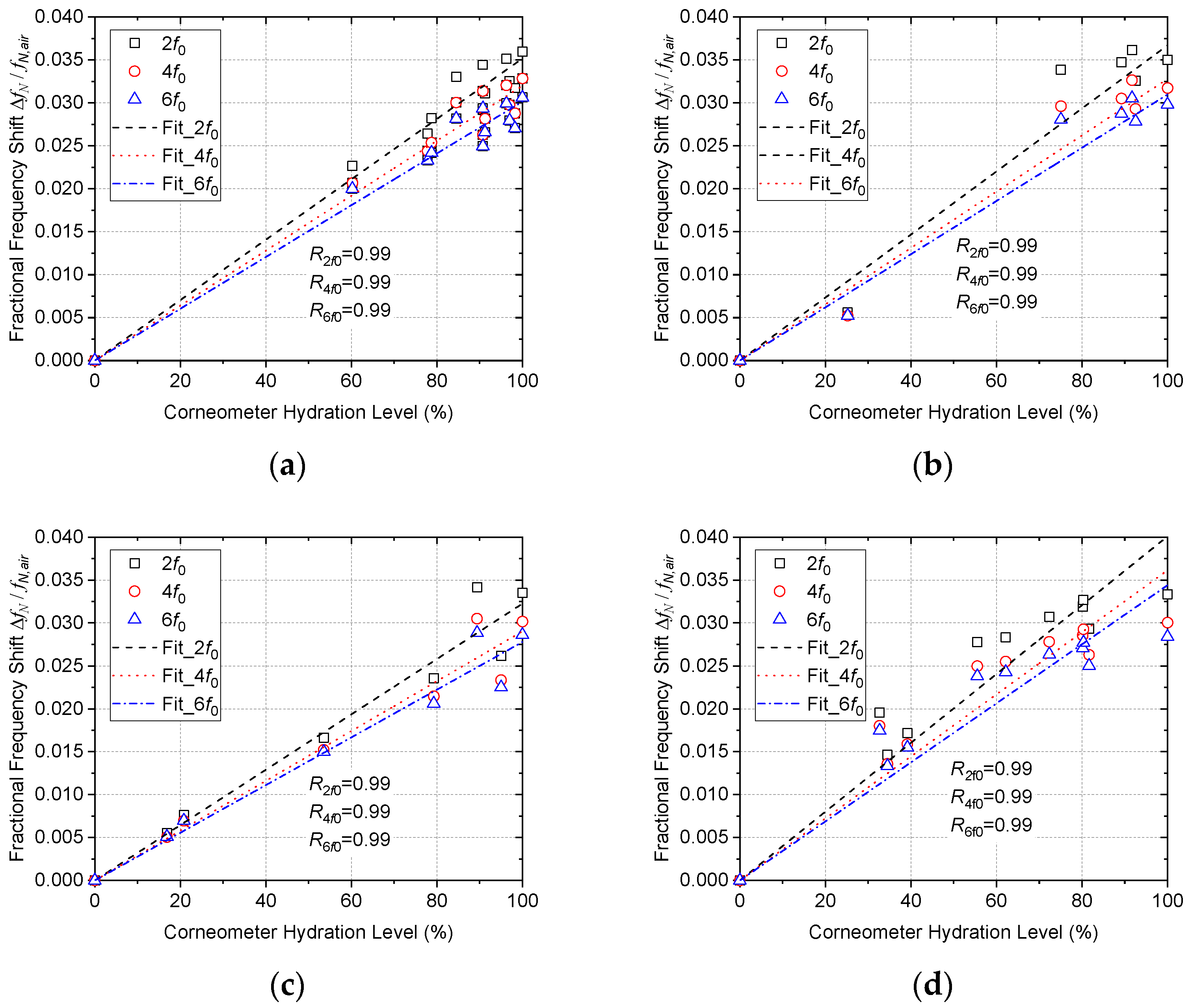
4. Data Analysis and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- World Health Organization. Preterm Birth. 2018. Available online: https://www.who.int/news-room/fact-sheets/detail/preterm-birth (accessed on 18 May 2022).
- World Health Organization. Systematic review on maternal mortality and morbidity: The global burden of preterm birth. Bull World Health Organ. 2010, 88, 31–38. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. Preterm Birth. 2021. Available online: https://www.cdc.gov/reproductivehealth/maternalinfanthealth/pretermbirth.htm (accessed on 18 May 2022).
- O’Hara, S.; Zelesco, M.; Sun, Z. Cervical length for predicting preterm birth and a comparison of ultrasonic measurement techniques. Australas. J. Ultrasound Med. 2013, 16, 124–134. [Google Scholar] [CrossRef] [PubMed]
- Feltovich, H.; Hall, T.J.; Berghella, V. Beyond cervical length: Emerging technologies for assessing the pregnant cervix. Am. J. Obstet. Gynecol. 2012, 207, 345–354. [Google Scholar] [CrossRef] [PubMed]
- Feltovich, H.; Drehfal, L. New techniques in evaluation of the cervix. Semin. Perinatol. 2017, 41, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Schoeller, D.A. Isotope tracers in metabolic research: Principles and practice of kinetic analysis. Q. Rev. Biol. 2017, 82, 43–44. [Google Scholar] [CrossRef]
- Thomasset, A. Bioelectrical properties of tissue impedance. Lyon Med. 1962, 207, 107–118. [Google Scholar]
- Faes, T.J.C.; Van Der Meij, H.A.; De Munck, J.C.; Heethaar, R.M. The electric resistivity of human tissues (100 Hz–10 MHz): A meta-analysis of review studies. Physiol. Meas. 1999, 20, R1–R10. [Google Scholar] [CrossRef]
- Matthie, J.; Zarowitz, B.; De Lorenzo, A.; Andreoli, A.; Katzarski, K.; Pan, G.; Withers, P. Analytic assessment of the various bioimpedance methods used to estimate body water. J. Appl. Physiol. 1998, 84, 1801–1816. [Google Scholar] [CrossRef]
- Vanloan, M.D.; Mayclyn, P.D. A new TOBEC instrument and procedure for the assessment of body composition: The use of Fourier coefficients to predict lean body mass and total body water. Am. J. Clin. Nutr. 1987, 45, 131–137. [Google Scholar] [CrossRef]
- Lorenzo, A.D.; Andreoli, A. Segmental bioelectrical impedance analysis. Curr. Opin. Clin. Nutr. Metab. Care 2003, 6, 551–556. [Google Scholar] [CrossRef]
- Jackobson, J.A. Musculoskeletal sonography and MR imaging: A role for both imaging methods. Radiol. Clin. North Am. 1999, 37, 713–735. [Google Scholar] [CrossRef]
- Peetrons, P. Ultrasound of muscles. Eur. Radiol. 2002, 12, 35–43. [Google Scholar] [CrossRef]
- Schick, F. Pulsed Magnetization Transfer Contrast MRI by a Sequence with Water Selective Excitation. J. Comput. Assist. Tomogr. 1996, 20, 73–79. [Google Scholar] [CrossRef]
- de Tejada, B.M.; Faltin, D.L.; Kinkel, K.; Guittier, M.J.; Boulvain, M.; Irion, O. Magnetic resonance imaging of the cervix in women at high risk for preterm delivery. J. Matern. Fetal Neonatal Med. 2011, 24, 1392–1397. [Google Scholar] [CrossRef]
- Keeton, J.T.; Hafley, B.S.; Eddy, S.M.; Moser, C.R.; McManus, B.J.; Leffler, T.P. Rapid determination of moisture and fat in meats by microwave and nuclear magnetic resonance analysis. J. AOAC Int. 2003, 86, 1193–1202. [Google Scholar] [CrossRef]
- Xu, X.; Wang, R.K. The role of water desorption on optical clearing of biotissue: Studied with near infrared reflectance spectroscopy. Med. Phys. 2003, 30, 1246–1253. [Google Scholar] [CrossRef]
- Kuon, R.J.; Shi, S.-Q.; Maul, H.; Sohn, C.; Balducci, J.; Shi, L.; Garfield, R.E. A novel optical method to assess cervical changes during pregnancy and use to evaluate the effects of progestins on term and preterm labor. Am. J. Obstet. Gynecol. 2011, 205, 82.e15–82.e20. [Google Scholar] [CrossRef] [PubMed]
- O’Connell, M.P.; Tidy, J.; Wisher, S.J.; Avis, N.J.; Brown, B.H.; Lindow, S.W. An in vivo comparative study of the pregnant and nonpregnant cervix using electrical impedance measurements. Br. J. Obstet. Gynecol. 2000, 107, 1040–1041. [Google Scholar] [CrossRef] [PubMed]
- McFarlin, B.L.; Bigelow, T.A.; Laybed, Y.; O’Brien, W.D.; Oelze, M.L.; Abramowicz, J. Ultrasonic attenuation estimation of the pregnant cervix: A preliminary report. Ultrasound Obstet. Gynecol. 2010, 36, 218–225. [Google Scholar] [CrossRef]
- O’Brien, C.M.; Vargis, E.; Paria, B.C.; Bennett, K.A.; Mahadevan-Jansen, A.; Reese, J. Raman spectroscopy provides a noninvasive approach for determining biochemical composition of the pregnant cervix in vivo. Acta Paediatr. 2014, 103, 715–721. [Google Scholar] [PubMed]
- Scharfetter, H.; Casanas, R.; Rosell, J. Biological tissue characterization by magnetic induction spectroscopy (MIS): Re-quirements and limitations. IEEE Trans. Biomed. Eng. 2003, 50, 870–880. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Healey, T.; Barker, A.; Brown, B.; Monk, C.; Anumba, D. Magnetic induction spectroscopy (MIS)—Probe design for cervical tissue measurements. Physiol. Meas. 2017, 38, 729–742. [Google Scholar] [CrossRef]
- Halim, S.F.A.; Zakaria, Z.; Pusppanathan, J.; Noor, A.M.; Norali, A.N.; Rahiman, M.H.F.; Muji, S.Z.M.; Rahim, R.A.; Engku-Husna, E.I.; Hassan, M.K.A.; et al. A Review on Magnetic Induction Spectroscopy Potential for Fetal Acidosis Examination. Sensors 2022, 22, 1334. [Google Scholar] [CrossRef]
- Wickett, R. Hardware and measuring principles: The Nova Dermal Phase Meter. In Bioengineering of the Skin. Water and the Stratum Corneum; Fluhr, J., Elsner, P., Berardesca, E., Maibach, H.I., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 263–274. [Google Scholar]
- Corneometer® CM 825, Courage-Khazaka.de. Available online: https://www.courage-khazaka.de/en/16-wissenschaftliche-produkte/alle-produkte/183-corneometer-e (accessed on 19 May 2022).
- La Gioia, A.; Porter, E.; Merunka, I.; Shahzad, A.; Salahuddin, S.; Jones, M.; O’Halloran, M. Open-Ended Coaxial Probe Technique for Dielectric Measurement of Biological Tissues: Challenges and Common Practices. Diagnostics 2018, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Stuchly, M.; Athey, T.; Samaras, G.; Taylor, G. Measurement of Radio Frequency Permittivity of Biological Tissues with an Open-Ended Coaxial Line: Part II—Experimental Results. IEEE Trans. Microw. Theory Tech. 1982, 30, 87–92. [Google Scholar] [CrossRef]
- Burdette, E.; Cain, F.; Seals, J. In Vivo Probe Measurement Technique for Determining Dielectric Properties at VHF through Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 1980, 28, 414–427. [Google Scholar] [CrossRef]
- Kraszewski, A.; Stuchly, M.A.; Stuchly, S.S.; Smith, A.M. In vivo and in vitro dielectric properties of animal tissues at radio frequencies. Bioelectromagnetics 1982, 3, 421–432. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Peyman, A.; Holden, S.; Gabriel, C. Mobile Telecommunications and Health Research Programme: Dielectric Properties of Tissues at Microwave Frequencies; Microwave Consultants Limited: London, UK, 2005. [Google Scholar]
- Abdilla, L.; Sammut, C.; Mangion, L.Z. Dielectric properties of muscle and liver from 500 MHz–40 GHz. Electromagn. Biol. Med. 2013, 32, 244–252. [Google Scholar] [CrossRef]
- Schwan, H.; Foster, K. RF-field interactions with biological systems: Electrical properties and biophysical mechanisms. Proc. IEEE 1980, 68, 104–113. [Google Scholar] [CrossRef]
- Gregory, A.; Clarke, R.; Hodgetts, T.; Symm, G. RF and Microwave Dielectric Measurements upon Layered Materials Using Coaxial Sensors; NPL Report MAT 13; National Physical Laboratory: Teddington, UK, 2008. [Google Scholar]
- Keysight Technologies. Basics of Measuring the Dielectric Properties of Materials (1–35) [Online]. Available online: https://www.keysight.com/gb/en/assets/7018-01284/application-notes/5989-2589.pdf (accessed on 26 October 2022).
- Pozar, D.M. Microwave Engineering, 3rd ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- O’Rourke, A.P.; Lazebnik, M.; Bertram, J.M.; Converse, M.C.; Hagness, S.C.; Webster, J.G.; Mahvi, D.M. Dielectric Properties of Human Normal, Malignant and Cirrhotic Liver Tissue: In Vivo and Ex Vivo Measurements from 0.5 to 20 GHz Using a Pre-cision Open-Ended Coaxial Probe. Phys. Med. Biol. 2007, 52, 4707–4719. [Google Scholar] [CrossRef] [PubMed]
- Stuchly, M.A.; Stuchly, S.S. Coaxial Line Reflection Methods for Measuring Dielectric Properties of Biological Substances at Radio and Microwave Frequencies-A Review. IEEE Trans. Instrum. Meas. 1980, 29, 176–183. [Google Scholar] [CrossRef]
- Athey, T.; Stuchly, M.; Stuchly, S. Measurement of Radio Frequency Permittivity of Biological Tissues with an Open-Ended Coaxial Line: Part I. IEEE Trans. Microw. Theory Tech. 1982, 30, 82–86. [Google Scholar] [CrossRef]
- Gabriel, C.; Grant, E.H.; Young, I.R. Use of time domain spectroscopy for measuring dielectric properties with a coaxial probe. J. Phys. E Sci. Instrum. 1986, 19, 843–846. [Google Scholar] [CrossRef]
- Alanen, E.; Lahtinen, T.; Nuutinen, J. Variational formulation of open-ended coaxial line in contact with layered biological medium. IEEE Trans. Biomed. Eng. 1998, 45, 1241–1248. [Google Scholar] [CrossRef]
- Hagl, D.; Popovic, D.; Hagness, S.C.; Booske, J.H.; Okoniewski, M. Sensing Volume of Open-Ended Coaxial Probes for Die-lectric Characterization of Breast Tissue at Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 2003, 51, 1194–1206. [Google Scholar] [CrossRef]
- Popovic, D.; Okoniewski, M.; Hagl, D.; Booske, J.H.; Hagness, S.C. Volume Sensing Properties of Open Ended Coaxial Probes for Dielectric Spectroscopy of Breast Tissue. In Proceedings of the IEEE Antennas and Propagation Society, Boston, MA, USA, 8–13 July 2001; pp. 254–257. [Google Scholar]
- Popovic, D.; McCartney, L.; Beasley, C.; Lazebnik, M.; Okoniewski, M.; Hagness, S.C.; Booske, J.H. Precision Open-Ended Coaxial Probes for in Vivo and Ex Vivo Dielectric Spectroscopy of Biological Tissues at Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 2005, 53, 1713–1721. [Google Scholar] [CrossRef]
- Fallahi, A.; Hashemizadeh, S.; Kuster, N. On the Dielectric Measurement of Thin Layers Using Open-Ended Coaxial Probes. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Wang, J.; Lim, E.G.; Leach, M.P.; Wang, Z.; Man, K.L. Open-Ended Coaxial Cable Selection for Meas-urement of Liquid Dielectric Properties via the Reflection Method. Math. Probl. Eng. 2020, 2020, 8942096. [Google Scholar]
- Shao, M.; Li, X.; Liu, Z.; Liang, X.; Lin, L.; Fan, H.; Xu, J. Time Domain Calibration Method of Open-Ended Coaxial Probe in Dielectric Measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Dilman, I.; Akinci, M.N.; Yilmaz, T.; Cayoren, M.; Akduman, I. A Method to Measure Complex Dielectric Permittivity With Open-Ended Coaxial Probes. IEEE Trans. Instrum. Meas. 2022, 71, 1–7. [Google Scholar] [CrossRef]
- Rowe, D.J.; Naylon, J.; Porch, A.; Barrow, D.A.; Allender, C.J. Microwave resonant sensor for real-time continuous-flow measurements of microfluidic systems. In Proceedings of the 14th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Groningen, The Netherlands, 3–7 October 2010; pp. 1004–1006. [Google Scholar]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C.J. Integrated microwave resonant device for dielectric analysis of mi-crofluidic systems. J. Phys. Conf. Ser. 2011, 310, 012004. [Google Scholar] [CrossRef]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C.J. Dielectric analysis of microfluidic systems with an integrated mi-crowave resonant device. In Proceedings of the 2011 41st European Microwave Conference, Manchester, UK, 10–13 October 2011; pp. 607–610. [Google Scholar]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C.J. Non-contact label-free dielectric spectroscopy of single-and multi-phase microfluidic systems. In Proceedings of the 16th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Seattle, WA, USA, 2–6 October 2011; pp. 891–893. [Google Scholar]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C.J. Novel Coupling Structure for the Resonant Coaxial Probe. IEEE Trans. Microw. Theory Tech. 2012, 60, 1699–1708. [Google Scholar] [CrossRef]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C. Microfluidic device for compositional analysis of solvent systems at microwave frequencies. Sens. Actuators B Chem. 2012, 169, 213–221. [Google Scholar] [CrossRef]
- Rowe, D.J.; Porch, A.; Barrow, D.A.; Allender, C.J. Microfluidic Microwave Sensor for Simultaneous Dielectric and Magnetic Characterization. IEEE Trans. Microw. Theory Tech. 2012, 61, 234–243. [Google Scholar] [CrossRef]
- Misra, D.K. Quasi-static analysis of open-ended coaxial lines. IEEE Trans. Microw. Theory Tech. 1987, 35, 925–928. [Google Scholar] [CrossRef]
- Gabriel, C.; Chan, T.Y.A.; Grant, E.H. Admittance models for open ended coaxial probes and their place in dielectric spectroscopy. Phys. Med. Biol. 1994, 39, 2183–2200. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-H.; Enkhbayar, B.; Bang, J.-H.; Ahn, B.-C.; Cha, E.-J. New formula for the reflection coefficient of an open-ended rectangular waveguide with or without an infinite flange. Prog. Electromagn. Res. M 2010, 12, 143–153. [Google Scholar] [CrossRef][Green Version]






| Harmonic | Frequency | Measured f0 | Bandwidth | QL | Q0 | Loss |
|---|---|---|---|---|---|---|
| Number | (MHz) | (MHz) | (MHz) | (dB) | ||
| 1f | 350 | 352.6 | 1.0 | 337.5 | 351.1 | 28.3 |
| 2f | 700 | 705.3 | 1.6 | 448.9 | 496.0 | 20.5 |
| 3f | 1050 | 1058.4 | 2.2 | 488.4 | 569.6 | 16.9 |
| 4f | 1400 | 1413.3 | 2.8 | 505.1 | 613.8 | 15.0 |
| 5f | 1750 | 1766.0 | 3.5 | 503.1 | 624.0 | 14.3 |
| 6f | 2100 | 2116.9 | 4.2 | 509.3 | 625.8 | 14.6 |
| 7f | 2450 | 2471.6 | 5.0 | 495.1 | 592.6 | 15.7 |
| 8f | 2800 | 2824.5 | 5.7 | 495.6 | 560.6 | 18.7 |
| 9f | 3150 | 3182.3 | 7.5 | 425.1 | 451.4 | 24.7 |
| 10f | 3500 | 3531.3 | N/A | N/A | N/A | 32.1 |
| 11f | 3850 | 3883.7 | 8.5 | 455.3 | 507.9 | 19.7 |
| 12f | 4200 | 4237.5 | 9.5 | 445.0 | 552.0 | 14.3 |
| 13f | 4550 | 4590.1 | 11.2 | 411.4 | 560.0 | 11.5 |
| 14f | 4900 | 4942.9 | 13.5 | 376.2 | 588.0 | 8.9 |
| 15f | 5250 | 5297.2 | 13.3 | 397.3 | 679.4 | 7.6 |
| 16f | 5600 | 5650.5 | 15.0 | 376.3 | 726.4 | 6.3 |
| 17f | 5950 | 6002.8 | 16.9 | 355.1 | 754.2 | 5.5 |
| 18f | 6300 | 6355.8 | 19.9 | 319.9 | 699.5 | 5.3 |
| 19f | 6650 | 6707.7 | 23.4 | 286.3 | 692.9 | 4.6 |
| 20f | 7000 | 7060.8 | 22.6 | 312.3 | 749.6 | 4.7 |
| 21f | 7350 | 7413.3 | 24.7 | 299.2 | 732.6 | 4.6 |
| 22f | 7700 | 7767.4 | 25.5 | 304.3 | 732.0 | 4.7 |
| 23f | 8050 | 8122.5 | 30.3 | 268.0 | 583.4 | 5.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Barker, E.; Abduljabar, A.A.; Anumba, D.; Porch, A. Cervical Tissue Hydration Level Monitoring by a Resonant Microwave Coaxial Probe. Sensors 2022, 22, 9527. https://doi.org/10.3390/s22239527
Choi H, Barker E, Abduljabar AA, Anumba D, Porch A. Cervical Tissue Hydration Level Monitoring by a Resonant Microwave Coaxial Probe. Sensors. 2022; 22(23):9527. https://doi.org/10.3390/s22239527
Chicago/Turabian StyleChoi, Heungjae, Emilia Barker, Ali A. Abduljabar, Dilly Anumba, and Adrian Porch. 2022. "Cervical Tissue Hydration Level Monitoring by a Resonant Microwave Coaxial Probe" Sensors 22, no. 23: 9527. https://doi.org/10.3390/s22239527
APA StyleChoi, H., Barker, E., Abduljabar, A. A., Anumba, D., & Porch, A. (2022). Cervical Tissue Hydration Level Monitoring by a Resonant Microwave Coaxial Probe. Sensors, 22(23), 9527. https://doi.org/10.3390/s22239527






