An Improved Synthesis Phase Unwrapping Method Based on Three-Frequency Heterodyne
Abstract
1. Introduction
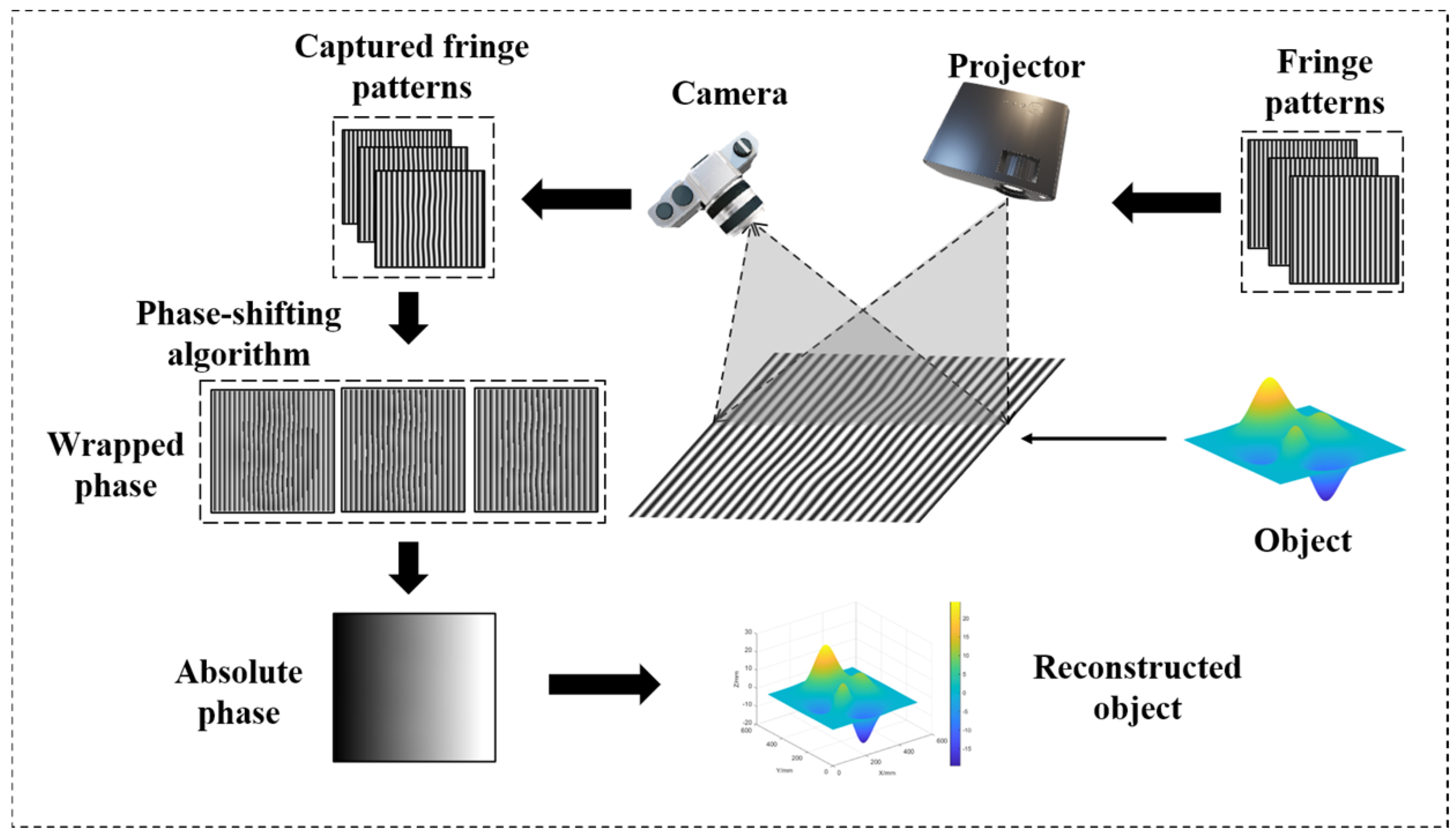
2. Principle
2.1. Wrapped Phase Extraction
2.2. Principle of Phase Unwrapping
2.3. The TFH Phase Unwrapping Algorithm
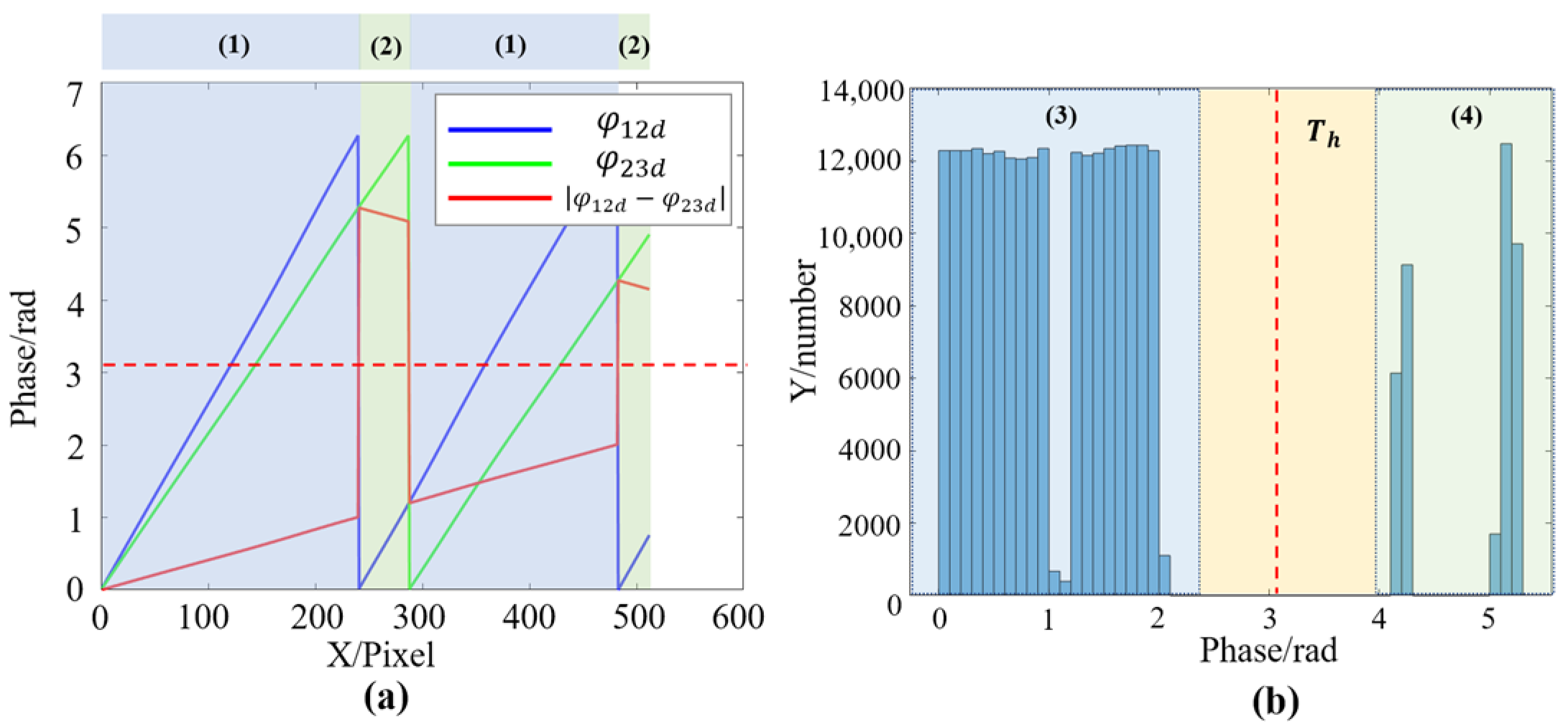
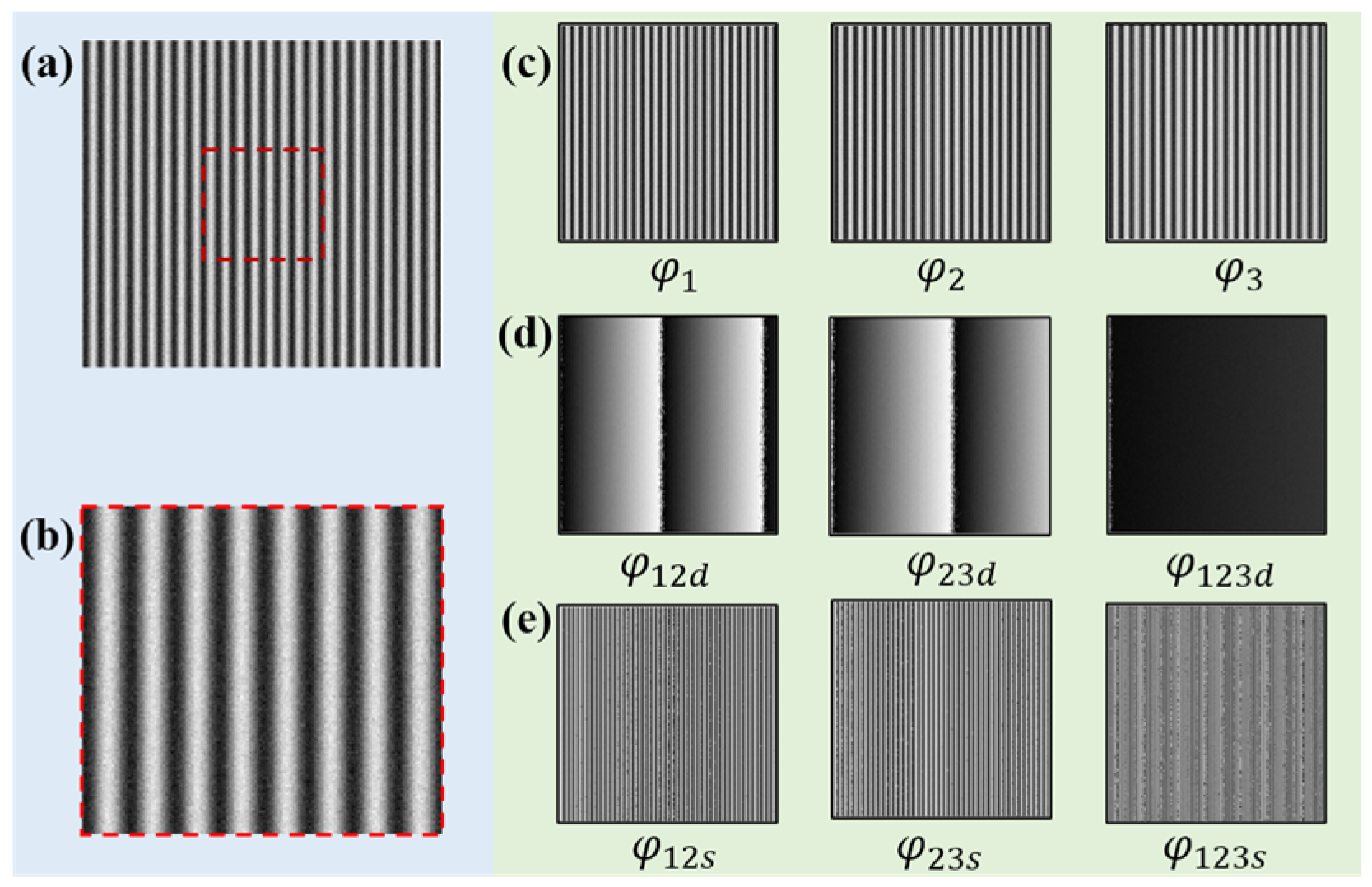
2.3.1. The Traditional TFH Phase Unwrapping Algorithm
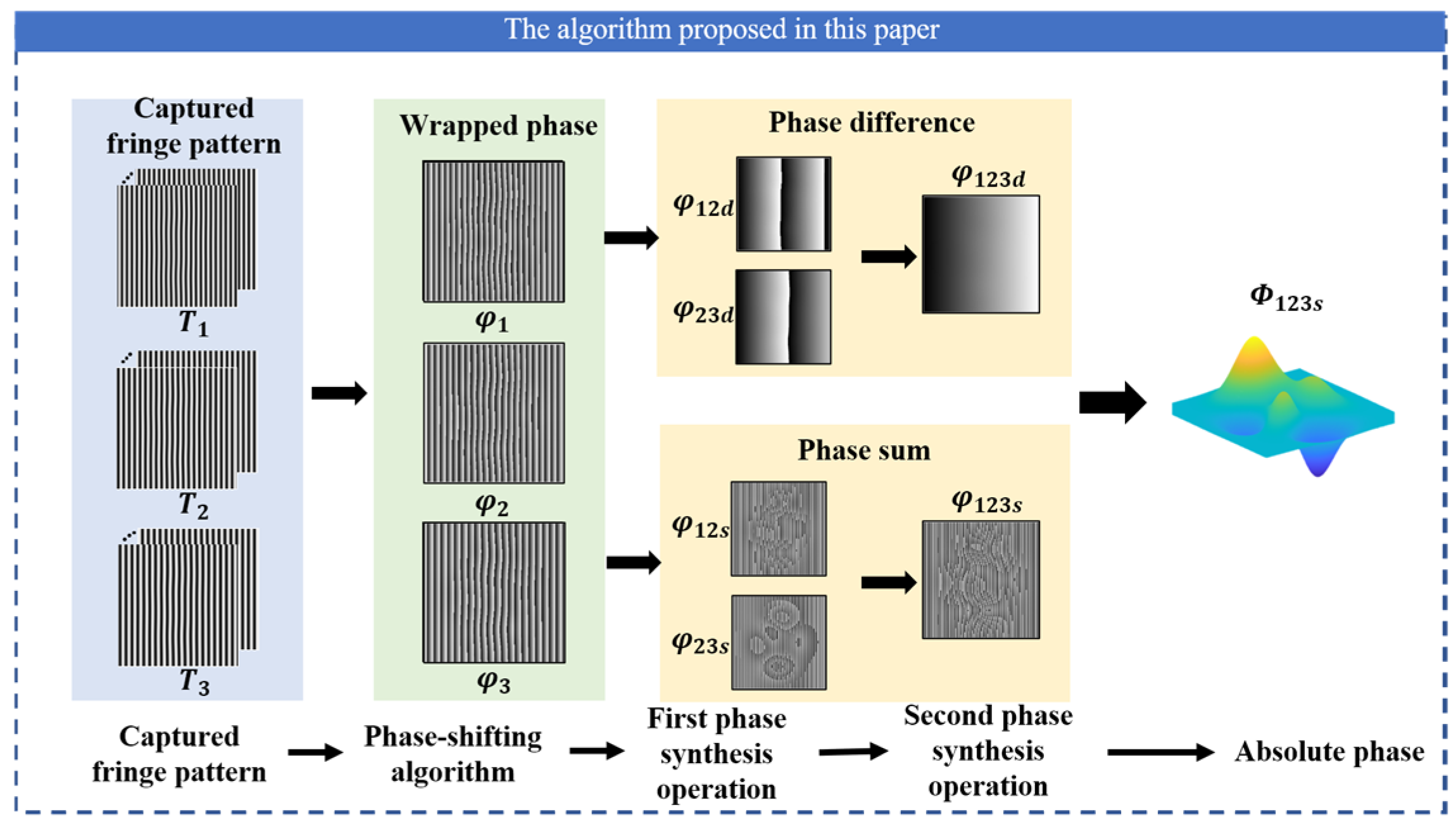
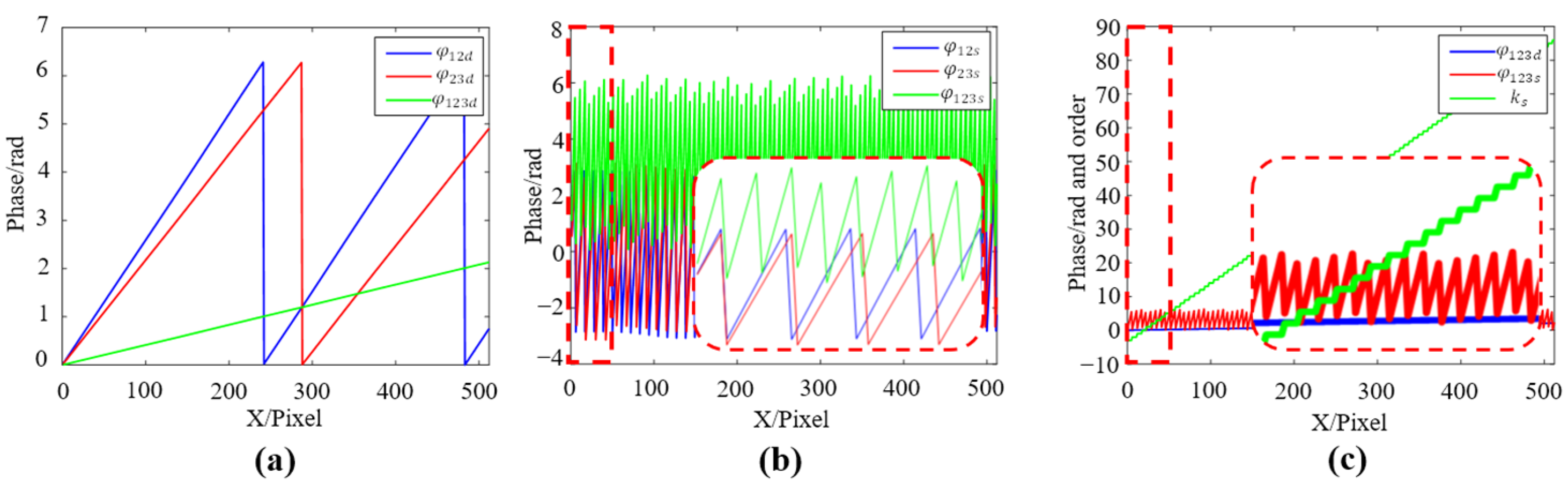
2.3.2. The Proposed Algorithm
2.3.3. Mathematical Derivation and Analysis
3. Simulation
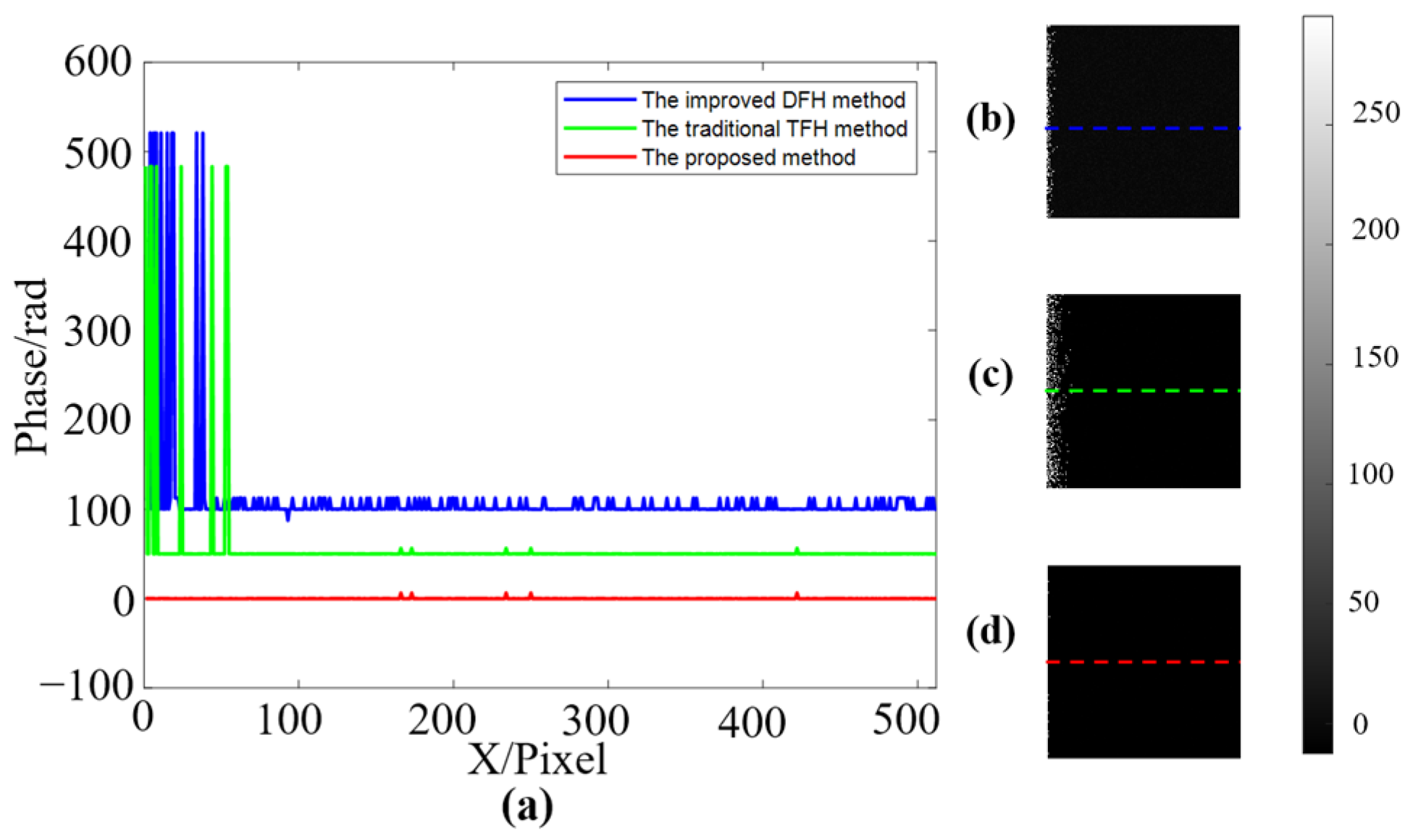
3.1. Phase Calculation from Fringe Patterns with Noise Added
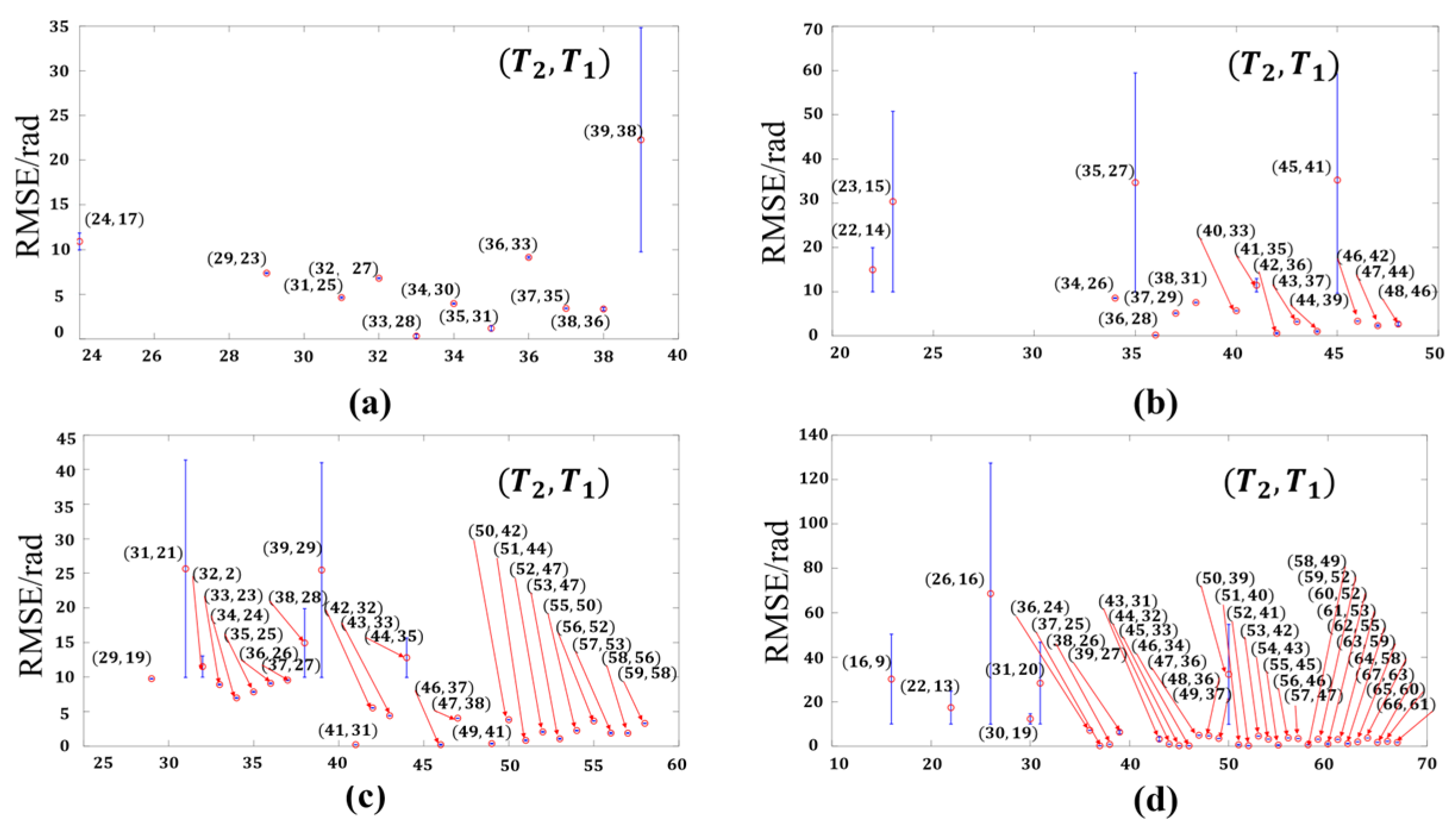
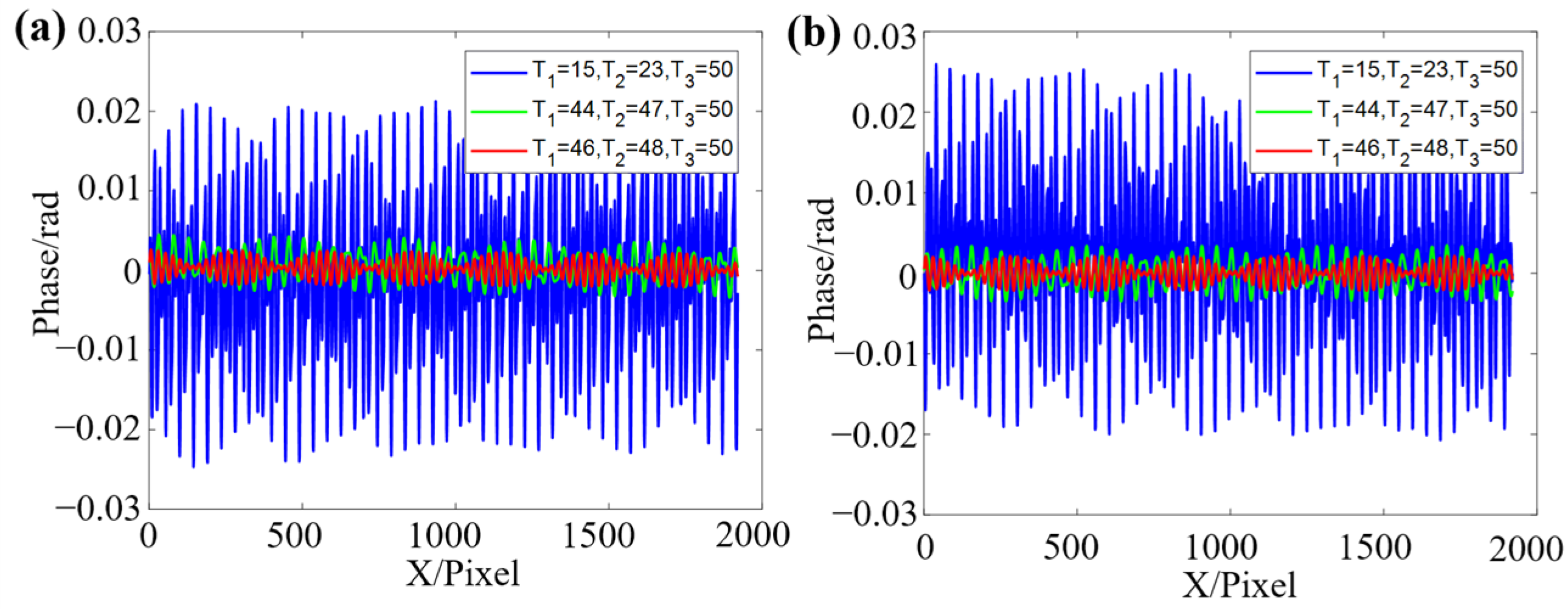
3.2. Effect of Fringe Period Selection on Phase Calculation
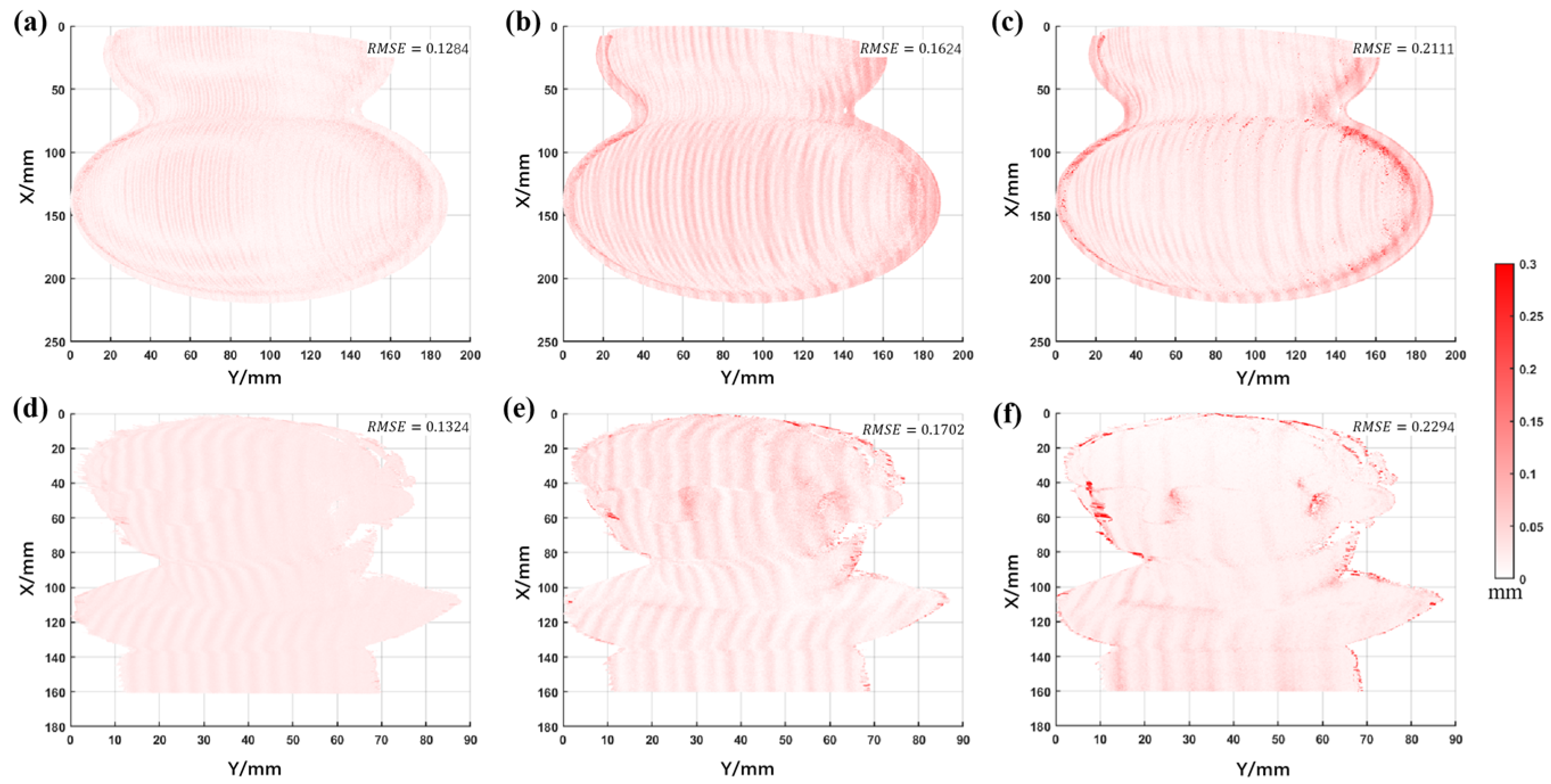
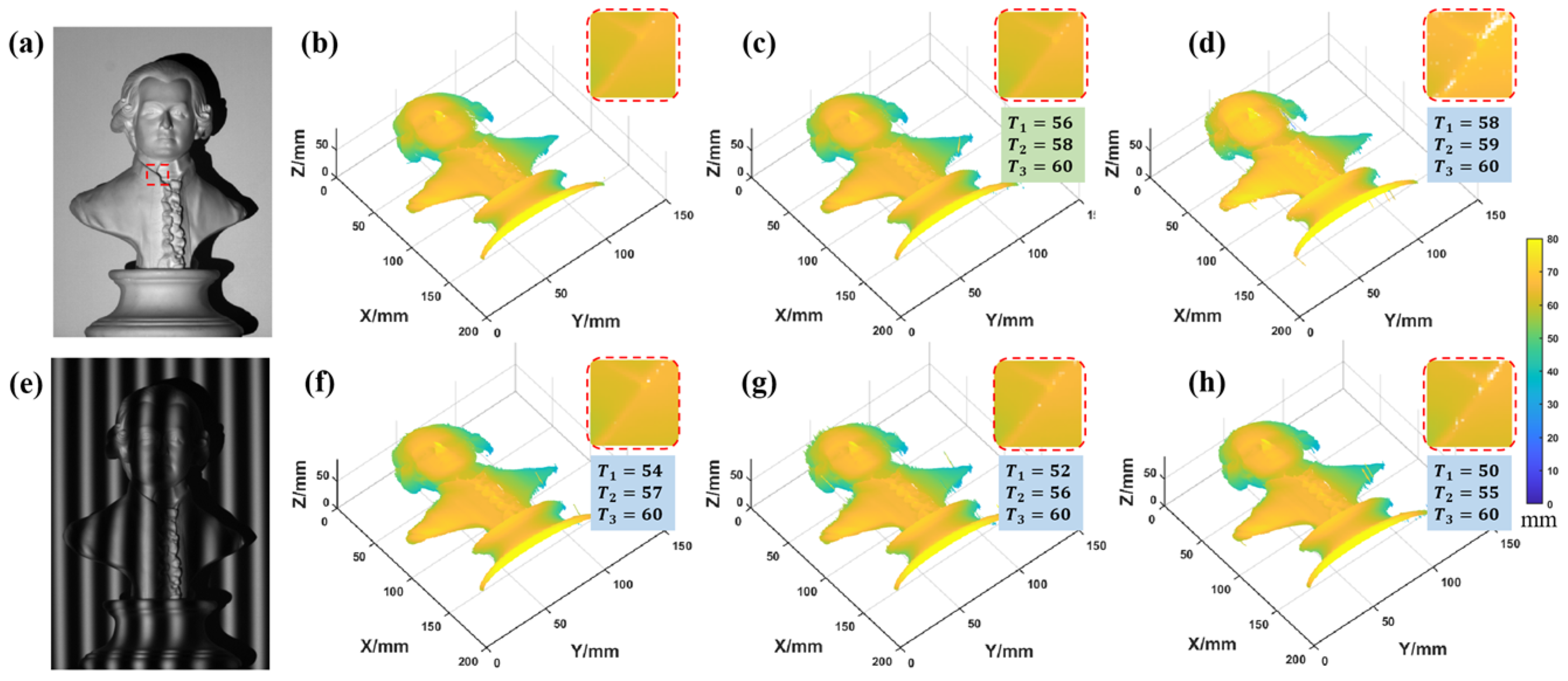
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Brown, G.M.; Song, M. Overview of 3-D shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Laser. Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Marrugo, A.G.; Gao, F.; Zhang, S. State-of-the-art active optical techniques for three-dimensional surface metrology: A review. J. Opt. Soc. Am. A 2020, 37, B60–B77. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Laser. Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Q. Dynamic 3-D shape measurement method: A review. Opt. Laser. Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Laser. Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Han, L.; Cheng, X.; Li, Z.; Zhong, K.; Shi, Y.; Jiang, H. A Robot-Driven 3D Shape Measurement System for Automatic Quality Inspection of Thermal Objects on a Forging Production Line. Sensors 2018, 18, 4368. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Zhang, Z.H. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Laser. Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Optics 1984, 23, 3105–3108. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Laser. Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Chen, Q.; Han, M.; Wang, Y.; Chen, W. An Improved Circular Fringe Fourier Transform Profilometry. Sensors 2022, 22, 6048. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Laser. Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Huntley, J.M.; Saldner, H. Temporal phase-unwrapping algorithm for automated interferogram analysis. Appl. Optics 1993, 32, 3047–3052. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Chen, W. Reliability-guided phase unwrapping algorithm: A review. Opt. Laser. Eng. 2004, 42, 245–261. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zhang, Q.; Su, X.; Asundi, A.; Kemao, Q. Quality-guided phase unwrapping technique: Comparison of quality maps and guiding strategies. Appl. Optics 2011, 50, 6214–6224. [Google Scholar] [CrossRef]
- Chen, K.; Xi, J.; Yu, Y. Quality-guided spatial phase unwrapping algorithm for fast three-dimensional measurement. Opt. Commun. 2013, 294, 139–147. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F. High-speed three-dimensional profilometry for multiple objects with complex shapes. Opt. Express 2012, 20, 19493–19510. [Google Scholar] [CrossRef]
- Ding, Y.; Xi, J.; Yu, Y.; Chicharo, J. Recovering the absolute phase maps of two fringe patterns with selected frequencies. Opt. Lett. 2011, 36, 2518–2520. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zheng, D.; Kemao, Q.; Christopoulos, G. Quaternary gray-code phase unwrapping for binary fringe projection profilometry. Opt. Laser. Eng. 2019, 121, 358–368. [Google Scholar] [CrossRef]
- Wan, Y.; Cao, Y.; Kofman, J. High-accuracy 3D surface measurement using hybrid multi-frequency composite-pattern temporal phase unwrapping. Opt. Express 2020, 28, 39165–39180. [Google Scholar] [CrossRef]
- Di, J.; Zhang, J.; Xi, T.; Ma, C.; Zhao, J. Improvement of measurement accuracy in digital holographic microscopy by using dual-wavelength technique. J. Micro-Nanolith. Mem. 2015, 14, 041313. [Google Scholar] [CrossRef]
- Hyun, J.S.; Zhang, S. Enhanced two-frequency phase-shifting method. Appl. Optics 2016, 55, 4395–4401. [Google Scholar] [CrossRef] [PubMed]
- Xing, S.; Guo, H. Correction of projector nonlinearity in multi-frequency phase-shifting fringe projection profilometry. Opt. Express 2018, 26, 16277–16291. [Google Scholar] [CrossRef]
- Li, J.; Guan, J.; Du, H.; Xi, J. Error self-correction method for phase jump in multi-frequency phase-shifting structured light. Appl. Optics 2021, 60, 949–958. [Google Scholar] [CrossRef]
- Zhang, S. Digital multiple wavelength phase shifting algorithm. Proc. SPIE 2009, 7432. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Laser. Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Mustafin, K.S.; Seleznev, V.A. Methods of increasing the sensitivity of holographic interferrometry. Sov. Phys Uspekhi. 1970, 13, 416. [Google Scholar] [CrossRef]
- Weigi, F. A generalized technique of two-wavelength, nondiffuse holographic interferometry. Appl. Optics 1971, 10, 187–192. [Google Scholar] [CrossRef] [PubMed]
- Wyant, J.C. Testing aspherics using two-wavelength holography. Appl. Optics. 1971, 10, 2113–2118. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Y.; Wyant, J.C. Two-wavelength phase shifting interferometry. Appl. Optics. 1984, 23, 4539–4543. [Google Scholar] [CrossRef]
- Servin, M.; Padilla, J.M.; Gonzalez, A.; Garnica, G. Temporal phase-unwrapping of static surfaces with 2-sensitivity fringe-patterns. Opt. Express 2015, 23, 15806–15815. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, C.; Si, S.; Li, X.; Lei, Z.; Li, Y. Extended depth-range dual-wavelength interferometry based on iterative two-step temporal phase-unwrapping. J. Mod. Optic. 2018, 65, 287–297. [Google Scholar] [CrossRef]
- Servin, M.; Padilla, M.; Garnica, G. Super-sensitive two-wavelength fringe projection profilometry with 2-sensitivities temporal unwrapping. Opt. Laser. Eng. 2018, 106, 68–74. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE T. Syst. Man Cy. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, Q. Dual-frequency fringe for improving measurement accuracy of three-dimensional shape measurement. Chin. Opt. Lett. 2021, 19, 102601. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Zhang, L.; Tao, T.; Hu, Y.; Yin, W.; Chen, Q. Calibration of fringe projection profilometry: A comparative review. Opt. Laser. Eng. 2021, 143, 106622. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE T. Pattern Anal. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Tian, P.; Li, H.; Wei, H.; Deng, G.; Zhou, S.; Ma, Z.; Wang, W.; He, L. An Improved Synthesis Phase Unwrapping Method Based on Three-Frequency Heterodyne. Sensors 2022, 22, 9388. https://doi.org/10.3390/s22239388
Liu J, Tian P, Li H, Wei H, Deng G, Zhou S, Ma Z, Wang W, He L. An Improved Synthesis Phase Unwrapping Method Based on Three-Frequency Heterodyne. Sensors. 2022; 22(23):9388. https://doi.org/10.3390/s22239388
Chicago/Turabian StyleLiu, Jiangtao, Peng Tian, Hongru Li, Hao Wei, Guoliang Deng, Shouhuan Zhou, Zeyu Ma, Wenwu Wang, and Liang He. 2022. "An Improved Synthesis Phase Unwrapping Method Based on Three-Frequency Heterodyne" Sensors 22, no. 23: 9388. https://doi.org/10.3390/s22239388
APA StyleLiu, J., Tian, P., Li, H., Wei, H., Deng, G., Zhou, S., Ma, Z., Wang, W., & He, L. (2022). An Improved Synthesis Phase Unwrapping Method Based on Three-Frequency Heterodyne. Sensors, 22(23), 9388. https://doi.org/10.3390/s22239388




