QoS-Aware Joint Task Scheduling and Resource Allocation in Vehicular Edge Computing
Abstract
1. Introduction
- We propose FEVEC, a Fast and Energy-efficient VEC framework to find the optimal offloading strategy. FEVEC comprehensively considers frequently changing network conditions and limited computation resources, aiming to minimize overall delay and energy consumption.
- We formalize the problem of devising an offloading strategy as a multi-objective optimization problem, and propose a multi-objective computing offloading method for VEC named MOV to obtain the optimal offloading policy. Compared with other works, this approach considers the collaboration between multiple RSUs and the application-specific QoS requirement, where an improved Non-dominated Sorting Genetic Algorithm-II (NSGA-II) is employed to generate the Pareto-optimal solutions with low complexity.
- We evaluate FEVEC using real-world and simulated vehicle trajectories. Extensive evaluations are provided to demonstrate the effectiveness of our proposed MOV compared to the state-of-the-art schemes; the proposed method leads to an improvement of about 20% on average compared with PSOCO [3].
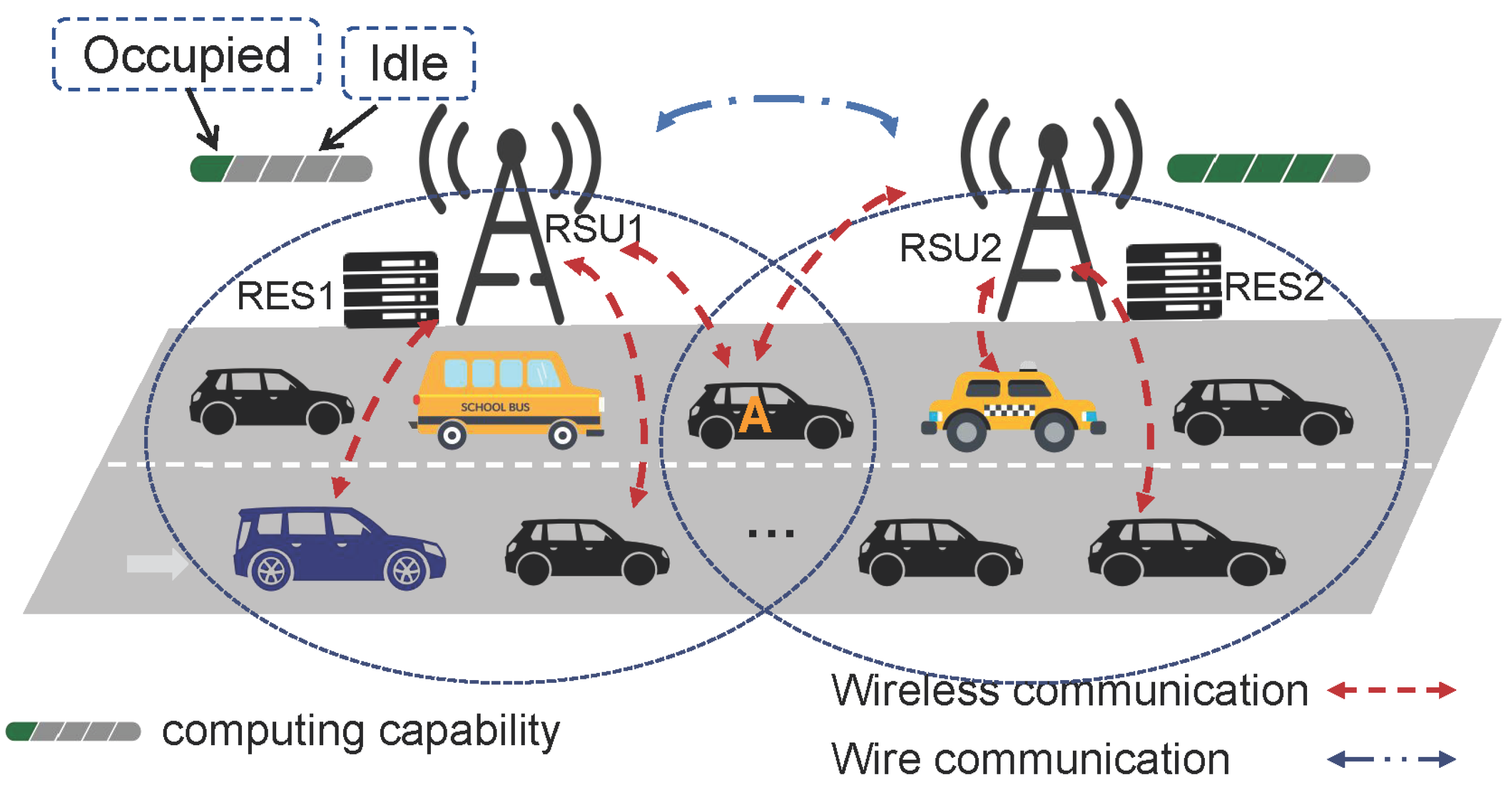
2. Motivation Example
3. System Model and Problem Formulation
3.1. Definitions and Assumptions
3.2. Communication Model
3.3. Computation Model
3.4. Problem Formalization
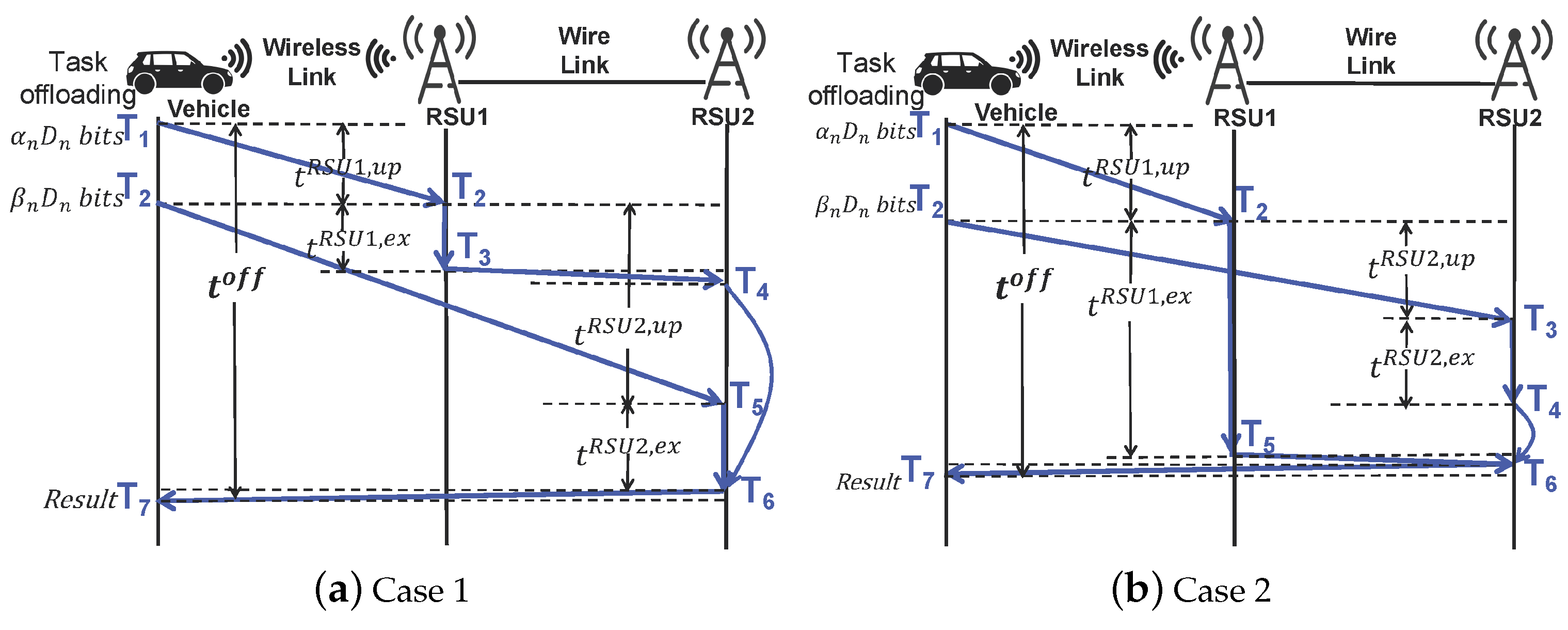
3.4.1. Delay Analysis
3.4.2. Energy Analysis
3.4.3. Task Offloading Problem
4. Computation Offloading Algorithm
| Algorithm 1 Multi-Objective computing offloading algorithm for VEC, MOV |
Input: The number of vehicles N, the offloading task , the NSGA-II algorithm parameters
|
4.1. Step 1: Vehicle Prejudgment
4.2. Step 2: Obtaining the Pareto-Optimal Solutions
4.3. Step 3: Selection of Optimal Offloading Strategy
5. Evaluation
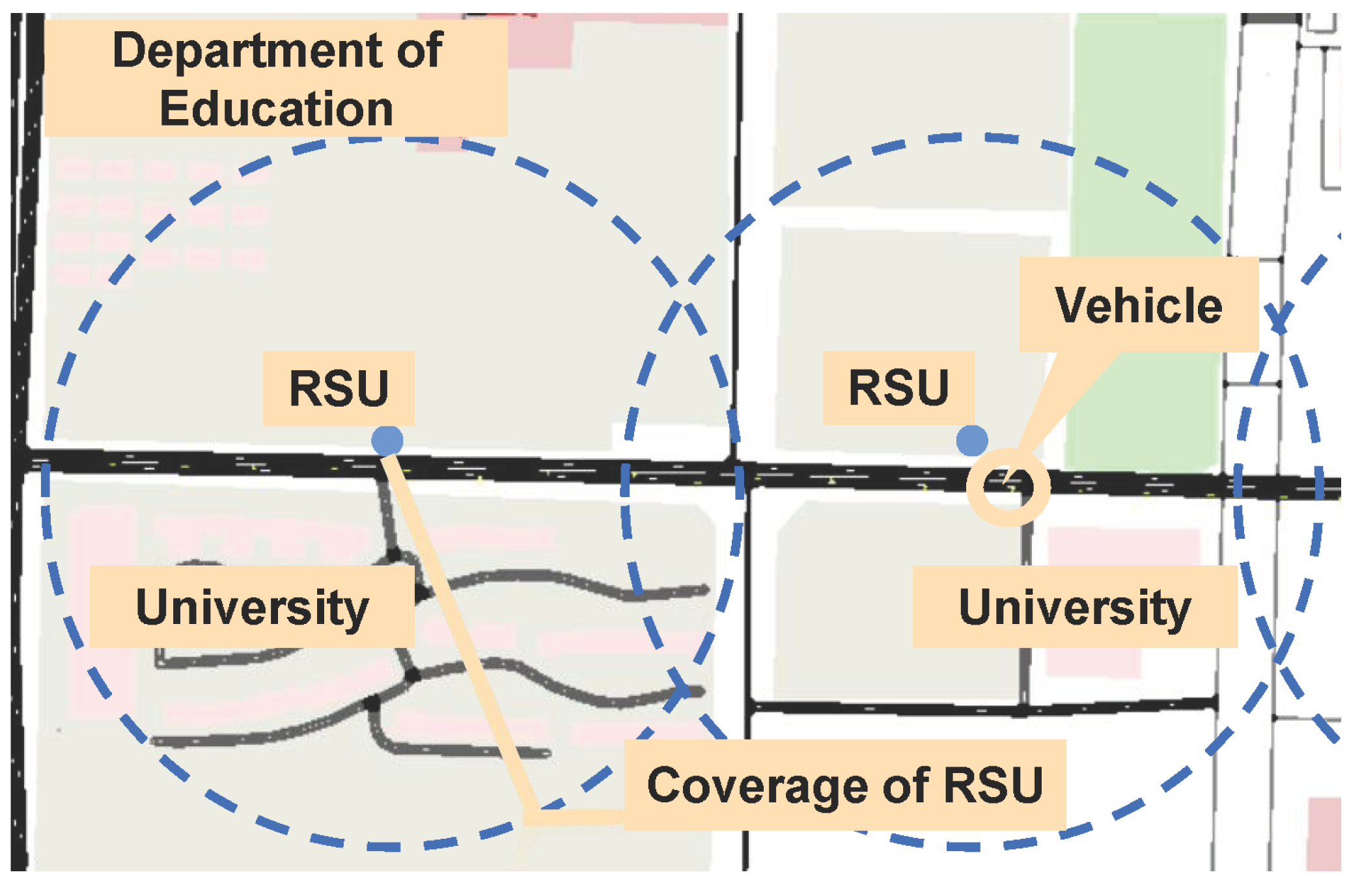
5.1. Simulation Setup
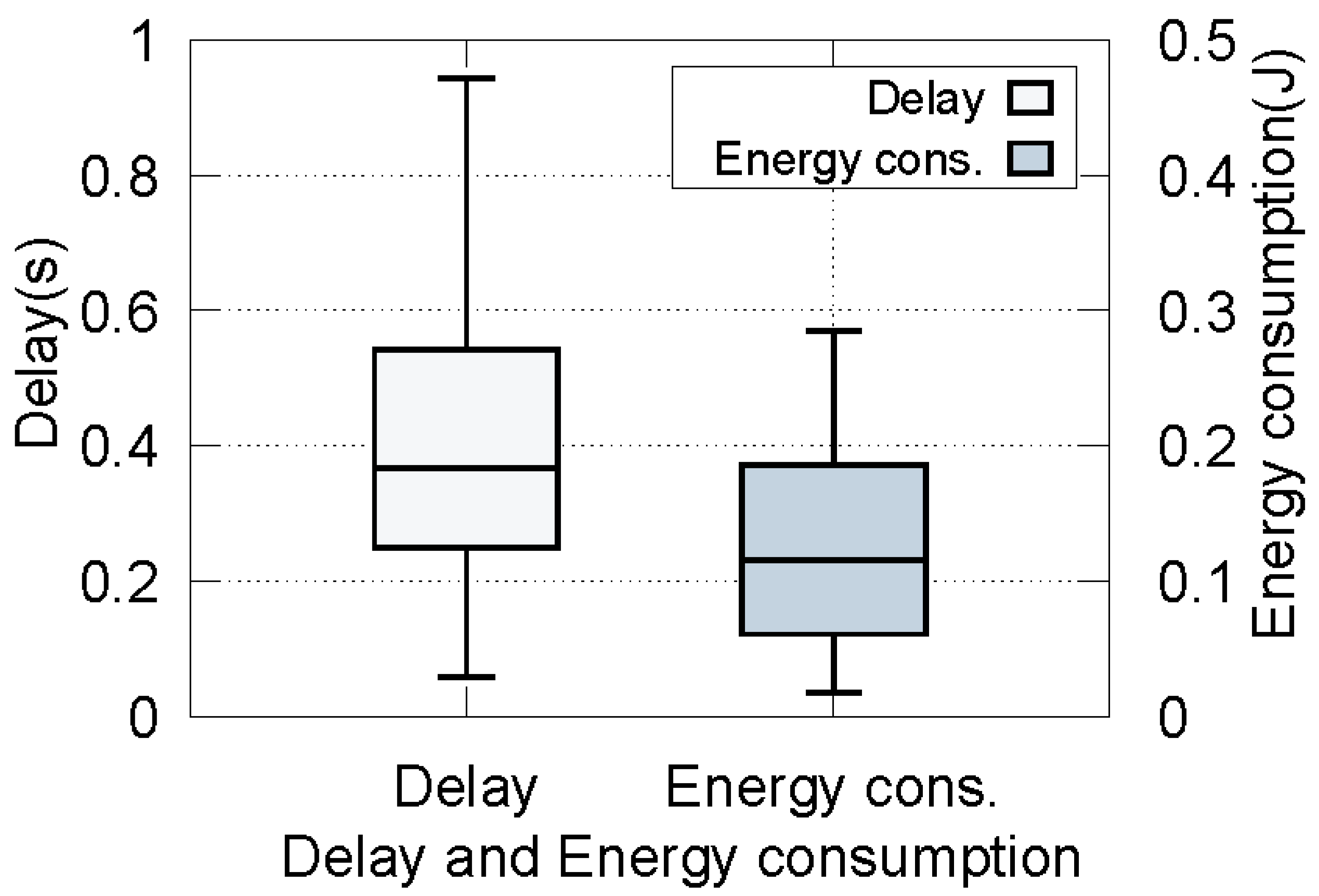
5.2. Simulation Results
5.2.1. Pareto-Optimal Solutions
5.2.2. The Validity of the Proposed Strategy
6. Related Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, K.; Mao, Y.; Leng, S.; He, Y.; Zhang, Y. Mobile-edge computing for vehicular networks: A promising network paradigm with predictive off-loading. IEEE Veh. Technol. Mag. 2017, 12, 36–44. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Pei, Q.; Maharjan, S.; Zhang, Y. Vehicular edge computing and networking: A survey. Mob. Netw. Appl. 2021, 26, 1145–1168. [Google Scholar] [CrossRef]
- Luo, Q.; Li, C.; Luan, T.; Shi, W. Minimizing the Delay and Cost of Computation Offloading for Vehicular Edge Computing. IEEE Trans. Serv. Comput. 2021, 15, 2897–2909. [Google Scholar] [CrossRef]
- Yaqoob, I.; Khan, L.U.; Kazmi, S.M.A.; Imran, M.; Guizani, N.; Hong, C.S. Autonomous Driving Cars in Smart Cities: Recent Advances, Requirements, and Challenges. IEEE Netw. 2020, 34, 174–181. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Q.; Gong, Y.; Zhang, K. Computation offloading and resource allocation for cloud assisted mobile edge computing in vehicular networks. IEEE Trans. Veh. Technol. 2019, 68, 7944–7956. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H.; Xie, S.; Zhang, Y. Deep reinforcement learning for offloading and resource allocation in vehicle edge computing and networks. IEEE Trans. Veh. Technol. 2019, 68, 11158–11168. [Google Scholar] [CrossRef]
- Dai, P.; Hu, K.; Wu, X.; Xing, H.; Yu, Z. Asynchronous Deep Reinforcement Learning for Data-Driven Task Offloading in MEC-Empowered Vehicular Networks. In Proceedings of the IEEE INFOCOM, Vancouver, BC, Canada, 10–13 May 2021. [Google Scholar]
- Wan, S.; Li, X.; Xue, Y.; Lin, W.; Xu, X. Efficient computation offloading for Internet of Vehicles in edge computing-assisted 5G networks. J. Supercomput. 2020, 76, 2518–2547. [Google Scholar] [CrossRef]
- Huang, M.; Zhai, Q.; Chen, Y.; Feng, S.; Shu, F. Multi-Objective Whale Optimization Algorithm for Computation Offloading Optimization in Mobile Edge Computing. Sensors 2021, 21, 2628. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, D.; Maharjan, S.; Zhang, Y. Joint Load Balancing and Offloading in Vehicular Edge Computing and Networks. IEEE Internet Things J. 2018, 6, 4377–4387. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, J.; Chen, L.; Yan, J.; Luo, Y. Efficient task scheduling for servers with dynamic states in vehicular edge computing. Comput. Commun. 2020, 150, 245–253. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Farrell, J.A. High-Precision Vehicle Navigation in Urban Environments using a MEM’s IMU and Single-frequency GPS Receiver. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2854–2867. [Google Scholar] [CrossRef]
- Ning, Z.; Wang, X.; Huang, J. Mobile edge computing-enabled 5G vehicular networks: Toward the integration of communication and computing. IEEE Veh. Technol. Mag. 2018, 14, 54–61. [Google Scholar] [CrossRef]
- Zhou, Z.; Feng, J.; Chang, Z.; Shen, X.S. Energy-Efficient Edge Computing Service Provisioning for Vehicular Networks: A Consensus ADMM Approach. IEEE Trans. Veh. Technol. 2019, 68, 5087–5099. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Feng, J.; Liu, Z.; Wu, C.; Ji, Y. AVE: Autonomous vehicular edge computing framework with ACO-based scheduling. IEEE Trans. Veh. Technol. 2017, 66, 10660–10675. [Google Scholar] [CrossRef]
- Huang, X.; He, L.; Chen, X.; Wang, L.; Li, F. Revenue and energy efficiency-driven delay constrained computing task offloading and resource allocation in a vehicular edge computing network: A deep reinforcement learning approach. IEEE Internet Things J. 2021, 9, 8852–8868. [Google Scholar] [CrossRef]
- White, J.S. Tables of normal percentile points. J. Am. Stat. Assoc. 1970, 65, 635–638. [Google Scholar] [CrossRef]
- Didi. Urban Traffic Time Index and Trajectory Data (New). Available online: https://gaia.didichuxing.com (accessed on 1 May 2021).
- Openstreetmap. Available online: https://master.apis.dev.openstreetmap.org (accessed on 1 April 2022).
- Wu, Y.; Xia, J.; Gao, C.; Ou, J.; Fan, C.; Ou, J.; Fan, D. Task offloading for vehicular edge computing with imperfect CSI: A deep reinforcement approach. Phys. Commun. 2022, 55, 101867. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Su, M.; Cao, C.; Dai, M.; Li, J.; Li, Y. Towards Fast and Energy-Efficient Offloading for Vehicular Edge Computing. In Proceedings of the 2022 IEEE 28th International Conference on Parallel and Distributed Systems (ICPADS), Nanjing, China, 10–12 January 2023. [Google Scholar]
- Chen, C.; Wang, Z.; Pei, Q.; He, C.; Dou, Z. Distributed Computation Offloading using Deep Reinforcement Learning in Internet of Vehicles. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9–11 August 2020. [Google Scholar]
- Lin, S.Y.; Huang, C.M.; Wu, T.Y. Multi-Access Edge Computing-Based Vehicle-Vehicle-RSU Data Offloading Over the Multi-RSU-Overlapped Environment. IEEE Open J. Intell. Transp. Syst. 2022, 3, 7–32. [Google Scholar] [CrossRef]
- Ning, Z.; Zhang, K.; Wang, X.; Guo, L.; Hu, X.; Huang, J.; Hu, B.; Kwok, R.Y. Intelligent edge computing in internet of vehicles: A joint computation offloading and caching solution. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2212–2225. [Google Scholar] [CrossRef]
- Zheng, J.; Luan, T.H.; Gao, L.; Zhang, Y.; Wu, Y. Learning based task offloading in digital twin empowered internet of vehicles. arXiv 2021, arXiv:2201.09076. [Google Scholar]
- Karimi, E.; Chen, Y.; Akbari, B. Task offloading in vehicular edge computing networks via deep reinforcement learning. Comput. Commun. 2022, 189, 193–204. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Shang, B.; Zhang, P. Joint Resource Allocation and Multi-Part Collaborative Task Offloading in MEC Systems. IEEE Trans. Veh. Technol. 2022, 71, 8877–8890. [Google Scholar] [CrossRef]
- Pang, S.; Wang, N.; Wang, M.; Qiao, S.; Zhai, X.; Xiong, N.N. A Smart Network Resource Management System for High Mobility Edge Computing in 5G Internet of Vehicles. IEEE Trans. Netw. Sci. Eng. 2021, 8, 3179–3191. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, J.; Zhou, H.; Lin, T.; Luo, G.; Shen, X. A Joint Service Migration and Mobility Optimization Approach for Vehicular Edge Computing. IEEE Trans. Veh. Technol. 2020, 69, 9041–9052. [Google Scholar] [CrossRef]






| Descriptions | Parameter | Value |
|---|---|---|
| Coverage radius of RSU | r | 200 m |
| The number of vehicles | N | 50–90 |
| Uplink bandwidth of RSU1 | 100 MHZ | |
| The uplink transmission power of vehicle n with RSU1 | 1 W | |
| The uplink power gains of vehicle n with RSU1 | 1 | |
| Path loss exponent | v | 3.5 |
| Coefficients related to power in vehicle and RSU1 [10] | , | , |
| Local maximum processing capacity | cycles/s | |
| RSU1 maximum processing capacity | cycles/s | |
| White Gaussian noise powers | −100 dBm | |
| The delay threshold for LPA | 0.8 s | |
| The speed of vehicle | s | 0–60 km/h |
| Notations | Descriptions |
|---|---|
| r | A coverage radius of one RSU |
| N | The number of vehicles |
| The data size of the task on the vehicle n | |
| Computation intensity (in CPU cycles per bit) | |
| Delay tolerance of the task | |
| Distance between vehicle n and RSU | |
| , , | Offloading ratio of vehicle n to RSU1, RSU2 and local |
| Uplink bandwidth of RSU1 | |
| M | The number of subchannels in the uplink of RSU1 |
| The uplink transmission power of vehicle n to RSU1 | |
| The uplink power gains of vehicle n to RSU1 | |
| White Gaussian noise powers on subchannel m | |
| v | Path loss exponent |
| , | Coefficients related to power in vehicle n and RSU1 |
| , | Processing capability for task and maximum processing capability of vehicle n |
| , | Processing capability for task and maximum processing capability of RSU1 |
| Indicator indicating whether subchannel m is allocated to vehicle n |
| The Number of Vehicles | Algorithm | QoS Value | Delay (s) | Energy Consumption (J) | ||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | |||
| ORO | 0.45 | 6.811 | 9.187 | 11.139 | 12.462 | |
| PLO | 0.47 | 58.858 | 123.820 | 0.080 | 3.332 | |
| PSOCO | 0.63 | 27.957 | 78.406 | 2.590 | 14.915 | |
| MOV | 0.74 | 23.834 | 53.703 | 3.180 | 10.342 | |
| ORO | 0.52 | 7.638 | 14.002 | 16.807 | 18.243 | |
| PLO | 0.54 | 64.372 | 140.077 | 0.147 | 3.535 | |
| PSOCO | 0.65 | 39.507 | 88.564 | 3.261 | 16.070 | |
| MOV | 0.71 | 27.243 | 55.769 | 5.002 | 13.850 | |
| ORO | 0.51 | 8.439 | 13.989 | 20.882 | 22.855 | |
| PLO | 0.49 | 83.505 | 190.345 | 1.255 | 4.950 | |
| PSOCO | 0.66 | 41.045 | 119.717 | 3.632 | 17.562 | |
| MOV | 0.75 | 31.626 | 65.433 | 5.669 | 17.310 | |
| The Number of Vehicles | Algorithm | Reward Value | ||
|---|---|---|---|---|
| Balance | Delay-sen. | Energy-sen. | ||
| P-PPO | 0.94 | 0.93 | 0.94 | |
| MOV | 0.97 | 0.96 | 0.98 | |
| P-PPO | 0.89 | 0.89 | 0.89 | |
| MOV | 0.92 | 0.94 | 0.90 | |
| P-PPO | 0.87 | 0.83 | 0.87 | |
| MOV | 0.92 | 0.88 | 0.93 | |
| Algorithm | Delay (s) | Energy Consumption (J) | QoS Value | ||||
|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Balance | Delay-sen. | Energy-sen. | |
| MOV-S. [23] | 21.33 | 58.27 | 3.72 | 10.15 | 0.61 | 0.72 | 0.68 |
| MOV | 15.42 | 47.15 | 3.81 | 14.03 | 0.68 | 0.86 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Su, M.; Duan, S.; Dai, M.; Li, J.; Li, Y. QoS-Aware Joint Task Scheduling and Resource Allocation in Vehicular Edge Computing. Sensors 2022, 22, 9340. https://doi.org/10.3390/s22239340
Cao C, Su M, Duan S, Dai M, Li J, Li Y. QoS-Aware Joint Task Scheduling and Resource Allocation in Vehicular Edge Computing. Sensors. 2022; 22(23):9340. https://doi.org/10.3390/s22239340
Chicago/Turabian StyleCao, Chenhong, Meijia Su, Shengyu Duan, Miaoling Dai, Jiangtao Li, and Yufeng Li. 2022. "QoS-Aware Joint Task Scheduling and Resource Allocation in Vehicular Edge Computing" Sensors 22, no. 23: 9340. https://doi.org/10.3390/s22239340
APA StyleCao, C., Su, M., Duan, S., Dai, M., Li, J., & Li, Y. (2022). QoS-Aware Joint Task Scheduling and Resource Allocation in Vehicular Edge Computing. Sensors, 22(23), 9340. https://doi.org/10.3390/s22239340







