Optimal Temporal Filtering of the Cosmic-Ray Neutron Signal to Reduce Soil Moisture Uncertainty
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Data
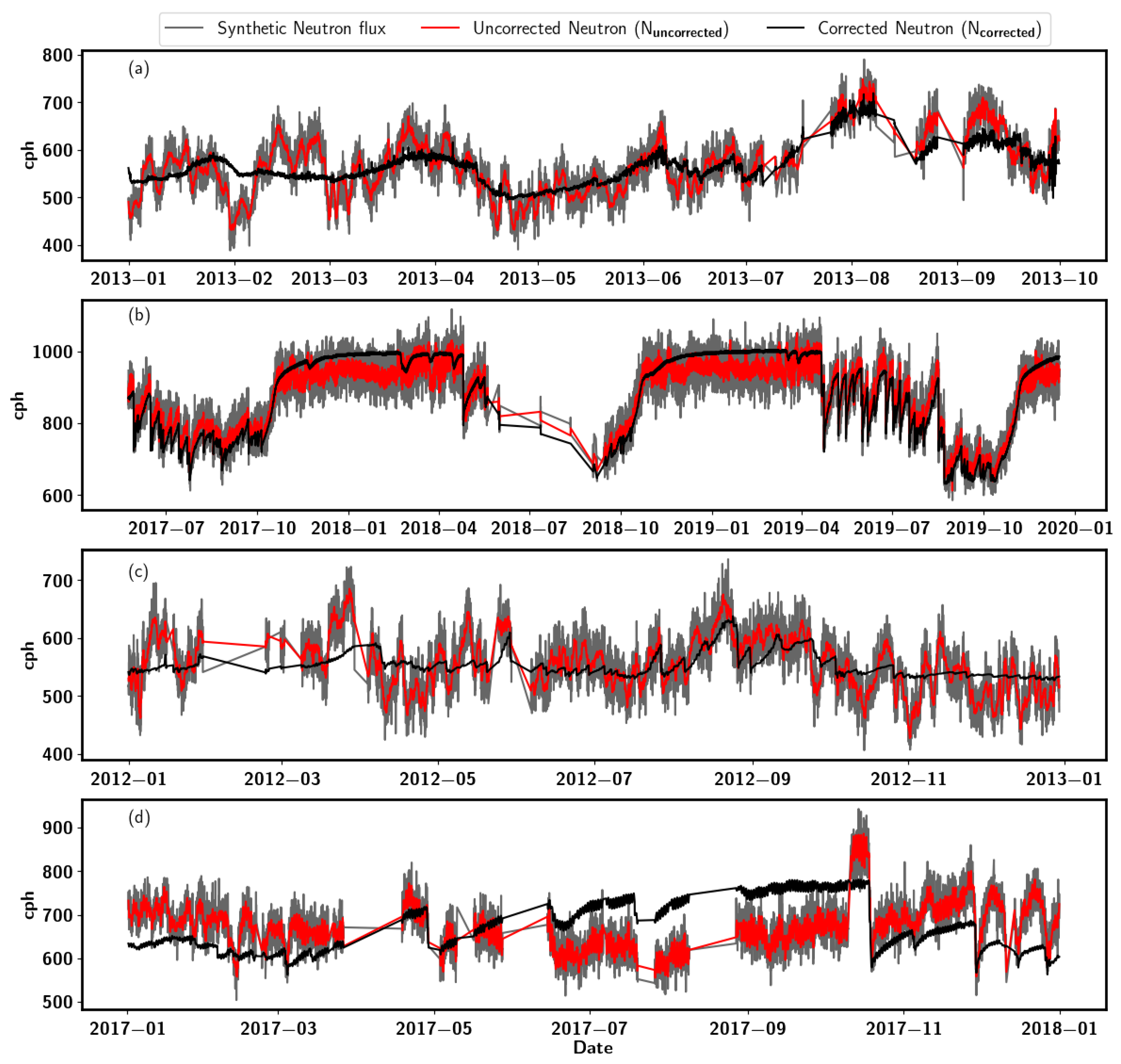
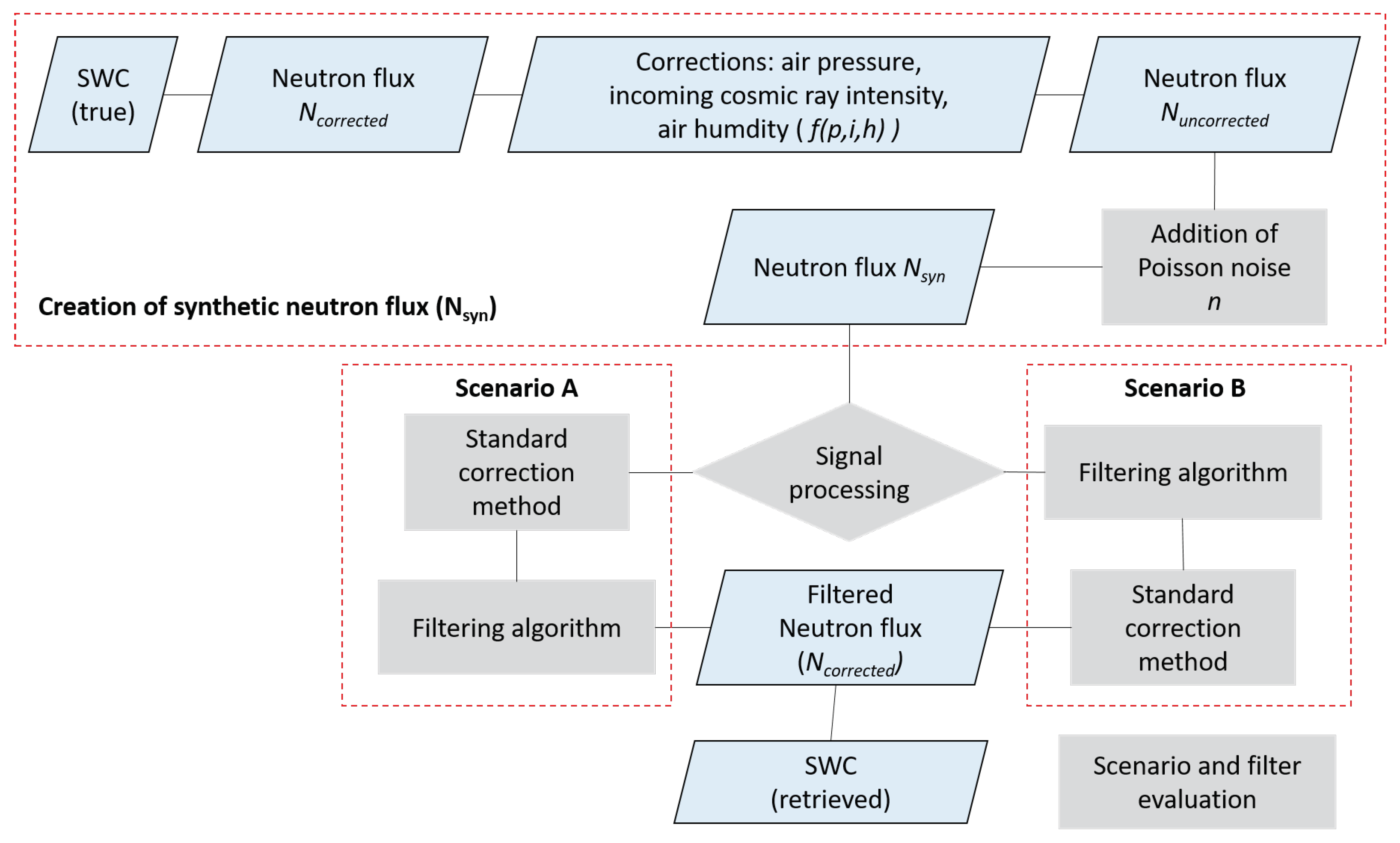
Generating Synthetic Neutron Signal for Selected Sites
2.3. Analysis
2.3.1. Moving Average
2.3.2. Savitzky–Golay Filter
2.3.3. Median Filter
2.3.4. Kalman Filter
2.3.5. Error Measurement
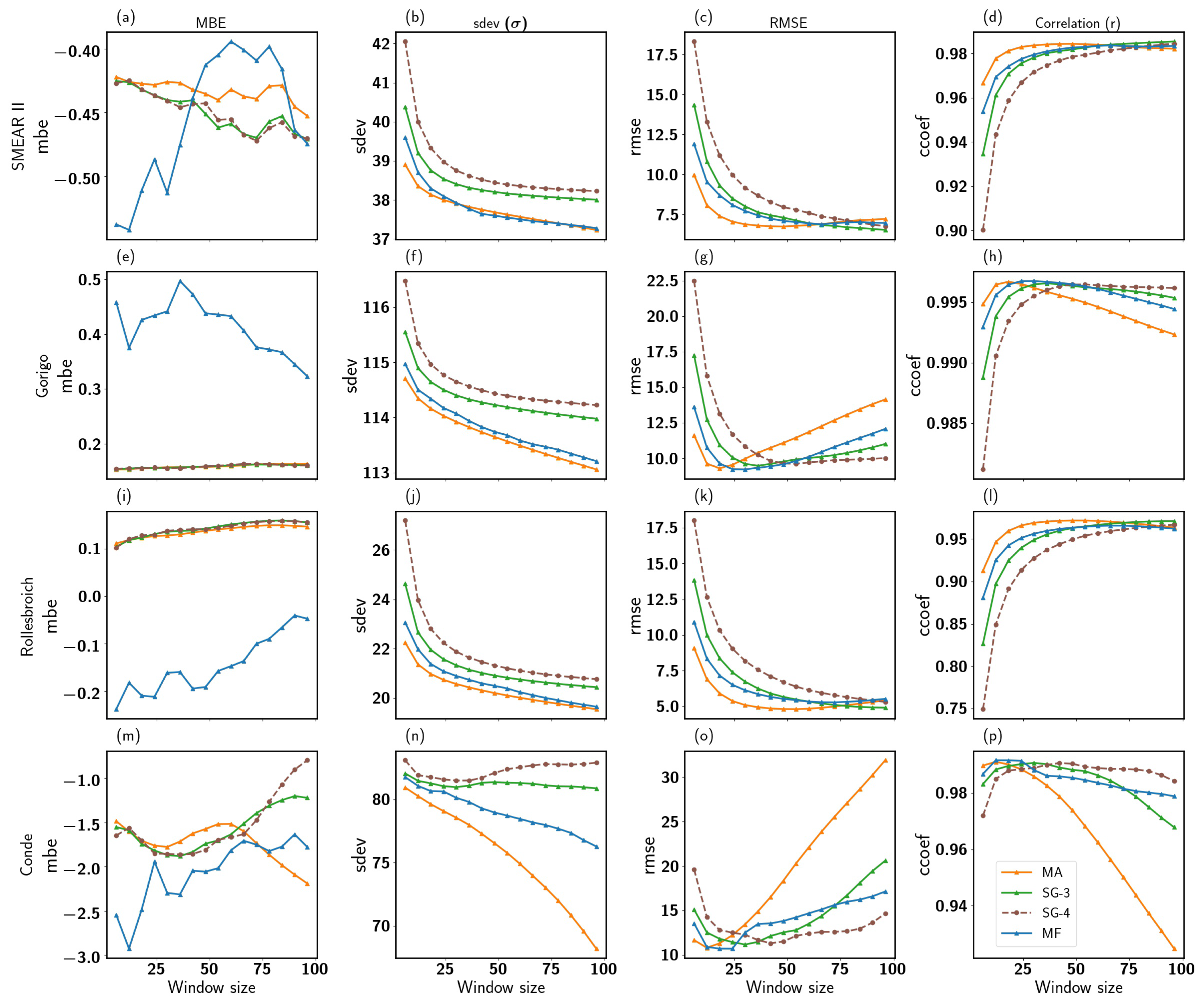
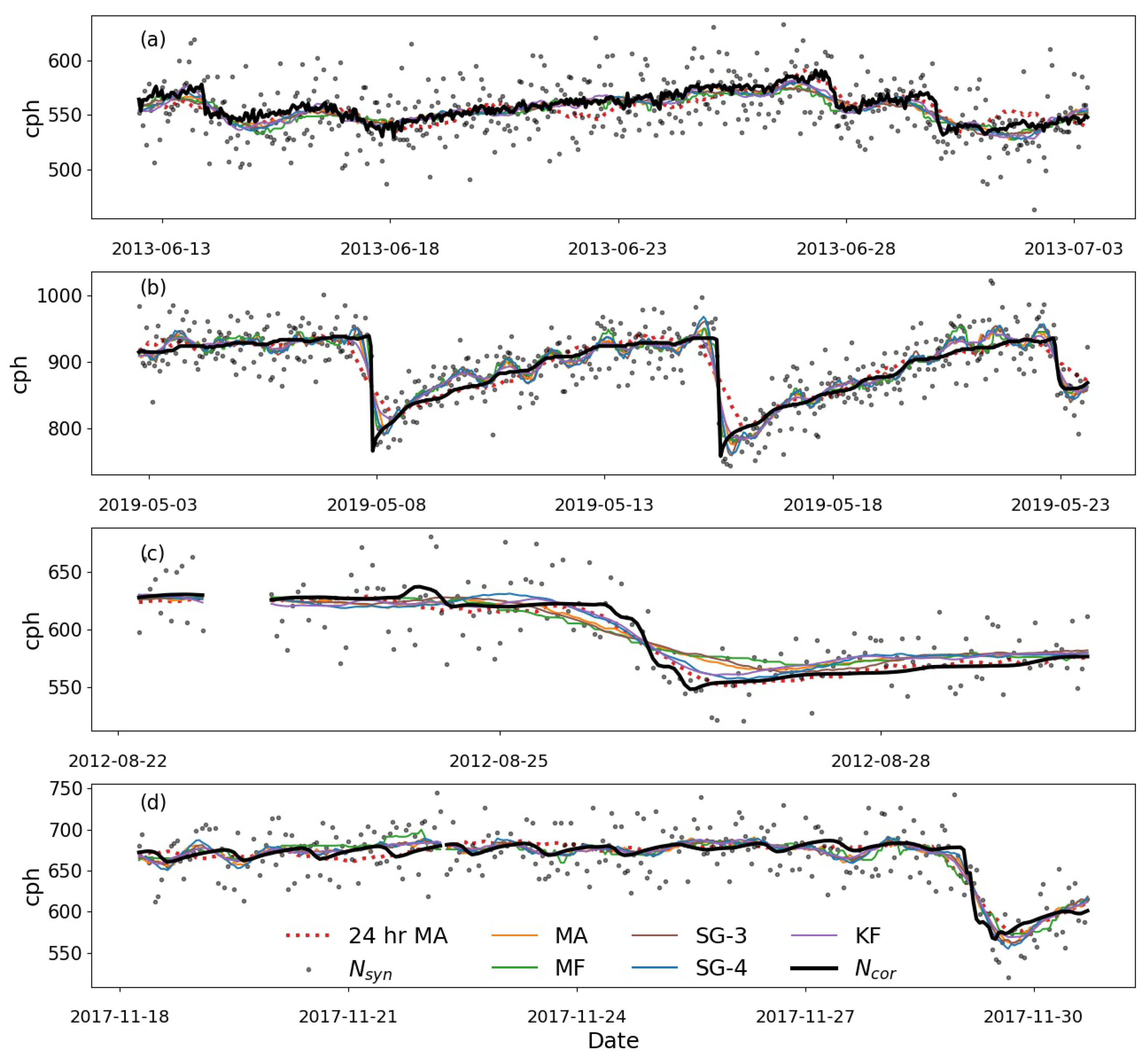
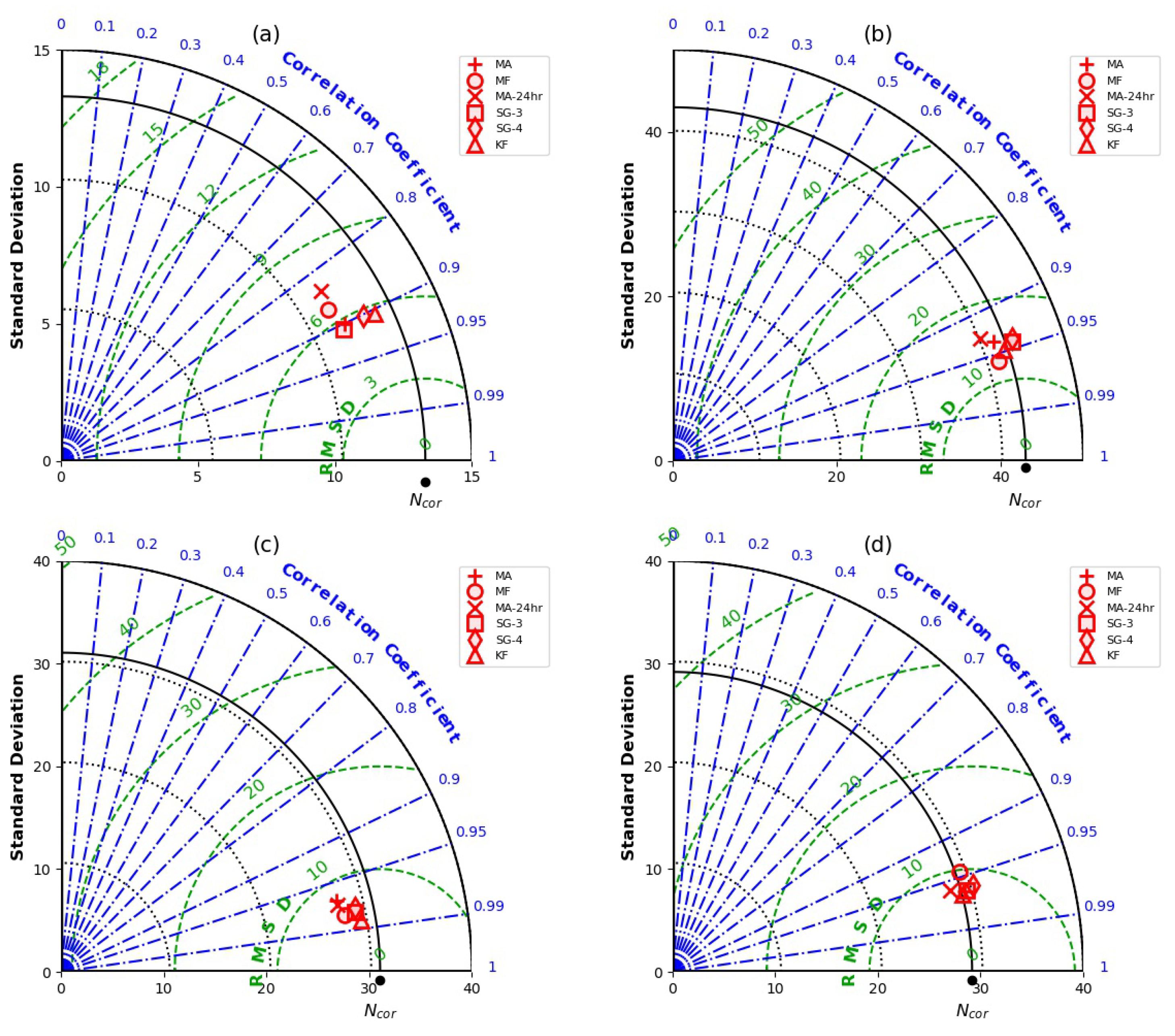
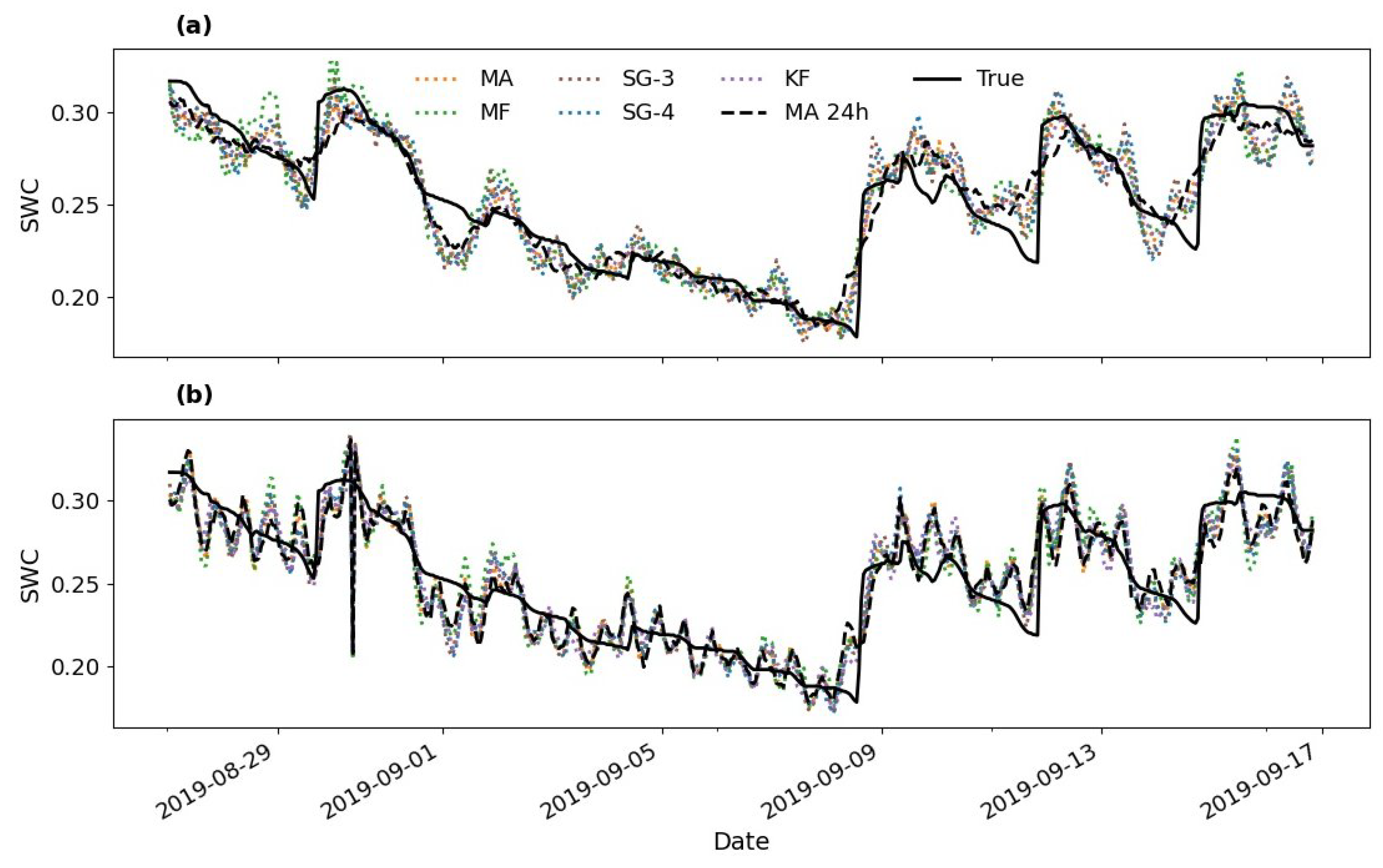
3. Results
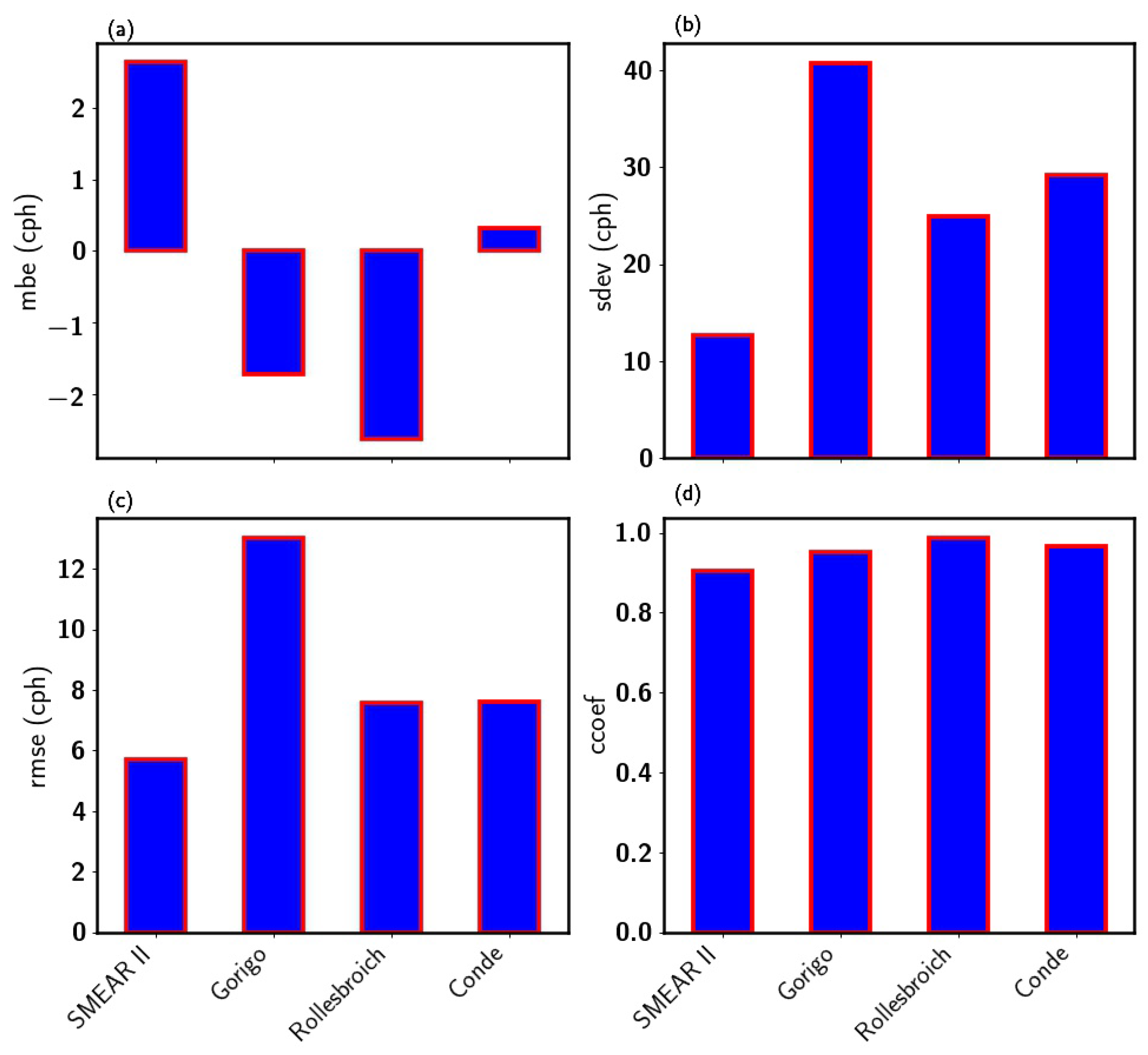
3.1. Evaluation of Filters’ Performance at the Four Sites
3.2. Optimal Filter and Window Length
3.3. Uncertainty Propagation from CRNS Standard Correction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LeMone, M.A.; Chen, F.; Alfieri, J.G.; Tewari, M.; Geerts, B.; Miao, Q.; Grossman, R.L.; Coulter, R.L. Influence of land cover and soil moisture on the horizontal distribution of sensible and latent heat fluxes in southeast Kansas during IHOP_2002 and CASES-97. J. Hydrometeorol. 2007, 8, 68–87. [Google Scholar] [CrossRef]
- Zhang, D.; Anthes, R.A. A high-resolution model of the planetary boundary layer—Sensitivity tests and comparisons with SESAME-79 data. J. Appl. Meteorol. 1982, 21, 1594–1609. [Google Scholar] [CrossRef]
- Clark, C.A.; Arritt, P.W. Numerical simulations of the effect of soil moisture and vegetation cover on the development of deep convection. J. Appl. Meteorol. Climatol. 1995, 34, 2029–2045. [Google Scholar] [CrossRef]
- Pielke Sr, R.A. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall. Rev. Geophys. 2001, 39, 151–177. [Google Scholar] [CrossRef]
- Ek, M.; Holtslag, A. Influence of soil moisture on boundary layer cloud development. J. Hydrometeorol. 2004, 5, 86–99. [Google Scholar] [CrossRef]
- Zwane, E.M. Impact of climate change on primary agriculture, water sources and food security in Western Cape, South Africa. Jàmbá J. Disaster Risk Stud. 2019, 11, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Shayanmehr, S.; Porhajašová, J.I.; Babošová, M.; Sabouhi Sabouni, M.; Mohammadi, H.; Rastegari Henneberry, S.; Shahnoushi Foroushani, N. The impacts of climate change on water resources and crop production in an arid region. Agriculture 2022, 12, 1056. [Google Scholar] [CrossRef]
- Sharma, P.K.; Kumar, D.; Srivastava, H.S.; Patel, P. Assessment of different methods for soil moisture estimation: A review. J. Remote Sens. GIS 2018, 9, 57–73. [Google Scholar]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.; Franz, T.E.; et al. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.B.; Mooney, H.A.; Schulze, E.D. A global budget for fine root biomass, surface area, and nutrient contents. Proc. Natl. Acad. Sci. USA 1997, 94, 7362–7366. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.B.; Liao, T.H. Robust retrieval of soil moisture at field scale across wide-ranging SAR incidence angles for soybean, wheat, forage, oat and grass. Remote Sens. Environ. 2021, 266, 112712. [Google Scholar] [CrossRef]
- Desilets, D.; Zreda, M.; Ferré, T.P. Nature’s neutron probe: Land surface hydrology at an elusive scale with cosmic rays. Water Resour. Res. 2010, 46, 11. [Google Scholar] [CrossRef]
- Baatz, R.; Hendricks Franssen, H.J.; Han, X.; Hoar, T.; Bogena, H.R.; Vereecken, H. Evaluation of a cosmic-ray neutron sensor network for improved land surface model prediction. Hydrol. Earth Syst. Sci. 2017, 21, 2509–2530. [Google Scholar] [CrossRef]
- Köhli, M.; Schrön, M.; Schmidt, U. Response functions for detectors in cosmic ray neutron sensing. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 902, 184–189. [Google Scholar] [CrossRef]
- Zreda, M.; Shuttleworth, W.; Zeng, X.; Zweck, C.; Desilets, D.; Franz, T.; Rosolem, R. COSMOS: The cosmic-ray soil moisture observing system. Hydrol. Earth Syst. Sci. 2012, 16, 4079–4099. [Google Scholar] [CrossRef]
- Schreiner-McGraw, A.P.; Vivoni, E.R.; Mascaro, G.; Franz, T.E. Closing the water balance with cosmic-ray soil moisture measurements and assessing their relation to evapotranspiration in two semiarid watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 329–345. [Google Scholar] [CrossRef]
- Bogena, H.; Huisman, J.; Baatz, R.; Hendricks Franssen, H.J.; Vereecken, H. Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario. Water Resour. Res. 2013, 49, 5778–5791. [Google Scholar] [CrossRef]
- Sigouin, M.J.; Si, B.C. Calibration of a non-invasive cosmic-ray probe for wide area snow water equivalent measurement. Cryosphere 2016, 10, 1181–1190. [Google Scholar] [CrossRef]
- Zhu, X.; Shao, M.; Zeng, C.; Jia, X.; Huang, L.; Zhang, Y.; Zhu, J. Application of cosmic-ray neutron sensing to monitor soil water content in an alpine meadow ecosystem on the northern Tibetan Plateau. J. Hydrol. 2016, 536, 247–254. [Google Scholar] [CrossRef]
- Bachelet, F.; Balata, P.; Iucci, N. Some properties of the radiation recorded by the IGY cosmic-ray neutron monitors in the lower atmosphere. Nuovo C. 1965, 40, 250–260. [Google Scholar] [CrossRef]
- Rosolem, R.; Shuttleworth, W.; Zreda, M.; Franz, T.E.; Zeng, X.; Kurc, S. The effect of atmospheric water vapor on neutron count in the cosmic-ray soil moisture observing system. J. Hydrometeorol. 2013, 14, 1659–1671. [Google Scholar] [CrossRef]
- Baatz, R.; Bogena, H.; Hendricks Franssen, H.J.; Huisman, J.; Montzka, C.; Vereecken, H. An empirical vegetation correction for soil water content quantification using cosmic ray probes. Water Resour. Res. 2015, 51, 2030–2046. [Google Scholar] [CrossRef]
- Schrön, M. Cosmic-ray Neutron Sensing and Its Applications to Soil and Land Surface Hydrology: On Neutron Physics, Method Development, and Soil Moisture Estimation Across Scales; Universität Potsdam: Potsdam, Germany, 2016. [Google Scholar]
- Heidbüchel, I.; Güntner, A.; Blume, T. Use of cosmic-ray neutron sensors for soil moisture monitoring in forests. Hydrol. Earth Syst. Sci. 2016, 20, 1269–1288. [Google Scholar] [CrossRef]
- Jakobi, J.; Huisman, J.A.; Schrön, M.; Fiedler, J.; Brogi, C.; Vereecken, H.; Bogena, H.R. Error estimation for soil moisture measurements with cosmic ray neutron sensing and implications for rover surveys. Front. Water 2020, 2, 10. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T. Field validation of a cosmic-ray neutron sensor using a distributed sensor network. Vadose Zone J. 2012, 11, vzj2012-0046. [Google Scholar] [CrossRef]
- Baroni, G.; Scheiffele, L.; Schrön, M.; Ingwersen, J.; Oswald, S. Uncertainty, sensitivity and improvements in soil moisture estimation with cosmic-ray neutron sensing. J. Hydrol. 2018, 564, 873–887. [Google Scholar] [CrossRef]
- Köhli, M.; Schrön, M.; Zreda, M.; Schmidt, U.; Dietrich, P.; Zacharias, S. Footprint characteristics revised for field-scale soil moisture monitoring with cosmic-ray neutrons. Water Resour. Res. 2015, 51, 5772–5790. [Google Scholar] [CrossRef]
- Schrön, M.; Rosolem, R.; Köhli, M.; Piussi, L.; Schröter, I.; Iwema, J.; Kögler, S.; Oswald, S.; Wollschläger, U.; Samaniego, L.; et al. Cosmic-ray neutron rover surveys of field soil moisture and the influence of roads. Water Resour. Res. 2018, 54, 6441–6459. [Google Scholar] [CrossRef]
- Chrisman, B.; Zreda, M. Quantifying mesoscale soil moisture with the cosmic-ray rover. Hydrol. Earth Syst. Sci. 2013, 17, 5097–5108. [Google Scholar] [CrossRef]
- Franz, T.E.; Wahbi, A.; Zhang, J.; Vreugdenhil, M.; Heng, L.; Dercon, G.; Strauss, P.; Brocca, L.; Wagner, W. Practical data products from cosmic-ray neutron sensing for hydrological applications. Front. Water 2020, 2, 9. [Google Scholar] [CrossRef]
- Korres, W.; Reichenau, T.; Fiener, P.; Koyama, C.; Bogena, H.R.; Cornelissen, T.; Baatz, R.; Herbst, M.; Diekkrüger, B.; Vereecken, H.; et al. Spatio-temporal soil moisture patterns–A meta-analysis using plot to catchment scale data. J. Hydrol. 2015, 520, 326–341. [Google Scholar] [CrossRef]
- Bogena, H.; Montzka, C.; Huisman, J.; Graf, A.; Schmidt, M.; Stockinger, M.; Von Hebel, C.; Hendricks-Franssen, H.; Van der Kruk, J.; Tappe, W.; et al. The TERENO-Rur hydrological observatory: A multiscale multi-compartment research platform for the advancement of hydrological science. Vadose Zone J. 2018, 17, 1–22. [Google Scholar] [CrossRef]
- Kolari, P.; Aalto, J.; Levula, J.; Kulmala, L.; Ilvesniemi, H.; Pumpanen, J. Hyytiälä SMEAR II Site Characteristics 2022. Available online: https://zenodo.org/record/5909681 (accessed on 21 September 2022).
- Aguirre-García, S.D.; Aranda-Barranco, S.; Nieto, H.; Serrano-Ortiz, P.; Sánchez-Cañete, E.P.; Guerrero-Rascado, J.L. Modelling actual evapotranspiration using a two source energy balance model with Sentinel imagery in herbaceous-free and herbaceous-cover Mediterranean olive orchards. Agric. For. Meteorol. 2021, 311, 108692. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating high-resolution daily soil moisture by using spatial downscaling techniques: A comparison of six machine learning algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Kennedy, H.L. Improving the frequency response of Savitzky–Golay filters via colored-noise models. Digit. Signal Process. 2020, 102, 102743. [Google Scholar] [CrossRef]
- Kwak, S.G.; Kim, J.H. Central limit theorem: The cornerstone of modern statistics. Korean J. Anesthesiol. 2017, 70, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Hassanpour, H. A time–frequency approach for noise reduction. Digit. Signal Process. 2008, 18, 728–738. [Google Scholar] [CrossRef]
- Mader, W.; Linke, Y.; Mader, M.; Sommerlade, L.; Timmer, J.; Schelter, B. A numerically efficient implementation of the expectation maximization algorithm for state space models. Appl. Math. Comput. 2014, 241, 222–232. [Google Scholar] [CrossRef]
- Bishara, A.J.; Hittner, J.B. Reducing bias and error in the correlation coefficient due to nonnormality. Educ. Psychol. Meas. 2015, 75, 785–804. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diagn. Med Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Kim, Y.; Bang, H. Introduction to Kalman filter and its applications. Introd. Implementations Kalman Filter 2018, 1, 1–16. [Google Scholar]
- Moosavi, S.R.; Qajar, J.; Riazi, M. A comparison of methods for denoising of well test pressure data. J. Pet. Explor. Prod. Technol. 2018, 8, 1519–1534. [Google Scholar] [CrossRef]
- Rasheed, A.H.; Hussein, H.M. Effect of different window size on median filter performance with variable noise densities. Int. J. Comput. Appl. 2017, 178, 22–27. [Google Scholar]
- Schafer, R.W. What is a Savitzky-Golay filter? [lecture notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Y.; Li, S.; Wang, Y.; Jia, R. Comparison of alternative strategies estimating the kinetic reaction rate of the gold cyanidation leaching process. ACS Omega 2019, 4, 19880–19894. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F. Optimum window length of Savitzky-Golay filters with arbitrary order. arXiv 2018, arXiv:1808.10489. [Google Scholar]
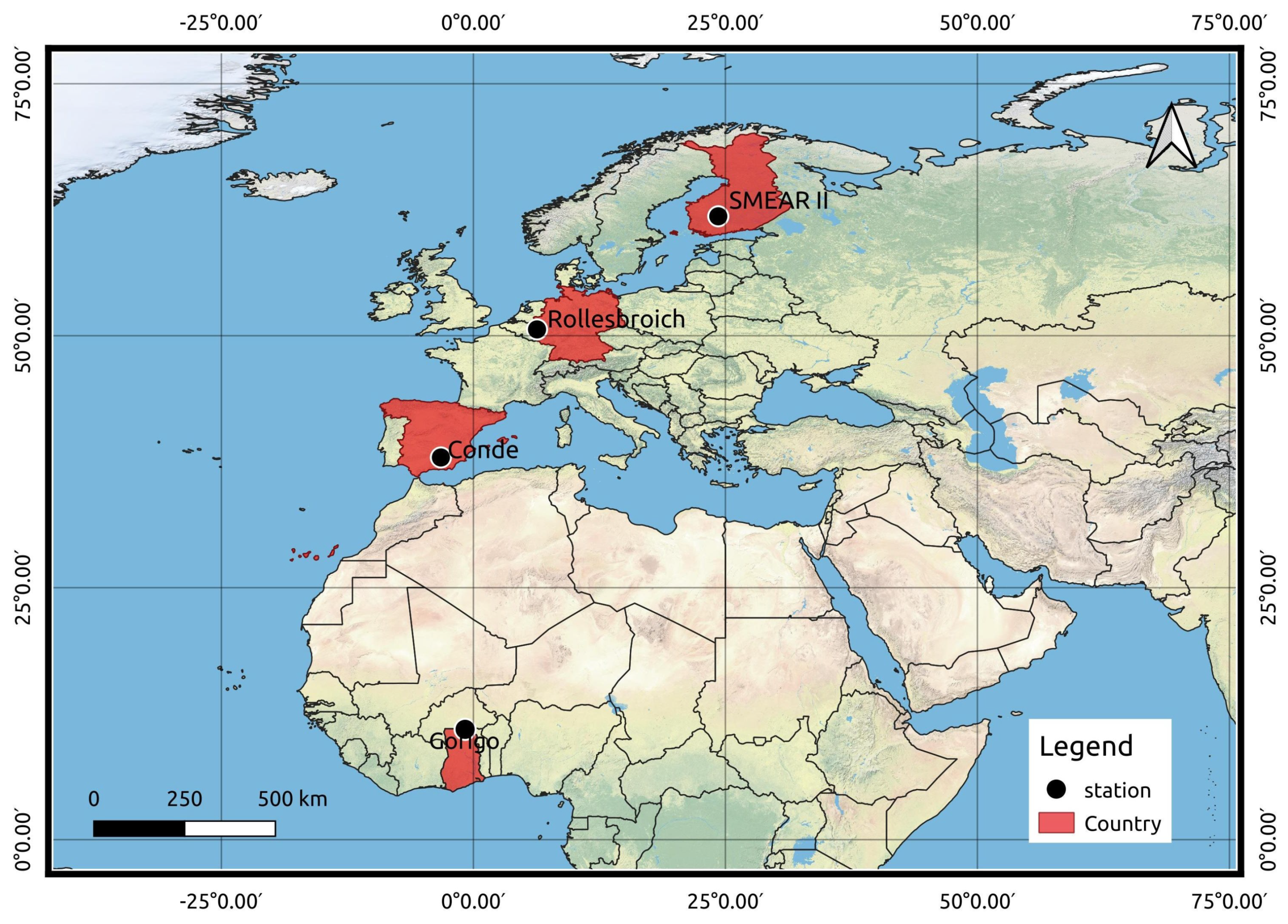

| Station | Lon/Lat | Bulk Density (g/cm) | Rigidity Cut-Off (GV) | Other Site Information |
|---|---|---|---|---|
| Gorigo | 0.82/10.93 | 1.54 | 14.68 | Highly degraded grassland |
| Loamy sand soil | ||||
| Rollesbroich | 6.30/50.63 | 1.09 | 3.27 | Managed grassland |
| Silty clay loam | ||||
| SMEAR II | 24.29/61.84 | 0.85 | 1.11 | Homogenous Scots pine trees |
| Silty sand [34] | ||||
| Conde | −3.22/37.91 | 1.37 | 8.33 | Evergreen trees and shrubs. |
| Clayey loam [35] |
| Station | True Neutron | Synthetic Neutron | KF-Filtered Neutron |
|---|---|---|---|
| Gorigo | 43.05 | 52.07 | 40.30 |
| Rollesbroich | 31.16 | 37.99 | 29.99 |
| SMEAR II | 13.31 | 26.34 | 12.63 |
| Conde | 29.24 | 39.74 | 29.20 |
| Station | MA (h) | MF (h) | SG-3 (h) | SG-4 (h) |
|---|---|---|---|---|
| Gorigo | 30 | 36 | 78 | 84 |
| Rollesbroich | 18 | 18 | 30 | 48 |
| SMEAR II | 36 | 42 | 54 | 84 |
| Conde | 18 | 12 | 30 | 36 |
| Filter | Scenario A (cm/cm) | Scenario B (cm/cm) |
|---|---|---|
| KF | 0.006 | 0.008 |
| MA (30 h) | 0.006 | 0.009 |
| SG-3 (78 h) | 0.007 | 0.009 |
| SG-4 (84 h) | 0.007 | 0.008 |
| MA (24 h) | 0.007 | 0.009 |
| MF (36 h) | 0.007 | 0.009 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davies, P.; Baatz, R.; Bogena, H.R.; Quansah, E.; Amekudzi, L.K. Optimal Temporal Filtering of the Cosmic-Ray Neutron Signal to Reduce Soil Moisture Uncertainty. Sensors 2022, 22, 9143. https://doi.org/10.3390/s22239143
Davies P, Baatz R, Bogena HR, Quansah E, Amekudzi LK. Optimal Temporal Filtering of the Cosmic-Ray Neutron Signal to Reduce Soil Moisture Uncertainty. Sensors. 2022; 22(23):9143. https://doi.org/10.3390/s22239143
Chicago/Turabian StyleDavies, Patrick, Roland Baatz, Heye Reemt Bogena, Emmanuel Quansah, and Leonard Kofitse Amekudzi. 2022. "Optimal Temporal Filtering of the Cosmic-Ray Neutron Signal to Reduce Soil Moisture Uncertainty" Sensors 22, no. 23: 9143. https://doi.org/10.3390/s22239143
APA StyleDavies, P., Baatz, R., Bogena, H. R., Quansah, E., & Amekudzi, L. K. (2022). Optimal Temporal Filtering of the Cosmic-Ray Neutron Signal to Reduce Soil Moisture Uncertainty. Sensors, 22(23), 9143. https://doi.org/10.3390/s22239143







