Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems
Abstract
:1. Introduction
- A modified TOSMO is applied to quickly estimate the approximate value of the uncertainty and exterior disturbance;
- The novel Prescribed Performance Function (PPF) does not contain a singularity problem and can flexibly adjust lower and upper bounds. Furthermore, it can extend the operation domain at a steady state compared to that of the conventional PPF. With the proposed PPF, the steady-state error boundaries will be symmetric to zero, so, when the transformed error converges to zero, the tracking error also converges to zero;
- A modified function of GFTSMM based on the transformed errors of the PPC is introduced; hence, the error variables quickly converge to the equilibrium point with the prescribed performance;
- The maximum overshoot, convergence index, and steady-state error can be managed within a predefined domain under the proposed controller;
- A novel solution ensures a finite-time stable position of the controlled ball and the possibility of performing different orbit tracking missions with an impressive performance in the terms of tracking accuracy, fast convergence, stabilization, and chattering reduction;
- The effectiveness of the designed control solution was confirmed by simulation and experiment;
- This controller is presented in a way that can be applied to real-time applications. In addition, it can apply not only to MLSs but also to a class of second-order nonlinear systems.
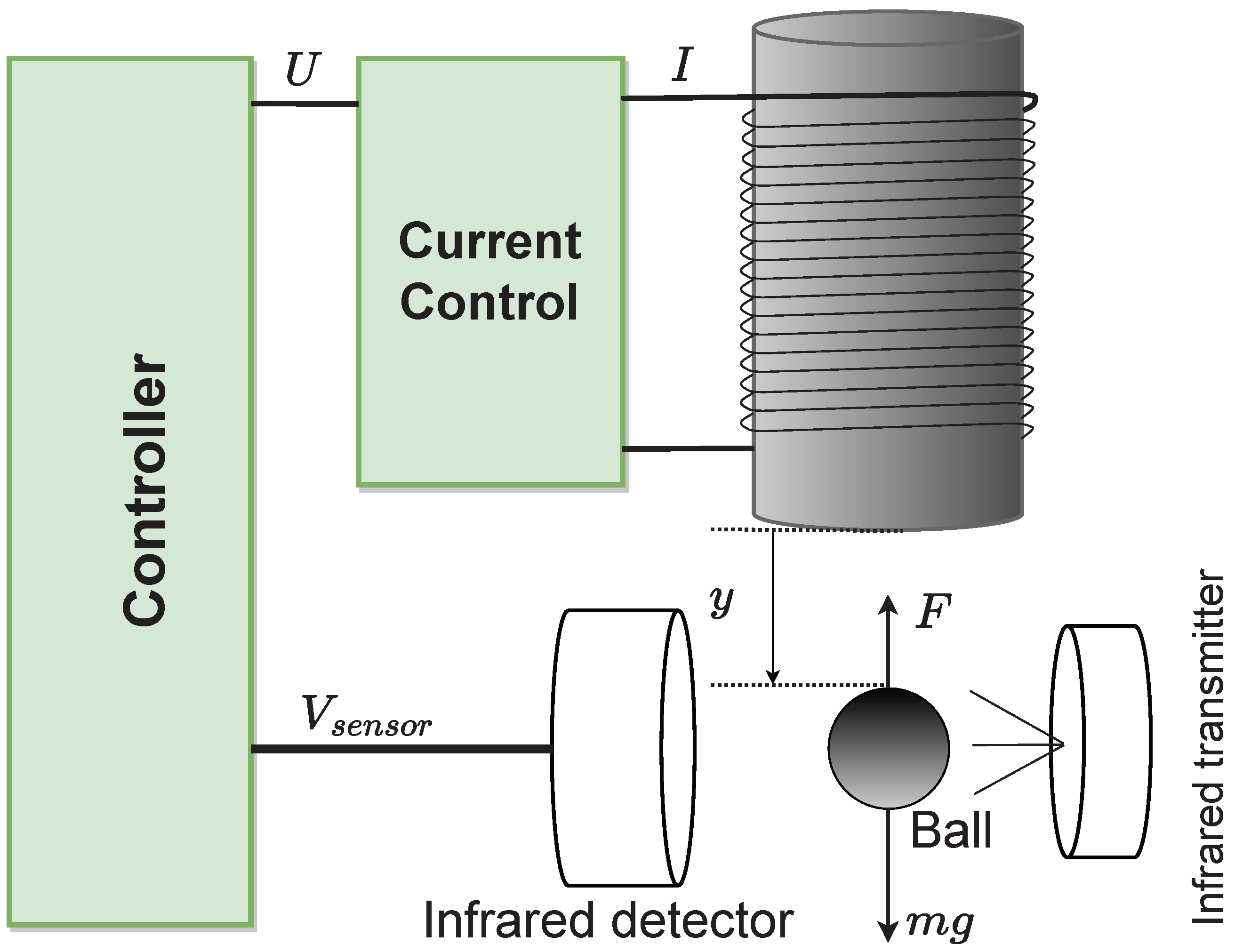
2. Problem Statements
3. Design of the Proposed Control Method
3.1. Design of the Sliding Mode Surface
3.2. Design of Global Fast Terminal Sliding Mode Control
3.3. Design of a Disturbance Observer for Magnetic Levitation Systems
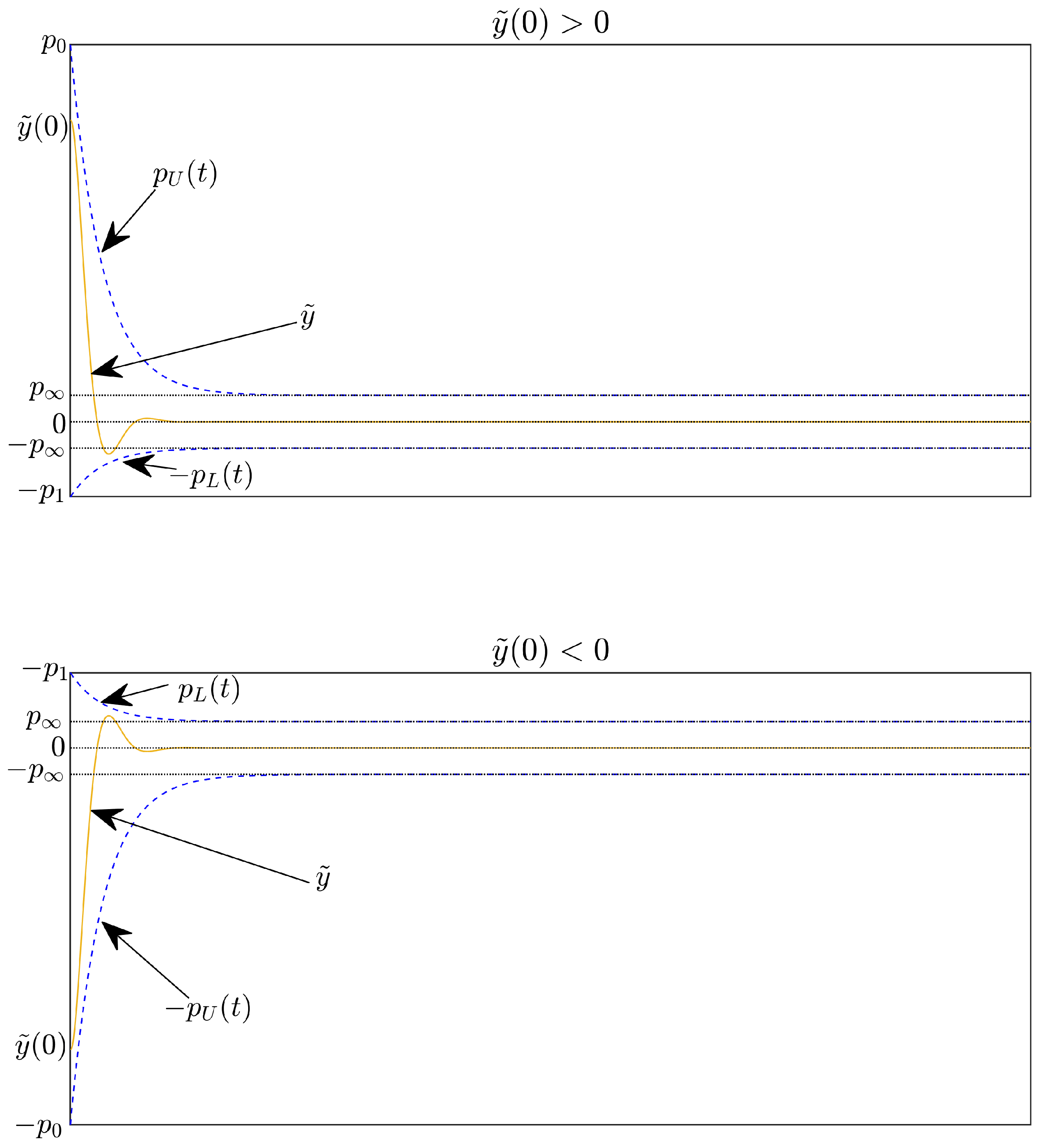
3.4. Prescribed Performance Control
- is a smooth and strictly increasing function;
- ;
- if ;
- .
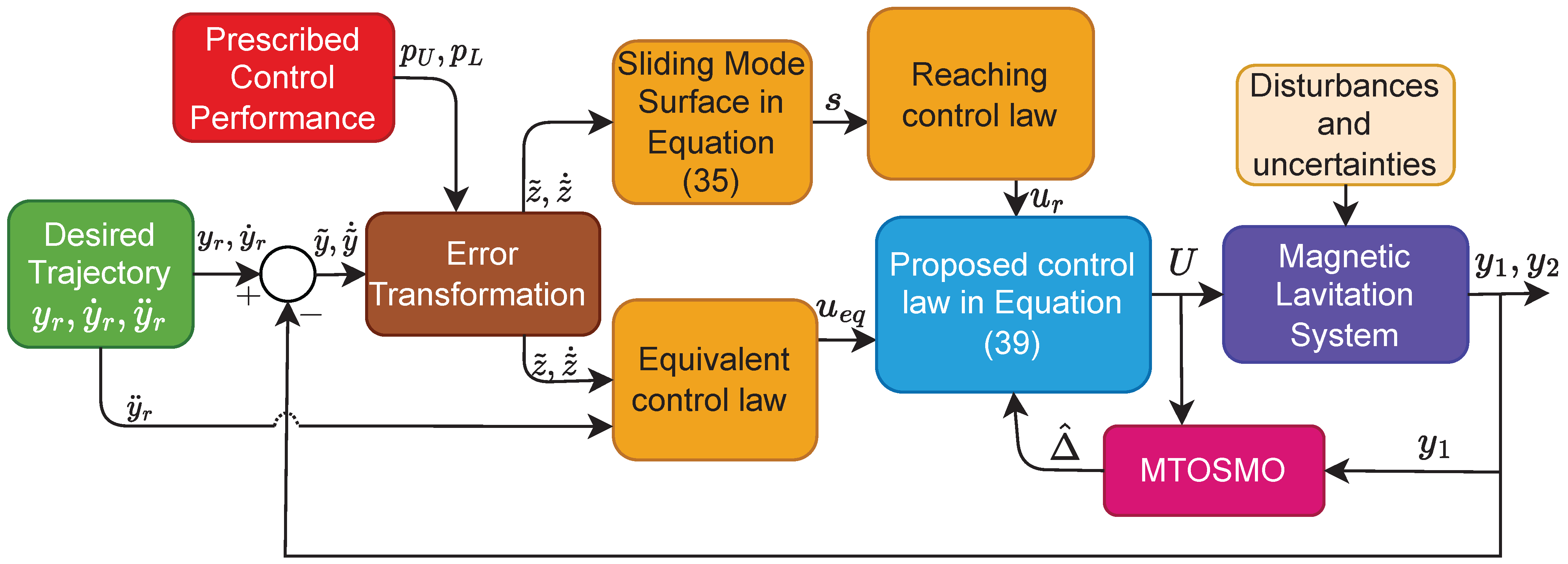
3.5. Proposed Controller Design
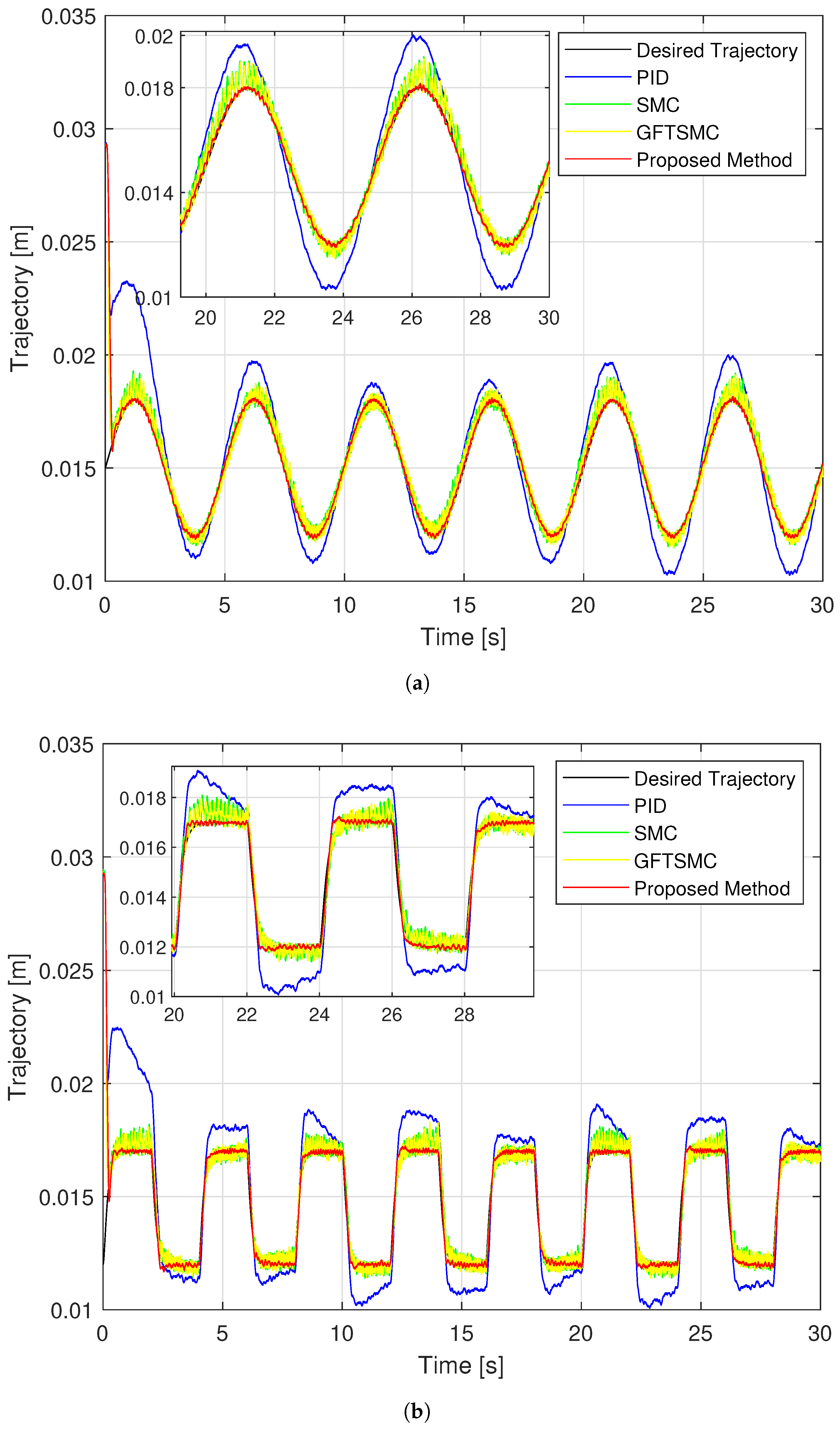
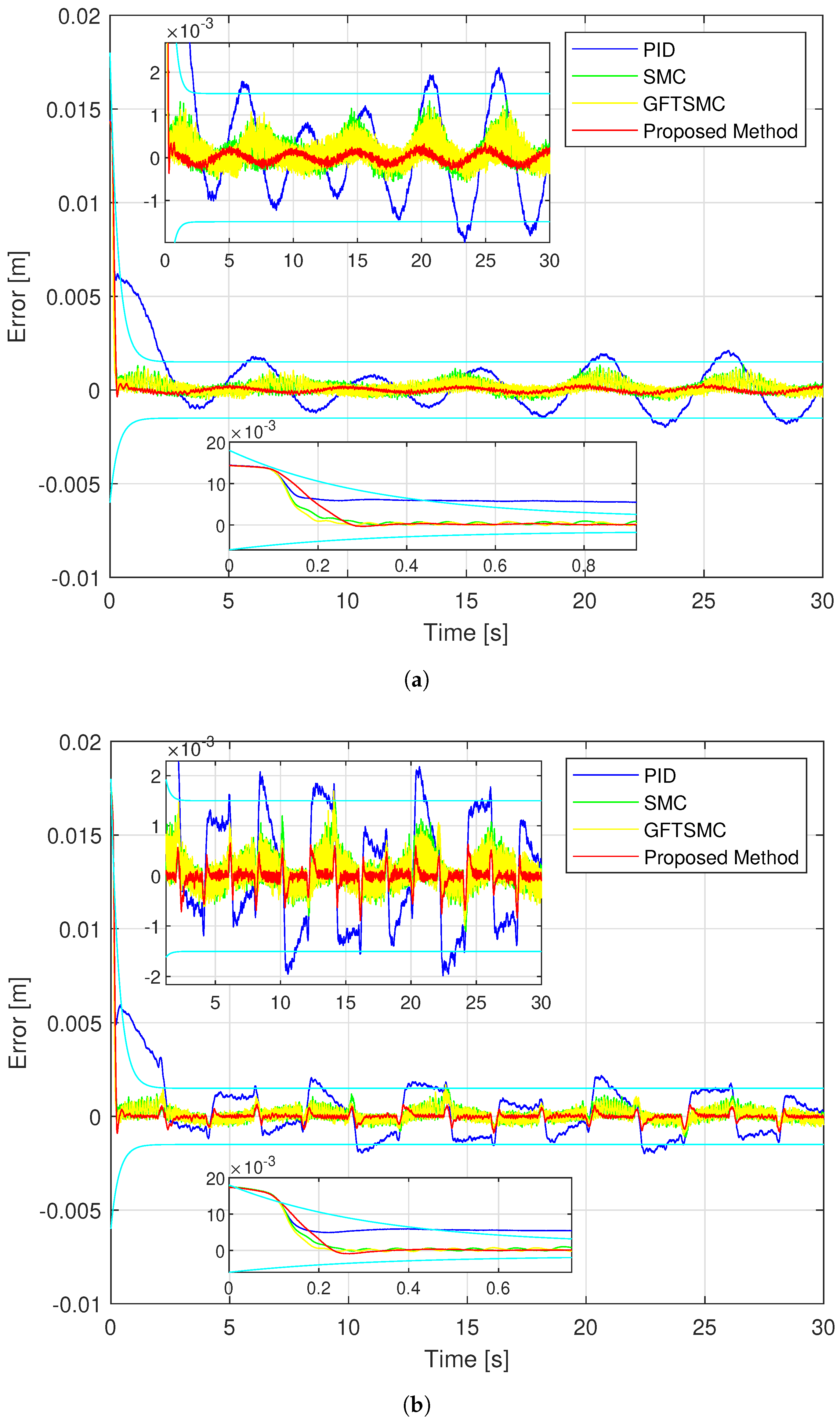
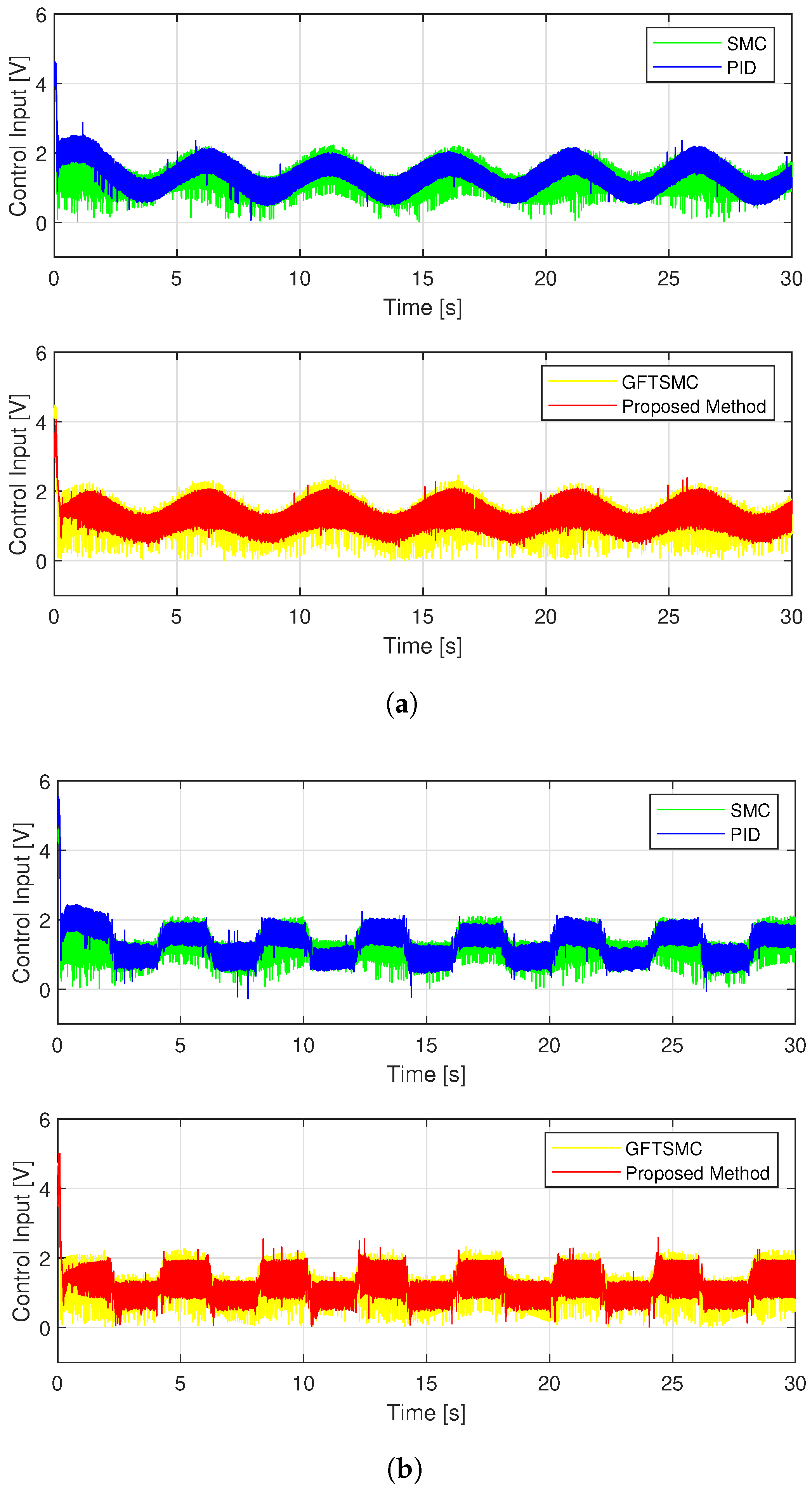
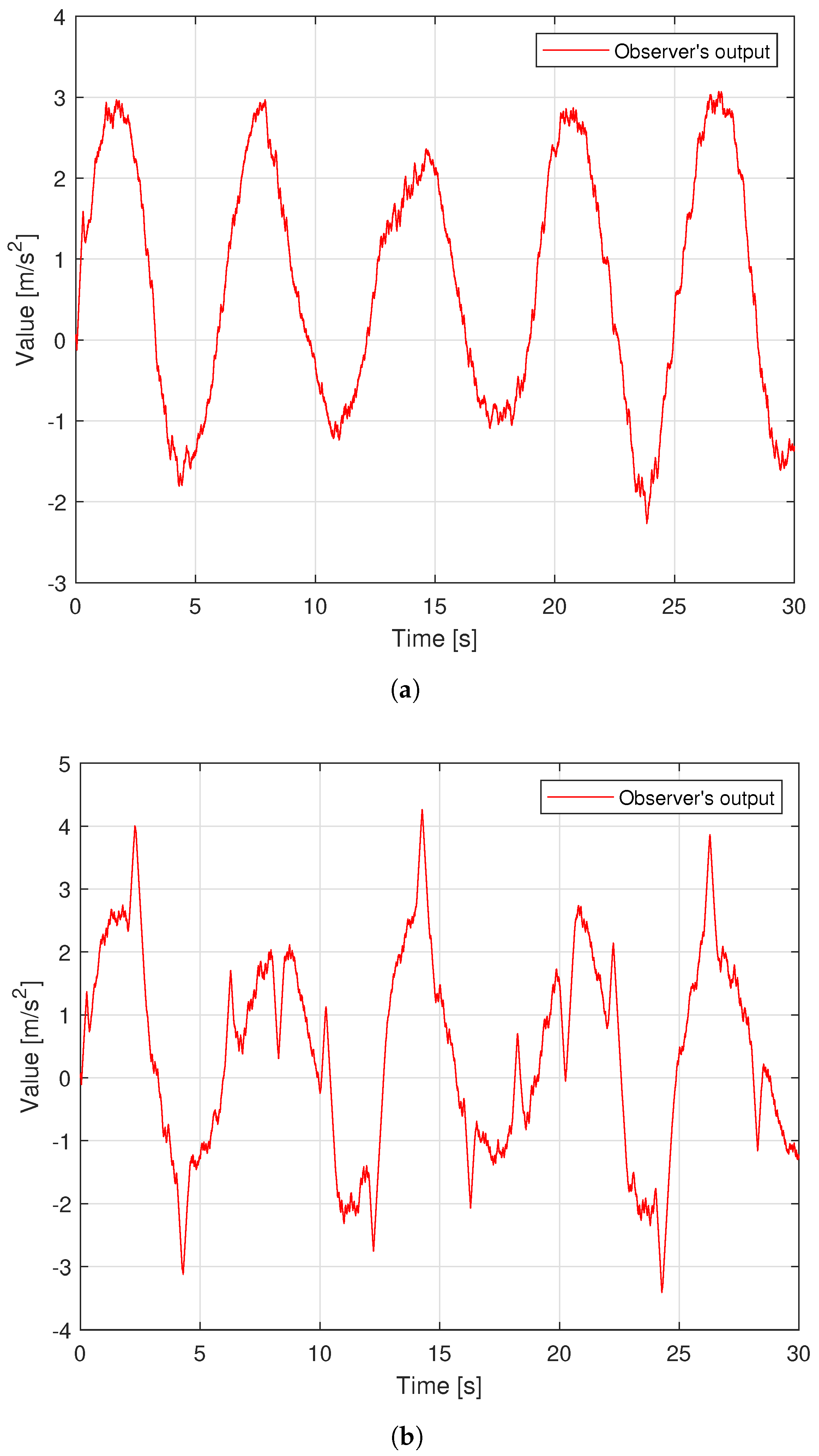
4. Simulation and Experimental Results
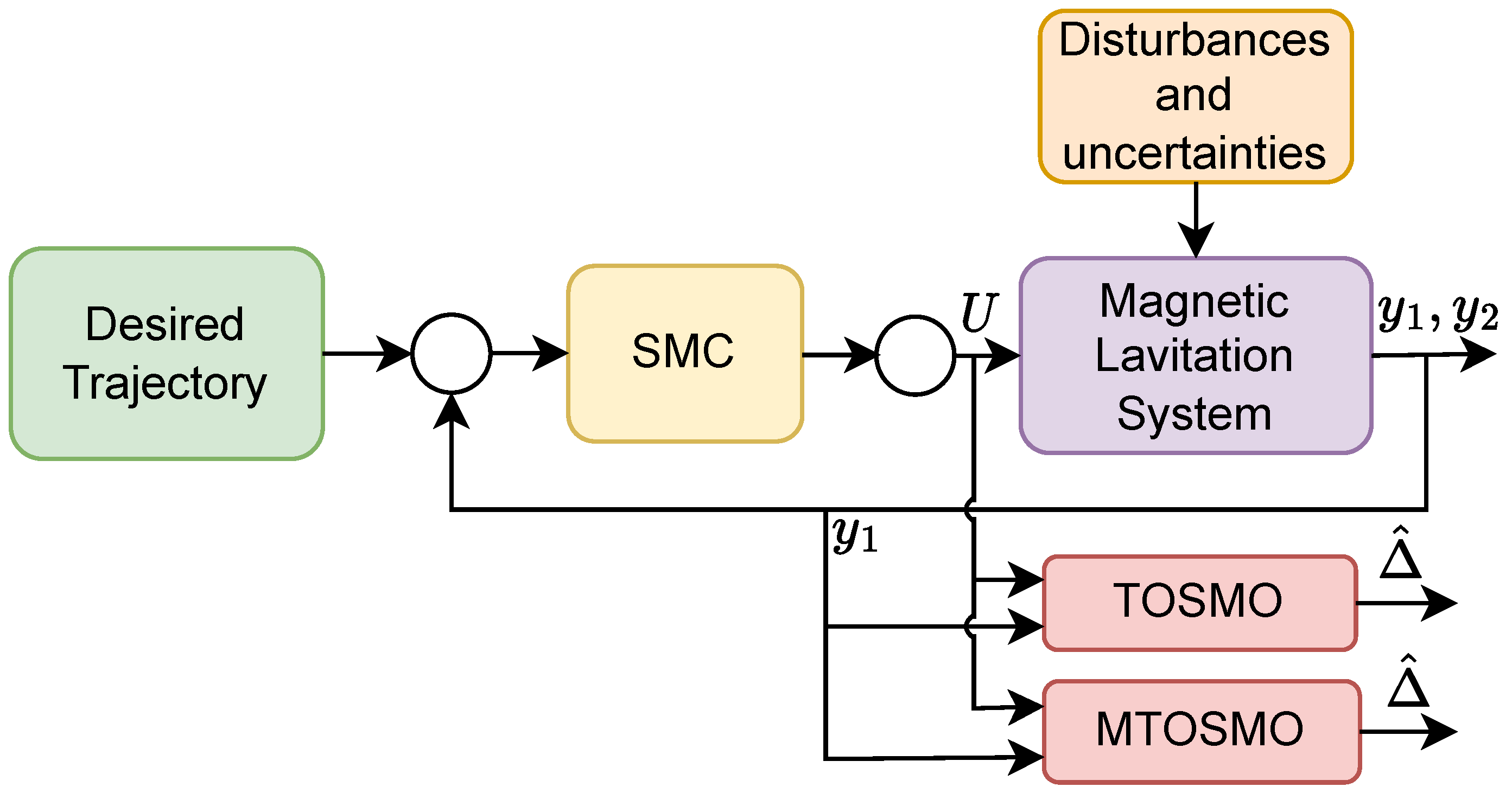
4.1. Simulation Results
- Step 1: simulates and evaluates the approximation ability of the proposed observer through a comparison between its approximation ability and the conventional TOSMO;
- Step 2: investigates the management of the terms of the proposed PPC including maximum overshoot and steady-state of the controlled errors;
- Step 3: compares the tracking accuracy, maximum overshoot and steady-state of the controlled errors among the four control methods through figures plotted from MATLAB and RMS methods;
- Step 4: considers the chattering behavior that appeared in the control signal of the four methods.
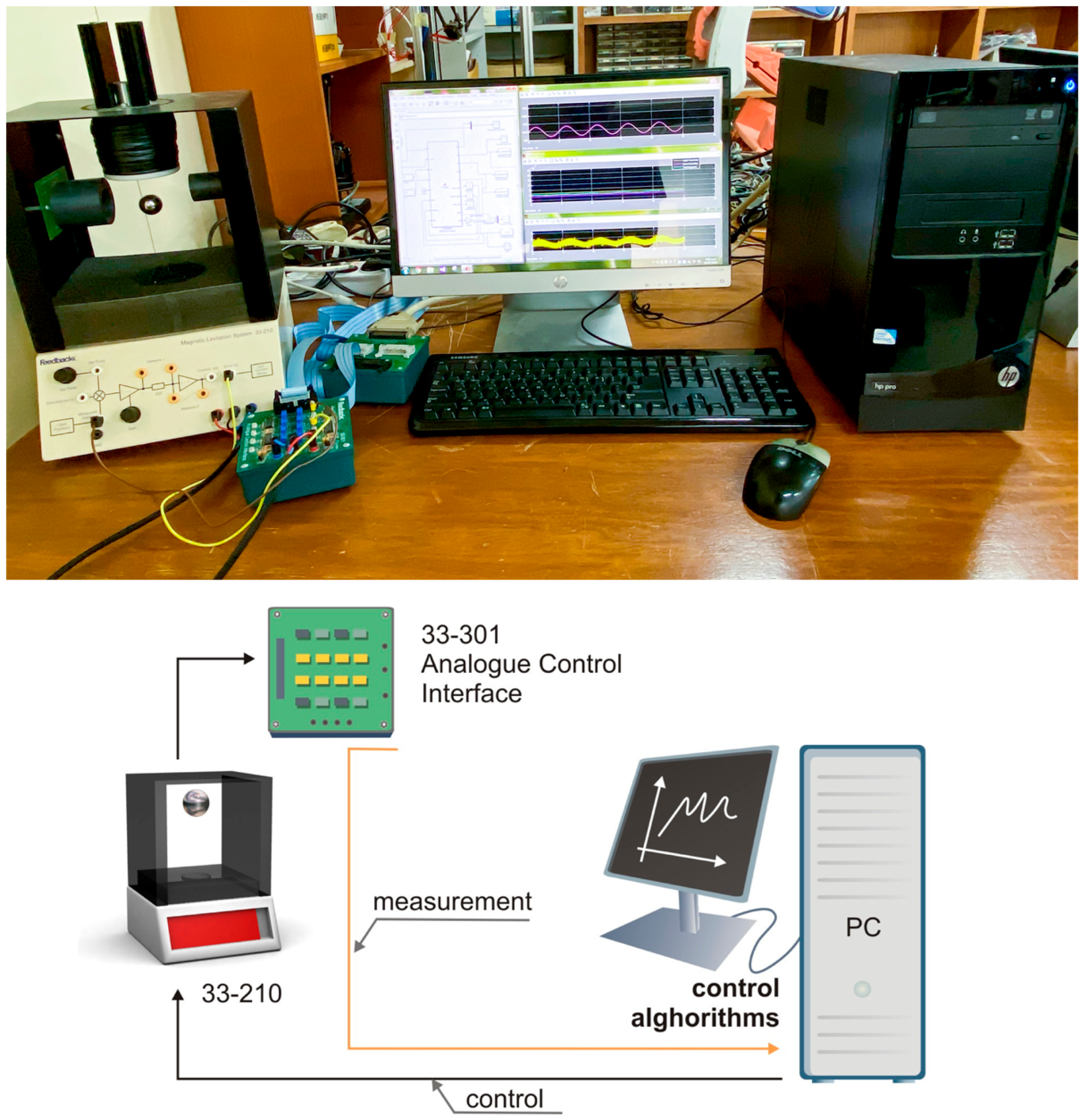
4.2. Experimental Results
5. Some Remarkable Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Golob, M.; Tovornik, B. Modeling and control of the magnetic suspension system. ISA Trans. 2003, 42, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Rong, J.; Yang, J. Adaptive Fixed-Time Position Precision Control for Magnetic Levitation Systems. IEEE Trans. Autom. Sci. Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Yu, L. Adaptive terminal sliding mode control for magnetic levitation systems with enhanced disturbance compensation. IEEE Trans. Ind. Electron. 2020, 68, 756–766. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. Implementation of an Adaptive Neural Terminal Sliding Mode for Tracking Control of Magnetic Levitation Systems. IEEE Access 2020, 8, 206931–206941. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A Novel Fixed-Time Control Algorithm for Trajectory Tracking Control of Uncertain Magnetic Levitation Systems. IEEE Access 2021, 9, 47698–47712. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. An Adaptive Terminal Sliding Mode Control Scheme via Neural Network Approach for Path-following Control of Uncertain Nonlinear Systems. Int. J. Control Autom. Syst. 2022, 20, 2081–2096. [Google Scholar] [CrossRef]
- Morales, R.; Feliu, V.; Sira-Ramirez, H. Nonlinear control for magnetic levitation systems based on fast online algebraic identification of the input gain. IEEE Trans. Control Syst. Technol. 2010, 19, 757–771. [Google Scholar] [CrossRef]
- El-Sousy, F.F.; Alattas, K.A.; Mofid, O.; Mobayen, S.; Asad, J.H.; Skruch, P.; Assawinchaichote, W. Non-Singular Finite Time Tracking Control Approach Based on Disturbance Observers for Perturbed Quadrotor Unmanned Aerial Vehicles. Sensors 2022, 22, 2785. [Google Scholar] [CrossRef]
- Alattas, K.A.; Mofid, O.; Alanazi, A.K.; Abo-Dief, H.M.; Bartoszewicz, A.; Bakouri, M.; Mobayen, S. Barrier Function Adaptive Nonsingular Terminal Sliding Mode Control Approach for Quad-Rotor Unmanned Aerial Vehicles. Sensors 2022, 22, 909. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, B.; Wang, G.; Mu, D. Adaptive Fast Non-Singular Terminal Sliding Mode Path Following Control for an Underactuated Unmanned Surface Vehicle with Uncertainties and Unknown Disturbances. Sensors 2021, 21, 7454. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Chen, M.; Kong, L. Predefined-time sliding mode formation control for multiple autonomous underwater vehicles with uncertainties. Chaos Solitons Fractals 2021, 144, 110680. [Google Scholar] [CrossRef]
- Manzanilla, A.; Ibarra, E.; Salazar, S.; Zamora, Á.E.; Lozano, R.; Munoz, F. Super-twisting integral sliding mode control for trajectory tracking of an Unmanned Underwater Vehicle. Ocean Eng. 2021, 234, 109164. [Google Scholar] [CrossRef]
- González-García, J.; Gómez-Espinosa, A.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Cuan-Urquizo, E.; Escobedo Cabello, J.A. Experimental Validation of a Model-Free High-Order Sliding Mode Controller with Finite-Time Convergence for Trajectory Tracking of Autonomous Underwater Vehicles. Sensors 2022, 22, 488. [Google Scholar] [CrossRef]
- Zheng, J.; Song, L.; Liu, L.; Yu, W.; Wang, Y.; Chen, C. Fixed-time sliding mode tracking control for autonomous underwater vehicles. Appl. Ocean Res. 2021, 117, 102928. [Google Scholar] [CrossRef]
- González-García, J.; Gómez-Espinosa, A.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Cuan-Urquizo, E.; Cabello, J.A.E. Model-Free High-Order Sliding Mode Controller for Station-Keeping of an Autonomous Underwater Vehicle in Manipulation Task: Simulations and Experimental Validation. Sensors 2022, 22, 4347. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. A backstepping global fast terminal sliding mode control for trajectory tracking control of industrial robotic manipulators. IEEE Access 2021, 9, 31921–31931. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Vo, A.T.; Kang, H.J. A Non-Singular Fast Terminal Sliding Mode Control Based on Third-Order Sliding Mode Observer for a Class of Second-Order Uncertain Nonlinear Systems and its Application to Robot Manipulators. IEEE Access 2020, 8, 78109–78120. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J.; Van, M. A Robust Observer-Based Control Strategy for n-DOF Uncertain Robot Manipulators with Fixed-Time Stability. Sensors 2021, 21, 7084. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Jin, X.Z.; Wu, X.M.; Wang, H.; Chi, J. Neural network-based fixed-time sliding mode control for a class of nonlinear Euler-Lagrange systems. Appl. Math. Comput. 2022, 415, 126718. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Vo, A.T.; Kang, H.J. A finite-time fault-tolerant control using non-singular fast terminal sliding mode control and third-order sliding mode observer for robotic manipulators. IEEE Access 2021, 9, 31225–31235. [Google Scholar] [CrossRef]
- Mu, C.; He, H. Dynamic behavior of terminal sliding mode control. IEEE Trans. Ind. Electron. 2017, 65, 3480–3490. [Google Scholar] [CrossRef]
- Solis, C.U.; Clempner, J.B.; Poznyak, A.S. Fast terminal sliding-mode control with an integral filter applied to a van der pol oscillator. IEEE Trans. Ind. Electron. 2017, 64, 5622–5628. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J.; Van, M. A Novel Active Fault-Tolerant Tracking Control for Robot Manipulators with Finite-Time Stability. Sensors 2021, 21, 8101. [Google Scholar] [CrossRef] [PubMed]
- Zhai, J.; Xu, G. A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 391–395. [Google Scholar] [CrossRef]
- Xu, S.S.D.; Chen, C.C.; Wu, Z.L. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A novel tracking control algorithm with finite-time disturbance observer for a class of second-order nonlinear systems and its applications. IEEE Access 2021, 9, 31373–31389. [Google Scholar] [CrossRef]
- Truong, T.N.; Kang, H.J.; Vo, A.T. An active disturbance rejection control method for robot manipulators. In Proceedings of the International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 190–201. [Google Scholar]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A Novel Prescribed-Performance-Tracking Control System with Finite-Time Convergence Stability for Uncertain Robotic Manipulators. Sensors 2022, 22, 2615. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J.; Le, T.D. An Advanced Terminal Sliding Mode Controller for Robot Manipulators in Position Tracking Problem. In Proceedings of the International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2022; pp. 518–528. [Google Scholar]
- Truong, T.N.; Vo, A.T.; Kang, H.J.; Le, T.D. An Observer-Based Fixed Time Sliding Mode Controller for a Class of Second-Order Nonlinear Systems and Its Application to Robot Manipulators. In Proceedings of the International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2022; pp. 529–543. [Google Scholar]
- Huang, J.; Zhang, M.; Ri, S.; Xiong, C.; Li, Z.; Kang, Y. High-order disturbance-observer-based sliding mode control for mobile wheeled inverted pendulum systems. IEEE Trans. Ind. Electron. 2019, 67, 2030–2041. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Tran, X.T.; Kang, H.J. A Novel High-Speed Third-Order Sliding Mode Observer for Fault-Tolerant Control Problem of Robot Manipulators. Actuators 2022, 11, 259. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Liu, Z.; Qu, Y.; Su, C.Y.; Jiang, B. Decentralized finite-time adaptive fault-tolerant synchronization tracking control for multiple UAVs with prescribed performance. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 11830–11862. [Google Scholar] [CrossRef]
- Koksal, N.; An, H.; Fidan, B. Backstepping-based adaptive control of a quadrotor UAV with guaranteed tracking performance. ISA Trans. 2020, 105, 98–110. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Y. Adaptive coordinated control of uncertain free-floating space manipulators with prescribed control performance. Nonlinear Dyn. 2019, 97, 1541–1566. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Sun, C. Prescribed Performance Fault-Tolerant Control for Uncertain Nonlinear MIMO System Using Actor-Critic Learning Structure. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4479–4490. [Google Scholar] [CrossRef]
- Huang, H.; He, W.; Li, J.; Xu, B.; Yang, C.; Zhang, W. Disturbance Observer-Based Fault-Tolerant Control for Robotic Systems With Guaranteed Prescribed Performance. IEEE Trans. Cybern. 2022, 52, 772–783. [Google Scholar] [CrossRef]
- Wang, S.; Na, J.; Chen, Q. Adaptive Predefined Performance Sliding Mode Control of Motor Driving Systems With Disturbances. IEEE Trans. Energy Convers. 2021, 36, 1931–1939. [Google Scholar] [CrossRef]
- Yang, P.; Su, Y. Proximate Fixed-Time Prescribed Performance Tracking Control of Uncertain Robot Manipulators. IEEE/ASME Trans. Mechatron. 2021, 27, 3275–3285. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y.; Chen, B. Fault-tolerant control of an aerial manipulator with guaranteed tracking performance. Int. J. Robust Nonlinear Control 2022, 32, 960–986. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
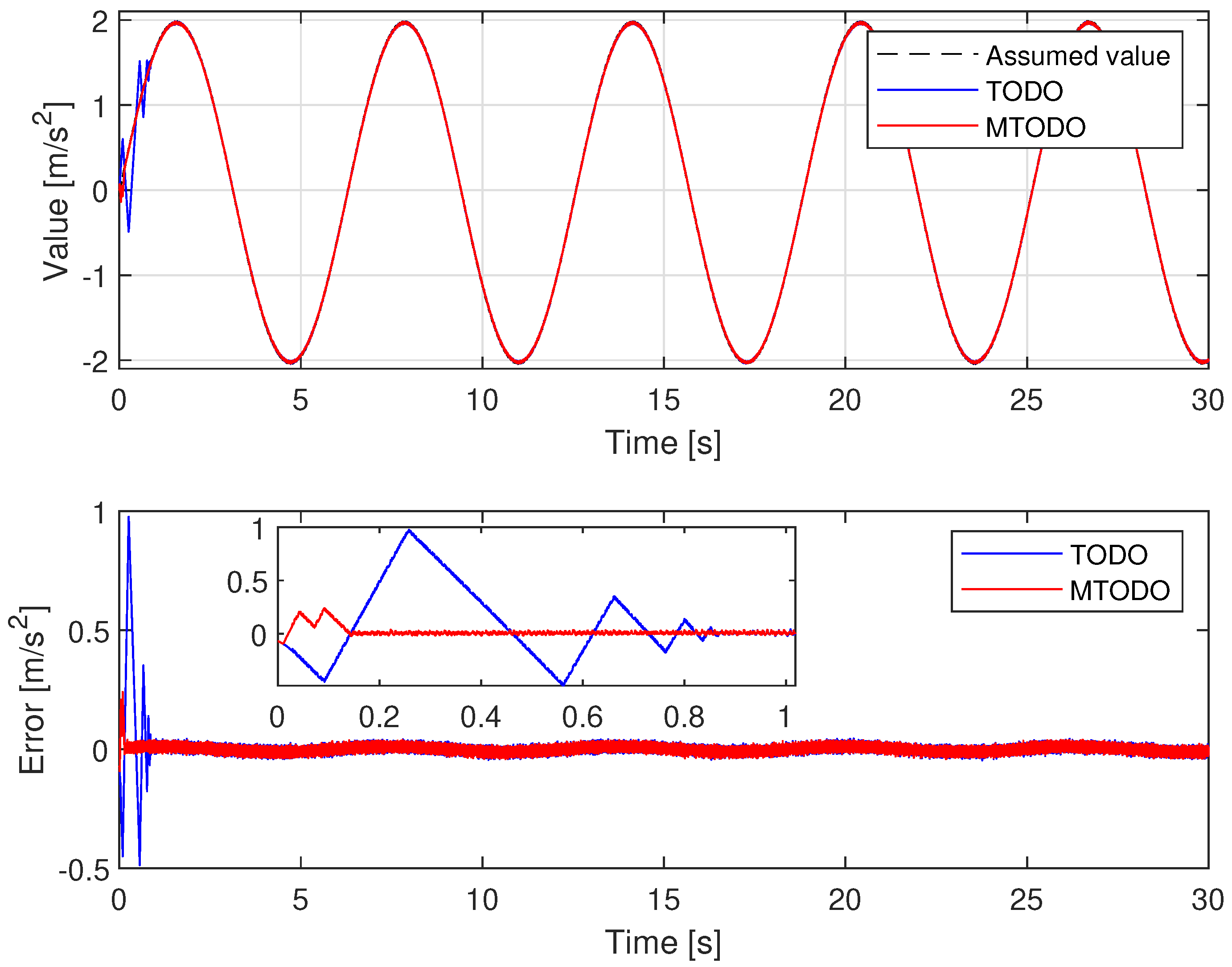

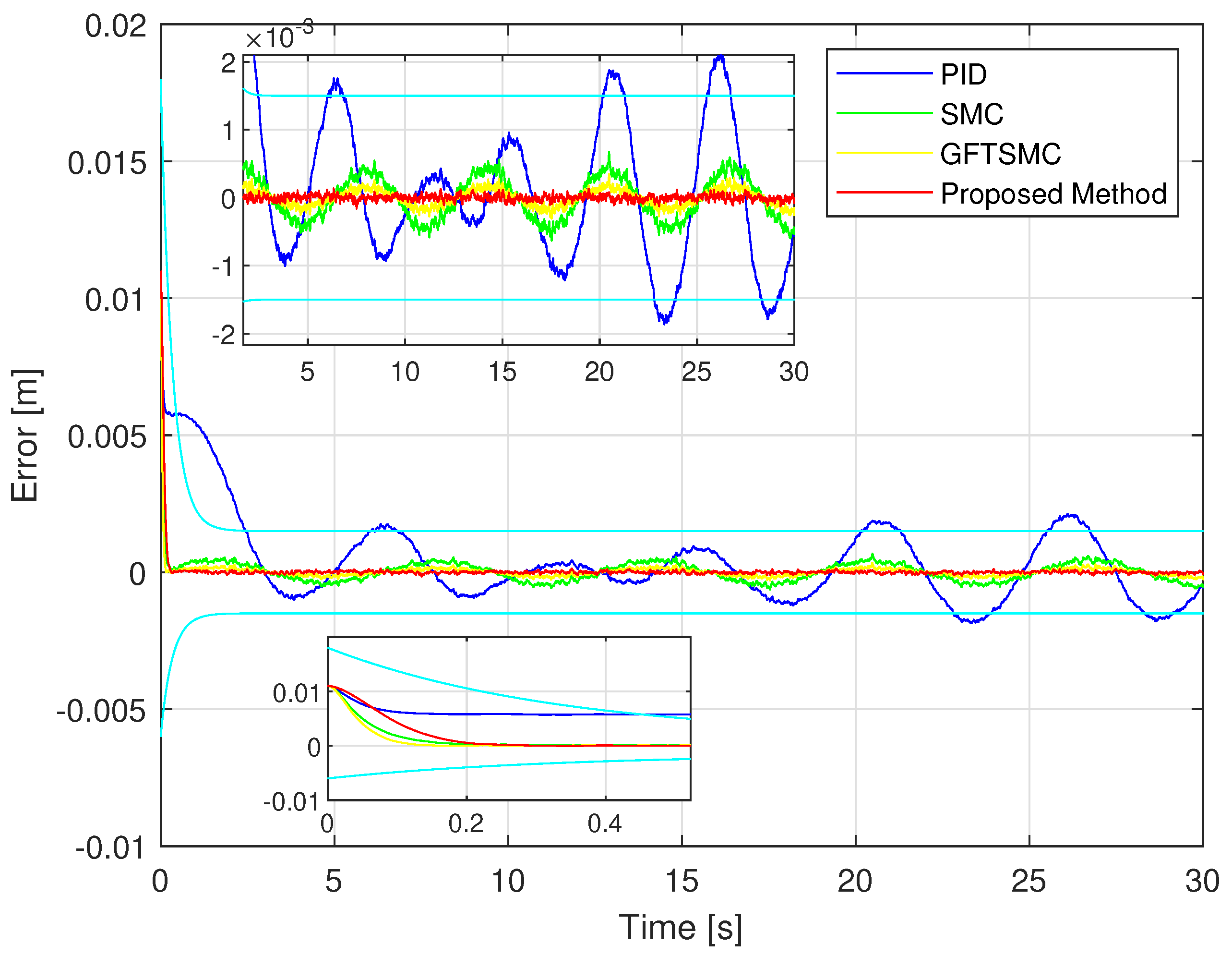
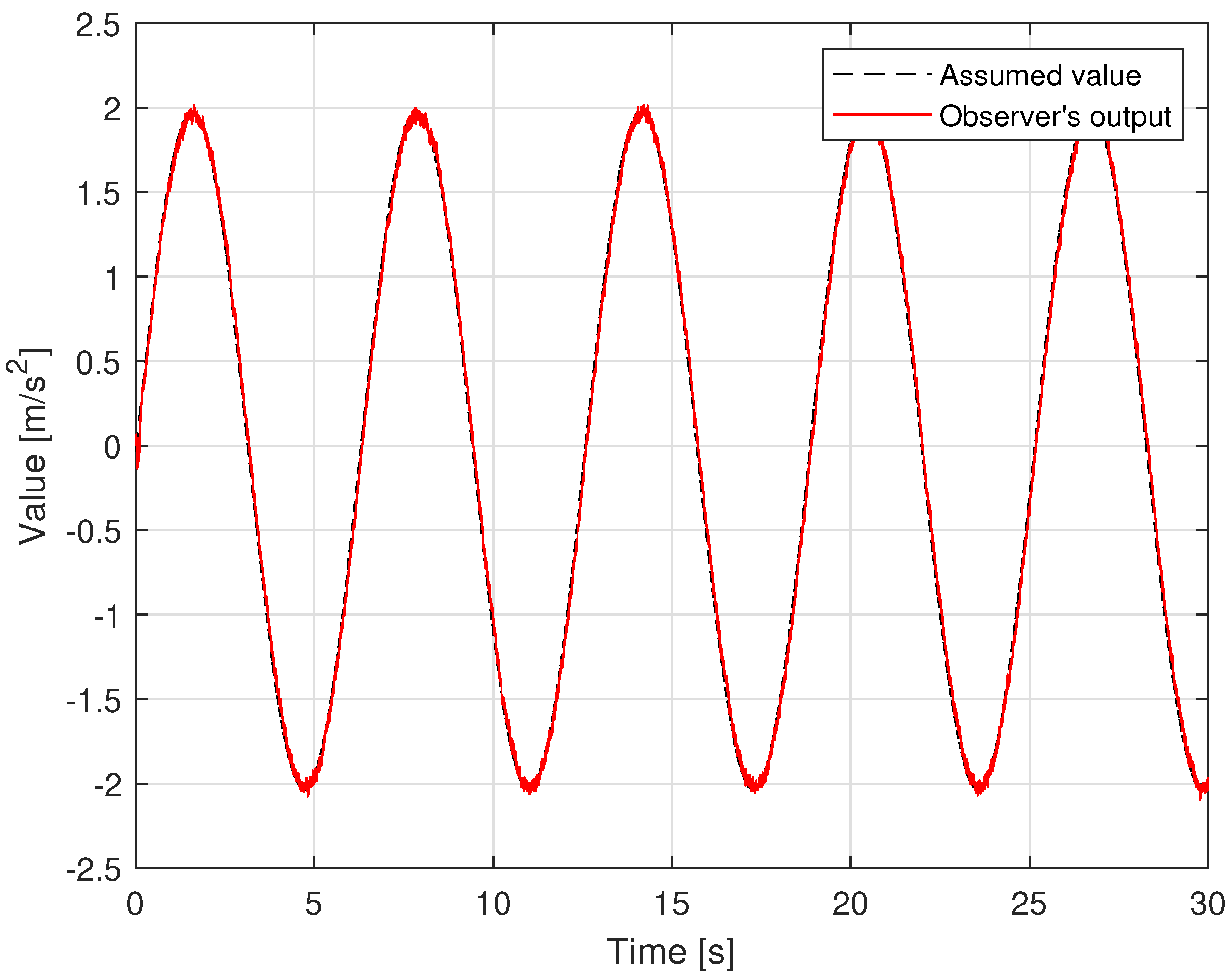

| System Parameters | Value | Unit |
|---|---|---|
| g | 9.81 | m/s |
| m | 0.02 | kg |
| Nm/A | ||
| K | 1.05 | A/V |
| 0.00136487 | (N.m/kg.V) |
| Controller | Symbol | Value |
|---|---|---|
| PID | ||
| SMC | ||
| GFTSMC | ||
| Proposed Method | ||
| Controller | RMSTE |
|---|---|
| PID | |
| SMC | |
| GFTSMC | |
| Proposed Method |
| Controller | RMSTE in Case of Sinusoidal Orbit | RMSTE in Case of a Rest-to-Rest Line |
|---|---|---|
| PID | ||
| SMC | ||
| GFTSMC | ||
| Proposed Method |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong, T.N.; Vo, A.T.; Kang, H.-J. Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems. Sensors 2022, 22, 9132. https://doi.org/10.3390/s22239132
Truong TN, Vo AT, Kang H-J. Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems. Sensors. 2022; 22(23):9132. https://doi.org/10.3390/s22239132
Chicago/Turabian StyleTruong, Thanh Nguyen, Anh Tuan Vo, and Hee-Jun Kang. 2022. "Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems" Sensors 22, no. 23: 9132. https://doi.org/10.3390/s22239132
APA StyleTruong, T. N., Vo, A. T., & Kang, H.-J. (2022). Real-Time Implementation of the Prescribed Performance Tracking Control for Magnetic Levitation Systems. Sensors, 22(23), 9132. https://doi.org/10.3390/s22239132








