Co-Occurrence Fingerprint Data-Based Heterogeneous Transfer Learning Framework for Indoor Positioning
Abstract
1. Introduction
- Within the HTL-CD framework, homogeneous knowledge transfer and knowledge transfer between heterogeneous domains can be attained. To cope with the heterogeneous problem caused by the collection device heterogeneity or real-time environmental changes, a projection from the source feature space to the target feature space was considered. In addition, by imposing a MMD restriction on the mapping matrix, the cross-domain marginal and conditional distributions were both aligned, giving rise to higher positioning accuracy and robustness in uncertain environment dynamics.
- The cross-domain correlation was evaluated with a correlation coefficient, which could precisely reflect whether and how the given source domain is effective in knowledge transferring to the target domain in both homogeneous and heterogeneous cases. Hence, it is possible to take full advantage of a fingerprint database and avoid the “negative transfer” issue.
- Through extending the current definition of co-occurrence data to a general-sense version, it was dramatically easier to collect co-occurrence fingerprint samples in FIPS. With the help of general-sense co-occurrence fingerprint data, joint sources, and target domains, the correlation between two arbitrary samples can be fairly evaluated, such that even in the existence of significant cross-domain divergence, an accurate and robust positioning performance can be achieved without resorting to common features or accurately labeled samples in the target domain.
2. Related Work
2.1. Classical Indoor Positioning Algorithms
2.1.1. Geometric-Based Methods
2.1.2. Vision-Based Methods
2.1.3. PDR
2.1.4. FIPS
2.2. Transfer Learning in FIPS
3. Problem Formulation
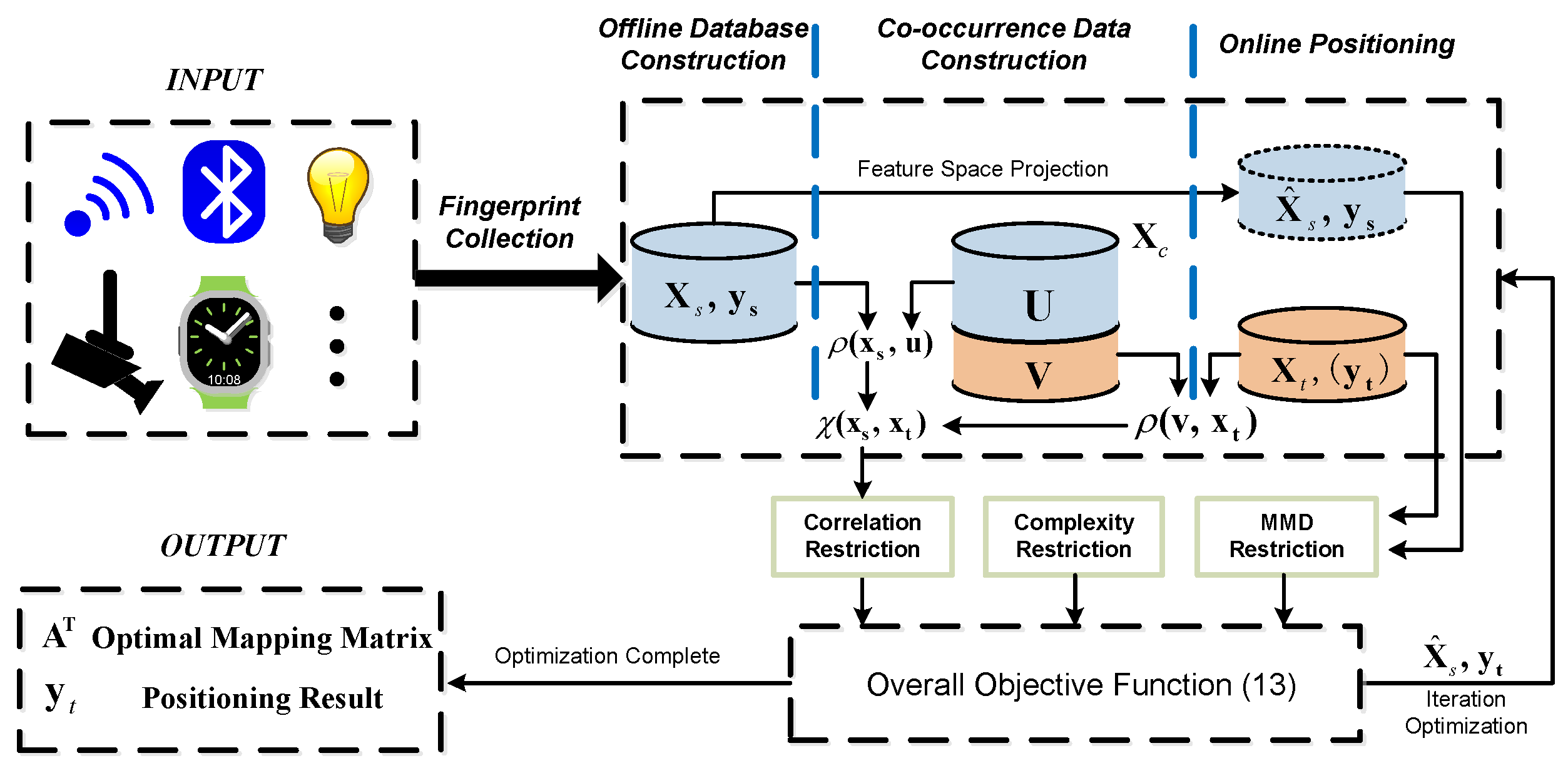
4. Htl-Cd Framework
4.1. MMD Restriction
4.2. Co-Occurrence Data Definition
4.2.1. Narrow-Sense Co-Occurrence Data
4.2.2. Wide-Sense Co-Occurrence Data
4.3. Correlation Restriction
4.4. Objective Function and Iterative Optimization
| Algorithm 1: HTL-CD framework for fingerprint positioning |
Require: , , , , , T |
Ensure: , |
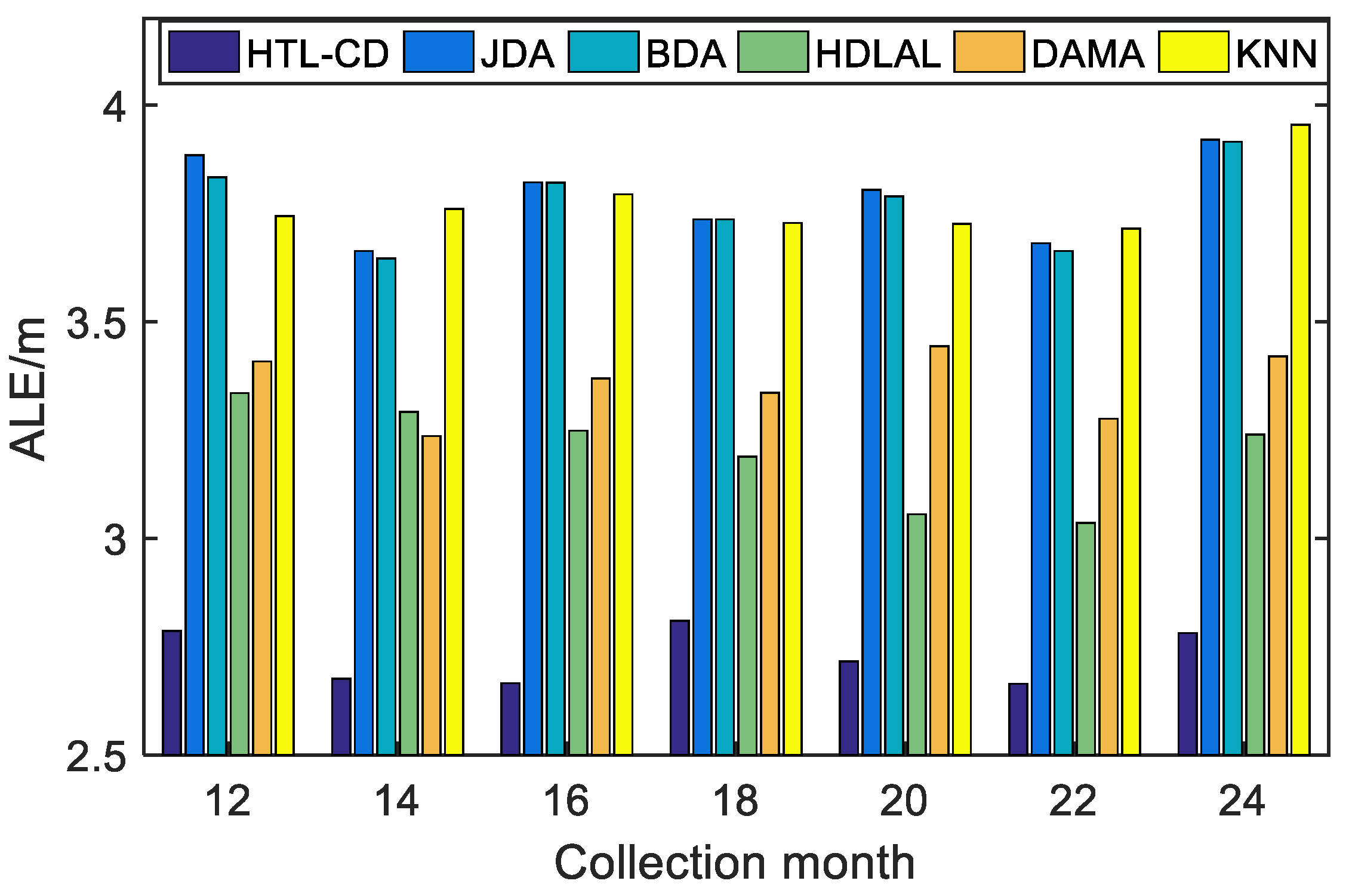
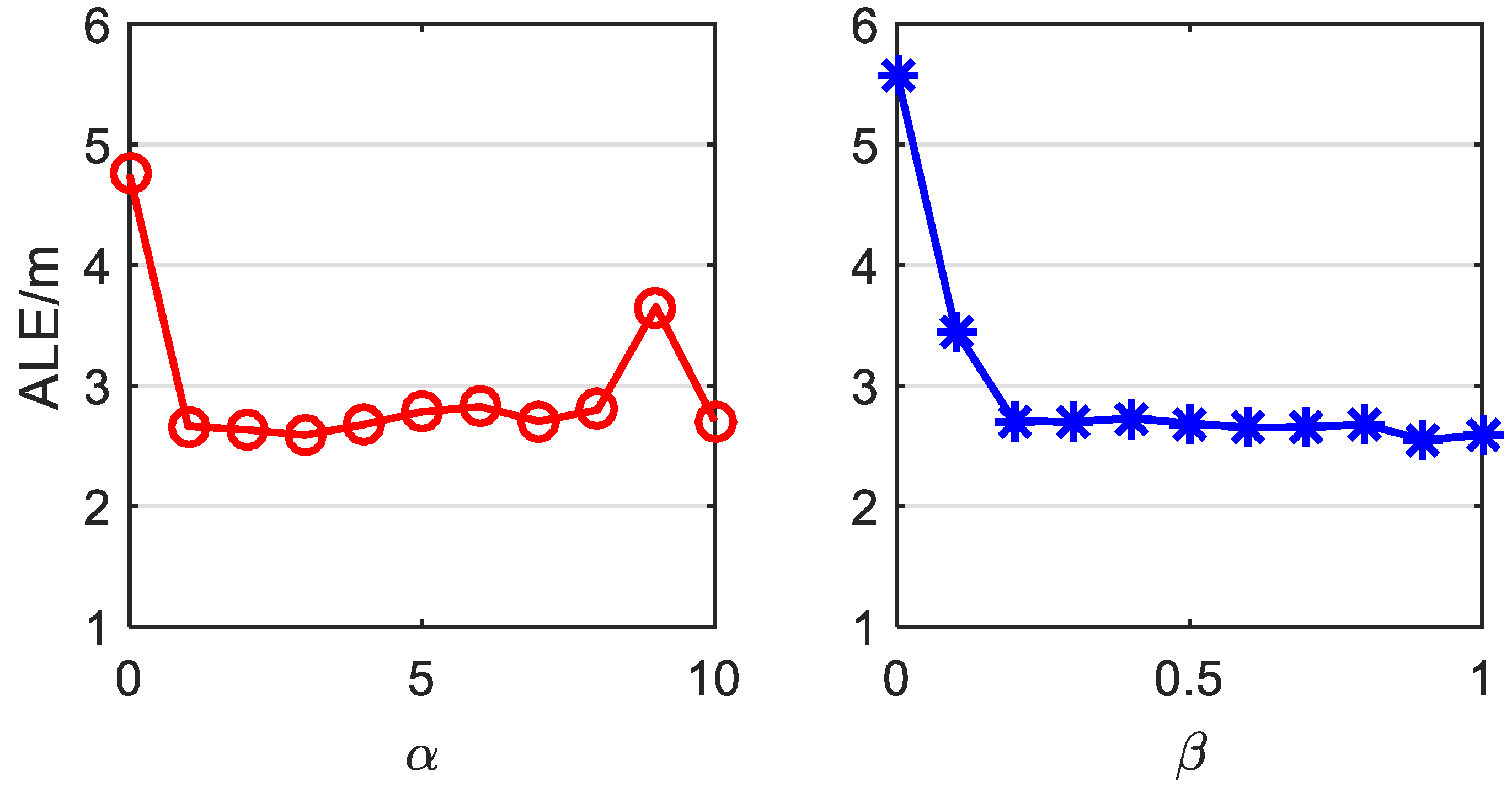
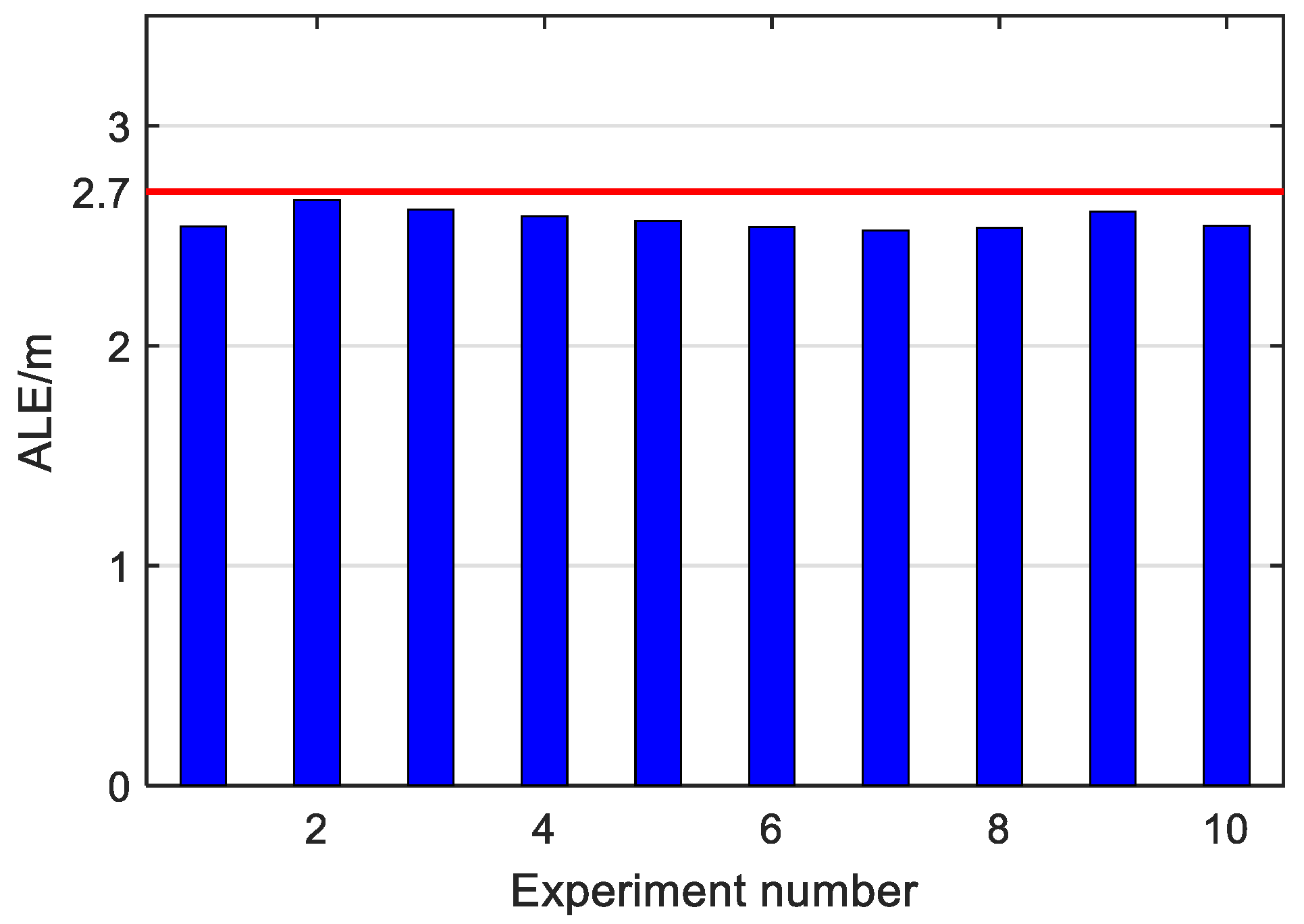
5. Experiment Results
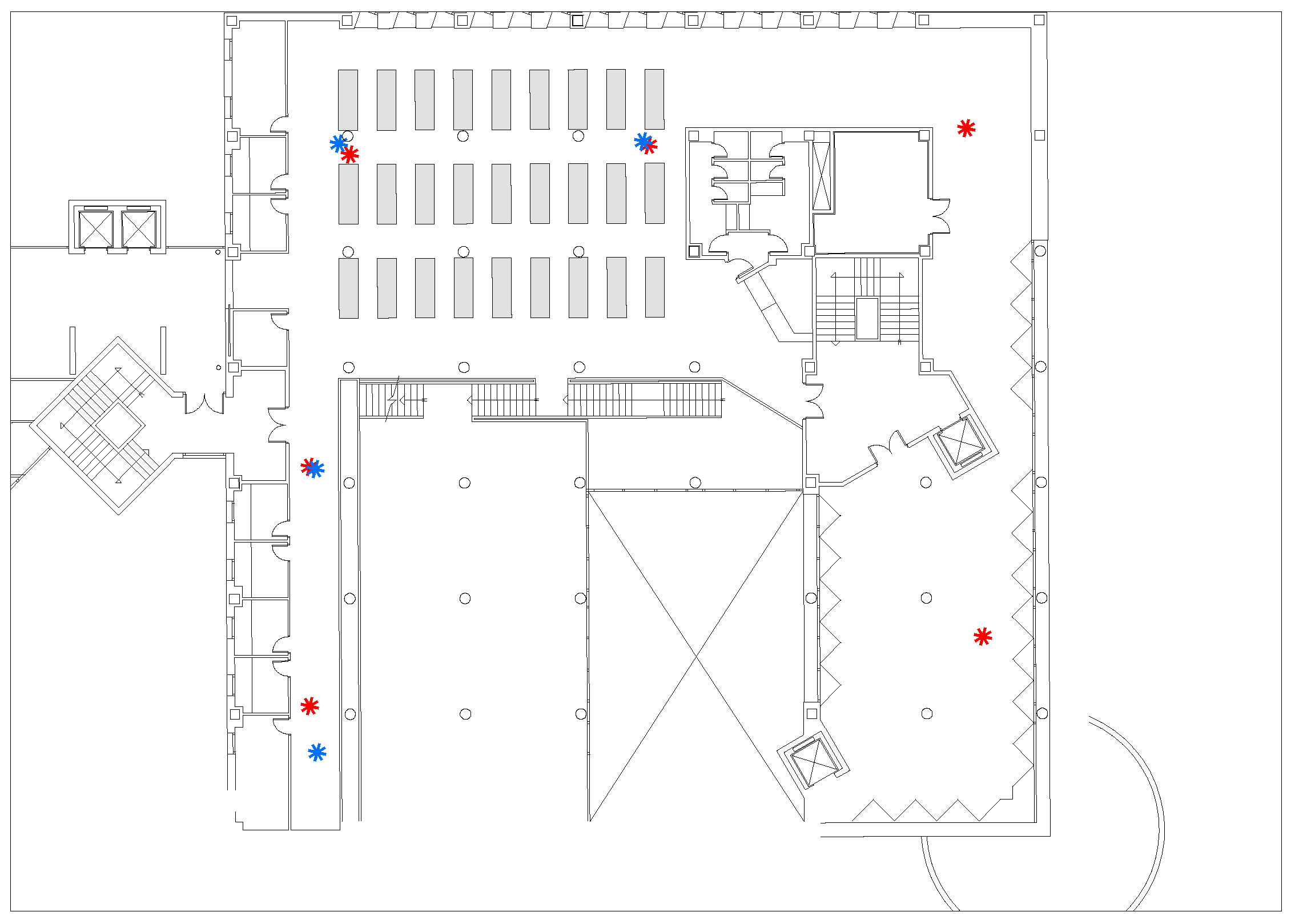
5.1. Environment Description
5.2. Positioning Results
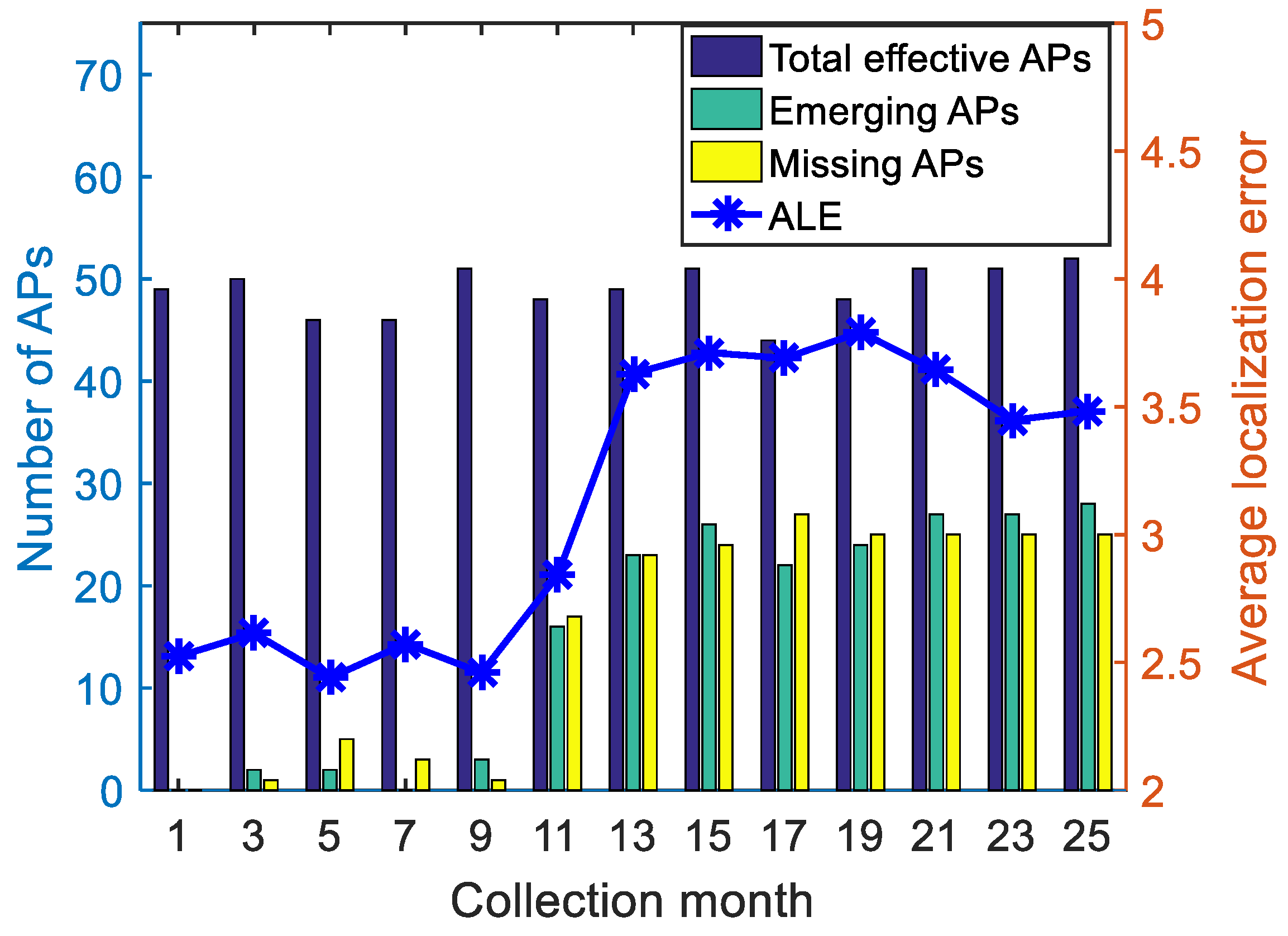
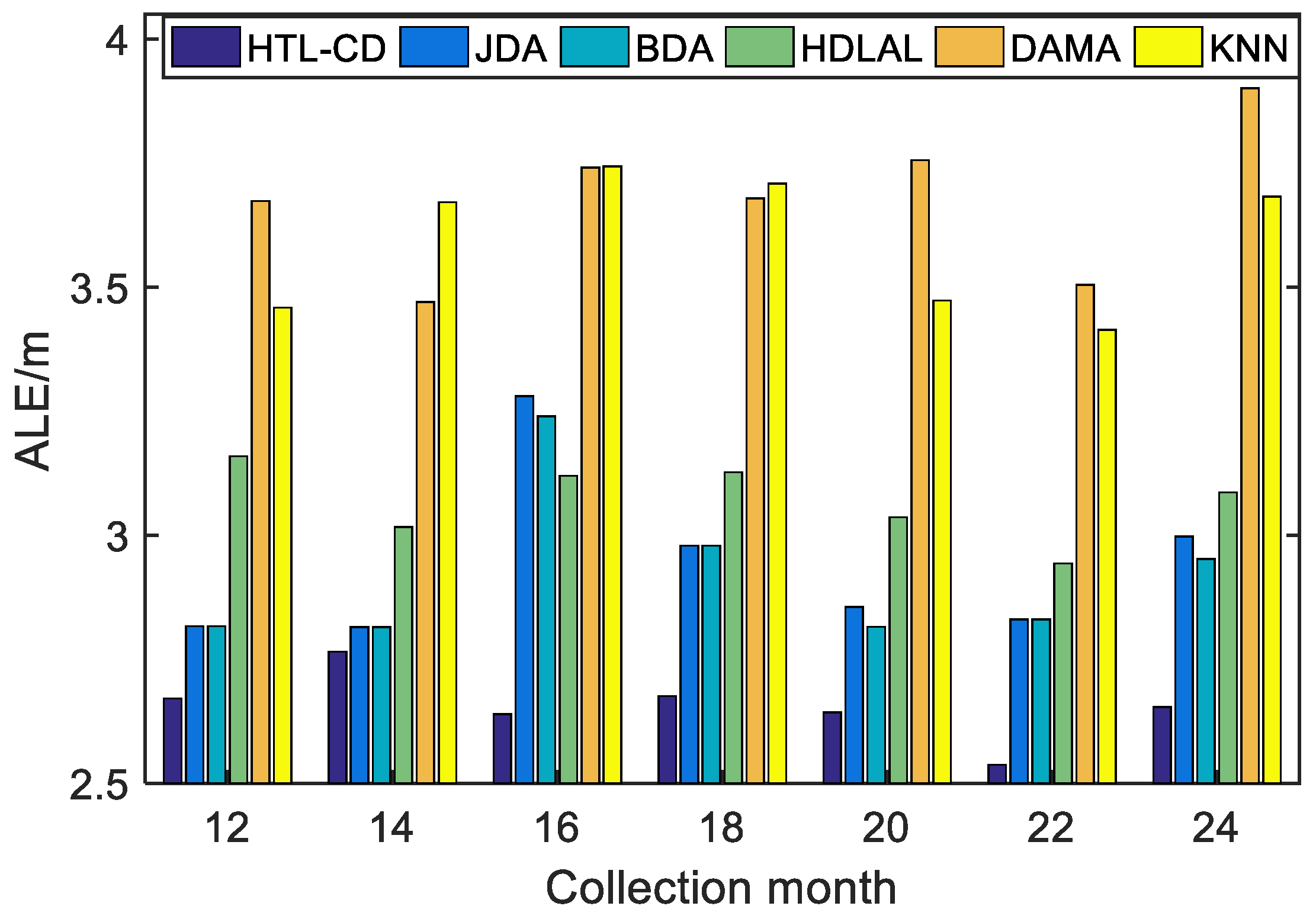
5.3. Robustness Analyses
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Lau, B.P.L.; Marakkalage, S.H.; Zhou, Y.; Hassan, N.U.; Yuen, C.; Zhang, M.; Tan, U.X. A survey of data fusion in smart city applications. Inf. Fusion 2019, 52, 357–374. [Google Scholar] [CrossRef]
- Ahmad, M.O.; Ahad, M.A.; Alam, M.A.; Siddiqui, F.; Casalino, G. Cyber-Physical Systems and Smart Cities in India: Opportunities, Issues, and Challenges. Sensors 2021, 21, 7714. [Google Scholar] [CrossRef]
- Tian, S.; Yang, W.; Le Grange, J.M.; Wang, P.; Huang, W.; Ye, Z. Smart healthcare: Making medical care more intelligent. Glob. Health J. 2019, 3, 62–65. [Google Scholar] [CrossRef]
- Men, J.; Jiang, P.; Zheng, S.; Kong, Y.; Zhao, Y.; Sheng, G.; Su, N.; Zheng, S. A multi-objective emergency rescue facilities location model for catastrophic interlocking chemical accidents in chemical parks. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4749–4761. [Google Scholar] [CrossRef]
- Lygouras, E.; Santavas, N.; Taitzoglou, A.; Tarchanidis, K.; Mitropoulos, A.; Gasteratos, A. Unsupervised human detection with an embedded vision system on a fully autonomous UAV for search and rescue operations. Sensors 2019, 19, 3542. [Google Scholar] [CrossRef]
- Sirmacek, B.; Riveiro, M. Occupancy prediction using low-cost and low-resolution heat sensors for smart offices. Sensors 2020, 20, 5497. [Google Scholar] [CrossRef] [PubMed]
- Tekler, Z.D.; Chong, A. Occupancy prediction using deep learning approaches across multiple space types: A minimum sensing strategy. Build. Environ. 2022, 226, 109689. [Google Scholar] [CrossRef]
- Esrafilian-Najafabadi, M.; Haghighat, F. Occupancy-based HVAC control systems in buildings: A state-of-the-art review. Build. Environ. 2021, 197, 107810. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Low, R.; Yuen, C.; Blessing, L. Plug-Mate: An IoT-based occupancy-driven plug load management system in smart buildings. Build. Environ. 2022, 223, 109472. [Google Scholar] [CrossRef]
- Zou, H.; Zhou, Y.; Jiang, H.; Chien, S.C.; Xie, L.; Spanos, C.J. WinLight: A Wi-Fi-based occupancy-driven lighting control system for smart building. Energy Build. 2018, 158, 924–938. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man, Cybern. Part C (Appl. Rev.) 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Charan, G.; Osman, T.; Hredzak, A.; Thawdar, N.; Alkhateeb, A. Vision-Position multi-modal beam prediction using real millimeter wave datasets. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 2727–2731. [Google Scholar]
- Hou, X.; Bergmann, J. Pedestrian dead reckoning with wearable sensors: A systematic review. IEEE Sens. J. 2020, 21, 143–152. [Google Scholar] [CrossRef]
- Dinh, T.M.T.; Duong, N.S.; Sandrasegaran, K. Smartphone-based indoor positioning using BLE iBeacon and reliable lightweight fingerprint map. IEEE Sens. J. 2020, 20, 10283–10294. [Google Scholar] [CrossRef]
- Wang, B.; Gan, X.; Liu, X.; Yu, B.; Jia, R.; Huang, L.; Jia, H. A novel weighted KNN algorithm based on RSS similarity and position distance for Wi-Fi fingerprint positioning. IEEE Access 2020, 8, 30591–30602. [Google Scholar] [CrossRef]
- Yang, C.; Shao, H.R. Wi-Fi-based indoor positioning. IEEE Commun. Mag. 2015, 53, 150–157. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Low, R.; Gunay, B.; Andersen, R.K.; Blessing, L. A scalable Bluetooth Low Energy approach to identify occupancy patterns and profiles in office spaces. Build. Environ. 2020, 171, 106681. [Google Scholar] [CrossRef]
- Niu, J.; Wang, B.; Shu, L.; Duong, T.Q.; Chen, Y. ZIL: An energy-efficient indoor localization system using ZigBee radio to detect Wi-Fi fingerprints. IEEE J. Sel. Areas Commun. 2015, 33, 1431–1442. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, G.; Wang, S. Wi-Fi sensing with channel state information: A survey. ACM Comput. Surv. (CSUR) 2019, 52, 1–36. [Google Scholar] [CrossRef]
- Hsieh, C.H.; Chen, J.Y.; Nien, B.H. Deep learning-based indoor localization using received signal strength and channel state information. IEEE Access 2019, 7, 33256–33267. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Ghamisi, P. Heterogeneous transfer learning for hyperspectral image classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3246–3263. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, Y.; Zhang, Y.; Yao, L. A robust indoor localization method with calibration strategy based on joint distribution adaptation. Wirel. Netw. 2021, 27, 1739–1753. [Google Scholar] [CrossRef]
- Feng, S.; Li, B.; Yu, H.; Liu, Y.; Yang, Q. Semi-Supervised Federated Heterogeneous Transfer Learning. Knowl.-Based Syst. 2022, 252, 109384. [Google Scholar] [CrossRef]
- Myagmar, B.; Li, J.; Kimura, S. Heterogeneous daily living activity learning through domain invariant feature subspace. IEEE Trans. Big Data 2020, 7, 922–929. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin, Germany, 2009; pp. 1–4. [Google Scholar]
- Ng, M.K.; Wu, Q.; Ye, Y. Co-transfer learning via joint transition probability graph based method. In Proceedings of the 1st International Workshop on Cross Domain Knowledge Discovery in Web and Social Network Mining, Beijing, China, 12–16 August 2012; pp. 1–9. [Google Scholar]
- Zhu, Y.; Chen, Y.; Lu, Z.; Pan, S.J.; Xue, G.R.; Yu, Y.; Yang, Q. Heterogeneous transfer learning for image classification. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]
- Mensink, T.; Gavves, E.; Snoek, C.G. Costa: Co-occurrence statistics for zero-shot classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2441–2448. [Google Scholar]
- Van Haute, T.; Verbeke, B.; De Poorter, E.; Moerman, I. Optimizing time-of-arrival localization solutions for challenging industrial environments. IEEE Trans. Ind. Inform. 2016, 13, 1430–1439. [Google Scholar] [CrossRef]
- Ye, X.; Rodríguez-Piñeiro, J.; Liu, Y.; Yin, X.; Pérez Yuste, A. A novel experiment-free site-specific TDOA localization performance-evaluation approach. Sensors 2020, 20, 1035. [Google Scholar] [CrossRef]
- Esteva, A.; Chou, K.; Yeung, S.; Naik, N.; Madani, A.; Mottaghi, A.; Liu, Y.; Topol, E.; Dean, J.; Socher, R. Deep learning-enabled medical computer vision. NPJ Digit. Med. 2021, 4, 1–9. [Google Scholar] [CrossRef]
- Morar, A.; Moldoveanu, A.; Mocanu, I.; Moldoveanu, F.; Radoi, I.E.; Asavei, V.; Gradinaru, A.; Butean, A. A comprehensive survey of indoor localization methods based on computer vision. Sensors 2020, 20, 2641. [Google Scholar] [CrossRef]
- Hoyer, L.; Steup, C.; Mostaghim, S. A Robot Localization Framework Using CNNs for Object Detection and Pose Estimation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 1388–1395. [Google Scholar]
- Trejos, K.; Rincón, L.; Bolaños, M.; Fallas, J.; Marín, L. 2D SLAM Algorithms Characterization, Calibration, and Comparison Considering Pose Error, Map Accuracy as Well as CPU and Memory Usage. Sensors 2022, 22, 6903. [Google Scholar] [CrossRef]
- Seel, T.; Kok, M.; McGinnis, R.S. Inertial sensors applications and challenges in a nutshell. Sensors 2020, 20, 6221. [Google Scholar] [CrossRef]
- Ibrahim, M.; Torki, M.; ElNainay, M. CNN based indoor localization using RSS time-series. In Proceedings of the 2018 IEEE Symposium on Computers and Communications (ISCC), Natal, Brazil, 25–28 June 2018; pp. 01044–01049. [Google Scholar]
- Pecorella, T.; Fantacci, R.; Picano, B. Improving CSI Prediction Accuracy with Deep Echo State Networks in 5G Networks. Sensors 2020, 20, 6475. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Chan, S.H.G.; Yu, L.; Liu, N. Maxlifd: Joint maximum likelihood localization fusing fingerprints and mutual distances. IEEE Trans. Mob. Comput. 2018, 18, 602–617. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, S.; Li, L.; Hu, F.; Ansari, N. Accurate Wi-Fi localization by unsupervised fusion of extended candidate location set. IEEE Internet Things J. 2018, 6, 2476–2485. [Google Scholar] [CrossRef]
- Guo, X.; Elikplim, N.R.; Ansari, N.; Li, L.; Wang, L. Robust Wi-Fi localization by fusing derivative fingerprints of RSS and multiple classifiers. IEEE Trans. Ind. Inform. 2019, 16, 3177–3186. [Google Scholar] [CrossRef]
- Mazlan, A.B.; Ng, Y.H.; Tan, C.K. A Fast Indoor Positioning Using a Knowledge-Distilled Convolutional Neural Network (KD-CNN). IEEE Access 2022, 10, 65326–65338. [Google Scholar] [CrossRef]
- Aqilah, B.M.; Ng, Y.H.; Chee, K.T. Teacher-Assistant Knowledge Distillation Based Indoor Positioning System. Sustainability 2022, 2022, 14652. [Google Scholar]
- Qin, F.; Zuo, T.; Wang, X. Ccpos: Wi-Fi fingerprint indoor positioning system based on CDAE-CNN. Sensors 2021, 21, 1114. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Moon, N. Random forest and Wi-Fi fingerprint-based indoor location recognition system using smart watch. Hum.-Centric Comput. Inf. Sci. 2019, 9, 1–14. [Google Scholar] [CrossRef]
- Bozinovski, S. Reminder of the first paper on transfer learning in neural networks, 1976. Informatica 2020, 44. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar]
- Sanodiya, R.K.; Yao, L. A subspace based transfer joint matching with Laplacian regularization for visual domain adaptation. Sensors 2020, 20, 4367. [Google Scholar] [CrossRef] [PubMed]
- Klus, R.; Klus, L.; Talvitie, J.; Pihlajasalo, J.; Torres-Sospedra, J.; Valkama, M. Transfer Learning for Convolutional Indoor Positioning Systems. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar]
- Korkmaz, O. Indoor Localization with Transfer Learning. In Proceedings of the 2022 30th Signal Processing and Communications Applications Conference (SIU), Safranbolu, Turkey, 15–18 May 2022; pp. 1–4. [Google Scholar]
- Li, L.; Guo, X.; Zhao, M.; Li, H.; Ansari, N. TransLoc: A heterogeneous knowledge transfer framework for fingerprint-based indoor localization. IEEE Trans. Wirel. Commun. 2021, 20, 3628–3642. [Google Scholar] [CrossRef]
- Gidey, H.T.; Guo, X.; Li, L.; Zhang, Y. Heterogeneous Transfer Learning for Wi-Fi Indoor Positioning Based Hybrid Feature Selection. Sensors 2022, 22, 5840. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Wu, Q.; Tan, M.; Ng, M.K.; Min, H.; Tsang, I.W. Online heterogeneous transfer by hedge ensemble of offline and online decisions. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3252–3263. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, Y.; Lu, G.; Li, J.; Zhang, D. Fast pore comparison for high resolution fingerprint images based on multiple co-occurrence descriptors and local topology similarities. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5721–5731. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Kofler, C.; Muhr, R.; Spöck, G. Classifying image stacks of specular silicon wafer back surface regions: Performance comparison of CNNs and SVMs. Sensors 2019, 19, 2056. [Google Scholar] [CrossRef]
- Mendoza-Silva, G.M.; Richter, P.; Torres-Sospedra, J.; Lohan, E.S.; Huerta, J. Long-term Wi-Fi fingerprinting dataset for research on robust indoor positioning. Data 2018, 3, 3. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Feng, W.; Shen, Z. Balanced distribution adaptation for transfer learning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1129–1134. [Google Scholar]
- Wang, C.; Mahadevan, S. Heterogeneous domain adaptation using manifold alignment. In Proceedings of the Twenty-second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1541–1546. [Google Scholar]

| Notation | Meaning |
|---|---|
| ,, | source/target/co-occurrence domain |
| ,, | source/target/co-occurrence feature matrix |
| , | source/target labels |
| ,, | number of source/target/co-occurrence samples |
| ,, | dimension of source/target/co-occurrence samples |
| , | mapping matrix, mapped source feature matrix |
| correlation matrix | |
| MMD matrix | |
| kernelized matrix | |
| column vectors with and elements of value 1 | |
| topology and regularization parameters | |
| T | iteration times |
| Frobenius norm of ⋆ | |
| transposition matrix of ⋆ | |
| fingerprint classifier |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Si, H.; Guo, X.; Zhong, K. Co-Occurrence Fingerprint Data-Based Heterogeneous Transfer Learning Framework for Indoor Positioning. Sensors 2022, 22, 9127. https://doi.org/10.3390/s22239127
Huang J, Si H, Guo X, Zhong K. Co-Occurrence Fingerprint Data-Based Heterogeneous Transfer Learning Framework for Indoor Positioning. Sensors. 2022; 22(23):9127. https://doi.org/10.3390/s22239127
Chicago/Turabian StyleHuang, Jian, Haonan Si, Xiansheng Guo, and Ke Zhong. 2022. "Co-Occurrence Fingerprint Data-Based Heterogeneous Transfer Learning Framework for Indoor Positioning" Sensors 22, no. 23: 9127. https://doi.org/10.3390/s22239127
APA StyleHuang, J., Si, H., Guo, X., & Zhong, K. (2022). Co-Occurrence Fingerprint Data-Based Heterogeneous Transfer Learning Framework for Indoor Positioning. Sensors, 22(23), 9127. https://doi.org/10.3390/s22239127





