An Improved Density Peak Clustering Algorithm for Multi-Density Data
Abstract
:1. Introduction
- (1)
- In order to solve the problem of unsatisfactory clustering effect caused by the uniqueness of data parameters of multi-density, the distance matrix is obtained by the distance between any two points of each data point, and the K-nearest neighbor matrix is obtained by row in ascending order. Draw a line graph of the K-nearest neighbor distance according to the parameter k, find the global bifurcation point for division, and obtain D = {D1, D2, ..., Dm}, where m is the number of divisions. Calculate the corresponding parameter truncation distance dci for each dci, where i ∈ [1,m].
- (2)
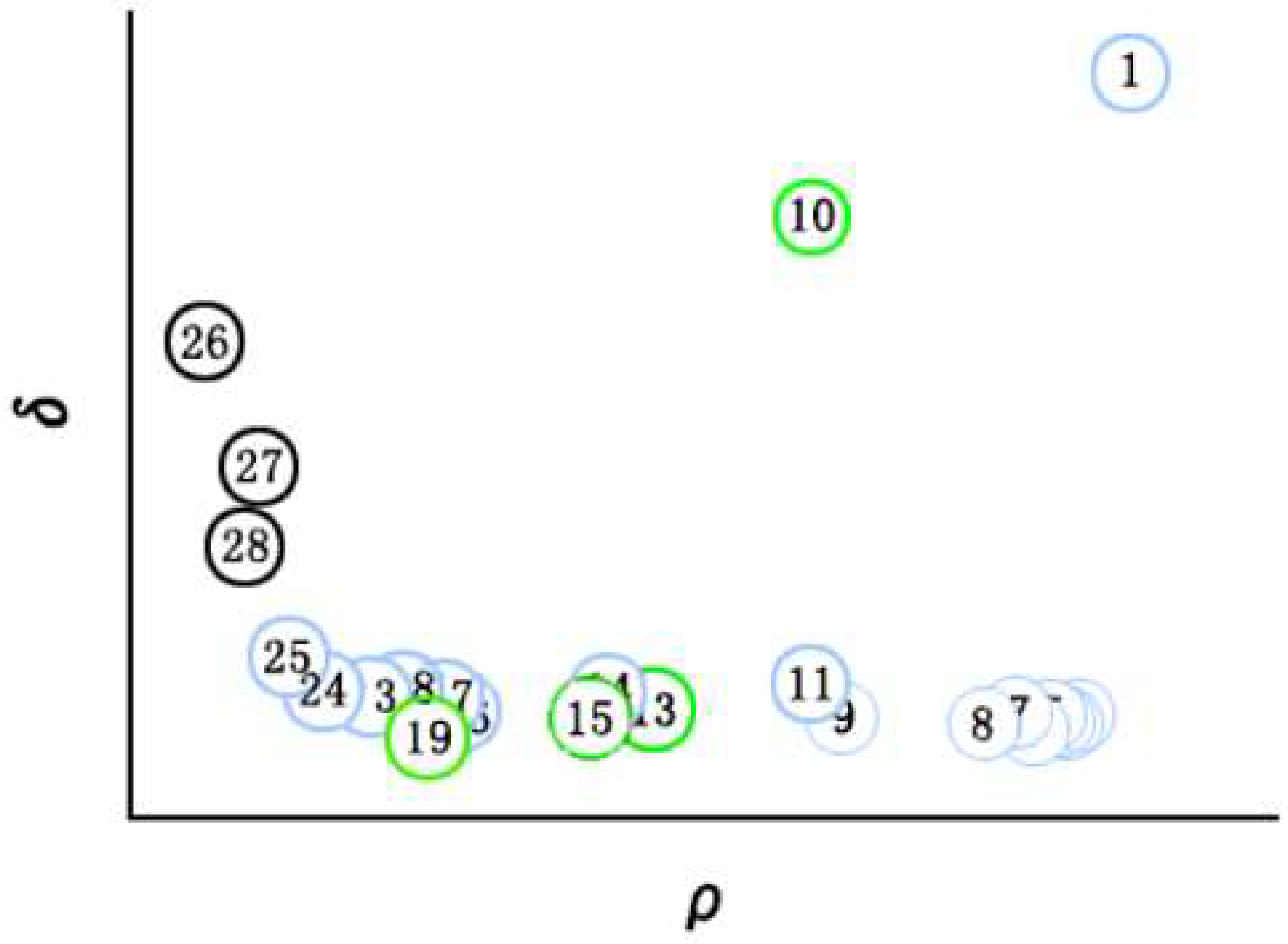
- In order to solve the problem of subjective selection of cluster centers, for each Di, calculate the local density ρj and data point distance δj of each data point, calculate the product of the two γj, and sort them in ascending order. Finally, draw the scatter plot of each data γj, calculate the height difference between two adjacent points, calculate the average height difference, and select the point higher than the average height difference as the center point of the preliminary cluster. Screen again according to the preparatory cluster center points to determine the cluster center and the number of clusters of each Di.
- (3)
- Each Di performs the DPC algorithm according to the obtained cluster center and dci to obtain a new cluster. Finally, the clusters are merged through the fusion rule to obtain the final cluster.
- (4)
- Comparative experiments are carried out from various perspectives on various artificial simulated datasets and UCI real datasets. From the perspective of various measurement indicators of clustering, the clustering quality of the F-DPC algorithm is the best; however, from the perspective of time consumption, the time consumption of the F-DPC algorithm increases with the increase in the amount of data, but the increase level is in the middle.
2. DPC Algorithm
2.1. DPC Algorithm Idea
2.2. DPC Algorithm Formula
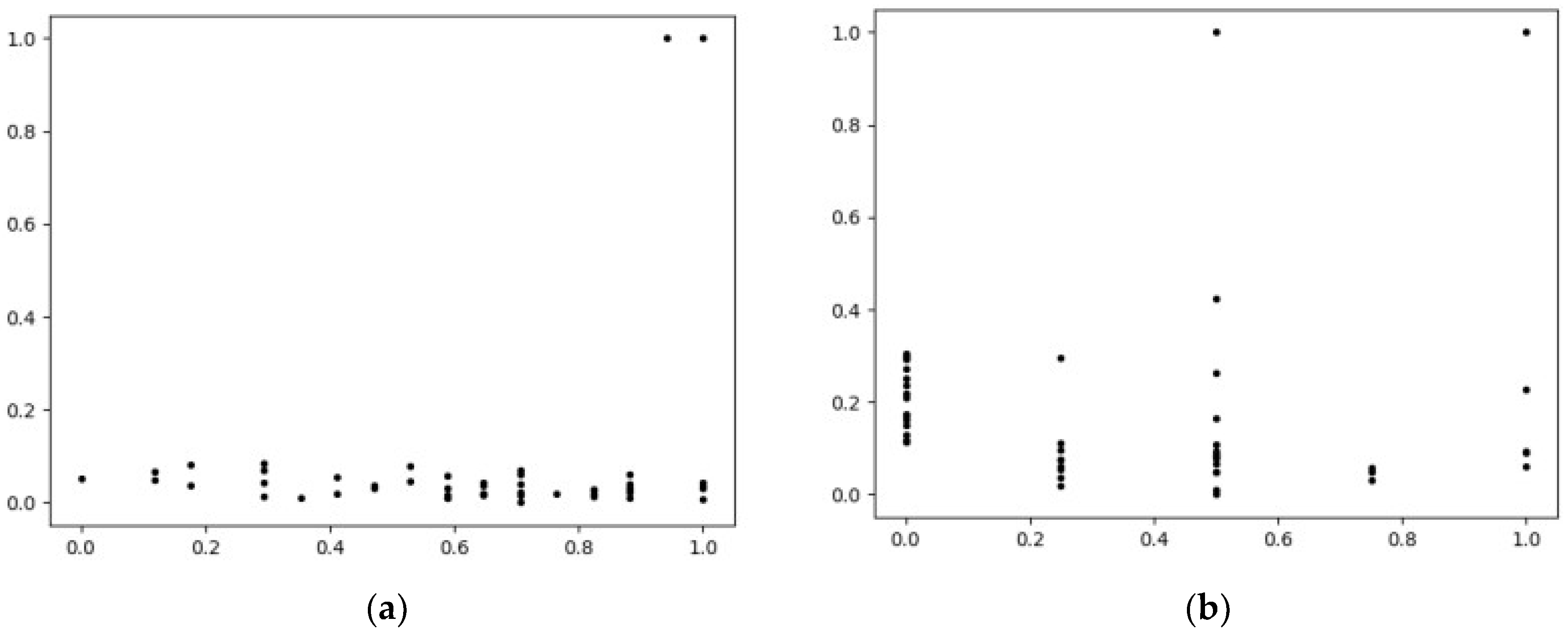
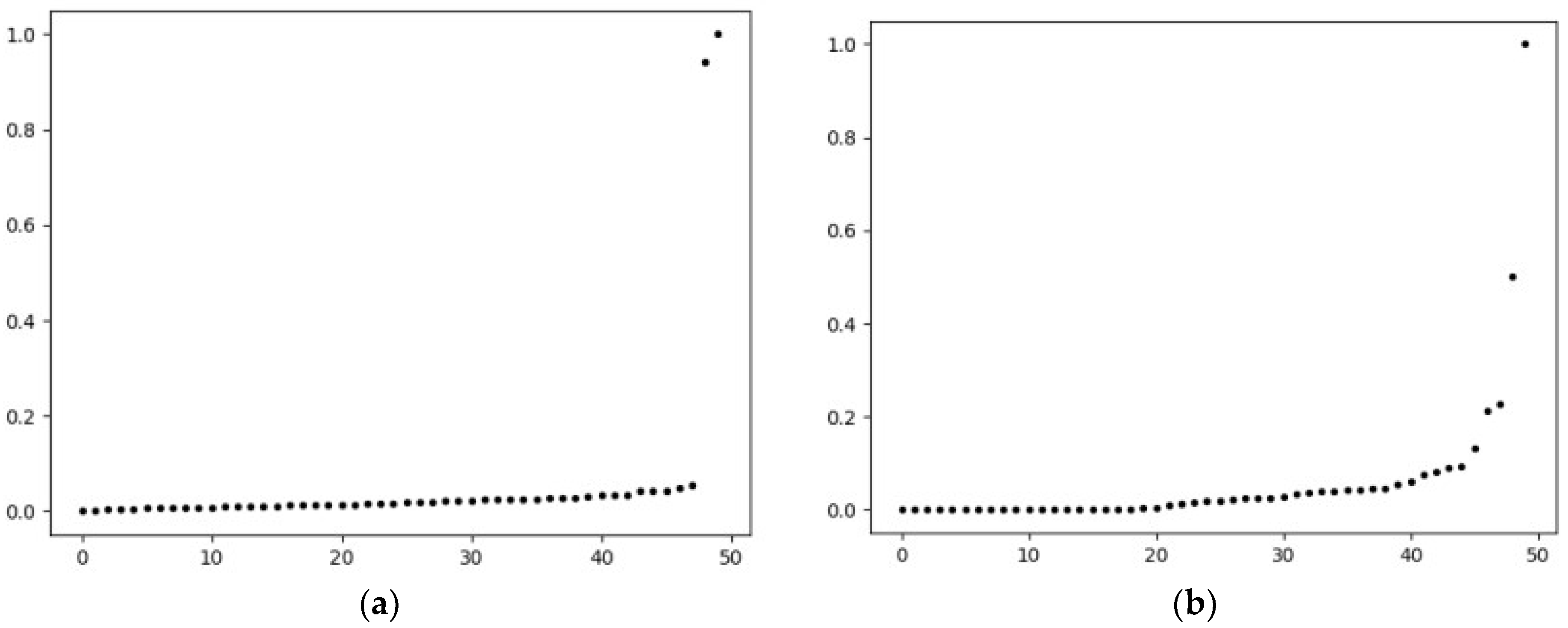
2.3. Selection of Cluster Centers
2.4. Selection of DPC Algorithm Parameters
2.5. Steps of DPC Algorithm
- (1)
- Calculate the distance between any two points.
- (2)
- Estimate the global parameter dc value.
- (3)
- Calculate the local density ρi of each point.
- (4)
- Calculate the data point distance δi for each point.
- (5)
- Draw a decision diagram according to (3) and (4).
- (6)
- Estimate the cluster center and the number of clusters.
- (7)
- The remaining points are assigned to the cluster of data points that are closest to the current point and whose local density is greater than that.
3. F-DPC Algorithm
3.1. The Basic Idea of F-DPC Algorithm
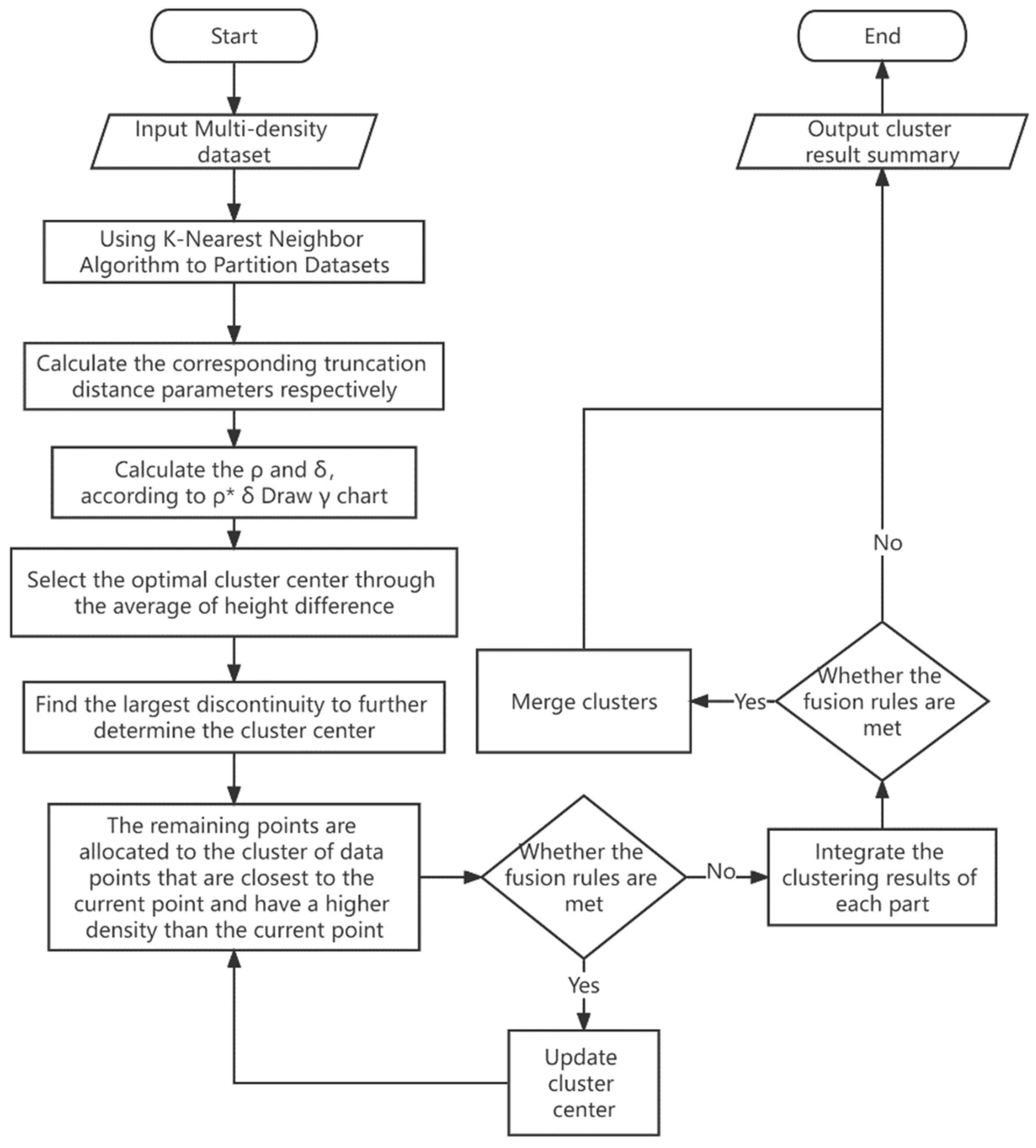
3.2. F-DPC Algorithm Design
3.2.1. K-Nearest Neighbor Algorithm to Divide Dataset
| Algorithm 1 Divide_Datasets. | ||
| Input: Multi-density Dataset D | ||
| Output: Dataset summary after dividing the dataset DD | ||
| 1 | X = read(D) // read data into X | |
| 2 | disMat = squareform(X) // Calculate the distance between any two points. | |
| 3 | for I in disMat | |
| 4 | i.sort() // Sort each row of data | |
| 5 | array.append(i[k]) // The kth nearest neighbor distance of each point is stored in an array. | |
| 6 | Use plt.plot to draw a distance line chart on the array; | |
| 7 | Calculate array[i + 1]-array[i] successively from the figure to find the point with obvious height difference, and mark array[i + 1] as the bifurcation point; | |
| 8 | Use index binding to divide the dataset into two parts left and right of the bifurcation point; | |
| 9 | return DD | |
3.2.2. Selection of Parameter Cut-Off Distance dc
| Algorithm 2 Parameter_Selection. | |
| Input: Currently partitioned dataset dd | |
| Output: Parameter dc | |
| 1 | disMat = squareform(dd) // Statistical data distance total to get distance matrix |
| 2 | position = int(n * (n − 1) * per/100) //per = 2%, N represents the number of currently divided datasets, and records the selected truncation distance dc position |
| 3 | dc = sort(t)[position + N] |
| 4 | return dc / / return parameter |
3.2.3. The Selection of Cluster Centers and the Number of Centers
| Algorithm 3 Select_Cluster_Center. | ||||
| Input: Currently partitioned dataset dd | ||||
| Output: cc | ||||
| 1 | Statistical local density is sorted and calculated and stored in normal_den; | |||
| 2 | for i in dd | |||
| 3 | Statistical local density is sorted and calculated and stored in normal_dis; | |||
| 4 | gama = normal_den*normal_dis // Preparing the product of the two parts for drawing the γ graph; | |||
| 5 | Use plt.plot to draw a gama graph for γ; | |||
| 6 | for j in range(len(gama)) | |||
| 7 | R.append(gama[i]-gama[i + 1]) //The height difference between front and rear is stored in R. | |||
| 8 | Calculate height difference mean in R, filter out the pre-cluster center is stored in K; | |||
| 9 | Compare the height difference in K, find the maximum height difference, and select the larger data point as the maximum discontinuity point; | |||
| 10 | Screen out the points greater than or equal to the maximum discontinuity point as the final cluster center and store it in cc, and update the labels of the dataset dd; | |||
| 11 | end for | |||
| 12 | end for | |||
| 13 | return cc | |||
3.2.4. Cluster Fusion
| Algorithm 4 Cluster_Fusion. | ||||
| Input: Dataset pp that needs fusion detection | ||||
| Output: Fusion clustering results | ||||
| 1 | for I in pp // Count any two clusters in the current dataset. | |||
| 2 | for j in pp | |||
| 3 | if there are two points with distance < dc and from two different labels | |||
| 4 | marked as adjacent samples and adjacent clusters; | |||
| 5 | end if | |||
| 6 | end for | |||
| 7 | if meet the fusion rules(The number of adjacent samples accounts for more than 2% of the total number of two adjacent clusters) | |||
| 8 | Update the cluster center cc to re-cluster, and perform fusion detection again after re-labeling; | |||
| 9 | Update dataset labels; | |||
| 10 | end if | |||
| 11 | return cluster // Return clustering results. | |||
3.3. Time Complexity Analysis of F-DPC Algorithm
- (1)
- Dataset division needs to traverse all data, count the distances of all data points to obtain a distance matrix and sort, where m is the total amount of data, so the time complexity is O(m2).
- (2)
- In the selection of parameters, the parameters are obtained by traversing the data distance of the current dataset, where n is the number of the current dataset, so the time complexity is O(n2).
- (3)
- In the selection of cluster centers, it is necessary to traverse all data points of the current divided dataset to calculate the γ value, and then traverse and draw the γ graph again to filter the cluster centers. The time complexity is O(n2), and then the final cluster centers are selected from the preselected cluster centers, where r represents the number of preselected cluster centers, r <= n, so the algorithm time complexity of the whole process is O(n2 * r).
- (4)
- DPC rule clustering needs to traverse the local density and data point distance of each data point. The traversal length is also the total number of data points in the current dataset n, and the algorithm time complexity is O(n).
- (5)
- In the process of cluster fusion, the process of finding adjacent clusters, traversing the distance of any current dataset data points to judge adjacent clusters and adjacent samples, the algorithm time complexity is O(n2).
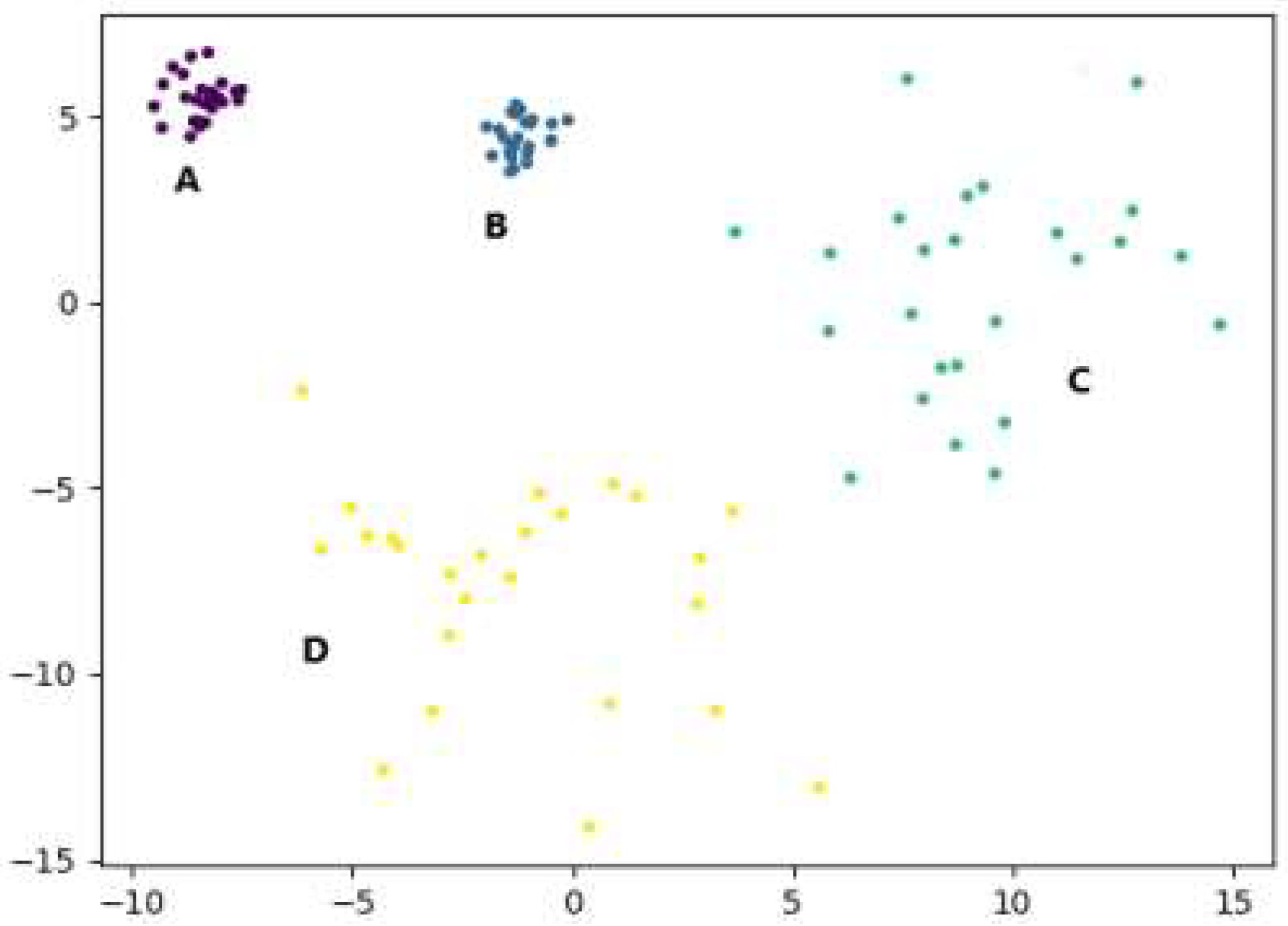
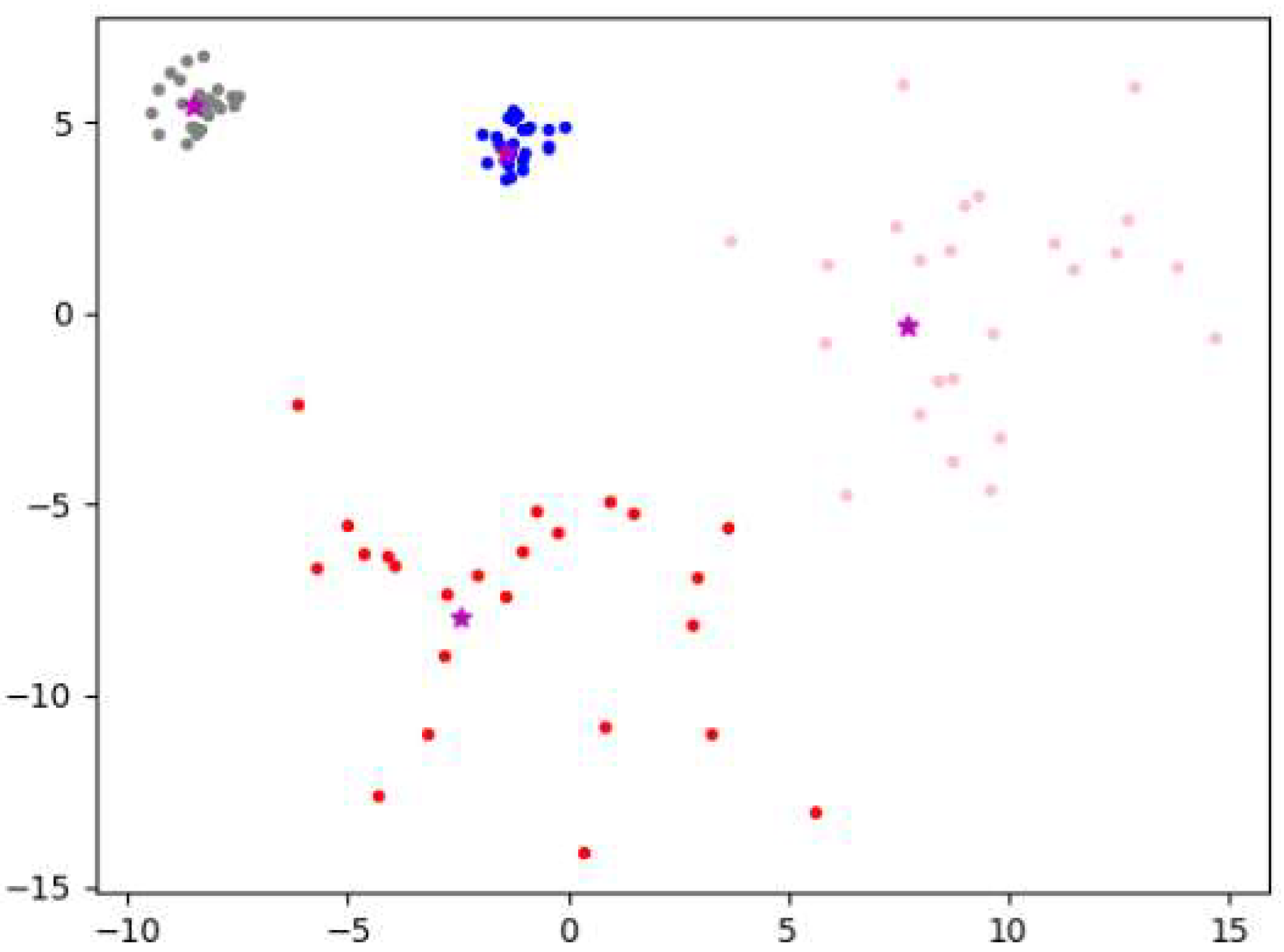
3.4. Algorithm Example Analysis
4. Discussion
4.1. Algorithm Evaluation Metrics
4.2. Analysis of Experimental Results on Artificial Synthetic Datasets
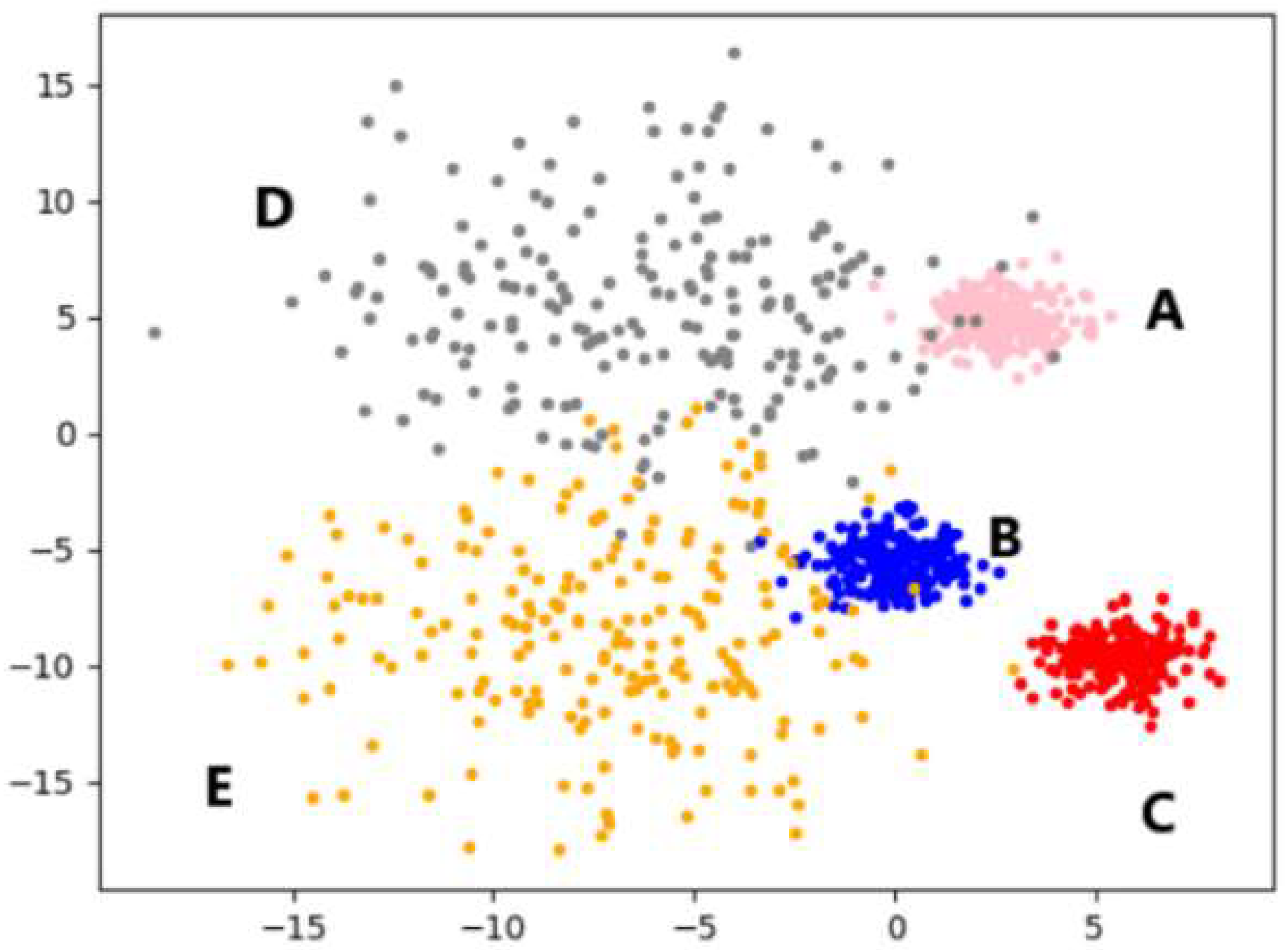
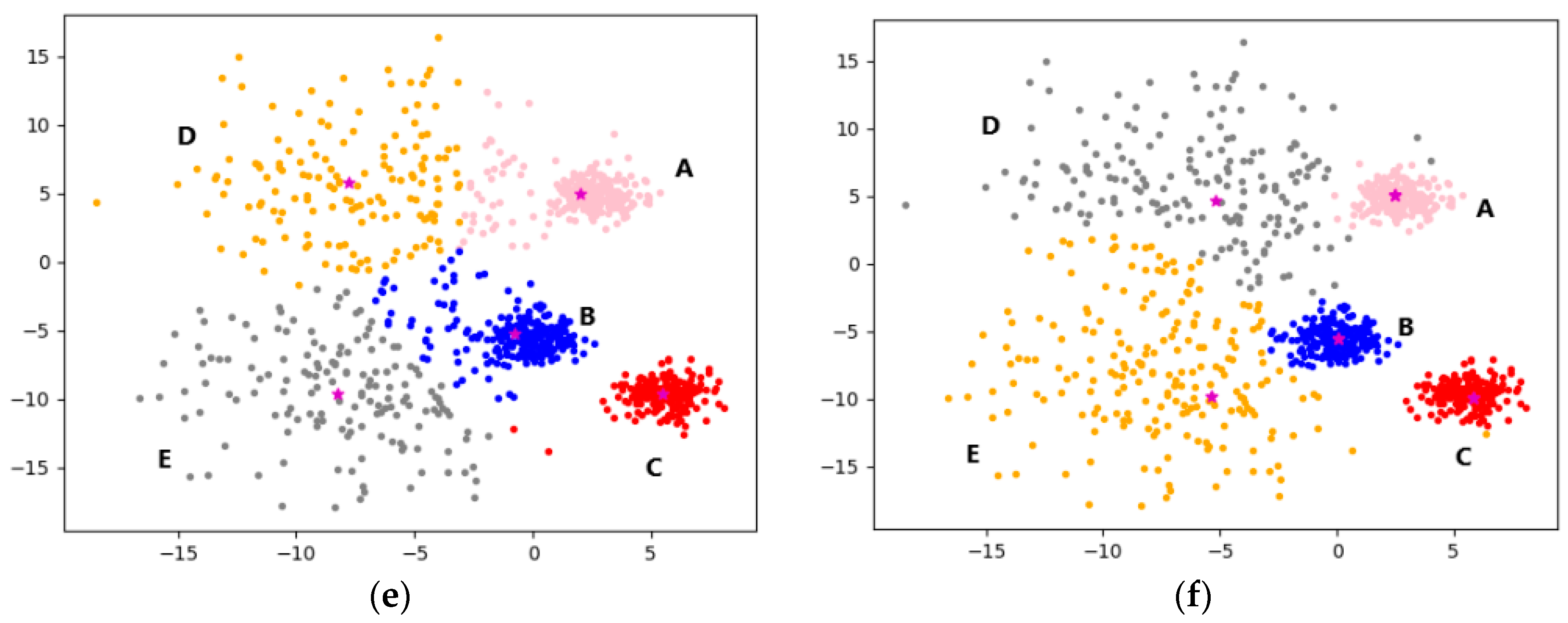
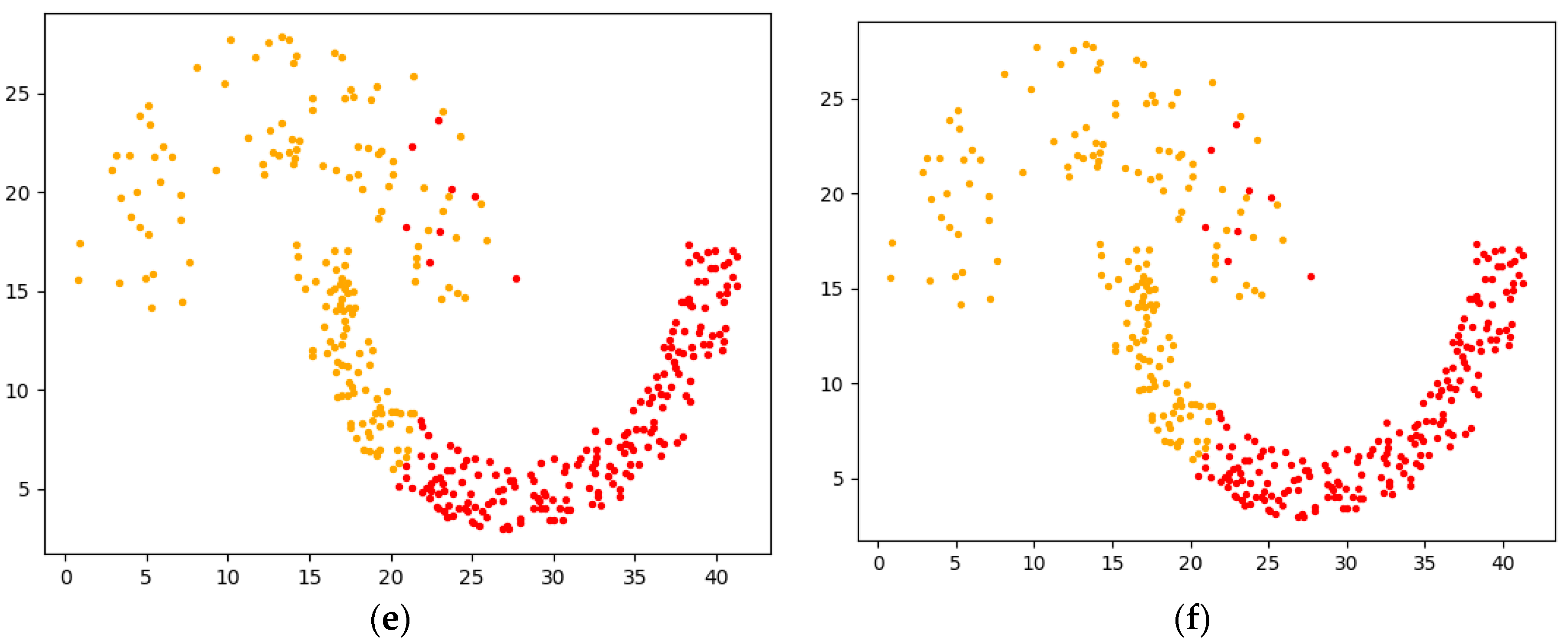
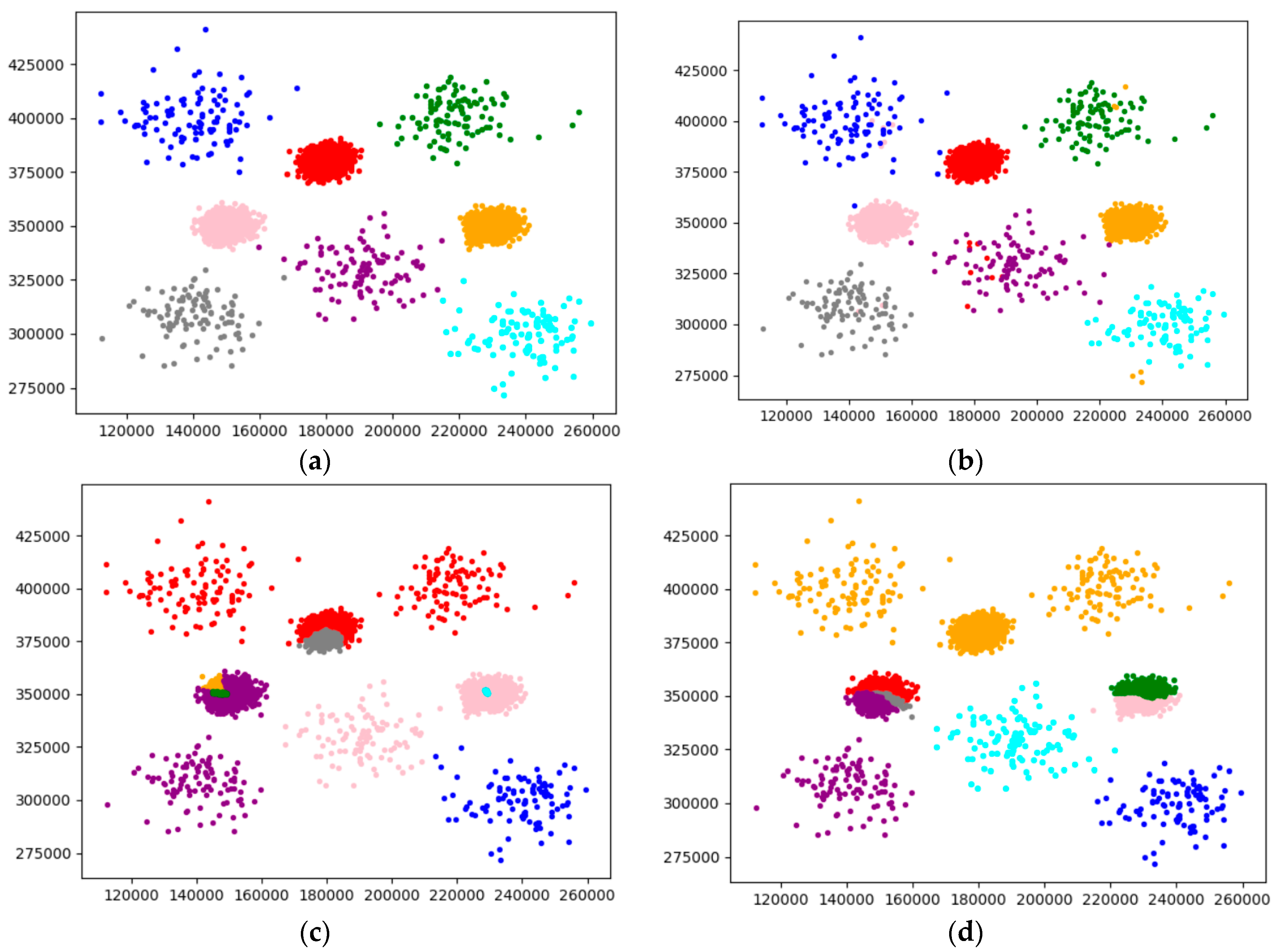
4.2.1. Experimental Analysis from the Perspective of Clustering Effect
4.2.2. Experimental Analysis from the Perspective of Clustering Quality
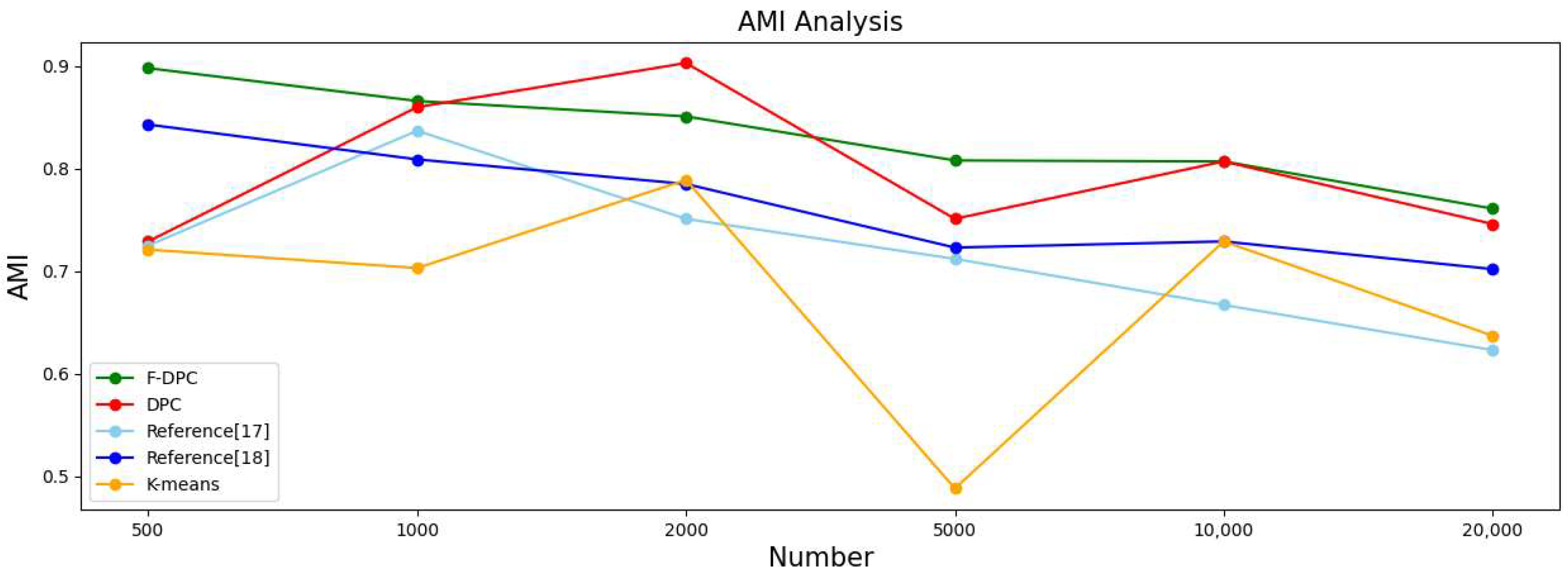
4.2.3. Experimental Analysis from the Perspective of Sample Size
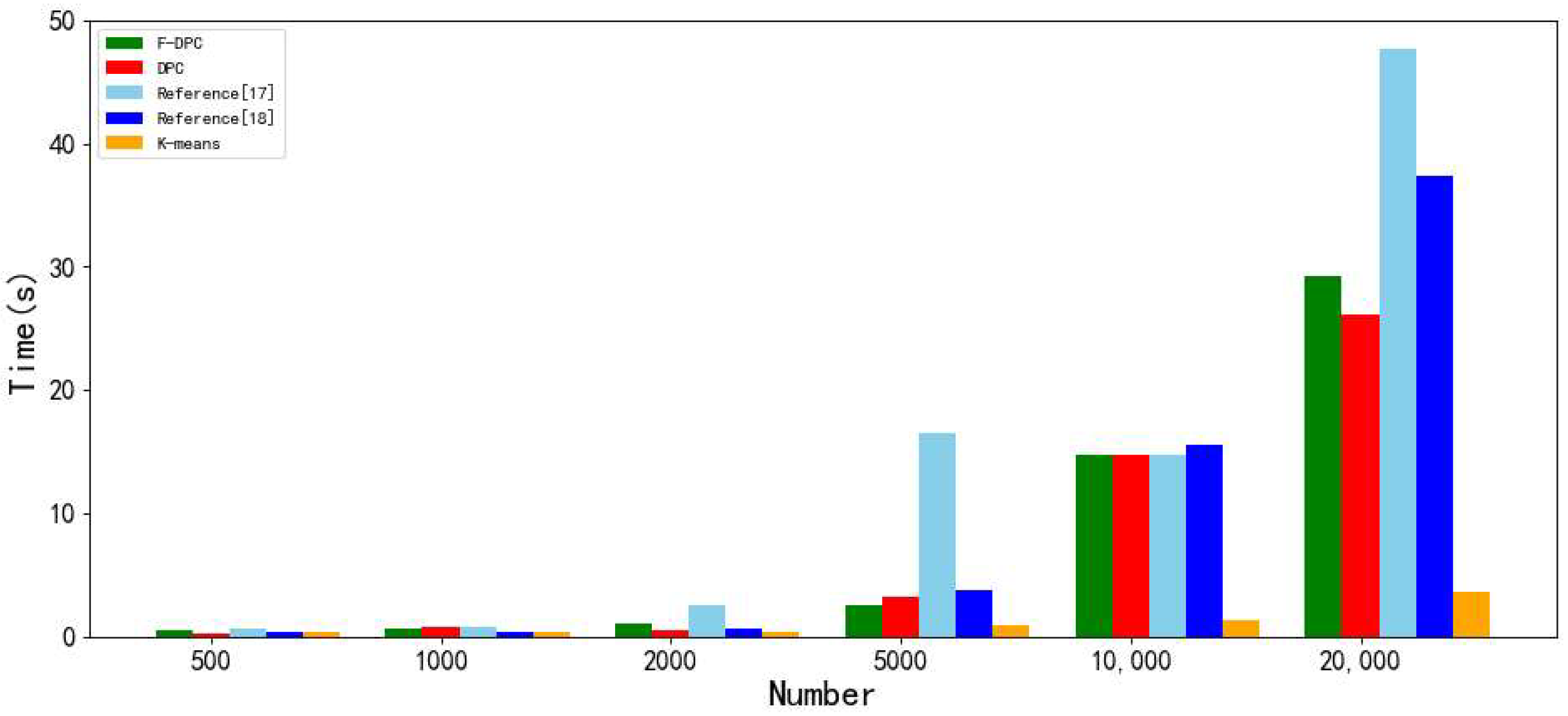
4.2.4. Experimental Analysis from the Perspective of Time Consumption
4.3. Analysis of Experimental Results on UCI Real Datasets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Zhou, Y. Overview of Clustering Algorithms. Comput. Appl. 2019, 39, 1869–1882. [Google Scholar]
- Gan, J.; Yang, X.; Lv, J.; Huang, H.; Xiao, L. Overview of Unsupervised Learning Algorithms in Artificial Intelligence. Strait Technol. Ind. 2019, 1, 134–135. [Google Scholar]
- Sun, R. A recognition method for visual image of sports video based on fuzzy clustering algorithm. Int. J. Inf. Commun. Technol. 2022, 20, 1–17. [Google Scholar] [CrossRef]
- Devi, S.S.; Anto, S.; Ibrahim, S.P.S. An efficient document clustering using hybridized harmony search K-means algorithm with multi-view point. Int. J. Cloud Comput. 2021, 10, 129–143. [Google Scholar] [CrossRef]
- Spathoulas, G.; Theodoridis, G.; Damiris, G.P. Using homomorphic encryption for privacy-preserving clustering of intrusion detection alerts. Int. J. Inf. Secur. 2021, 20, 347–370. [Google Scholar] [CrossRef]
- Kang, Y.; Jia, Q.; Gao, S.; Zeng, X.; Wang, Y.; Angsuesser, S.; Liu, Y.; Ye, X.; Fei, T. Extracting human emotions at different places based on facial expressions and spatial clustering analysis. Trans. GIS 2019, 23, 450–480. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, S.; Deng, Z. Several Problems in Cluster Analysis Research. Control. Decis. 2012, 27, 321–328. [Google Scholar]
- Han, J.; Kamber, M. Concept and Technology of Data Mining; Machinery Industry Press: Beijing, China, 2012. [Google Scholar]
- Wu, D.; Wu, C. Research on the time-dependent split delivery green vehicle routing problem for fresh agricultural products with multiple time windows. Agriculture 2022, 12, 793. [Google Scholar] [CrossRef]
- Xu, G.; Bai, H.; Xing, J.; Luo, T.; Xiong, N.N. SG-PBFT: A secure and highly efficient distributed blockchain PBFT consensus algorithm for intelligent Internet of vehicles. J. Parallel Distrib. Comput. 2022, 164, 1–11. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Zhou, Y.Q.; Luo, Q.F.; Deng, W. Optimal reactive power dispatch using an improved slime Mould algorithm. Energy Rep. 2021, 7, 8742–8759. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.G.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Processing 2022, 167, 108576. [Google Scholar] [CrossRef]
- Chen, H.Y.; Fang, M.; Xu, S. Hyperspectral remote sensing image classification with CNN based on quantum genetic-optimized sparse representation. IEEE Access 2020, 8, 99900–99909. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Song, Y.; Zhao, H.M. Differential evolution algorithm with wavelet basis function and optimal mutation strategy for complex optimization problem. Appl. Soft Comput. 2021, 100, 106724. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.J.; Liu, Y.; Deng, W.Q.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2022. [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.; Cheng, K. Analysis of Weibo Public Sentiment Based on Density Peak Optimization K-means Clustering Algorithm. Comput. Digit. Eng. 2022, 50, 726–729+735. [Google Scholar]
- Tian, S.; Ding, L.; Zheng, J. K-means text clustering algorithm based on density peak optimization. Comput. Eng. Des. 2017, 38, 1019–1023. [Google Scholar]
- Liu, L.; Yu, D. Density Peaks Clustering Algorithm Based on Weighted k-Nearest Neighbors and Geodesic Distance. IEEE Access 2020, 8, 168282–168296. [Google Scholar] [CrossRef]
- Wang, F. Research on Adaptive Density Peak Clustering Algorithm; Xi’an University of Technology: Xi’an, China, 2021. [Google Scholar]
- Tao, X.; Li, Q.; Guo, W.; Ren, C.; He, Q.; Liu, R.; Zou, J. Adaptive weighted over-sampling for imbalanced datasets based on density peaks clustering with heuristic filtering. Inf. Sci. 2020, 519, 43–73. [Google Scholar] [CrossRef]
- Yin, L.; Li, M.; Chen, H.; Deng, W. An Improved Hierarchical Clustering Algorithm Based on the Idea of Population Reproduction and Fusion. Electronics 2022, 11, 2735. [Google Scholar] [CrossRef]
- Niu, S.; Ou, Y.; Ling, J.; Gu, G. Multi-density fast clustering algorithm using regional division. Comput. Eng. Appl. 2019, 55, 61–66+102. [Google Scholar]
- Shan, Y.; Li, S.; Li, F.; Cui, Y.; Li, S.; Zhou, M.; Li, X. A Density Peaks Clustering Algorithm With Sparse Search and K-d Tree. IEEE Access 2022, 10, 74883–74901. [Google Scholar] [CrossRef]
- Jiang, D.; Zang, W.; Sun, R.; Wang, Z.; Liu, X. Adaptive density peaks clustering based on k-nearest neighbor and gini coefficient. IEEE Access 2020, 8, 113900–113917. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, M.; Xiang, Y. Fast Searching Density Peak Clustering Algorithm Based on Shared Nearest Neighbor and Adaptive Clustering Center. Symmetry 2020, 12, 2014. [Google Scholar] [CrossRef]
- Tong, W.; Liu, S.; Gao, X.-Z. A density-peak-based clustering algorithm of automatically determining the number of clusters. Neurocomputing 2020, 458, 655–666. [Google Scholar] [CrossRef]
- Xu, X.; Ding, S.; Xu, H.; Liao, H.; Xue, Y. A feasible density peaks clustering algorithm with a merging strategy. Soft Comput. 2018, 23, 5171–5183. [Google Scholar] [CrossRef]
- Yang, X.; Cai, Z.; Li, R.; Zhu, W. GDPC: Generalized density peaks clustering algorithm based on order similarity. Int. J. Mach. Learn. Cybern. 2020, 12, 719–731. [Google Scholar] [CrossRef]
- Deng, W.; Ni, H.C.; Liu, Y.; Chen, H.L.; Zhao, H.M. An adaptive differential evolution algorithm based on belief space and generalized opposition-based learning for resource allocation. Appl. Soft Comput. 2022, 127, 109419. [Google Scholar] [CrossRef]
- Song, Y.J.; Cai, X.; Zhou, X.B.; Zhang, B.; Chen, H.L.; Li, Y.G.; Deng, W.Q.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.R.; Zhou, X.B.; Zhou, Y.Q.; Sun, Y.Z.; Zhu, W.H.; Chen, H.Y.; Deng, W.Q.; Chen, H.L.; Zhao, H.M. Multi-strategy particle swarm and ant colony hybrid optimization for airport taxiway planning problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Zhou, X.B.; Ma, H.J.; Gu, J.G.; Chen, H.L.; Deng, W. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism. Eng. Appl. Artif. Intell. 2022, 114, 105139. [Google Scholar] [CrossRef]
- Ren, Z.; Han, X.; Yu, X.; Skjetne, R.; Leira, B.J.; Sævik, S.; Zhu, M. Data-driven simultaneous identification of the 6DOF dynamic model and wave load for a ship in waves. Mech. Syst. Signal Processing 2023, 184, 109422. [Google Scholar] [CrossRef]
- Chen, H.Y.; Miao, F.; Chen, Y.J.; Xiong, Y.J.; Chen, T. A hyperspectral image classification method using multifeature vectors and optimized KELM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Yao, R.; Guo, C.; Deng, W.; Zhao, H.M. A novel mathematical morphology spectrum entropy based on scale-adaptive techniques. ISA Trans. 2022, 126, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Li, T.Y.; Shi, J.Y.; Deng, W.; Hu, Z.D. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 2022, 121, 108731. [Google Scholar] [CrossRef]
- Zhao, H.M.; Liu, J.; Chen, H.Y.; Chen, J.; Li, Y.; Xu, J.J.; Deng, W. Intelligent diagnosis using continuous wavelet transform and gauss convolutional deep belief network. IEEE Trans. Reliab. 2022, 1–11. [Google Scholar] [CrossRef]
- Xu, X.; Ding, S.; Ding, L. Research progress of density peak clustering algorithm. J. Softw. 2022, 33, 1800–1816. [Google Scholar]
- Li, T.; Yue, S.; Sun, C. General density-peaks-clustering algorithm. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, C.; Ding, S.; Xu, X.; Du, S.; Shi, T. Fast density peaks clustering algorithm in polar coordinate system. Appl. Intell. 2022, 52, 14478–14490. [Google Scholar] [CrossRef]
- Parmar, M.; Wang, D.; Zhang, X.; Tan, A.-H.; Miao, C.; Jiang, J.; Zhou, Y. REDPC: A residual error-based density peak clustering algorithm. Neurocomputing 2018, 348, 82–96. [Google Scholar] [CrossRef]
- Zhuo, L.; Li, K.; Liao, B.; Lia, H.; Wei, X.; Lib, K. HCFS: A Density Peak Based Clustering Algorithm Employing A Hierarchical Strategy. IEEE Access 2019, 7, 74612–74624. [Google Scholar] [CrossRef]
- Dou, X. Overview of KNN Algorithm. Commun. World 2018, 10, 273–274. [Google Scholar]
- Sinsomboonthong, S. Performance Comparison of New Adjusted Min-Max with Decimal Scaling and Statistical Column Normalization Methods for Artificial Neural Network Classification. Int. J. Math. Math. Sci. 2022, 2022, 1–9. [Google Scholar] [CrossRef]
- Pandey, A.; Achin, J. Comparative analysis of KNN algorithm using various normalization techniques. Int. J. Comput. Netw. Inf. Secur. 2017, 9, 36. [Google Scholar] [CrossRef] [Green Version]
- Li, M. Improvement of K-Means Algorithm and Its Application in Text Clustering; Jiangnan University: Wuxi, China, 2018. [Google Scholar]
- Ge, L.; Chen, Y.; Zhou, Y. Research Status and Analysis of Density Peak Clustering Algorithms. Guangxi Sci. 2022, 29, 277–286. [Google Scholar]
- Xue, X.; Gao, S.; Peng, H.; Wu, H. Density Peak Clustering Algorithm Based on K-Nearest Neighbors and Multi-Class Merging. J. Jilin Univ. 2019, 57, 111–120. [Google Scholar] [CrossRef]
- Vinh, N.X.; Julien, E.; James, B. Information theoretic measures for clusterings comparison: Is a correction for chance necessary? In Proceedings of the 26th annual international conference on machine learning, Montreal, QC, Canada, 14–18 June 2009. [Google Scholar]
- Hubert, L.; Phipps, A. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Wang, C.X.; Liu, L.G. Feature matching using quasi-conformal maps. Front. Inf. Technol. Electron. Eng. 2017, 18, 644–657. [Google Scholar] [CrossRef]
- Al Alam, P.; Constantin, J.; Constantin, I.; Lopez, C. Partitioning of Transportation Networks by Efficient Evolutionary Clustering and Density Peaks. Algorithms 2022, 15, 76. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, X.; Wang, T.; Du, K.; Fu, C. An Adaptive Ellipse Distance Density Peak Fuzzy Clustering Algorithm Based on the Multi-target Traffic Radar. Sensors 2020, 20, 4920. [Google Scholar] [CrossRef]
- Sun, L.; Ci, S.; Liu, X.; Zheng, X.; Yu, Q.; Luo, Y. A privacy-preserving density peak clustering algorithm in cloud computing. Concurr. Comput. Pr. Exper. 2020, 32, e5641. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Du, H. A Collaborative Filtering Recommendation Algorithm Based on Density Peak Clustering. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS), Macao, China, 13–16 December 2019; pp. 45–49. [Google Scholar] [CrossRef]
- Chen, Y.; Du, Y.; Cao, X. Density Peak Clustering Algorithm Based on Differential Privacy Preserving. In Science of Cyber Security. SciSec 2019. Lecture Notes in Computer Science; Liu, F., Xu, J., Xu, S., Yung, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 11933. [Google Scholar] [CrossRef]
- Yu, C.; Zhou, S.; Song, M.; Chang, C.I. Semisupervised hyperspectral band selection based on dual-constrained low-rank representation. IEEE Geosci. Remote. S. 2022, 19, 5503005.1-5. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.C.; Wu, T.H.; Bao, X.G. Solving the family traveling salesperson problem in the adleman–lipton model based on DNA computing. IEEE Trans. NanoBioscience 2021, 21, 75–85. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, Z.; Li, G.; Liu, Y.; Yang, R.; Liu, H. Optimal search mapping among sensors in heterogeneous smart homes. Math. Biosci. Eng. 2023, 20, 1960–1980. [Google Scholar] [CrossRef]
- Yu, C.; Liu, C.; Yu, H.; Song, M.; Chang, C.I. Unsupervised domain adaptation with dense-based compaction for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12287–12299. [Google Scholar] [CrossRef]



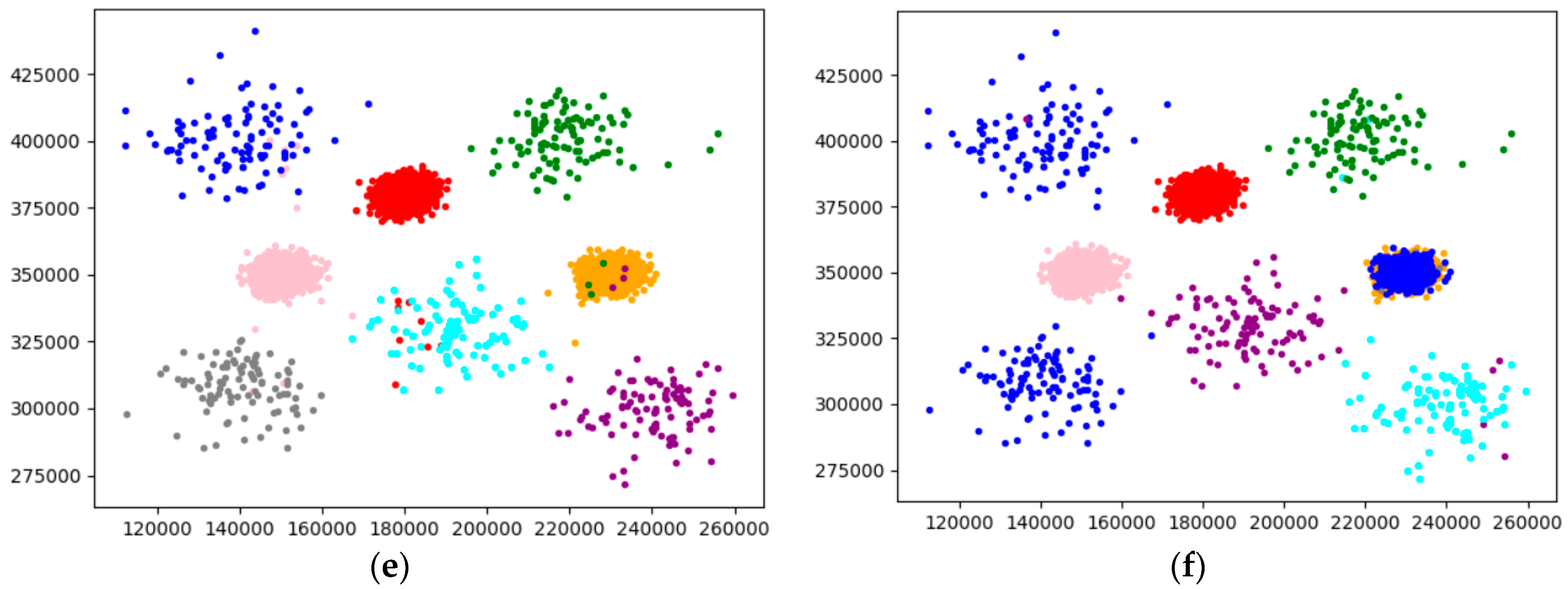
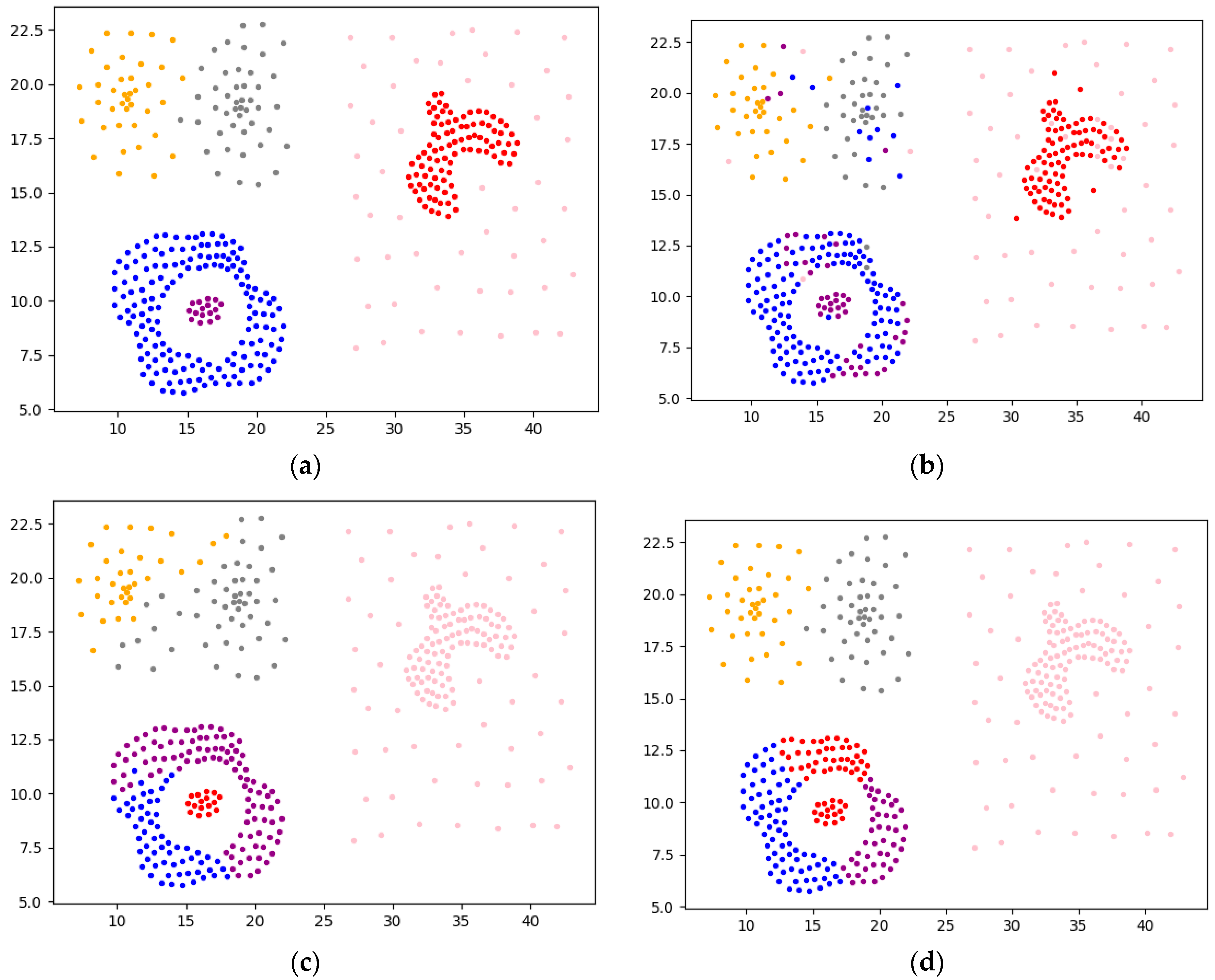
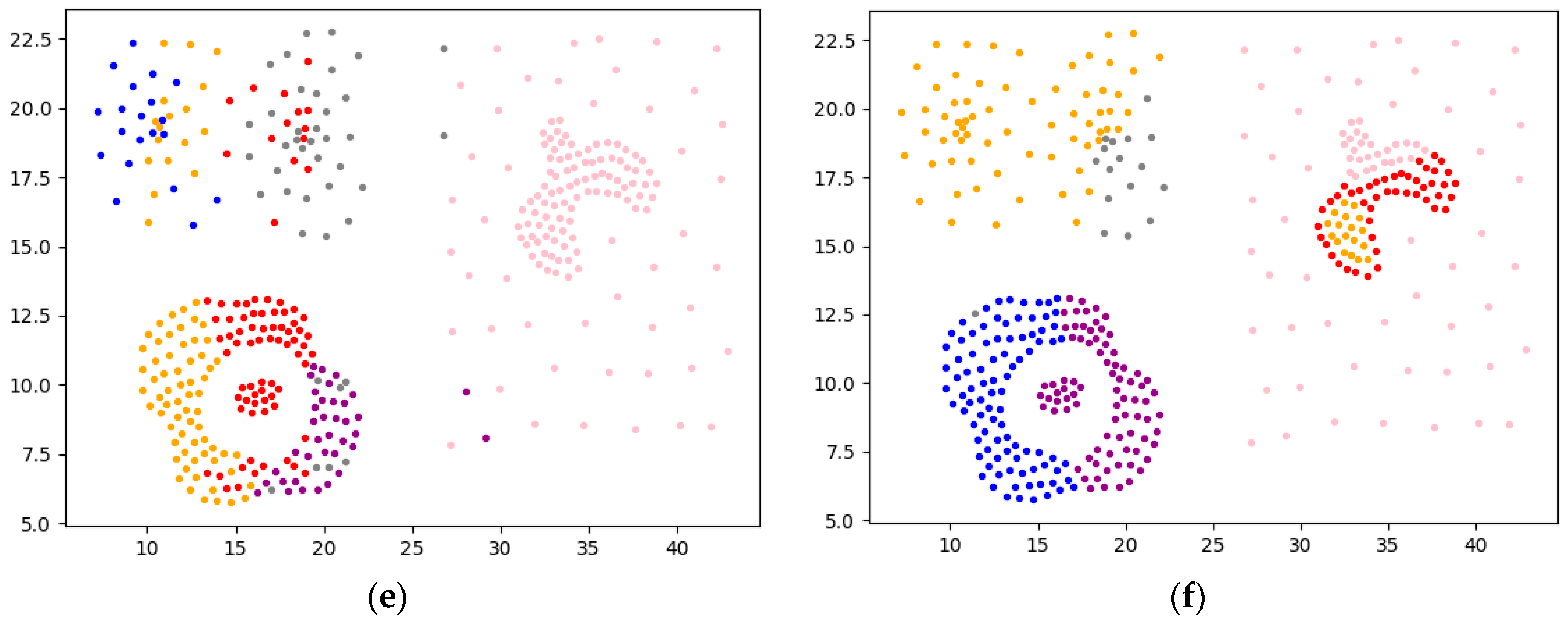

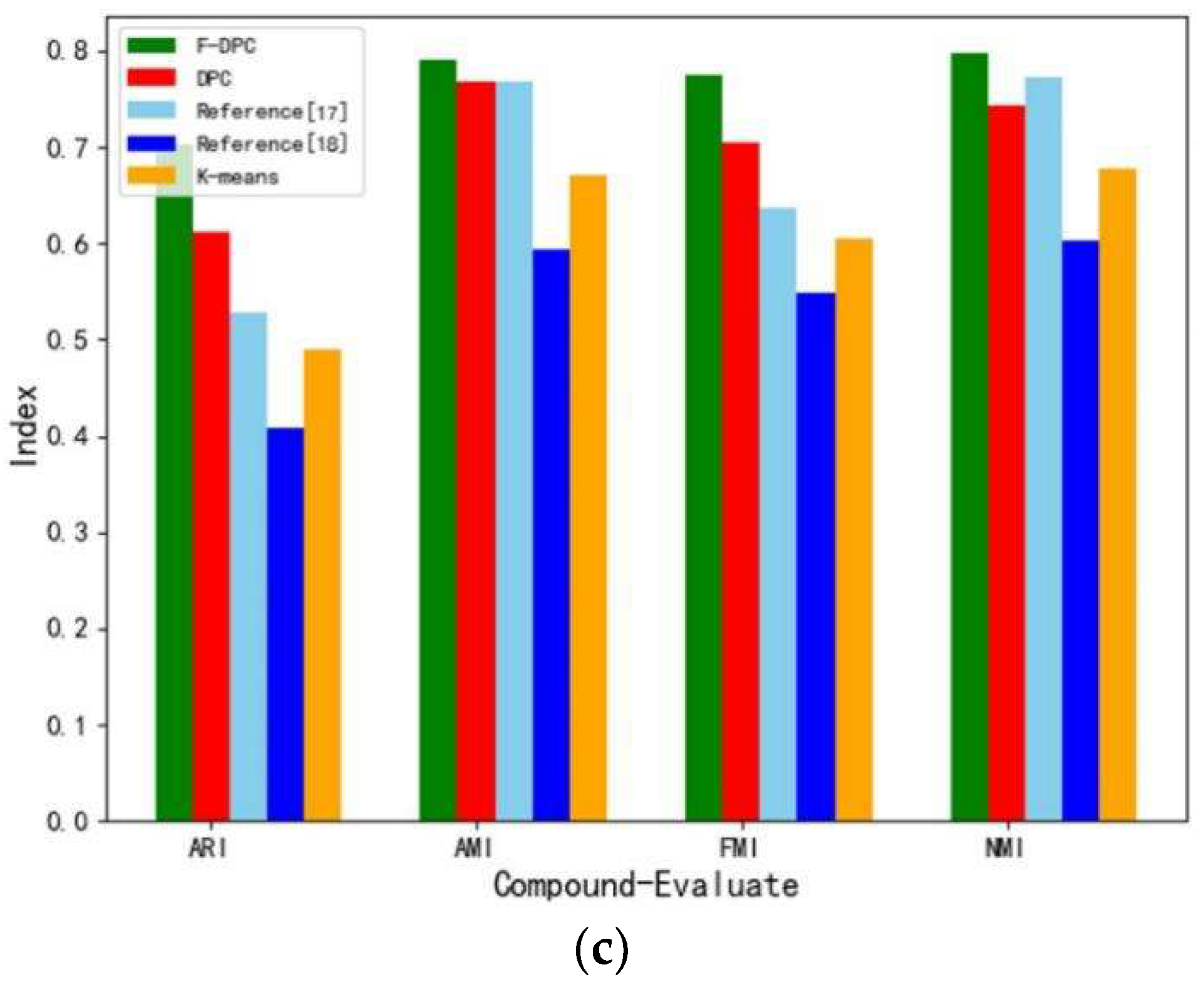
| Algorithm | Jain | Unbalance | Compound | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARI | AMI | FMI | NMI | ARI | AMI | FMI | NMI | ARI | AMI | FMI | NMI | |
| F-DPC | 0.768 | 0.684 | 0.918 | 0.685 | 0.994 | 0.982 | 0.995 | 0.981 | 0.703 | 0.791 | 0.774 | 0.797 |
| DPC | 0.643 | 0.595 | 0.729 | 0.595 | 0.731 | 0.787 | 0.804 | 0.783 | 0.612 | 0.769 | 0.705 | 0.744 |
| Reference [17] | 0.052 | 0.164 | 0.591 | 0.166 | 0.650 | 0.774 | 0.743 | 0.775 | 0.527 | 0.767 | 0.637 | 0.772 |
| Reference [18] | 0.265 | 0.260 | 0.674 | 0.262 | 0.993 | 0.981 | 0.995 | 0.980 | 0.409 | 0.594 | 0.548 | 0.602 |
| K-means | 0.265 | 0.260 | 0.674 | 0.262 | 0.816 | 0.837 | 0.866 | 0.838 | 0.490 | 0.671 | 0.605 | 0.677 |
| Algorithm | 500 | 1000 | 2000 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | F1 | ARI | AMI | Time(s) | ACC | F1 | ARI | AMI | Time(s) | ACC | F1 | ARI | AMI | Time(s) | |
| F-DPC | 0.964 | 0.963 | 0.909 | 0.898 | 0.52 | 0.942 | 0.941 | 0.871 | 0.866 | 0.73 | 0.931 | 0.932 | 0.839 | 0.851 | 1.12 |
| DPC | 0.831 | 0.831 | 0.682 | 0.729 | 0.34 | 0.911 | 0.902 | 0.865 | 0.860 | 0.79 | 0.910 | 0.910 | 0.905 | 0.903 | 0.53 |
| Reference [17] | 0.702 | 0.643 | 0.607 | 0.725 | 0.68 | 0.921 | 0.911 | 0.811 | 0.837 | 0.83 | 0.811 | 0.804 | 0.662 | 0.751 | 2.59 |
| Reference [18] | 0.921 | 0.921 | 0.823 | 0.843 | 0.43 | 0.897 | 0.891 | 0.769 | 0.809 | 0.44 | 0.881 | 0.881 | 0.739 | 0.785 | 0.72 |
| K-means | 0.628 | 0.632 | 0.584 | 0.721 | 0.41 | 0.571 | 0.524 | 0.569 | 0.703 | 0.39 | 0.881 | 0.881 | 0.739 | 0.785 | 0.49 |
| Algorithm | 5000 | 10,000 | 20,000 | ||||||||||||
| ACC | F1 | ARI | AMI | Time(s) | ACC | F1 | ARI | AMI | Time(s) | ACC | F1 | ARI | AMI | Time(s) | |
| F-DPC | 0.904 | 0.904 | 0.792 | 0.808 | 2.62 | 0.910 | 0.909 | 0.798 | 0.807 | 14.71 | 0.892 | 0.883 | 0.752 | 0.761 | 29.24 |
| DPC | 0.870 | 0.873 | 0.723 | 0.751 | 3.34 | 0.900 | 0.901 | 0.782 | 0.807 | 14.82 | 0.823 | 0.824 | 0.732 | 0.746 | 26.12 |
| Reference [17] | 0.782 | 0.767 | 0.603 | 0.712 | 16.51 | 0.631 | 0.542 | 0.523 | 0.667 | 14.81 | 0.835 | 0.712 | 0.588 | 0.623 | 47.62 |
| Reference [18] | 0.841 | 0.830 | 0.669 | 0.723 | 3.86 | 0.851 | 0.836 | 0.683 | 0.729 | 15.61 | 0.732 | 0.802 | 0.675 | 0.702 | 37.33 |
| K-means | 0.280 | 0.211 | 0.344 | 0.488 | 0.96 | 0.851 | 0.836 | 0.683 | 0.729 | 1.32 | 0.623 | 0.622 | 0.705 | 0.637 | 3.62 |
| Datasets | Number | Feature | Class |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Wine | 178 | 13 | 3 |
| Seed | 210 | 7 | 3 |
| Vowel | 871 | 3 | 6 |
| WDBC | 569 | 30 | 2 |
| Algorithm | Iris | Wine | Seed | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | ARI | AMI | FMI | ACC | ARI | AMI | FMI | ACC | ARI | AMI | FMI | |
| F-DPC | 0.898 | 0.722 | 0.720 | 0.824 | 0.552 | 0.355 | 0.378 | 0.560 | 0.788 | 0.962 | 0.971 | 0.985 |
| DPC | 0.876 | 0.702 | 0.719 | 0.801 | 0.491 | 0.154 | 0.150 | 0.467 | 0.611 | 0.332 | 0.467 | 0.641 |
| Reference [17] | 0.891 | 0.731 | 0.767 | 0.822 | 0.501 | 0.143 | 0.176 | 0.438 | 0.623 | 0.443 | 0.578 | 0.667 |
| Reference [18] | 0.888 | 0.716 | 0.738 | 0.811 | 0.542 | 0.133 | 0.175 | 0.437 | 0.982 | 0.972 | 0.960 | 0.981 |
| K-means | 0.890 | 0.716 | 0.739 | 0.811 | 0.540 | 0.132 | 0.175 | 0.438 | 0.981 | 0.929 | 0.898 | 0.953 |
| Algorithm | Vowel | WDBC | ||||||||||
| ACC | ARI | AMI | FMI | ACC | ARI | AMI | FMI | |||||
| F-DPC | 0.356 | 0.372 | 0.502 | 0.499 | 0.690 | 0.688 | 0.624 | 0.723 | ||||
| DPC | 0.241 | 0.352 | 0.469 | 0.497 | 0.689 | 0.663 | 0.605 | 0.625 | ||||
| Reference [17] | 0.242 | 0.313 | 0.465 | 0.459 | 0.628 | 0.613 | 0.589 | 0.622 | ||||
| Reference [18] | 0.143 | 0.314 | 0.438 | 0.441 | 0.519 | 0.466 | 0.483 | 0.469 | ||||
| K-means | 0.233 | 0.290 | 0.446 | 0.422 | 0.501 | 0.422 | 0.428 | 0.482 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Wang, Y.; Chen, H.; Deng, W. An Improved Density Peak Clustering Algorithm for Multi-Density Data. Sensors 2022, 22, 8814. https://doi.org/10.3390/s22228814
Yin L, Wang Y, Chen H, Deng W. An Improved Density Peak Clustering Algorithm for Multi-Density Data. Sensors. 2022; 22(22):8814. https://doi.org/10.3390/s22228814
Chicago/Turabian StyleYin, Lifeng, Yingfeng Wang, Huayue Chen, and Wu Deng. 2022. "An Improved Density Peak Clustering Algorithm for Multi-Density Data" Sensors 22, no. 22: 8814. https://doi.org/10.3390/s22228814
APA StyleYin, L., Wang, Y., Chen, H., & Deng, W. (2022). An Improved Density Peak Clustering Algorithm for Multi-Density Data. Sensors, 22(22), 8814. https://doi.org/10.3390/s22228814