Acoustic Emission Source Characterisation during Fatigue Crack Growth in Al 2024-T3 Specimens
Abstract
1. Introduction
- A novel method of waveform selection based on the peak frequency of AE waveforms is presented. This allows a better prediction of the fatigue crack growth. Thus, the results from this study can help make a better decision on the inspection interval of components.
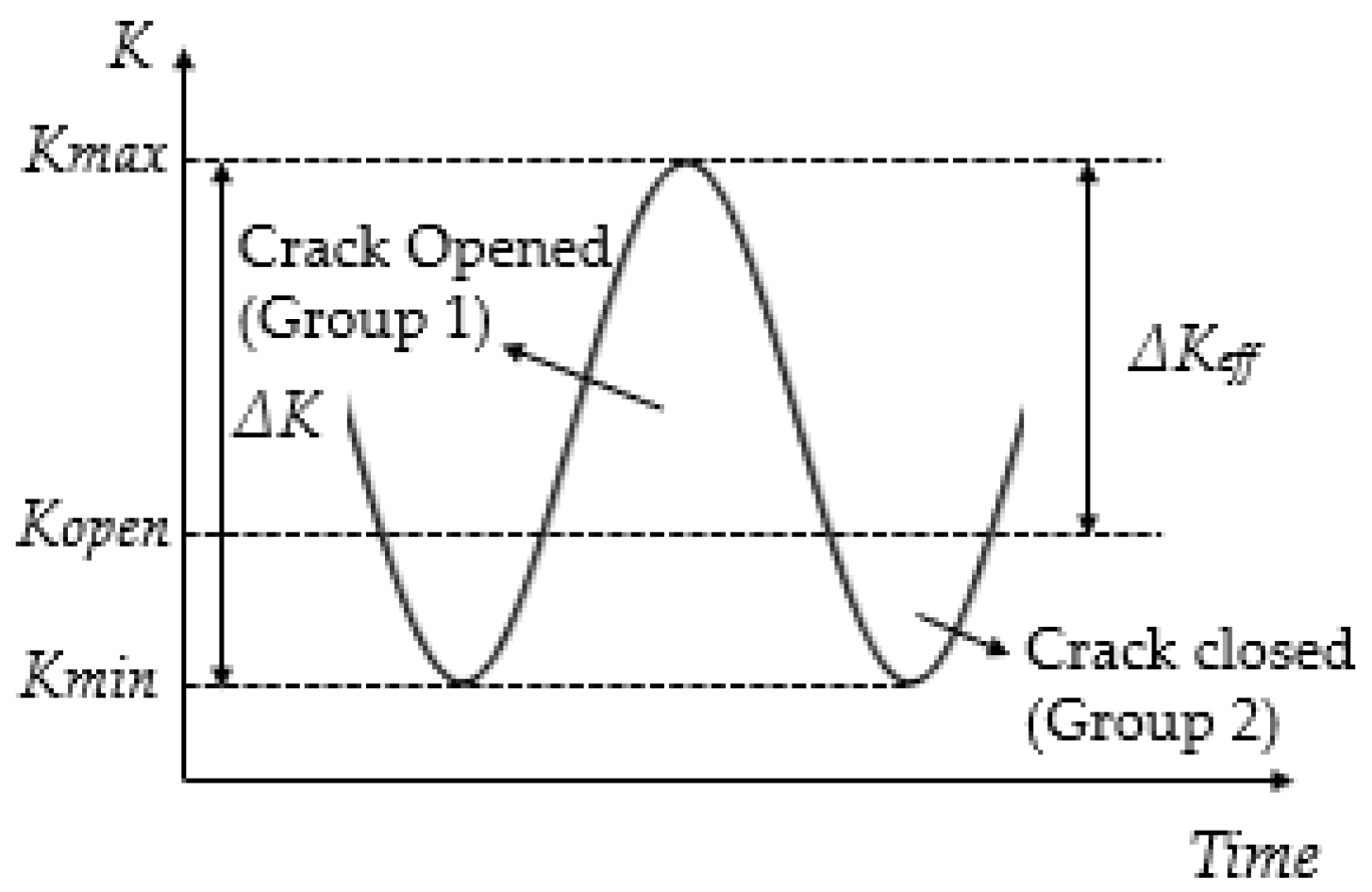
- The AE data collected are divided into two groups based on crack open and closure conditions at different crack lengths, and the corresponding dominant peak frequency of each group is presented to provide a basis of the waveform selection. Understanding AE waveforms from different sources also helps with AE source characterisation.
- The methodology in the current research can be extended and applied to other metallic materials.
2. Materials and Methods
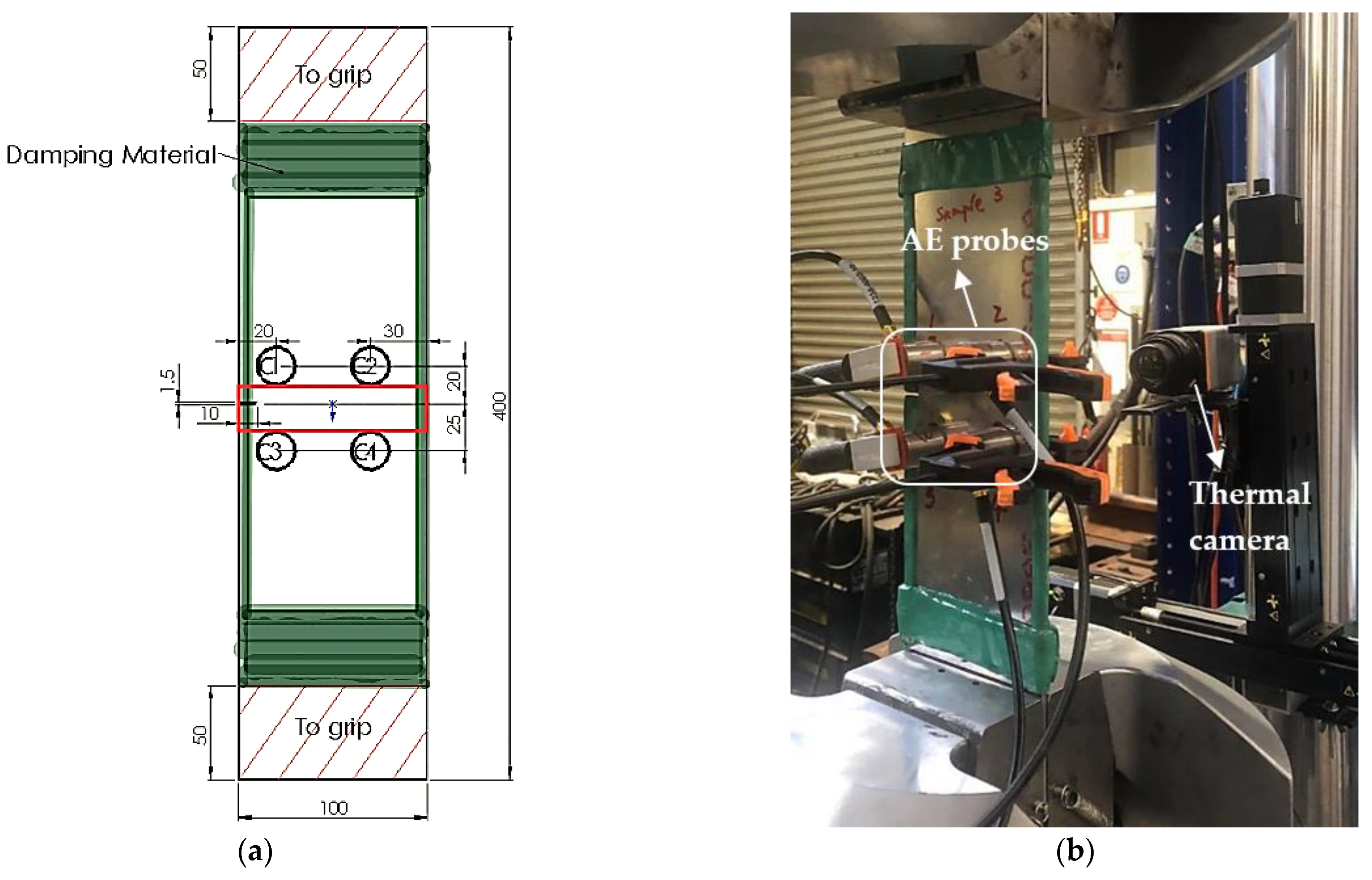
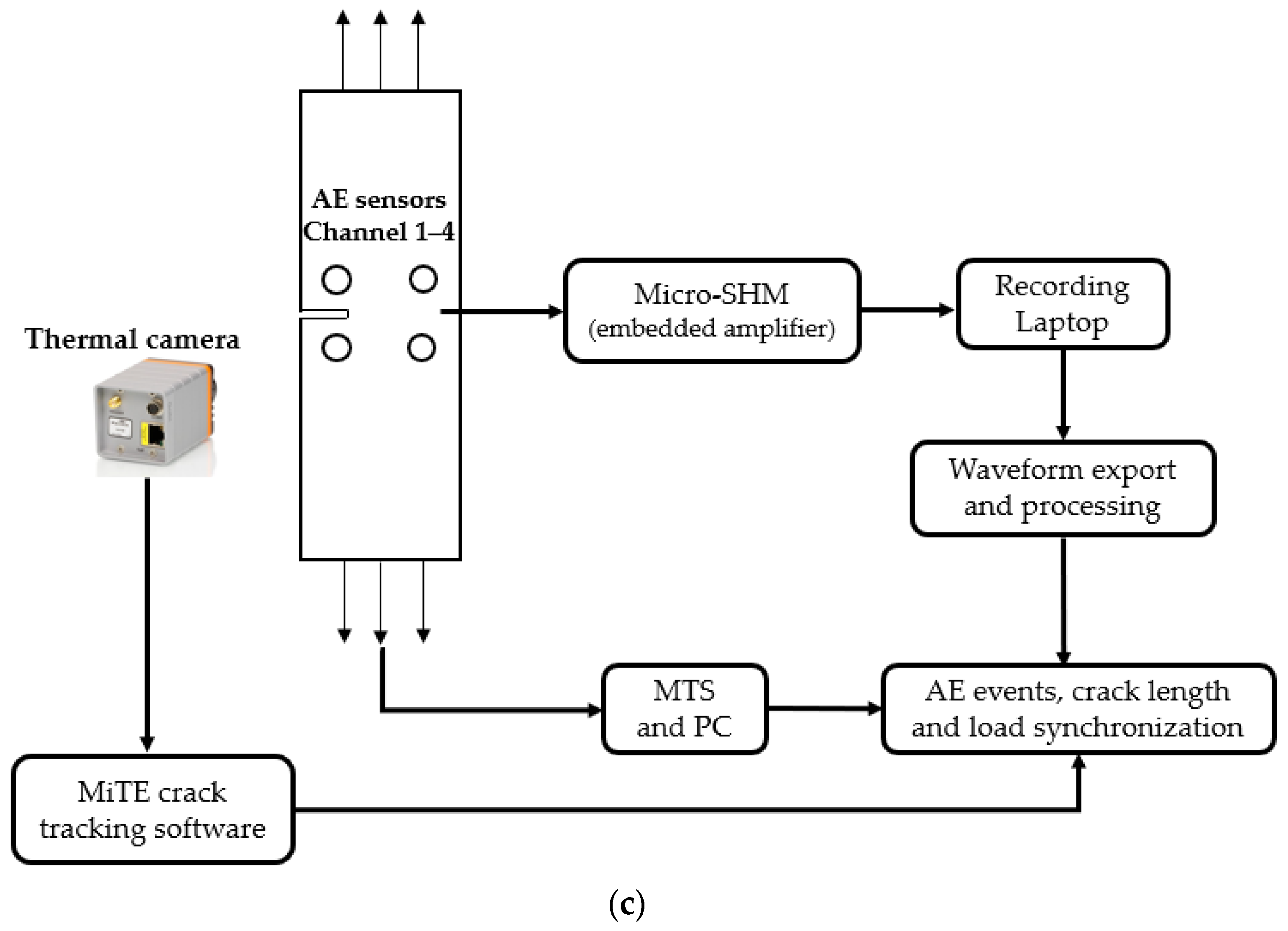
2.1. Experimental Set-Up and Equipment
2.2. Data Processing
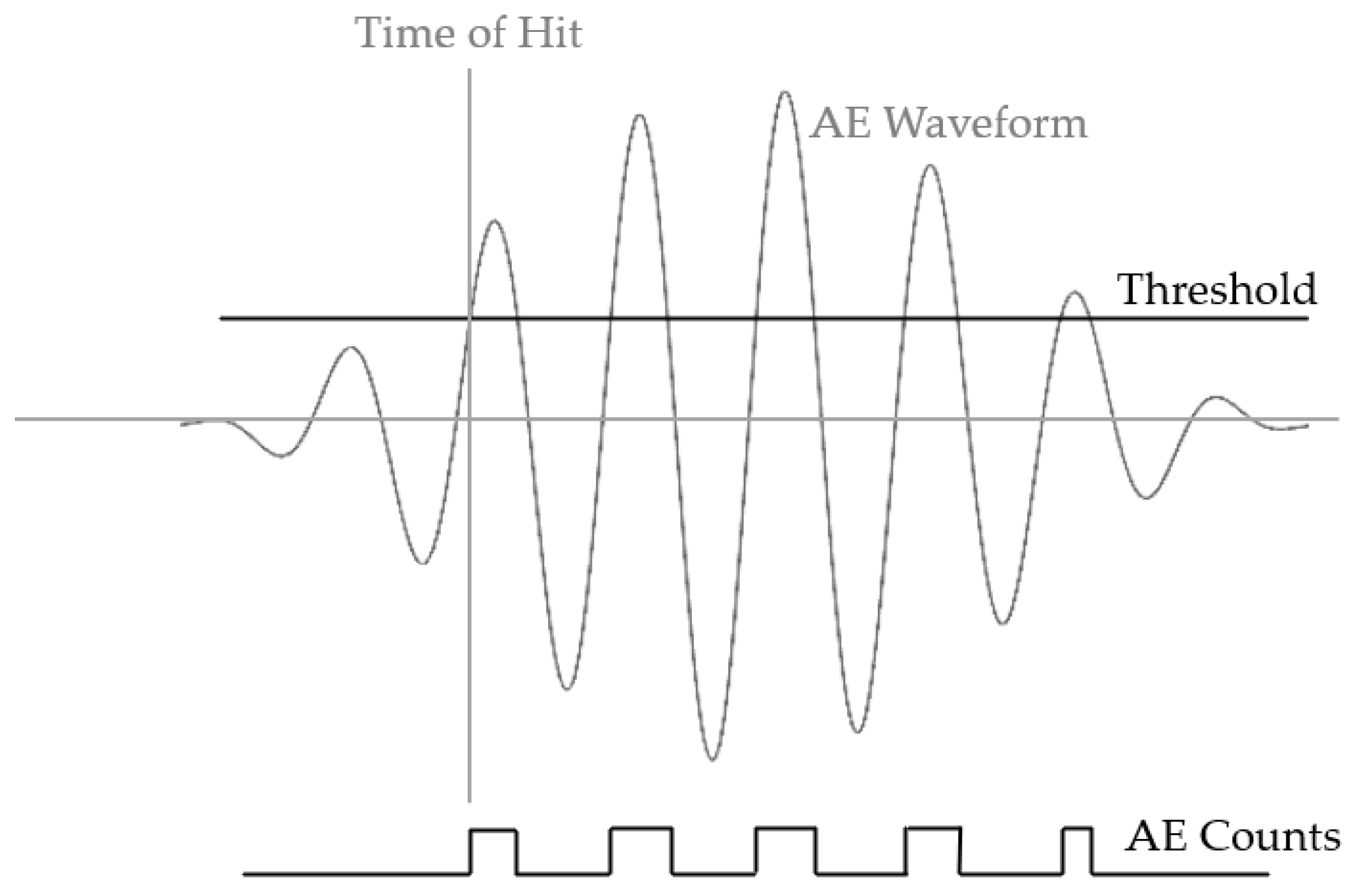
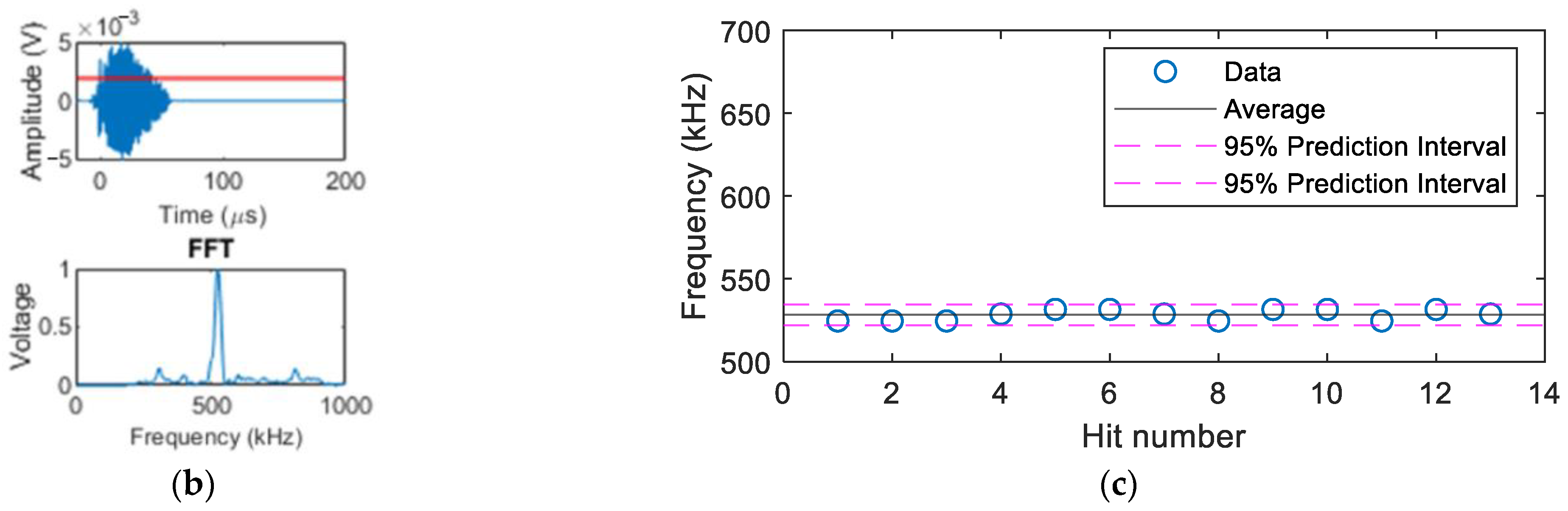
2.2.1. Processing of AE Waveforms
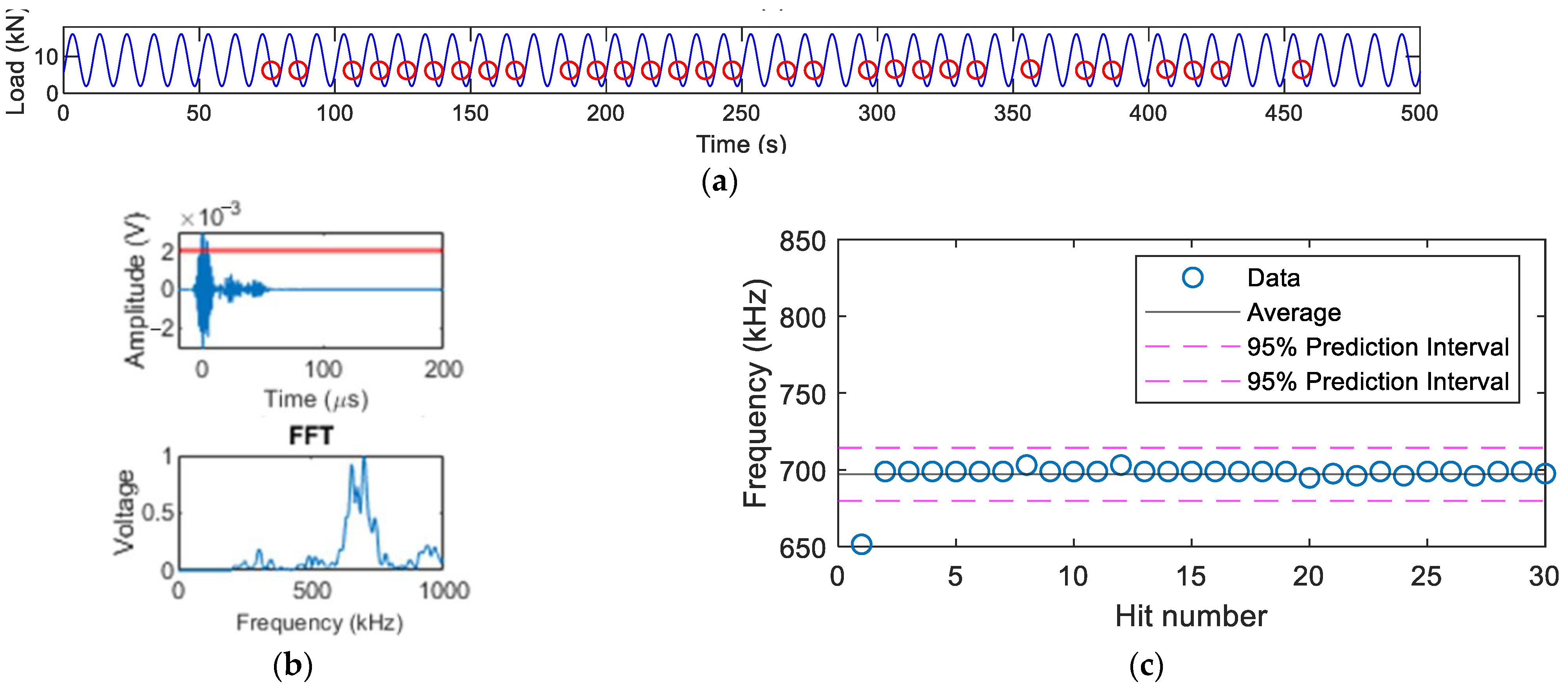
2.2.2. Synchronisation of AE Hits with Load
3. Results and Discussion
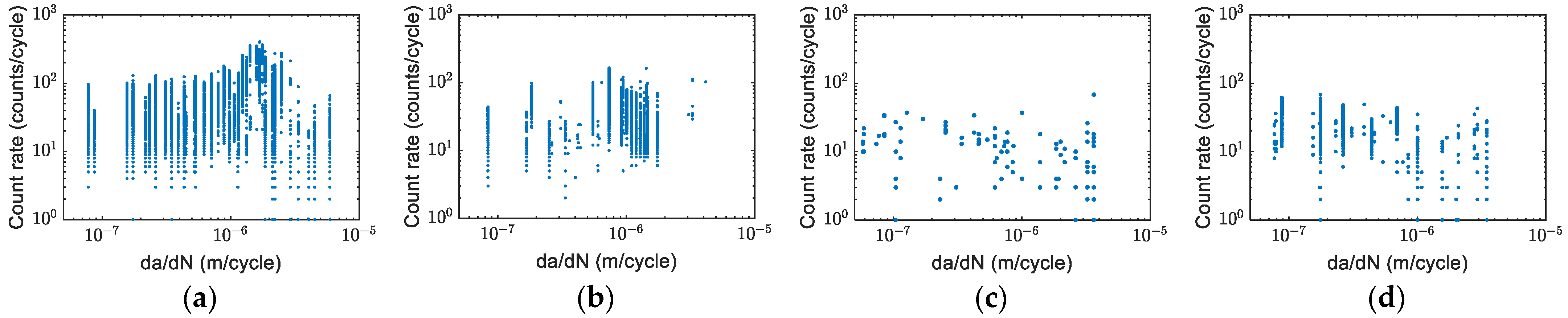
3.1. Fatigue Crack Growth and Count Rate
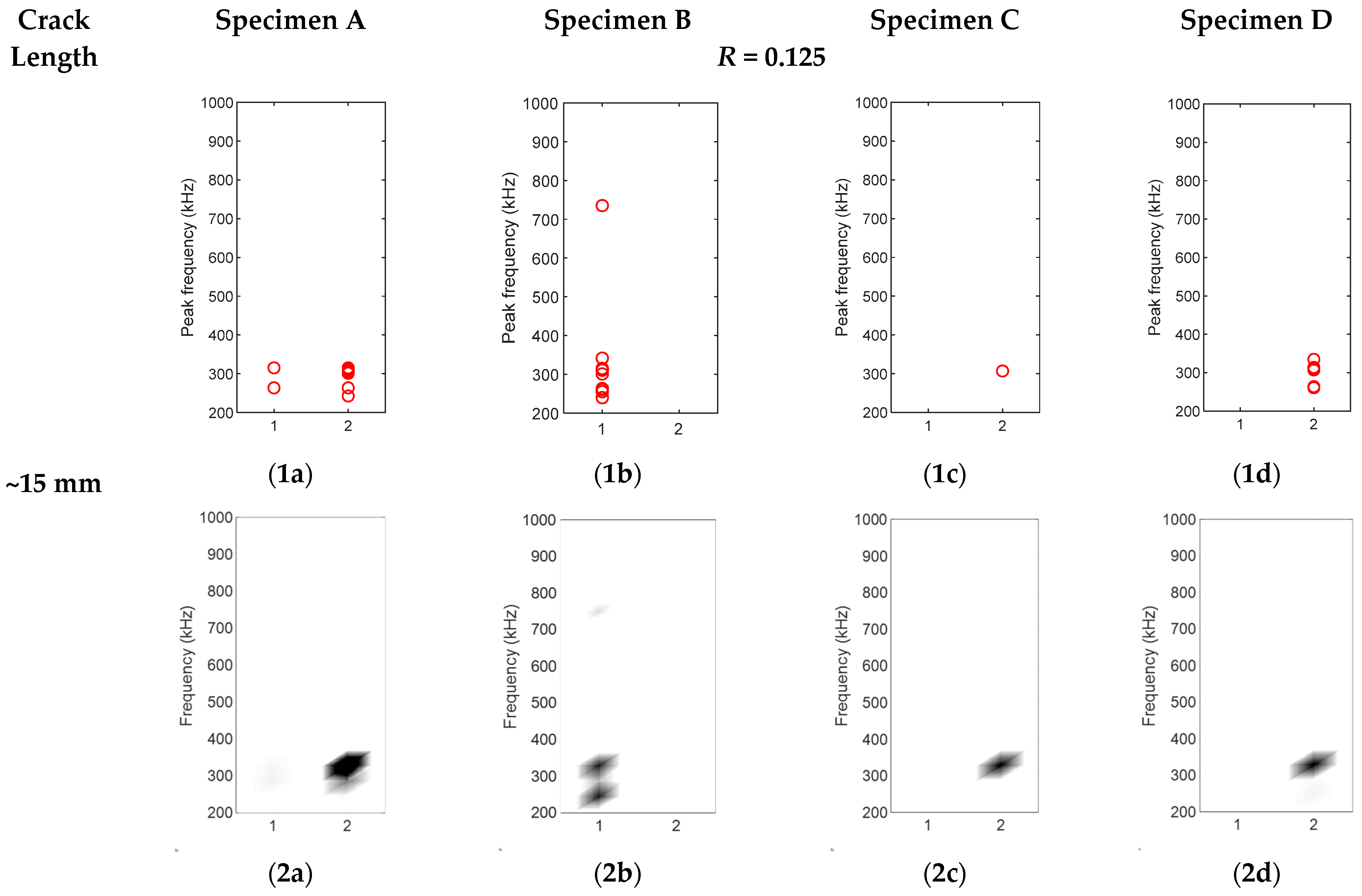
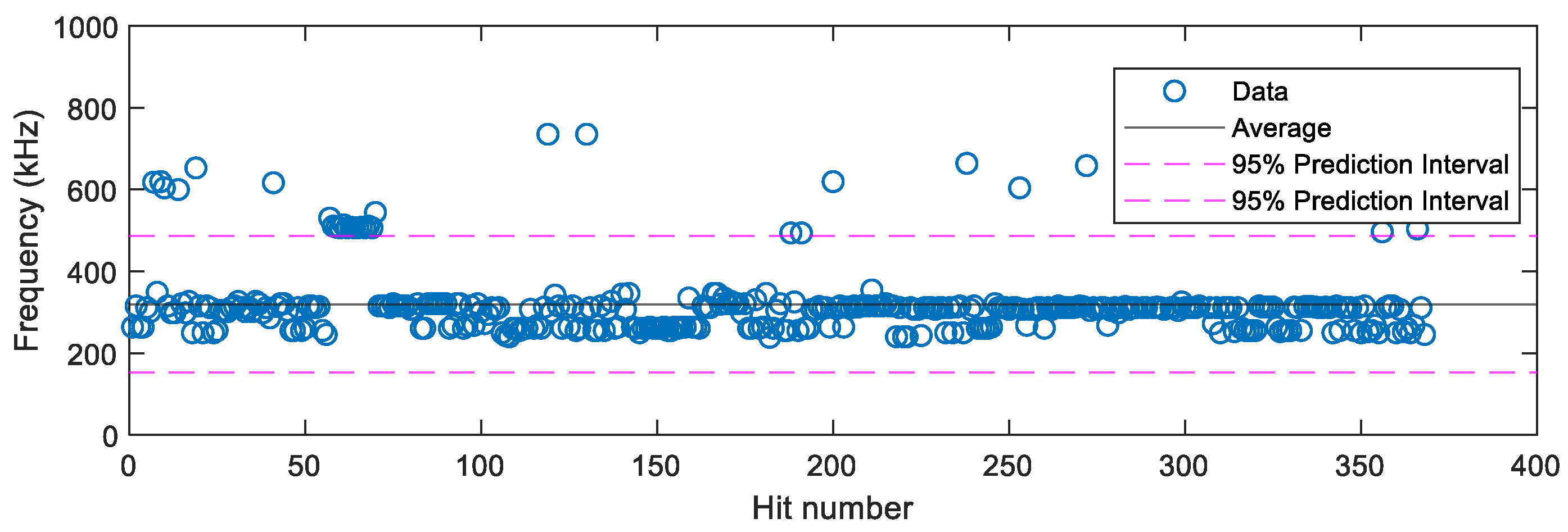
3.2. Source Characterisation of Synchronised Hits
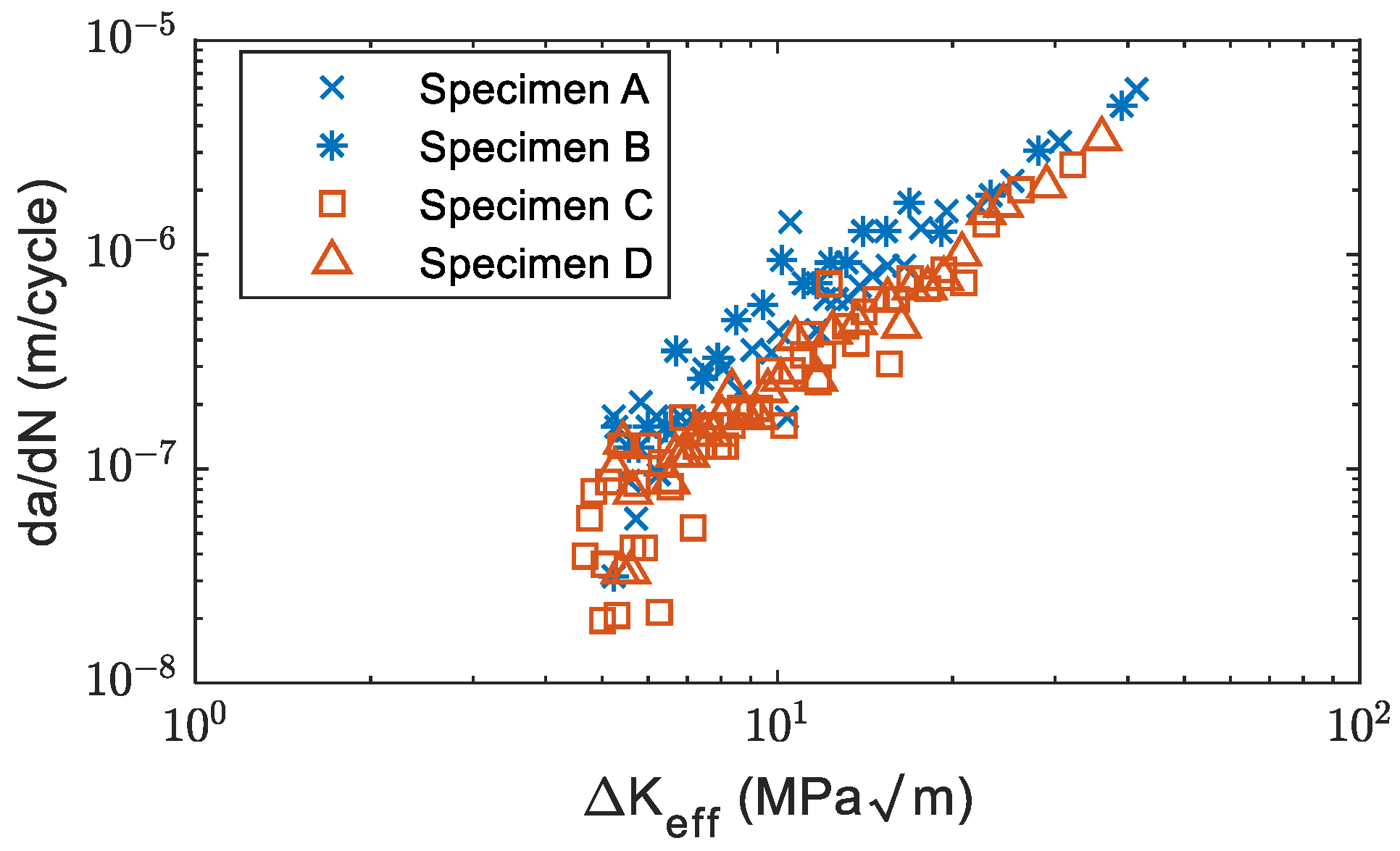
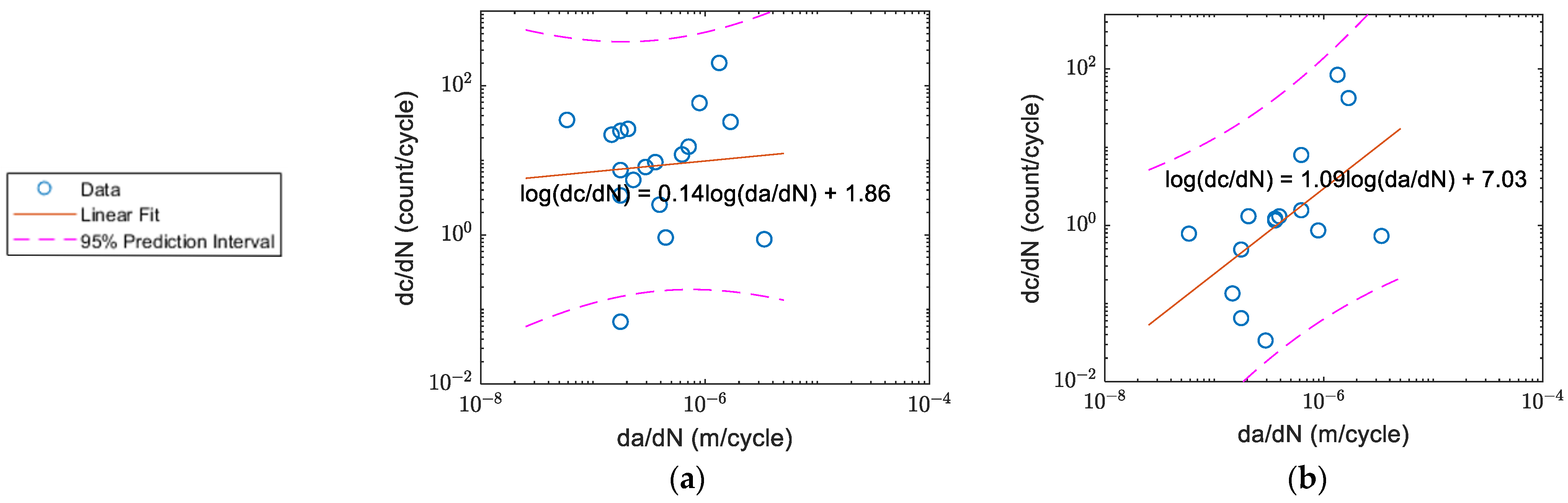
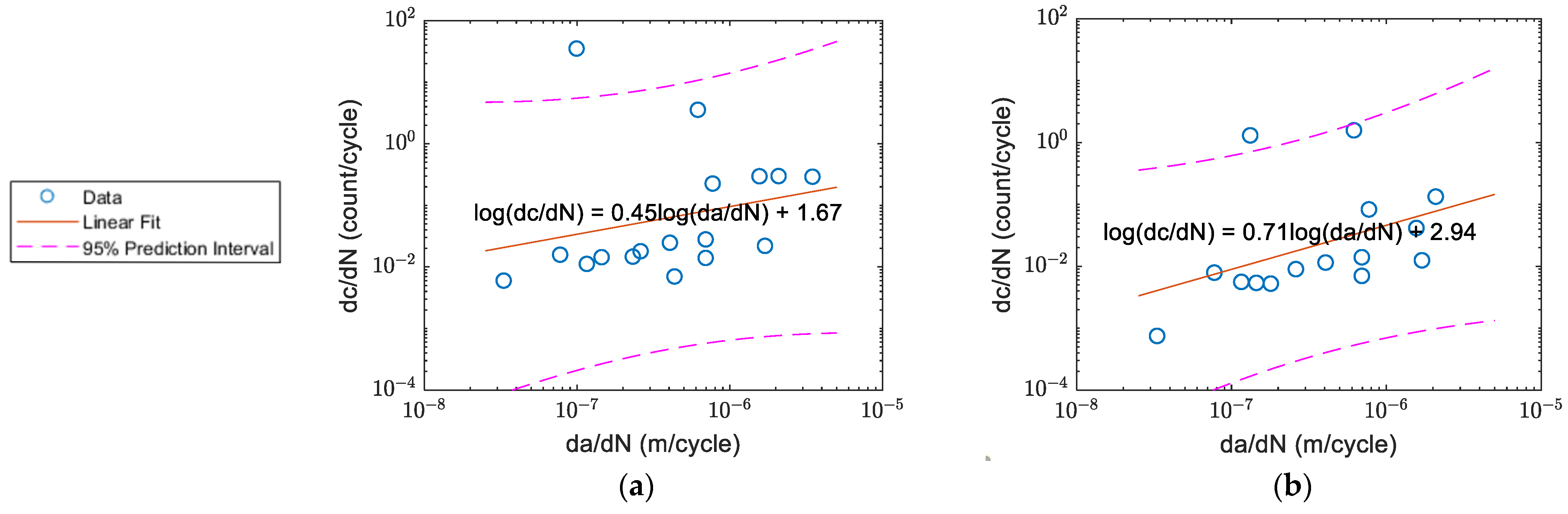
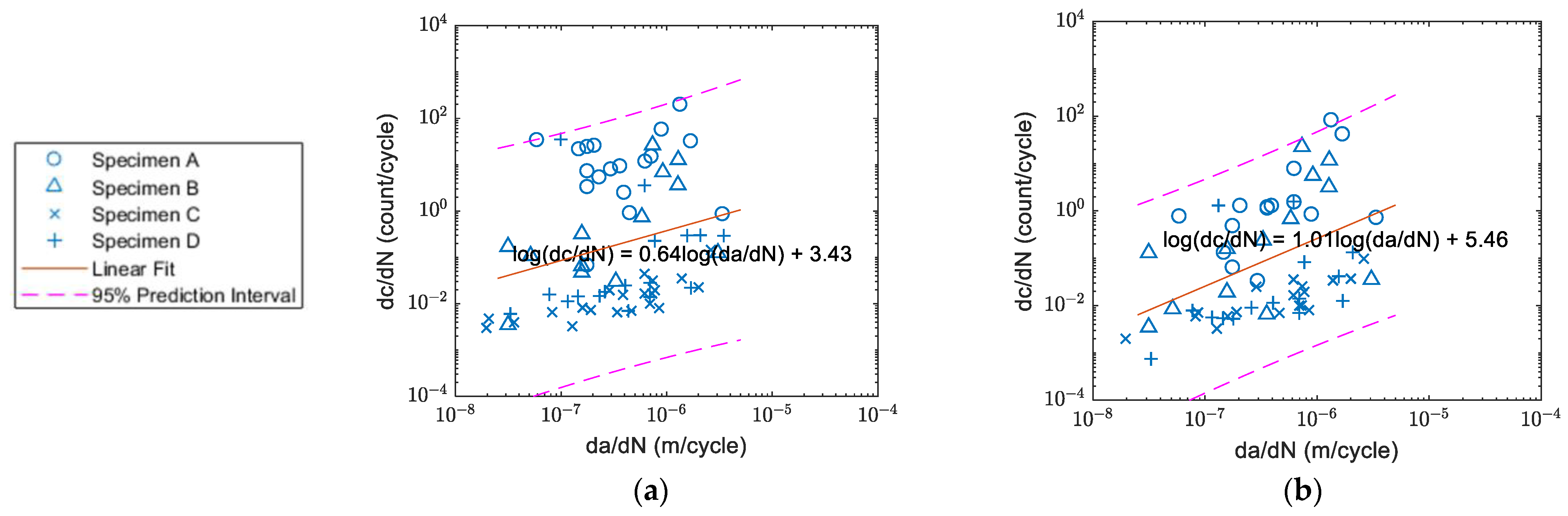
3.3. The Linear Relationship between Count Rate and Crack Growth Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mouritz, A.P. Introduction to Aerospace Materials; Woodhead Publishing Limited: Sawston, UK, 2012. [Google Scholar]
- Cousland, S.M.K.; Scala, C.M. Acoustic emission from the aluminium alloy 6061-T651. J. Mater. Sci. Lett. 1984, 3, 268–270. [Google Scholar] [CrossRef]
- Roberts, T.M.; Talebzadeh, M. Acoustic emission monitoring of fatigue crack propagation. J. Constr. Steel Res. 2003, 59, 659–712. [Google Scholar] [CrossRef]
- Chang, H.; Han, E.; Wang, J.Q.; Ke, W. Acoustic emission study of corrosion fatigue crack propagation mechanism for LY12CZ and 7075-T6 aluminum alloys. J. Mater. Sci. 2005, 40, 5669–5674. [Google Scholar] [CrossRef]
- Bhuiyan, M.Y.; Giurgiutiu, V. The signatures of acoustic emission waveforms from fatigue crack advancing in thin metallic plates. Smart Mater. Struct. 2018, 27, 015019. [Google Scholar] [CrossRef]
- Wisner, B.; Kontsos, A. In situ monitoring of particle fracture in aluminium alloys. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 581–596. [Google Scholar] [CrossRef]
- Jeong, S.-M.; Hong, S.; Oh, J.-S. A New Fracture Detection Algorithm of Low Amplitude Acoustic Emission Signal Based on Kalman Filter-Ripple Voltage. Sensors 2021, 21, 4247. [Google Scholar] [CrossRef]
- Yu, S.; Fan, C.; Zhao, Y. Hypervelocity Impact Detection and Location for Stiffened Structures Using a Probabilistic Hyperbola Method. Sensors 2022, 22, 3003. [Google Scholar] [CrossRef]
- MISTRAS Group Inc. Micro-SHM User’s Manual; MISTRAS Group: Junction, NJ, USA, 2017. [Google Scholar]
- Scala, C.M.; Cousland, S.M. Acoustic Emission during Fatigue Crack Propagation in the Aluminium Alloys 2024 and 2124. Mater. Sci. Eng. 1983, 61, 211–218. [Google Scholar] [CrossRef]
- Yu, J.; Ziehl, P.; Zárate, B.; Caicedo, J. Prediction of fatigue crack growth in steel bridge components using acoustic emission. J. Constr. Steel Res. 2011, 67, 1254–1260. [Google Scholar] [CrossRef]
- Gagar, D.; Foote, P.; Irving, P. A novel closure based approach for fatigue crack length estimation using the acoustic emission technique in structural health monitoring applications. Smart Mater. Struct. 2014, 23, 105033. [Google Scholar] [CrossRef]
- Chai, M.; Zhang, Z.; Duan, Q. A new qualitative acoustic emission parameter based on Shannon’s entropy for damage monitoring. Mech. Syst. Signal Process. 2018, 100, 617–629. [Google Scholar] [CrossRef]
- D’Angela, D.; Ercolino, M. Acoustic emission entropy: An innovative approach for structural health monitoring of fracture-critical metallic components subjected to fatigue loading. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1041–1058. [Google Scholar] [CrossRef]
- Hassan, F.; Mahmood, A.K.B.; Yahya, N.; Saboor, A.; Abbas, M.Z.; Khan, Z.; Rimsan, M. State-of-the-Art Review on the Acoustic Emission Source Localization Techniques. IEEE Access 2021, 9, 101246–101266. [Google Scholar] [CrossRef]
- Hamstad, M. Acoustic emission signals generated by monopole (pencil lead break) versus dipole sources: Finite element modeling and experiments. J. Acoust. Emiss. 2007, 25, 92–106. [Google Scholar]
- Maslouhi, A. Fatigue crack growth monitoring in aluminum using acoustic emission and acousto-ultrasonic methods. Struct. Control. Health Monit. 2011, 18, 790–806. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Kordatos, E.Z.; Matikas, T.E. Acoustic emission for fatigue damage characterization in metal plates. Mech. Res. Commun. 2011, 38, 106–110. [Google Scholar] [CrossRef]
- Cousland, S.M.; Scala, C. Acoustic emission during the plastic deformation of aluminium alloys 2024 and 2124. Mater. Sci. Eng. 1983, 57, 23–29. [Google Scholar] [CrossRef]
- Joseph, R.; Giurgiutiu, V. Analytical and Experimental Study of Fatigue-Crack-Growth AE Signals in Thin Sheet Metals. Sensors 2020, 20, 5835. [Google Scholar] [CrossRef]
- Joseph, R.; Bhuiyan, M.Y.; Giurgiutiu, V. Acoustic emission from vibration of cracked sheet-metal samples. Eng. Fract. Mech. 2019, 217, 106544. [Google Scholar] [CrossRef]
- Wisner, B.; Mazur, K.; Perumal, V.; Baxevanakis, K.P.; An, L.; Feng, G.; Kontsos, A. Acoustic emission signal processing framework to identify fracture in aluminum alloys. Eng. Fract. Mech. 2019, 210, 367–380. [Google Scholar] [CrossRef]
- Pomponi, E.; Vinogradov, A. A real-time approach to acoustic emission clustering. Mech. Syst. Signal Process. 2013, 40, 791–804. [Google Scholar] [CrossRef]
- Han, Z.; Luo, H.; Sun, C.; Li, J.; Papaelias, M.; Davis, C. Acoustic emission study of fatigue crack propagation in extruded AZ31 magnesium alloy. Mater. Sci. Eng. A 2014, 597, 270–278. [Google Scholar] [CrossRef]
- Li, D.; Kuang, K.S.C.; Koh, C.G. Fatigue crack sizing in rail steel using crack closure-induced acoustic emission waves. Meas. Sci. Technol. 2017, 28, 065601. [Google Scholar] [CrossRef]
- Chai, M.; Hou, X.; Zhang, Z.; Duan, Q. Identification and prediction of fatigue crack growth under different stress ratios using acoustic emission data. Int. J. Fatigue 2022, 160, 106860. [Google Scholar] [CrossRef]
- Rajic, N.; Rowlands, D. Thermoelastic stress analysis with a compact low-cost microbolometer system. Quant. InfraRed Thermogr. J. 2013, 10, 135–158. [Google Scholar] [CrossRef]
- Rajic, N.; Brooks, C. Automated Crack Detection and Crack Growth Rate Measurement Using Thermoelasticity. Procedia Eng. 2017, 188, 463–470. [Google Scholar] [CrossRef]
- Elber, W. Fatigue Crack Closure under Cyclic Tension. Eng. Fract. Mech. 1970, 2, 37–45. [Google Scholar]
- Newman, J.C., Jr. A crack opening stress equation for fatigue crack growth. Int. J. Fract. 1984, 24, R131–R135. [Google Scholar] [CrossRef]
- Rice, J.R. Mechanics of Crack Tip Deformation and Extension by Fatigue. In Fatigue Crack Propagation; ASTM STP 415; Springer: Berlin/Heidelberg, Germany, 1967; pp. 247–311. [Google Scholar]
- Correia, J.A.; De Jesus, A.M.; Moreira, P.M.; Tavares, P.J. Crack closure effects on fatigue crack propagation rates: Application of a proposed theoretical model. Adv. Mater. Sci. Eng. 2016, 2016, 3026745. [Google Scholar] [CrossRef]
- Volpe, J.A. Damage Tolerance Assessment Handbook; Research and Special Programs Administration, National Transportation Systems Center: Camgridge, MA, USA, 1993.
- Chandran, K.S.R. A new approach to the mechanics of fatigue crack growth in metals: Correlation of mean stress (stress ratio) effects using the change in net-section strain energy. Acta Mater. 2017, 135, 201–214. [Google Scholar] [CrossRef]









| Authors | Metallic Material | Sources | Frequency Contents |
|---|---|---|---|
| Bhuiyan and Giurgiutiu [5] | Al2024-T3 | Crack extension | 100 kHz, 230 kHz, 450 kHz, and 550 kHz |
| Joseph, Bhuiyan, and Giurgiutiu [21] | Al2024-T3 | Rubbing and clapping at adjacent crack surfaces | 40 kHz, 100 kHz, and 300–400 kHz |
| Wisner et al. [22] | Al2024-T3 | Particle fracture | 450–550 kHz |
| Pomponi and Vinogradov [23] | CuZr alloy | Plastic deformation | 280–480 kHz |
| Ductile crack growth Particle fracture | 300–480 kHz 480–500 kHz | ||
| Han et al. [24] | AZ31 magnesium alloy | Twinning | 140 kHz, 250 kHz, and 370 kHz |
| Plastic events related to twinning | 150 kHz, 250 kHz, and 370 kHz | ||
| Crack extension | 150 kHz | ||
| Li, Kuang, and Koh [25] | Rail steel | Crack propagation | 100–350 kHz and 400–650 kHz |
| Crack closure | 100–350 kHz | ||
| Chai et al. [26] | 316LN stainless steel | Fatigue crack growth | 90–160 kHz |
| Crack Length | Specimen A and B | Specimen C and D | ||
|---|---|---|---|---|
| U | U | |||
| ~15 mm | R = 0.125 (for crack initiation) | |||
| 0.53 | 0.54 | 0.53 | 0.54 | |
| ~30 mm | R = 0.125 | R = 0.5 | ||
| 0.53 | 0.54 | 0.64 | 0.72 | |
| ~70 mm | R = 0.125 | R = 0.5 | ||
| 0.44 | 0.64 | 0.60 | 0.80 | |
| Specimens | Before the Selection | After the Selection |
|---|---|---|
| A | Slope | |
| 0.14 | 1.09 | |
| B | Slope | |
| 1.13 | 1.20 | |
| C | Slope | |
| 0.55 | 0.65 | |
| D | Slope | |
| 0.45 | 0.71 | |
| A, B, C, D | Slope | |
| 0.64 | 1.01 | |
| Standard error | ||
| 1.38 | 1.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Vien, B.S.; Davies, C.; Chiu, W.K. Acoustic Emission Source Characterisation during Fatigue Crack Growth in Al 2024-T3 Specimens. Sensors 2022, 22, 8796. https://doi.org/10.3390/s22228796
Yao X, Vien BS, Davies C, Chiu WK. Acoustic Emission Source Characterisation during Fatigue Crack Growth in Al 2024-T3 Specimens. Sensors. 2022; 22(22):8796. https://doi.org/10.3390/s22228796
Chicago/Turabian StyleYao, Xinyue, Benjamin Steven Vien, Chris Davies, and Wing Kong Chiu. 2022. "Acoustic Emission Source Characterisation during Fatigue Crack Growth in Al 2024-T3 Specimens" Sensors 22, no. 22: 8796. https://doi.org/10.3390/s22228796
APA StyleYao, X., Vien, B. S., Davies, C., & Chiu, W. K. (2022). Acoustic Emission Source Characterisation during Fatigue Crack Growth in Al 2024-T3 Specimens. Sensors, 22(22), 8796. https://doi.org/10.3390/s22228796








