A Novel Two-Axis Differential Resonant Accelerometer Based on Graphene with Transmission Beams
Abstract
:1. Introduction
2. Model Design and Establishment
2.1. Structure of Accelerometer
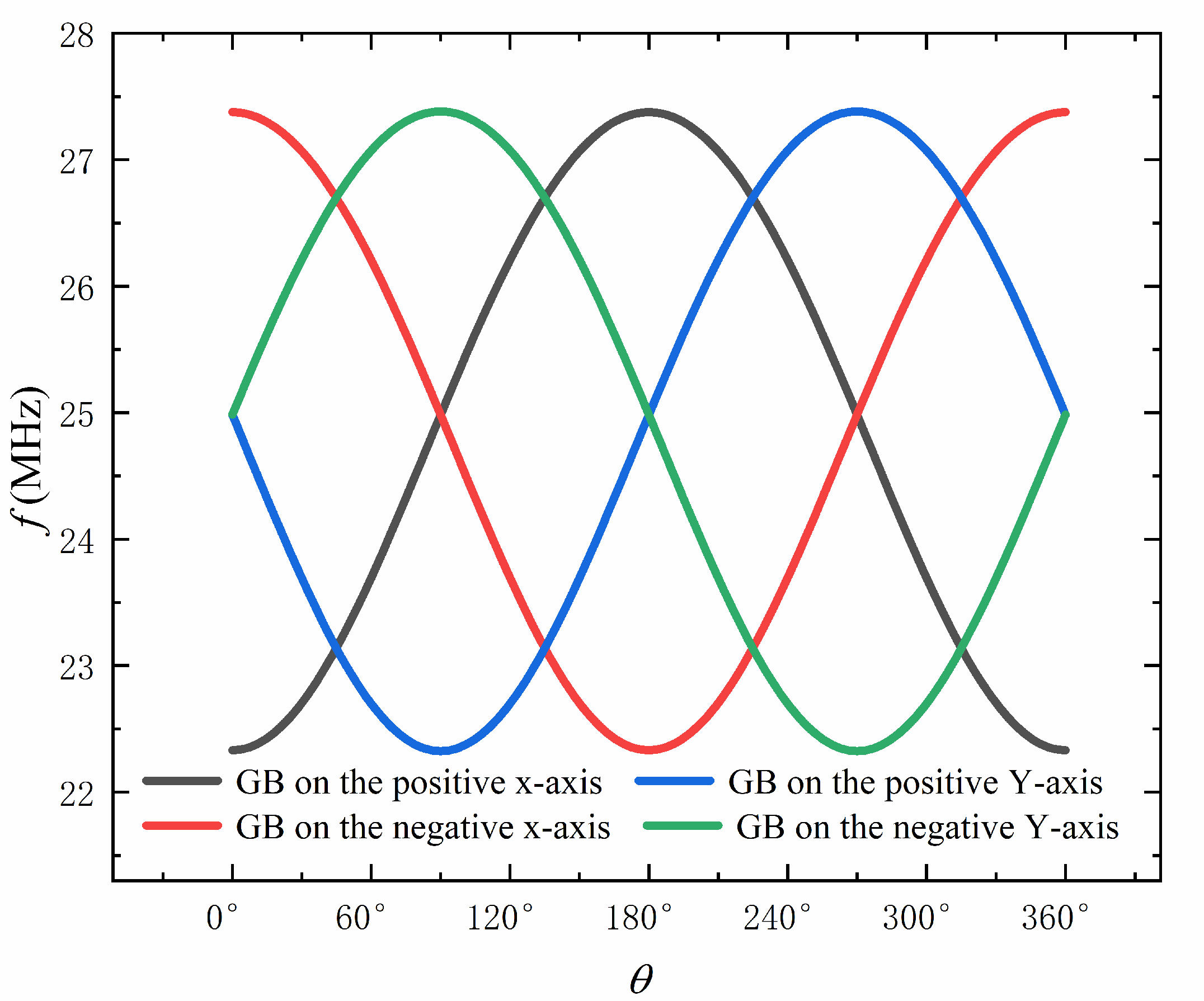
2.2. Working Principle of the Accelerometer
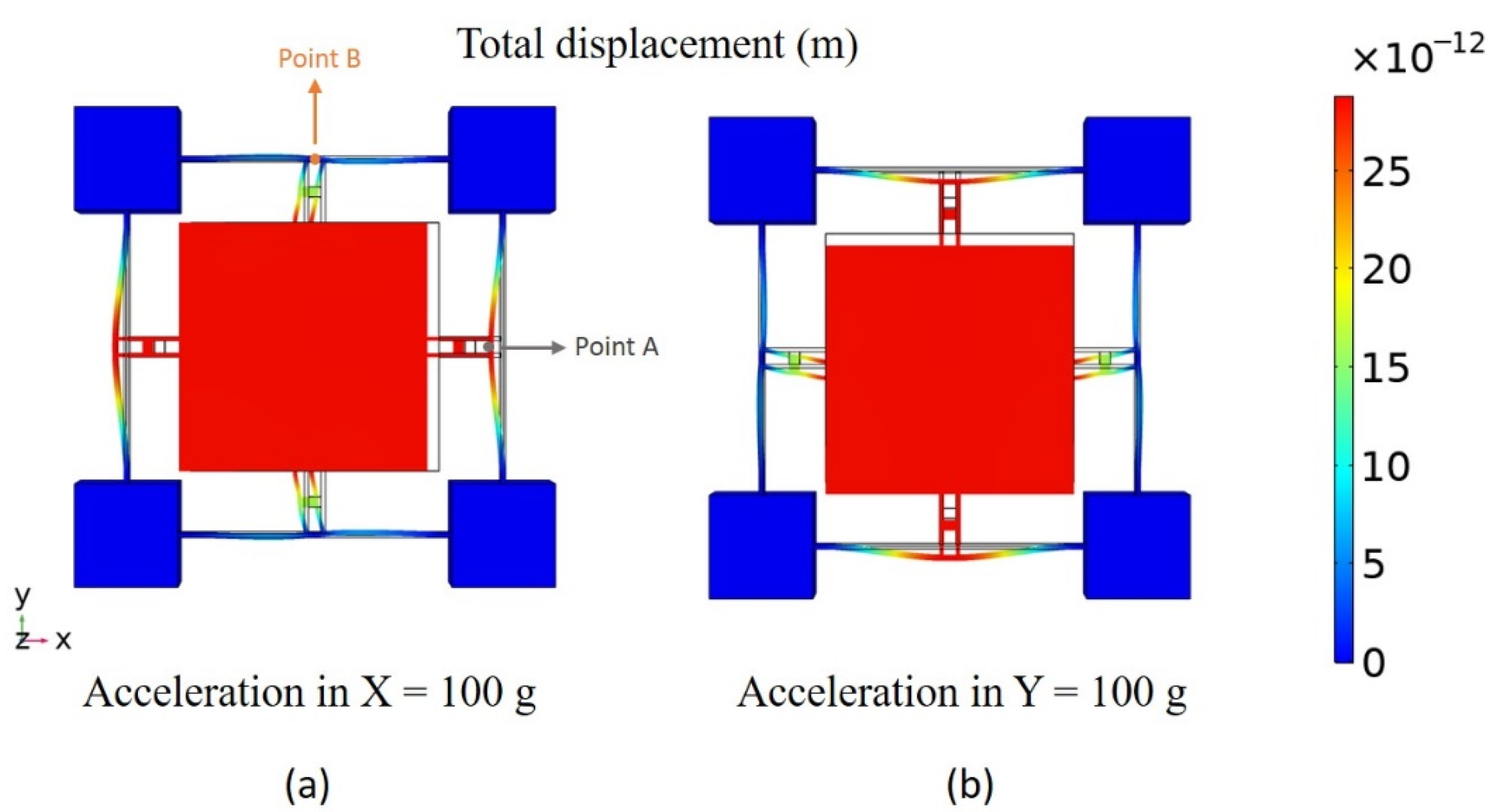
3. Modeling and Simulation
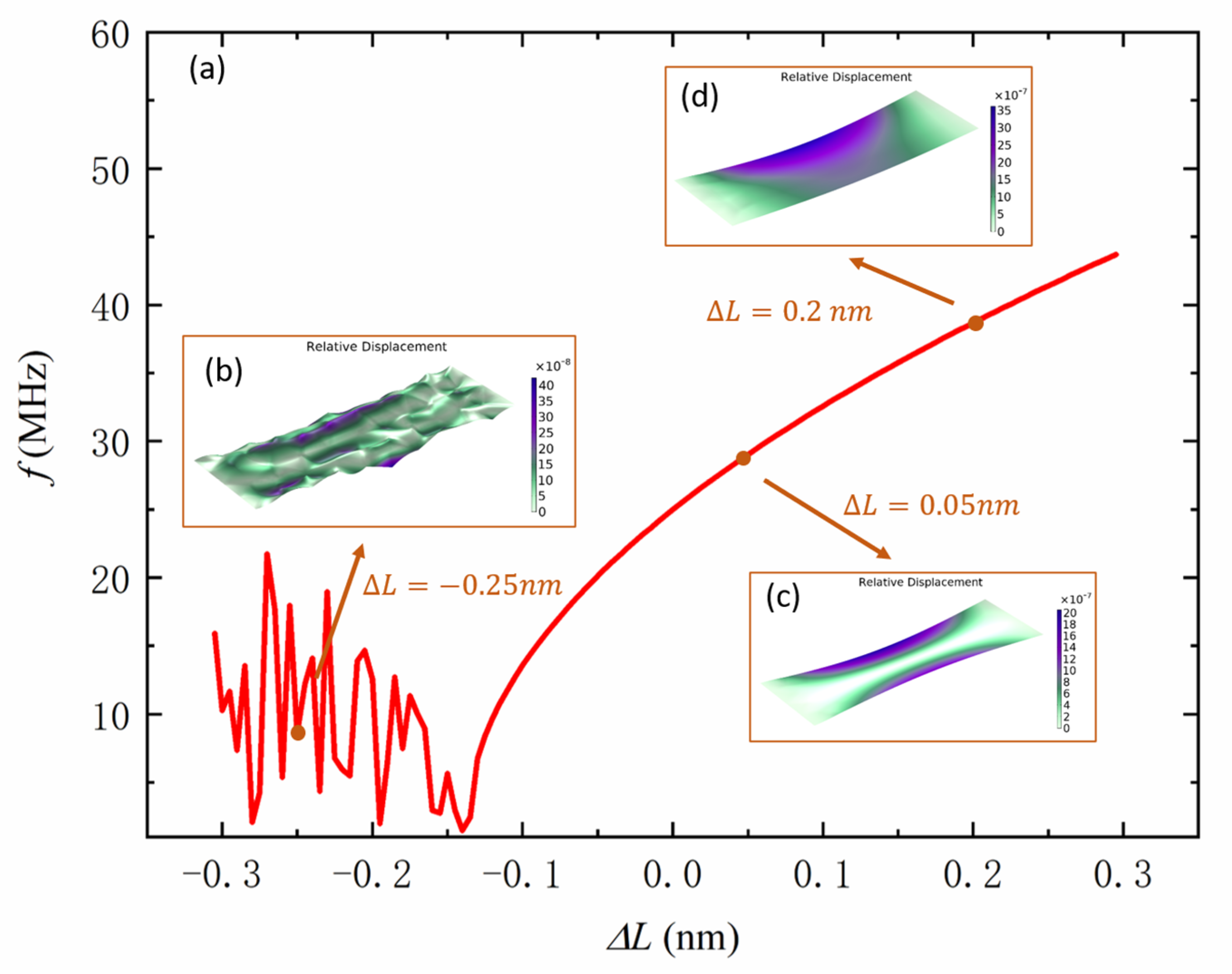
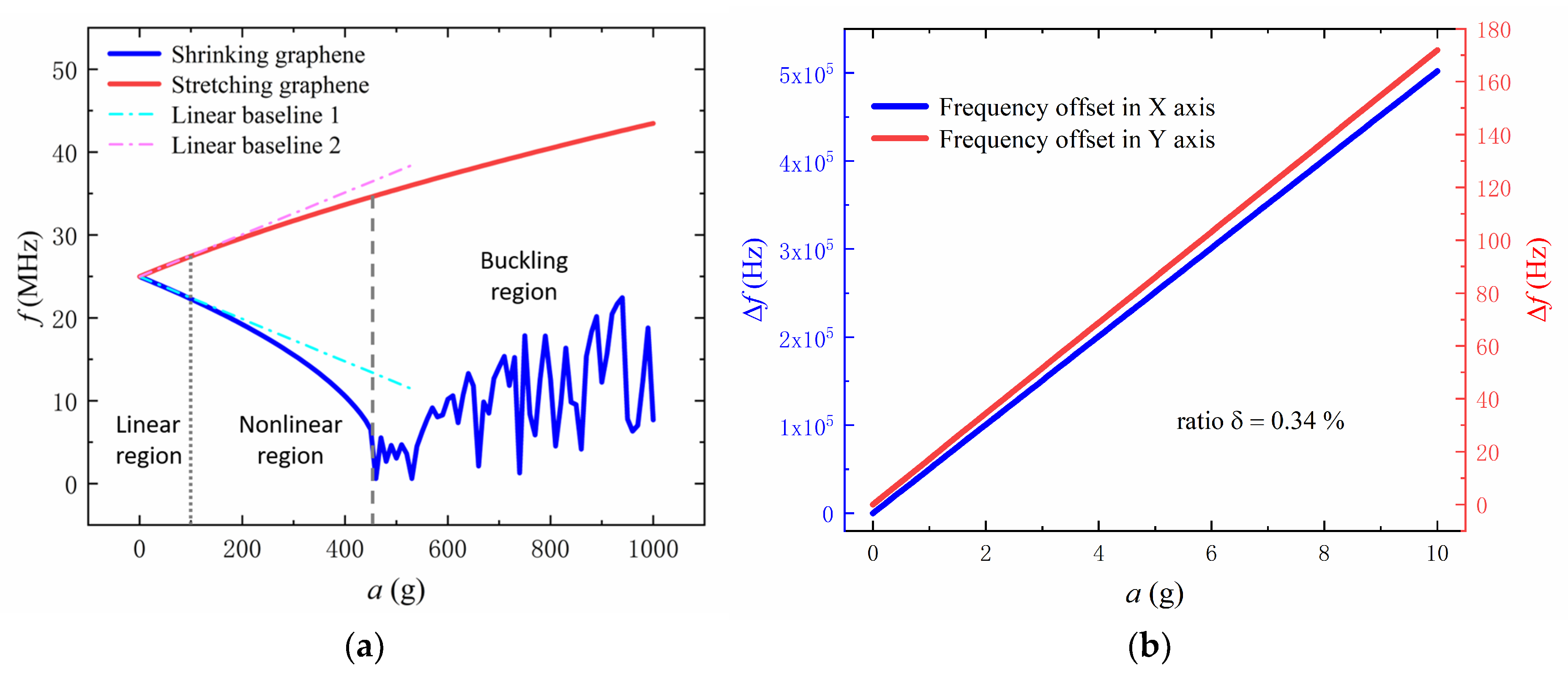
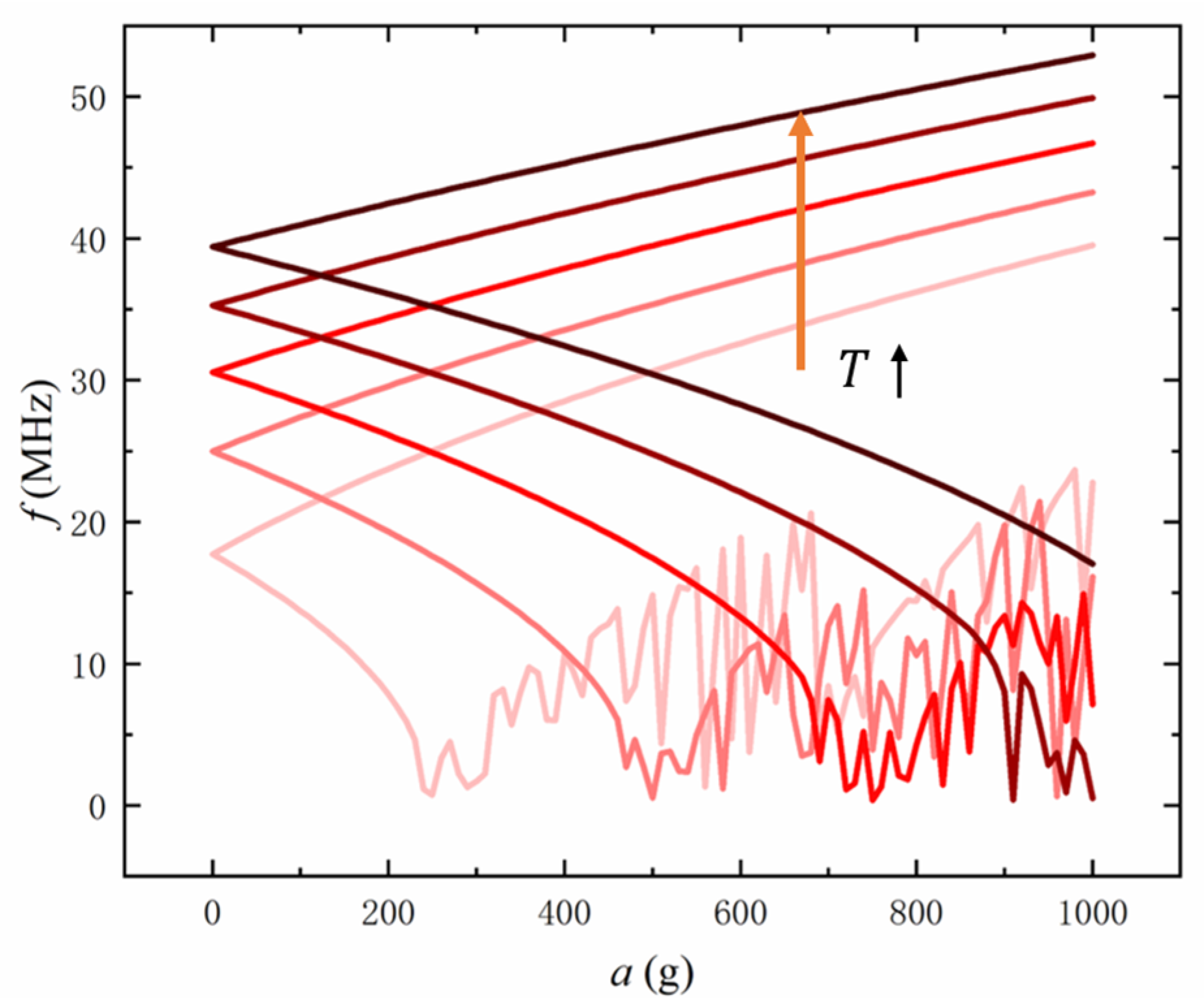
4. Optimization and Results
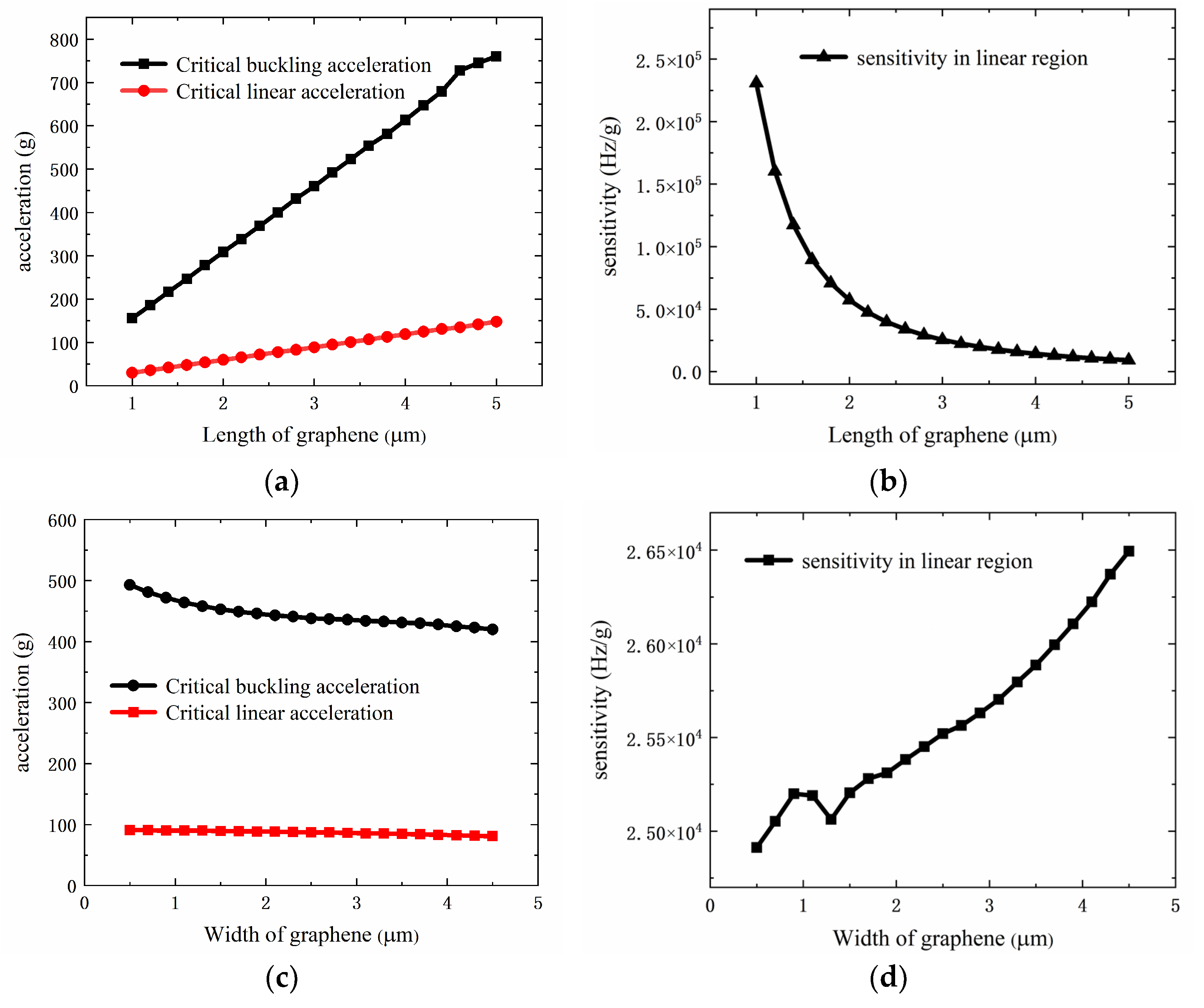
4.1. Parameter Optimization of Graphene Beam
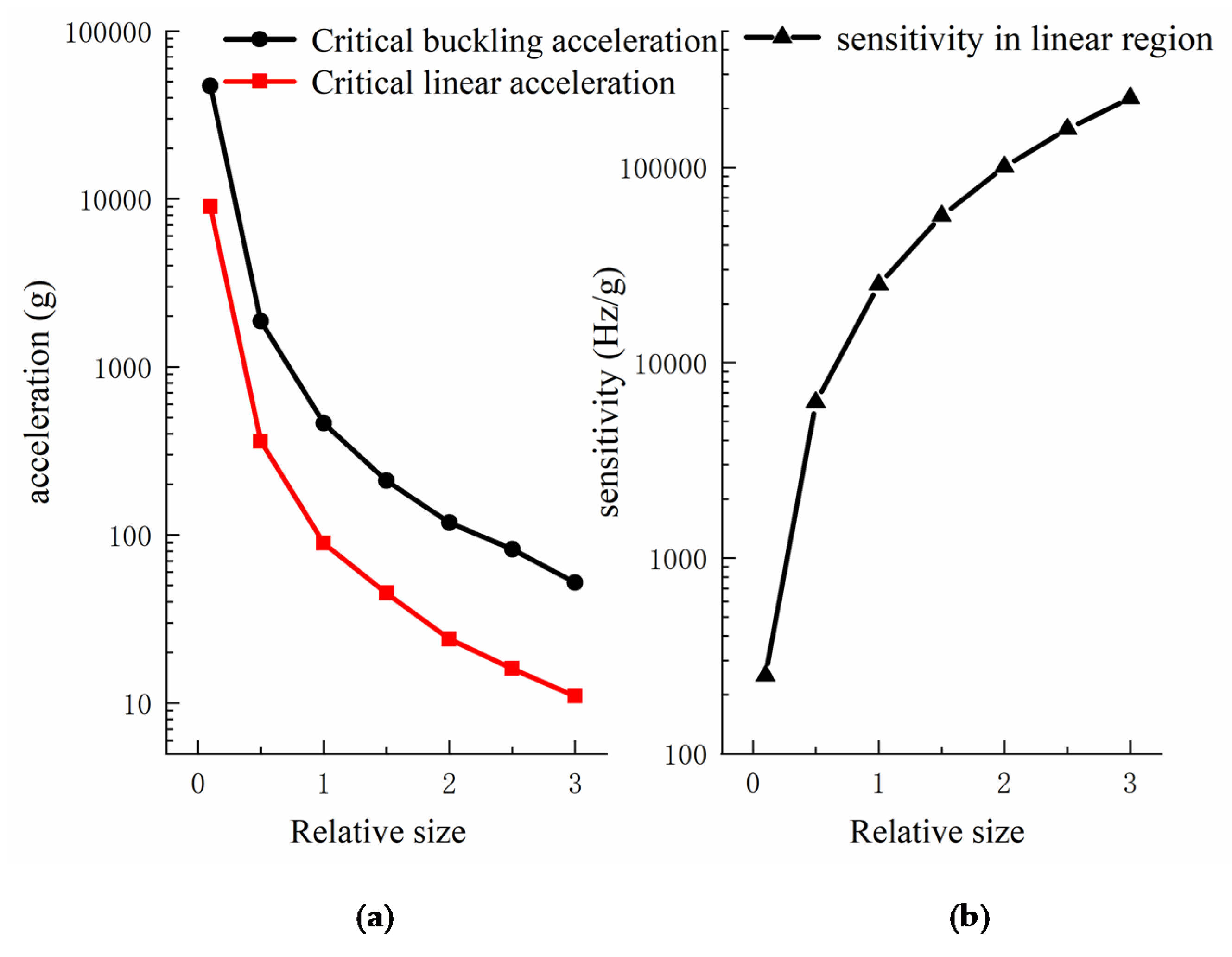
4.2. Size Optimization of Force Transfer Structure
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhao, Y.; Cheng, R.; Yu, Z.; Liu, Y. A resonant sensor composed of quartz double ended tuning fork and silicon substrate for digital acceleration measurement. Rev. Sci. Instrum. 2014, 85, 35004. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Si, C.; Han, G.; Zhao, Y.; Ning, J.; Yang, F. A Novel Fabrication Method for a Capacitive MEMS Accelerometer Based on Glass-Silicon Composite Wafers. Micromachines 2021, 12, 102. [Google Scholar] [CrossRef] [PubMed]
- Jency, J.G.; Sekar, M.; Sankar, A.R. Damping analysis of a quad beam MEMS piezoresistive accelerometer. Int. J. Model. Simul. 2021, 41, 256–264. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, B.; Cai, Y.; Liu, W.; Tovstopyat, A.; Sun, C. A Novel Tri-Axial Piezoelectric MEMS Accelerometer with Folded Beams. Sensors 2021, 21, 453. [Google Scholar] [CrossRef]
- Han, C.; Li, C.; Zhao, Y.; Li, B. High-Stability Quartz Resonant Accelerometer with Micro-Leverages. J. Microelectromechanical Syst. 2021, 30, 184–192. [Google Scholar] [CrossRef]
- Chen, C.; Hone, J. Graphene Nanoelectromechanical Systems. Proc. IEEE 2013, 101, 1766–1779. [Google Scholar] [CrossRef]
- Butscher, S.; Milde, F.; Hirtschulz, M.; Malić, E.; Knorr, A. Hot electron relaxation and phonon dynamics in graphene. Appl. Phys. Lett. 2007, 91, 203103. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef] [Green Version]
- Guan, F.; Kumaravadivel, P.; Averin, D.V.; Du, X. Tuning strain in flexible graphene nanoelectromechanical resonators. Appl. Phys. Lett. 2015, 107, 193102. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Varshney, U.; Lu, Y. Electronic applications of graphene mechanical resonators. IET Circuits Devices Syst. 2015, 9, 413–419. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van Der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.W.; Lee, J.H.; Hwang, H.J.; Kim, K.S. Developing accelerometer based on graphene nanoribbon resonators. Phys. Lett. A 2012, 376, 3248–3255. [Google Scholar] [CrossRef]
- Kang, J.W.; Park, J.H.; Lee, G.Y.; Kim, K.S. Molecular Dynamics Simulation on Crossroad-Type Graphene-Resonator Accelerometer. J. Comput. Theor. Nanosci. 2015, 12, 4186–4190. [Google Scholar] [CrossRef]
- Byun, K.R.; Kim, K.S.; Hwang, H.J.; Kang, J.W. Sensitivity of Graphene-Nanoribbon-Based Accelerometer with Attached Mass. J. Comput. Theor. Nanosci. 2013, 10, 1886–1891. [Google Scholar] [CrossRef]
- Moreno, D.; Fan, X.; Niklaus, F.; Villanueva, L.G. Proof of Concept of a Graphene-Based Resonant Accelerometer. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021. [Google Scholar]
- Shi, F.T.; Fan, S.C.; Li, C.; Peng, X.B. Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors 2018, 18, 2266. [Google Scholar] [CrossRef] [Green Version]
- Beijing University of Aeronautics and Astronautics. A Resonant Graphene Biaxial Accelerometer. CN201710501462.5, 27 June 2017. [Google Scholar]
- Yang, B.; Wang, X.; Dai, B.; Liu, X. A new z-axis resonant micro-accelerometer based on electrostatic stiffness. Sensors 2015, 15, 687–702. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Fan, S.C.; Li, C.; Yu, C.F. Research progress of silicon resonant MEMS accelerometer. Transducer Microsyst. Technol. 2011, 30, 4–7. [Google Scholar]
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef] [Green Version]
- Fardindoost, S.; Alipour, A.; Mohammadi, S.; Gokyar, S.; Sarvari, R.; Demir, H.V. Flexible strain sensors based on electrostatically actuated graphene flakes. J. Micromech. Microeng. 2015, 25, 75016. [Google Scholar] [CrossRef]
- Ilic, B.; Krylov, S.; Craighead, H.G. Theoretical and experimental investigation of optically driven nanoelectromechanical oscillators. J. Appl. Phys. 2010, 107, 34311. [Google Scholar] [CrossRef]
- Wang, Q. Simulations of the bending rigidity of graphene. Phys. Lett. A 2010, 374, 1180–1183. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; van der Zande, A.M.; Paulo, A.S.; Lassagne, B.; McEuen, P.L.; Bachtold, A. Imaging Mechanical Vibrations in Suspended Graphene Sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, S.; Shi, S.; Wang, X. Nanomechanics and vibration analysis of graphene sheets via a 2D plate model. J. Phys. D Appl. Phys. 2014, 47, 45104. [Google Scholar] [CrossRef]
- Ang, W.T.; Khosla, P.K.; Riviere, C.N. Nonlinear Regression Model of a Low-g MEMS Accelerometer. IEEE Sens. J. 2007, 7, 81–88. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, C.; Cai, Q. An accurate calibration method for accelerometer nonlinear scale factor on a low-cost three-axis turntable. Meas. Sci. Technol. 2014, 25, 25102–25108. [Google Scholar] [CrossRef]
- Caspani, A.; Comi, C.; Corigliano, A.; Langfelder, G.; Tocchio, A. Compact biaxial micromachined resonant accelerometer. J. Micromech. Microeng. 2013, 23, 105012. [Google Scholar] [CrossRef]
- Ding, H.; Zhao, J.; Ju, B.F.; Xie, J. A high-sensitivity biaxial resonant accelerometer with two-stage microleverage mechanisms. J. Micromech. Microeng. 2015, 26, 15011. [Google Scholar] [CrossRef]
- Yang, B.; Zhao, H.; Dai, B.; Liu, X. A new silicon biaxial decoupled resonant micro-accelerometer. Microsyst. Technol. 2014, 21, 109–115. [Google Scholar] [CrossRef]
- Zhao, L.; Dai, B.; Yang, B.; Liu, X. Design and simulations of a new biaxial silicon resonant micro-accelerometer. Microsyst. Technol. 2016, 22, 2829–2834. [Google Scholar] [CrossRef]
- Chen, C.; Rosenblatt, S.; Bolotin, K.I.; Kalb, W.; Kim, P.; Kymissis, I.; Stormer, H.L.; Heinz, T.F.; Hone, J. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; Van Der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable atomic membranes from graphene sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef] [Green Version]
- Zande, A.M.; Barton, R.A.; Alden, J.S.; Ruiz-Vargas, C.S.; Whitney, W.S.; Pham, P.H.; Park, J.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Large-Scale Arrays of Single-Layer Graphene Resonators. Nano Lett. 2010, 10, 4869–4873. [Google Scholar] [CrossRef]
- Kwon, O.K.; Lee, J.H.; Park, J.; Kim, K.S.; Kang, J.W. Molecular dynamics simulation study on graphene-nanoribbon-resonators tuned by adjusting axial strain. Curr. Appl. Phys. 2013, 13, 360–365. [Google Scholar] [CrossRef]
- Jung, M.; Rickhaus, P.; Zihlmann, S.; Eichler, A.; Makk, P.; Schönenberger, C. GHz nanomechanical resonator in an ultraclean suspended graphene p–n junction. Nanoscale 2019, 11, 4355–4361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, V.P.; Li, X.; Guney, M.G.; Paramesh, J.; Mukherjee, T.; Fedder, G.K. Hourglass-beam Nanogram-proof-mass Array: Toward a High Dynamic Range Accelerometer. In Proceedings of the IEEE International Symposium on Inertial Sensors & Systems, Naples, FL, USA, 1–5 April 2019; IEEE: Piscataway Township, NJ, USA, 2019. [Google Scholar]
- Nam, K.B.; Yeo, J.H.; Hu, Q.; Kim, M.J.; Oh, B.; Yoo, J.B. Fabrication of extreme ultraviolet lithography pellicle with nanometer-thick graphite film by sublimation of camphor supporting layer. Nanotechnology 2021, 32, 465301. [Google Scholar] [CrossRef]

| Structure | |
|---|---|
| Proof mass | |
| H beam (the long) | |
| H beam (the short) | |
| Crossbeam | |
| The suspended part of graphene |
| Reference | Materials | Dimension | Volume | Sensitivity (Hz/g) | Cross Sensitivity |
|---|---|---|---|---|---|
| Caspani et al. [28] | Silicon-based | biaxial | |||
| Ding et al. [29] | Silicon-based | biaxial | |||
| Yang et al. [30] | Silicon-based | biaxial | (X-axis) (Y-axis) | (X-axis) (Y-axis) | |
| Shi et al. [16] | Graphene-based | uniaxial | - | ||
| Morenoet et al. [15] | Graphene-based | uniaxial | (proof mass) | 1935 | - |
| This work | Graphene-based | biaxial | 50,919 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Hu, F.; Zhang, Y.; Zheng, J.; Qin, S. A Novel Two-Axis Differential Resonant Accelerometer Based on Graphene with Transmission Beams. Sensors 2022, 22, 641. https://doi.org/10.3390/s22020641
Xiao Y, Hu F, Zhang Y, Zheng J, Qin S. A Novel Two-Axis Differential Resonant Accelerometer Based on Graphene with Transmission Beams. Sensors. 2022; 22(2):641. https://doi.org/10.3390/s22020641
Chicago/Turabian StyleXiao, Yang, Feng Hu, Yuchen Zhang, Jiaxing Zheng, and Shiqiao Qin. 2022. "A Novel Two-Axis Differential Resonant Accelerometer Based on Graphene with Transmission Beams" Sensors 22, no. 2: 641. https://doi.org/10.3390/s22020641
APA StyleXiao, Y., Hu, F., Zhang, Y., Zheng, J., & Qin, S. (2022). A Novel Two-Axis Differential Resonant Accelerometer Based on Graphene with Transmission Beams. Sensors, 22(2), 641. https://doi.org/10.3390/s22020641





