Shape–Texture Debiased Training for Robust Template Matching †
Abstract
:1. Introduction
- •
- We created a new benchmark; compared to the existing standard benchmark, it is more challenging, provides a far larger number of image pairs, and is better able to discriminate between the performance of different template matching methods.
- •
- By training a CNN to be more sensitive to shape information and combining features from both early and late layers, we created a feature space in which the performance of most template matching algorithms is improved.
- •
- Using this feature space together with an existing template matching method, DIM [30], we obtained state-of-art results on both the standard and new datasets.
2. Related Work
2.1. Template Matching
2.2. Deep Features
3. Methods
3.1. Training CNN with Stylised Data
3.2. DIM Template Matching Algorithm
4. Results
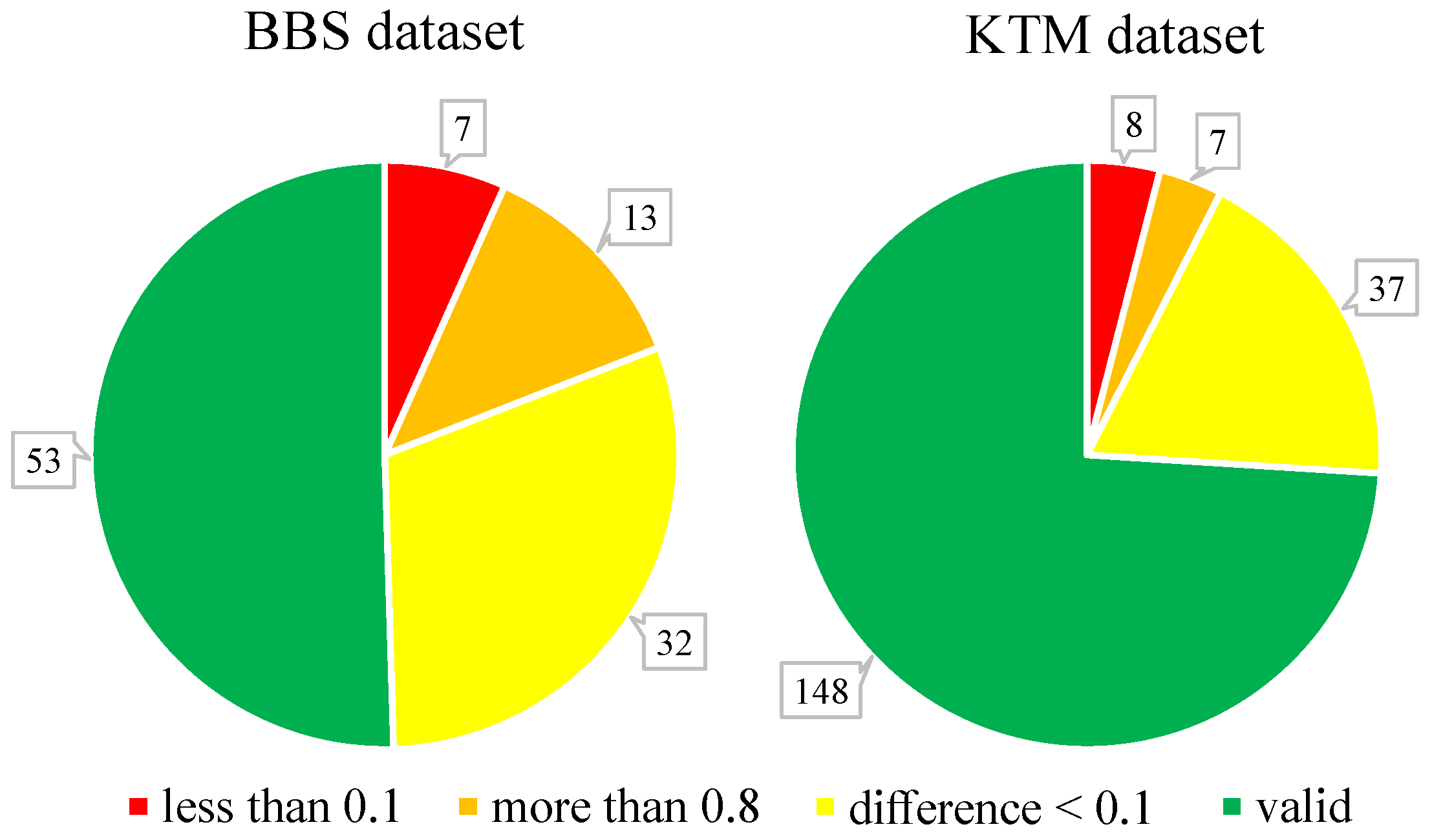
4.1. Dataset Preparation
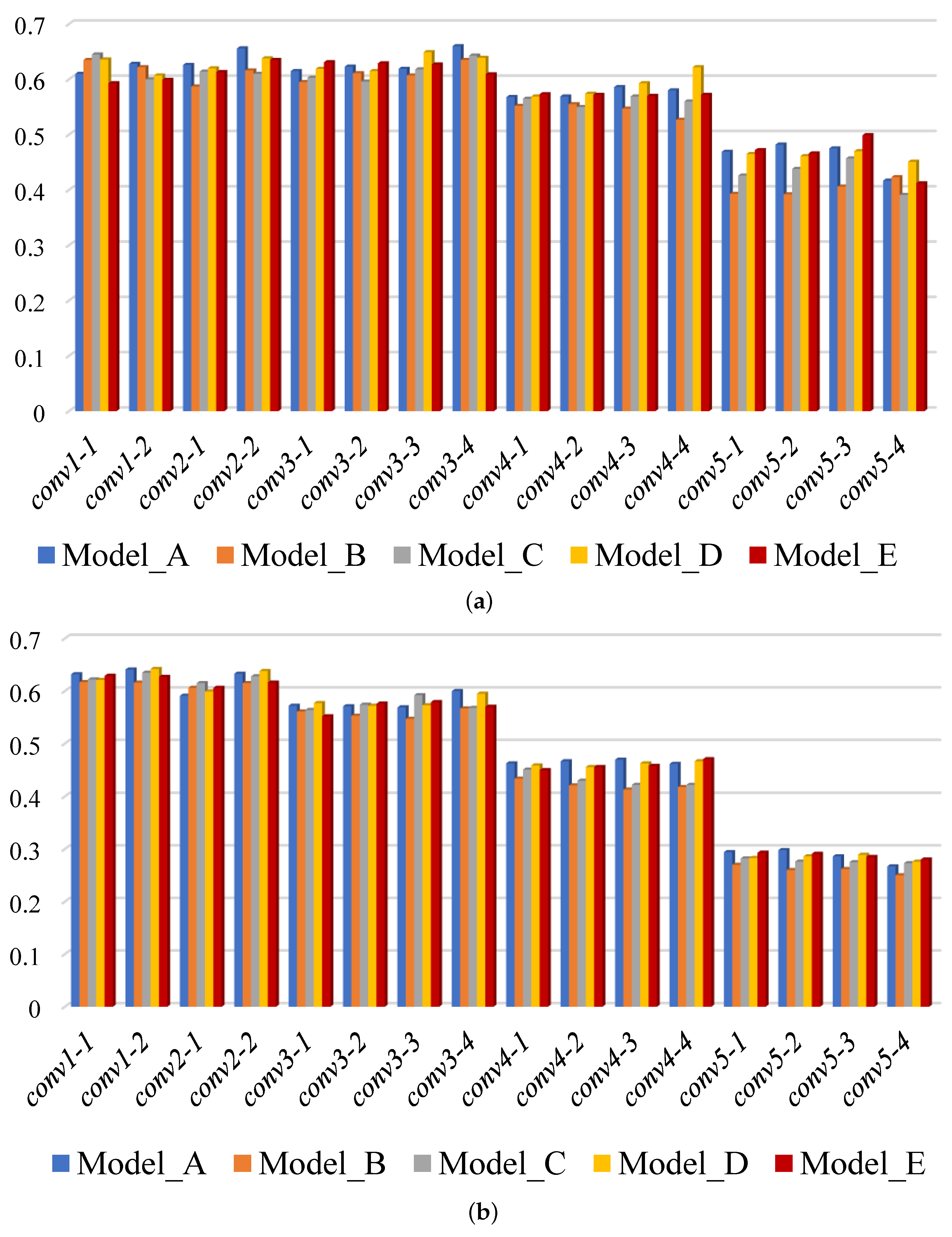
4.2. Template Matching Using Features from Individual Convolutional Layers
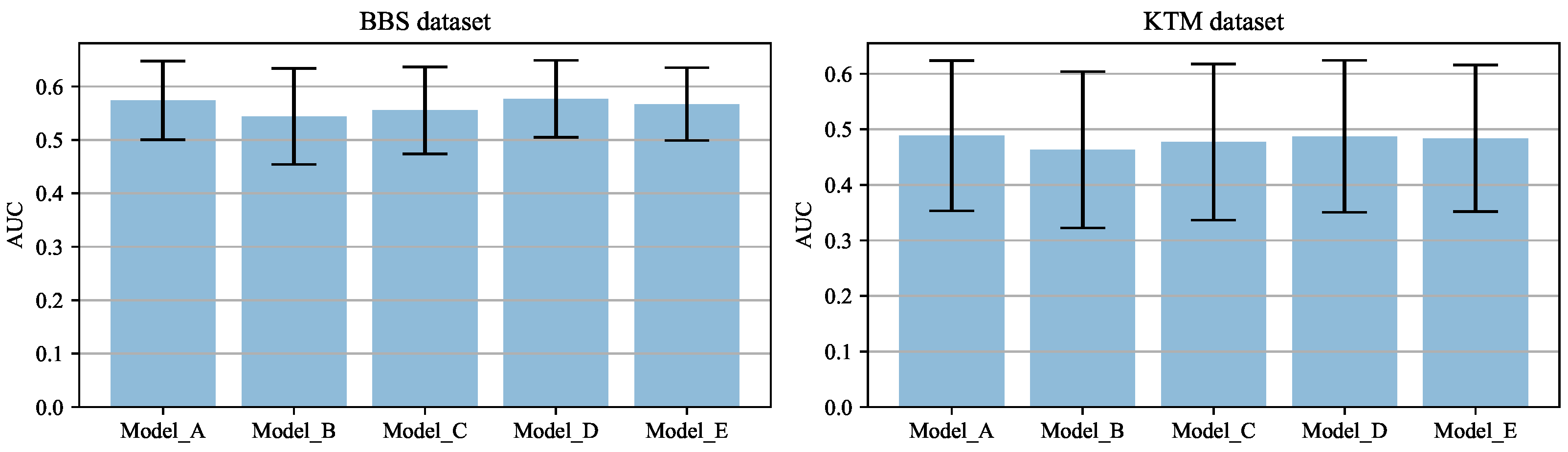
4.3. Template Matching Using Features from Multiple Convolutional Layers
4.4. Comparison with Other Methods
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, B.; Spratling, M.W. Explaining away results in more robust visual tracking. Vis. Comput. 2022, 1–15. [Google Scholar] [CrossRef]
- Gao, B.; Spratling, M.W. More Robust Object Tracking via Shape and Motion Cue Integration. Signal Process. 2022, 22, 108628. [Google Scholar] [CrossRef]
- Ahuja, K.; Tuli, P. Object recognition by template matching using correlations and phase angle method. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 1368–1373. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar]
- Chhatkuli, A.; Pizarro, D.; Bartoli, A. Stable template-based isometric 3D reconstruction in all imaging conditions by linear least-squares. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 708–715. [Google Scholar]
- Oron, S.; Dekel, T.; Xue, T.; Freeman, W.T.; Avidan, S. Best-buddies similarity—Robust template matching using mutual nearest neighbors. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1799–1813. [Google Scholar] [PubMed]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Dou, J.; Qin, Q.; Tu, Z. Robust image matching based on the information of SIFT. Optik 2018, 171, 850–861. [Google Scholar]
- Lee, H.; Kwon, H.; Robinson, R.M.; Nothwang, W.D. DTM: Deformable template matching. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 1966–1970. [Google Scholar]
- Sibiryakov, A. Fast and high-performance template matching method. In Proceedings of the CVPR 2011, Washington, DC, USA, 20–25 June 2011; pp. 1417–1424. [Google Scholar]
- Arslan, O.; Demirci, B.; Altun, H.; Tunaboylu, N.S. A novel rotation-invariant template matching based on HOG and AMDF for industrial laser cutting applications. In Proceedings of the 2013 9th International Symposium on Mechatronics and Its Applications (ISMA), Amman, Jordan, 9–11 April 2013; pp. 1–5. [Google Scholar]
- Antipov, G.; Berrani, S.A.; Ruchaud, N.; Dugelay, J.L. Learned vs. hand-crafted features for pedestrian gender recognition. In Proceedings of the 23rd ACM international Conference on Multimedia, Brisbane, Australia, 26–30 October 2015; pp. 1263–1266. [Google Scholar]
- Chan, T.H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A simple deep learning baseline for image classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Liang, M.; Hu, X. Recurrent convolutional neural network for object recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3367–3375. [Google Scholar]
- Wohlhart, P.; Lepetit, V. Learning descriptors for object recognition and 3d pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3109–3118. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional siamese networks for object tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Amsterdam, The Netherlands, 2016; pp. 850–865. [Google Scholar]
- Ma, C.; Huang, J.B.; Yang, X.; Yang, M.H. Robust visual tracking via hierarchical convolutional features. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2709–2723. [Google Scholar] [CrossRef]
- Cheng, J.; Wu, Y.; AbdAlmageed, W.; Natarajan, P. QATM: Quality-Aware Template Matching For Deep Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 11553–11562. [Google Scholar]
- Kat, R.; Jevnisek, R.; Avidan, S. Matching pixels using co-occurrence statistics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1751–1759. [Google Scholar]
- Kim, J.; Kim, J.; Choi, S.; Hasan, M.A.; Kim, C. Robust template matching using scale-adaptive deep convolutional features. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 708–711. [Google Scholar]
- Talmi, I.; Mechrez, R.; Zelnik-Manor, L. Template matching with deformable diversity similarity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 175–183. [Google Scholar]
- Zhang, Z.; Yang, X.; Gao, H. Weighted smallest deformation similarity for NN-based template matching. IEEE Trans. Ind. Inform. 2020, 16, 6787–6795. [Google Scholar]
- Lai, J.; Lei, L.; Deng, K.; Yan, R.; Ruan, Y.; Jinyun, Z. Fast and robust template matching with majority neighbour similarity and annulus projection transformation. Pattern Recognit. 2020, 98, 107029. [Google Scholar] [CrossRef]
- Kriegeskorte, N. Deep neural networks: A new framework for modeling biological vision and brain information processing. Annu. Rev. Vis. Sci. 2015, 1, 417–446. [Google Scholar] [CrossRef] [PubMed]
- Geirhos, R.; Rubisch, P.; Michaelis, C.; Bethge, M.; Wichmann, F.A.; Brendel, W. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. arXiv 2018, arXiv:1811.12231. [Google Scholar]
- Li, Y.; Yu, Q.; Tan, M.; Mei, J.; Tang, P.; Shen, W.; Yuille, A.; Xie, C. Shape-Texture Debiased Neural Network Training. arXiv 2020, arXiv:2010.05981. [Google Scholar]
- Spratling, M.W. Explaining away results in accurate and tolerant template matching. Pattern Recognit. 2020, 104, 107337. [Google Scholar] [CrossRef]
- Gao, B.; Spratling, M.W. Robust Template Matching via Hierarchical Convolutional Features from a Shape Biased CNN. In Proceedings of the The International Conference on Image, Vision and Intelligent Systems (ICIVIS 2021), Changsha, China, 15–17 June 2021; pp. 333–344. [Google Scholar]
- Korman, S.; Milam, M.; Soatto, S. OATM: Occlusion aware template matching by consensus set maximization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2675–2683. [Google Scholar]
- Kersten, D.; Mamassian, P.; Yuille, A. Object perception as Bayesian inference. Annu. Rev. Psychol. 2004, 55, 271–304. [Google Scholar] [CrossRef] [Green Version]
- Spratling, M.W. Unsupervised learning of generative and discriminative weights encoding elementary image components in a predictive coding model of cortical function. Neural Comput. 2012, 24, 60–103. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, X.; Belongie, S. Arbitrary style transfer in real-time with adaptive instance normalization. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 1501–1510. [Google Scholar]
- Lochmann, T.; Deneve, S. Neural processing as causal inference. Curr. Opin. Neurobiol. 2011, 21, 774–781. [Google Scholar] [CrossRef]
- Lochmann, T.; Ernst, U.A.; Deneve, S. Perceptual inference predicts contextual modulations of sensory responses. J. Neurosci. 2012, 32, 4179–4195. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Object tracking benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed]
- Liang, P.; Blasch, E.; Ling, H. Encoding color information for visual tracking: Algorithms and benchmark. IEEE Trans. Image Process. 2015, 24, 5630–5644. [Google Scholar] [CrossRef] [PubMed]



| Name | Training | Fine-Tuning | Rank of Shape Sensitivity |
|---|---|---|---|
| Model_A | IN | - | 4 |
| Model_B | SIN | - | 1 |
| Model_C | IN + SIN | - | 2 |
| Model_D | IN + SIN | IN | 3 |
| Model_E | IN | - | - |
| (a) Evaluation on BBS dataset. | ||||||||
| Layer | conv3_3 | conv3_4 | conv4_1 | conv4_2 | conv4_3 | conv4_4 | ||
| AUC | ||||||||
| Layer | ||||||||
| conv1_1 | 0.710 | 0.705 | 0.713 | 0.697 | 0.698 | 0.711 | ||
| 0.707↓ | 0.714↑ | 0.704↓ | 0.718↑ | 0.710↑ | 0.708↓ | |||
| 0.692↓ | 0.673↓ | 0.700↓ | 0.711↑ | 0.697↓ | 0.694↓ | |||
| conv1_2 | 0.686 | 0.686 | 0.674 | 0.655 | 0.680 | 0.683 | ||
| 0.686 | 0.687↑ | 0.707↑ | 0.696↑ | 0.690↑ | 0.710↑ | |||
| 0.658↓ | 0.659↓ | 0.675↑ | 0.695↑ | 0.683↑ | 0.677↓ | |||
| conv2_1 | 0.658 | 0.670 | 0.664 | 0.653 | 0.662 | 0.667 | ||
| 0.659↑ | 0.669↓ | 0.665↑ | 0.671↑ | 0.683↑ | 0.693↑ | |||
| 0.686↑ | 0.663↓ | 0.666↑ | 0.690↑ | 0.687↑ | 0.687↑ | |||
| conv2_2 | 0.659 | 0.661 | 0.653 | 0.641 | 0.659 | 0.663 | ||
| 0.665↑ | 0.667↑ | 0.676↑ | 0.679↑ | 0.676↑ | 0.682↑ | |||
| 0.682↑ | 0.653↓ | 0.688↑ | 0.684↑ | 0.672↑ | 0.691↑ | |||
| (b) Evaluation on KTM dataset. | ||||||||
| Layer | conv3_3 | conv3_4 | conv4_1 | conv4_2 | conv4_3 | conv4_4 | ||
| AUC | ||||||||
| Layer | ||||||||
| conv1_1 | 0.687 | 0.684 | 0.677 | 0.668 | 0.670 | 0.678 | ||
| 0.689↑ | 0.691↑ | 0.682↑ | 0.695↑ | 0.684↑ | 0.687↑ | |||
| 0.672↓ | 0.676↓ | 0.664↓ | 0.672↑ | 0.675↑ | 0.678 | |||
| conv1_2 | 0.687 | 0.689 | 0.682 | 0.685 | 0.675 | 0.682 | ||
| 0.680↓ | 0.694↑ | 0.695↑ | 0.697↑ | 0.691↑ | 0.690↑ | |||
| 0.668↑ | 0.672↓ | 0.670↓ | 0.669↓ | 0.669↓ | 0.673↓ | |||
| conv2_1 | 0.634 | 0.633 | 0.647 | 0.645 | 0.655 | 0.639 | ||
| 0.642↑ | 0.651↑ | 0.665↑ | 0.671↑ | 0.668↑ | 0.666↑ | |||
| 0.658↑ | 0.673↑ | 0.643↓ | 0.648↑ | 0.665↑ | 0.660↑ | |||
| conv2_2 | 0.642 | 0.651 | 0.664 | 0.661 | 0.669 | 0.669 | ||
| 0.657↑ | 0.664↑ | 0.670↑ | 0.673↑ | 0.669 | 0.669 | |||
| 0.657↑ | 0.665↑ | 0.640↑ | 0.651↓ | 0.665↓ | 0.670↑ | |||
| (a) Evaluation on BBS dataset. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layers | ||||||||||
| AUC | 0.728 | 0.727 | 0.724 | 0.724 | 0.723 | 0.722 | 0.720 | 0.720 | 0.720 | 0.720 |
| (b) Evaluation on KTM dataset. | ||||||||||
| Layers | ||||||||||
| AUC | 0.711 | 0.709 | 0.708 | 0.706 | 0.706 | 0.705 | 0.705 | 0.705 | 0.705 | 0.704 |
| Feature | BBS Dataset | KTM Dataset | |||||
|---|---|---|---|---|---|---|---|
| AUC | Colour | Deep | Deep (Proposed) | Colour | Deep (Proposed) | ||
| Method | |||||||
| SSD | 0.46 | - | 0.54 | 0.42 | 0.54 | ||
| NCC | 0.48 | 0.63 [23] | 0.67 | 0.42 | 0.67 | ||
| ZNCC | 0.54 | - | 0.67 | 0.48 | 0.67 | ||
| BBS | 0.55 | 0.60 [7] | 0.54 | 0.44 | 0.55 | ||
| CoTM | 0.54 1 | 0.67 [22] | 0.64 | 0.51 | 0.56 | ||
| DDIS | 0.64 | - | 0.66 | 0.63 | 0.68 | ||
| QATM | - | 0.62 2 | 0.66 | - | 0.64 | ||
| DIM | 0.69 | - | 0.73 | 0.60 | 0.71 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Spratling, M.W. Shape–Texture Debiased Training for Robust Template Matching. Sensors 2022, 22, 6658. https://doi.org/10.3390/s22176658
Gao B, Spratling MW. Shape–Texture Debiased Training for Robust Template Matching. Sensors. 2022; 22(17):6658. https://doi.org/10.3390/s22176658
Chicago/Turabian StyleGao, Bo, and Michael W. Spratling. 2022. "Shape–Texture Debiased Training for Robust Template Matching" Sensors 22, no. 17: 6658. https://doi.org/10.3390/s22176658
APA StyleGao, B., & Spratling, M. W. (2022). Shape–Texture Debiased Training for Robust Template Matching. Sensors, 22(17), 6658. https://doi.org/10.3390/s22176658






