Deep Learning-Based 3D Measurements with Near-Infrared Fringe Projection
Abstract
:1. Introduction
2. Principles
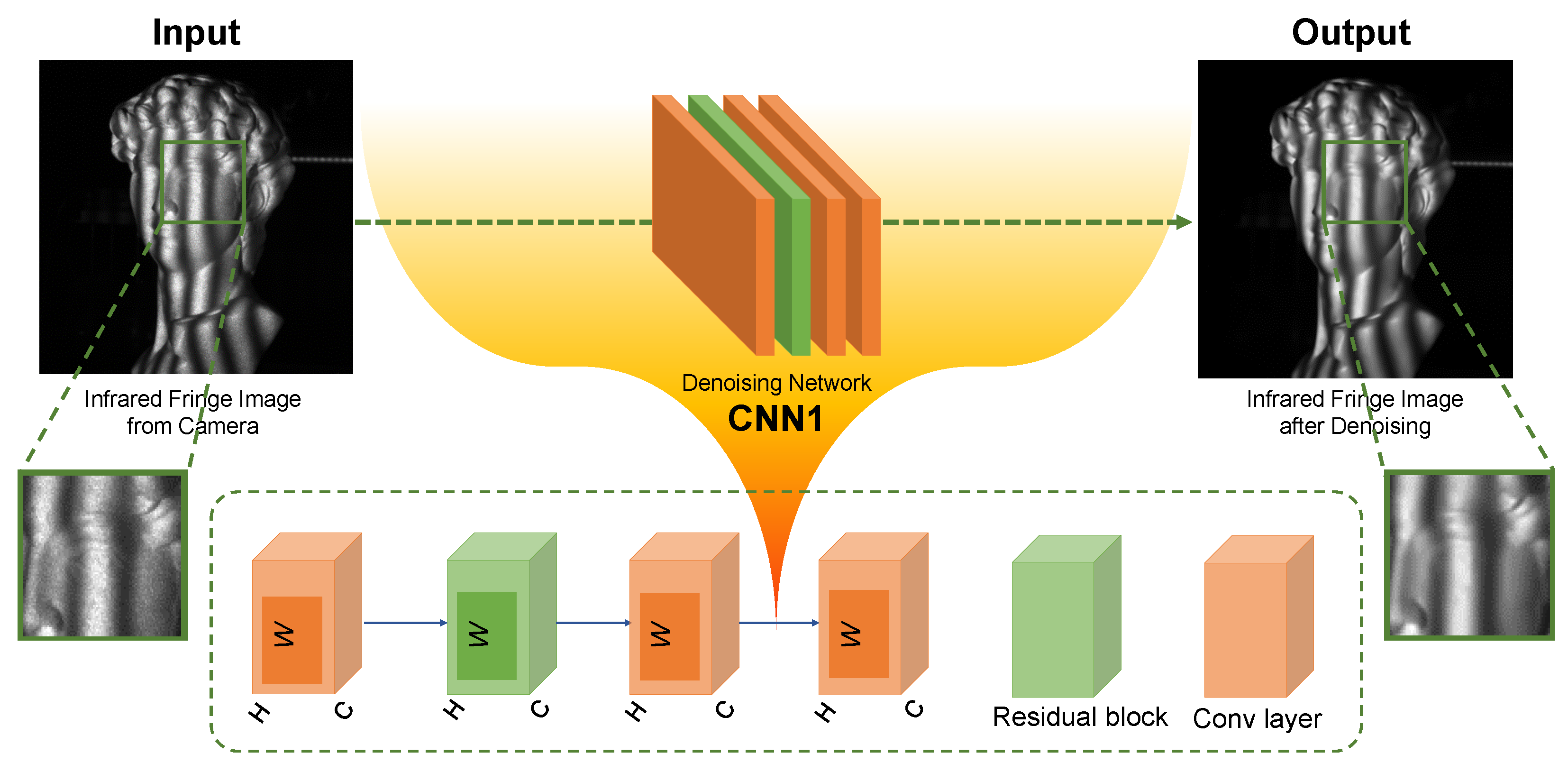
2.1. The Elimination of Speckle Noise in NIR Fringe Pattern Using Deep Learning
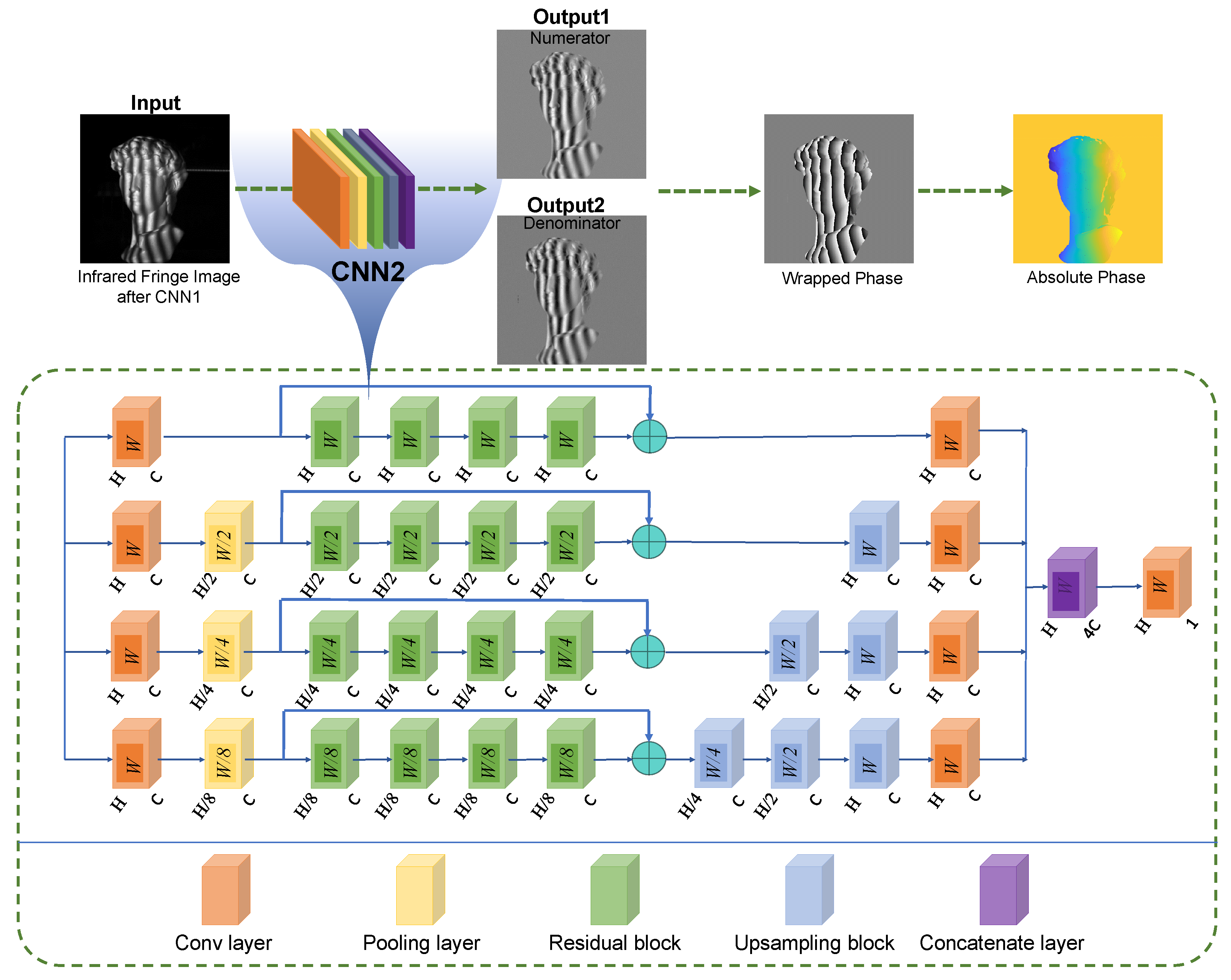
2.2. Analysis of Denoised Fringe Pattern Using Deep Learning
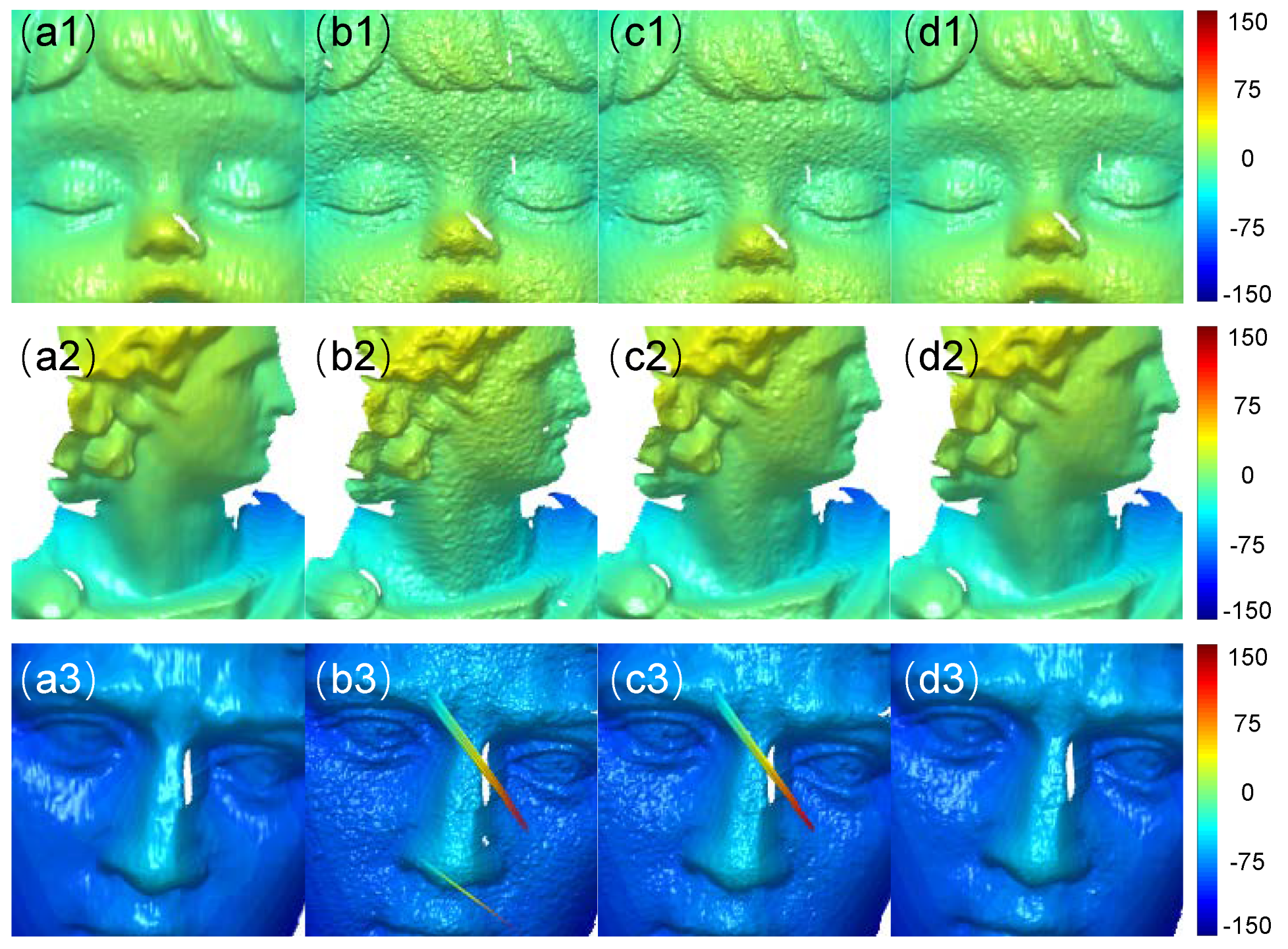
3. Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, H.; Wang, Z. Accurate 3D shape reconstruction from single structured-light Image via fringe-to-fringe network. Photonics 2021, 8, 459. [Google Scholar] [CrossRef]
- Zhang, Z.; Towers, C.E.; Towers, D.P. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency selection. Opt. Express 2006, 14, 6444–6455. [Google Scholar] [CrossRef]
- Nguyen, H.; Tran, T.; Wang, Y.; Wang, Z. Three-dimensional shape reconstruction from single-shot speckle image using deep convolutional neural networks. Opt. Lasers Eng. 2021, 143, 106639. [Google Scholar] [CrossRef]
- Machineni, R.C.; Spoorthi, G.E.; Vengala, K.S.; Gorthi, S.; Gorthi, R.K. End-to-end deep learning-based fringe projection framework for 3D profiling of objects. Comput. Vis. Image Underst. 2020, 199, 103023. [Google Scholar] [CrossRef]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Lu, L.; Suresh, V.; Zheng, Y.; Wang, Y.; Xi, J.; Li, B. Motion induced error reduction methods for phase shifting profilometry: A review. Opt. Lasers Eng. 2021, 141, 106573. [Google Scholar] [CrossRef]
- Barbastathis, G.; Ozcan, A.; Situ, G. On the use of deep learning for computational imaging. Optica 2019, 6, 921–943. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q.; Zuo, C.; Feng, S. High-speed high dynamic range 3D shape measurement based on deep learning. Opt. Lasers Eng. 2020, 134, 106245. [Google Scholar] [CrossRef]
- Shi, J.; Zhu, X.; Wang, H.; Song, L.; Guo, Q. Label enhanced and patch based deep learning for phase retrieval from single frame fringe pattern in fringe projection 3D measurement. Opt. Express 2019, 27, 28929–28943. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe pattern denoising based on deep learning. Opt. Commun. 2019, 437, 148–152. [Google Scholar] [CrossRef]
- Jeon, W.; Jeong, W.; Son, K.; Yang, H. Speckle noise reduction for digital holographic images using multi-scale convolutional neural networks. Opt. Lett. 2018, 43, 4240–4243. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Q.; Gu, G.; Tao, T.; Zhang, L.; Hu, Y.; Yin, W.; Zuo, C. Fringe pattern analysis using deep learning. Adv. Photonics 2019, 1, 025001. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Yin, W.; Gu, G.; Chen, Q. Micro deep learning profilometry for high-speed 3D surface imaging. Opt. Lasers Eng. 2019, 121, 416–427. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Tao, T.; Hu, Y.; Li, Y.; Chen, Q.; Zuo, C. Deep-learning-enabled geometric constraints and phase unwrapping for single-shot absolute 3D shape measurement. Apl Photonics 2020, 5, 046105. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light. Sci. Appl. 2022, 11, 39. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Zhang, L.; Yin, W.; Chen, Q. Generalized framework for non-sinusoidal fringe analysis using deep learning. Photonics Res. 2021, 9, 1084–1098. [Google Scholar] [CrossRef]
- Feng, S.; Zuo, C.; Hu, Y.; Li, Y.; Chen, Q. Deep-learning-based fringe-pattern analysis with uncertainty estimation. Optica 2021, 8, 1507–1510. [Google Scholar] [CrossRef]
- Li, Y.; Qian, J.; Feng, S.; Chen, Q.; Zuo, C. Deep-learning-enabled dual-frequency composite fringe projection profilometry for single-shot absolute 3D shape measurement. Opto-Electron. Adv. 2022, 5, 210021. [Google Scholar] [CrossRef]
- Muhire, D.; Tounsi, Y.; Zada, S.; Siari, A.; Nassim, A. Wiener Teager–Kaiser energy method for phase derivative estimation: Application to speckle interferometry. Opt. Eng. 2017, 56, 114101. [Google Scholar] [CrossRef]
- Leng, J.; Zhou, J.; Lang, X.; Li, X. Two-stage method to suppress speckle noise in digital holography. Opt. Rev. 2015, 22, 844–852. [Google Scholar] [CrossRef]
- Kemao, Q.; Wang, H.; Gao, W. Windowed Fourier transform for fringe pattern analysis: Theoretical analyses. Appl. Opt. 2008, 47, 5408–5419. [Google Scholar] [CrossRef]
- Kemao, Q. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Hao, F.; Tang, C.; Xu, M.; Lei, Z. Batch denoising of ESPI fringe patterns based on convolutional neural network. Appl. Opt. 2019, 58, 3338–3346. [Google Scholar] [CrossRef]
- Danielyan, A.; Katkovnik, V.; Egiazarian, K. BM3D frames and variational image deblurring. IEEE Trans. Image Process. 2011, 21, 1715–1728. [Google Scholar] [CrossRef] [Green Version]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]







| Time Cost of Fringe Analysis | BM3D/s | Our Method/s |
|---|---|---|
| Scene 1 | 1.983 | 0.0648 |
| Scene 2 | 1.995 | 0.0673 |
| Scene 3 | 1.997 | 0.0633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, Y.; Ji, Y.; Qian, J.; Che, Y.; Zuo, C.; Chen, Q.; Feng, S. Deep Learning-Based 3D Measurements with Near-Infrared Fringe Projection. Sensors 2022, 22, 6469. https://doi.org/10.3390/s22176469
Wang J, Li Y, Ji Y, Qian J, Che Y, Zuo C, Chen Q, Feng S. Deep Learning-Based 3D Measurements with Near-Infrared Fringe Projection. Sensors. 2022; 22(17):6469. https://doi.org/10.3390/s22176469
Chicago/Turabian StyleWang, Jinglei, Yixuan Li, Yifan Ji, Jiaming Qian, Yuxuan Che, Chao Zuo, Qian Chen, and Shijie Feng. 2022. "Deep Learning-Based 3D Measurements with Near-Infrared Fringe Projection" Sensors 22, no. 17: 6469. https://doi.org/10.3390/s22176469
APA StyleWang, J., Li, Y., Ji, Y., Qian, J., Che, Y., Zuo, C., Chen, Q., & Feng, S. (2022). Deep Learning-Based 3D Measurements with Near-Infrared Fringe Projection. Sensors, 22(17), 6469. https://doi.org/10.3390/s22176469








