Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter
Abstract
:1. Introduction
2. Localization without Accelerometers
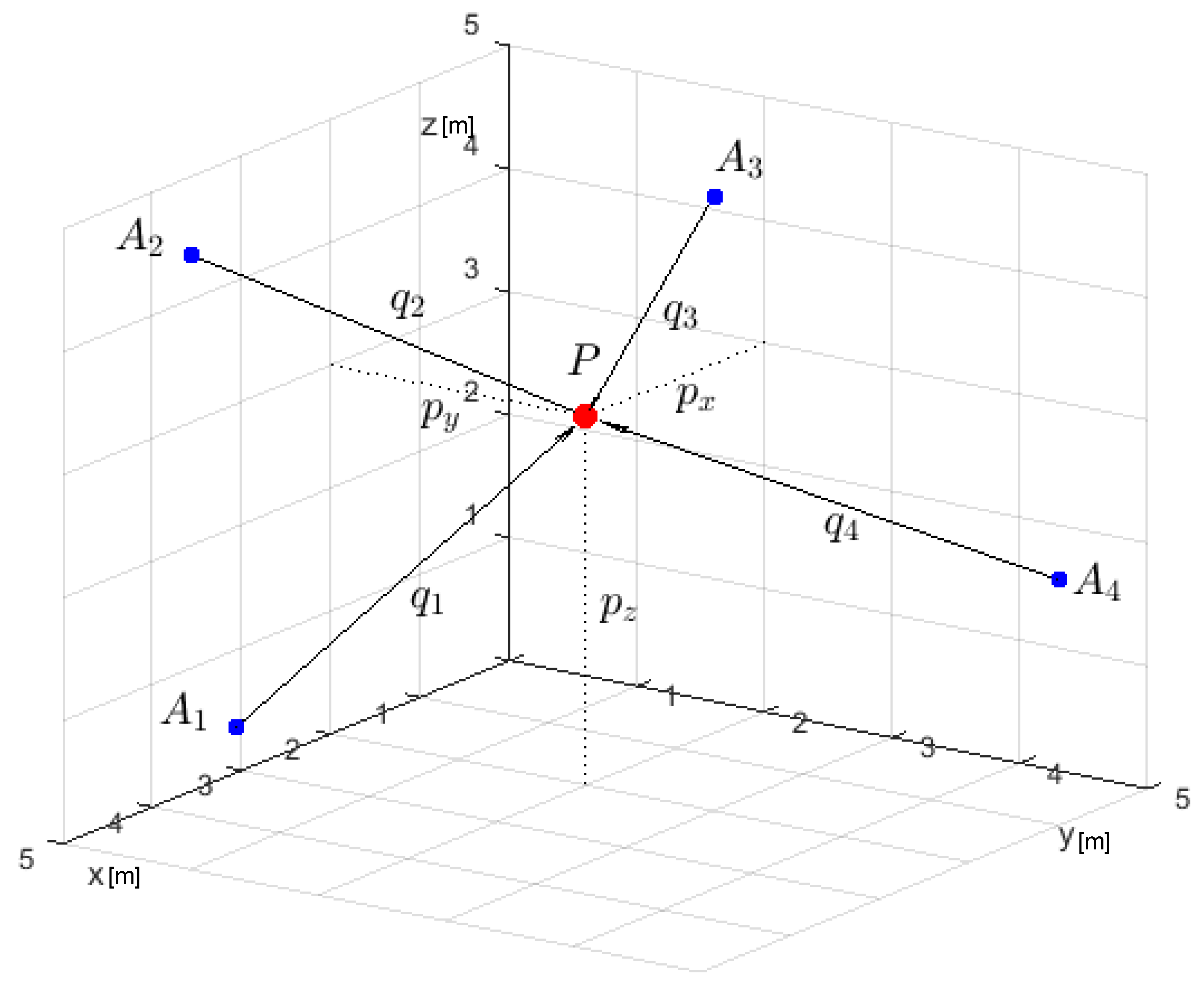
2.1. Determination of the Direct Kinematics for Anchors
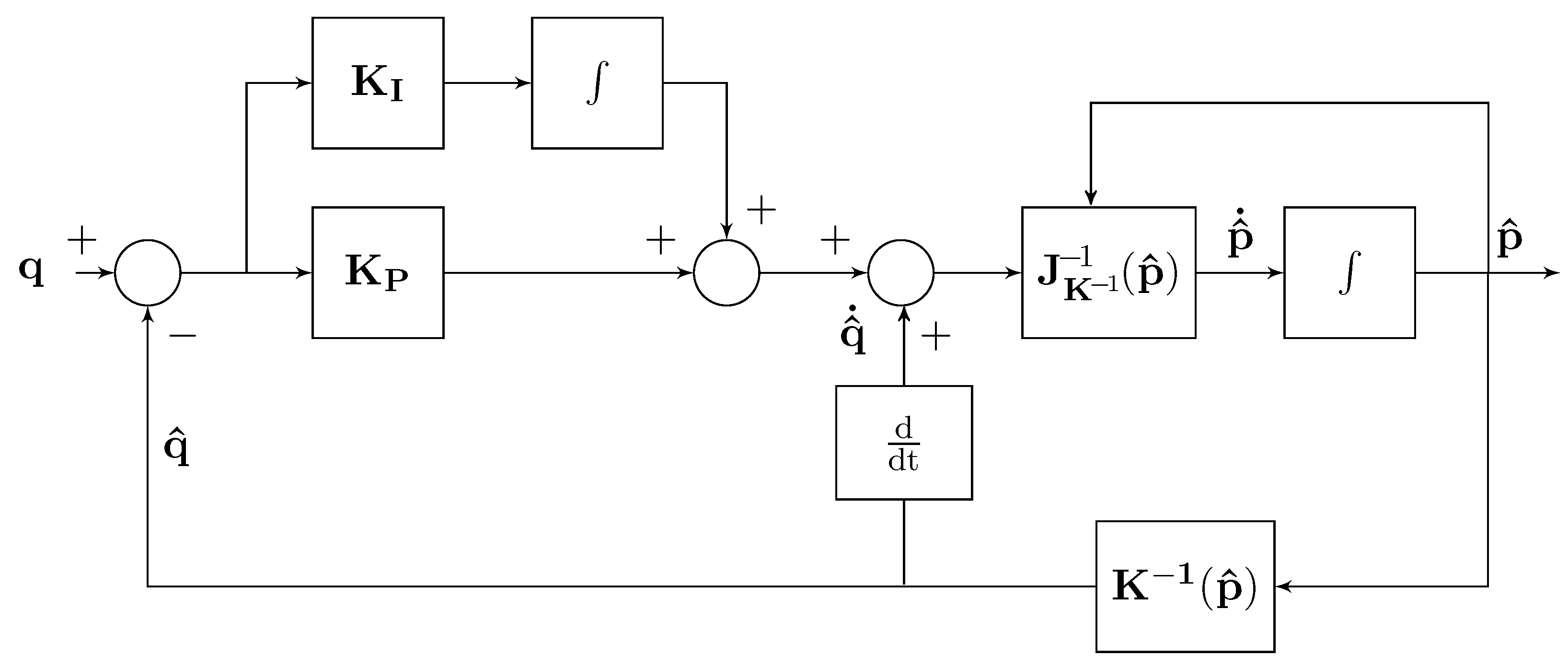
2.2. A New Closed-Loop Localization Algorithm
2.3. Using Three Anchors
2.4. Using Anchors
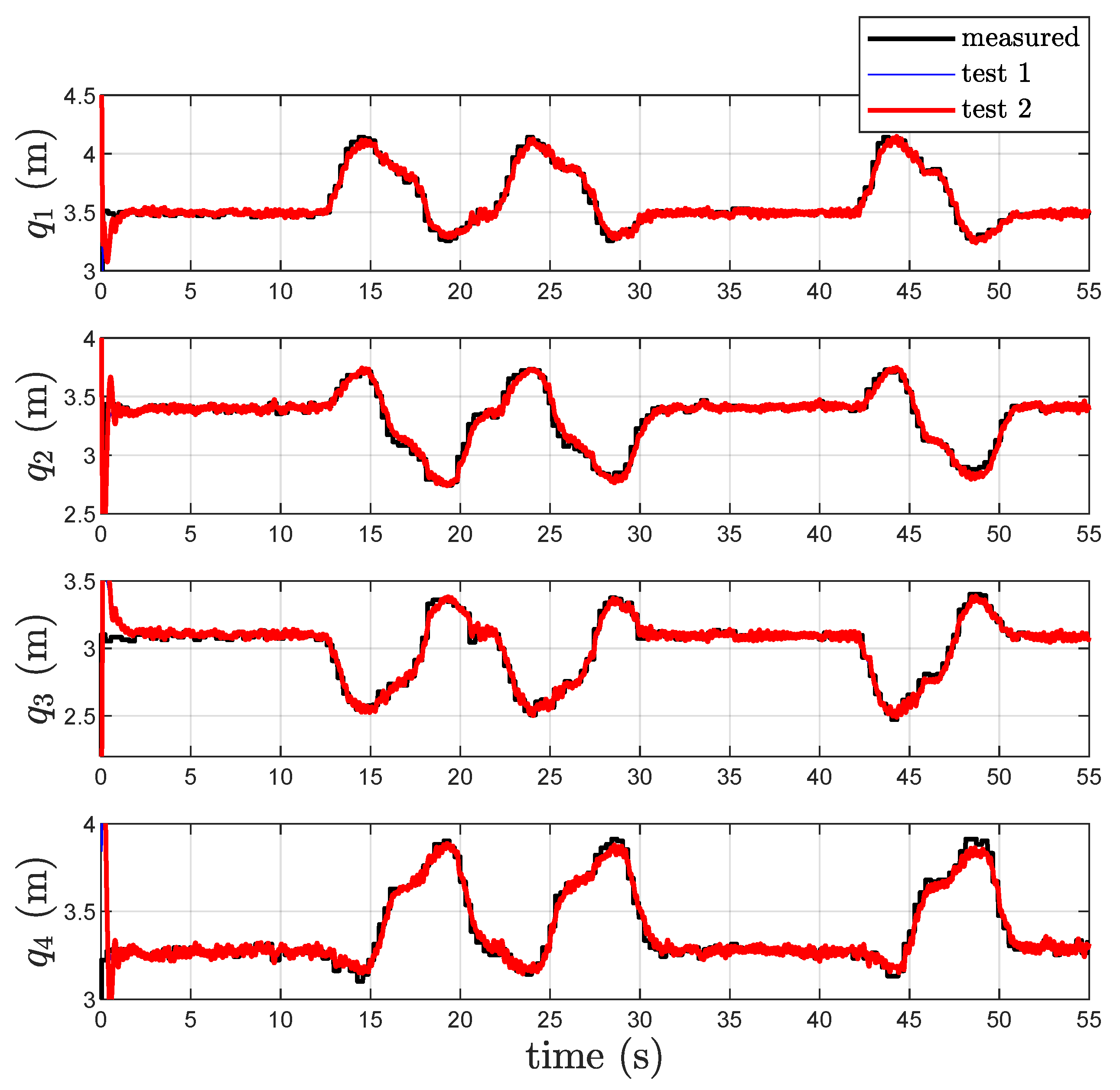
2.5. Experimental Results Using Four Anchors
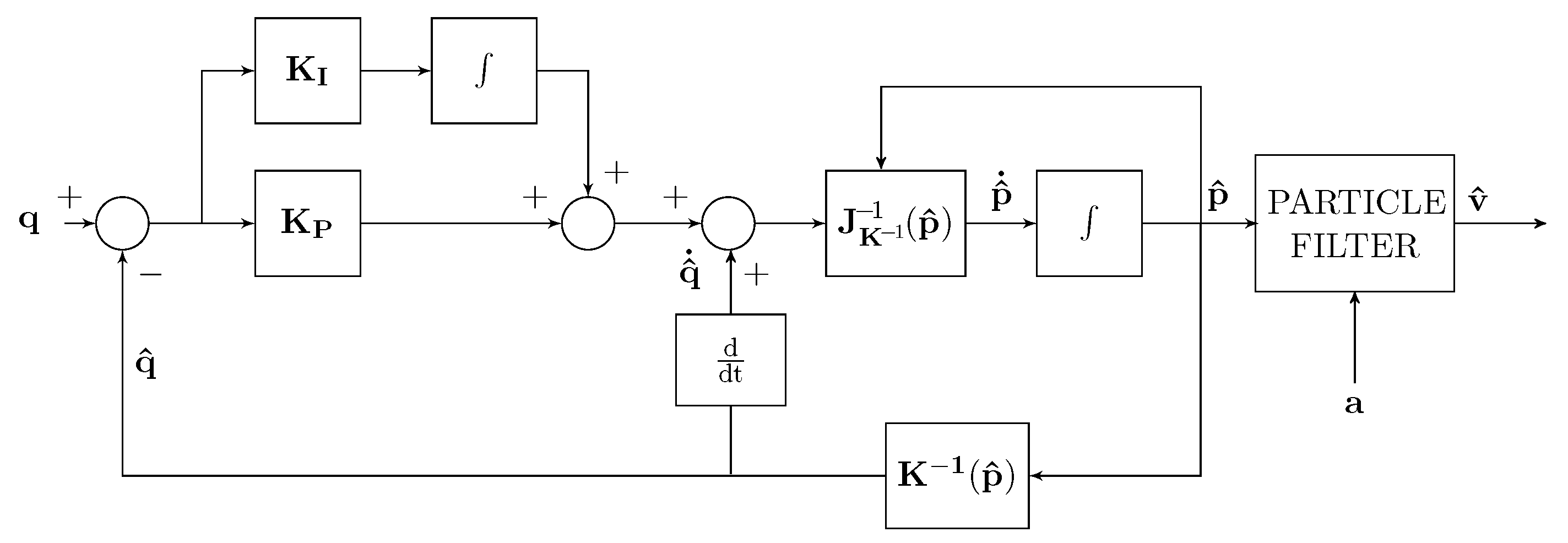
3. Velocity Estimation
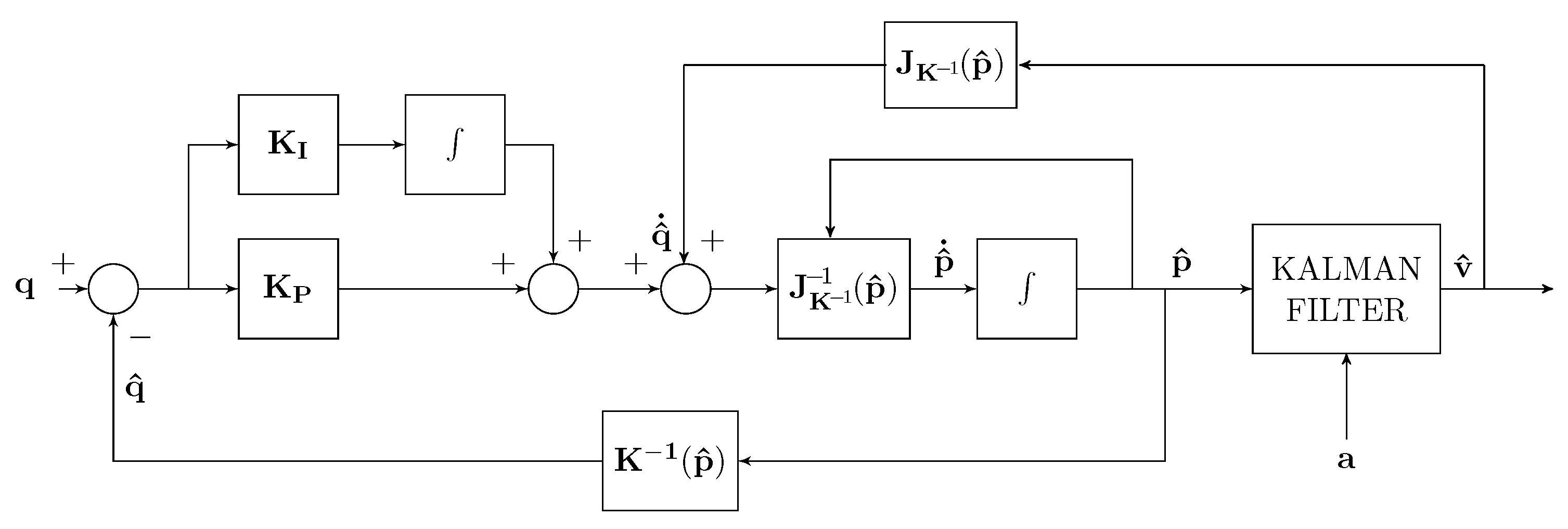
3.1. Kalman–Bucy Filter
3.2. Particle Filter as Alternative to the Kalman–Bucy Filter
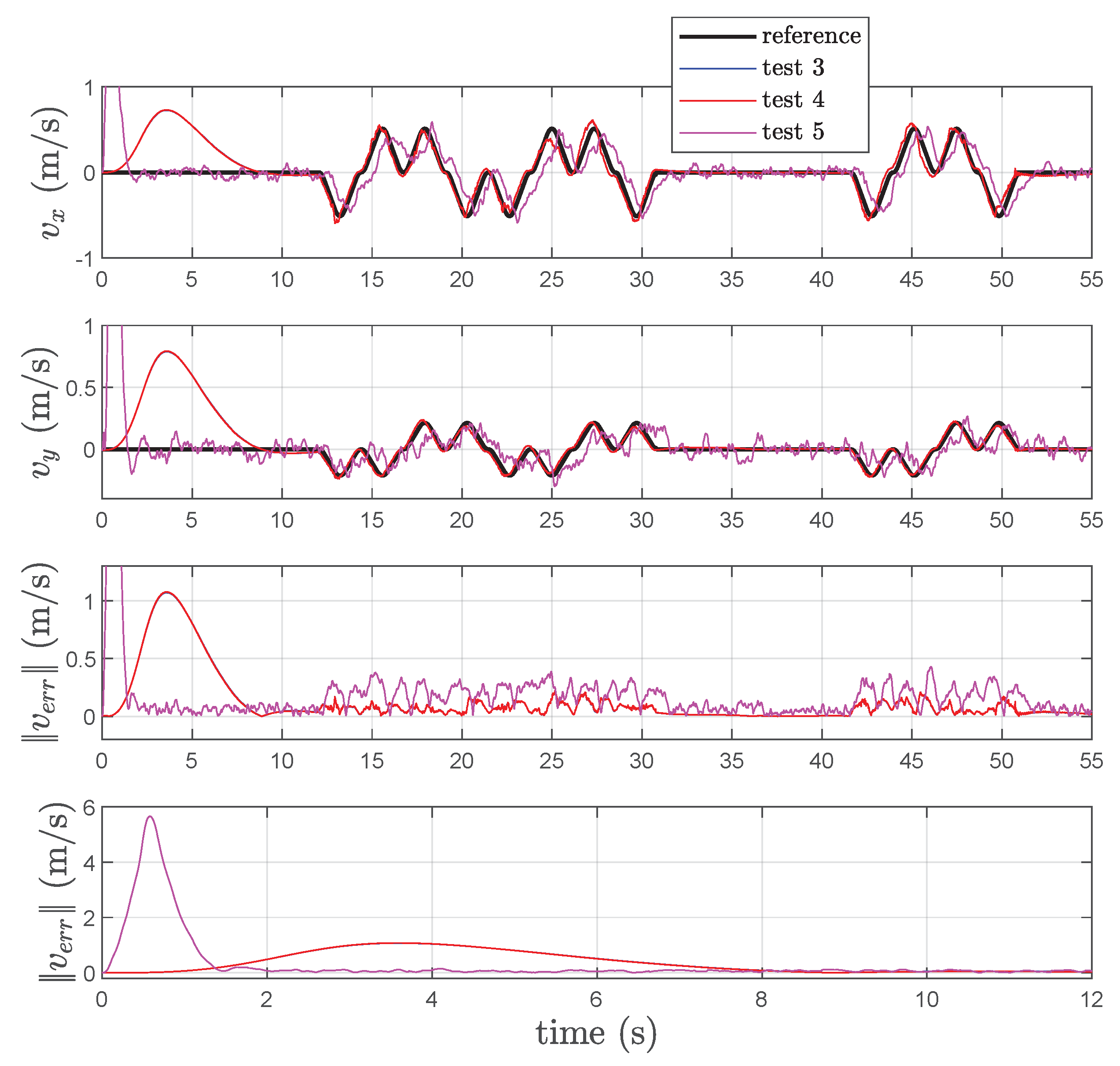
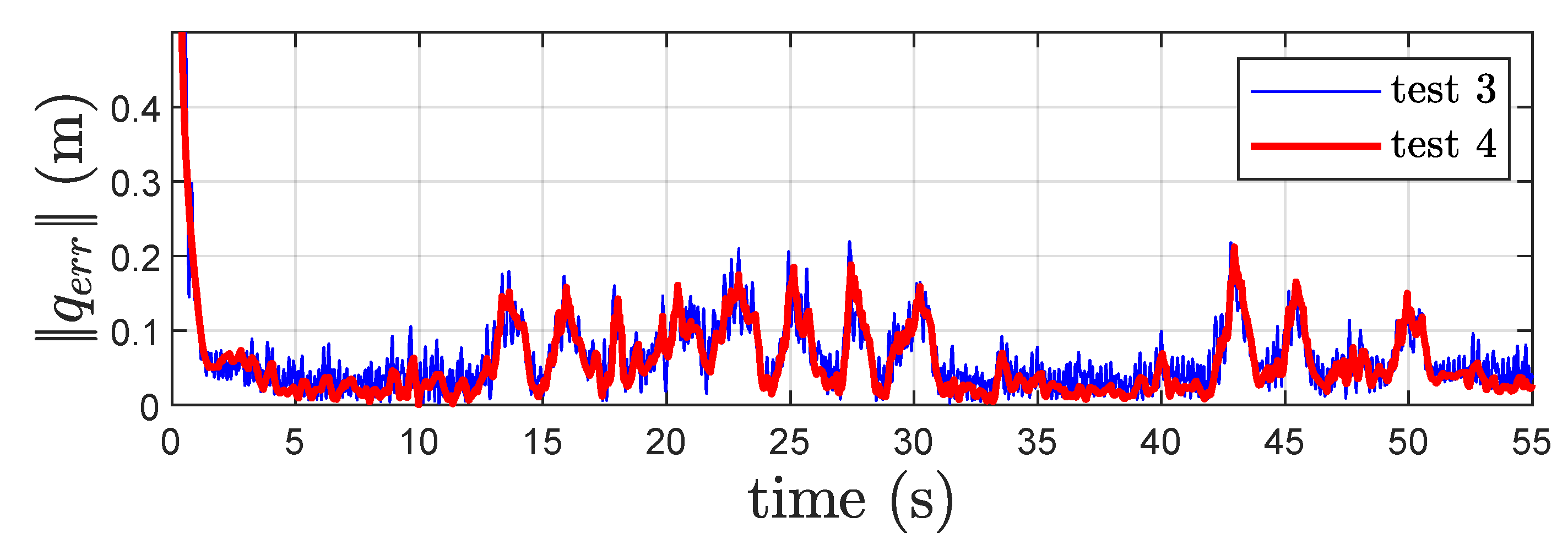
3.3. Experimental Results for the Velocity Estimation Schemes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Description of the Experimental Setup

References
- Monica, S.; Ferrari, G. Robust UWB-Based Localization with Application to Automated Guided Vehicles. Adv. Intell. Syst. 2020, 3, 2000083. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Alonge, F.; D’Ippolito, F.; Fagiolini, A.; Garraffa, G.; Sferlazza, A. Trajectory robust control of autonomous quadcopters based on model decoupling and disturbance estimation. Int. J. Adv. Robot. Syst. 2021, 18, 1729881421996974. [Google Scholar] [CrossRef]
- Hamel, T.; Mahony, R. Attitude estimation on SO(3) based on direct inertial measurements. In Proceedings of the IEEE International Conference on Robotics and Automation, IEEE, Orlando, FL, USA, 15–19 May 2006; pp. 2170–2175. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, W.; Ghogho, M.; Yuan, B. Mathematical Model and Matlab Simulation of Strapdown inertial navigation system. Model. Simul. Eng. 2012, 2012, 264537. [Google Scholar] [CrossRef] [Green Version]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Fossen, T.I. Marine Control Systems: Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics: Trondheim, Norway, 2002. [Google Scholar]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. Ocean. Eng. IEEE J. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Alonge, F.; D’Ippolito, F.; Garraffa, G.; Sferlazza, A. A Hybrid Observer for Localization of Mobile Vehicles with Asynchronous Measurements. Asian J. Control 2019, 21, 1506–1521. [Google Scholar] [CrossRef]
- Li, M.G.; Zhu, H.; You, S.Z.; Tang, C.Q. UWB-Based Localization System Aided With Inertial Sensor for Underground Coal Mine Applications. IEEE Sens. J. 2020, 20, 6652–6669. [Google Scholar] [CrossRef]
- Lee, J.; Moon, J.; Kim, S. UWB-based Multiple UAV Control System for Indoor Ground Vehicle Tracking. In Proceedings of the 2021 IEEE VTS 17th Asia Pacific Wireless Communications Symposium (APWCS), Osaka, Japan, 30–31 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Lee, H.; Kim, W.; Seo, J. Simulation of UWB Radar-Based Positioning Performance for a UAV in an Urban Area. In Proceedings of the 2018 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), JeJu, Korea, 24–26 June 2018; pp. 206–212. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef] [Green Version]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Dardari, D.; Closas, P.; Djurić, P.M. Indoor Tracking: Theory, Methods, and Technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef] [Green Version]
- You, W.; Li, F.; Liao, L.; Huang, M. Data Fusion of UWB and IMU Based on Unscented Kalman Filter for Indoor Localization of Quadrotor UAV. IEEE Access 2020, 8, 64971–64981. [Google Scholar] [CrossRef]
- Yao, L.; Wu, Y.W.A.; Yao, L.; Liao, Z.Z. An integrated IMU and UWB sensor based indoor positioning system. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Kulikov, R.S. Integrated UWB/IMU system for high rate indoor navigation with cm-level accuracy. In Proceedings of the 2018 Moscow Workshop on Electronic and Networking Technologies (MWENT), Moscow, Russia, 14–16 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Foy, W.H. Position-location solutions by Taylor-series estimation. IEEE Trans. Aerosp. Electron. Syst. 1976, 2, 187–194. [Google Scholar] [CrossRef]
- Manolakis, D.E. Efficient solution and performance analysis of 3-D position estimation by trilateration. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1239–1248. [Google Scholar] [CrossRef]
- Navidi, W.; Murphy, W.S., Jr.; Hereman, W. Statistical methods in surveying by trilateration. Comput. Stat. Data Anal. 1998, 27, 209–227. [Google Scholar] [CrossRef]
- Guo, K.; Qiu, Z.; Miao, C.; Zaini, A.H.; Chen, C.L.; Meng, W.; Xie, L. Ultra-wideband-based localization for quadcopter navigation. Unmanned Syst. 2016, 4, 23–34. [Google Scholar] [CrossRef]
- Murphy, W.S.; Hereman, W. Determination of a Position in Three Dimensions Using Trilateration and Approximate Distances; Department of Mathematical and Computer Science (MCS), Colorado School of Mines: Golden, CO, USA, 1995. [Google Scholar]
- Coope, I. Reliable computation of the points of intersection of n spheres in Rn. ANZIAM J. 2000, 42, C461–C477. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.; Anderson, B.D.; Morse, A.S. Localization with imprecise distance information in sensor networks. In Proceedings of the Proceedings of the 44th IEEE Conference on Decision and Control, IEEE, Seville, Spain, 15–15 December 2005; pp. 2829–2834.
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhou, B.; Huang, P.; Xue, W.; Li, Q.; Zhu, J.; Qiu, L. Kalman filter-based data fusion of wi-fi rtt and pdr for indoor localization. IEEE Sens. J. 2021, 21, 8479–8490. [Google Scholar] [CrossRef]
- Shaukat, N.; Ali, A.; Javed Iqbal, M.; Moinuddin, M.; Otero, P. Multi-sensor fusion for underwater vehicle localization by augmentation of rbf neural network and error-state kalman filter. Sensors 2021, 21, 1149. [Google Scholar] [CrossRef]
- Liu, J.; Guo, G. Vehicle localization during GPS outages with extended Kalman filter and deep learning. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Garraffa, G.; Sferlazza, A.; D’Ippolito, F.; Alonge, F. Localization Based on Parallel Robots Kinematics As an Alternative to Trilateration. IEEE Trans. Ind. Electron. 2022, 69, 999–1010. [Google Scholar] [CrossRef]
- DecaWave. DW1000 User Manual; Version 2.11.; DecaWave: Dublin, Ireland, 2017. [Google Scholar]
- Siciliano, B. The Tricept robot: Inverse kinematics, manipulability analysis and closed-loop direct kinematics algorithm. Robotica 1999, 17, 437–445. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Chen, Z. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond. Statistics 2003, 182, 9257. [Google Scholar] [CrossRef]




| Test Name | Estimation Algorithm |
|---|---|
| Test 1 | The one already proposed in [32]. |
| Test 2 | Localization without accelerometers as in Equation (8). |
| Mean Value [m] | Variance [m] | |
|---|---|---|
| Test 1 | 0.045 | 0.00910 |
| Test 2 | 0.053 | 0.01187 |
| Test Name | Estimation Algorithm |
|---|---|
| Test 3 | Differentiator and Kalman–Bucy filter (cf. Figure 5). |
| Test 4 | Estimation of by Kalman–Bucy filter (cf. Figure 6). |
| Test 5 | Differentiator and particle filter (cf. Figure 7). |
| Error Mean Value [m] | Error Variance [m] | |
|---|---|---|
| Test 3 | 0.045 | 0.00911 |
| Test 4 | 0.053 | 0.01187 |
| Test 5 | 0.064 | 0.04008 |
| Error Mean Value [m] | Error Variance [m] | |
|---|---|---|
| Test 3 | 0.125 | 0.04860 |
| Test 4 | 0.125 | 0.04877 |
| Test 5 | 0.198 | 0.20147 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonge, F.; Cusumano, P.; D’Ippolito, F.; Garraffa, G.; Livreri, P.; Sferlazza, A. Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter. Sensors 2022, 22, 6308. https://doi.org/10.3390/s22166308
Alonge F, Cusumano P, D’Ippolito F, Garraffa G, Livreri P, Sferlazza A. Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter. Sensors. 2022; 22(16):6308. https://doi.org/10.3390/s22166308
Chicago/Turabian StyleAlonge, Francesco, Pasquale Cusumano, Filippo D’Ippolito, Giovanni Garraffa, Patrizia Livreri, and Antonino Sferlazza. 2022. "Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter" Sensors 22, no. 16: 6308. https://doi.org/10.3390/s22166308
APA StyleAlonge, F., Cusumano, P., D’Ippolito, F., Garraffa, G., Livreri, P., & Sferlazza, A. (2022). Localization in Structured Environments with UWB Devices without Acceleration Measurements, and Velocity Estimation Using a Kalman–Bucy Filter. Sensors, 22(16), 6308. https://doi.org/10.3390/s22166308








