Piezoelectric Energy Harvesting from Low-Frequency Vibrations Based on Magnetic Plucking and Indirect Impacts
Abstract
1. Introduction
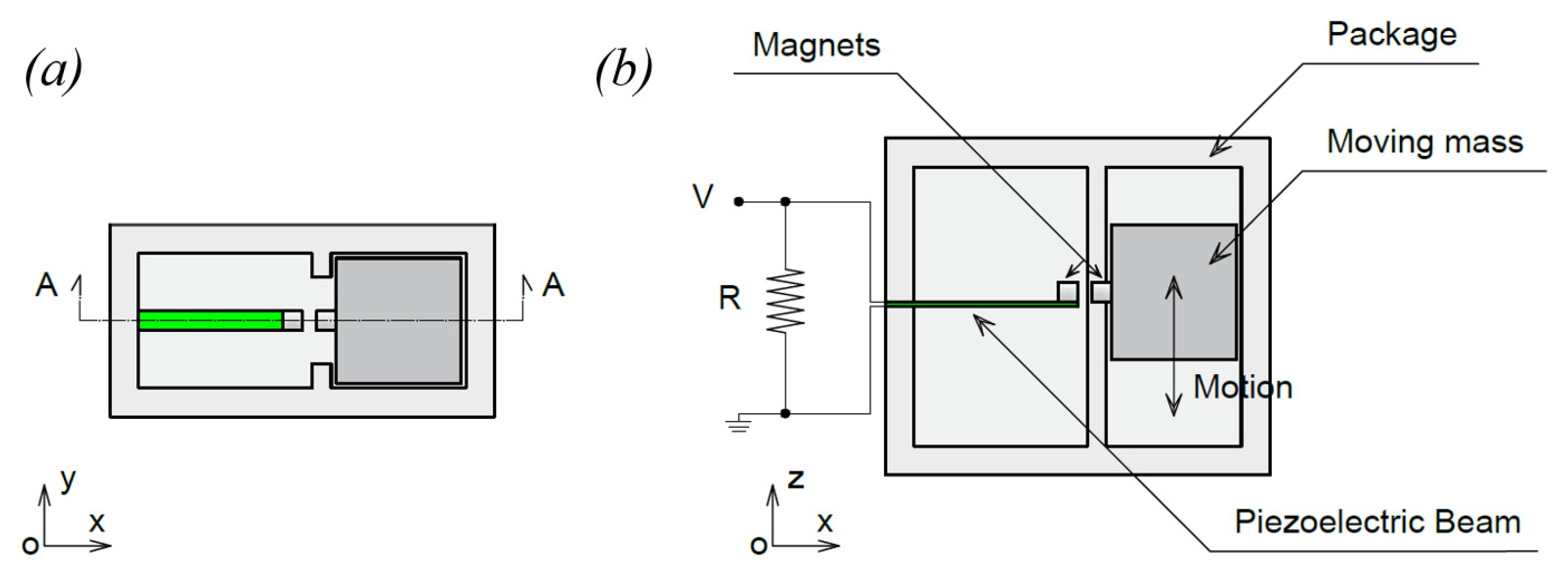
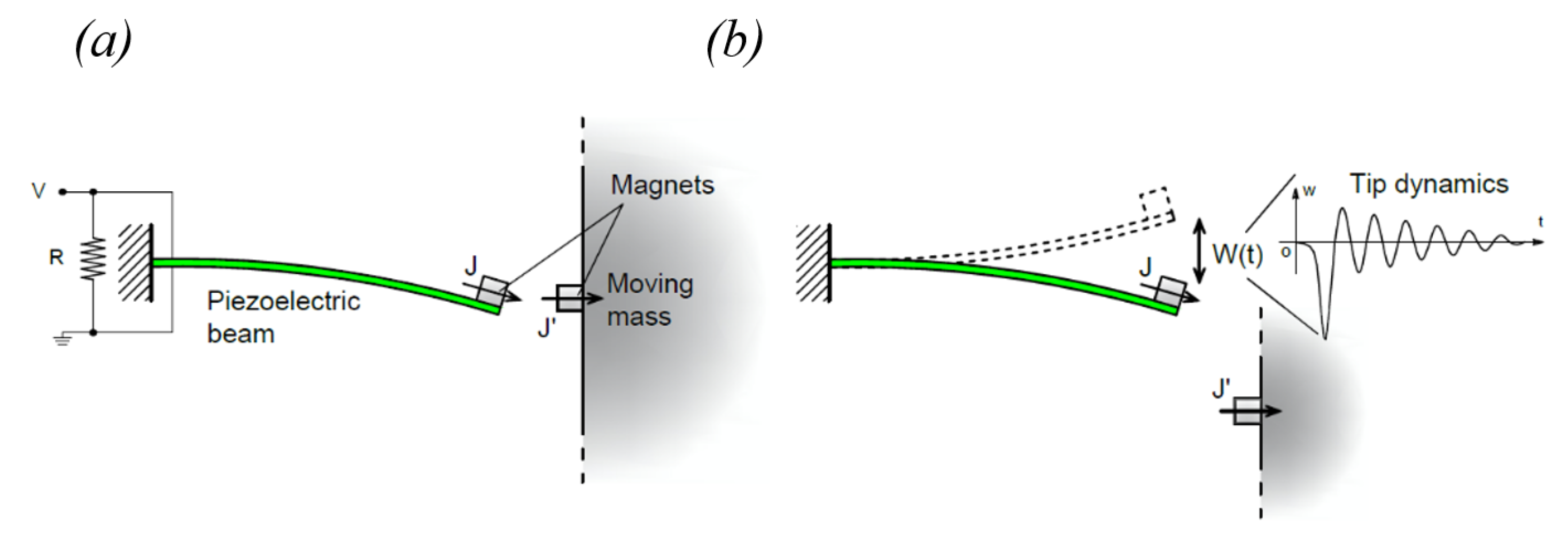
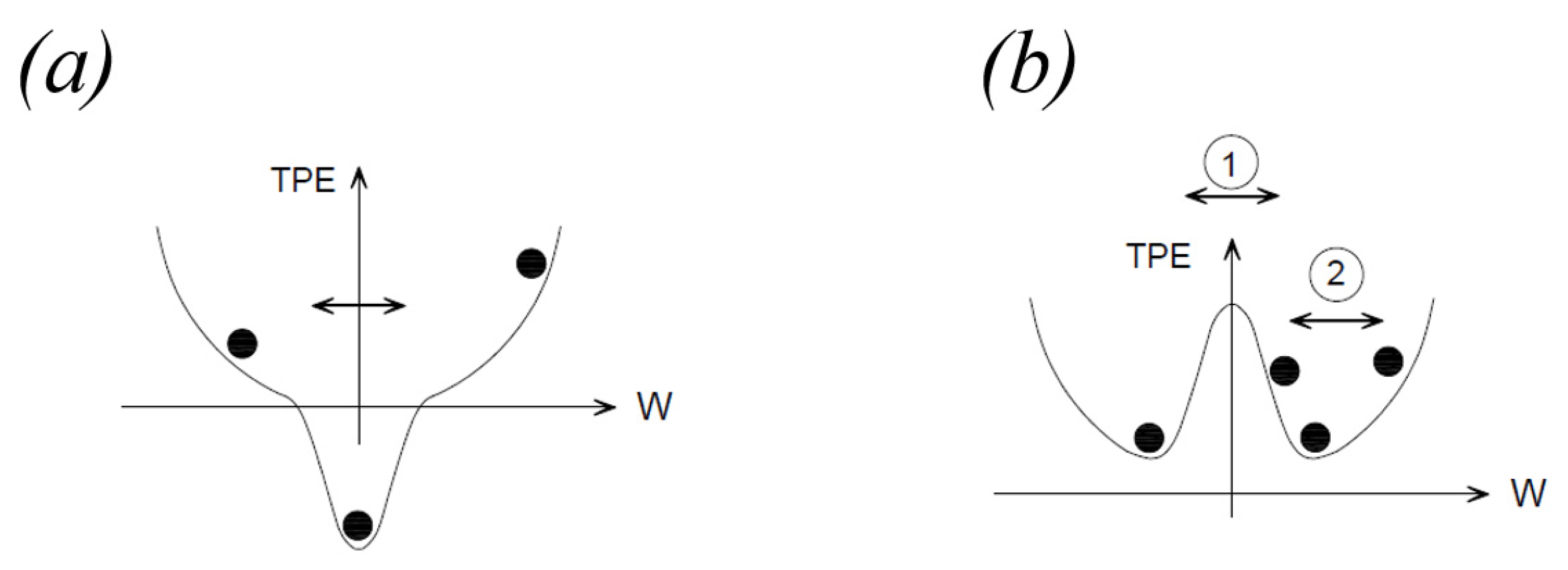
2. Description of the Piezoelectric Energy Harvester
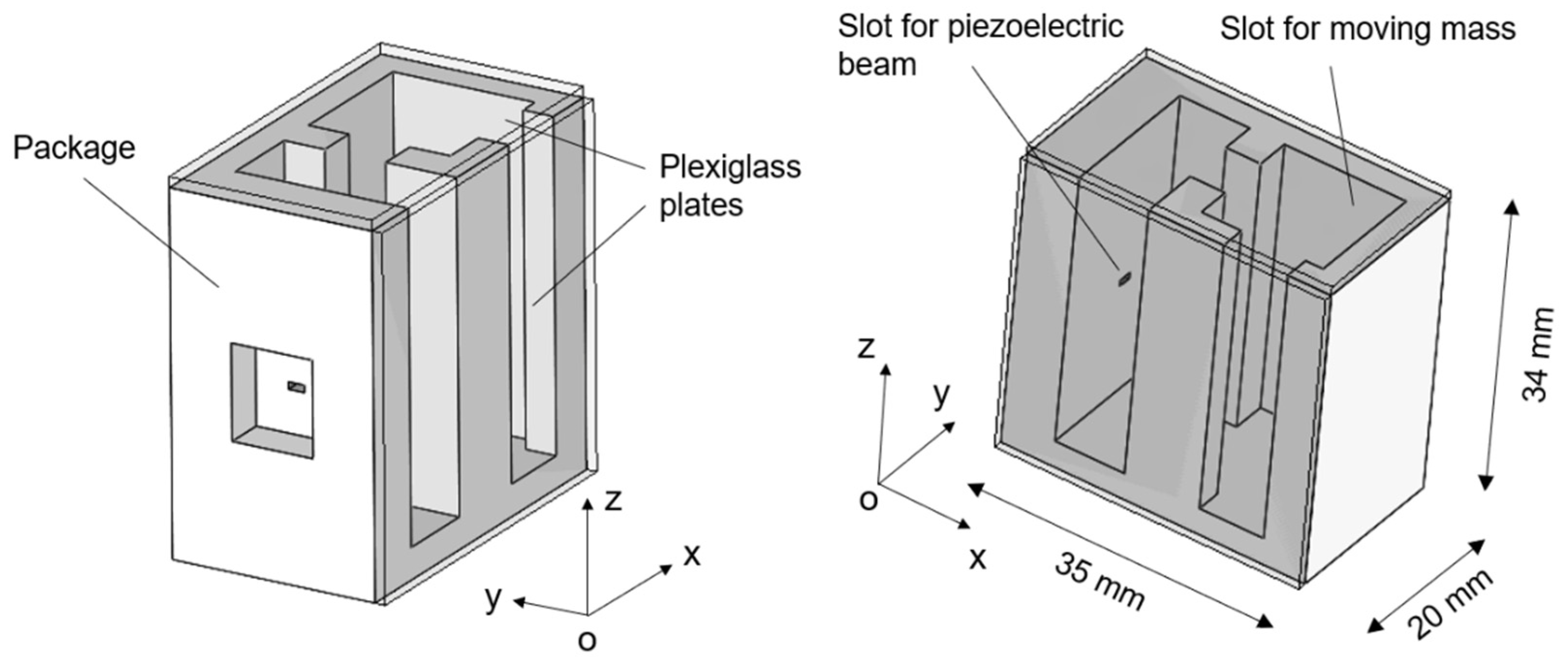
3. Design and Fabrication
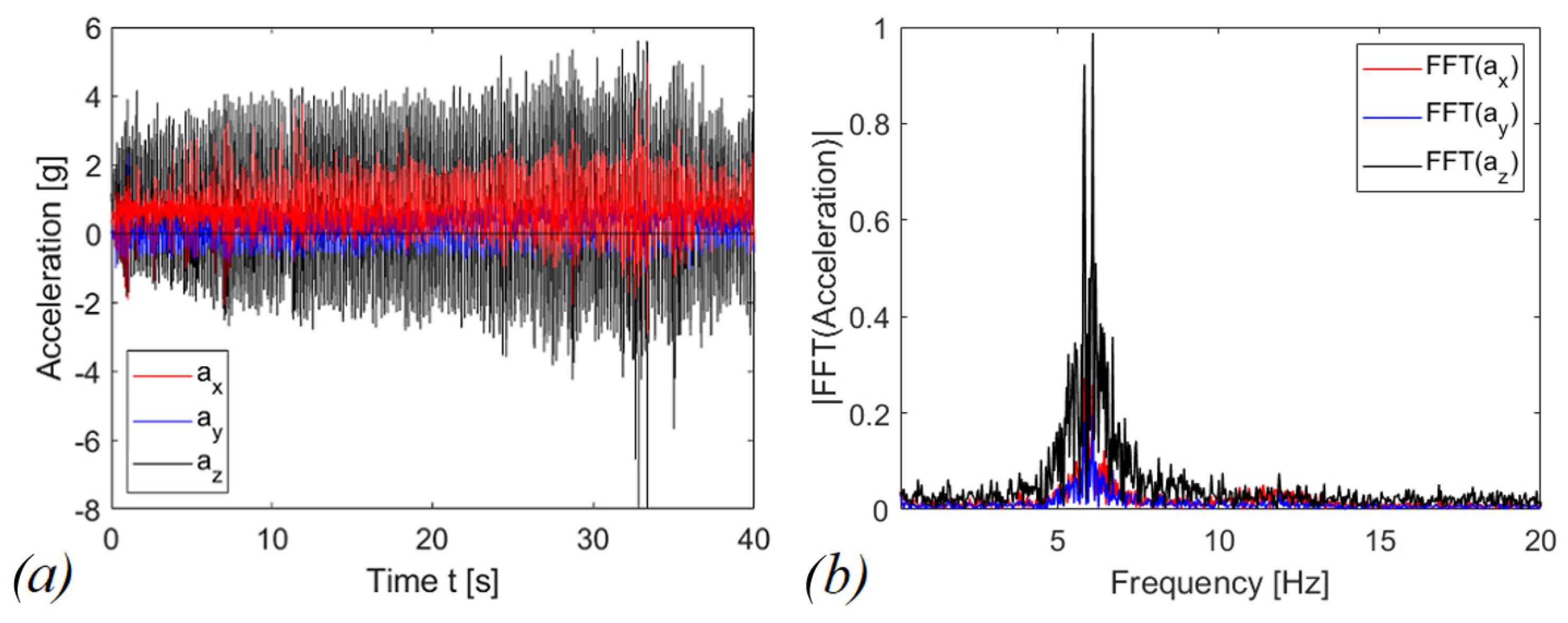
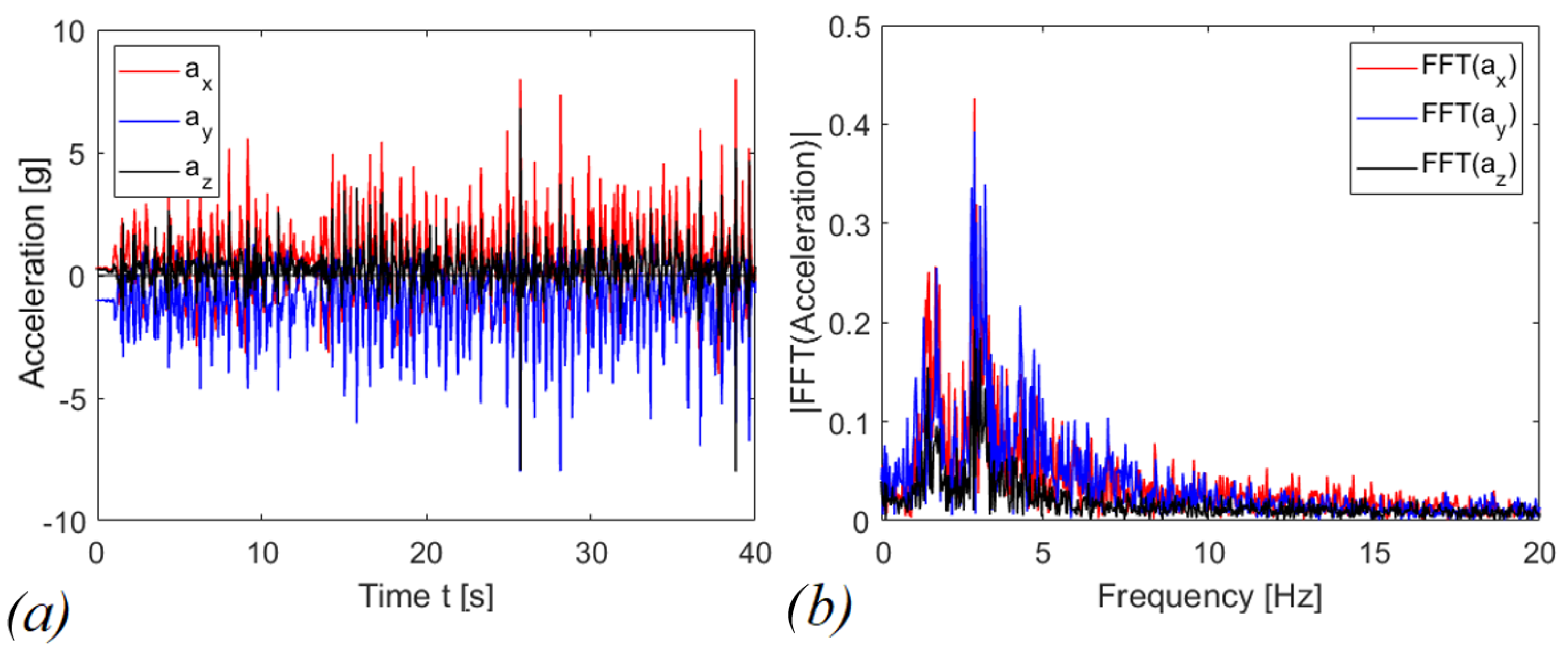
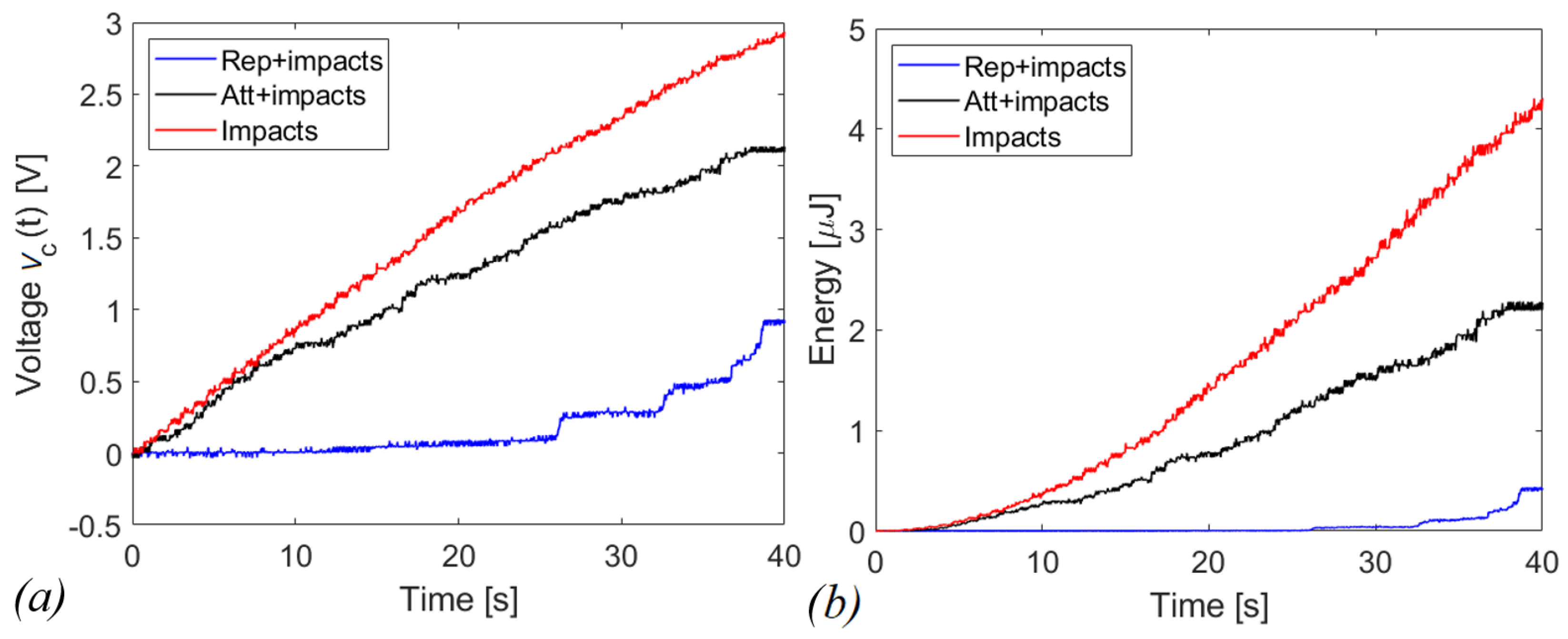
4. Experimental Results
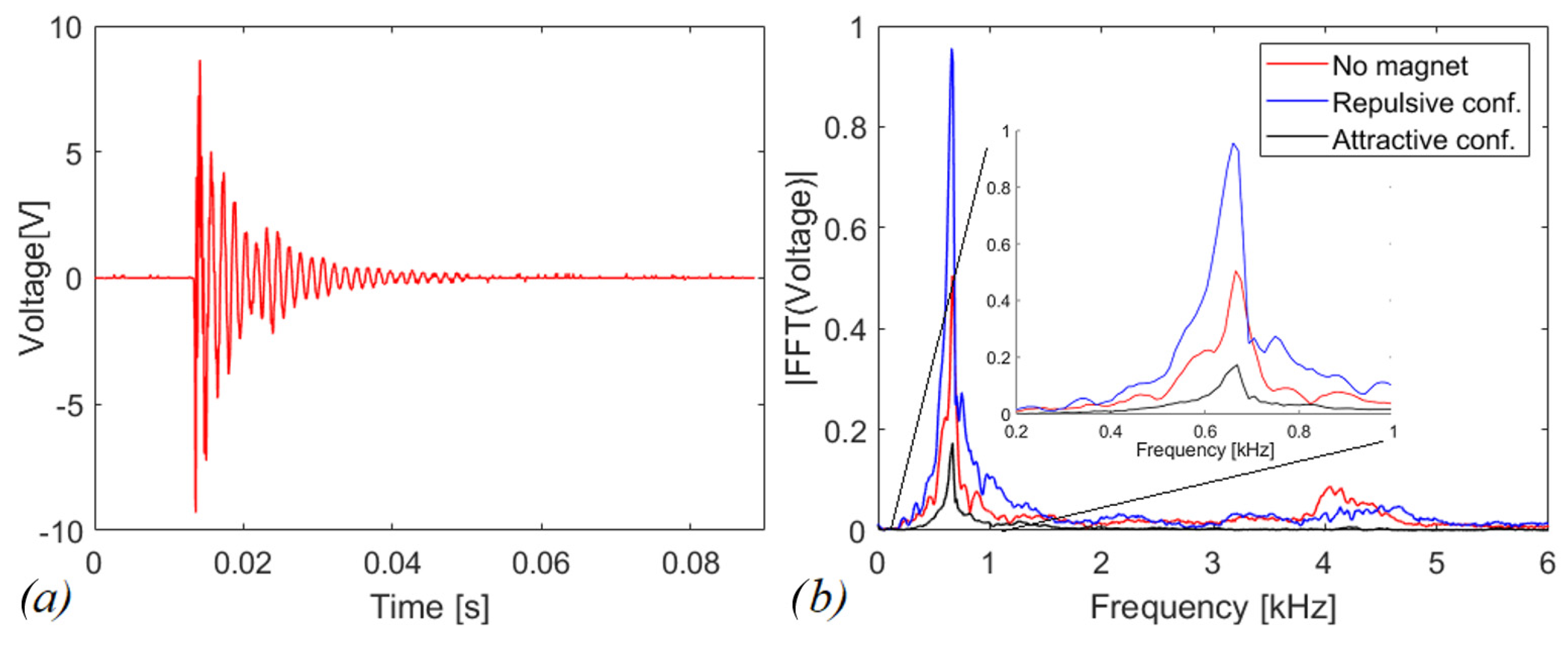
4.1. Free Vibration of the Piezoelectric Beam
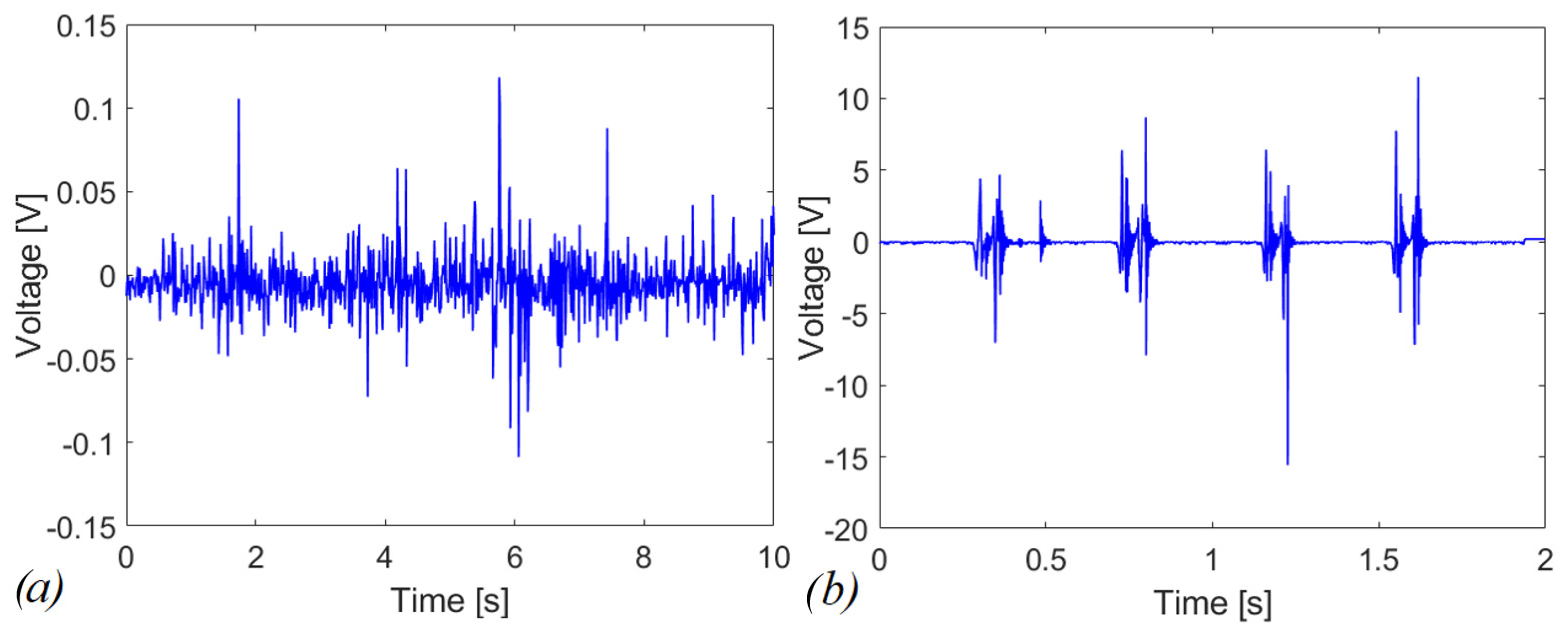
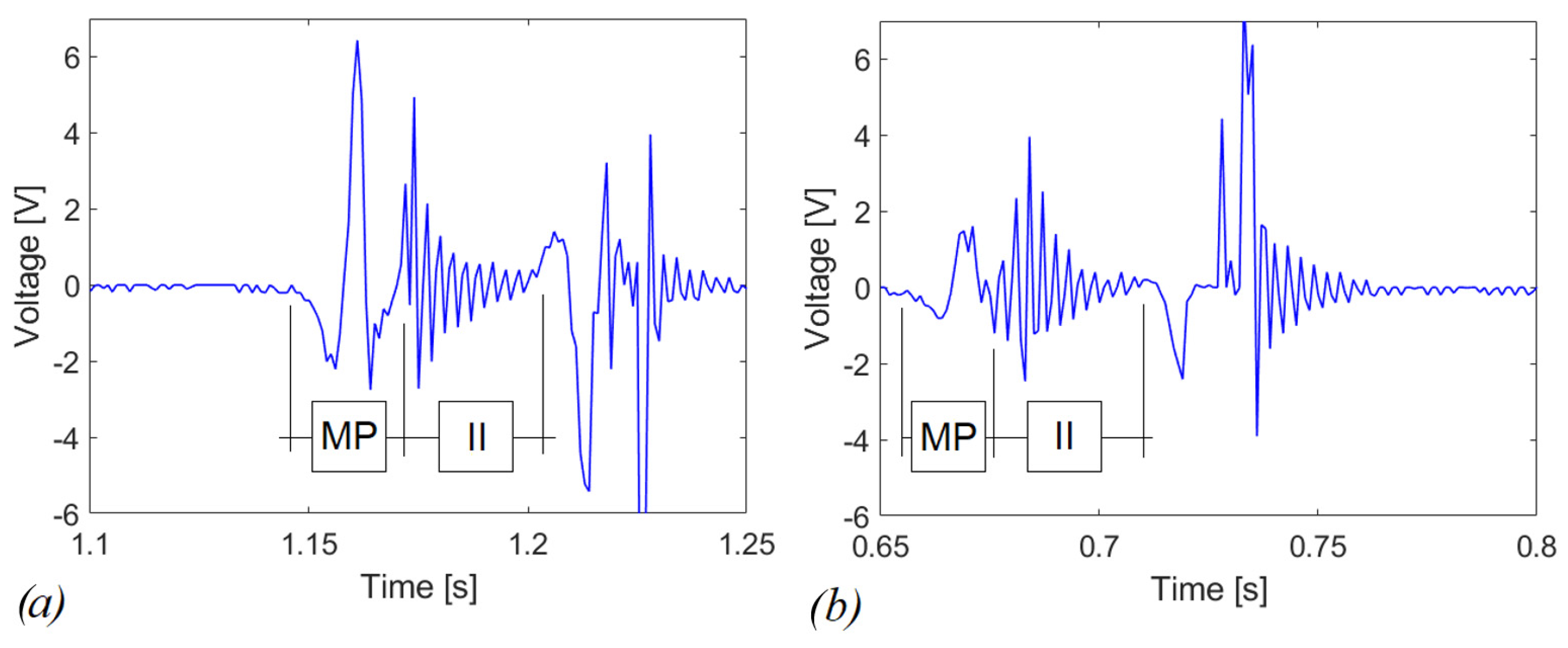
4.2. Experimental Tests in Open Circuit
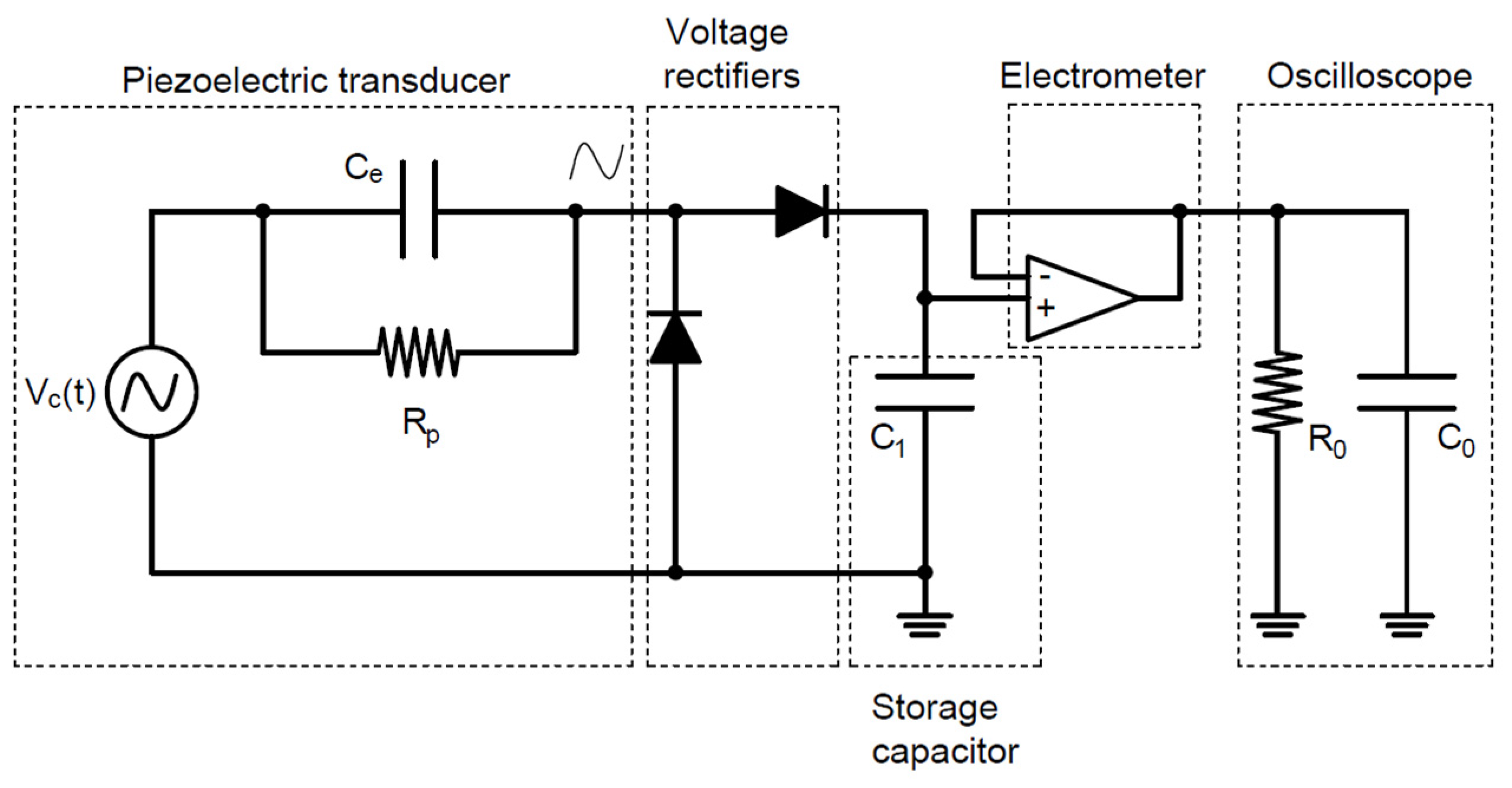
4.3. Experimental Tests with a Connected Circuit
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Corigliano, A.; Ardito, R.; Comi, C.; Frangi, A.; Ghisi, A.; Mariani, S. Mechanics of Microsystem, 1st ed.; Wiley: Chichester, UK, 2018. [Google Scholar]
- Tewar, D.; Baul, S. Microelectromechanical System (MEMS) Market by Type (Sensors, & Actuators), and Application (Consumer Electronics, Automotive, Industrial, Aerospace & Defense, Healthcare, and Telecommunication, and Others): Global Opportunity Analysis and Industry Forecast, 2019–2026; Allied Market Research: Portland, OR, USA, 2019. [Google Scholar]
- Priya, S.; Inman, D. Energy Harvesting Technologies, 1st ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Ertruk, A.; Inman, J.D. Piezoelectric Energy Harvesting, 1st ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Spies, P.; Mateu, L.; Pollak, M. Handbook of Energy Harvesting Power Supplies and Applications; Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy Scavenging for Wireless Sensor Networks; Springer Science + Business Media: New York, NY, USA, 2004. [Google Scholar]
- Maamer, B.; Boughamoura, A.; Fath El-Bab, A.M.R.; Francis, A.L. A review on design improvements and techniques for mechanical energy harvesting using piezoelectric and electromagnetic schemes. Energy Convers. Manag. 2019, 199, 111973. [Google Scholar] [CrossRef]
- Antonsson, E.K.; Mann, R.W. The frequency content of gait. J. Biomech. 1985, 18, 39–47. [Google Scholar] [CrossRef]
- Jeon, Y.B.; Sood, R.; Jeong, J.H.; Kim, S.G. MEMS power generator with transverse mode thin film PZT. Sens. Actuators A Phys. 2005, 122, 16–22. [Google Scholar] [CrossRef]
- Dutoit, N.E.; Wardle, B.L.; Kim, S.G. Design Considerations for MEMS-Scale Piezoelectric Mechanical Vibration Energy Harvesters. Integr. Ferroelectr. 2005, 71, 121–160. [Google Scholar] [CrossRef]
- Nastro, A.; Pienazza, N.; Baù, M.; Aceti, P.; Rouvala, M.; Ardito, R.; Ferrari, M.; Corigliano, A.; Ferrari, V. Wearable Ball-Impact Piezoelectric Multi-Converters for Low-Frequency Energy Harvesting from Human Motion. Sensors 2022, 22, 772. [Google Scholar] [CrossRef]
- Halim, M.A.; Kabir, M.H.; Cho, H.; Park, J.Y. A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion. Micromachines 2019, 10, 701. [Google Scholar] [CrossRef]
- Ju, S.; Ji, C.H. Impact-based piezoelectric vibration energy harvester. Appl. Energy 2018, 214, 139–151. [Google Scholar] [CrossRef]
- Speciale, A.; Ardito, R.; Baù, M.; Ferrari, M.; Ferrari, V.; Frangi, A. Snap-through buckling mechanism for frequency-up conversion in piezoelectric energy harvesting. Appl. Sci. 2020, 10, 3614. [Google Scholar] [CrossRef]
- Xu, R.; Haluk, A.; Kim, S.G. Buckled MEMS beams for energy harvesting from low frequency vibrations. Research 2019, 2019, 1087946. [Google Scholar] [CrossRef]
- Shin, Y.H.; Choi, J.; Kim, S.J.; Kim, S.; Maurya, D.; Sung, T.H.; Priya, S.; Kang, C.Y.; Song, H.C. Automatic resonance tuning mechanism for ultra-wide bandwidth mechanical energy harvesting. Nano Energy 2020, 77, 104986. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Y.; Li, T.; Yan, Z.; Tan, T. A flute-inspired broadband piezoelectric vibration energy harvesting device with mechanical intelligent design. Appl. Energy 2021, 303, 117577. [Google Scholar] [CrossRef]
- Bonnin, M.; Traversa, F.L.; Bonani, F. An impedance matching solution to increase the harvested power and efficiency of nonlinear piezoelectric energy harvesters. Energies 2022, 15, 2764. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, W.; Hajj, M.R.; Zhang, W.; Tan, T. Ultra-broadband piezoelectric energy harvesting via bistable multi-hardening and multi-softening. Nonlinear Dyn. 2020, 100, 1057–1077. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, S. Performance investigations of nonlinear piezoelectric energy harvesters with a resonant circuit under white Gaussian noises. Nonlinear Dyn. 2021, 103, 183–196. [Google Scholar] [CrossRef]
- Pillatsch, P.; Yeatman, E.; Holmes, S. Magnetic plucking of piezoelectric beams for frequency up-converting energy harvesters. Smart Mater. Struct. 2014, 23, 025009. [Google Scholar] [CrossRef]
- Pillatsch, P.; Yeatman, E.; Holmes, A.S. A piezoelectric frequency up-converting energy harvester with rotating proof mass for human body applications. Sens. Actuators 2014, 206, 178–185. [Google Scholar] [CrossRef]
- Dauksevicius, R.; Kleiva, A.; Grigaliunas, V. Analysis of magnetic plucking dynamics in a frequency up-converting piezoelectric energy harvester. Smart Mater. Struct. 2018, 27, 085016. [Google Scholar] [CrossRef]
- Kuang, Y.; Yang, Z. Design and characteristion of a piezoelectric knee-joint energy harvester with frequency up-conversion through magnetic plucking. Smart Mater. Struct. 2015, 25, 085209. [Google Scholar] [CrossRef]
- Pozzi, M. Magnetic plucking of piezoelectric bimorphs for a wearable energy harvester. Smart Mater. Struct. 2016, 25, 045008. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, H.; Wu, Z.; Huang, Z.; Mao, H.; Cao, Y. Broadband spring connected bi-stable piezo-electric vibration energy harvester with variable potential barrier. Results Phys. 2020, 18, 1033173. [Google Scholar] [CrossRef]
- Baù, M.; Alghisi, D.; Dalola, S.; Ferrari, M.; Ferrari, V. Multi-frequency array of nonlinear piezoelectric converters for vibration energy harvesting. Smart Mater. Struct. 2020, 29, 085047. [Google Scholar] [CrossRef]
- Ardito, R.; Corigliano, A.; Gafforelli, G.; Valzasina, G.; Procopio, F.; Zafalon, R. Advanced model for fast assessment of piezoelectric micro energy harvesters. Front. Mater. 2016, 3, 17. [Google Scholar] [CrossRef]
- Gafforelli, G.; Ardito, R.; Corigliano, A. Improved one-dimensional model for piezoelectric laminates for energy harvesters including three dimensional effects. Compos. Struct. 2015, 127, 369–381. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan and Co.: London, UK, 1877. [Google Scholar]
- Akoun, G.; Yonnet, J. 3D Analytical calculation of the forces extered between two cuboidal magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar] [CrossRef]
- Yonnet, J.P.; Allag, H. Three-dimensional analytical calculation of permanent magnets interactions by “magnetic node” representation. IEEE Trans. Magn. 2011, 47, 2050–2055. [Google Scholar] [CrossRef]
- Rakotoarison, H.L.; Yonnet, J.P.; Delinchant, B. Using coulombian approach for modelling scalar potential and magnetic field of a permanent magnet with radial polarization. IEEE Trans. Magn. 2007, 43, 1261–1264. [Google Scholar] [CrossRef]
- Schomburg, W.K.; Reinertz, O.; Sackmann, J.; Schmitz, K. Equations for the approximate calculation of forces between cuboid magnets. J. Magn. Magn. Mater. 2020, 506, 166694. [Google Scholar] [CrossRef]
- Rosso, M.; Corigliano, A.; Ardito, R. Numerical and experimental evaluation of the magnetic interaction for frequency up-conversion in piezoelectric vibration energy harvesters. Meccanica 2022, 57, 1139–1154. [Google Scholar] [CrossRef]
- Clough, R.; Penzien, J. Dynamics of Structures, 3rd ed.; Computers & Structures Inc.: Berkeley, CA, USA, 2003. [Google Scholar]







| Material | ρ [kg/m3] | E [GPa] | ν [-] | d31 [pC/N] | ε33s [-] | t [mm] | Width [mm] | Length [mm] |
|---|---|---|---|---|---|---|---|---|
| Titanium | 4500 | 115 | 0.3 | - | - | 0.065 | 1.5 | 15 |
| PZT | 7500 | 60 | 0.3 | 212 | 2000 | 0.280 per layer | 1.5 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosso, M.; Nastro, A.; Baù, M.; Ferrari, M.; Ferrari, V.; Corigliano, A.; Ardito, R. Piezoelectric Energy Harvesting from Low-Frequency Vibrations Based on Magnetic Plucking and Indirect Impacts. Sensors 2022, 22, 5911. https://doi.org/10.3390/s22155911
Rosso M, Nastro A, Baù M, Ferrari M, Ferrari V, Corigliano A, Ardito R. Piezoelectric Energy Harvesting from Low-Frequency Vibrations Based on Magnetic Plucking and Indirect Impacts. Sensors. 2022; 22(15):5911. https://doi.org/10.3390/s22155911
Chicago/Turabian StyleRosso, Michele, Alessandro Nastro, Marco Baù, Marco Ferrari, Vittorio Ferrari, Alberto Corigliano, and Raffaele Ardito. 2022. "Piezoelectric Energy Harvesting from Low-Frequency Vibrations Based on Magnetic Plucking and Indirect Impacts" Sensors 22, no. 15: 5911. https://doi.org/10.3390/s22155911
APA StyleRosso, M., Nastro, A., Baù, M., Ferrari, M., Ferrari, V., Corigliano, A., & Ardito, R. (2022). Piezoelectric Energy Harvesting from Low-Frequency Vibrations Based on Magnetic Plucking and Indirect Impacts. Sensors, 22(15), 5911. https://doi.org/10.3390/s22155911











