Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning
Abstract
:1. Introduction
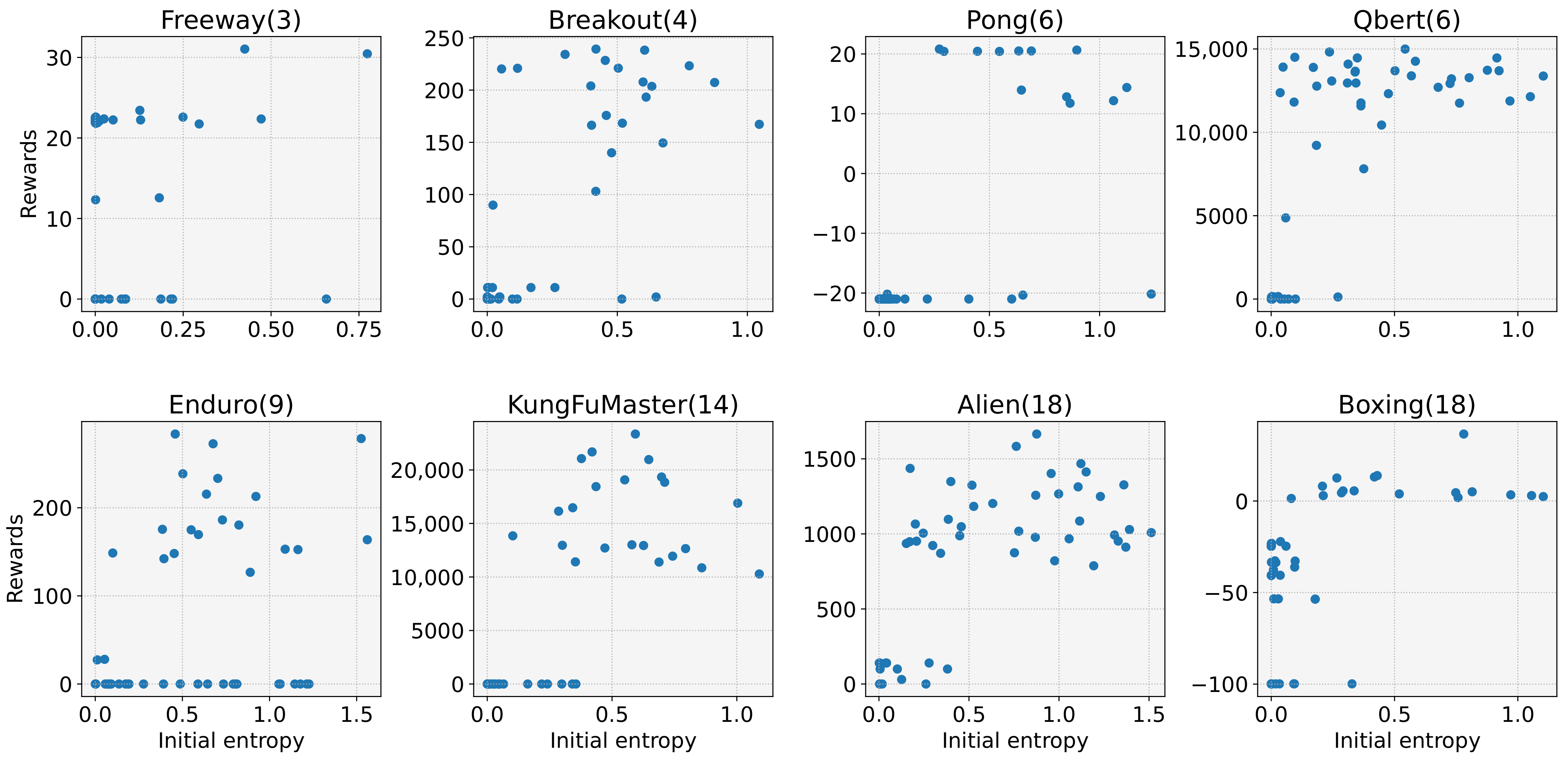
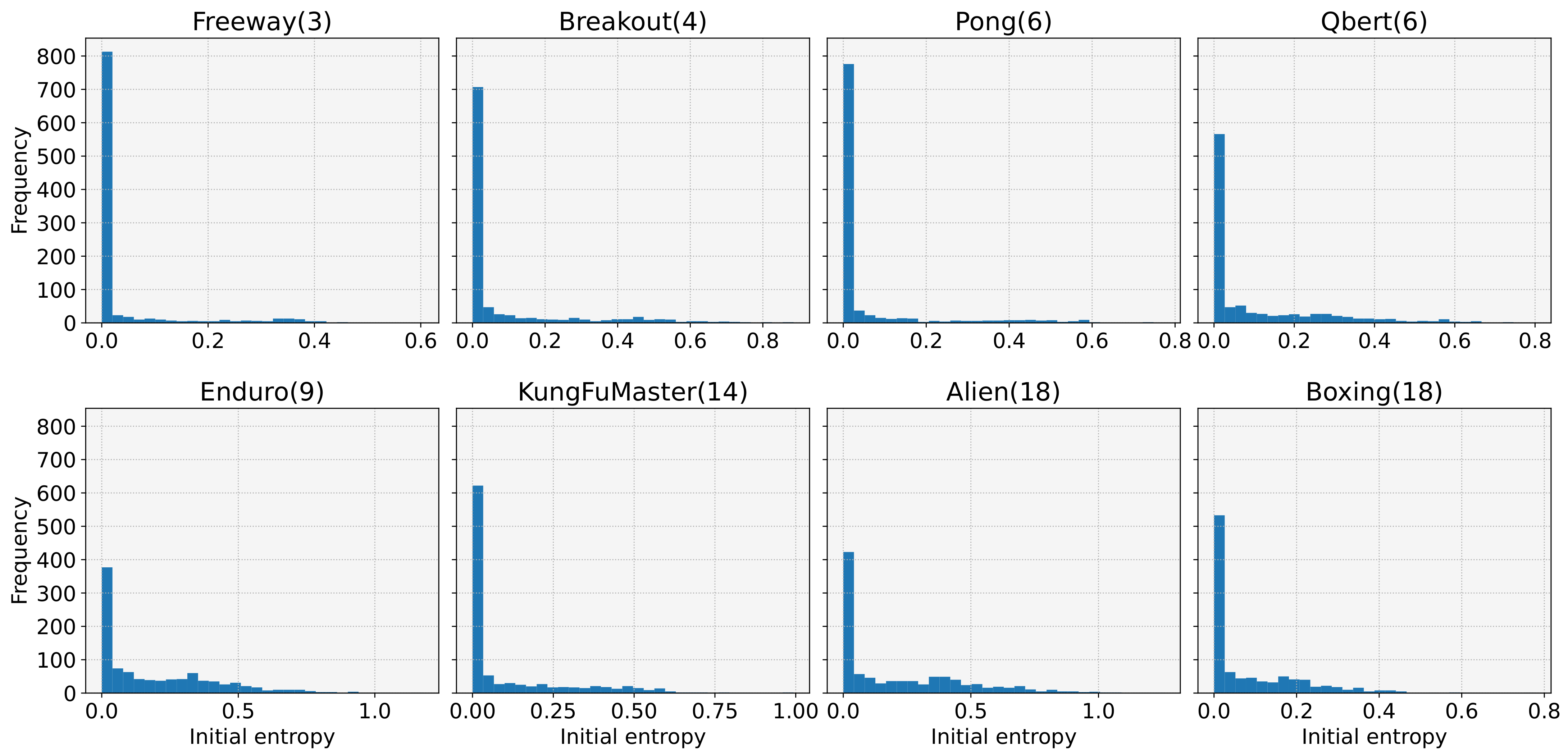
- We reveal a cause of frequent learning failures despite the ease of the tasks. Our investigations show that the model with low initial entropy significantly increases the probability of learning failures, and that the initial entropy is biased towards a low value for various tasks. Moreover, we observe that the initial entropy varies depending on the task and initial weight of the model. These dependencies make it difficult to control the initial entropy of the discrete control tasks;
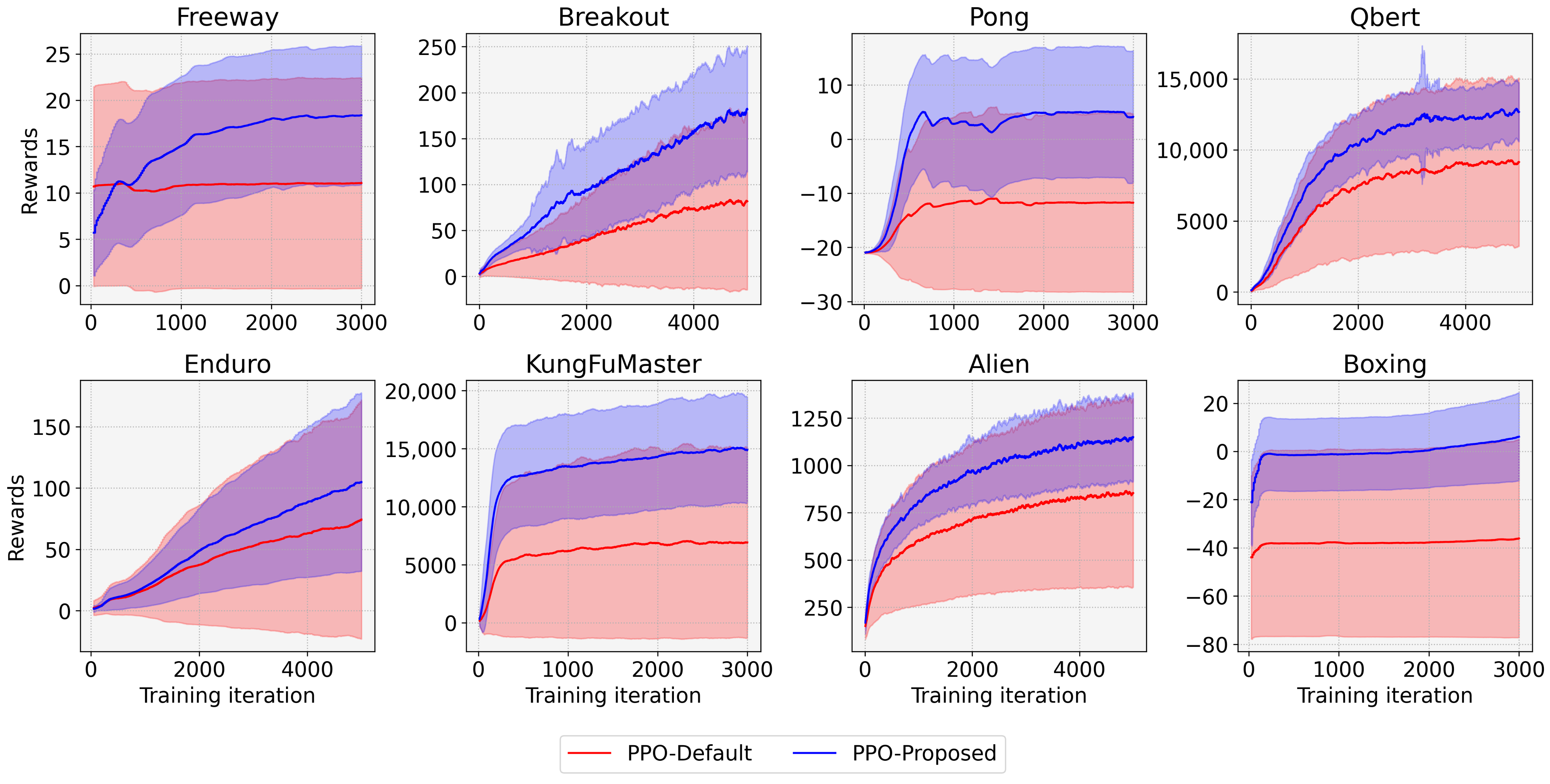
- We devise entropy-aware model initialization, a simple yet powerful learning strategy that exploits the effect of the initial entropy that we have analyzed. The devised learning strategy repeats the model initialization and entropy measurements until the initial entropy exceeds an entropy threshold. It can be used with any reinforcement learning algorithm because the proposed strategy just provides a well-initialized model to a DRL algorithm. The experimental results show that entropy-aware model initialization significantly reduces learning failures and improves performance, stability, and learning speed.
2. Effect of Initial Entropy in DRL
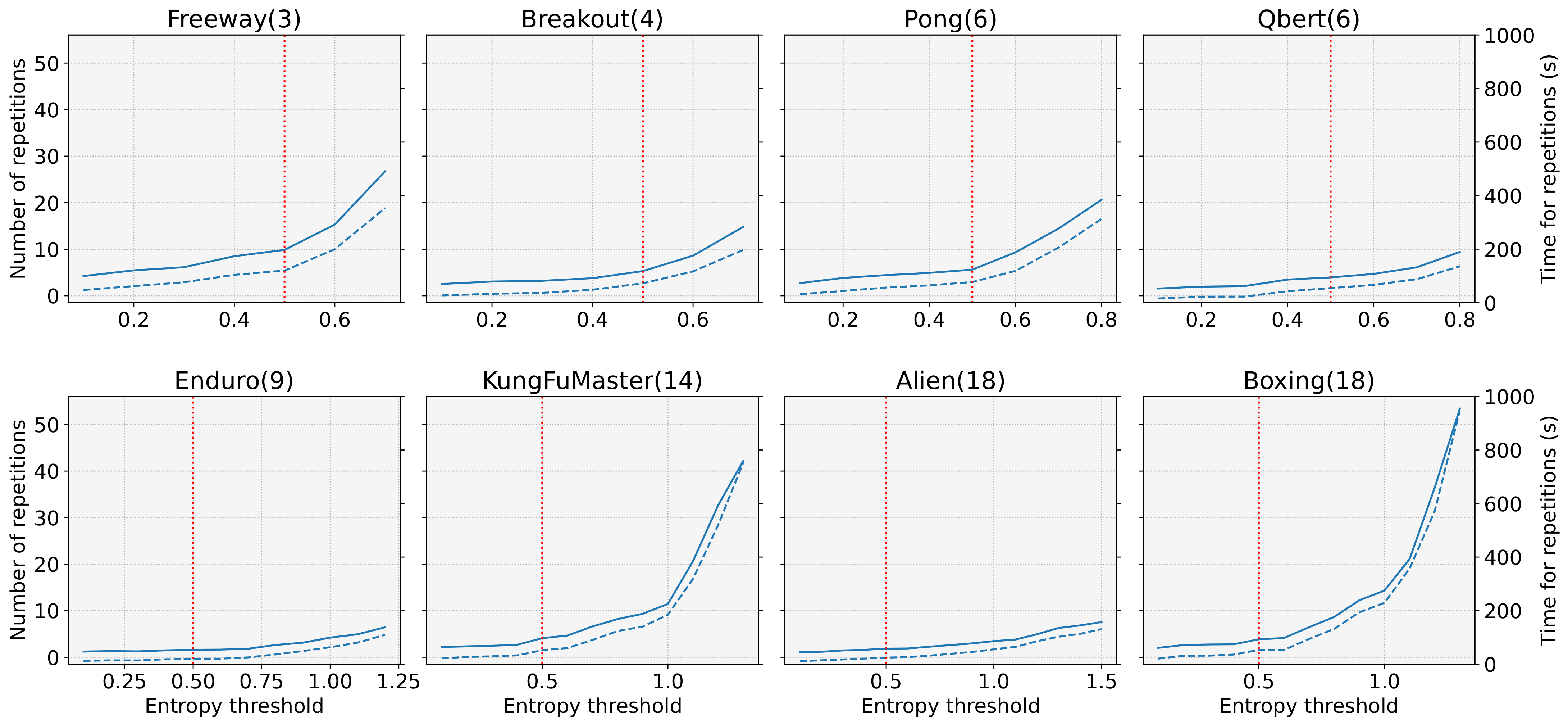
3. Entropy-Aware Model Initialization
| Algorithm 1: Entropy-aware model initialization. |
 |
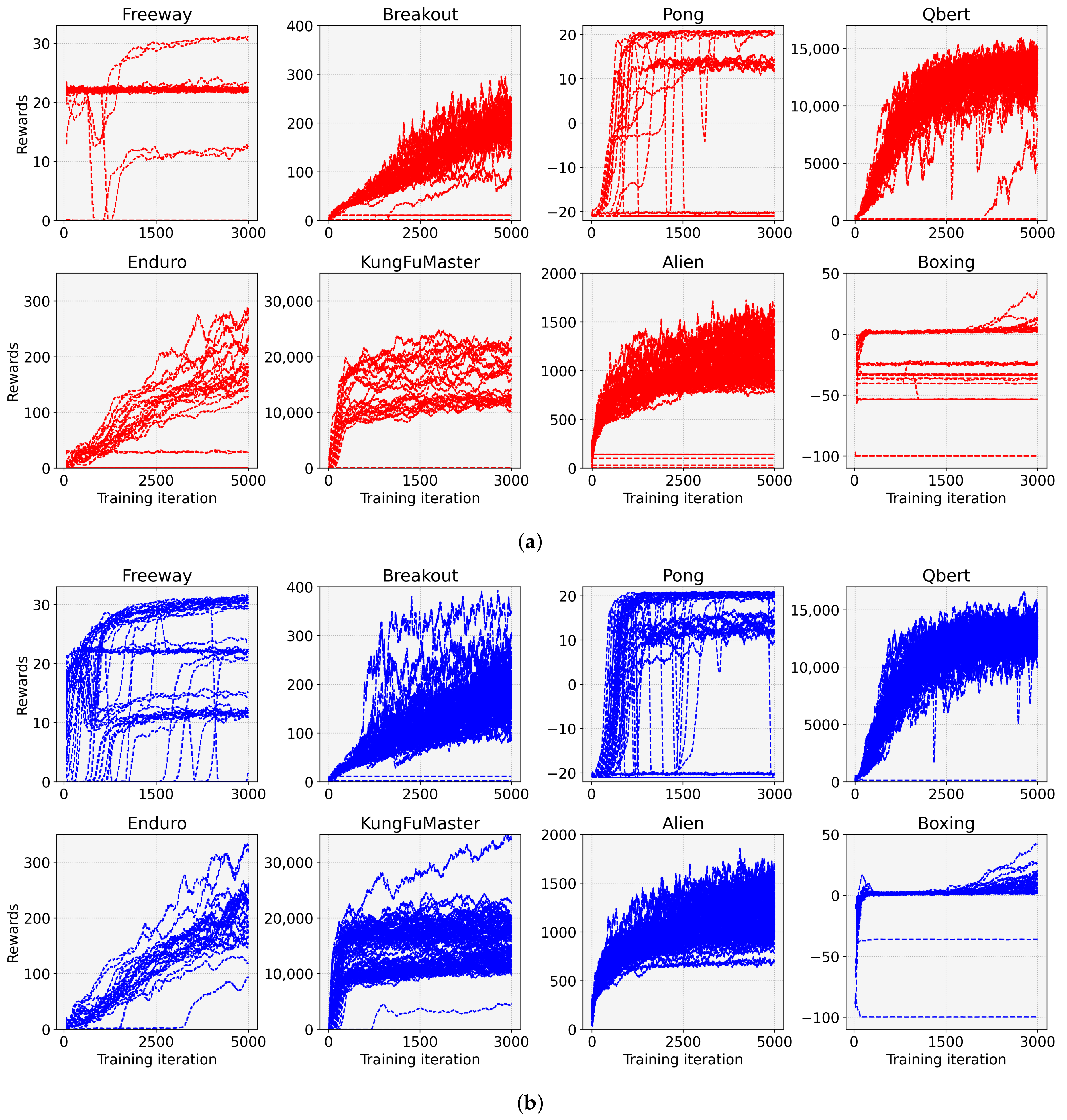
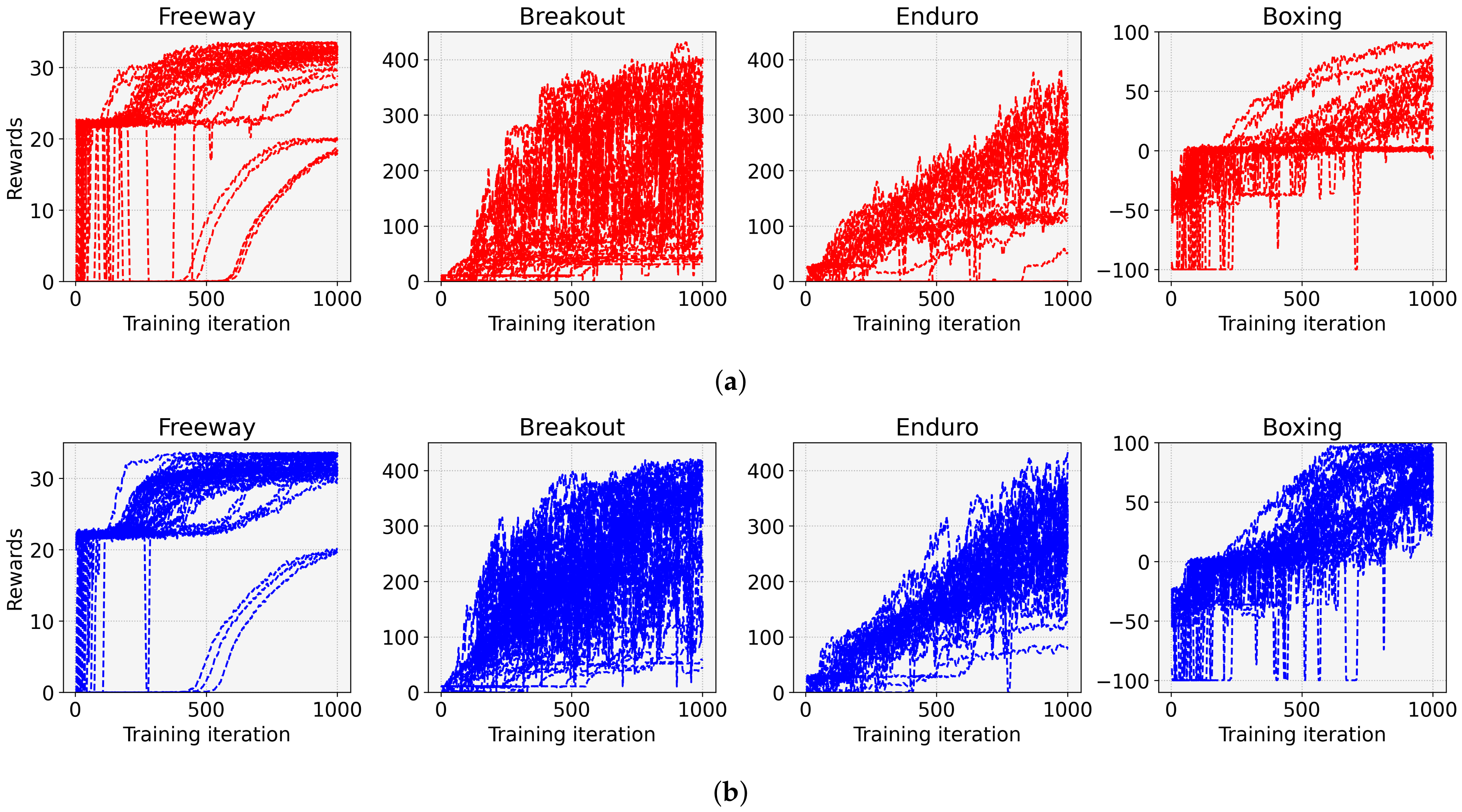
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Merrick, K.; Jin, L.; Abbass, H.A. Hierarchical Deep Reinforcement Learning for Continuous Action Control. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 5174–5184. [Google Scholar] [CrossRef] [PubMed]
- Haarnoja, T.; Pong, V.; Zhou, A.; Dalal, M.; Abbeel, P.; Levine, S. Composable Deep Reinforcement Learning for Robotic Manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 6244–6251. [Google Scholar]
- Lathuilière, S.; Massé, B.; Mesejo, P.; Horaud, R. Neural network based reinforcement learning for audio–visual gaze control in human–robot interaction. Pattern Recognit. Lett. 2019, 118, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Jang, S.; Choi, C. Prioritized Environment Configuration for Drone Control with Deep Reinforcement Learning. Hum. Centric Comput. Inf. Sci. 2022, 12, 1–16. [Google Scholar]
- Zhang, Q.; Ma, X.; Yang, Y.; Li, C.; Yang, J.; Liu, Y.; Liang, B. Learning to Discover Task-Relevant Features for Interpretable Reinforcement Learning. IEEE Robot. Autom. Lett. 2021, 6, 6601–6607. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the Game of Go without Human Knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Patel, D.; Hazan, H.; Saunders, D.J.; Siegelmann, H.T.; Kozma, R. Improved Robustness of Reinforcement Learning Policies upon Conversion to Spiking Neuronal Network Platforms Applied to Atari Breakout Game. Neural Netw. 2019, 120, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Nicholaus, I.T.; Kang, D.K. Robust experience replay sampling for multi-agent reinforcement learning. Pattern Recognit. Lett. 2021, 155, 135–142. [Google Scholar] [CrossRef]
- Ghesu, F.C.; Georgescu, B.; Zheng, Y.; Grbic, S.; Maier, A.; Hornegger, J.; Comaniciu, D. Multi-scale Deep Reinforcement Learning for Real-time 3D-landmark Detection in CT Scans. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 41, 176–189. [Google Scholar] [CrossRef] [PubMed]
- Raghu, A.; Komorowski, M.; Celi, L.A.; Szolovits, P.; Ghassemi, M. Continuous state-space models for optimal sepsis treatment: A deep reinforcement learning approach. In Proceedings of the Machine Learning for Healthcare Conference, Boston, MA, USA, 18–19 August 2017; pp. 147–163. [Google Scholar]
- Zarkias, K.S.; Passalis, N.; Tsantekidis, A.; Tefas, A. Deep Reinforcement Learning for Financial Trading using Price Trailing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3067–3071. [Google Scholar]
- Tsantekidis, A.; Passalis, N.; Tefas, A. Diversity-driven Knowledge Distillation for Financial Trading using Deep Reinforcement Learning. Neural Netw. 2021, 140, 193–202. [Google Scholar] [CrossRef]
- Ishii, S.; Yoshida, W.; Yoshimoto, J. Control of Exploitation–Exploration Meta-parameter in Reinforcement Learning. Neural Netw. 2002, 15, 665–687. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Wang, H.; Zhang, H.; Li, M.; Xiang, M.; Luo, C.; Ren, P. Underwater Image Enhancement with Reinforcement Learning. IEEE J. Ocean. Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-critic: Off-policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Seo, Y.; Chen, L.; Shin, J.; Lee, H.; Abbeel, P.; Lee, K. State Entropy Maximization with Random Encoders for Efficient Exploration. In Proceedings of the International Conference on Machine Learning (ICML), Online, 18–24 July 2021; pp. 9443–9454. [Google Scholar]
- Zhang, Y.; Vuong, Q.H.; Song, K.; Gong, X.Y.; Ross, K.W. Efficient Entropy for Policy Gradient with Multidimensional Action Space. arXiv 2018, arXiv:1806.00589. [Google Scholar]
- Ahmed, Z.; Le Roux, N.; Norouzi, M.; Schuurmans, D. Understanding the Impact of Entropy on Policy Optimization. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 151–160. [Google Scholar]
- Chen, J.; Li, S.E.; Tomizuka, M. Interpretable End-to-End Urban Autonomous Driving with Latent Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5068–5078. [Google Scholar] [CrossRef]
- Williams, R.J. Simple Statistical Gradient-following Algorithms for Connectionist Reinforcement Learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef] [Green Version]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Zhao, R.; Sun, X.; Tresp, V. Maximum Entropy-regularized Multi-goal Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 7553–7562. [Google Scholar]
- Wang, Z.; Zhang, Y.; Yin, C.; Huang, Z. Multi-agent Deep Reinforcement Learning based on Maximum Entropy. In Proceedings of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; Volume 4, pp. 1402–1406. [Google Scholar]
- Shi, W.; Song, S.; Wu, C. Soft Policy Gradient Method for Maximum Entropy Deep Reinforcement Learning. arXiv 2019, arXiv:1909.03198. [Google Scholar]
- Cohen, A.; Yu, L.; Qiao, X.; Tong, X. Maximum Entropy Diverse Exploration: Disentangling Maximum Entropy Reinforcement Learning. arXiv 2019, arXiv:1911.00828. [Google Scholar]
- Andrychowicz, M.; Raichuk, A.; Stańczyk, P.; Orsini, M.; Girgin, S.; Marinier, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Michalski, M.; et al. What Matters for On-policy Deep Actor-critic Methods? A Large-scale Study. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Liang, E.; Liaw, R.; Nishihara, R.; Moritz, P.; Fox, R.; Goldberg, K.; Gonzalez, J.; Jordan, M.; Stoica, I. RLlib: Abstractions for Distributed Reinforcement Learning. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 3053–3062. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 20 July 2022).
- Guadarrama, S.; Korattikara, A.; Ramirez, O.; Castro, P.; Holly, E.; Fishman, S.; Wang, K.; Gonina, E.; Wu, N.; Kokiopoulou, E.; et al. TF-Agents: A library for Reinforcement Learning in TensorFlow. 2018. Available online: https://github.com/tensorflow/agents (accessed on 20 July 2022).
- Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; Plappert, M.; Radford, A.; Schulman, J.; Sidor, S.; Wu, Y.; Zhokhov, P. OpenAI Baselines. 2017. Available online: https://github.com/openai/baselines (accessed on 20 July 2022).
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Bellemare, M.; Srinivasan, S.; Ostrovski, G.; Schaul, T.; Saxton, D.; Munos, R. Unifying count-based exploration and intrinsic motivation. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Gym Documentation. 2022. Available online: https://www.gymlibrary.ml/ (accessed on 20 July 2022).
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact Solutions to the Nonlinear Dynamics of Learning in Deep Linear Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Dulac-Arnold, G.; Evans, R.; van Hasselt, H.; Sunehag, P.; Lillicrap, T.; Hunt, J.; Mann, T.; Weber, T.; Degris, T.; Coppin, B. Deep Reinforcement Learning in Large Discrete Action Spaces. arXiv 2015, arXiv:1512.07679. [Google Scholar]
- Tang, Y.; Agrawal, S. Discretizing Continuous Action Space for On-Policy Optimization. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5981–5988. [Google Scholar]


| Size of Action Space | ||||
|---|---|---|---|---|
| 6 | 18 | |||
| Task | Pong | Qbert | Alien | Boxing |
| Seed 01 | ||||
| Seed 02 | ||||
| Seed 03 | ||||
| Seed 04 | ||||
| Seed 05 | ||||
| Seed 06 | ||||
| Seed 07 | ||||
| Seed 08 | ||||
| Seed 09 | ||||
| Seed 10 | ||||
| STD | ||||
| Size of Action Space | ||||
|---|---|---|---|---|
| 3 | 4 | 9 | 14 | |
| Task | Freeway | Breakout | Enduro | KungFuMaster |
| Seed 01 | ||||
| Seed 02 | ||||
| Seed 03 | ||||
| Seed 04 | ||||
| Seed 05 | ||||
| Seed 06 | ||||
| Seed 07 | ||||
| Seed 08 | ||||
| Seed 09 | ||||
| Seed 10 | ||||
| STD | ||||
| Task | Method | Avg. Reward | STD of Reward | Min Reward | Max Reward |
|---|---|---|---|---|---|
| Freeway | Default | 11.067 | 11.369 | 0 | 31.04 |
| Proposed | 18.376 | 7.479 | 0 | 31.55 | |
| Breakout | Default | 81.847 | 97.855 | 0 | 239.27 |
| Proposed | 181.905 | 68.739 | 2 | 348.67 | |
| Pong | Default | −11.736 | 16.507 | −21 | 20.82 |
| Proposed | 4.119 | 12.319 | −21 | 20.86 | |
| Qbert | Default | 9141.865 | 5913.837 | 0 | 14,994.75 |
| Proposed | 12,671.130 | 2068.368 | 125 | 15,605.00 | |
| Enduro | Default | 74.247 | 97.230 | 0 | 283.69 |
| Proposed | 104.804 | 72.493 | 0 | 326.18 | |
| KungFuMaster | Default | 6926.000 | 8241.017 | 0 | 23,356.00 |
| Proposed | 14,896.011 | 4562.688 | 0 | 34,334.00 | |
| Alien | Default | 854.550 | 498.047 | 0 | 1665.00 |
| Proposed | 1148.814 | 233.470 | 693.60 | 1665.30 | |
| Boxing | Default | −36.100 | 41.182 | −99.94 | 36.55 |
| Proposed | 6.113 | 18.284 | −99.88 | 42.10 |
| Task | Method | Avg. Reward | STD of Reward | Min Reward | Max Reward |
|---|---|---|---|---|---|
| Freeway | Default | 29.839 | 4.710 | 18.06 | 33.41 |
| Proposed | 31.199 | 3.094 | 19.59 | 33.59 | |
| Breakout | Default | 198.892 | 131.255 | 31.00 | 398.53 |
| Proposed | 287.870 | 106.686 | 45.36 | 412.72 | |
| Enduro | Default | 141.083 | 115.656 | 0 | 328.90 |
| Proposed | 285.711 | 79.364 | 78.26 | 432.87 | |
| Boxing | Default | 25.184 | 30.662 | −7.51 | 90.07 |
| Proposed | 78.129 | 15.385 | 48.09 | 99.39 |
| Task | Average Number of Initialization (#) | Average Time for Initialization (s) | Time Overhead (%) |
|---|---|---|---|
| Freeway | 9.86 | 119.993 | 4.000 |
| Breakout | 5.30 | 72.544 | 1.451 |
| Pong | 5.62 | 77.335 | 2.578 |
| Qbert | 3.94 | 54.540 | 1.091 |
| Enduro | 1.60 | 20.516 | 0.410 |
| KungFuMaster | 4.10 | 52.141 | 1.738 |
| Alien | 1.84 | 24.536 | 0.491 |
| Boxing | 3.86 | 53.115 | 1.771 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, S.; Kim, H.-I. Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning. Sensors 2022, 22, 5845. https://doi.org/10.3390/s22155845
Jang S, Kim H-I. Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning. Sensors. 2022; 22(15):5845. https://doi.org/10.3390/s22155845
Chicago/Turabian StyleJang, Sooyoung, and Hyung-Il Kim. 2022. "Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning" Sensors 22, no. 15: 5845. https://doi.org/10.3390/s22155845
APA StyleJang, S., & Kim, H.-I. (2022). Entropy-Aware Model Initialization for Effective Exploration in Deep Reinforcement Learning. Sensors, 22(15), 5845. https://doi.org/10.3390/s22155845






