Asymmetrical Artificial Potential Field as Framework of Nonlinear PID Loop to Control Position Tracking by Nonholonomic UAVs
Abstract
:1. Introduction
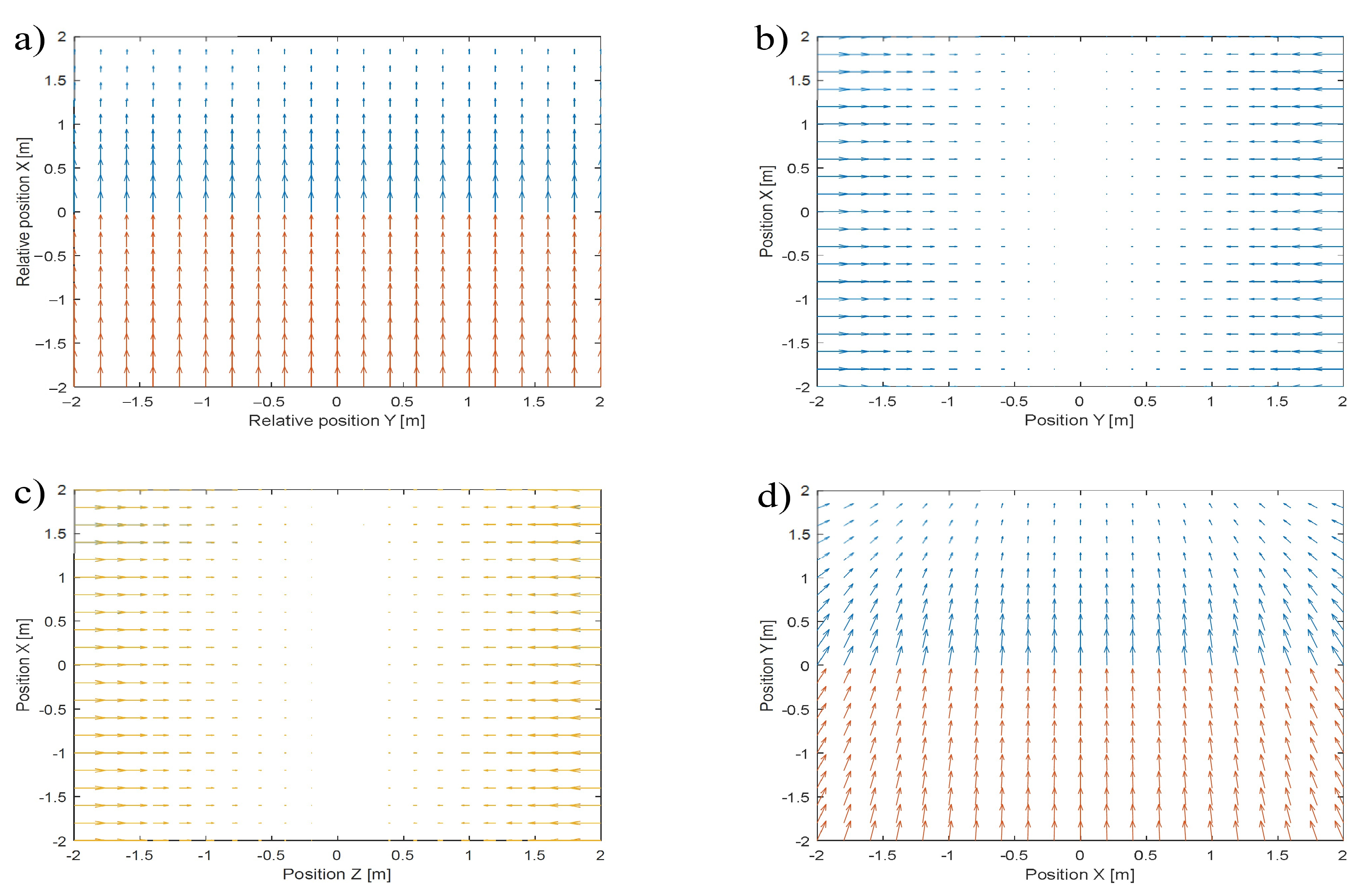
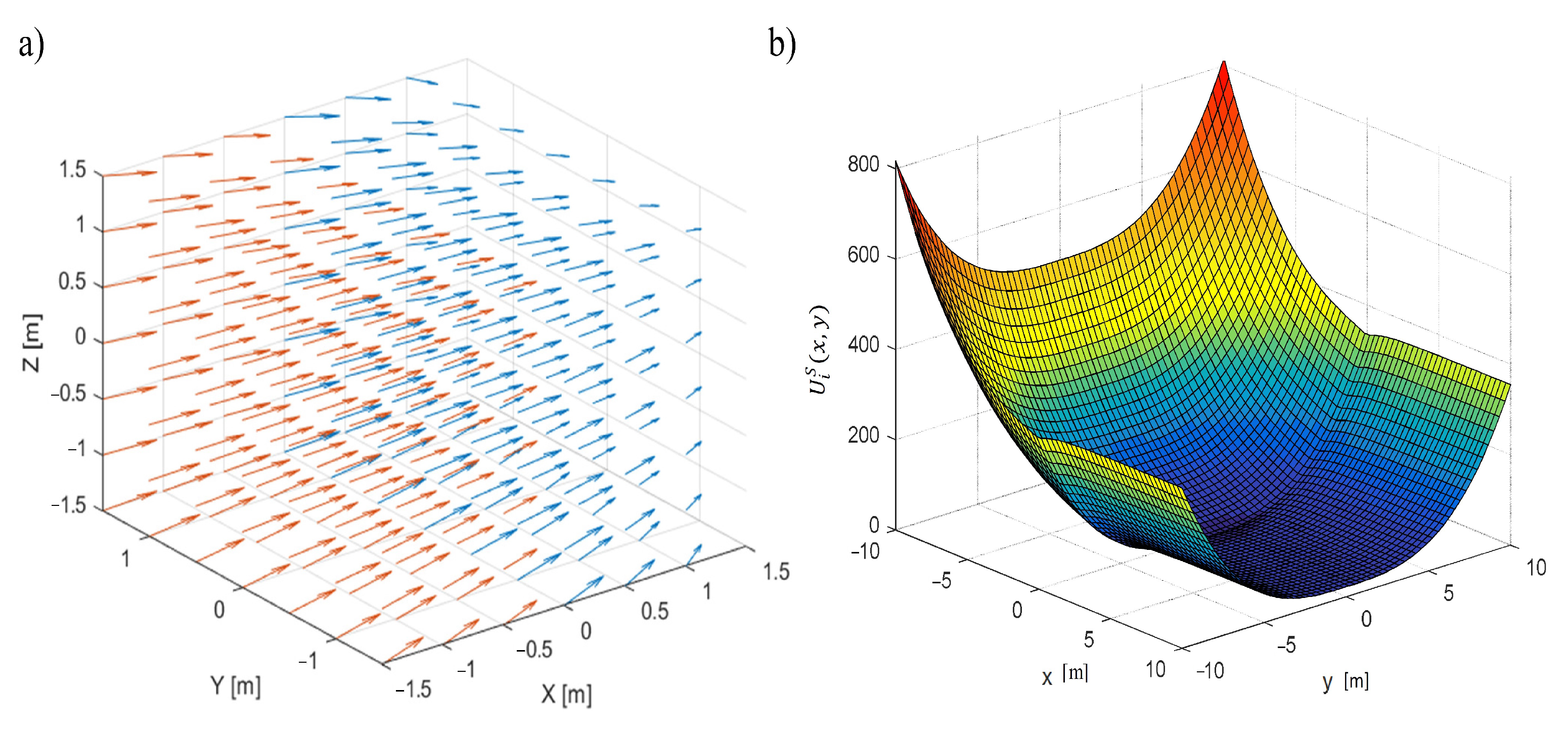
2. Artificial Asymmetrical Potential Field as Nonlinear Proportional Term
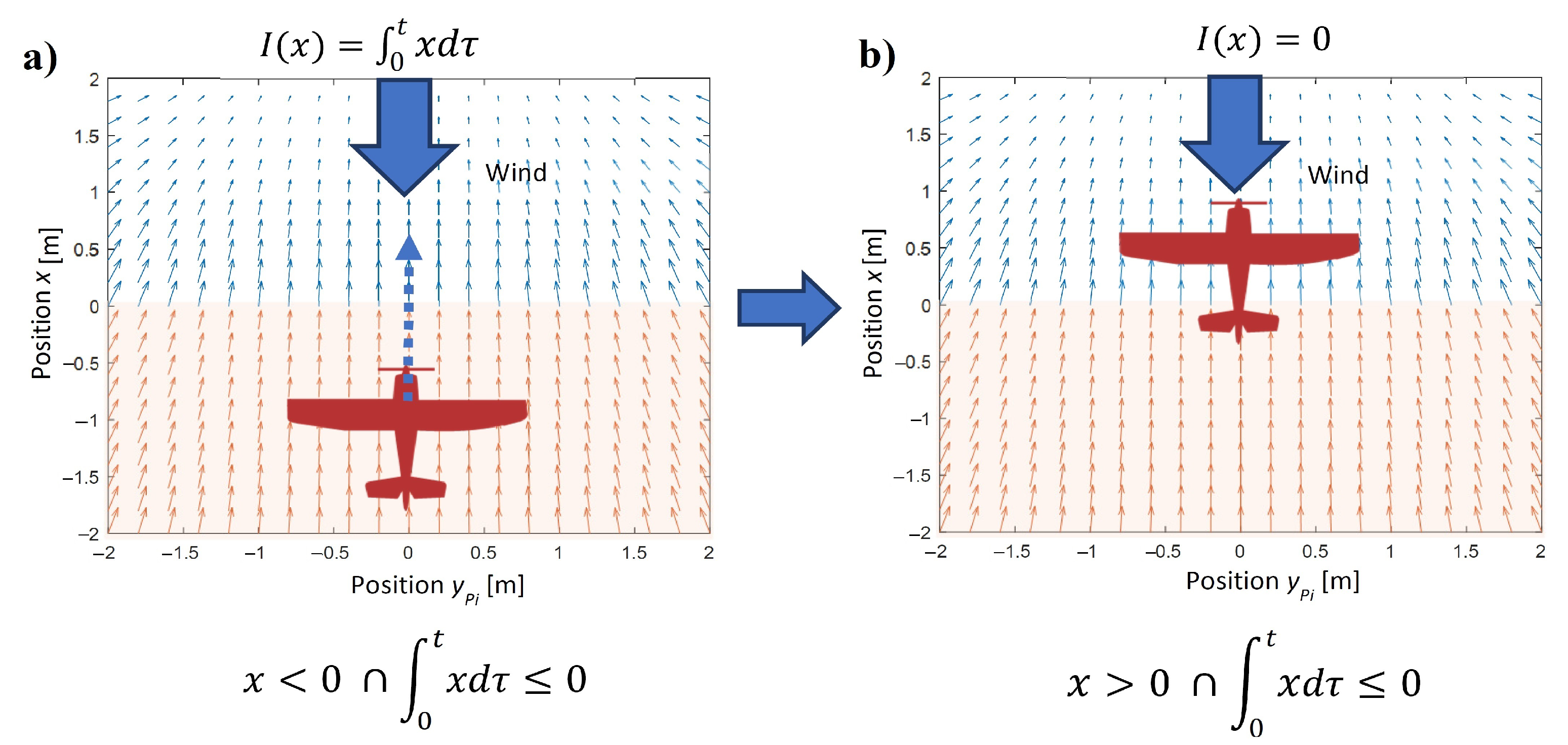
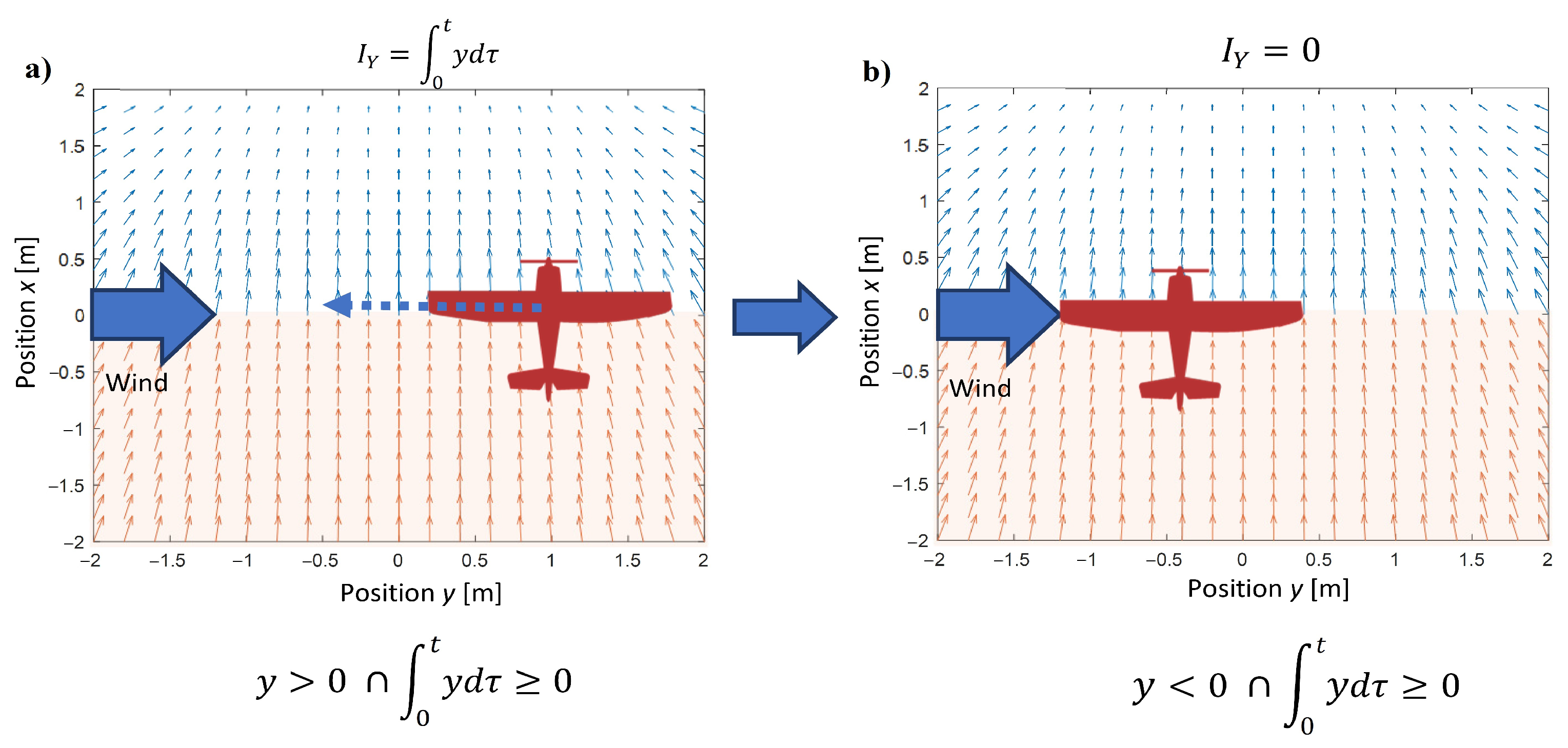
3. Nonlinear Integral Term of PID Control Loop
4. Nonlinear Derivative Term of PID Control Loop
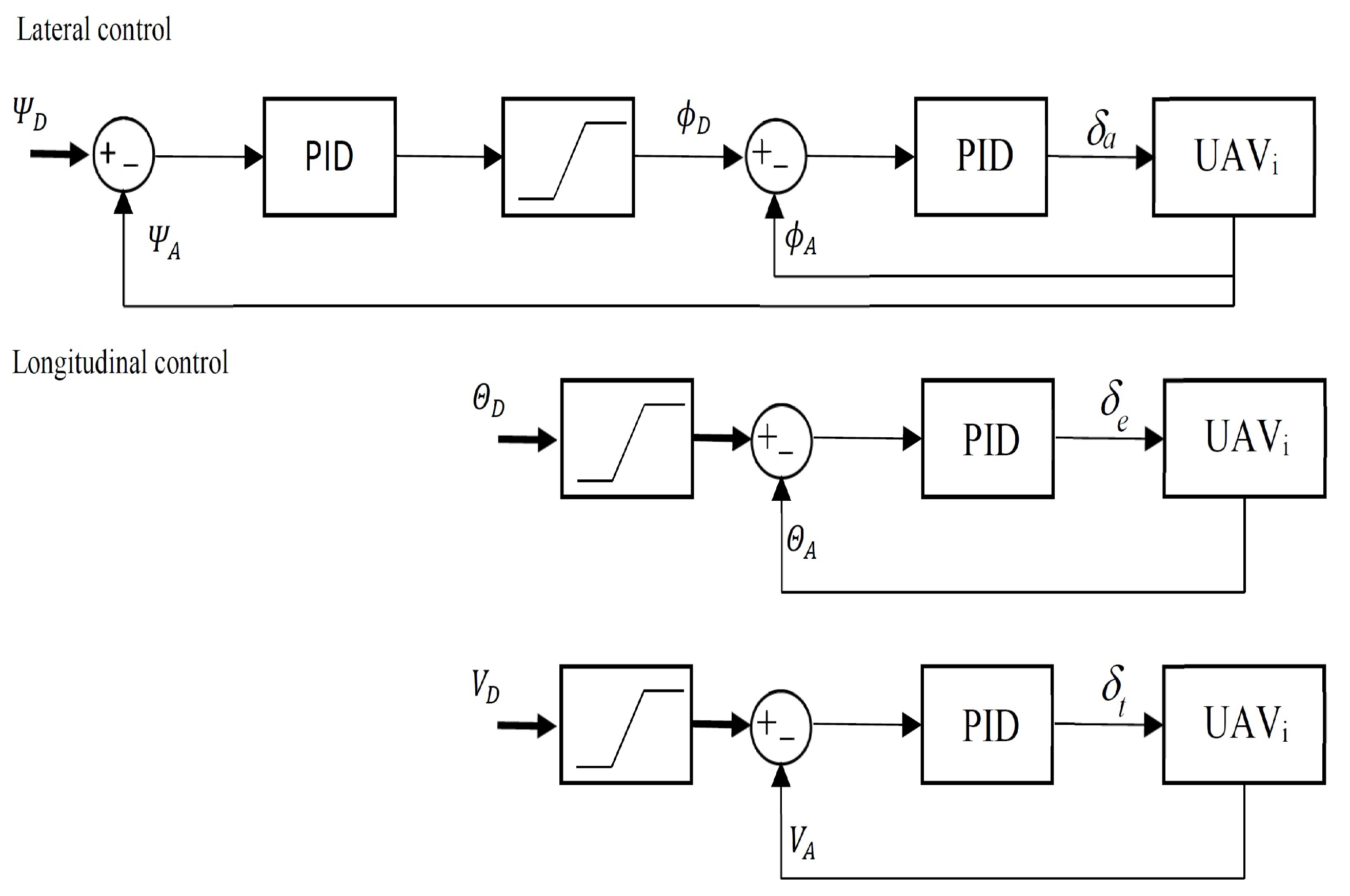
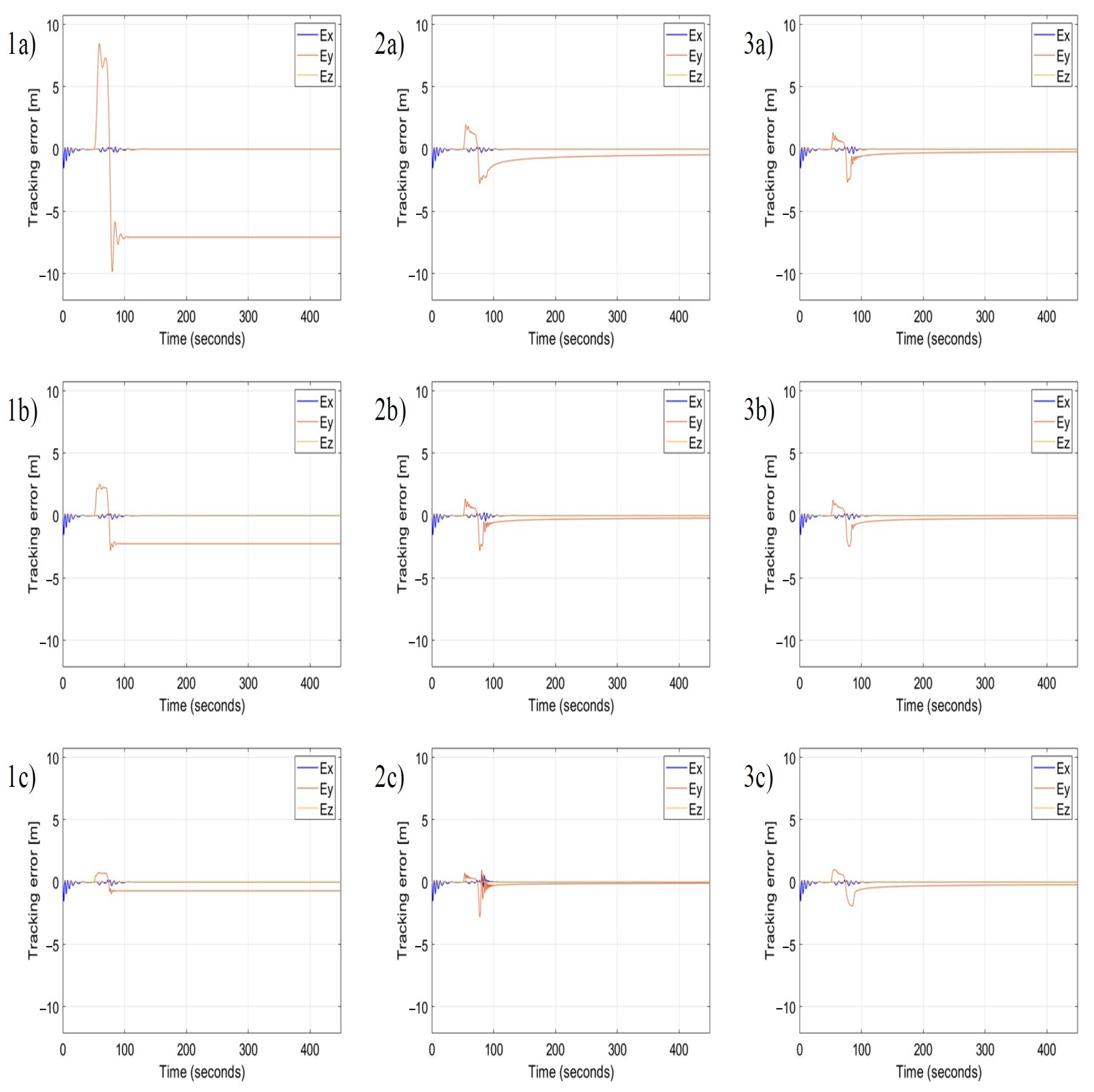
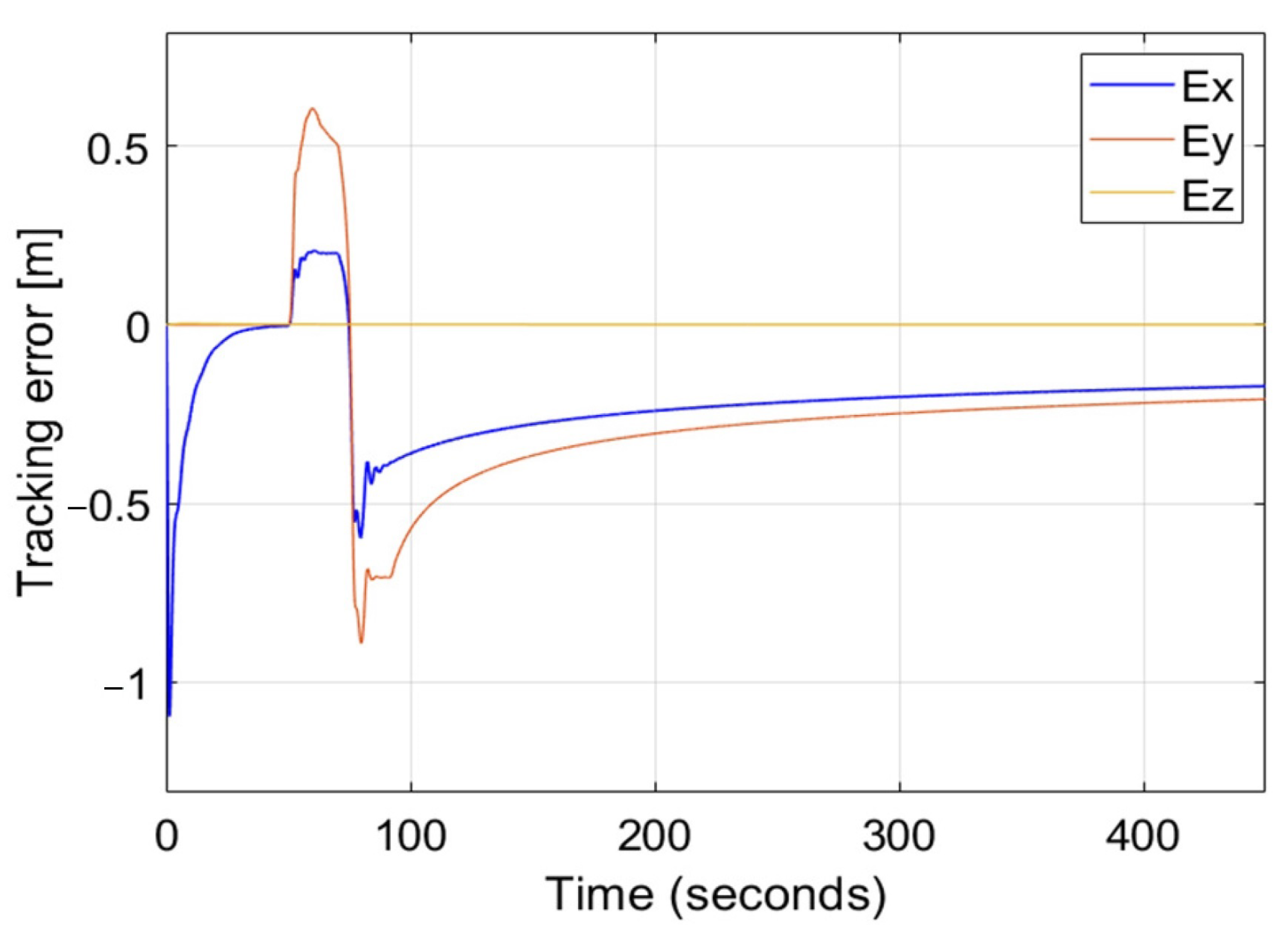
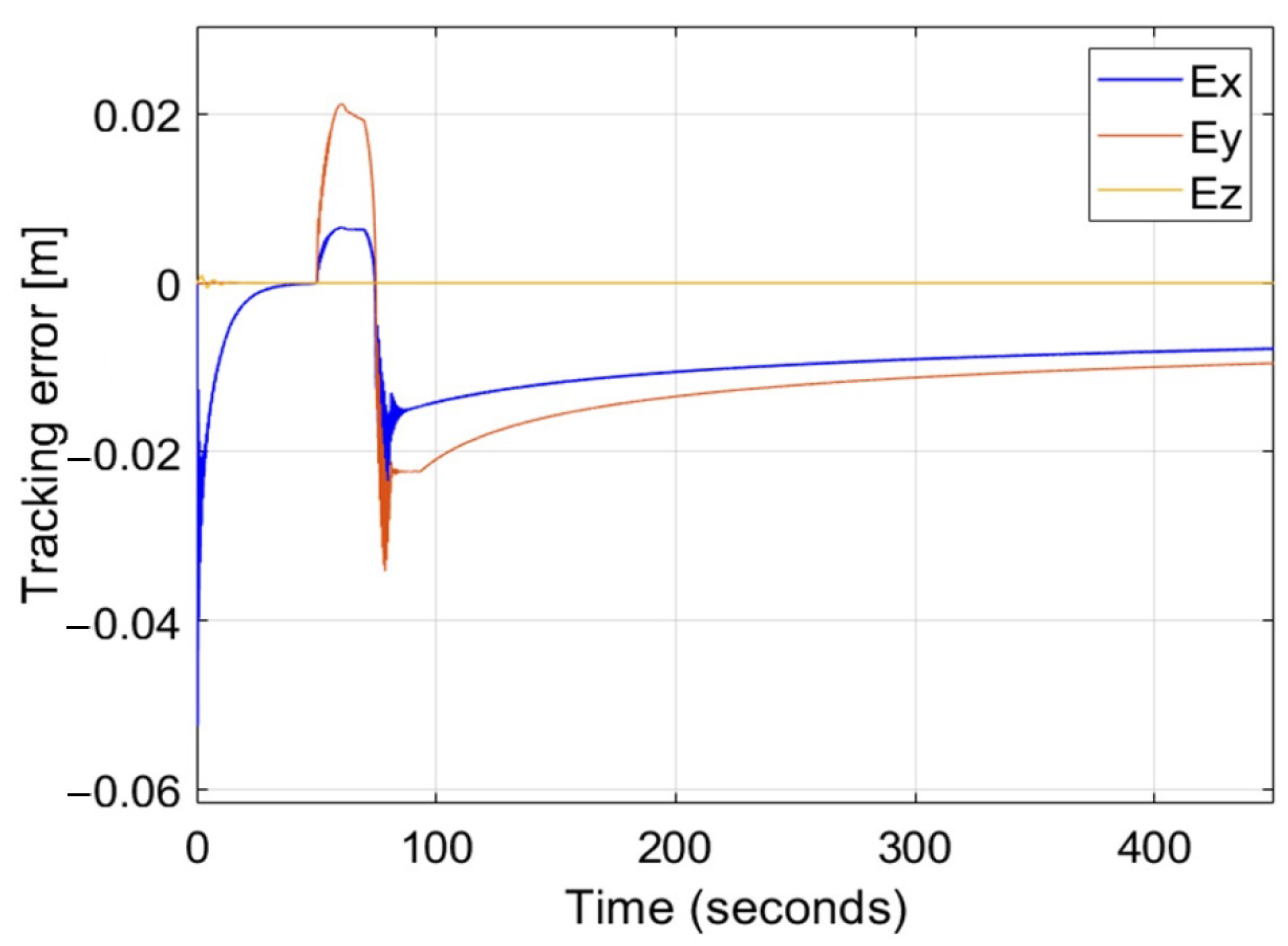
5. Numerical Simulations
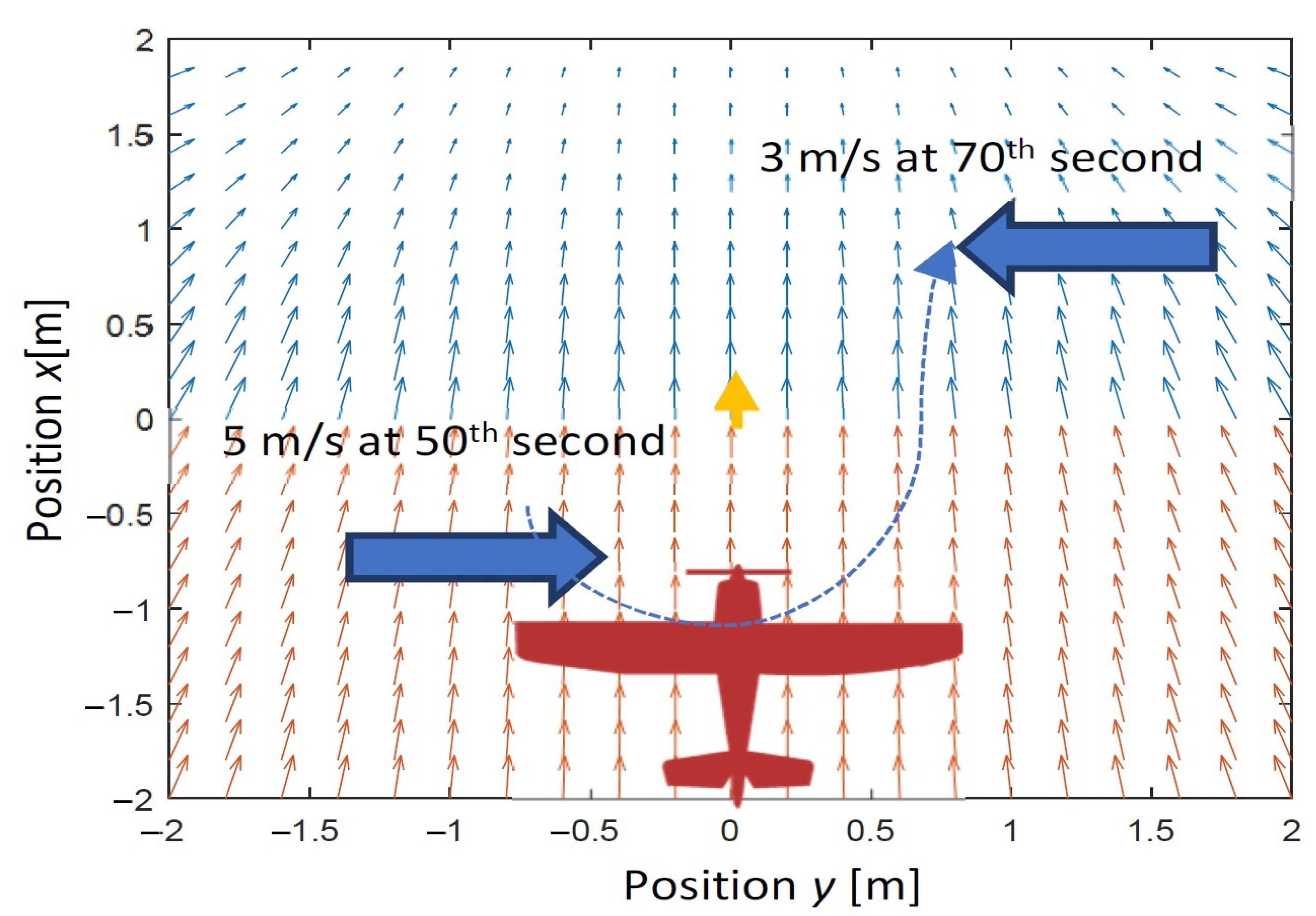
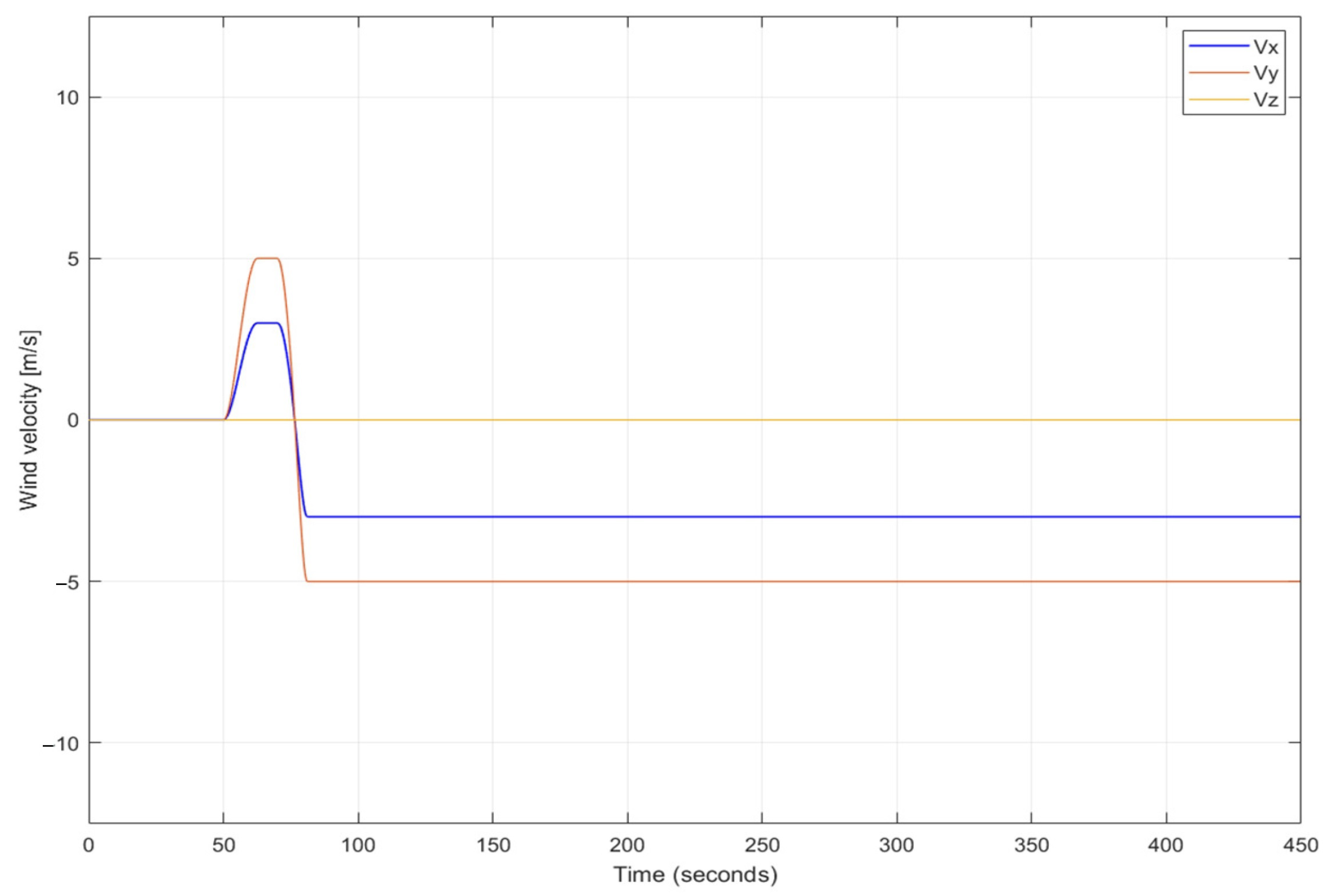
5.1. Lateral Wind Gust Case
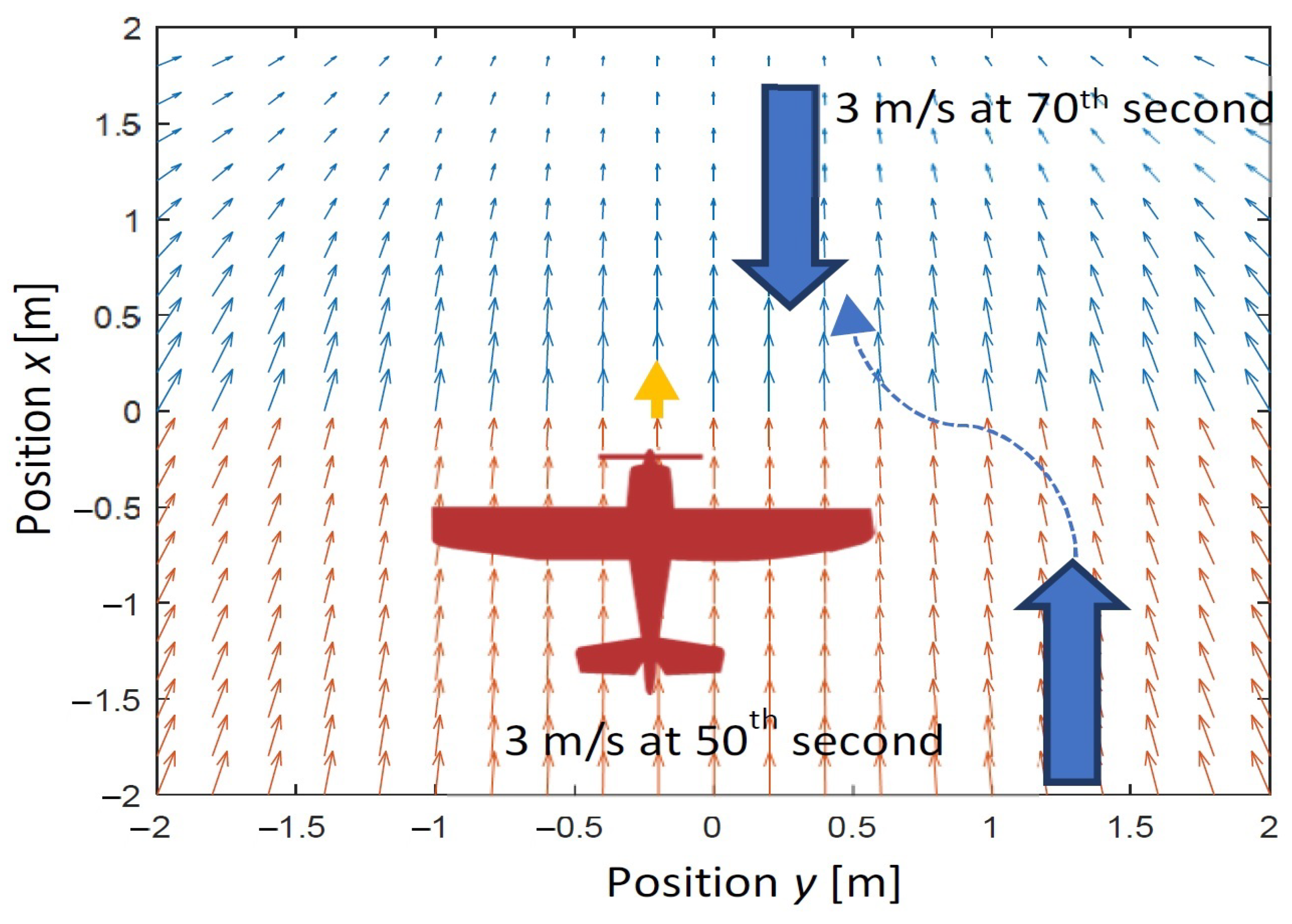
5.2. Longitudinal wind Gust Case
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambroziak, L.; Ciężkowski, M. Virtual Electric Dipole Field Applied to Autonomous Formation Flight Control of Unmanned Aerial Vehicles. Sensors 2021, 21, 4540. [Google Scholar] [CrossRef] [PubMed]
- Dongwoo, L.; Seung-Keun, K.; Jinyoung, S. Design of a Track Guidance Algorithm for Formation Flight of UAVs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Kownacki, C. Multi-UAV Flight Using Virtual Structure combined with Behavioral Approach. Acta Mech. Autmatica 2016, 10, 92–99. [Google Scholar] [CrossRef] [Green Version]
- Ambroziak, L.; Ciężkowski, M.; Wolniakowski, A.; Romaniuk, S.; Bożko, A.; Ołdziej, D.; Kownacki, C. Experimental tests of hybrid VTOL unmanned aerial vehicle designed for surveillance missions and operations in maritime conditions from ship-based helipads. J. Field Robot. 2022, 39, 203–217. [Google Scholar] [CrossRef]
- Daewon, L.; Tyler, R.; Kim, H.J. Autonomous landing of a VTOL UAV on a moving platform using image-based visual servoin. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012. [Google Scholar] [CrossRef]
- Hsiu-Min, C.; Dongqing, H.; Akio, N. Autonomous Target Tracking of UAV Using High-Speed Visual Feedback. Appl. Sci. 2019, 9, 4552. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Pu, F.; Wang, Z.; Chen, H.; Xu, Z. Detection, Tracking, and Geolocation of Moving Vehicle From UAV Using Monocular Camera. IEEE Access 2019, 7, 101160–101170. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, L.; Xiong, H. Person Tracking and Frontal Face Capture with UAV. In Proceedings of the IEEE 18th International Conference on Communication Technology, Chongqing, China, 8–11 October 2018. [Google Scholar] [CrossRef]
- Berry, C.A. Mobile Robotics for Multidisciplinary Study; Morgan & Claypool: Chicago, IL, USA, 2015. [Google Scholar]
- Pin, F.G.; Killough, S.M. A New Family of Omnidirectional and Holonomic Wheeled Platforms for Mobile Robots. IEEE Trans. Robot. Autom. 1994, 10, 480–489. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhen, Z. Multivariable adaptive distributed leader-follower flight control for multiple UAVs formation. Aeronaut. J. 2017, 121, 877–900. [Google Scholar] [CrossRef]
- Wilson, D.B.; Göktoǧan, H.; Sukkarieh, S. A Vision Based Relative Navigation Framework for Formation Flight. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar] [CrossRef]
- Gosiewski, Z.; Ambroziak, L. Two stage switching control for autonomous formation flight of unmanned aerial vehicles. Aerosp. Sci. Technol. 2015, 46, 221–226. [Google Scholar]
- Zhang, J.; Yan, J.; Zhang, P. Fixed-wing UAV Formation Control Design with Collision Avoidance Based on an Improved Artificial Potential Field. IEEE Access 2018, 6, 78342–78351. [Google Scholar] [CrossRef]
- Norman, L.H.M.; Hugh, L.H.T. Formation UAV flight control using virtual structure and motion synchronization. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008. [Google Scholar] [CrossRef]
- Hu, J.; Sun, X.; He, L. Time-Varying Formation Tracking for Multiple UAVs with Nonholonomic Constraints and Input Quantization via Adaptive Backstepping Control. Int. J. Aeronaut. Space Sci. 2019, 20, 710–721. [Google Scholar] [CrossRef]
- Chen, Y.B.; Luo, G.C.; Mei, Y.S.; Yu, J.Q.; Su, X.L. UAV path planning using artificial potential field. Int. J. Syst. Sci. 2016, 47, 1407–1420. [Google Scholar] [CrossRef]
- Frew, E.W.; Lawrence, D.A.; Dixon, C.; Elston, J.; Pisano, W.J. Lyapunov Guidance Vector. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007. [Google Scholar] [CrossRef]
- Nagao, Y.; Uchiyama, K. Formation flight of fixed-wing UAVs using artificial potential field. In Proceedings of the 29th Congress of the International Council of the Aerospace Sciences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Kownacki, C.; Ambroziak, L. Local and asymmetrical potential field approach to leader tracking problem in rigid formations of fixed-wing UAVs. Aerosp. Sci. Technol. 2017, 68, 465–474. [Google Scholar] [CrossRef]
- Kownacki, C.; Ambroziak, L. Adaptation Mechanism of Asymmetrical Potential Field Improving Precision of Position Tracking in the Case of Nonholonomic UAVs. Robotica 2019, 37, 1823–1834. [Google Scholar] [CrossRef]
- Daewon, L.; Taeyoung, L.; Farhad, G. Geometric Nonlinear PID Control of a Quadrotor UAV on SE(3). In Proceedings of the European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Zamora, J.J.; Camarillo-GóMez, K.A.; PéRez-Soto, G.I.; RodríGuez-ReséNdiz, J. Comparison of PD, PID and Sliding-Mode Position Controllers for V–Tail Quadcopter Stability. IEEE Access 2018, 6, 38086–38096. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Fuentes-Silva, C.; Hernández-Alvarado, R.; Falcón, M.D.C.P.T. Self-Tuning Neural Network PID with Dynamic Response Control. IEEE Access 2021, 9, 65206–65215. [Google Scholar] [CrossRef]
- García-Martínez, J.R.; Cruz-Miguel, E.E.; Carrillo-Serrano, R.V.; Mendoza-Mondragón, F.; Toledano-Ayala, M.; Rodríguez-Reséndiz, J. A PID-Type Fuzzy Logic Controller-Based Approach for Motion Control Applications. Sensors 2020, 20, 5323. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Moorhouse, D.J.; Woodcock, R.J. Background Information and User Guide for MIL-F-8785C, Military Specification—Flying Qualities of Piloted Airplanes; Report; Air Force Wright Aeronautical Labs Wright-Patterson AFB: Dayton, OH, USA, 1982. [Google Scholar]
- Langelaan, J.W.; Alley, N.; Neidhoefer, J. Wind Field Estimation for Small Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2011, 34, 1016–1030. [Google Scholar] [CrossRef]

| Symbol | Description |
|---|---|
| UAV | Unmanned aerial vehicle |
| APF | Artificial potential field |
| AAPF | Asymmetrical artificial potential field |
| Proportional integral derivative controller (function of x, y, or z) | |
| Proportional term (function of x, y, or z) | |
| Integral term (function of x, y, or z) | |
| Derivative term (function of x, y, or z) | |
| Proportional–integral term (function of x, y, or z) | |
| Tracked point velocity | |
| Gain coefficients of AAPF (proportional term) | |
| Rotation matrix of angular rate of heading angle | |
| Gain coefficient of rotation matrix | |
| Angular rate of heading angle of tracked point | |
| Asymmetrical artificial potential function | |
| Gradient of artificial potential function | |
| Velocity vector field | |
| , | Gain coefficients of integral term for x |
| Gain coefficient of integral term for y | |
| Gain coefficient of integral term for z | |
| , | Gain coefficients of derivative term for x |
| , | Gain coefficients of derivative term for y |
| , | Gain coefficients of derivative term for z |
| Controller (Subfigure) | ||||||||
|---|---|---|---|---|---|---|---|---|
| P (1a) | 10.0 | 10.0 | 0.01 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| P (1b) | 10.0 | 10.0 | 1 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| P (1c) | 10.0 | 10.0 | 10.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| PI (2a) | 10.0 | 10.0 | 1 | 0.3 | 0.1 | 0.1 | 0.0 | 0.0 |
| PI (2b) | 10.0 | 10.0 | 1 | 0.3 | 1.0 | 1.0 | 0.0 | 0.0 |
| PI (2c) | 10.0 | 10.0 | 1 | 0.3 | 10.0 | 10.0 | 0.0 | 0.0 |
| PID (3a) | 10.0 | 10.0 | 1 | 0.3 | 1.0 | 1.0 | 0.1 | 0.1 |
| PID (3b) | 10.0 | 10.0 | 1 | 0.3 | 1.0 | 1.0 | 1.0 | 1.0 |
| PID (3c) | 10.0 | 10.0 | 1 | 0.3 | 1.0 | 1.0 | 10.0 | 10.0 |
| Controller (Subfigure) | ||||||||
|---|---|---|---|---|---|---|---|---|
| P (1a) | 0.1 | 0.1 | 10.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| P (1b) | 1.0 | 1.0 | 10.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| P (1c) | 10.0 | 10.0 | 10.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| PI (2a) | 1.0 | 1.0 | 10.0 | 0.3 | 0.1 | 0.1 | 0.0 | 0.0 |
| PI (2b) | 1.0 | 1.0 | 10.0 | 0.3 | 1.0 | 1.0 | 0.0 | 0.0 |
| PI (2c) | 1.0 | 1.0 | 10.0 | 0.3 | 10.0 | 10.0 | 0.0 | 0.0 |
| PID (3a) | 1.0 | 1.0 | 10.0 | 0.3 | 1.0 | 1.0 | 0.1 | 0.1 |
| PID (3b) | 1.0 | 1.0 | 10.0 | 0.3 | 1.0 | 1.0 | 1.0 | 1.0 |
| PID(3c) | 1.0 | 1.0 | 10.0 | 0.3 | 1.0 | 1.0 | 10.0 | 10.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kownacki, C.; Ambroziak, L. Asymmetrical Artificial Potential Field as Framework of Nonlinear PID Loop to Control Position Tracking by Nonholonomic UAVs. Sensors 2022, 22, 5474. https://doi.org/10.3390/s22155474
Kownacki C, Ambroziak L. Asymmetrical Artificial Potential Field as Framework of Nonlinear PID Loop to Control Position Tracking by Nonholonomic UAVs. Sensors. 2022; 22(15):5474. https://doi.org/10.3390/s22155474
Chicago/Turabian StyleKownacki, Cezary, and Leszek Ambroziak. 2022. "Asymmetrical Artificial Potential Field as Framework of Nonlinear PID Loop to Control Position Tracking by Nonholonomic UAVs" Sensors 22, no. 15: 5474. https://doi.org/10.3390/s22155474
APA StyleKownacki, C., & Ambroziak, L. (2022). Asymmetrical Artificial Potential Field as Framework of Nonlinear PID Loop to Control Position Tracking by Nonholonomic UAVs. Sensors, 22(15), 5474. https://doi.org/10.3390/s22155474






