Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks
Abstract
:1. Introduction
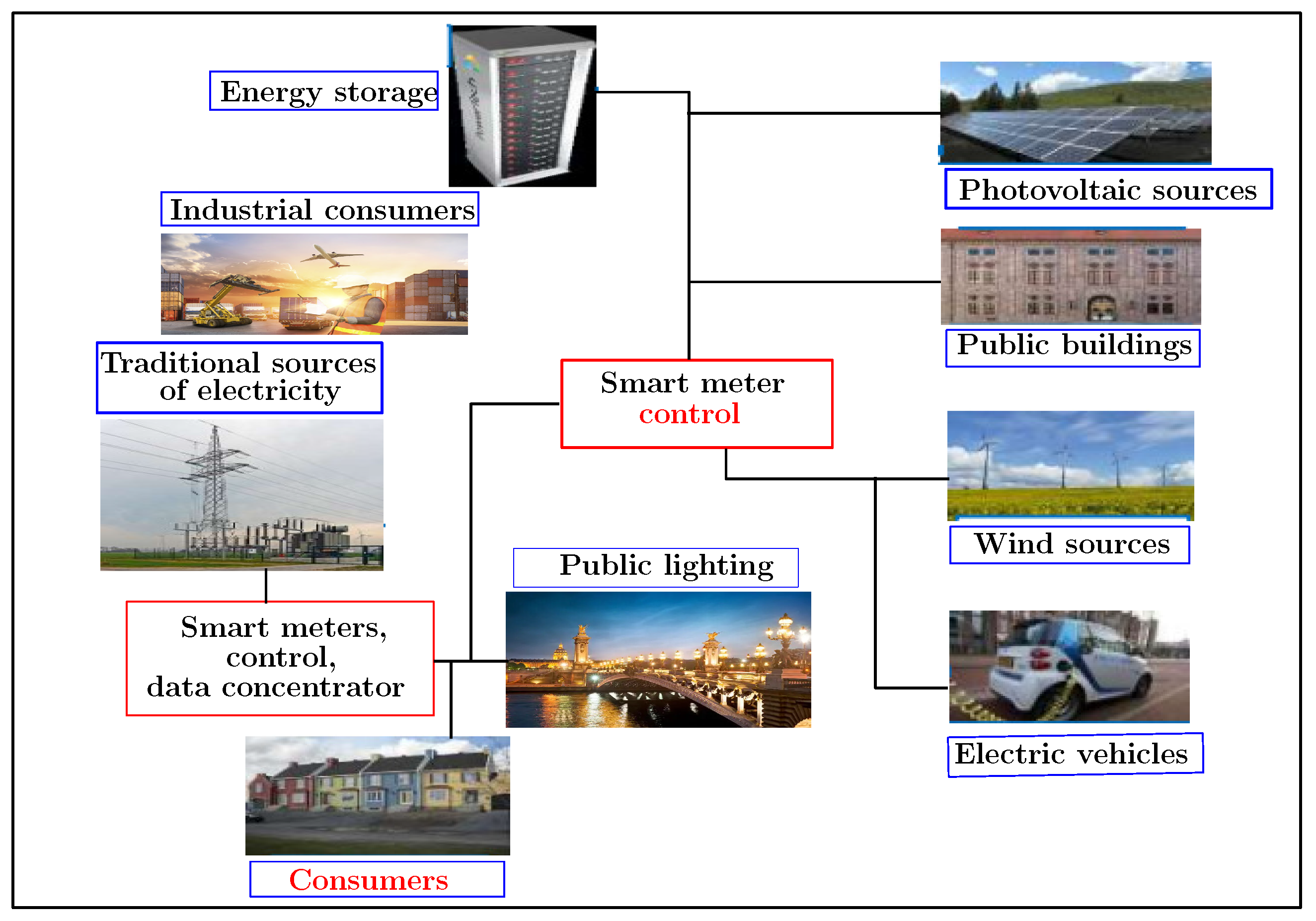
2. Context of This Work
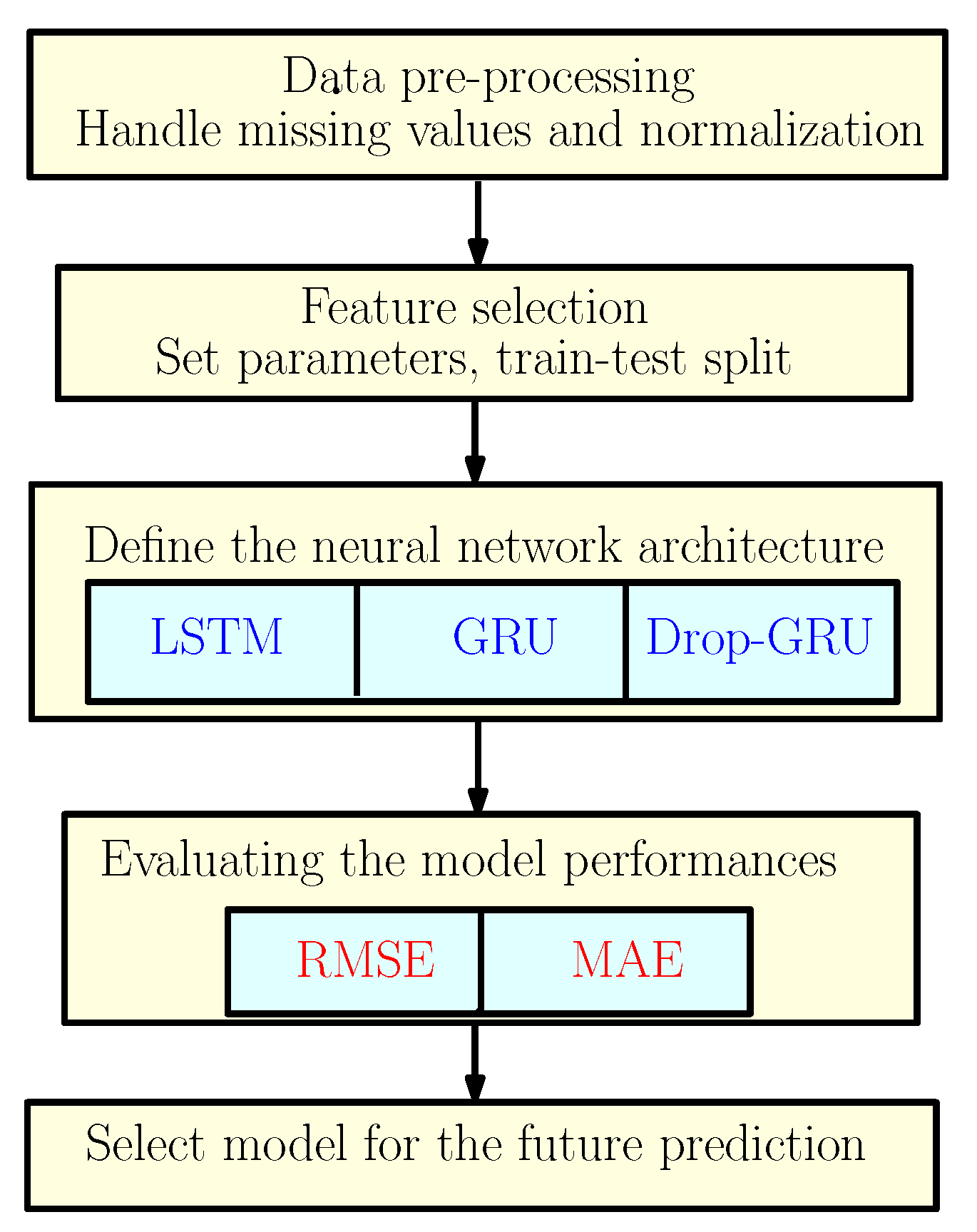
3. Materials and Methods
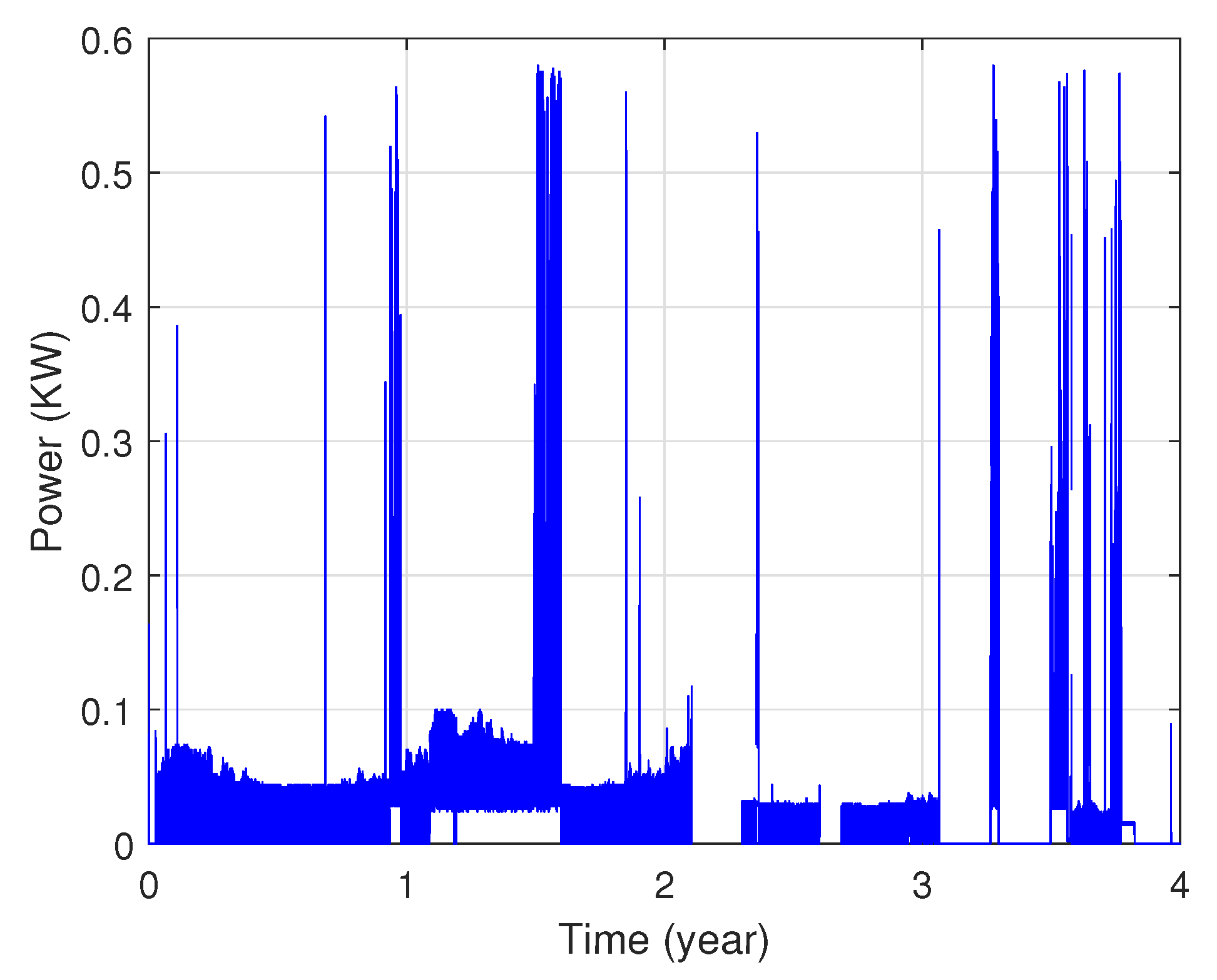
3.1. Data Analysis
- Nature of consumers: inhabitants, factories, hospitals, offices, etc.;
- Climatology: humidity, temperatures, sunshine, wind speed, etc.;
- Days of the week, weekends, holidays, etc.
3.2. Data Pre-Processing
- Some raw data have “holes”: the process of Exponential Moving Average () is used to fill in the missing information.The is a type of moving average that gives a greater weight and significance to the most recent data points. The EMA formula is given as:where the smoothing constant is equal towith n as the number of time periods.The formula is based on the previous day’s value. Since it has to start the computations somewhere, the initial value for the first calculation will actually be an . It is calculated by taking the arithmetic mean of a given set of values over a specified period of time.The formula for computing the SMA is presented as:whereA denotes the average in period n.
- Consumption profiles have different types of data: the process of reduced centered standardization is applied. The normalisation is performed by and the formula is given as:where:
3.3. LSTM Neural Network Model
- The input layer is mainly used for preprocessing the original data;
- The hidden layer is used to optimize the parameters and training the data;
- The output layer is used to predict the data according to the model trained in the hidden layer.
3.4. LSTM Network Parameters
3.5. GRU Neural Network Model
3.6. Neural Network Model Setup
3.6.1. Gradient Descent Algorithm
3.6.2. Dropout
3.6.3. Training and Testing Dataset
3.7. Performance Evaluation Indicators
4. Experimental Results
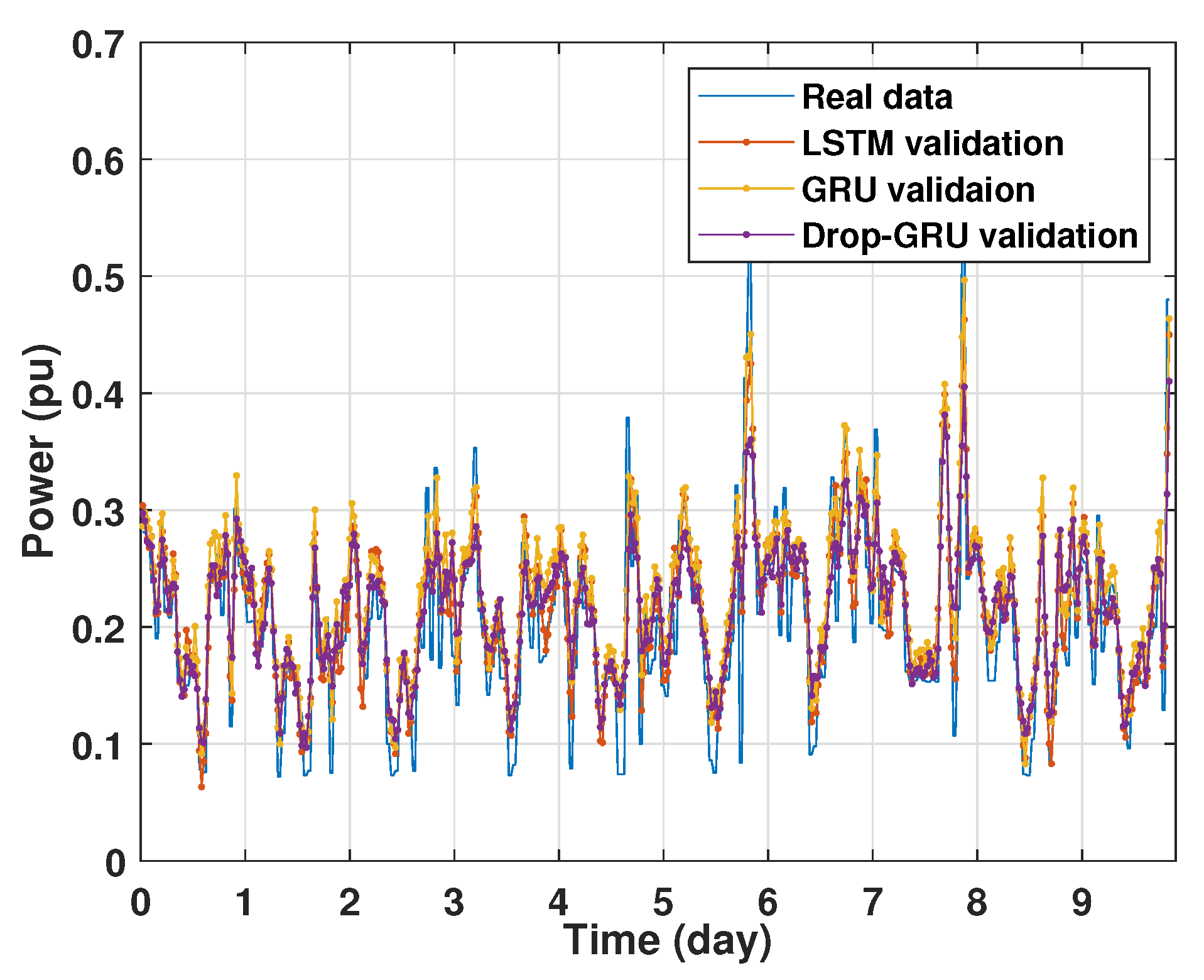
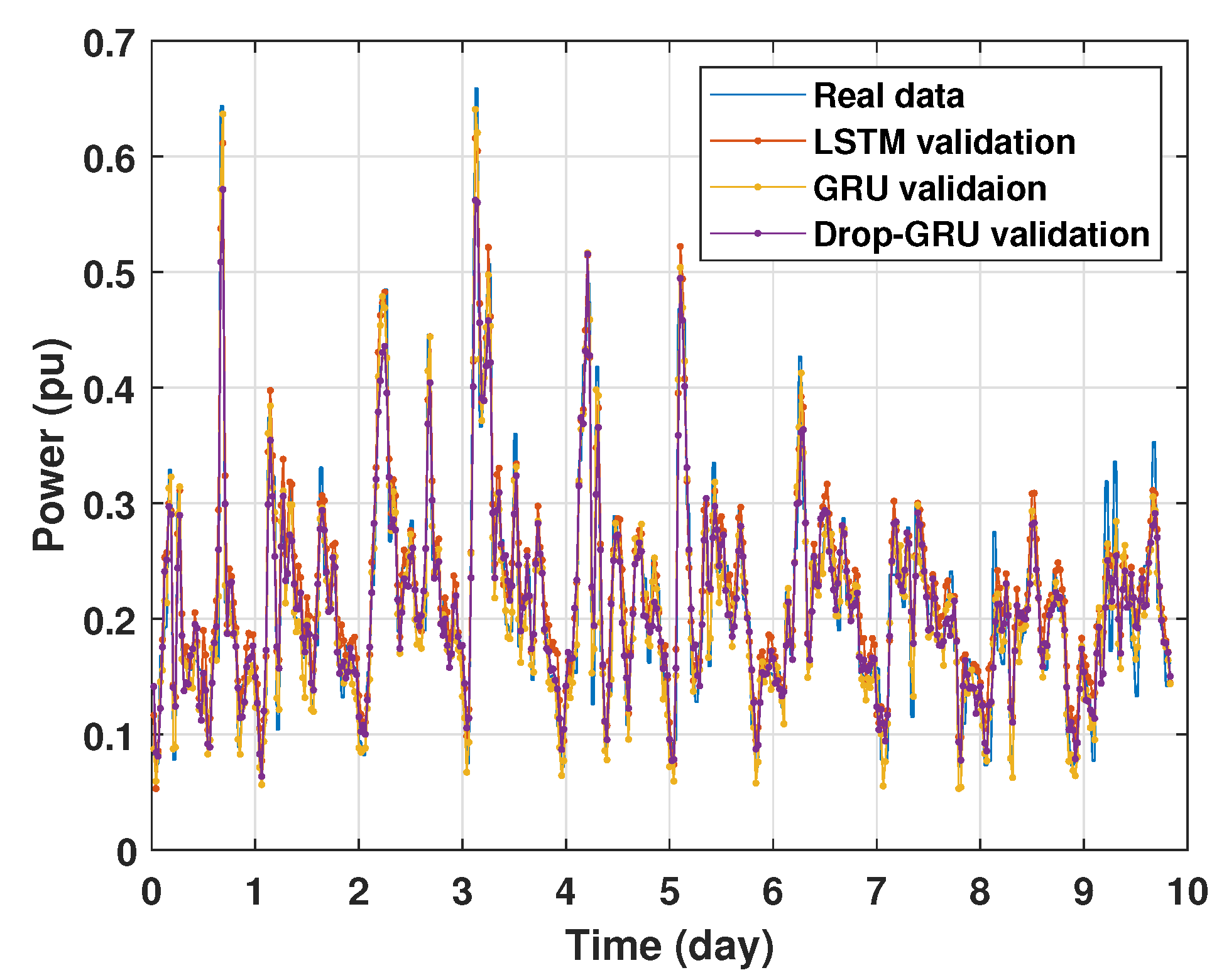
4.1. Training and Validation Processes
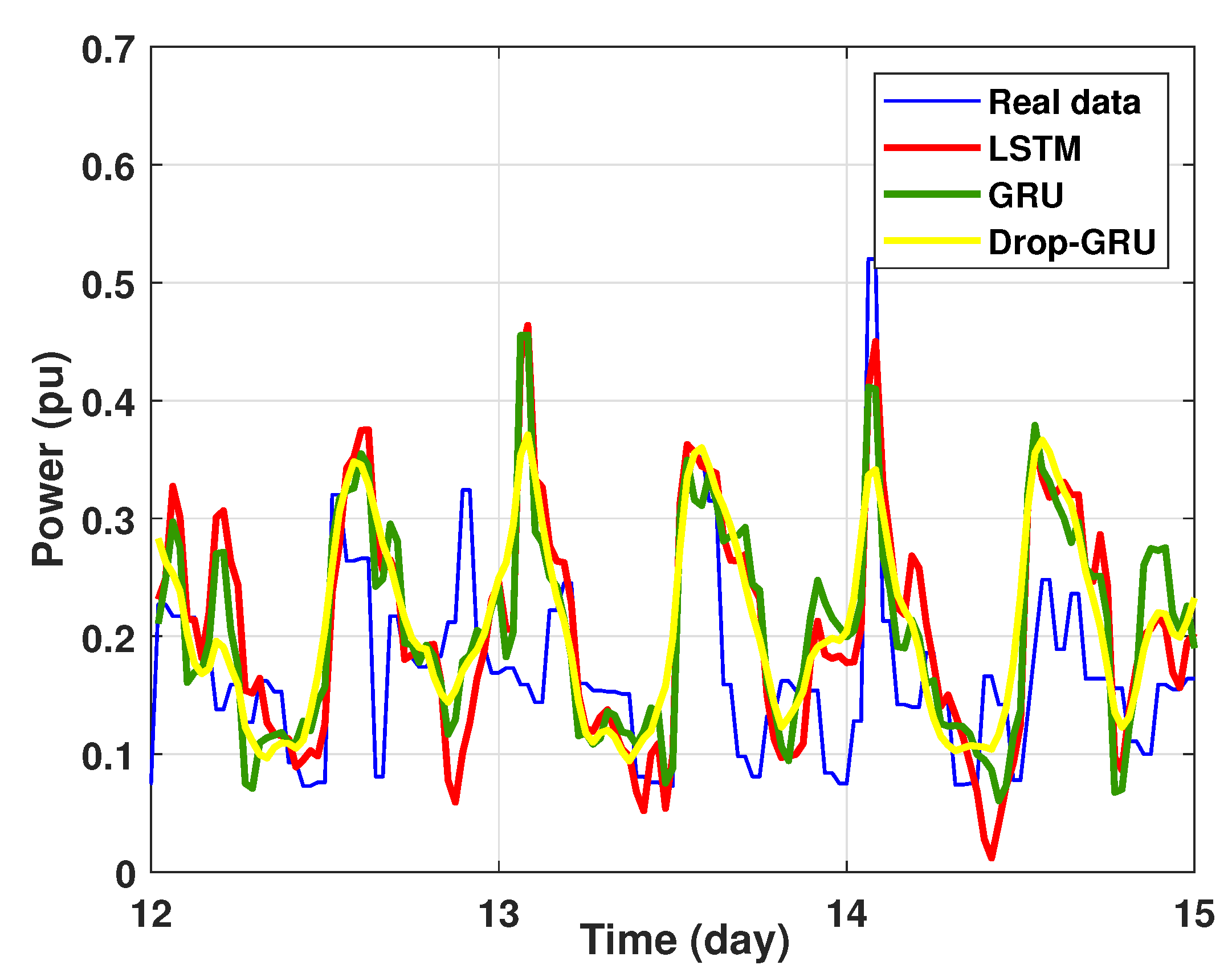
4.2. Prediction of Power Consumption
- Experiment 1: 1 Day prediction
- Experiment 2: 3 Days prediction
- Experiment 3: 7 Days prediction
- Experiment 4: 15 Days prediction
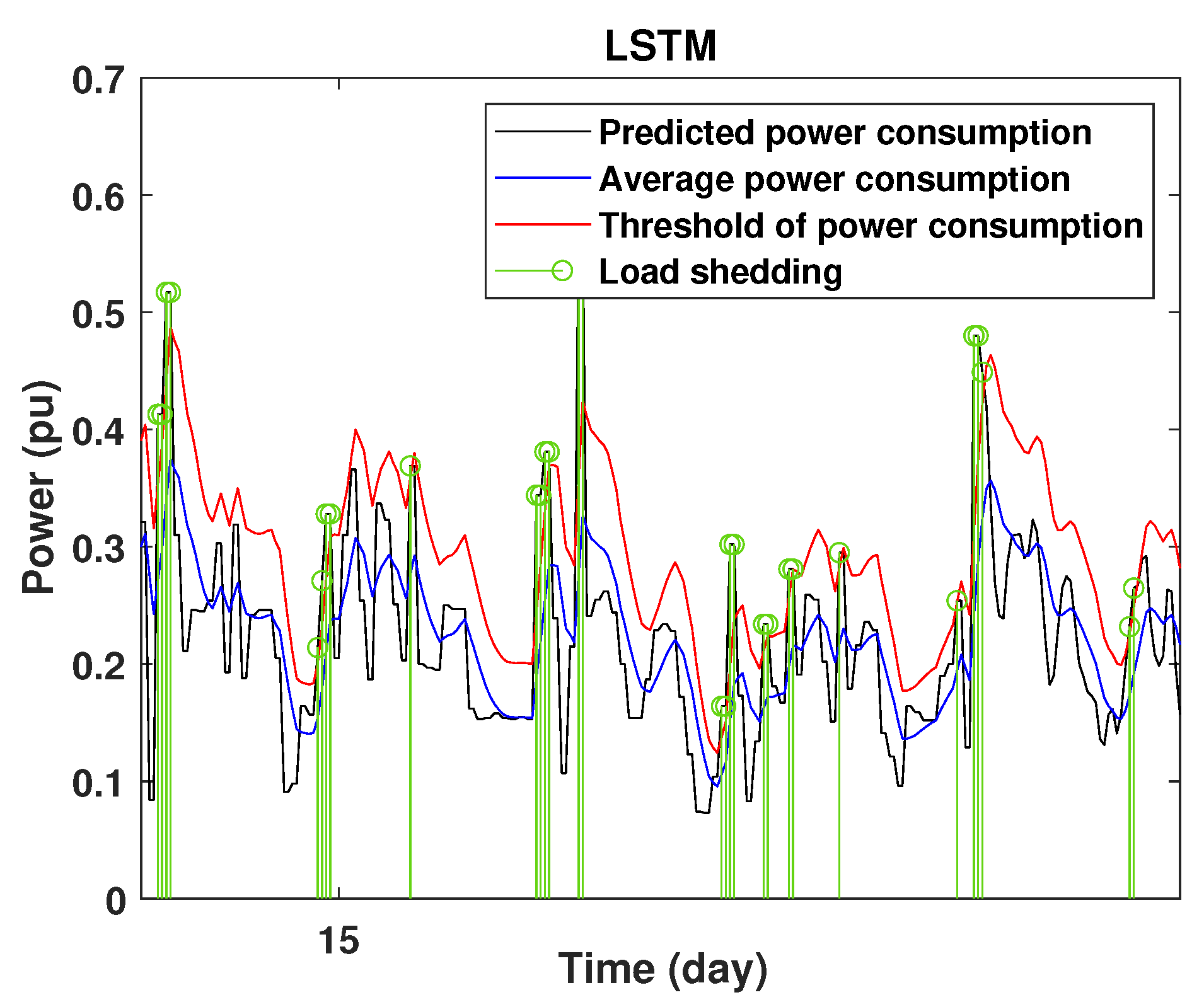
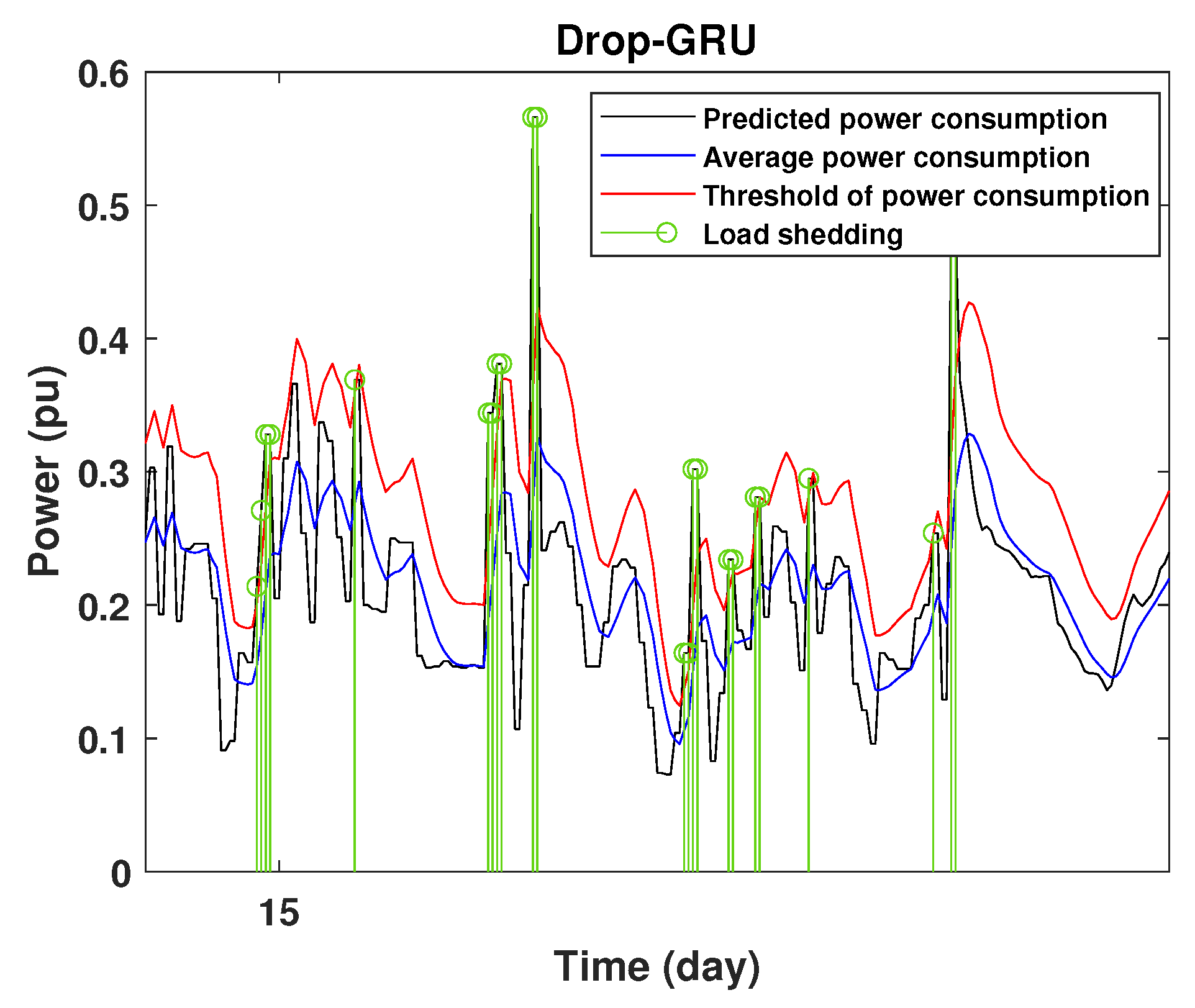
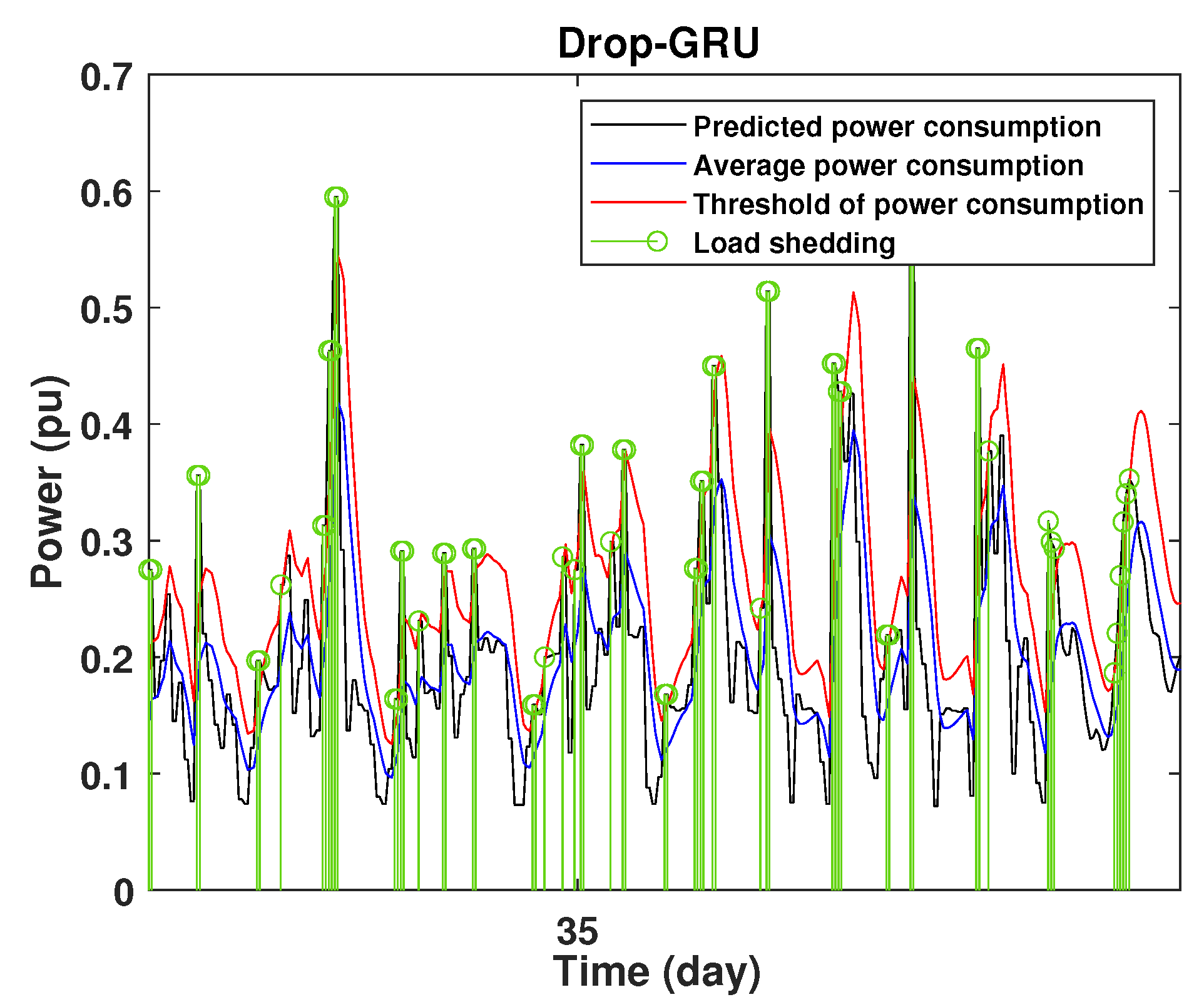
4.3. Detection of Power Consumption Peaks and Load Shedding
4.4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, K.; Wang, X.; Du, Y.; Jin, N.; Huang, H.; Zhou, H. Multi-step short-term power consumption forecasting with a hybrid deep learning strategy. Energies 2018, 11, 3089. [Google Scholar] [CrossRef] [Green Version]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar]
- Chen, K. APSO-LSTM: An improved LSTM neural network model based on APSO algorithm. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; p. 012151. [Google Scholar]
- Karevan, Z.; Suykens, J.A. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Tsai, Y.T.; Zeng, Y.R.; Chang, Y.S. Air pollution forecasting using RNN with LSTM. In Proceedings of the 2018 IEEE 16th International Conference on Dependable, Autonomic and Secure Computing, 16th International Conference on Pervasive Intelligence and Computing, 4th International Conference on Big Data Intelligence and Computing and Cyber Science and Technology Congress (DASC/PiCom/DataCom/CyberSciTech), Athens, Greece, 12–15 August 2018; pp. 1074–1079. [Google Scholar]
- Jin, Z.; Yang, Y.; Liu, Y. Stock closing price prediction based on sentiment analysis and LSTM. Neural Comput. Appl. 2019, 32, 9713–9729. [Google Scholar] [CrossRef]
- Shakya, A.; Michael, S.; Saunders, C.; Armstrong, D.; Pandey, P.; Chalise, S.; Tonkoski, R. Solar irradiance forecasting in remote microgrids using markov switching model. IEEE Trans. Sustain. Energy 2016, 8, 895–905. [Google Scholar] [CrossRef]
- Rendon-Sanchez, J.F.; de Menezes, L.M. Structural combination of seasonal exponential smoothing forecasts applied to load forecasting. Eur. J. Oper. Res. 2019, 275, 916–924. [Google Scholar] [CrossRef]
- Cao, T.D.; Delahoche, L.; Marhic, B.; Masson, J.B. Occupancy Forecasting using two ARIMA Strategies. In Proceedings of the ITISE 2019: International Conference on Time Series and Forecasting, Granada, Spain, 25–27 September 2019; Volume 2. [Google Scholar]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Qu, H.; Liu, S. Optimal forecast combination based on neural networks for time series forecasting. Appl. Soft Comput. 2018, 66, 1–17. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, Y.; Ivy, J.; Capan, M.; Arnold, R.; Huddleston, J.M.; Chi, M. Early diagnosis and prediction of sepsis shock by combining static and dynamic information using convolutional-LSTM. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 219–228. [Google Scholar]
- Kim, K.; Kim, D.K.; Noh, J.; Kim, M. Stable forecasting of environmental time series via long short term memory recurrent neural network. IEEE Access 2018, 6, 75216–75228. [Google Scholar] [CrossRef]
- Heidari, A.; Khovalyg, D. Short-term energy use prediction of solar-assisted water heating system: Application case of combined attention-based LSTM and time-series decomposition. Sol. Energy 2020, 207, 626–639. [Google Scholar] [CrossRef]
- Tovar, M.; Robles, M.; Rashid, F. PV Power Prediction, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México. Energies 2020, 13, 6512. [Google Scholar] [CrossRef]
- Zhang, T.; Song, S.; Li, S.; Ma, L.; Pan, S.; Han, L. Research on gas concentration prediction models based on LSTM multidimensional time series. Energies 2019, 12, 161. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Kong, C.; Hao, X.; Chen, W. A short-term load forecasting method based on GRU-CNN hybrid neural network model. Math. Probl. Eng. 2020, 2020, 1428104. [Google Scholar] [CrossRef] [Green Version]
- Shiang, E.P.L.; Chien, W.C.; Lai, C.F.; Chao, H.C. Gated recurrent unit network-based cellular trafile prediction. In Proceedings of the 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; pp. 471–476. [Google Scholar]
- Ghaziasgar, M.; Naeini, A.T. Neural Network for Routing in a Directed and Weighted Graph. In Proceedings of the 2008 Eighth International Conference on Intelligent Systems Design and Applications, Kaohsuing, Taiwan, 26–28 November 2008; pp. 631–636. [Google Scholar]
- Wen, L.; Zhou, K.; Yang, S. Load demand forecasting of residential buildings using a deep learning model. Electr. Power Syst. Res. 2020, 179, 106073. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Le, H.V.; Tran, V.Q.; Pham, B.T. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Probl. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. EA-LSTM: Evolutionary attention-based LSTM for time series prediction. Knowl.-Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef] [Green Version]
- Sommer, F.; et Stuke, M. An efficient and fast method to calculate integral experimental correlation coefficients–S2Cor. Ann. Nucl. Energy 2021, 157, 108209. [Google Scholar] [CrossRef]
















| m | ||||
|---|---|---|---|---|
| The weights between the input layer and the hidden layer. | Recursive weights in the hidden layer. | The bias of the hidden layer. | The weights between the hidden layer and the output layer. | The bias of the output layer. |
| Number of Days to Predict | 1 Day | 3 Days | 7 Days | 15 Days |
|---|---|---|---|---|
| Data size (measure) | 288 | 720 | 1680 | 3600 |
| Number of training data | 240 | 576 | 1344 | 1880 |
| Number of data to predict | 48 | 144 | 336 | 720 |
| Number of units (LSTM /GRU) in the hidden layer (h) | 280 | 600 | 750 | 1000 |
| Number of inputs for the LSTM/GRU network (n) | 200 | 300 | 300 | 600 |
| Number of outputs for the LSTM/GRU network (m) | 1 | 1 | 1 | 1 |
| Number of trainable weights (NTW) for the LSTM network | 539,001 | 2,163,001 | 3,153,751 | 6,405,001 |
| Number of iterations | 100 | 100 | 100 | 200 |
| Algorithm | Evaluation Indices | Number of Days to Predict | |||
|---|---|---|---|---|---|
| 1 Day | 3 Days | 7 Days | 15 Days | ||
| LSTM | RMSE | 0.0508 | 0.0904 | 0.0844 | 0.0837 |
| MAE | 0.0399 | 0.0682 | 0.0606 | 0.0583 | |
| R | 0.9666 | 0.8716 | 0.8045 | 07337 | |
| Execution time (s) | 4.8058 | 9.1943 | 11.67130 | 43.8825 | |
| GRU | RMSE | 0.0466 | 0.0868 | 0.0823 | 0.0873 |
| MAE | 0.0381 | 0.0678 | 0.0616 | 0.0621 | |
| R | 0.9708 | 0.8781 | 0.8155 | 0.7067 | |
| Execution time (s) | 4.0829 | 7.7684 | 9.6836 | 33.6734 | |
| Drop-GRU | RMSE | 0.0472 | 0.0727 | 0.0866 | 0.0813 |
| MAE | 0.0363 | 0.0555 | 0.0612 | 0.0574 | |
| R | 0.9696 | 0.9097 | 0.8287 | 0.7482 | |
| Execution time (s) | 4.1069 | 7.7501 | 9.5361 | 33.5519 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. https://doi.org/10.3390/s22114062
Mahjoub S, Chrifi-Alaoui L, Marhic B, Delahoche L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors. 2022; 22(11):4062. https://doi.org/10.3390/s22114062
Chicago/Turabian StyleMahjoub, Sameh, Larbi Chrifi-Alaoui, Bruno Marhic, and Laurent Delahoche. 2022. "Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks" Sensors 22, no. 11: 4062. https://doi.org/10.3390/s22114062
APA StyleMahjoub, S., Chrifi-Alaoui, L., Marhic, B., & Delahoche, L. (2022). Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors, 22(11), 4062. https://doi.org/10.3390/s22114062







