Abstract
Recent industrial robotics covers a broad part of the manufacturing spectrum and other human everyday life applications; the performance of these devices has become increasingly important. Positioning accuracy and repeatability, as well as operating speed, are essential in any industrial robotics application. Robot positioning errors are complex due to the extensive combination of their sources and cannot be compensated for using conventional methods. Some robot positioning errors can be compensated for only using machine learning (ML) procedures. Reinforced machine learning increases the robot’s positioning accuracy and expands its implementation capabilities. The provided methodology presents an easy and focused approach for industrial in situ robot position adjustment in real-time during production setup or readjustment cases. The scientific value of this approach is a methodology using an ML procedure without huge external datasets for the procedure and extensive computing facilities. This paper presents a deep q-learning algorithm applied to improve the positioning accuracy of an articulated KUKA youBot robot during operation. A significant improvement of the positioning accuracy was achieved approximately after 260 iterations in the online mode and initial simulation of the ML procedure.
1. Introduction
In complex manufacturing, articulated robots are chosen more frequently because of their advantages: multidegree-of-freedom (multi-DOF), wide working space, offline programming (OLP) capability, and high dexterity [1]. OLP significantly saves operating time and investment in the development of complex-shaped objects for the production process [2]. Nevertheless, OLP often does not ensure the required accuracy and repeatability; even using the most advanced robotic system, the motion parameters, namely, coordinate, velocity, acceleration, deceleration, and required positioning tolerance, have to be adjusted manually before operation [3]. However, sometimes even the final adjustment does not provide the desired accuracy due to the actual positioning errors. The value of errors depends on the robot characteristics and manipulation task [4]. Errors that depend on robot characteristics include inaccuracies in the assembly, transmission gear backlashes, and arm compliance [5]. In addition, kinematic mistakes occur due to serially connected links that accumulate errors related to drives, mechanisms, and joints from the robot base to the end effector [6,7,8,9]. Manipulation task performance depends on environmental conditions, applied load, stiffness of mounting surface, and tool characteristics, such as rotation speed, angle, and even lubrication [10]. Moreover, robot movement trajectory and setpoint position in the workspace influence its positioning accuracy [11]. Additionally, the robot’s movement is always affected by dynamic processes. Therefore, such a complex origin of positioning errors limits the implementation of common error compensation techniques [12,13,14,15,16,17,18]. Therefore, new and reliable methods, such as visual recognition systems and machine learning (ML) algorithms, can be applied to improve robot positioning accuracy and repeatability during operation [19,20,21,22].
One of the widely used ML algorithms to control physical equipment is the deep q-learning algorithm, which belongs to the reinforcement learning ML type [23]. It allows a robot to find the best positioning accuracy through trial-and-error interactions with the environment rather than requiring positive or negative labels [24,25,26,27,28,29]. As a part of the general robotic operation optimization technique, it gradually finds the best positioning method and seeks to discover the most considerable cumulative reward value in each iteration There are two main advantages of using the deep q-learning algorithm in an industrial robot case: the possibility to introduce gathered live video data into it [30,31] and the possibility to avoid the commonly known ML problems such as overfitting. The principle of deep q-learning is based on the perception of the environment [32], the state of the robot, and respective actions to achieve the maximum reward. Previous research proved this algorithm’s suitability for defining the robot tool position using visual data, finding the best combination of robot motion parameters, and generating output results with corrected setpoint coordinates [26,29,33].
Since online robot training is a time-consuming procedure, the values of positioning accuracy can be determined using ML simulation for actual cases. The simulation lasting less than five minutes replaces physical experiments lasting more than five hours. The convenience of the simulation is that it only requires a computer (except when it is necessary to collect input data from the real robotic system). However, any simulation cannot perfectly represent real-world conditions due to assumptions and simplifications used to describe various unknown or undefined physical effects. Therefore, even if the algorithm works well, simulation results require validation from experiments performed in operational conditions. Consequently, simulation is an excellent method to select the most promising combinations of algorithm parameters for testing in the real world.
The main aim of this paper is to present a methodology for the improvement of industrial robot accuracy and repeatability using the deep q-learning algorithm with optimal parameters. The methodology was evaluated by comparing simulations and experiments using the KUKA youBot articulated robot as a workbench.
2. State-of-the-Art
This section reviews the machine learning-based methods used to improve the performance of mechatronic and robotic systems or their components. From the perspective of industrial robotics, the main ML implementation fields and goals are: sensor data analysis—to increase object detection/recognition accuracy; tool path generation—to optimize motion trajectory or energy consumption; and robot calibration and positioning errors analysis—to save operational time and increase positioning accuracy.
2.1. Trajectory Generation and Its Accuracy
Trajectory generation is an essential task for robots and robotic systems operating in all possible applications. Trajectory defines robot movement quality in terms of the accuracy of static points at the end of the trajectory, intermediate points as waypoints within, and acceleration levels during the entire movement cycle. Good trajectory uses minimum possible intermediate points, defines paths using higher-order curves, and uses internal robot interpolation facilities as the fastest and most efficient resource. Issues of accuracy cover the entity of volumetric (or, in case, planar) coordinates of the target as a basis for error definition at the actual robot position. Angular coordinate deviation questions are often left behind except when manipulation tasks raise the requirement to ensure precise tool orientation [34,35].
The accuracy of a robot’s trajectory and the required computational resources strictly depend on the trajectory generation method. Recently, more and more attention is being paid to the automatic trajectory generation by copying human movements, for example, in surgery, where movement trajectory is of vital importance. Wang and Majewicz Fey developed a special ML procedure that implements a neural network for robot trajectory generation [36]. The proposed method uses human gesture analysis as input and successfully transforms it into a final robot motion. During experimental validation, highly competitive accuracies were achieved of 92.5% for suturing, 95.4% for needle passing, and 91.3% in the knot-tying operations.
A summarized overview of various ML approaches for the improvement of robot positioning accuracy and generation of trajectory is provided in Table 1.

Table 1.
Summary of research focused on trajectory generation and its accuracy.
An overview of the references shows that there are three main directions of ML implementation in the field of positioning accuracy enhancement and trajectory generation:
- The development of new methods for manipulator calibration to compensate for the positioning errors regardless of their nature. It is performed similar to our methodology.
- Implementation of ML into the robot controller to solve kinematic problems occurring in complex structure manipulators where traditional methods are not suitable or require a lot of computational resources.
- Implementation of ML into the trajectory generation process to enhance or generate input data to optimize generated trajectory.
2.2. Object Grasping
Using a robot as a manipulator, a device for pick-and-place tasks, and a general device with a changeable load or end-of-arm tool embraces a general problem of grasping. The variety of objects from solid to almost liquid state and their different geometric shapes raises the requirements for object manipulation. However, this issue faces limitations such as maximal acceptable forces or accelerations during the motion. Solutions existing in the grasping area developed a tree-like structure of standard objects and assigned solutions such as two- or three-finger grabbers. Nevertheless, individual problems raise tasks for original designs and conceptions. The implementation of ML procedures recently covers grabbing parameters, but, unfortunately, ideas and applications must be generated only by human beings. ML in this area can adjust grabbing parameters to the optimal values.
The manipulation of complex geometry objects that slightly change their position or orientation due to grasping action is a difficult task [22]. Typically, directions and amplitudes of such movements are chaotic and hardly predictable due to arising uncertainties. The authors raise the hypothesis that concerning the required positioning accuracy, the machine learning-based classification method and computer vision system could be used to define the object’s actual position after grasping. Such a solution could provide crucial information for real-time movement trajectory correction. A similar object recognition problem is mentioned in [45], where a composite structure inspection system consisting of an industrial robot and laser profilometer is described. The robot actuates the profilometer and quickly scans the part’s profile, providing profile height data as a grayscale image. A convolutional neural network detects defects and assigns them to a certain class. Product assignment to a particular class defines the required adjustments in the binding material allocation algorithm, which typically results in trajectory changes of the robot or other device placing the binder.
Luo et al. [46] presented a reinforcement learning-based solution for force/torque control to assemble a tight-fit gear wheel set. Experiments showed that using reinforcement learning, the robot provided fewer assembly errors due to part misalignment. Lie et al. [47] implemented the least squares support vector machines method for image classification to sort coal and gangue. The proposed system reached the identification accuracy of coal 88.3%, and the identification accuracy of the gangue sample was 90.0% with 0.130 s average total time for one sample recognition. Reviews by Li et al. [48] and Bai et al. [49] analyze the research progress in implementing machine learning for robotic grasping, including aspects of machine vision or tactile feedback. A condensed review of the related research is provided in Table 2.

Table 2.
Summary of research on robot grasping technology enhancement using machine learning.
The result of the performed review reveals three main directions on how ML can be used in the grasping process:
- The combination of ML and computer vision ensures more precise object detection and recognition as well as a more accurate definition of optimal grabbing position and grabber orientation.
- ML can be used to analyze and process position or force feedback signals when it is necessary to adjust the final robot tool position for successful grasping.
- ML significantly improves the manipulation process of unstable objects that can change their position or shape due to the low stiffness, grasping impact, or gravity forces.
2.3. Sensor and Instrumentation
The intelligent application of robots and robotic systems requires sensors and their data processing systems. Such systems recently armed with machine learning algorithms can achieve high efficiency and early detection of issues. The implementation of ML procedures can also sharpen these systems by increasing their accuracy or resolution. The use of the sensors allows the creation of systems with artificial (synthetic) ontology, which opens a space for further application of ML procedures. Instrumentation in robotics covers fault detections of the system, early detection of defects, failure prevention, and other issues required for successful task execution. A big issue in robotics is applications with virtual and augmented reality, allowing one to enhance the approach of synthetic ontology. This field of research lays on the frontier of applied science, and achievements there will bring significant changes in robot perception.
Ribeiro et al. [53] used ML to increase the accuracy of human movement trajectory tracking using inertial measurement units. Their proposed method defines zero velocity and evaluates the regression of translations in periods of movement. Xiao et al. [54] proposed the implementing of ML to decrease IMU tracking errors by learning typical error patterns and later compensating for them. As a result, the obtained trajectory could be transformed easier and faster into robot motion commands.
Cheng et al. in [55] proposed a fault prediction method for industrial robots. It measures the electrical current used by the motors and analyzes it in time and frequency domains. The main diagnostic parameters are the magnitude fluctuation index and signal-to-noise ratio. The magnitude fluctuation index is extracted in the time domain using Hilbert transformation, and the signal-to-noise ratio is defined as the ratio between frequencies in the spectrum obtained by the short Fourier transformation. The Gaussian mixture model detects failure by clustering the obtained parameters as normal and faulty.
The outcome of the review of research focused on sensors and instrumentation in robotics is listed in Table 3.

Table 3.
Summary of research on sensors and instrumentation in robotics.
The analysis of references related to ML-based sensing and instrumentation in robotics emphasizes that the mainstream in this field is human movement trajectory tracking and its transformation into the robot control program. Another actual research direction is the implementation of ML for internal robot parameter monitoring to predict possible faults and unwanted impacts from the environment, for example, contact with other objects.
The provided analysis of ML applications in the field of robotics covers specific areas mentioned in the highlighted references that focus on various aspects but mainly result in the increase in accuracy, efficiency, or functionality. Nevertheless, this area is not limited by these research items. The wide variety of robotic tasks creates a considerable space for unique and individual solutions.
3. Materials and Methods
3.1. Deep Q-Learning-Based KUKA YouBot Control Method
The KUKA youBot articulated robot [59] controlled by a unique software platform consisting of six merged modules (Figure 1) was used in our research. All software modules, mainly written in Python language, operate simultaneously and perform individual functions. Communication with external devices is performed through additional drivers, libraries, and robot operating system (ROS). The latter communicates with the robot using dedicated drivers and libraries provided by the manufacturer.
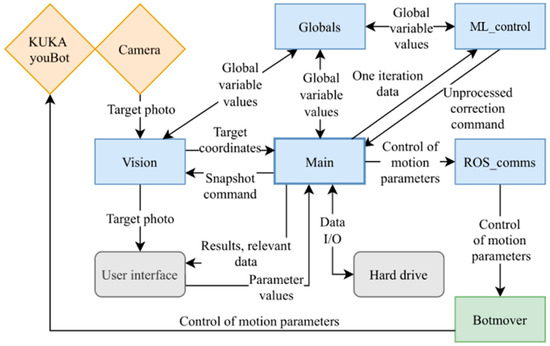
Figure 1.
Control system scheme: blue—Python programs, green—C++ program, yellow—physical peripherals, grey—physical computer elements and accessories.
The created ML_control module contains the deep q-learning algorithm [60]. It receives the values of global variables from the Globals module, which synchronizes Globals’ variable values among several Python programs running on the control system. The ML_control module communicates with the Main, accepting input values and sending the ML algorithm’s output value.
The user interface was realized within the Main module, which controls the flow of the experiment. The Main module also includes experiment and simulation algorithms and the data input/output functions. The Main sends the command to the Vision module, which takes a photo of the target using a digital microscope, identifies the target, calculates its center coordinates, and sends them back to the Main.
The Botmover module gives low-level access to the robot control parameters and allows control of the KUKA youBot by an external program. The primary function of this module is to control robot joint angles based on coordinate requirements received from the Main via ROS_comms. Once a set of coordinates and a command to move to that position are received, angle values for each joint are calculated by solving the inverse kinematic task. Then, by employing youBot libraries and drivers, the joint angle data are sent to the robot to perform the corresponding motion. Such a method enables close to real-time control of the robot from the Main module. The Botmover runs in an infinite loop until interruption by the user or another program.
Communication between the Botmover and other programs runs in asynchronous mode. It is based on the publisher–subscriber principle and is realized via means and libraries of ROS. The ROS_comms module acts as an intermediary between the Botmover program written in C++ and the Python programs. It enables full control of the robot parameters and movements directly from other Python applications.
3.2. Implementation of the Method
The simulation and experiment algorithm (Figure 2) running in the Main module is a cycle performing certain functions that repeat many iterations (400–4000). The cycle begins by inputting five values from the previous cycle into the ML. If the cycle runs for the first time, the parameter’s value is zero. In the other cases, the algorithm takes the correction step and the deviation values in the y and z directions from the previous cycle.
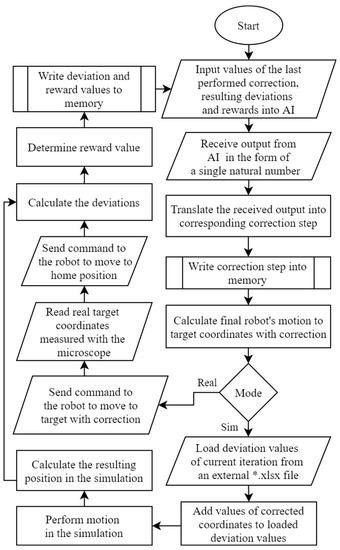
Figure 2.
Principle of experimental and simulation algorithms in Main module (from Figure 1).
The output from the ML goes in the form of a single natural number, thus converting it into the appropriate correction step stored in the memory. The correction step is a correction performed in one iteration and exists in the form of a vector (value and direction). Firstly, this is where an array of vectors is created containing all defined vectors. Then, the accepted ML output is assumed to be an index of that array. Each ML output value is assigned with the corresponding correction step. The vector components of the correction step are defined with the coordinates of the target in space to obtain the corrected coordinates.
The goal of the algorithm is to obtain corrected coordinates. The correction steps are cumulative. They continue to add the results of the current iteration to the results of all previous iterations. After defining the corrected coordinates, the robot receives the command to execute them in real-time. The Vision module takes the target picture, calculates the actual target coordinates, and sends a command to return the robot to the “home” position. The actual coordinates of the target are compared with the theoretical ones to determine the deviation values and directions.
After determining the deviations, the ML algorithm activates the reward function, which determines the value of the reward depending on the obtained deviations value. The value of the reward indicates to the algorithm how much the performed action corresponds to the desired result.
A positive reward indicates that the current iteration achieved the desired result. The magnitude of the reward is proportional to the result achievement level. A positive reward is given as output when one of the two conditions is fulfilled: (I) the deviation found in the current iteration must be smaller than in the previous iteration; (II) the deviation in the current iteration is less than half of the average deviation when the robot moves without correction. A negative reward is received when: (I) the measured deviation in the current iteration is greater than or equal to the deviation in the previous iteration; (II) or the threshold is exceeded (correction value is so high that any deviation compensation is impossible).
Such a reward function motivates the algorithm to perform actions that would reduce the deviations in each iteration until, in an ideal situation, a specific optimal point (average deviation reduced by half) is reached. However, due to the stochastic nature of some sources of positioning errors, it would be very difficult or impossible to reach such a point. Nevertheless, it is useful to have such a point as the goal is an ideal deviation value that must fit as close as possible.
The resulting deviation and reward values are stored in memory at the end of each iteration. Afterward, a learning cycle is restarted for a new iteration.
For speed and convenience, the Main module can also perform simulations with or without the use of collected real data. The simulation uses most of the same blocks of the Main code and the actual experiment code (Figure 2). The difference is that instead of sending commands to the robot and the camera, the simulation uses data collected experimentally when the robot was moving thousands of iterations without correction. These data represent the actual positioning accuracy of the robot. Such a dataset gives a possibility to use it in an unlimited number of simulations. Moreover, it minimizes the required number of iterations by loading the algorithm memory with real data before performing the online training.
3.3. Methodology of the Research
By using data representing experimentally obtained actual coordinates when the robot moves without correction, many simulations were performed in advance to speed up the experiments and define the best combination of algorithm parameters.
The deep q-learning algorithm with parameters providing the most seemingly successful results was further tested experimentally.
All experiments were performed at maximum operating speed when all joints were rotating at 90°/s to test the worst possible conditions at which the accuracy is mainly affected by inertial forces. The trajectory of the robot movement, the “home”, and target positions (Figure 3) were chosen so that all robot joints would move by similar angles during movements.

Figure 3.
Robot “home” position (A) and the target position (B). The robot moved between these two positions during each cycle of the experiments. 1—target, 2—robot, and 3—microscope.
The experiment began by finding the theoretical target. The robot moved to the “home” and “target” positions 100 times, while the Vision module defined the target center coordinates and sent them to the ML_control memory. The ML_control calculated the target’s average coordinates, further used in the training procedure algorithm.
The algorithm was trained using parameter values obtained from simulations. The robot moved from the “home” position to the target position with the target coordinate correction. A digital microscope took a picture of the target and sent it to the Vision module to detect the target position in the picture and define its center coordinates. The obtained coordinates were transferred to the Main module, which processed the data and wrote them to memory. The Main module calculated the deviation in y and z directions and wrote data into memory. Then the procedure activated the reward function and saved the determined reward for the deep q-learning algorithm in computer memory. Horizontal (y), vertical (z), and absolute deviations, as well as previous correction steps, were transferred into the machine learning algorithm. The algorithm calculated the values of the coordinate corrections for the next iteration. In the simulation run of 4000 iterations, experimental tests stopped after completing 800 iterations since further training did not give any improvement.
4. Results
4.1. Results of the Simulation
The standard deep q-learning algorithm has four main parameters: activation function, optimizer, replay memory, and temperature [49]. The activation function defines the algorithm’s output for a given input or set of inputs. An optimizer is a parameter that controls interconnections among neurons (synapses) and affects how the final algorithm works over a long period. The replay memory is a function that allows the algorithm to use the previous experience to decide on the present. Temperature is a parameter that regulates the exploration–exploitation ratio. The efficiency of the deep q-learning algorithm depends on the combination of these parameters.
The appropriate algorithm configuration and its parameters were obtained from the simulation procedure. The ML algorithm made coordinate corrections to compensate for the positioning errors, thus improving the robot’s positioning accuracy after a number of training cycles of the machine learning algorithm. The number of training cycles for the machine learning algorithm was small enough to make training practical in terms of time (e.g., the total training took no more than a few hours). After developing the optimal algorithm, multiple variations of the parameters were tested and evaluated in the simulations. By varying each parameter, tens of 4000 iteration length simulations were performed to find the best combination of their values.
The quality of the defined parameter combinations was evaluated by the standard deviation of the mean error values of the last 300 iterations (Figure 4) and the stability of the long-term process. These values show how strongly the results vary when a certain parameter is changed. The lower standard deviation value means that the smaller parameter change affects the result.
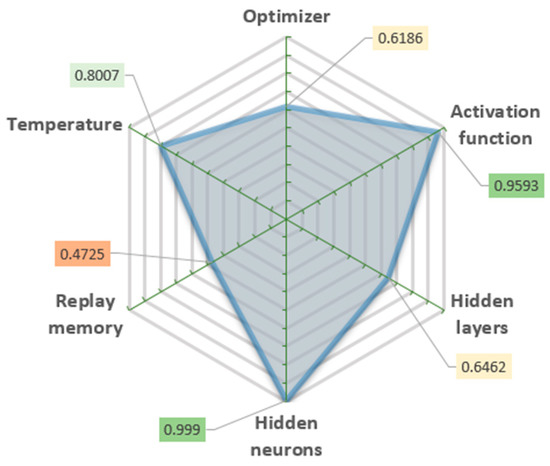
Figure 4.
Algorithm configuration parameters and their significance.
The determined optimal combination of parameters shows that an extensive artificial neural network is not required for this purpose, but an extensive amount of replay memory is useful. Simulations have shown that an increase in at least one or both mentioned parameters does not significantly improve the results, and it prolongs simulation time. A higher temperature value indicates a high algorithm operating stability.
4.2. Results of the Experiment
Robot positioning accuracy was evaluated using the algorithm parameters determined from the simulations. The dependency of relative position vs. the number of iterations shows how the position of the robot end effector changes during 800 motion cycles (Figure 5). It is seen that internal sensors do not notice the position drift when the robot works without the correction. The positioning deviation (curve 2, without correction) has practically the same amplitudes and trends in both y- and z-axes: 0.08 mm (from 1.10 to 1.18 mm) in the z-axis and 0.07 mm in the y-axis (from 1.08 mm to 1.15 mm). This difference might be explained by the fact that the load carried by the robot affects the movement of the robot mainly in the vertical direction.
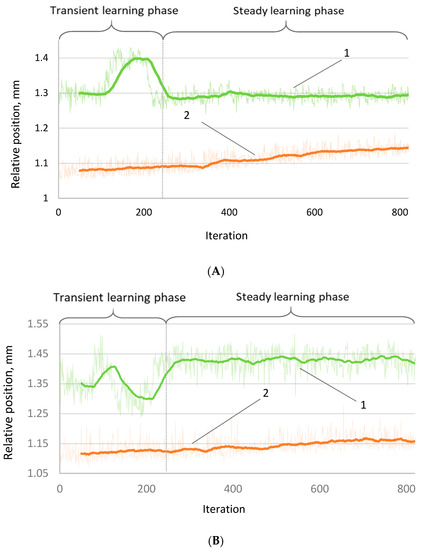
Figure 5.
Variation of positioning of the final coordinates of (A) y-axis; (B) z-axis. 1—with correction and 2—without correction.
The dependencies of the corrected position vs. iteration (Figure 5) show a completely different trend than the uncorrected case: large variations in position coordinates in the learning position of approximately 220 iterations. This behavior is highly expected because the algorithm at the beginning of the training performs “exploration”. At the end of this stage, there was a drastic change in the accuracy characteristics, and these coordinate values became much more stable. As in the case of uncorrected motion, the amplitude of fluctuations in the vertical axis is larger than in the horizontal axis. However, the adjusted positioning shows many more stable trends in the process perspective—both coordinates remain approximately constant.
The absolute error in terms of the number of iterations used to determine the robot’s positioning accuracy changes over time (Figure 6). As was expected, the positioning deviation increases with the number of iterations, and significant random error value fluctuations are observed in the short run.
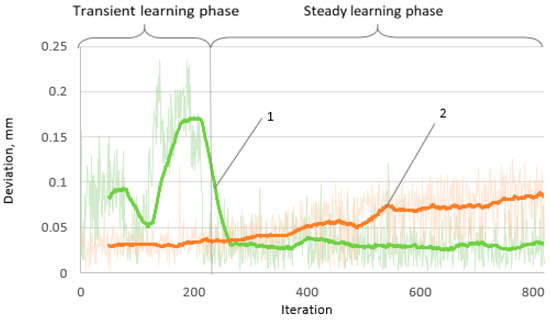
Figure 6.
Variation of positioning deviation (error) with respect to the number of iterations: 1—with correction and 2—without correction.
The position deviation graph shows a distinct picture of the ML outcome from the original state. Here, after the end of the transient learning phase, when the steady learning phase begins, it is obvious that the value of the error remains approximately constant and is equal to that which occurs at the beginning of the uncorrected positioning. Such a situation indicates that the algorithm successfully eliminates positioning drift, although the mean error value remains similar to that which appears at the very beginning of the uncorrected positioning.
5. Discussion
There are a few algorithms that have been used for similar research, and each one has its own set of approaches that focuses on distinct factors. More detailed information about the methods and their achievements is provided in Table 1. Our research brings fresh results for machine learning integration into the robotic system as the strategy to increase robot positioning accuracy.
Our key finding is that applying different parameters to the ML algorithm helps us separate the relevance of certain characteristics and choose where we should concentrate our efforts. The importance of the algorithm setup parameters to achieve better learning procedure results is shown in Figure 4. This analysis might save time and resources in future studies, as well as improve the efficiency of the research.
Nevertheless, the proposed methodology faces limitations, too. Initially, this procedure is useful in case of a small number of points of interest in the trajectory. A considerable amount of data will require the entire mapping of the robot workspace rather than positioning error compensation ad hoc. The proposed ML procedure focused on the individual case of position, robot configuration in this position, and carrying load or end-of-arm tool.
The advantage of this methodology is that it is easy to use in the installed robot environment, where a particular task is processed, and the learning process brings an optimal value of robot position compensation for the analyzed case. Running the procedure does not require a ML professional; this is affordable for robot operators when the general script for the learning process is uploaded into a robot control system. Such a situation is advantageous in the real operation environment, especially for production process adjustment after its changes.
Although the principle of positioning error compensation is similar everywhere, the methods for achieving the result are very different (Table 1). Only similar robotic systems, signal fusion, and algorithms can be compared. The two closest studies to our method performed on 6 DOF robots with an image recognition system using deep reinforcement learning yielded an accuracy improvement of 20% and 50.3%, respectively [37,39]. Our algorithm reached a 66.6% improvement in positioning accuracy, decreasing the absolute positioning error value from 0.09 mm to 0.03 mm.
As a scope of this research, the activity mainly focuses on one aspect of the robotic accuracy issues. A few further steps toward a multifunctional solution are required to make these results more applicable. Specifically, this research develops an algorithm for compensating position errors using visual control, performed by the optical sensor, which requires the installation of a camera with corresponding optics, with a magnifying ratio not less than 50×. During this ML process, the algorithm is constantly searching for the best path to reduce positioning errors after learning; therefore, the final number of loops does not exist. Continuous procedure during its run decreases error, but the best-achieved result with the time passing fluctuates due to process exploration. Therefore, the best learning result could be chosen separately from the learning history. On the other hand, the continuous learning mode loses a bit in positioning accuracy but remains flexible for the compensation values adjustment in case of external condition change (loads, thermal conditions, etc.).
Future studies could focus on eliminating the necessity to add visual control into the ML algorithm. This could be accomplished by locking/freezing compensation coordinates discovered without the use of visual sensors. To eliminate the constant need for a camera, it is possible to use distance sensors or their array and keep feeding the algorithm with live data from them together with internal robot sensor data. Future robotic systems possibly will be supplied with an internally installed ML technique using externally mounted sensors, indicating absolute positions of the robot’s trajectory points of interest.
6. Conclusions
This research provides an attempt to improve robot positioning accuracy using ML techniques. The implemented deep q-learning algorithm demonstrated efficiency by decreasing the robot position error from 0.09 mm to 0.03 mm. This result appeared as an outcome after approximately 800 iterations of the training process.
The newly created methodology improves the reliability and accuracy of robot positioning and decreases the duration of the ML procedure. This algorithm developed on the workbench allows accounting control of an unlimited number of variables per iteration with the proposed ML algorithm. This methodology is realized through the graphical user interface, which allows real-time monitoring of the procedure progress and control.
Nevertheless, the experimental learning process took a long time; therefore, there is an interest in and space for ML process simulation, which increase learning process efficiency. For this purpose, the original robot position deviations on the required point were stored and later used as simulation input. The developed methodology for simulation with many input parameters uses a special neural network. The simulation process lets us choose optimal activation and optimizer functions as well as the size of replay memory and the value of temperature. Moreover, after excessive trials, we defined the optimal size of the artificial neural network; it took one hidden layer with 37 neurons. The values obtained from the simulation were validated experimentally and confirmed initial assumptions of the proposed methodology. The robot positioning drift in the target point was efficiently compensated for externally without access to the internal robot control system.
The developed methodology of the online ML procedure is useful for all types of industrial robots. It is unrelated to the robot control system since it runs on independent external hardware. Our findings create a base of user-friendly and in-place online ML procedures that need adjusting to the level of the end user. Future research includes the analysis of different types of ML algorithms, the development of sensor fusion methods for online robot accuracy control, and further development of the algorithm focused on improving the accuracy of the entire robot trajectory.
Author Contributions
Conceptualization, V.B., D.V. and A.D.; methodology, M.S.; software, A.P. and M.S.; validation, A.P. and M.S.; formal analysis, A.P. and M.S.; investigation, M.S. and A.D.; data curation, A.P. and M.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S., A.P., V.B., A.D., D.V. and I.M.-V.; visualization, M.S. and A.D.; supervision, V.B. and I.M.-V.; funding acquisition, V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received financial support from the Research Council of Lithuania (LMTLT), No. P-LLT-21-6, State Education Development Agency of Latvia, Ministry of Science and Technology (MOST) of Taiwan.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shen, N.Y.; Guo, Z.M.; Li, J.; Tong, L.; Zhu, K. A practical method of improving hole position accuracy in the robotic drilling process. Int. J. Adv. Manuf. Technol. 2018, 96, 2973–2987. [Google Scholar] [CrossRef]
- Anandan, T.M. Demystify robot programming: Software suppliers are disproving preconceptions about robot offline programming (OLP) being too complicated or not cost-effective. Control Eng. 2019, 66, M1. [Google Scholar]
- Nguyen, H.-N.; Le, P.-N.; Kang, H.-J. A new calibration method for enhancing robot position accuracy by combining a robot model–based identification approach and an artificial neural network–based error compensation technique. Adv. Mech. Eng. 2019, 11, 168781401882293. [Google Scholar] [CrossRef] [Green Version]
- Abdelaal, M. A Study of Robot Control Programing for an Industrial Robotic Arm. In Proceedings of the ACCS/PEIT International Conference on Advanced Control Circuits Systems (ACCS) Systems & International Conference on New Paradigms in Electronics & Information Technology, Hurgada, Egypt, 17–20 November 2019; pp. 23–28. [Google Scholar] [CrossRef]
- Kubela, T.; Pochyly, A.; Singule, V. Assessment of industrial robots accuracy in relation to accuracy improvement in machining processes. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference, PEMC, Varna, Bulgaria, 25–28 September 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA; pp. 720–725. [Google Scholar]
- Klimchik, A.; Pashkevich, A. Robotic manipulators with double encoders: Accuracy improvement based on advanced stiffness modeling and intelligent control. IFAC-PapersOnLine 2018, 51, 740–745. [Google Scholar] [CrossRef]
- Ma, L.; Bazzoli, P.; Sammons, P.M.; Landers, R.G.; Bristow, D.A. Modeling and calibration of high-order joint-dependent kinematic errors for industrial robots. Robot. Comput. Integr. Manuf. 2018, 50, 153–167. [Google Scholar] [CrossRef]
- Su, H.; Yang, C.; Ferrigno, G.; De Momi, E. Improved human-robot collaborative control of redundant robot for teleoperated minimally invasive surgery. IEEE Robot. Autom. Lett. 2019, 4, 1447–1453. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Yu, L.; Jia, H.; Zhao, H.; Xia, H. Absolute positioning accuracy improvement in an industrial robot. Sensors 2020, 20, 4354. [Google Scholar] [CrossRef]
- Bi, Z.M.; Miao, Z.; Zhang, B.; Zhang, C.W.J. The state of the art of testing standards for integrated robotic systems. Robot. Comput. Integr. Manuf. 2020, 63, 101893. [Google Scholar] [CrossRef]
- Hazeleger, L.; Beerens, R.; van de Wouw, N. Proportional–Integral–Derivative-Based Learning Control for High-Accuracy Repetitive Positioning of Frictional Motion Systems. IEEE Trans. Control Syst. Technol. 2020, 29, 1652–1663. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Ge, K.; Ding, H. A contour error definition, estimation approach and control structure for six-dimensional robotic machining tasks. Robot. Comput. Integr. Manuf. 2022, 73, 102235. [Google Scholar] [CrossRef]
- Zhu, D.; Feng, X.; Xu, X.; Yang, Z.; Li, W.; Yan, S.; Ding, H. Robotic grinding of complex components: A step towards efficient and intelligent machining–challenges, solutions, and applications. Robot. Comput. Integr. Manuf. 2020, 65, 101908. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, D.; Zhang, H.; Yan, S.; Ding, H. TCP-based calibration in robot-assisted belt grinding of aero-engine blades using scanner measurements. Int. J. Adv. Manuf. Technol. 2017, 90, 635–647. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, D.; Zhang, H.; Yan, S.; Ding, H. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades. Chin. J. Aeronaut. 2019, 32, 2368–2382. [Google Scholar] [CrossRef]
- Peng, J.; Yang, Z.; Ma, T. Position/force tracking impedance control for robotic systems with uncertainties based on adaptive Jacobian and neural network. Complexity 2019, 2019, 1406534. [Google Scholar] [CrossRef]
- Shang, D.; Li, Y.; Liu, Y.; Cui, S. Research on the Motion Error Analysis and Compensation Strategy of the Delta Robot. Mathematics 2019, 7, 411. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.N.; Zhou, J.; Kang, H.J. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network. Neurocomputing 2015, 151, 996–1005. [Google Scholar] [CrossRef]
- Park, I.W.; Lee, B.J.; Cho, S.H.; Hong, Y.D.; Kim, J.H. Laser-based kinematic calibration of robot manipulator using differential kinematics. IEEE/ASME Trans. Mechatron. 2012, 17, 1059–1067. [Google Scholar] [CrossRef]
- Wu, H.; Tizzano, W.; Andersen, T.T.; Andersen, N.A.; Ravn, O. Hand-Eye Calibration and Inverse Kinematics of Robot Arm Using Neural Network. Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2014; Volume 274, pp. 581–591. [Google Scholar]
- Zakhama, A.; Charrabi, L.; Jelassi, K. Intelligent Selective Compliance Articulated Robot Arm robot with object recognition in a multi-agent manufacturing system. Int. J. Adv. Robot. Syst. 2019, 16, 172988141984114. [Google Scholar] [CrossRef] [Green Version]
- Aivaliotis, P.; Zampetis, A.; Michalos, G.; Makris, S. A Machine Learning Approach for Visual Recognition of Complex Parts in Robotic Manipulation. Procedia Manuf. 2017, 11, 423–430. [Google Scholar] [CrossRef]
- Ribeiro, T.; Gonçalves, F.; Garcia, I.; Lopes, G.; Ribeiro, A.F. Q-Learning for Autonomous Mobile Robot Obstacle Avoidance. In Proceedings of the 19th IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC) 2019, Porto, Portugal, 24–26 April 2019. [Google Scholar] [CrossRef]
- Parak, R.; Matousek, R. Comparison of multiple reinforcement learning and deep reinforcement learning methods for the task aimed at achieving the goal. Mendel 2021, 27, 1–8. [Google Scholar] [CrossRef]
- Haarnoja, T.; Pong, V.; Zhou, A.; Dalal, M.; Abbeel, P.; Levine, S. Composable Deep Reinforcement Learning for Robotic Manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6244–6251. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, Y.Z.; Lin, S.S. Robotic Arm Assistance System Based on Simple Stereo Matching and Q-Learning Optimization. IEEE Sens. J. 2020, 20, 10945–10954. [Google Scholar] [CrossRef]
- Jiang, L.; Huang, H.; Ding, Z. Path planning for intelligent robots based on deep Q-learning with experience replay and heuristic knowledge. IEEE/CAA J. Autom. Sin. 2020, 7, 1179–1189. [Google Scholar] [CrossRef]
- Chu, C.; Takahashi, K.; Hashimoto, M. Comparison of deep reinforcement learning algorithms in a robot manipulator control application. In Proceedings of the International Symposium on Computer, Consumer and Control (IS3C) 2020, Taiwan, China, 13–16 November 2020; pp. 284–287. [Google Scholar] [CrossRef]
- Koushik, A.M.; Hu, F.; Kumar, S. Deep q-learning-based node positioning for throughput-optimal communications in dynamic UAV swarm network. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 554–566. [Google Scholar] [CrossRef]
- Gankidi, P.R.; Thangavelautham, J. FPGA architecture for deep learning and its application to planetary robotics. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 4–11 March 2017; IEEE Computer Society: Washington, DC, USA, 2017. [Google Scholar]
- Edu, J.; Wang, Z.; Xie, Y.; Yang, Z.; Bayen, A.; Jadbabaie, A.; Pappas, G.J.; Parrilo, P.; Recht, B.; Tomlin, C.; et al. A Theoretical Analysis of Deep Q-Learning Jianqing Fan. PMLR 2020, 120, 486–489. [Google Scholar]
- Gordón, C.; Encalada, P.; Lema, H.; León, D.; Castro, C.; Chicaiza, D. Intelligent Autonomous Navigation of Robot Kuka Youbot. Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2020; Volume 1038, pp. 954–967. [Google Scholar]
- Rahman, M.M.; Rashid, S.M.H.; Hossain, M.M. Implementation of Q learning and deep Q network for controlling a self balancing robot model. Robot. Biomim. 2018, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Zheng, Y.; Shuai, Y.; Yang, J.; Yang, S.; Tian, Y. Kinematics analysis and trajectory planning of 6-DOF robot. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1749–1754. [Google Scholar] [CrossRef]
- Xie, F.; Chen, L.; Li, Z.; Tang, K. Path smoothing and feed rate planning for robotic curved layer additive manufacturing. Robot. Comput. Integr. Manuf. 2020, 65, 101967. [Google Scholar] [CrossRef]
- Wang, Z.; Majewicz Fey, A. Deep learning with convolutional neural network for objective skill evaluation in robot-assisted surgery. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1959–1970. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Lan, R. An end-to-end calibration method for welding robot laser vision systems with deep reinforcement learning. IEEE Trans. Instrum. Meas. 2020, 69, 4270–4280. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Luo, X. Data-driven Industrial Robot Arm Calibration: A Machine Learning Perspective. In Proceedings of the 2021 IEEE International Conference on Networking, Sensing and Control (ICNSC), Xiamen, China, 3–5 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, C.T.; Do, V.P.; Lee, B.R. A novel indirect calibration approach for robot positioning error compensation based on neural network and hand-eye vision. Appl. Sci. 2019, 9, 1940. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Cao, G.; Qu, Y. Safety analysis via forward kinematics of delta parallel robot using machine learning. Saf. Sci. 2019, 117, 243–249. [Google Scholar] [CrossRef]
- Yuan, P.; Chen, D.; Wang, T.; Cao, S.; Cai, Y.; Xue, L. A compensation method based on extreme learning machine to enhance absolute position accuracy for aviation drilling robot. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Burström, G.; Buerger, C.; Hoppenbrouwers, J.; Nachabe, R.; Lorenz, C.; Babic, D.; Homan, R.; Racadio, J.M.; Grass, M.; Persson, O.; et al. Machine learning for automated 3-dimensional segmentation of the spine and suggested placement of pedicle screws based on intraoperative cone-beam computer tomography. J. Neurosurg. Spine 2019, 31, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Yang, G.; Zheng, T.; Wang, Y.; Yang, K.; Fang, Z. An accuracy enhancement method for a cable-driven continuum robot with a flexible backbone. IEEE Access 2020, 8, 37474–37481. [Google Scholar] [CrossRef]
- Alamdar, A.; Samandi, P.; Hanifeh, S.; Kheradmand, P.; Mirbagheri, A.; Farahmand, F.; Sarkar, S. Investigation of a Hybrid Kinematic Calibration Method for the “Sina” Surgical Robot. IEEE Robot. Autom. Lett. 2020, 5, 5276–5282. [Google Scholar] [CrossRef]
- Sacco, C.; Baz Radwan, A.; Anderson, A.; Harik, R.; Gregory, E. Machine learning in composites manufacturing: A case study of Automated Fiber Placement inspection. Compos. Struct. 2020, 250, 112514. [Google Scholar] [CrossRef]
- Luo, J.; Solowjow, E.; Wen, C.; Ojea, J.A.; Agogino, A.M.; Tamar, A.; Abbeel, P. Reinforcement learning on variable impedance controller for high-precision robotic assembly. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3080–3087. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Duan, Y.; He, X.; Yang, M. Image positioning and identification method and system for coal and gangue sorting robot. Int. J. Coal Prep. Util. 2020. [Google Scholar] [CrossRef]
- Li, Y.; Lei, Q.; Cheng, C.; Zhang, G.; Wang, W.; Xu, Z. A review: Machine learning on robotic grasping. In Proceedings of the Eleventh International Conference on Machine Vision (ICMV 2018), Munich, Germany, 1–3 November 2018; Nikolaev, D.P., Radeva, P., Verikas, A., Zhou, J., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11041, p. 54. [Google Scholar]
- Bai, Q.; Li, S.; Yang, J.; Song, Q.; Li, Z.; Zhang, X. Object Detection Recognition and Robot Grasping Based on Machine Learning: A Survey. IEEE Access 2020, 8, 181855–181879. [Google Scholar] [CrossRef]
- Causo, A.; Chong, Z.H.; Luxman, R.; Kok, Y.Y.; Yi, Z.; Pang, W.C.; Meixuan, R.; Teoh, Y.S.; Jing, W.; Tju, H.S.; et al. A robust robot design for item picking. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7421–7426. [Google Scholar] [CrossRef]
- Al Khawli, T.; Anwar, M.; Alzaabi, A.; Sunda-Meya, A.; Islam, S. Machine Learning for Robot-Assisted Industrial Automation of Aerospace Applications. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 3695–3698. [Google Scholar] [CrossRef]
- Deng, Z.; Zheng, X.; Zhang, L.; Zhang, J. A learning framework for semantic reach-to-grasp tasks integrating machine learning and optimization. Rob. Auton. Syst. 2018, 108, 140–152. [Google Scholar] [CrossRef]
- Ribeiro, P.M.S.; Matos, A.C.; Santos, P.H.; Cardoso, J.S. Machine learning improvements to human motion tracking with imus. Sensors 2020, 20, 6383. [Google Scholar] [CrossRef]
- Xiao, X.; Zarar, S. Machine Learning for Placement-Insensitive Inertial Motion Capture. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6716–6721. [Google Scholar] [CrossRef]
- Cheng, F.; Raghavan, A.; Jung, D.; Sasaki, Y.; Tajika, Y. High-accuracy unsupervised fault detection of industrial robots using current signal analysis. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 17–20 June 2019. [Google Scholar] [CrossRef]
- Koike, R.; Sakaino, S.; Tsuji, T. Hysteresis compensation in force/torque sensor based on machine learning. In Proceedings of the IECON 2018–44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2769–2774. [Google Scholar] [CrossRef]
- Kastner, L.; Frasineanu, V.C.; Lambrecht, J. A 3D-Deep-Learning-based Augmented Reality Calibration Method for Robotic Environments using Depth Sensor Data. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 1135–1141. [Google Scholar] [CrossRef]
- Zwiener, A.; Geckeler, C.; Zell, A. Contact Point Localization for Articulated Manipulators with Proprioceptive Sensors and Machine Learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 323–329. [Google Scholar] [CrossRef]
- Gordon, C.; Lema, H.; Leon, D.; Encalada, P. Human rescue based on autonomous robot KUKA youbot with deep learning approach. In Proceedings of the 2019 6th International Conference on eDemocracy and eGovernment, ICEDEG, Quito, Ecuador, 24–26 April 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA; pp. 318–323. [Google Scholar]
- Petronis, A.; Bučinskas, V.; Šumanas, M.; Dzedzickis, A.; Petrauskas, L.; Sitiajev, N.E.; Morkvenaite-Vilkonciene, I. Improving Positioning Accuracy of an Articulated Robot Using Deep Q-Learning Algorithms. Advances in Intelligent Systems and Computing; AISC: Chicago, IL, USA, 2020; Volume 1140, pp. 257–266. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).