A Novel Method for Source Tracking of Chemical Gas Leakage: Outlier Mutation Optimization Algorithm
Abstract
:1. Introduction
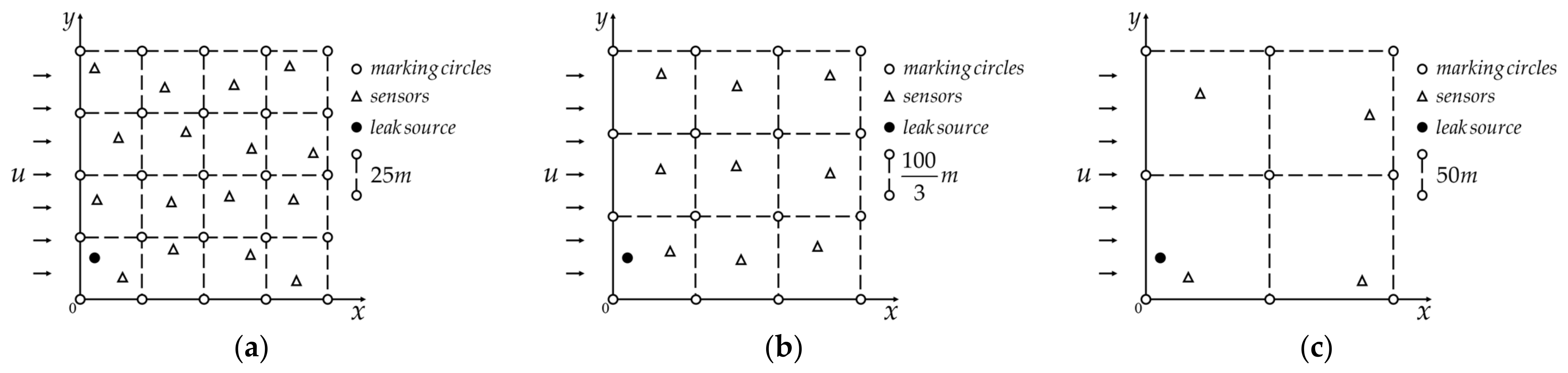
- Traditional gas leakage accident application examples usually take the position and number of the storage tank or environmental variables as known conditions. In order to illustrate that the OMO algorithm has the best comprehensive performance in the gas leakage traceability problem under flat terrain conditions, randomness is introduced to the various variables that will affect the calculation results of the Gaussian plume model, which can make the application examples created in this article to be strongly representative.
- The introduction of sensor information defect conditions: the number of sensors in the three types of application examples is 16, 9, 4, respectively, and the intensity of the information defect increases in turn, which is a challenge to the exploration integrity of the optimization algorithm, but it is also an important part to prove the advantages of OMO algorithm.
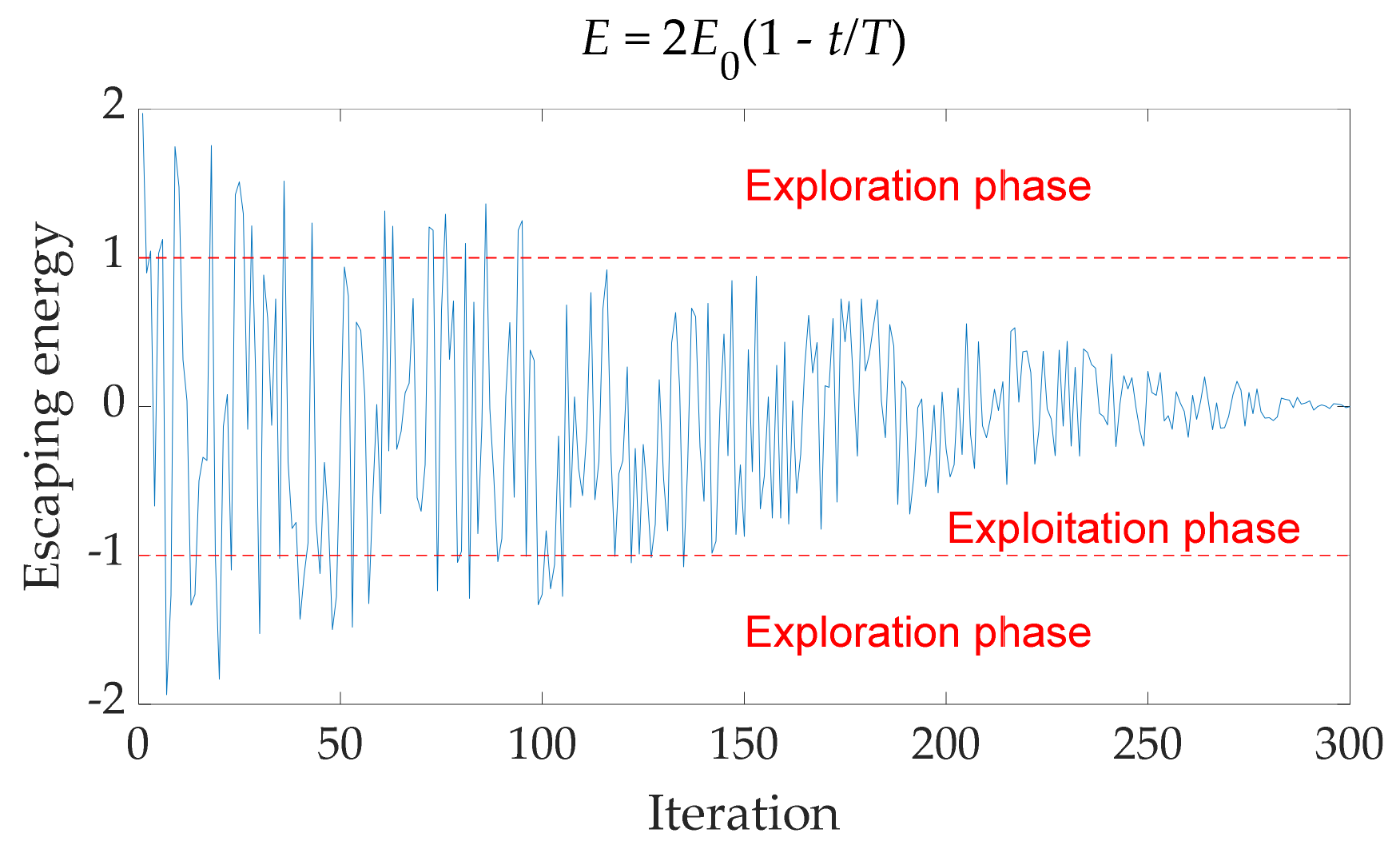
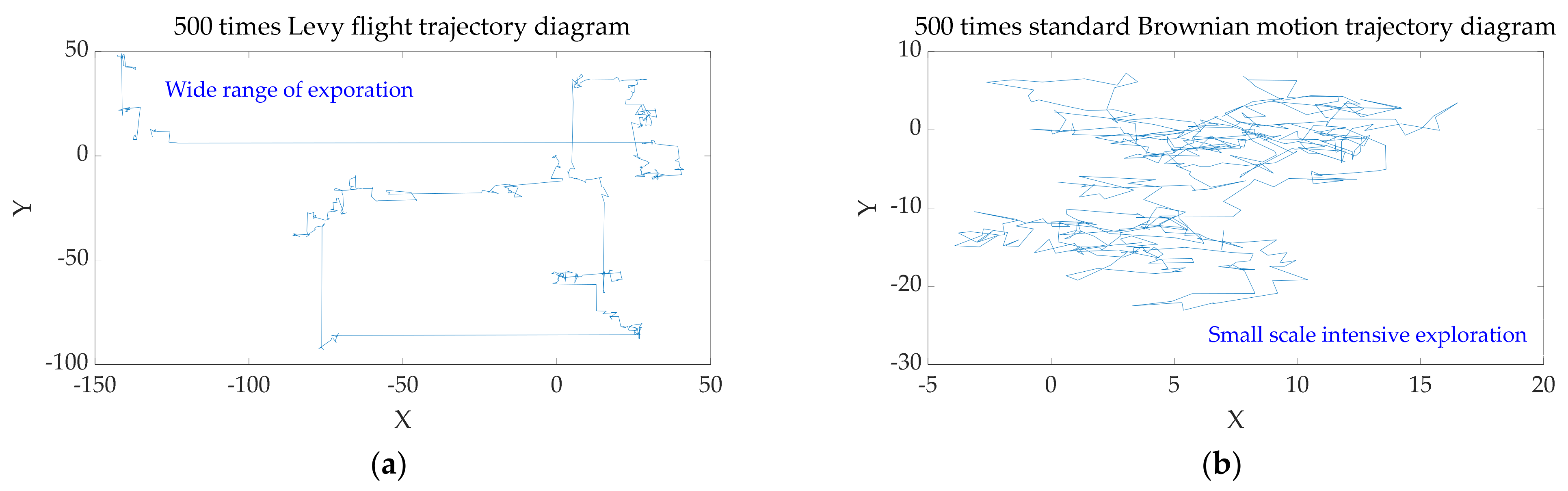
- The OMO algorithm is different from other swarm intelligence algorithms. The exploration phase of the OMO algorithm is dominated by outliers, and the exploration method introduces the Levi flight, which aims to avoid the local optimum with a high degree of exploration. In the exploitation phase of the OMO algorithm, two-way selection improves the convergence speed and accuracy. The complementarity of the encirclement and mutation strategies has become a major feature of the algorithm.
- The research on the parameter law of the OMO algorithm and the introduction of precision control parameters enable the OMO algorithm to adjust parameters reasonably in practical applications and quickly adapt to various application scenarios.
2. Methodology
2.1. Gaussian Plume Model
- The concentration of leaking gas conforms to Gaussian distribution in the y-axis section and the z-axis section;
- The leakage intensity of the leaking gas is continuous and uniform;
- The ambient wind speed remains constant during the gas leak process, and the default direction is along the positive x-axis;
- The model ignores the effects of any chemical reactions, including sedimentation and decomposition;
- The leaked gas follows the ideal gas equation of state and the law of conservation of mass.
2.2. Outlier Mutation Optimization (OMO) Algorithm
- ;
- ;
- , independent of .
3. Experimental Design
3.1. Chemical Gas Leakage Accident Application Example
3.2. Chemical Gas Leakage’s Source Tracking Model
3.3. Other Details and Pseudocode of OMO Algorithm
| Algorithm 1. Pseudocode of OMO algorithm. |
| Inputs: The population size N, maximum number of iterations T, Speed Control Constant SH, SR Outputs: Data required for drawing plotData, the location of prey preyLocation and its fitness value preyEnergy |
| Initialize the random population Xi(i = 1, 2, …, N), plotData, preyLocation, preyEnergy and step parameters α, β for (each iteration t) do for (each predator Xi) do Update the escape energy E and Epara using Equations (3) and (4) if (|E| ≥ 1) then Exploration phase Update the location vector using Equation (8) if (|E| < 1) then Exploitation phase if (r > 0.5) then Besiege strategy Update the location vector using Equations (13), (14), (16), (17) if (r ≤ 0.5) then Mutant strategy Update the location vector using Equations (13)–(17) Checkup population boundary and correct individual Calculate the fitness values of predator population Set preyLocation and preyEnergy as the location of prey and its fitness based on the minimum value between last prey and current population Update plotData and record them Return plotData, preyLocation, preyEnergy |
4. Results and Discussion
4.1. Results
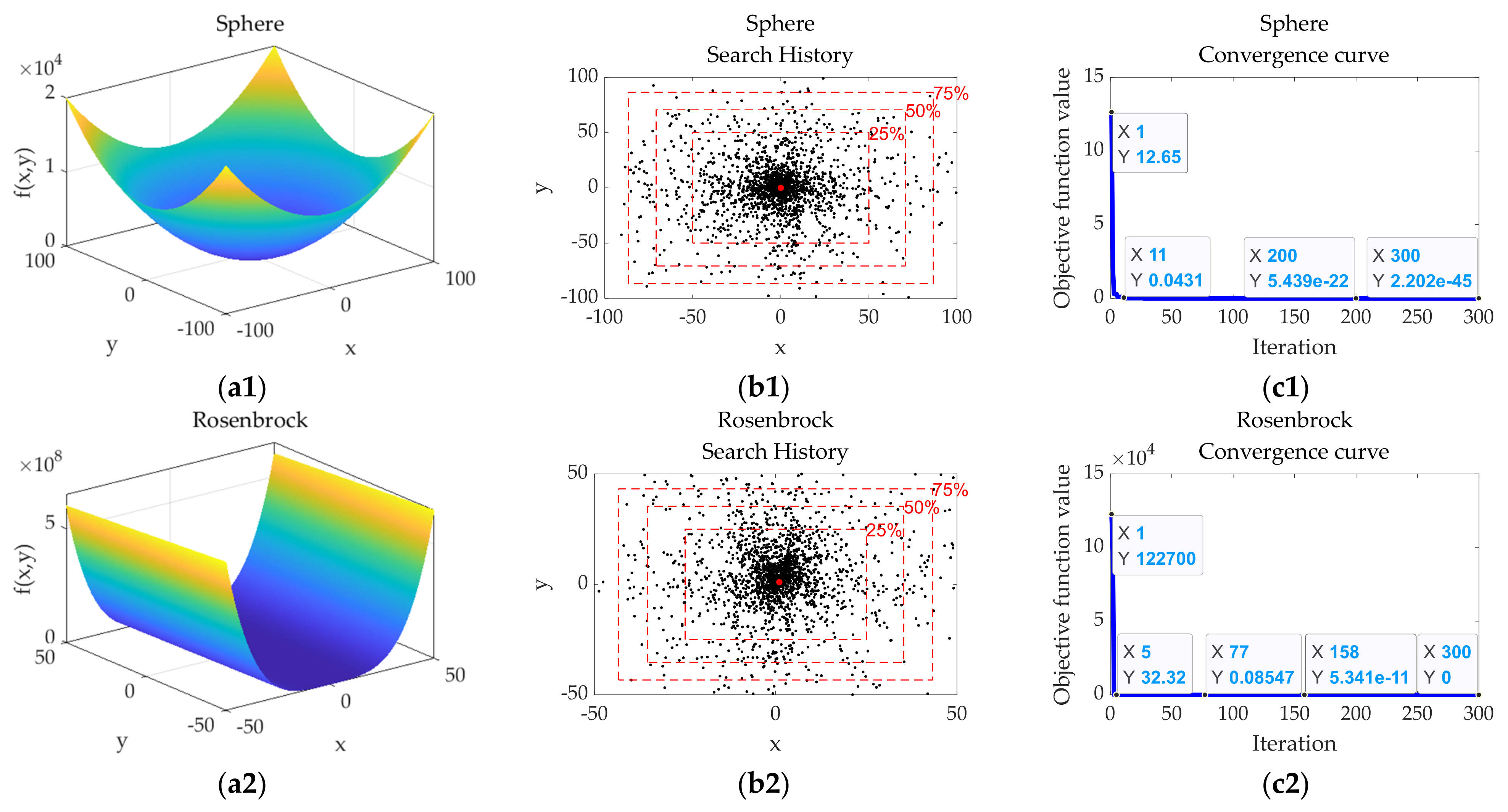
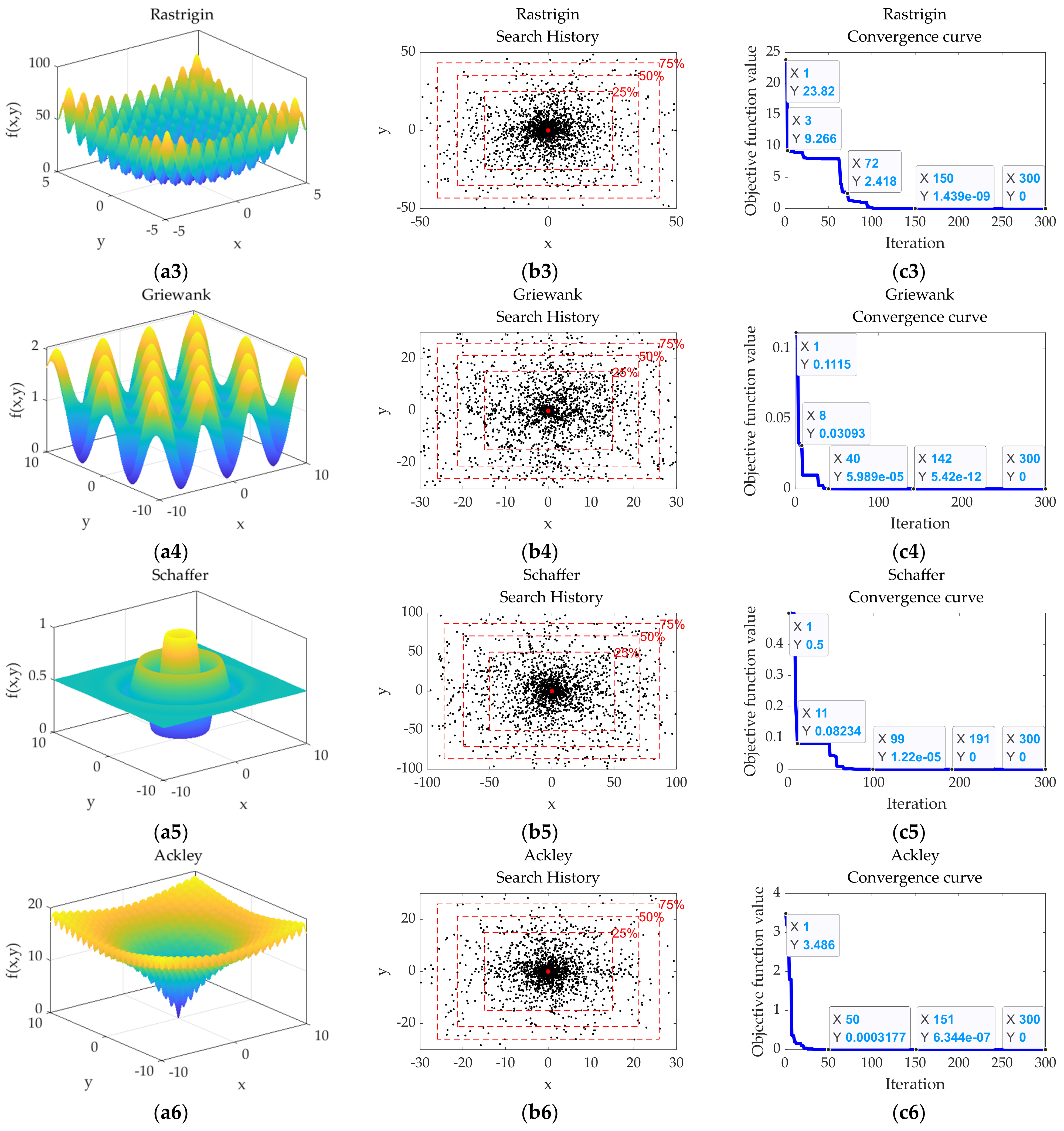
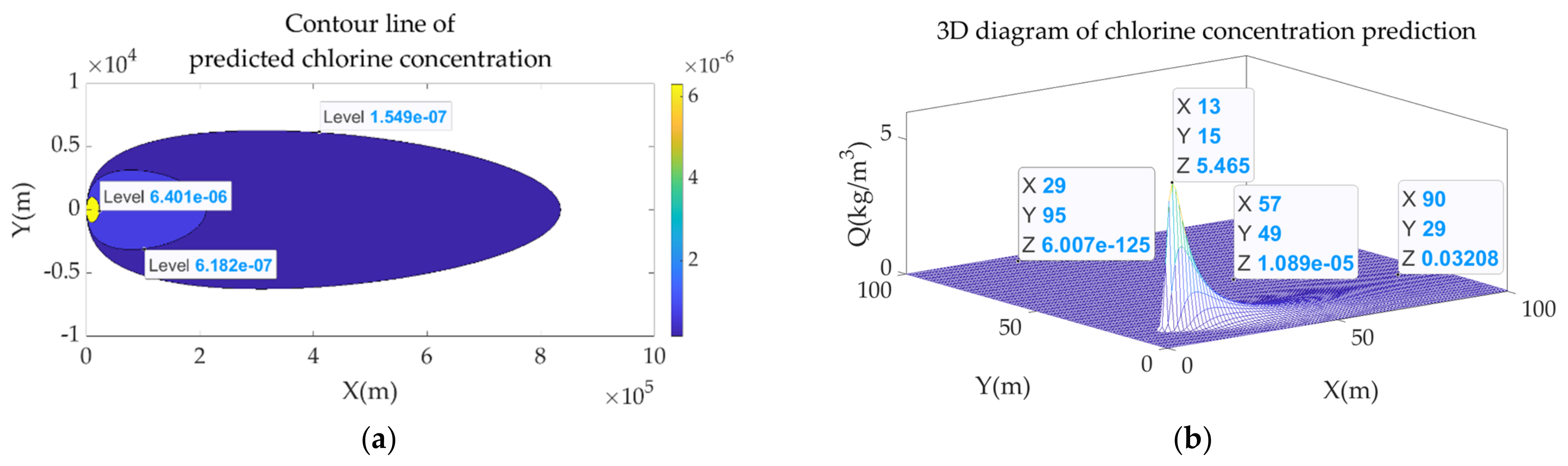
4.1.1. Qualitative Results of OMO Algorithm
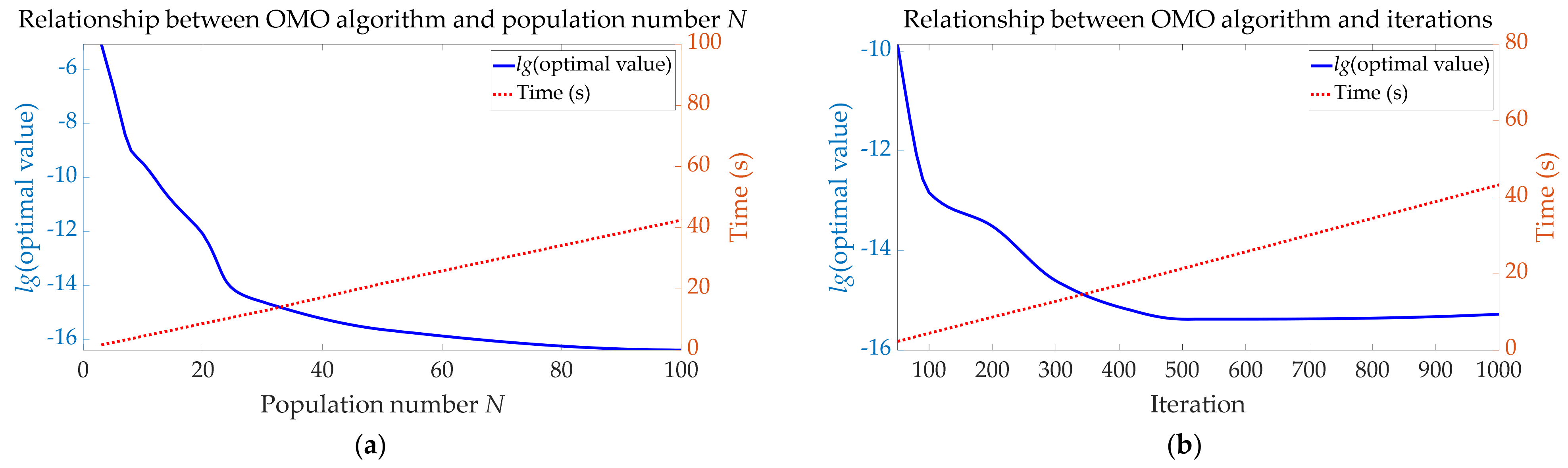
4.1.2. Relationship between OMO Algorithm and Population Number N
- The time-requirement of the OMO algorithm is approximately proportional to the population number N;
- The accuracy of the OMO algorithm gradually increases as the population number N increases;
- When the population number 3 < N < 5, the accuracy of the OMO algorithm is relatively low; when the population number 3 < N < 25, the accuracy of the OMO algorithm is significantly improved with the increase of N; when the population number N > 25, the increased speed of OMO algorithm’s accuracy with the increase of N gradually decreases and stabilizes.
4.1.3. Relationship between OMO Algorithm and Iterations
- The time-requirement of the OMO algorithm is approximately proportional to the iterations;
- The accuracy of the OMO algorithm gradually increases as the iterations increase;
- When the iterations <100, the accuracy of the OMO algorithm is significantly improved with the increase of iterations; when the 100 < iterations < 500, the accuracy of the OMO algorithm is slightly improved with the increase of iterations; when the iterations >500, the increased speed of the OMO algorithm’s accuracy with the increase of iterations gradually decreases and stabilizes.
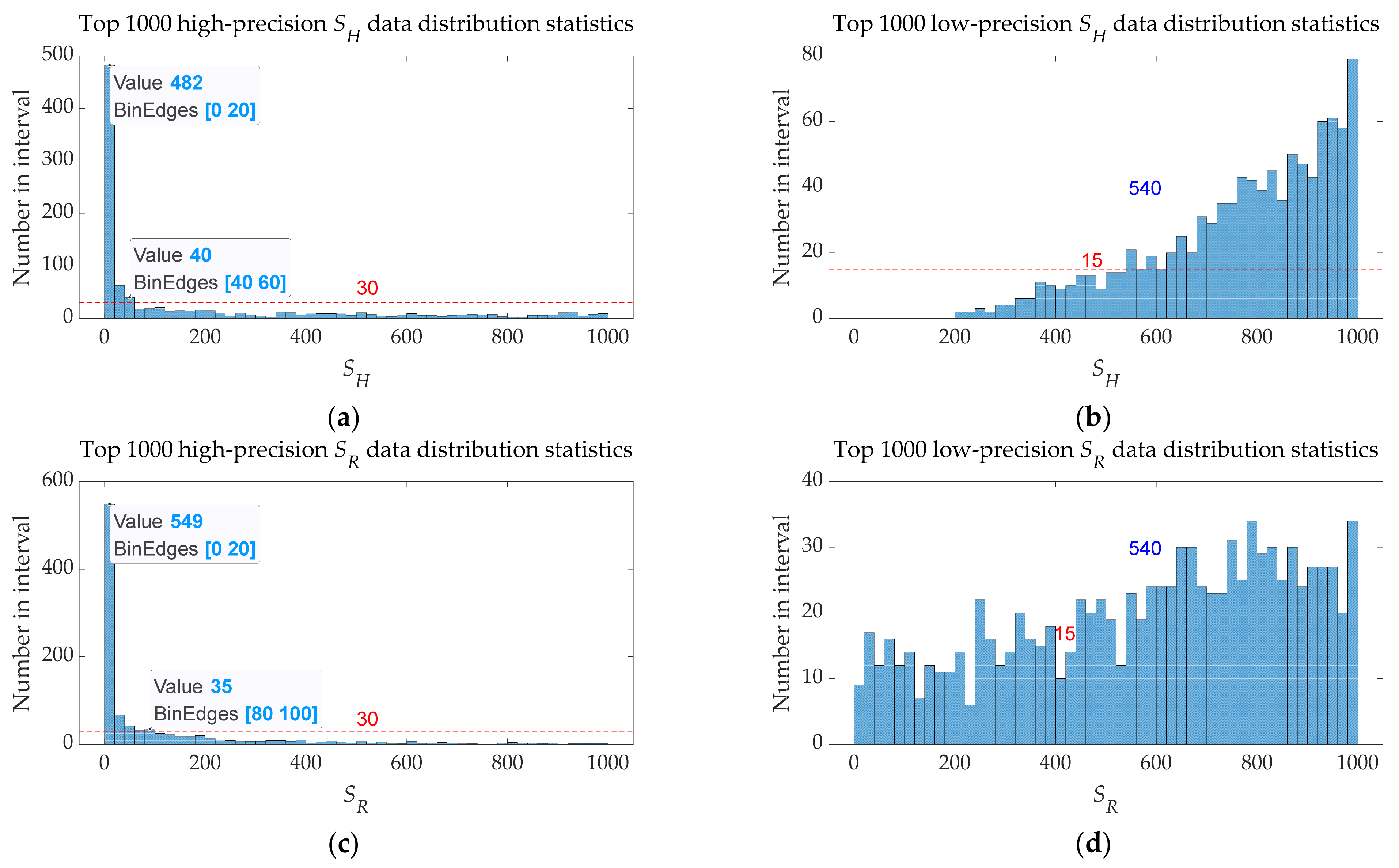
4.1.4. Relationship between OMO Algorithm and Speed Control Constant
- Changing the values of SH and SR will have a certain impact on the accuracy of the OMO algorithm, but random values of SH and SR will have a high probability to get a more satisfactory result.
- High-precision OMO algorithm results are often accompanied by suitable exploration steps (influenced by SH), and low-precision OMO algorithm results are often accompanied by too-large exploration steps. The reason why some SH are too large but can also achieve accuracy of the algorithm is mainly due to the random allocation of super boundary data, but in the chemical gas leakage accident model established by this paper, the best value of SH is 1–60.
- High-precision OMO algorithm results are often accompanied by suitable exploitation steps (influenced by SR), and low-precision OMO algorithm results are often accompanied by too large exploitation steps. Logarithmic processing has been performed in the step length parameter of the standard Brownian motion to ensure that the exploitation space is small enough in the final stage and the space has been explored completely; therefore, a small-range change of SR will have little effect on the accuracy of the OMO algorithm. In the chemical gas leakage accident model established by this paper, the best value of SR is 1–100.
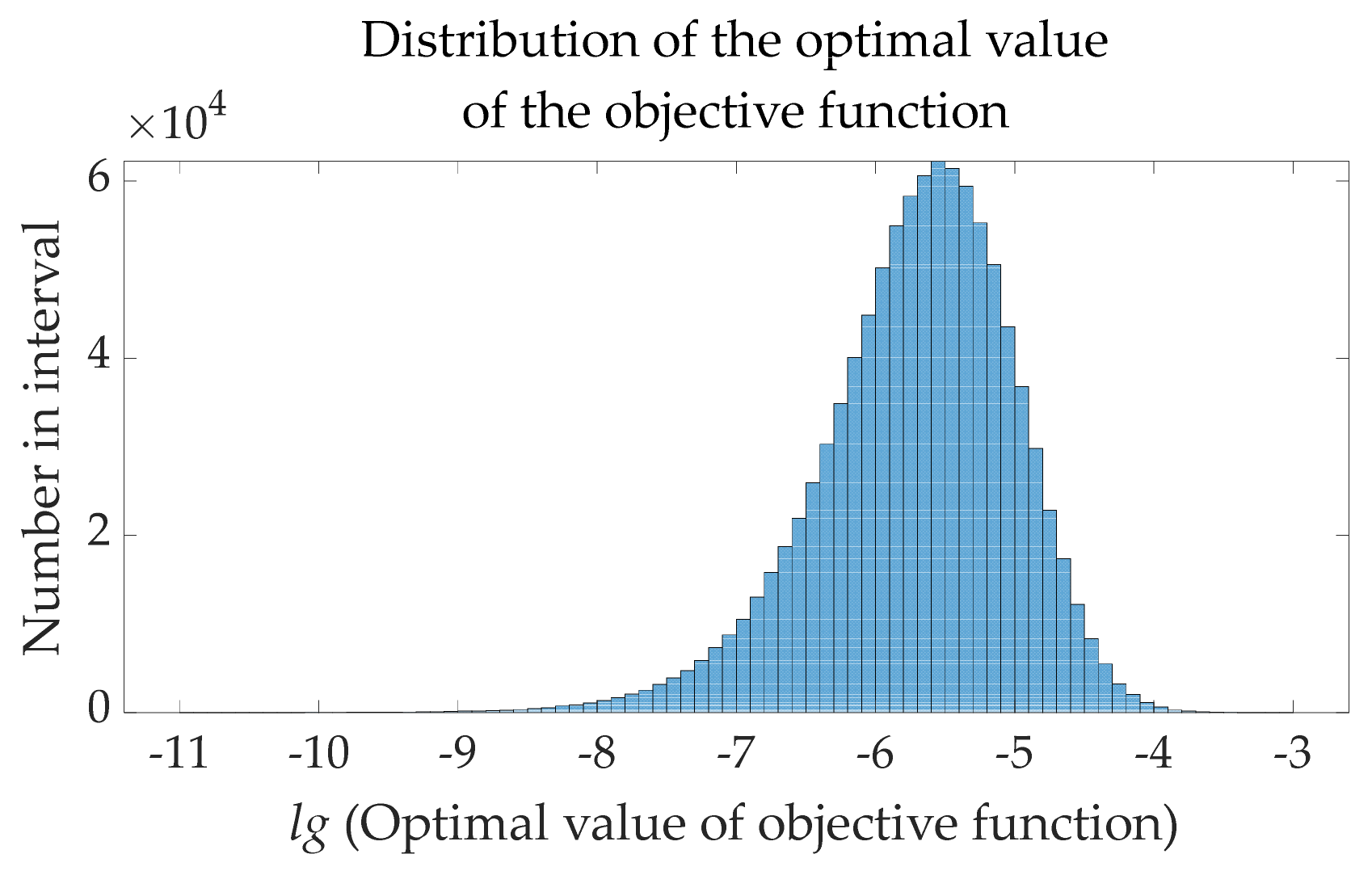
4.1.5. Robustness Analysis under the Influence of White Gaussian Noise (WGN)
4.1.6. Comparative Analysis among Optimization Algorithms
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Long, S.; Zhao, L.; Shi, T.; Li, J.; Yang, J.; Liu, H.; Mao, G.; Qiao, Z.; Yang, Y. Pollution control and cost analysis of wastewater treatment at industrial parks in Taihu and Haihe water basins, China. J. Clean. Prod. 2018, 172, 2435–2442. [Google Scholar] [CrossRef]
- Park, H.-S.; Rene, E.R.; Choi, S.-M.; Chiu, A.S.F. Strategies for sustainable development of industrial park in Ulsan, South Korea—From spontaneous evolution to systematic expansion of industrial symbiosis. J. Environ. Manag. 2008, 87, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, R.; Worden, S.; Cao, H.; Li, C. Public participation in environmental governance initiatives of chemical industrial parks. J. Clean. Prod. 2021, 305, 127092. [Google Scholar] [CrossRef]
- Yet-Pole, I.; Fu, J.M. Risk analysis of a cross-regional toxic chemical disaster by using the integrated mesoscale and microscale consequence analysis model. J. Loss Prev. Process. Ind. 2021, 71, 104424. [Google Scholar]
- Jiang, Y.; Xu, Z.; Wei, J.; Teng, G. Fused CFD-interpolation model for real-time prediction of hazardous gas dispersion in emergency rescue. J. Loss Prev. Process. Ind. 2020, 63, 103988. [Google Scholar] [CrossRef]
- Nooralishahi, P.; Lopez, F.; Maldague, X. A Drone-Enabled Approach for Gas Leak Detection Using Optical Flow Analysis. Appl. Sci. 2021, 11, 1412. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G.; Khakzad, N. Integrating safety and security resources to protect chemical industrial parks from man-made domino effects: A dynamic graph approach. Reliab. Eng. Syst. Saf. 2019, 191, 106470. [Google Scholar] [CrossRef]
- Gas Leak Accidents that Made the Headlines in the Past. Available online: https://www.deccanherald.com/national/gas-leak-accidents-that-made-the-headlines-in-the-past-834754.html (accessed on 25 June 2021).
- Acute Exposure Guideline Levels (AEGLs). Available online: https://response.restoration.noaa.gov/oil-and-chemical-spills/chemical-spills/resources/acute-exposure-guideline-levels-aegls.html (accessed on 10 July 2021).
- Ammonia Results-AEGL Program. Available online: https://www.epa.gov/aegl/ammonia-results-aegl-programs (accessed on 10 July 2021).
- Chlorine Results-AEGL Program. Available online: https://www.epa.gov/aegl/chlorine-results-aegl-program (accessed on 10 July 2021).
- Phosgene Results-AEGL Program. Available online: https://www.epa.gov/aegl/phosgene-results-aegl-program (accessed on 10 July 2021).
- Hou, Q.; Zhu, W. An EKF-Based Method and Experimental Study for Small Leakage Detection and Location in Natural Gas Pipelines. Appl. Sci. 2019, 9, 3193. [Google Scholar] [CrossRef]
- Huang, Y.; Xiu, G.; Lu, Y.; Gao, S.; Li, L.; Chen, L.; Huang, Q.; Yang, Y.; Che, X.; Chen, X.; et al. Application of an emission profile-based method to trace the sources of volatile organic compounds in a chemical industrial park. Sci. Total Environ. 2021, 768, 144694. [Google Scholar] [CrossRef]
- Singh, S.K.; Rani, R. A least-squares inversion technique for identification of a point release: Application to Fusion Field Trials 2007. Atmos. Environ. 2014, 92, 104–117. [Google Scholar] [CrossRef]
- Singh, S.K.; Rani, R. Assimilation of concentration measurements for retrieving multiple point releases in atmosphere: A least-squares approach to inverse modelling. Atmos. Environ. 2015, 119, 402–414. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Huang, L.; Zhang, X. Source term estimation of hazardous material releases using hybrid genetic algorithm with composite cost functions. Eng. Appl. Artif. Intell. 2018, 75, 102–113. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, E.S.; Shin, D. Deep Neural Networks for Source Tracking of Chemical Leaks and Improved Chemical Process Safety. In 13th International Symposium on Process Systems Engineering (PSE 2018); Mario, R.E., Marianthi, G.I., Gavin, P.T., Eds.; Elsevier Ltd.: San Diego, CA, USA, 2018; Volume 44, pp. 2359–2364. [Google Scholar]
- Althuwaynee, O.F.; Pokharel, B.; Aydda, A.; Balogun, A.L.; Kim, S.W.; Park, H.J. Spatial identification and temporal prediction of air pollution sources using conditional bivariate probability function and time series signature. J. Expo. Sci. Environ. Epidemiol. 2020, 31, 709–726. [Google Scholar] [CrossRef]
- Yang, Z.; Yao, Q.; Buser, M.D.; Alfieri, J.G.; Li, H.; Torrents, A.; McConnell, L.L.; Downey, P.M.; Hapeman, C.J. Modification and validation of the Gaussian plume model (GPM) to predict ammonia and particulate matter dispersion. Atmos. Pollut. Res. 2020, 11, 1063–1072. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Son, H.; Yi, W. Development of PUFF-Gaussian dispersion model for the prediction of atmospheric distribution of particle concentration. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Ye, W.; Zhou, B.; Tu, Z.; Xiao, X.; Yan, J.; Wu, T.; Wu, F.; Zheng, C.; Tittel, F.K. Leakage source location based on Gaussian plume diffusion model using a near-infrared sensor. Infrared Phys. Technol. 2020, 109, 103411. [Google Scholar] [CrossRef]
- Ban, M.; Yu, J.; Shahidehpour, M.; Guo, D.; Yao, Y. Considering the Differentiating Health Impacts of Fuel Emissions in Optimal Generation Scheduling. IEEE Trans. Sustain. Energy 2020, 11, 15–26. [Google Scholar] [CrossRef]
- Pirhalla, M.; Heist, D.; Perry, S.; Tang, W.; Brouwer, L. Simulations of dispersion through an irregular urban building array. Atmos. Environ. 2021, 258, 118500. [Google Scholar] [CrossRef]
- Hanna, S. Britter and McQuaid (B&M) 1988 workbook nomograms for dense gas modeling applied to the Jack Rabbit II chlorine release trials. Atmos. Environ. 2020, 232, 117539. [Google Scholar]
- Long, C.; Qi, H.; Zhang, Y. A dynamic model of gas diffusion. Dyn. Contin. Discret. Impulsive Syst. Ser. B Appl. Algorithms 2006, 13, 706–709. [Google Scholar]
- Zhang, X.; Li, J.; Zhu, J.; Qiu, L. Computational fluid dynamics study on liquefied natural gas dispersion with phase change of water. Int. J. Heat Mass Transf. 2015, 91, 347–354. [Google Scholar] [CrossRef]
- Bellegoni, M.; Ovidi, F.; Landucci, G.; Tognotti, L.; Galletti, C. CFD analysis of the influence of a perimeter wall on the natural gas dispersion from an LNG pool. Process Saf. Environ. Prot. 2021, 148, 751–764. [Google Scholar] [CrossRef]
- Huh, C.; Choi, S.; Lee, J.M. Concentration model for gas releases in buildings and the mitigation effect. J. Loss Prev. Process Ind. 2020, 65, 104135. [Google Scholar] [CrossRef]
- Ma, D.; Tan, W.; Wang, Q.; Zhang, Z.; Gao, J.; Zeng, Q.; Wang, X.; Xia, F.; Shi, X. Application and improvement of swarm intelligence optimization algorithm in gas emission source identification in atmosphere. J. Loss Prev. Process Ind. 2018, 56, 262–271. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Q.; Shi, L.; Yang, Q. Underwater gas pipeline leakage source localization by distributed fiber-optic sensing based on particle swarm optimization tuning of the support vector machine. Appl. Opt. 2016, 55, 242–247. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. Int. J. Escience 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Li, J.; Xin, Z. Locating unknown number of multi-point hazardous gas leaks using Principal Component Analysis and a Modified Genetic Algorithm. Atmos. Environ. 2020, 230, 117515. [Google Scholar] [CrossRef]
- Steffelbauer, D.B.; Günther, M.; Fuchs-Hanusch, D. Leakage Localization with Differential Evolution: A Closer Look on Distance Metrics. In Proceedings of the 18th International Conference on Water Distribution System Analysis (WDSA), Cartagena, Colombia, 24–28 July 2016; Elsevier Science BV: Amsterdam, The Netherlands, 2017; Volume 186, pp. 444–451. [Google Scholar]
- Zheng, X.; Chen, Z. Inverse calculation approaches for source determination in hazardous chemical releases. J. Loss Prev. Process Ind. 2011, 24, 293–301. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. Direct Search Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Lin, C.-C.; Yeh, H.-D. An Optimization Approach to Leak Detection in Pipe Networks Using Simulated Annealing. Water Resour. Manag. 2015, 29, 4185–4201. [Google Scholar] [CrossRef]
- Sousa, J.; Ribeiro, L.; Muranho, J.; Marques, A.S. Locating leaks in water distribution networks with simulated annealing and graph theory. In Computing and Control for the Water Industry; Ulanicki, B., Kapelan, Z., Boxall, J., Eds.; Elsevier Ltd.: San Diego, CA, USA, 2015; Volume 119, pp. 63–71. [Google Scholar]
- Jiao, S.B.; Fan, L.; Wu, P.Y.; Qiao, L.; Wang, Y.; Xie, G. Assessment of leakage degree of underground heating primary pipe network based on chaotic simulated annealing neural network. In Proceedings of the Chinese Automation Congress, Jinan, China, 20–22 October 2017; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Jaward, M.H.; Bull, D.; Canagarajah, N. Sequential Monte Carlo methods for contour tracking of contaminant clouds. Signal Process. 2010, 90, 249–260. [Google Scholar] [CrossRef]
- Quy, T.B.; Kim, J.M. Real-Time Leak Detection for a Gas Pipeline Using a k-NN Classifier and Hybrid AE Features. Sensors 2021, 21, 367. [Google Scholar] [CrossRef]
- Husnawati; Fitriana, G.F.; Nurmaini, S. The development of hybrid methods in simple swarm robots for gas leak localization. In Proceedings of the 2017 International Conference on Signals and Systems, Bali, Indonesia, 16–18 May 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Ma, T.; Liu, S.; Xiao, H. Multirobot searching method of natural gas leakage sources on offshore platform using ant colony optimization. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420959012. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, B.; Wang, R.; Zhu, Z.; Wang, Y.; Qiu, X. Atmospheric dispersion prediction and source estimation of hazardous gas using artificial neural network, particle swarm optimization and expectation maximization. Atmos. Environ. 2018, 178, 158–163. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Zhang, W.; Xu, N.; Guo, Z.; Wu, G. Improved PSO-Based Method for Leak Detection and Localization in Liquid Pipelines. IEEE Trans. Ind. Inform. 2018, 14, 3143–3154. [Google Scholar] [CrossRef]
- Wang, R.; Chen, B.; Qiu, S.; Ma, L.; Zhu, Z.; Wang, Y.; Qiu, X. Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm. Atmosphere 2018, 9, 119. [Google Scholar] [CrossRef]
- Lalle, Y.; Abdelhafidh, M.; Fourati, L.C.; Rezgui, J. A hybrid optimization algorithm based on K-means plus plus and Multi-objective Chaotic Ant Swarm Optimization for WSN in pipeline monitoring. In Proceedings of the 15th IEEE International Wireless Communications and Mobile Computing Conference, Tangier, Morocco, 24–28 June 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Lateb, M.; Meroney, R.N.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, M.C. On the use of numerical modelling for near-field pollutant dispersion in urban environments—A review. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef]
- Jung, Y.R.; Park, W.G.; Park, O.H. Pollution dispersion anaysis using the puff model with numerical flow field data. Mech. Res. Commun. 2003, 30, 277–286. [Google Scholar] [CrossRef]
- Xu, H.-X.; Li, G.; Yang, S.-L.; Xu, X. Modeling and simulation of haze process based on Gaussian model. In Proceedings of the 11th International Computer Conference on Wavelet Active Media Technology and Information Processing, Chengdu, China, 19–21 December 2014; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Stockie, J.M. The Mathematics of Atmospheric Dispersion Modeling. Siam Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Brusca, S.; Famoso, F.; Lanzafame, R.; Mauro, S.; Garrano, A.M.C.; Monforte, P. Theoretical and experimental study of Gaussian Plume model in small scale systems. In Energy Procedia, Proceedings of the 71st Conference of the Italian Thermal Machines Engineering Association, Politecnico Torino, Turin, Italy, 14–16 September 2016; Masoero, M.C., Arsie, I., Eds.; Elsevier Ltd.: San Diego, CA, USA, 2016. [Google Scholar]
- Yang, Y.; Zheng, Z.; Bian, K.; Song, L.; Han, Z. Real-Time Profiling of Fine-Grained Air Quality Index Distribution Using UAV Sensing. IEEE Internet Things J. 2018, 5, 186–198. [Google Scholar] [CrossRef]
- Jain, R.K.; Cui, Z.C.; Domen, J.K. Environmental Impact of Mining and Mineral Processing: Management, Monitoring, and Auditing Strategies; Elsevier Ltd.: San Diego, CA, USA, 2016; pp. 87–90. [Google Scholar]
- Ma, D.; Zhang, Z. Contaminant dispersion prediction and source estimation with integrated Gaussian-machine learning network model for point source emission in atmosphere. J. Hazard. Mater. 2016, 311, 237–245. [Google Scholar] [CrossRef]
- Cao, B.; Cui, W.; Chen, C.; Chen, Y. Development and uncertainty analysis of radionuclide atmospheric dispersion modeling codes based on Gaussian plume model. Energy 2020, 194, 116925. [Google Scholar] [CrossRef]
- Kahl, J.D.W.; Chapman, H.L. Atmospheric stability characterization using the Pasquill method: A critical evaluation. Atmos. Environ. 2018, 187, 196–209. [Google Scholar] [CrossRef]
- Kaasik, M.; Geertsema, G.; Scheele, R. Validation of Gaussian plume model Aeropol against Cabauw field experiment. Int. J. Environ. Pollut. 2017, 62, 369–384. [Google Scholar] [CrossRef]
- Wang, H.; Song, W.; Zio, E.; Kudreyko, A.; Zhang, Y. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Measurement 2020, 161, 107904. [Google Scholar] [CrossRef]
- Song, W.; Cattani, C.; Chi, C.H. Multifractional Brownian motion and quantum-behaved particle swarm optimization for short term power load forecasting: An integrated approach. Energy 2020, 194, 116847. [Google Scholar] [CrossRef]
- Cavalca, D.L.; Fernandes, R.A.S. Gradient-based mechanism for PSO algorithm: A comparative study on numerical benchmarks. In Proceedings of the IEEE Congress on Evolutionary Computation (IEEE CEC) as part of the IEEE World Congress on Computational Intelligence (IEEE WCCI), Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Bakwad, K.M.; Pattnaik, S.S.; Sohi, B.S.; Devi, S.; Panigrahi, B.K.; Gollapudi, S.V.R.S. Multimodal Function Optimization Using Synchronous Bacterial Foraging Optimization Technique. IETE J. Res. 2010, 56, 80–87. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]


| Ammonia | Chlorine | Phosgene | |
|---|---|---|---|
| AEGL-1 | 30 | 0.5 | NR |
| AEGL-2 | 160 | 2.0 | 0.3 |
| AEGL-3 | 1100 | 20 | 0.75 |
| Algorithm Classification | Strengths | Weaknesses | Instances |
|---|---|---|---|
| Swarm Intelligence (SI) algorithms based on gas dispersion models | High degree of freedom in the exploration phase, fast calculation speed, and accurate result in the exploitation phase | Insufficient random exploration may make the result fall into local optimal solution | Particle Swarm Optimization (PSO) Algorithm [30,31] Ant Colony Optimization (ACO) Algorithm [30] Firefly Algorithm [30] Harris Hawks Optimization (HHO) Algorithm [32] |
| Evolutionary algorithms based on gas dispersion models | No need to distinguish the exploration and exploitation phases; controllable search ability (coefficient of variation) | High evolutionary generations will reduce population diversity | Genetic Algorithm (GA) [17,33] Differential Evolution (DE) Algorithm [34] |
| Direct optimization algorithms based on gas dispersion models | Low algorithm complexity and fast calculation speed | Easy to fall into local optimal solution | Pattern Search (PS) Algorithm [35,36] Simulated Annealing (SA) Algorithm [37,38,39] Least Squares Algorithm [15,16] |
| Methods based on big data or probabilistic analysis | No need to build a scene model, not restricted by geographical conditions | Need for much prior knowledge and observation data, slow calculation speed | Deep Neural Networks [18] Big Data with Probability Function [19] Sequential Monte Carlo Methods [40] K-Nearest Neighbor Classifier [41] |
| Other methods | Advanced technology, high accuracy | High technical and economic requirements | Drone-Enabled Participation [6] Random Walk Robot Participation [42,43] Hybrid Optimization Algorithm [44,45,46,47] |
| Cloud Condition | Solar Radiation Angle α | ||
|---|---|---|---|
| α > 60° | 35°< α ≤ 60° | 15° < α ≤ 35° | |
| Cloud cover 4/8, or thin clouds at high altitude | Strong | Medium | Weak |
| Cloud cover 5/8–7/8, cloud height 2134–4877 m | Medium | Weak | Weak |
| Cloud cover 5/8–7/8, cloud height lower than 2134 m | Weak | Weak | Weak |
| Wind Speed | Under Sunshine | Without Sunshine | |||
|---|---|---|---|---|---|
| Strong | Medium | Weak | Cloud Cover ≥4/8 | Cloud Cover ≤3/8 | |
| 0–2 | A | A–B | B | F | F |
| 2–3 | A–B | B | C | E | F |
| 3–4 | B | B–C | C | D | E |
| 4–6 | C | C–D | D | D | D |
| >6 | D | D | D | D | D |
| Stability Level | ||
|---|---|---|
| A–B | ||
| C | ||
| D | ||
| E–F |
| Function Name | Function Equation | Range | Optimal Solution and Value |
|---|---|---|---|
| Sphere | |||
| Rosenbrock | |||
| Rastrigin | |||
| Griewank | |||
| Schaffer | |||
| Ackley |
| Optimization Algorithm | Parameter | Value |
|---|---|---|
| DE/GA | Scaling factor F | 0.5 |
| Crossover probability Cr | 0.5 | |
| HHO | σν | 1 |
| β | 1.5 | |
| PS | Initial point | (0, 0, 0) |
| SA | Initial point | (0, 0, 0) |
| PSO | Inertia factor | 0.3 |
| 1 | ||
| 1 | ||
| Grey Wolf Optimization (GWO) [63] | Convergence constant a | [2, 0] |
| Slap Swarm Algorithm (SSA) [64] | Convergence constant a | [2, 0] |
| Whale Optimization Algorithm (WOA) [65] | Convergence constant c1 | [2, 0] |
| Target Parameter | Expected Value | Calculated Value | Relative Error (%) |
|---|---|---|---|
| Time (s) | − | 12.743 | − |
| (m) | 8 | 8.158 | 1.971 |
| (m) | 15 | 15.020 | 0.131 |
| Q (kg/s) | 80 | 79.045 | 1.193 |
| Optimal value | 0 | 2.464e-15 | − |
| Target Parameter | Expected Value | Calculated Value | Relative Error (%) |
|---|---|---|---|
| Time (s) | − | 10.304 | − |
| (m) | 8 | 8.287 | 3.593 |
| (m) | 15 | 15.444 | 2.960 |
| Q (kg/s) | 80 | 76.909 | 3.864 |
| Optimal value | 0 | 2.356e-13 | − |
| Target Parameter | Expected Value | Calculated Value | Relative Error (%) |
|---|---|---|---|
| Time (s) | − | 8.644 | − |
| (m) | 8 | 10.725 | 34.068 |
| (m) | 15 | 14.190 | 5.401 |
| Q (kg/s) | 80 | 84.612 | 5.765 |
| Optimal value | 0 | 5.694e-23 | − |
| Target Parameter | Expected Value | Calculated Value | Relative Error (%) |
|---|---|---|---|
| Time (s) | − | 6.697 | − |
| (m) | 8 | 8.285 | 3.568 |
| (m) | 15 | 15.069 | 0.459 |
| Q (kg/s) | 80 | 79.896 | 0.131 |
| Optimal value | 0 | 2.029e-10 | − |
| Population Number N | Optimal Value | Time (s) |
|---|---|---|
| 3 | 8.450e-6 | 1.678 |
| 5 | 2.130e-7 | 2.490 |
| 8 | 9.622e-10 | 3.712 |
| 10 | 3.253e-10 | 4.561 |
| 15 | 1.187e-11 | 6.591 |
| 20 | 7.940e-13 | 8.680 |
| 25 | 7.228e-15 | 10.723 |
| 30 | 2.464e-15 | 12.743 |
| 50 | 2.339e-16 | 21.753 |
| 100 | 4.073e-17 | 42.479 |
| Iterations | Optimal Value | Time (s) |
|---|---|---|
| 50 | 1.384e-10 | 2.249 |
| 100 | 1.457e-13 | 4.405 |
| 200 | 3.067e-14 | 8.623 |
| 300 | 2.464e-15 | 12.743 |
| 400 | 7.305e-16 | 16.975 |
| 500 | 4.157e-16 | 21.311 |
| 1000 | 5.238e-16 | 43.213 |
| SH | SR | Optimal Value |
|---|---|---|
| 4 | 6 | 1.447e-11 |
| 23 | 3 | 1.690e-11 |
| 2 | 43 | 2.405e-11 |
| 15 | 2 | 2.683e-11 |
| 1 | 3 | 3.602e-11 |
| 137 | 1 | 3.679e-11 |
| 422 | 440 | 4.382e-4 |
| 709 | 469 | 4.384e-4 |
| 495 | 844 | 4.396e-4 |
| 869 | 42 | 6.804e-4 |
| 865 | 76 | 7.124e-4 |
| 973 | 329 | 7.846e-4 |
| SNR (dB) | Q (kg/s) | Optimal Value | ||
|---|---|---|---|---|
| 0 | 14.916 | 12.956 | 61.406 | 5.565e-2 |
| 0.3 | 15.173 | 14.886 | 54.400 | 6.340e-2 |
| 0.6 | 11.520 | 13.130 | 82.052 | 3.102e-2 |
| 1 | 12.125 | 13.927 | 57.669 | 2.614e-2 |
| 5 | 11.808 | 14.294 | 78.303 | 1.128e-2 |
| 10 | 9.047 | 14.618 | 73.611 | 3.658e-3 |
| 15 | 9.563 | 15.179 | 71.538 | 1.071e-3 |
| 20 | 7.383 | 14.727 | 77.701 | 3.932e-4 |
| 30 | 8.405 | 15.271 | 80.032 | 8.574e-5 |
| 50 | 8.175 | 14.977 | 79.100 | 4.209e-7 |
| 100 | 7.906 | 14.848 | 81.372 | 3.680e-11 |
| Target Parameters | OMO | PS | SA | PSO | GA | DE | HHO | GWO | SSA | WOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 12.743 | 4.910 | 3.028 | 2.223 | 6.049 | 10.129 | 12.373 | 13.196 | 13.514 | 13.160 |
| (m) | 8.158 | 6.207 | 5.565 | 7.410 | 6.379 | 7.435 | 8.528 | 5.276 | 6.849 | 8.779 |
| (m) | 15.020 | 14.501 | 10.905 | 14.175 | 13.890 | 15.028 | 14.530 | 14.740 | 15.026 | 13.188 |
| (kg/s) | 79.045 | 62.406 | 43.929 | 83.694 | 75.824 | 81.038 | 76.953 | 83.620 | 84.956 | 76.095 |
| relative error (%) | 1.971 | 22.418 | 30.433 | 7.379 | 20.262 | 7.064 | 6.606 | 34.044 | 14.391 | 9.741 |
| relative error (%) | 0.131 | 3.326 | 27.297 | 5.497 | 7.399 | 0.186 | 3.132 | 1.732 | 0.171 | 12.080 |
| relative error (%) | 1.193 | 21.993 | 45.089 | 4.617 | 5.220 | 1.298 | 3.809 | 4.525 | 6.195 | 4.882 |
| Optimal value | 2.464e-15 | 2.309e-6 | 9.492e-3 | 5.625e-8 | 3.302e-4 | 3.697e-13 | 8.531e-7 | 2.712e-7 | 6.317e-9 | 2.434e-5 |
| Target Parameters | OMO | PS | SA | PSO | GA | DE | HHO | GWO | SSA | WOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 10.304 | 4.429 | 2.990 | 1.638 | 3.867 | 8.406 | 10.263 | 11.170 | 11.364 | 11.083 |
| (m) | 8.287 | 4.111 | 10.667 | 9.549 | 5.668 | 8.854 | 9.644 | 1.855 | 7.312 | 4.460 |
| (m) | 15.444 | 12.990 | 12.908 | 13.352 | 13.661 | 15.001 | 15.533 | 10.150 | 13.190 | 12.100 |
| (kg/s) | 76.909 | 95.762 | 52.081 | 90.098 | 79.938 | 85.554 | 73.722 | 92.250 | 83.853 | 83.342 |
| relative error (%) | 3.593 | 48.618 | 33.335 | 19.363 | 29.151 | 10.675 | 20.544 | 76.814 | 8.598 | 44.252 |
| relative error (%) | 2.960 | 13.400 | 13.947 | 10.986 | 8.926 | 0.010 | 3.555 | 32.332 | 12.065 | 19.336 |
| relative error (%) | 3.864 | 19.703 | 34.899 | 12.622 | 0.077 | 6.943 | 7.847 | 15.313 | 4.816 | 4.178 |
| Optimal value | 2.356e-13 | 9.689e-7 | 6.450e-4 | 5.182e-8 | 6.226e-6 | 1.459e-11 | 2.012e-7 | 4.987e-7 | 1.960e-8 | 3.161e-4 |
| Target Parameters | OMO | PS | SA | PSO | GA | DE | HHO | GWO | SSA | WOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 8.644 | 3.206 | 2.954 | 1.341 | 3.046 | 7.219 | 8.833 | 9.301 | 9.536 | 9.390 |
| (m) | 10.725 | 2.677 | 12.369 | 2.101 | 6.126 | 4.446 | 10.669 | 3.628 | 12.061 | 4.878 |
| (m) | 14.190 | 7.641 | 15.168 | 9.720 | 10.597 | 9.392 | 15.471 | 9.127 | 8.076 | 11.870 |
| (kg/s) | 84.612 | 127.404 | 43.551 | 106.466 | 100.159 | 101.978 | 58.645 | 80.567 | 104.305 | 72.035 |
| relative error (%) | 34.068 | 66.536 | 54.607 | 73.732 | 23.427 | 44.428 | 33.368 | 54.653 | 50.768 | 39.026 |
| relative error (%) | 5.401 | 49.060 | 1.121 | 35.200 | 29.354 | 37.386 | 3.137 | 39.151 | 46.160 | 20.864 |
| relative error (%) | 5.765 | 59.255 | 45.562 | 33.082 | 25.199 | 27.472 | 26.694 | 0.709 | 30.382 | 9.956 |
| Optimal value | 5.694e-23 | 1.401e-11 | 1.384e-6 | 5.373e-10 | 3.371e-10 | 1.075e-11 | 9.049e-19 | 5.915e-12 | 7.136e-14 | 2.514e-9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Z.; Xu, Z.; Li, D.; Wei, J. A Novel Method for Source Tracking of Chemical Gas Leakage: Outlier Mutation Optimization Algorithm. Sensors 2022, 22, 71. https://doi.org/10.3390/s22010071
Xia Z, Xu Z, Li D, Wei J. A Novel Method for Source Tracking of Chemical Gas Leakage: Outlier Mutation Optimization Algorithm. Sensors. 2022; 22(1):71. https://doi.org/10.3390/s22010071
Chicago/Turabian StyleXia, Zhiyu, Zhengyi Xu, Dan Li, and Jianming Wei. 2022. "A Novel Method for Source Tracking of Chemical Gas Leakage: Outlier Mutation Optimization Algorithm" Sensors 22, no. 1: 71. https://doi.org/10.3390/s22010071
APA StyleXia, Z., Xu, Z., Li, D., & Wei, J. (2022). A Novel Method for Source Tracking of Chemical Gas Leakage: Outlier Mutation Optimization Algorithm. Sensors, 22(1), 71. https://doi.org/10.3390/s22010071







