Miniature Optical Particle Counter and Analyzer Involving a Fluidic-Optronic CMOS Chip Coupled with a Millimeter-Sized Glass Optical System †
Abstract
1. Introduction
1.1. Particulate Matter and Air Quality Monitoring
1.2. Toward Further Miniaturization of Optical PM Sensors
1.3. Lorenz-Mie Theory and Scattering Signatures
2. Designing the Optical System
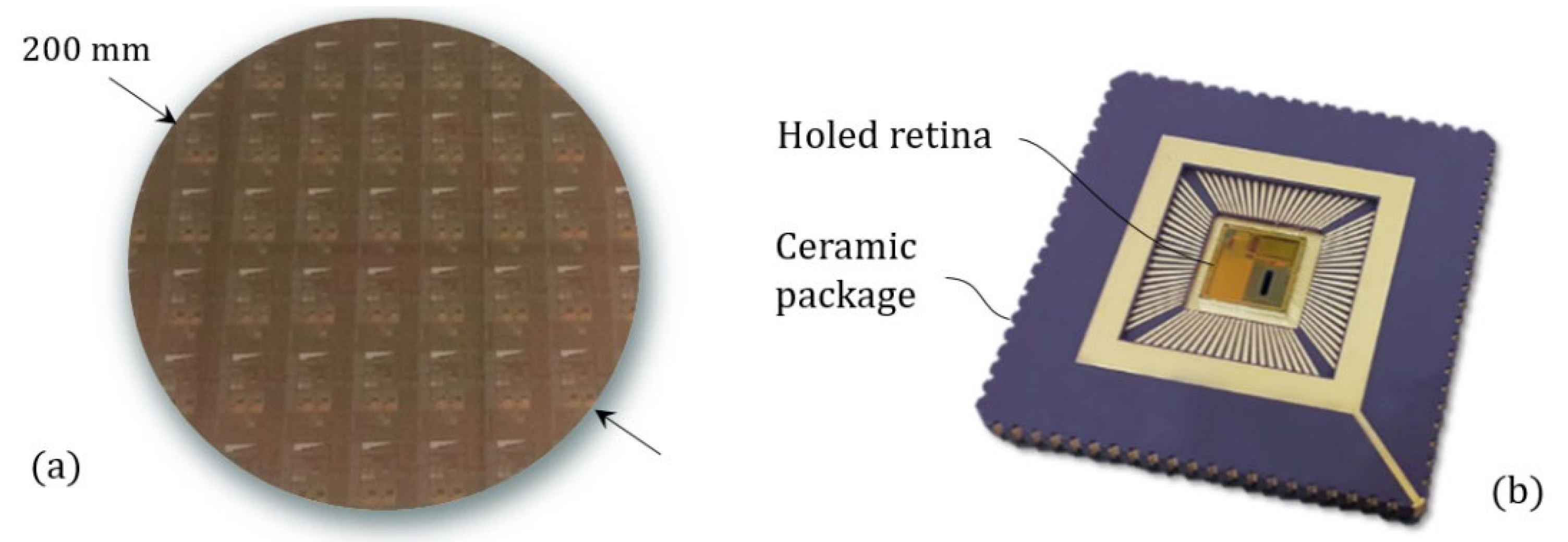
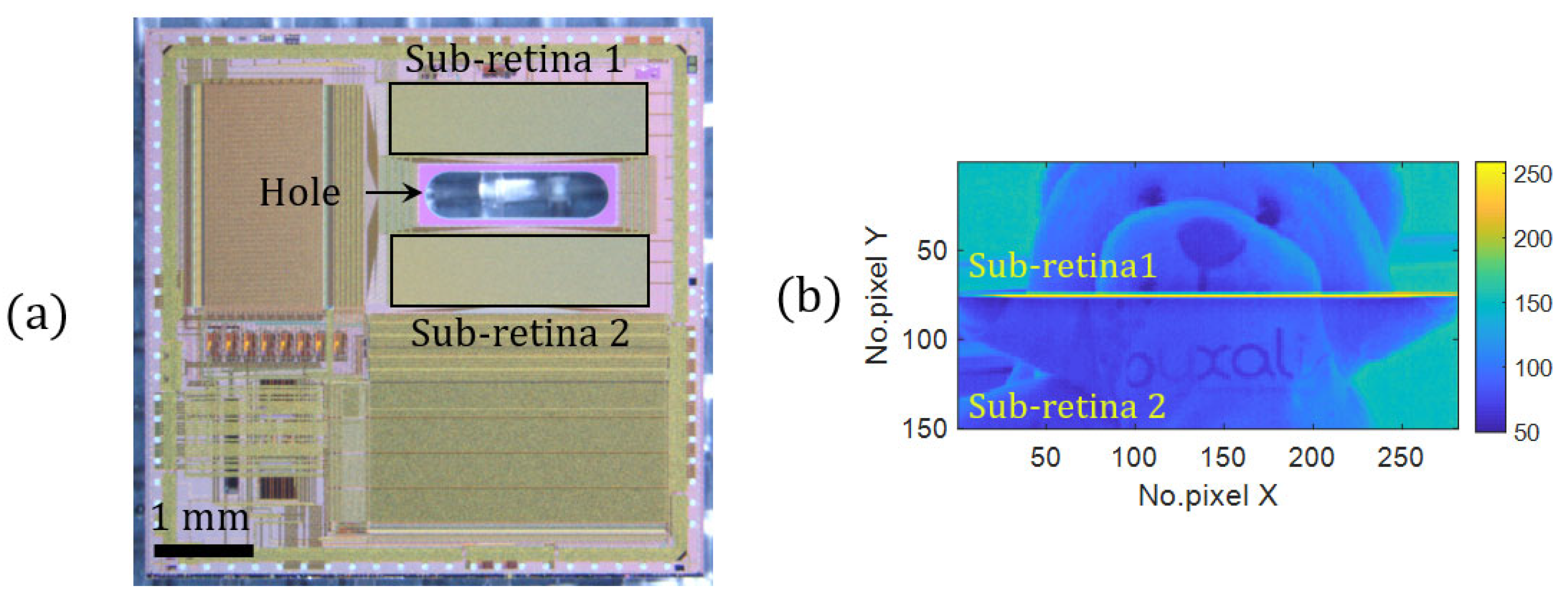
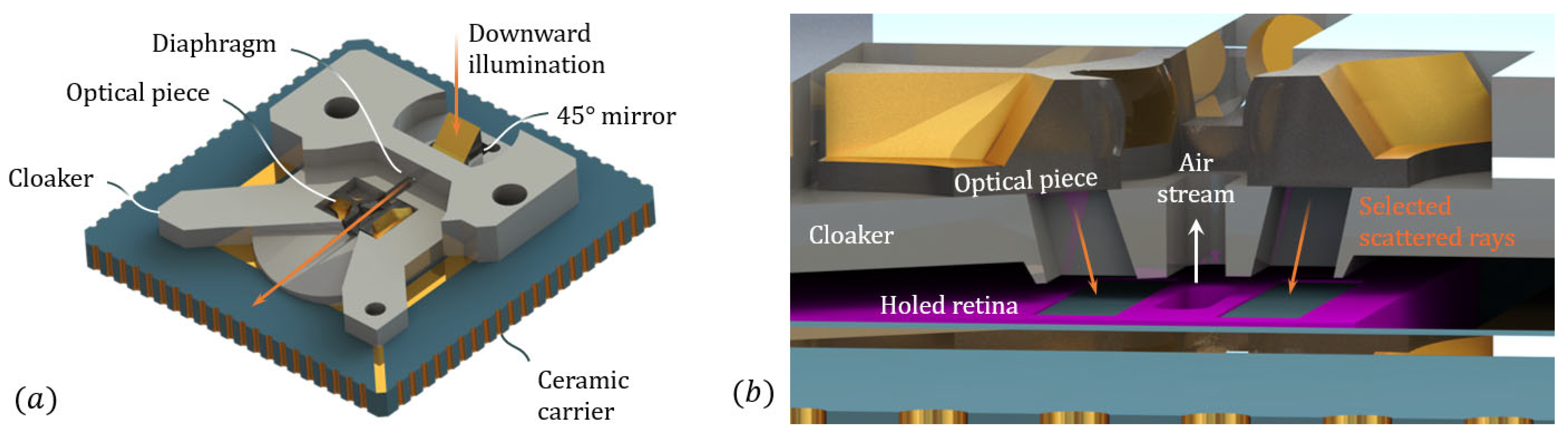
2.1. Holed Retina, an Opto-Fluidic CMOS Chip
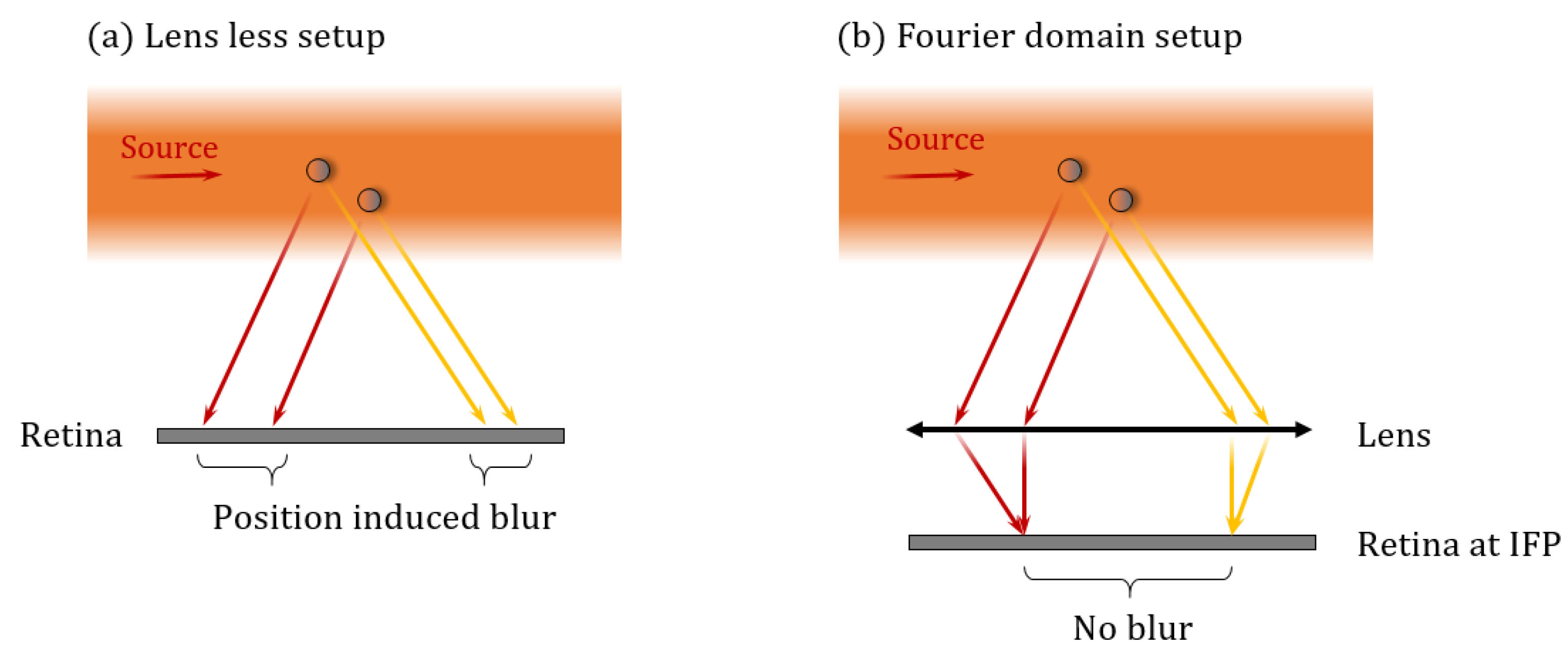
2.2. Difficulties Encoutered Using a Lens-less Setup
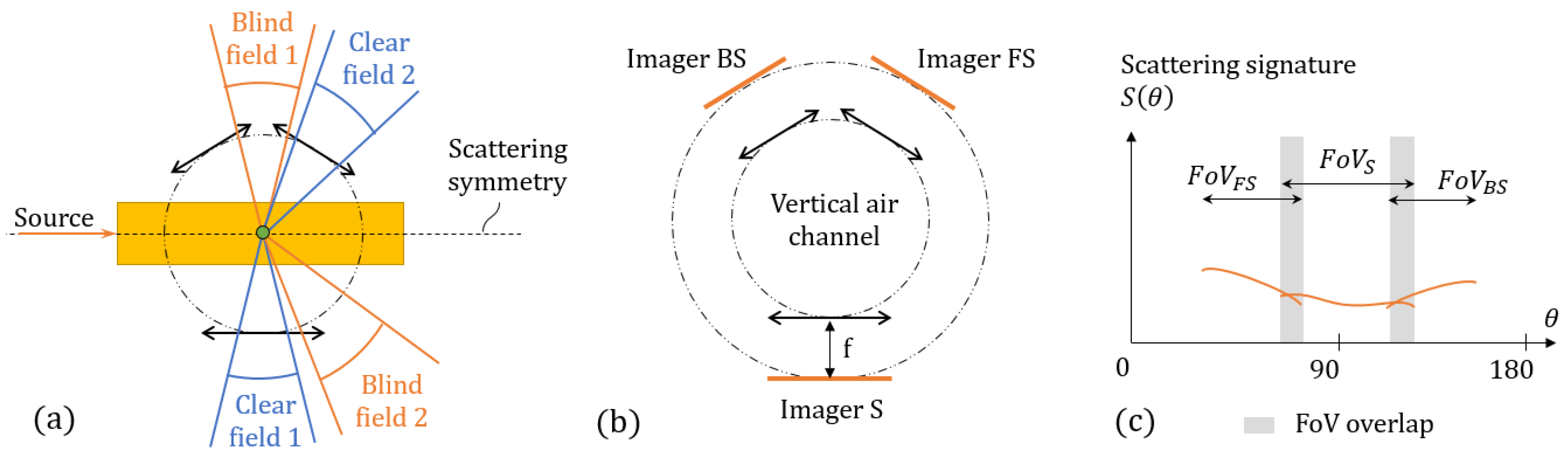
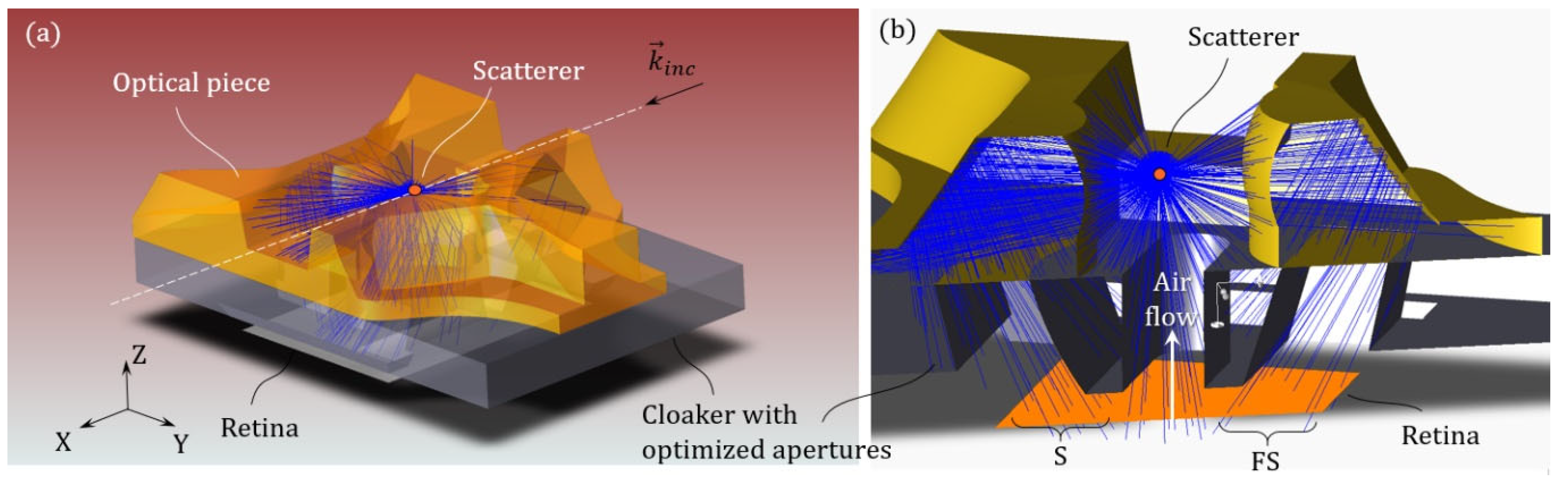
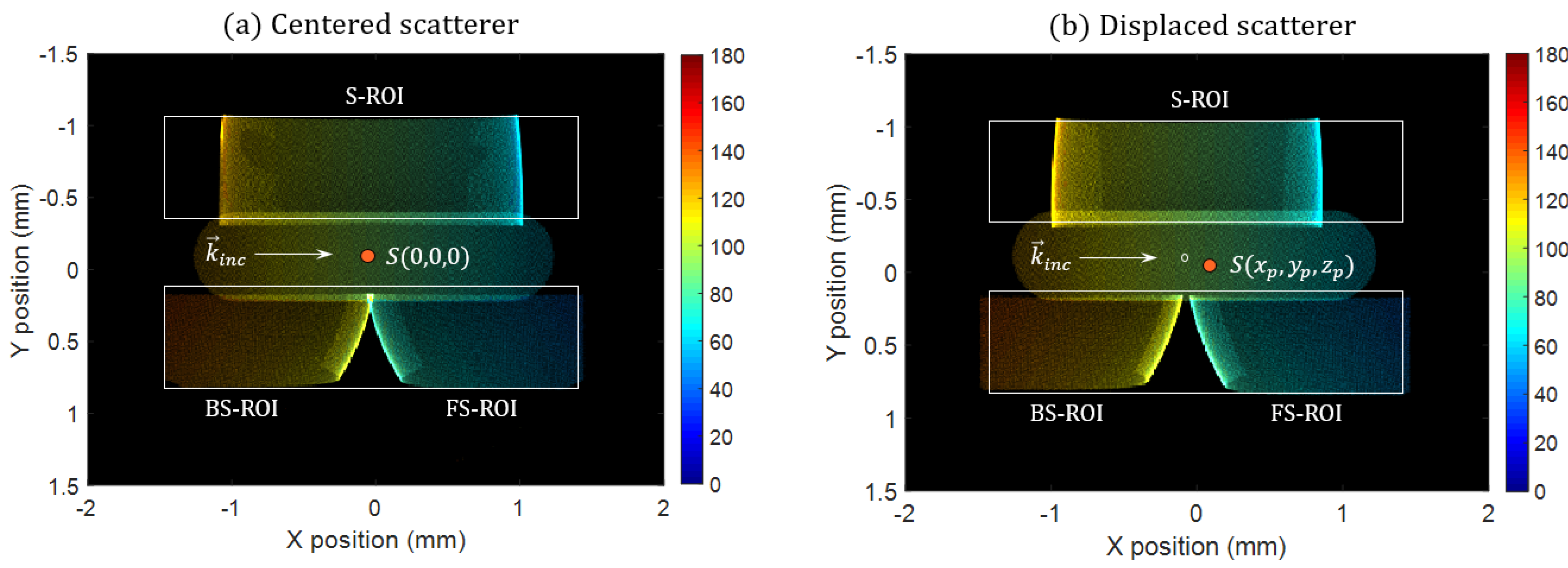
2.3. Achieving Position Insensitivity
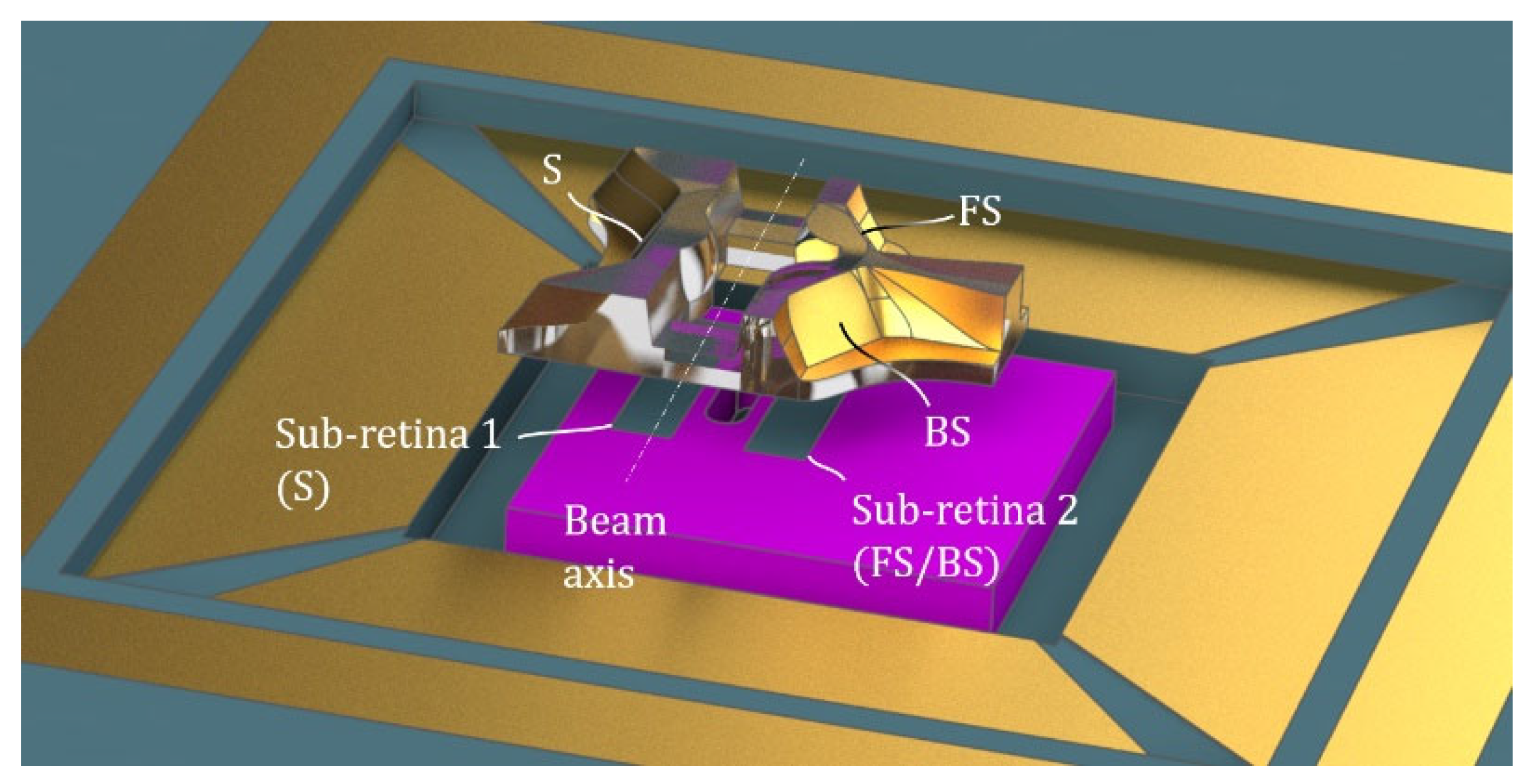
2.4. Assymetric Crown Assembly and Signature Reconstruction
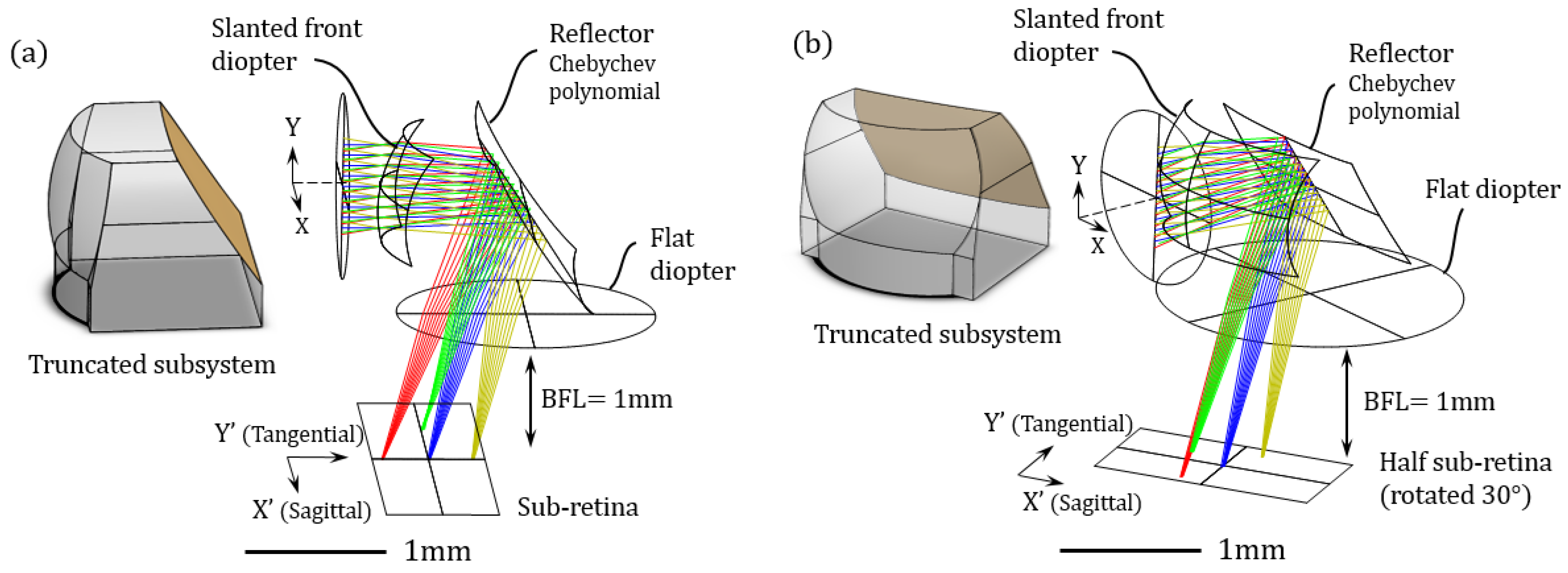
2.5. Compact Optical Subsystems with Coincidental Fourier Planes
2.6. Merging the Subsystems and Coupling with the Holed Retina
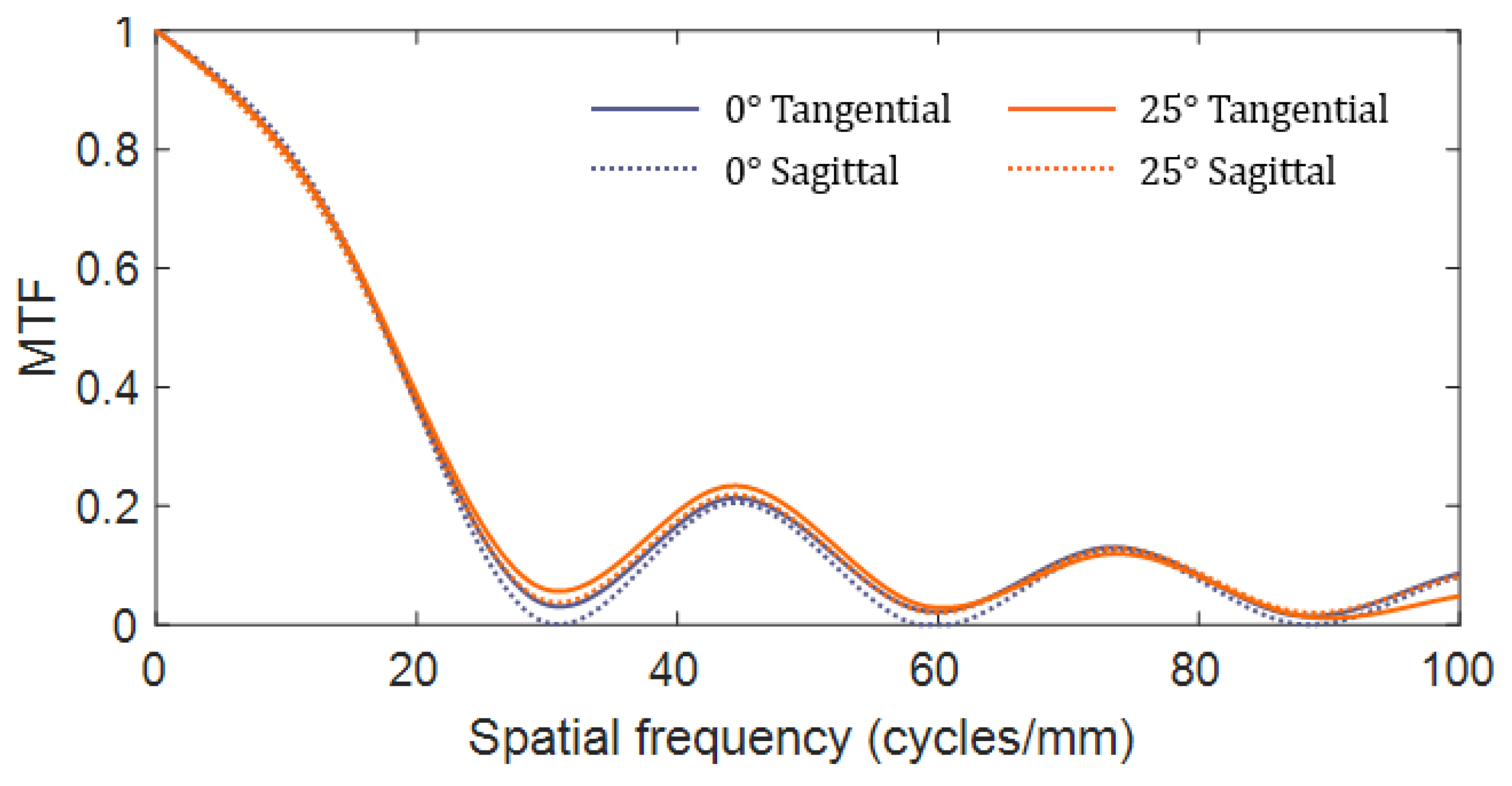
2.7. Angular Response at the Coincidental Fourier Plane
3. Fabrication Process
3.1. Micro-Machining on Glass
3.2. Mirror Deposition
4. Characterization
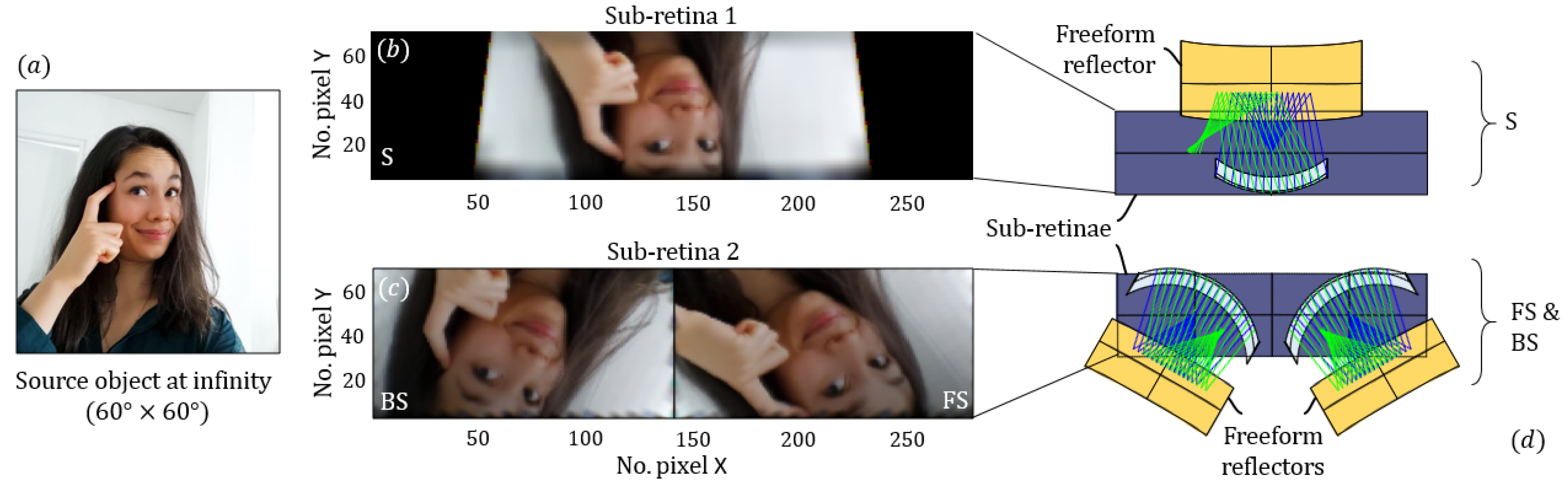
4.1. Experimental Setup
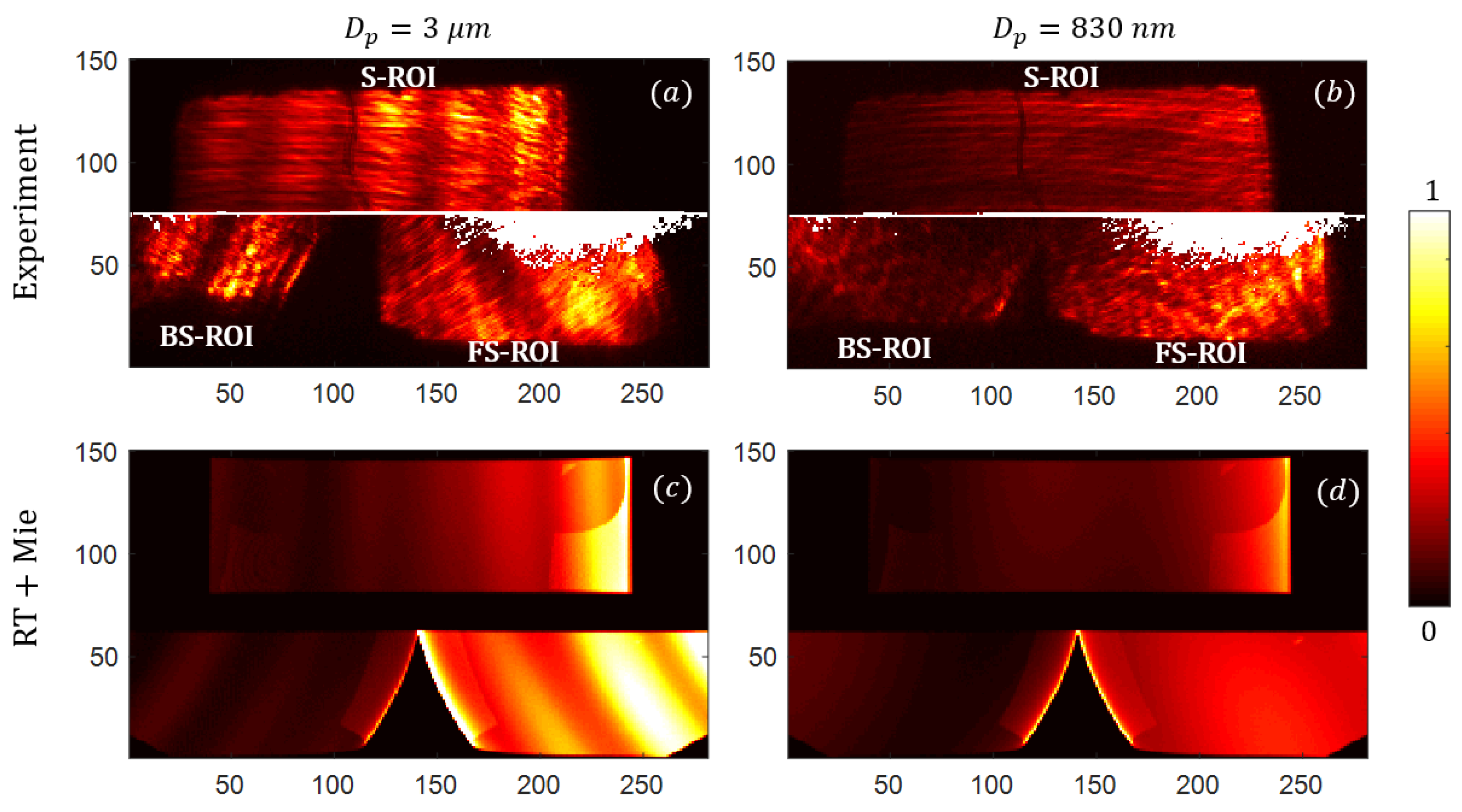
4.2. Experimental Images of Scattering Signatures
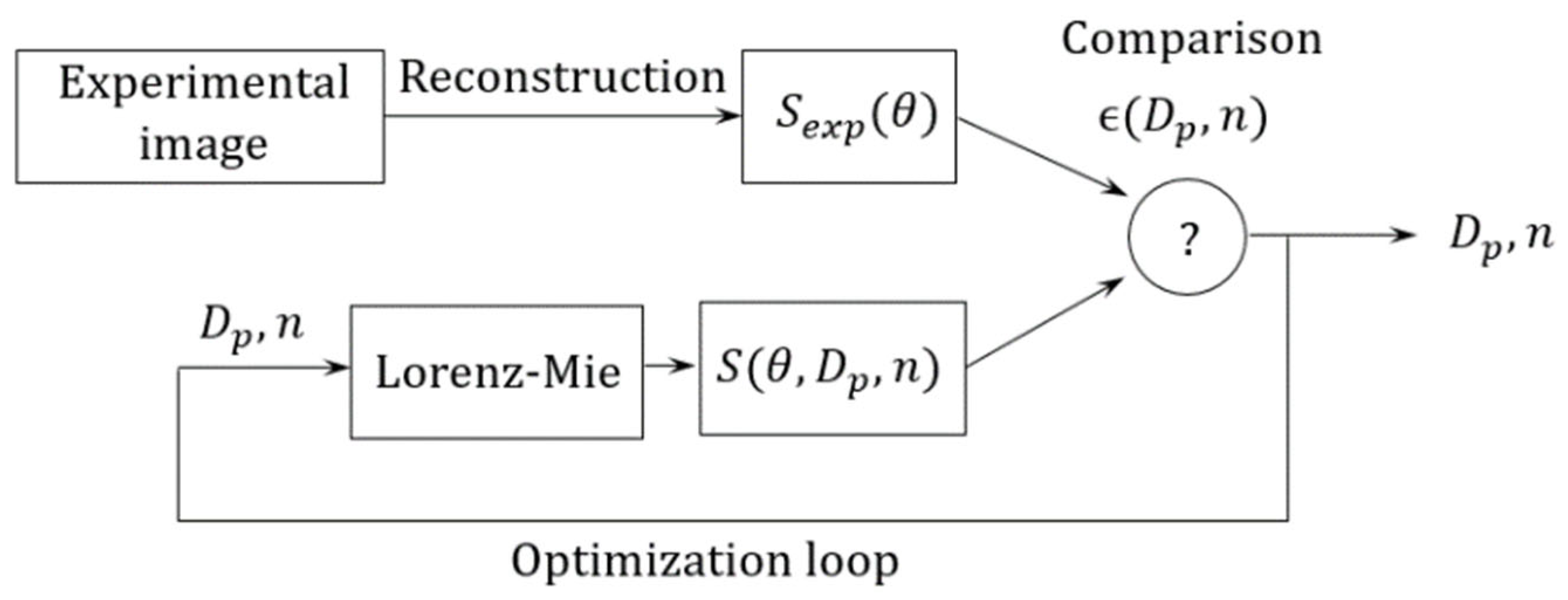
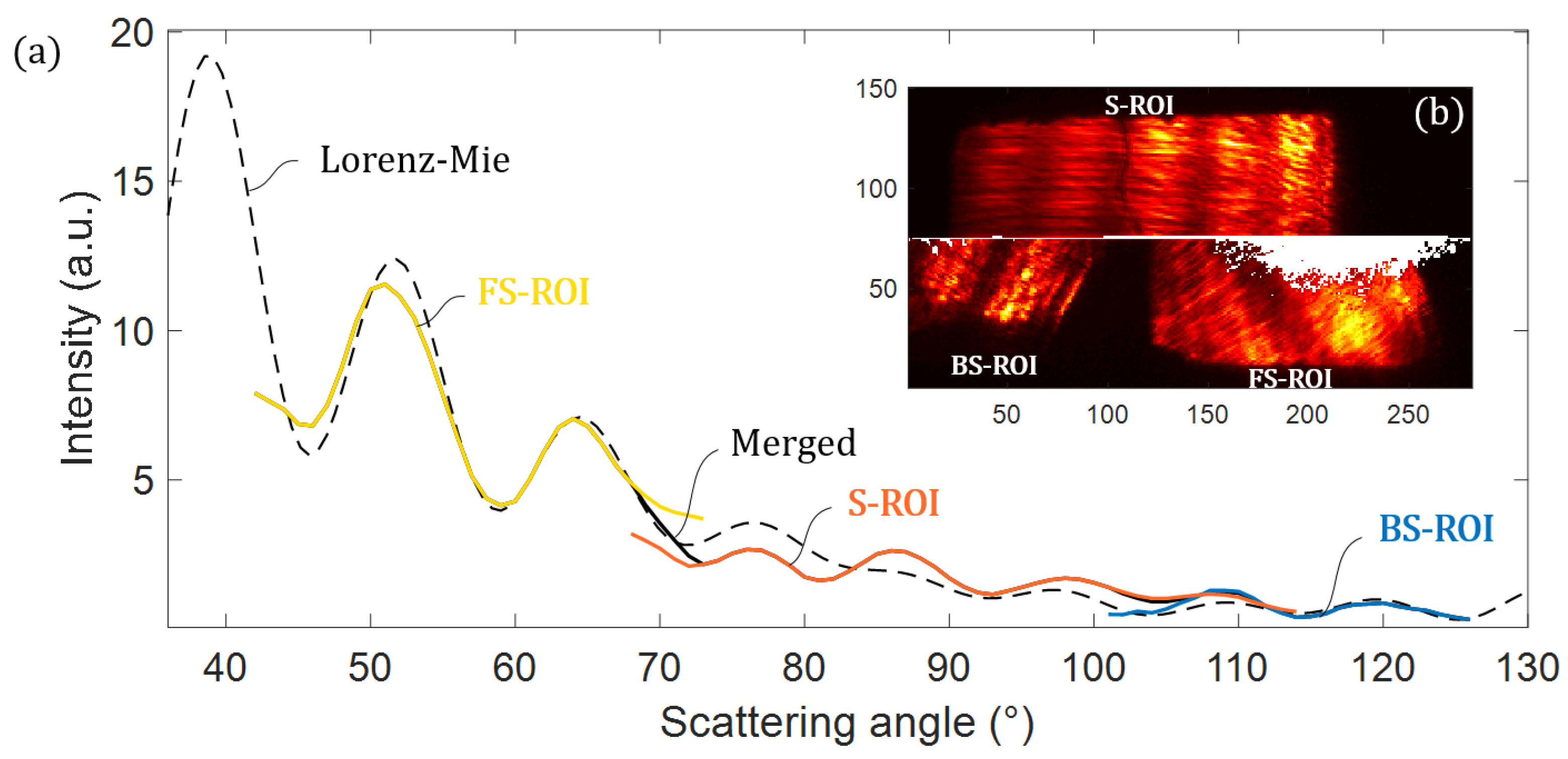
4.3. Reconstruction of Scattering Signatures
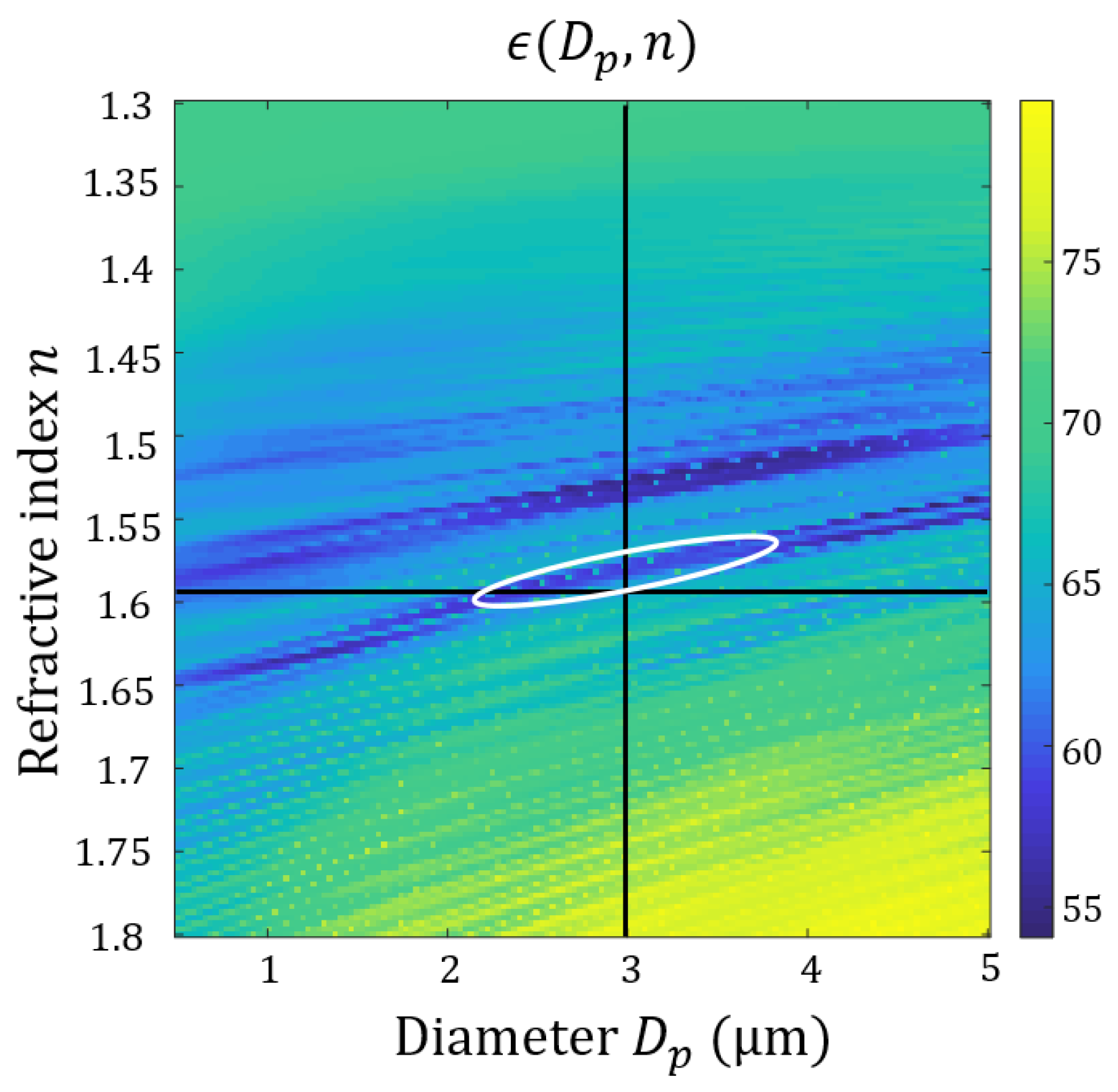
5. Discussion about Particle Identification
6. Conclusions
7. Patents
- Boutami, S. and Nicoletti, S., Optical detector of particles, 2018, Patent Application EP3574301, WO2018138223, FR3062209, KR20190112049
- Jobert, G., Optical particle detector, 2018, Patent Application EP3598102, US20200033246, FR3083864.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B

References
- Hamra, G.B.; Guha, N.; Cohen, A.; Laden, F.; Raaschou-Nielsen, O.; Samet, J.M.; Vineis, P.; Forastiere, F.; Saldiva, P.; Yorifuji, T.; et al. Outdoor Particulate Matter Exposure and Lung Cancer: A Systematic Review and Meta-Analysis. Environ. Health Perspect. 2014. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.O.; Thundiyil, J.G.; Stolbach, A. Clearing the Air: A Review of the Effects of Particulate Matter Air Pollution on Human Health. J. Med. Toxicol. 2012, 8, 166–175. [Google Scholar] [CrossRef]
- Cohen, A.J.; Samet, J.M.; Straif, K.; International Agency for Research on Cancer. Air Pollution and Cancer; International Agency for Research on Cancer: Lyon, France, 2013; ISBN 978-92-832-2161-6.
- Vineis, P.; Husgafvel-Pursiainen, K. Air Pollution and Cancer: Biomarker Studies in Human Populations †. Carcinogenesis 2005, 26, 1846–1855. [Google Scholar] [CrossRef] [PubMed]
- United States Environmental Protection Agency. Integrated Science Assessment for Particulate Matter (External Review Draft, 2018); U.S. Environmental Protection Agency: Washington, DC, USA, 2018; p. 1879.
- Cormier, S.A.; Lomnicki, S.; Backes, W.; Dellinger, B. Origin and Health Impacts of Emissions of Toxic By-Products and Fine Particles from Combustion and Thermal Treatment of Hazardous Wastes and Materials. Environ. Health Perspect. 2006, 114, 810–817. [Google Scholar] [CrossRef]
- Howard, V. Statement of Evidence: Particulate Emission and Health (An Bord Plenala, Proposed Ringaskiddy Waste-to-Energy Facility). Available online: http://www.durhamenvironmentwatch.org/Incinerator%20Health/CVHRingaskiddyEvidenceFinal1.pdf (accessed on 3 January 2018).
- Sioutas, C.; Delfino, R.J.; Singh, M. Exposure Assessment for Atmospheric Ultrafine Particles (UFPs) and Implications in Epidemiologic Research. Environ. Health Perspect. 2005, 113, 947–955. [Google Scholar] [CrossRef]
- Fuzzi, S.; Baltensperger, U.; Carslaw, K.; Decesari, S.; Denier van der Gon, H.; Facchini, M.C.; Fowler, D.; Koren, I.; Langford, B.; Lohmann, U.; et al. Particulate Matter, Air Quality and Climate: Lessons Learned and Future Needs. Atmos. Chem. Phys. 2015, 15, 8217–8299. [Google Scholar] [CrossRef]
- Clouds and Aerosols. In Climate Change 2013—The Physical Science Basis; Intergovernmental Panel on Climate Change, Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 571–658. ISBN 978-1-107-41532-4. [Google Scholar]
- Jacobson, M.Z. Control of Fossil-Fuel Particulate Black Carbon and Organic Matter, Possibly the Most Effective Method of Slowing Global Warming. J. Geophys. Res. 2002, 107, 4410. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the Role of Black Carbon in the Climate System: A Scientific Assessment: Black Carbon in the Climate System. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Ramanathan, V.; Carmichael, G. Global and Regional Climate Changes Due to Black Carbon. Nat. Geosci. 2008, 1, 221–227. [Google Scholar] [CrossRef]
- Wang, C. A Modeling Study on the Climate Impacts of Black Carbon Aerosols: Climate Aspects of Black Carbon. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- McMurry, P.H.; Shepherd, M.F.; Vickery, J.S. (Eds.) Particulate Matter Science for Policy Makers: A NARSTO Assessment; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0-521-84287-7. [Google Scholar]
- Singer, B.C.; Delp, W.W. Response of Consumer and Research Grade Indoor Air Quality Monitors to Residential Sources of Fine Particles. Indoor Air 2018, 28, 624–639. [Google Scholar] [CrossRef] [PubMed]
- Lowther, S.D.; Jones, K.C.; Wang, X.; Whyatt, J.D.; Wild, O.; Booker, D. Particulate Matter Measurement Indoors: A Review of Metrics, Sensors, Needs, and Applications. Environ. Sci. Technol. 2019, 53, 11644–11656. [Google Scholar] [CrossRef] [PubMed]
- Kaliszewski, M.; Włodarski, M.; Młyńczak, J.; Kopczyński, K. Comparison of Low-Cost Particulate Matter Sensors for Indoor Air Monitoring during COVID-19 Lockdown. Sensors 2020, 17, 7290. [Google Scholar] [CrossRef]
- Budde, M.; El Masri, R.; Riedel, T.; Beigl, M. Enabling Low-Cost Particulate Matter Measurement for Participatory Sensing Scenarios. In Proceedings of the 12th International Conference on Mobile and Ubiquitous Multimedia—MUM ’13; ACM Press: Lulȩ, Sweden, 2013; pp. 1–10. [Google Scholar]
- Jayaratne, R.; Liu, X.; Thai, P.; Dunbabin, M.; Morawska, L. The Influence of Humidity on the Performance of a Low-Cost Air Particle Mass Sensor and the Effect of Atmospheric Fog. Atmos. Meas. Tech. 2018, 11, 4883–4890. [Google Scholar] [CrossRef]
- Snider, G.; Weagle, C.L.; Martin, R.V.; van Donkelaar, A.; Conrad, K.; Cunningham, D.; Gordon, C.; Zwicker, M.; Akoshile, C.; Artaxo, P.; et al. SPARTAN: A Global Network to Evaluate and Enhance Satellite-Based Estimates of Ground-Level Particulate Matter for Global Health Applications. Atmos. Meas. Tech. 2015, 8, 505–521. [Google Scholar] [CrossRef]
- Wendt, E.A.; Quinn, C.W.; Miller-Lionberg, D.D.; Tryner, J.; L’Orange, C.; Ford, B.; Yalin, A.P.; Pierce, J.R.; Jathar, S.; Volckens, J. A low-cost monitor for simultaneous measurement of fine particulate matter and aerosol optical depth – Part 1: Specifications and testing. Atmos. Meas. Tech. 2019, 12, 5431–5441. [Google Scholar] [CrossRef]
- Nguyen, T.N.T.; Luu, V.H.; Pham, V.H.; Bui, Q.H.; Nguyen, T.K.O. Particulate Matter Concentration Mapping from Satellite Imagery. In TORUS 3—Toward an Open Resource Using Services; Laffly, D., Ed.; Wiley: Hoboken, NJ, USA, 2020; pp. 103–130. ISBN 978-1-78630-601-2. [Google Scholar]
- Liu, H.; Li, Q.; Shi, T.; Hu, S.; Wu, G.; Zhou, Q. Application of Sentinel 2 MSI Images to Retrieve Suspended Particulate Matter Concentrations in Poyang Lake. Remote Sens. 2017, 9, 761. [Google Scholar] [CrossRef]
- van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global Estimates of Fine Particulate Matter Using a Combined Geophysical-Statistical Method with Information from Satellites, Models, and Monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar] [CrossRef] [PubMed]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.W.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The Changing Paradigm of Air Pollution Monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef] [PubMed]
- Borghi, F.; Spinazzè, A.; Rovelli, S.; Campagnolo, D.; Del Buono, L.; Cattaneo, A. Domenico Cavallo Miniaturized Monitors for Assessment of Exposure to Air Pollutants: A Review. Int. J. Environ. Res. Public Health 2017, 14, 909. [Google Scholar] [CrossRef]
- Amaral, S.; de Carvalho, J.; Costa, M.; Pinheiro, C. An Overview of Particulate Matter Measurement Instruments. Atmosphere 2015, 6, 1327–1345. [Google Scholar] [CrossRef]
- Li, J. Recent Advances in Low-Cost Particulate Matter Sensor: Calibration and Application. Engineering and Applied Science Theses & Dissertations. Ph.D. Thesis, Washington University, St. Louis, MO, USA, 2019. [Google Scholar]
- Kelly, K.E.; Whitaker, J.; Petty, A.; Widmer, C.; Dybwad, A.; Sleeth, D.; Martin, R.; Butterfield, A. Ambient and Laboratory Evaluation of a Low-Cost Particulate Matter Sensor. Environ. Pollut. 2017, 221, 491–500. [Google Scholar] [CrossRef]
- Jobert, G.; Barritault, P.; Fournier, M.; Boutami, S.; Jobert, D.; Marchant, A.; Michelot, J.; Monsinjon, P.; Lienhard, P.; Nicoletti, S. Miniature Particulate Matter Counter and Analyzer Based on Lens-Free Imaging of Light Scattering Signatures with a Holed Image Sensor. Sens. Actuators Rep. 2020, 100010. [Google Scholar] [CrossRef]
- Li, X.; Iervolino, E.; Santagata, F.; Wei, J.; Yuan, C.A.; Sarro, P.M.; Zhang, G.Q. Miniaturized Particulate Matter Sensor for Portable Air Quality Monitoring Devices. In Proceedings of the IEEE SENSORS 2014 Proceedings; IEEE: Valencia, Spain, 2014; pp. 2151–2154. [Google Scholar]
- Dong, M.; Iervolino, E.; Santagata, F.; Zhang, G.; Zhang, G. Silicon Microfabrication Based Particulate Matter Sensor. Sens. Actuators A Phys. 2016, 247, 115–124. [Google Scholar] [CrossRef]
- Qiao, Y.; Tao, J.; Zhang, Y.; Qiu, J.; Hong, X.; Wu, J.; Chen, C.-H. Sub-Micro Particle Matter Detection for Metal 3-D Printing Workshop. IEEE Sens. J. 2019, 19, 4932–4939. [Google Scholar] [CrossRef]
- Nicoletti, S. Particle Detector and Method for Manufacturing Such a Detector 2012. Available online: https://permalink.orbit.com/RenderStaticFirstPage?XPN=B5lJYIF%252BxRQ1zTc2PWcWRHfDUqlXTJ5uwQdFuycu4uk%3D%26n%3D1&id=0&base= (accessed on 3 May 2021).
- Vincent, J.H. Aerosol Sampling; John Wiley & Sons, Ltd.: Chichester, UK, 2007; ISBN 978-0-470-06023-0. [Google Scholar]
- Tryner, J.; Quinn, C.; Windom, B.C.; Volckens, J. Design and Evaluation of a Portable PM2.5 Monitor Featuring a Low-Cost Sensor in Line with an Active Filter Sampler. Environ. Sci. Process. Impacts 2019, 21, 1403–1415. [Google Scholar] [CrossRef]
- Mahdavipour, O.; Fahimi, D.; Paprotny, I. Microfabricated Air-Microfluidics Virtual Impactor with Groove-Based Envelope-Flow Particle Focusing System. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII); IEEE: Berlin, Germany, 2019; pp. 805–808. [Google Scholar]
- Mulholland, G.W.; Choi, M.Y. Measurement of the Mass Specific Extinction Coefficient for Acetylene and Ethene Smoke Using the Large Agglomerate Optics Facility. Symp. Combust. 1998, 27, 1515–1522. [Google Scholar] [CrossRef]
- Kullenberg, G. Scattering of Light by Sargasso Sea Water. Deep Sea Res. Oceanogr. Abstr. 1968, 15, 423–432. [Google Scholar] [CrossRef]
- Bartholdi, M.; Salzman, G.C.; Hiebert, R.D.; Kerker, M. Differential Light Scattering Photometer for Rapid Analysis of Single Particles in Flow. Appl. Opt. 1980, 19, 1573. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, Y.C.; Pottsmith, H.C. Instruments for Particle Size and Settling Velocity Observations in Sediment Transport. Mar. Geol. 2000, 168, 89–114. [Google Scholar] [CrossRef]
- Heim, M.; Mullins, B.J.; Umhauer, H.; Kasper, G. Performance Evaluation of Three Optical Particle Counters with an Efficient “Multimodal” Calibration Method. J. Aerosol Sci. 2008, 39, 1019–1031. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Kalume, A.; Wang, C.; Santarpia, J.L. Opto-Aerodynamic Focusing of Aerosol Particles. Aerosol Sci. Technol. 2018, 52, 13–18. [Google Scholar] [CrossRef]
- Weinert, D.; Cleary, T.G.; Mulholland, G.W.; Beever, P. Light Scattering Characteristics and Size Distribution of Smoke and Nuisance Aerosols. Fire Saf. Sci. 2003, 7, 209–220. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: Hoboken, NJ, USA, 1983; ISBN 978-0-471-29340-8. [Google Scholar]
- Hulst, H.C. van de Light Scattering by Small Particles; Dover Publications: Mineola, NY, USA, 1981; ISBN 978-0-486-64228-4. [Google Scholar]
- Gouesbet, G.; Gréhan, G. Generalized Lorenz-Mie Theories; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-17194-9. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-Matrix Computations of Light Scattering by Nonspherical Particles: A Review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Fournier, M.; Barritault, P.; Jobert, G.; Marchant, A.; Boutami, S.; Michelot, J.; Lienhard, P.; Nicoletti, S.; Duraffourg, L. A Miniaturized Optical Sensor for Particulate Matter Detection. In Proceedings of the Photonic Instrumentation Engineering VII; Soskind, Y., Busse, L.E., Eds.; SPIE: San Francisco, CA, USA, 2020; p. 43. [Google Scholar]
- Michelot, J.; Monsinjon, P.; Caranana, J.; Menard, A.; Dubois, M.; Lesire, A.; Bouvier, C.; Cohet, S.; Caranhac, S. Creapyx: An Innovative Pixel Evaluation Platform; French Space Agency: Toulouse, France, 2015. [Google Scholar]
- Dupont, B.; Caranana, J.; Pinoncely, P.A.; Michelot, J.; Bouvier, C.; Cohet, S.; Jourdain, P.; Monsinjon, P. A Dual-Core Highly Programmable 120dB Image Sensor. Electron. Imaging 2016, 2016, 1–3. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005; ISBN 978-0-9747077-2-3. [Google Scholar]
- Jobert, G.; Fournier, M.; Boutami, S.; Jamois, C.; Lovera, A.; Braga, D.; Seassal, C. Millimeter-Sized Particle Sensor Using a Wide Field of View Monolithic Lens Assembly for Light Scattering Analysis in Fourier Domain. In Proceedings of the Photonic Instrumentation Engineering VII; Soskind, Y., Busse, L.E., Eds.; SPIE: San Francisco, CA, USA, 2020; p. 24. [Google Scholar]
- Ye, J.; Chen, L.; Li, X.; Yuan, Q.; Gao, Z. Review of Optical Freeform Surface Representation Technique and Its Application. Opt. Eng. 2017, 56, 1. [Google Scholar] [CrossRef]
- Li, L.; Yi, A.Y. Design and Fabrication of a Freeform Microlens Array for a Compact Large-Field-of-View Compound-Eye Camera. Appl. Opt. 2012, 51, 1843. [Google Scholar] [CrossRef]
- Sortino, M.; Totis, G.; Kuljanic, E. Comparison of Injection Molding Technologies for the Production of Micro-Optical Devices. Procedia Eng. 2014, 69, 1296–1305. [Google Scholar] [CrossRef]
- Thiele, S.; Gissibl, T.; Giessen, H.; Herkommer, A.M. Ultra-Compact on-Chip LED Collimation Optics by 3D Femtosecond Direct Laser Writing. Opt. Lett. 2016, 41, 3029. [Google Scholar] [CrossRef]
- Thiele, S.; Arzenbacher, K.; Gissibl, T.; Giessen, H.; Herkommer, A.M. 3D-Printed Eagle Eye: Compound Microlens System for Foveated Imaging. Sci. Adv. 2017, 3, e1602655. [Google Scholar] [CrossRef] [PubMed]
- Bellouard, Y. The Femtoprint Project. J. Laser Micro/Nanoeng. 2012, 7, 1–10. [Google Scholar] [CrossRef]
- Krol, D.M. Femtosecond Laser Modification of Glass. J. Non-Cryst. Solids 2008, 354, 416–424. [Google Scholar] [CrossRef]
- Ross, C.A.; MacLachlan, D.G.; Choudhury, D.; Thomson, R.R. Optimisation of Ultrafast Laser Assisted Etching in Fused Silica. Optics Express 2018, 26, 24343. [Google Scholar] [CrossRef] [PubMed]
- Boreman, G.D. Modulation Transfer Function in Optical & Electro-Optical Systems; Tutorial Texts in Optical Engineering; SPIE Press: Bellingham, WA, USA, 2001; ISBN 978-0-8194-4143-0. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jobert, G.; Barritault, P.; Fournier, M.; Monpeurt, C.; Boutami, S.; Jamois, C.; Bernasconi, P.; Lovera, A.; Braga, D.; Seassal, C. Miniature Optical Particle Counter and Analyzer Involving a Fluidic-Optronic CMOS Chip Coupled with a Millimeter-Sized Glass Optical System. Sensors 2021, 21, 3181. https://doi.org/10.3390/s21093181
Jobert G, Barritault P, Fournier M, Monpeurt C, Boutami S, Jamois C, Bernasconi P, Lovera A, Braga D, Seassal C. Miniature Optical Particle Counter and Analyzer Involving a Fluidic-Optronic CMOS Chip Coupled with a Millimeter-Sized Glass Optical System. Sensors. 2021; 21(9):3181. https://doi.org/10.3390/s21093181
Chicago/Turabian StyleJobert, Gabriel, Pierre Barritault, Maryse Fournier, Cyrielle Monpeurt, Salim Boutami, Cécile Jamois, Pietro Bernasconi, Andrea Lovera, Daniele Braga, and Christian Seassal. 2021. "Miniature Optical Particle Counter and Analyzer Involving a Fluidic-Optronic CMOS Chip Coupled with a Millimeter-Sized Glass Optical System" Sensors 21, no. 9: 3181. https://doi.org/10.3390/s21093181
APA StyleJobert, G., Barritault, P., Fournier, M., Monpeurt, C., Boutami, S., Jamois, C., Bernasconi, P., Lovera, A., Braga, D., & Seassal, C. (2021). Miniature Optical Particle Counter and Analyzer Involving a Fluidic-Optronic CMOS Chip Coupled with a Millimeter-Sized Glass Optical System. Sensors, 21(9), 3181. https://doi.org/10.3390/s21093181




