A Low-Cost Water Depth and Electrical Conductivity Sensor for Detecting Inputs into Urban Stormwater Networks
Abstract
1. Introduction
2. Sensor Development
2.1. Measured Parameters and Existing Research
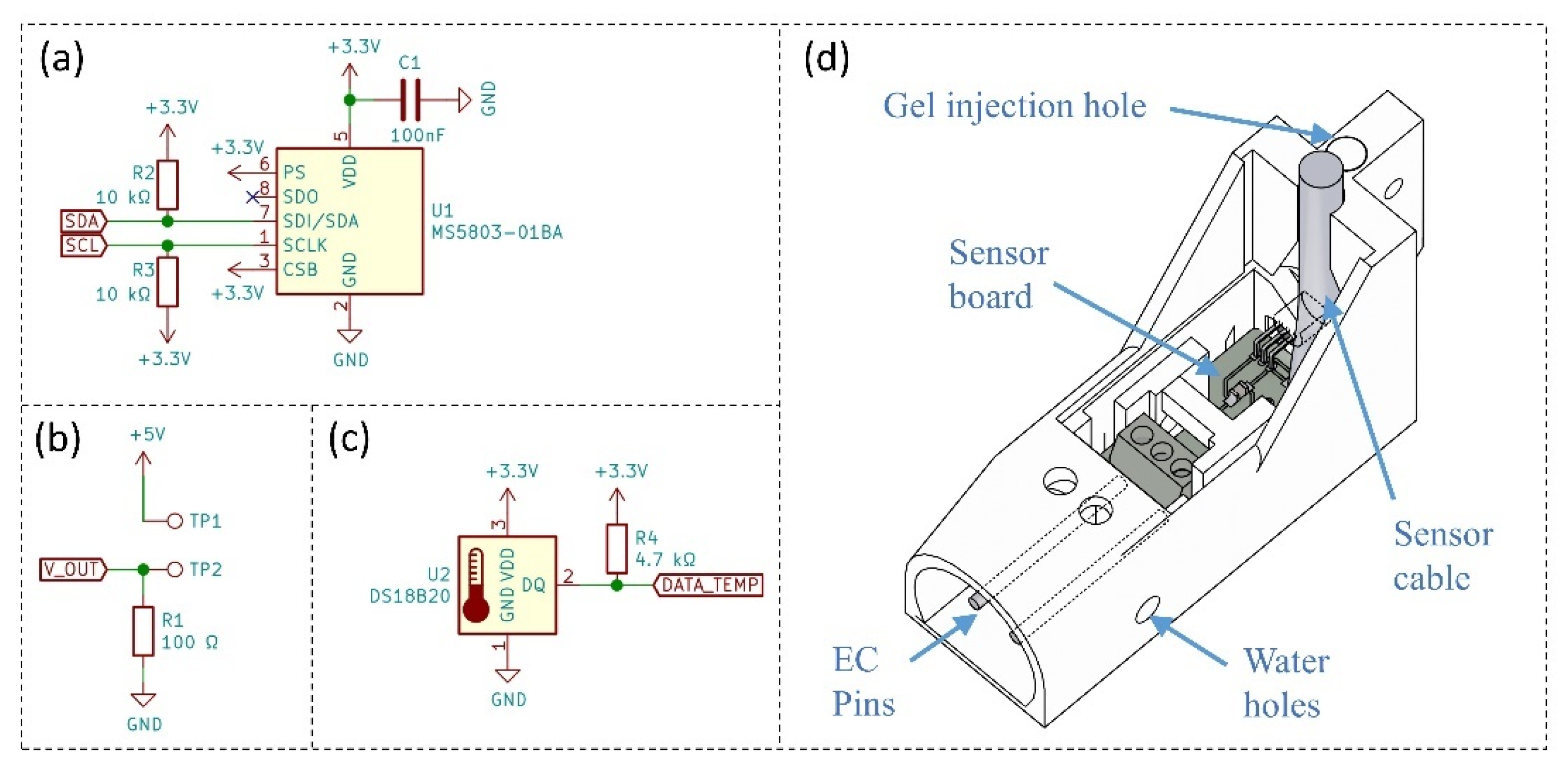
2.2. Depth and Temperature Sensors
2.3. Electrical Conductivity Sensor
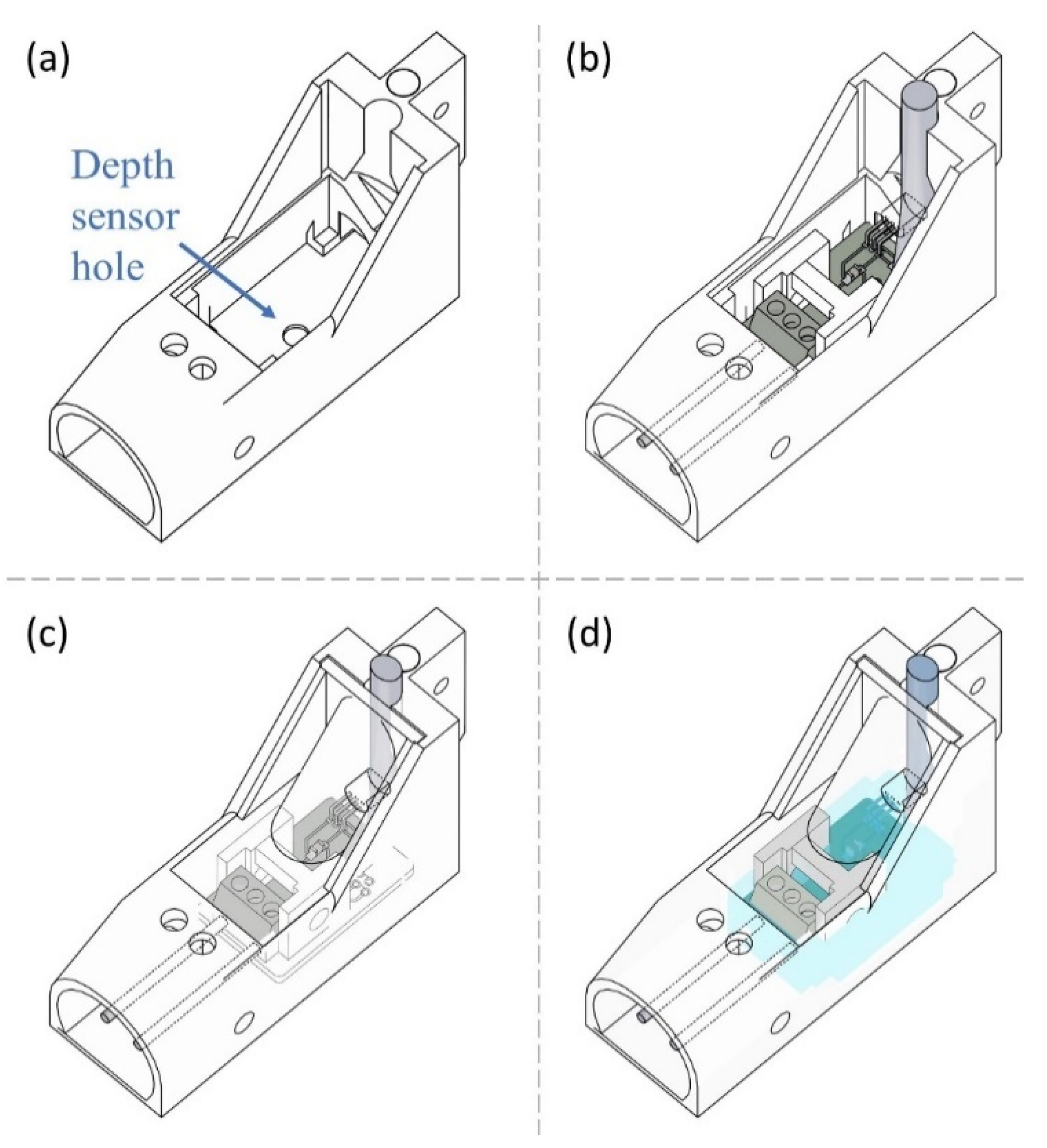
2.4. Structural Design
3. Material and Methods
3.1. Depth Sensor
3.1.1. Laboratory Water Column Test
3.1.2. In Situ Comparison between Low-Cost and a High-End Sensor
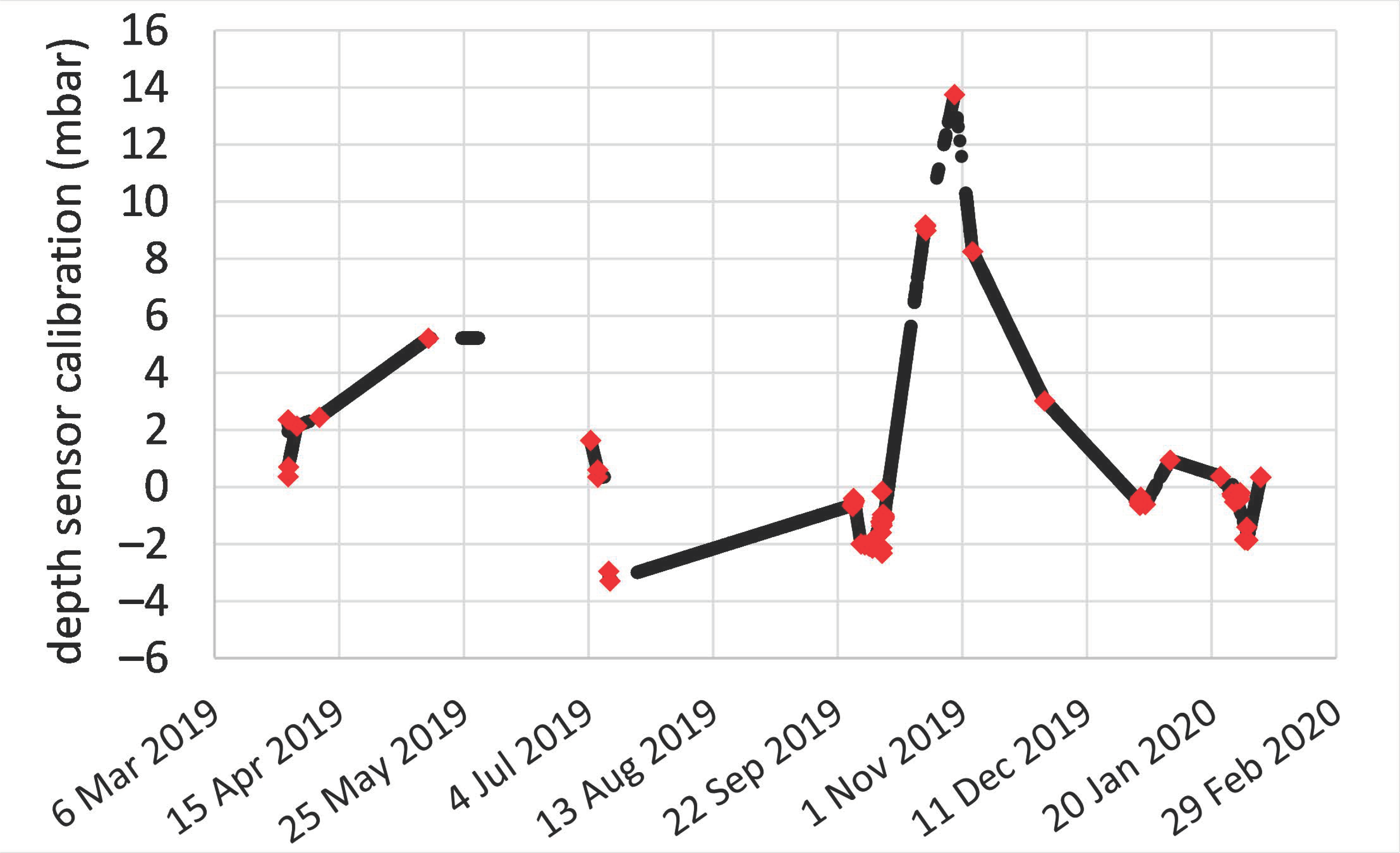
3.1.3. Accounting for Depth Sensor Drift
3.2. Conductivity Sensor
3.2.1. Lab Testing
3.2.2. Field Comparison
4. Results and Discussion
4.1. Depth Sensor
4.1.1. Laboratory Study
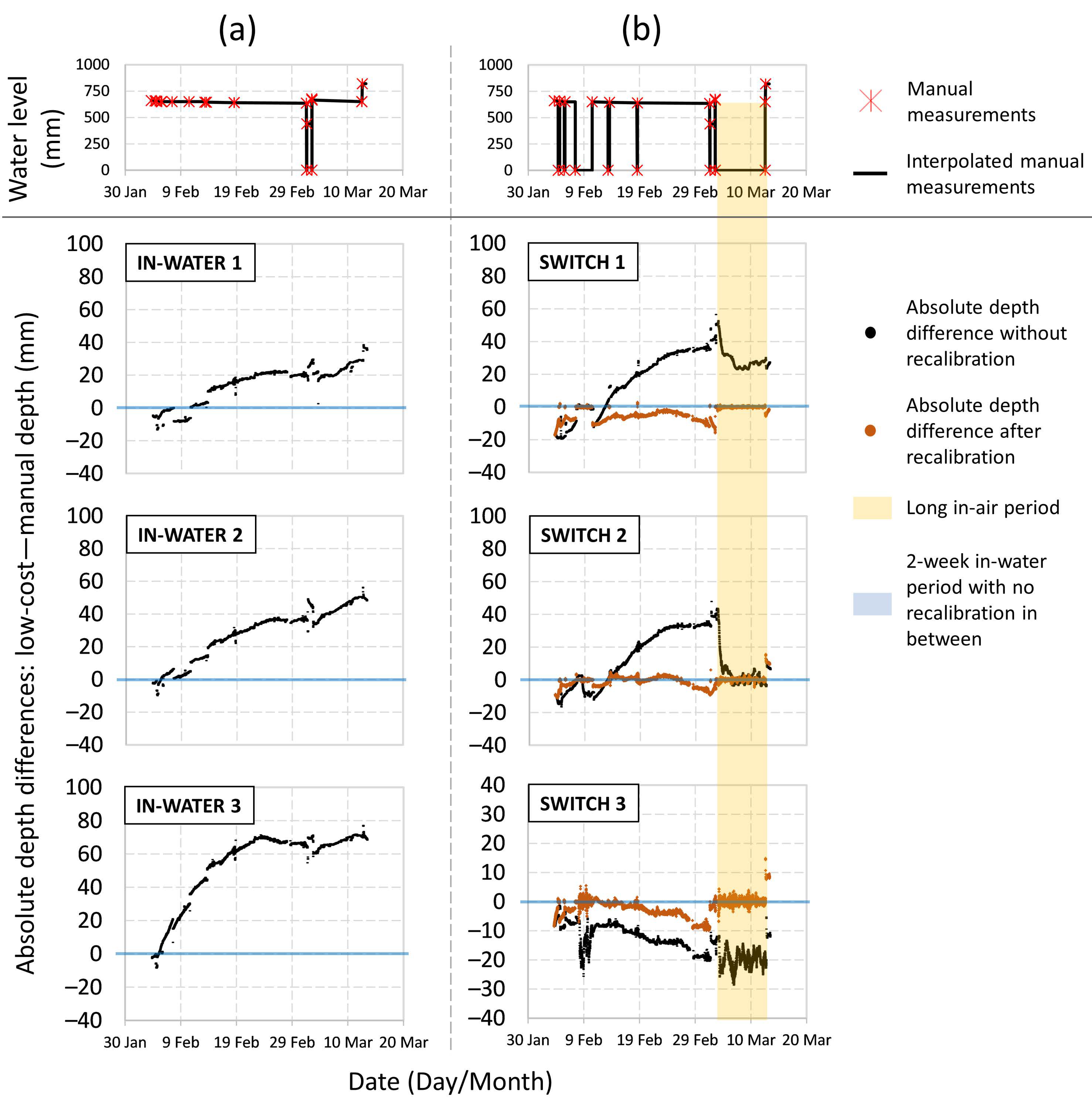
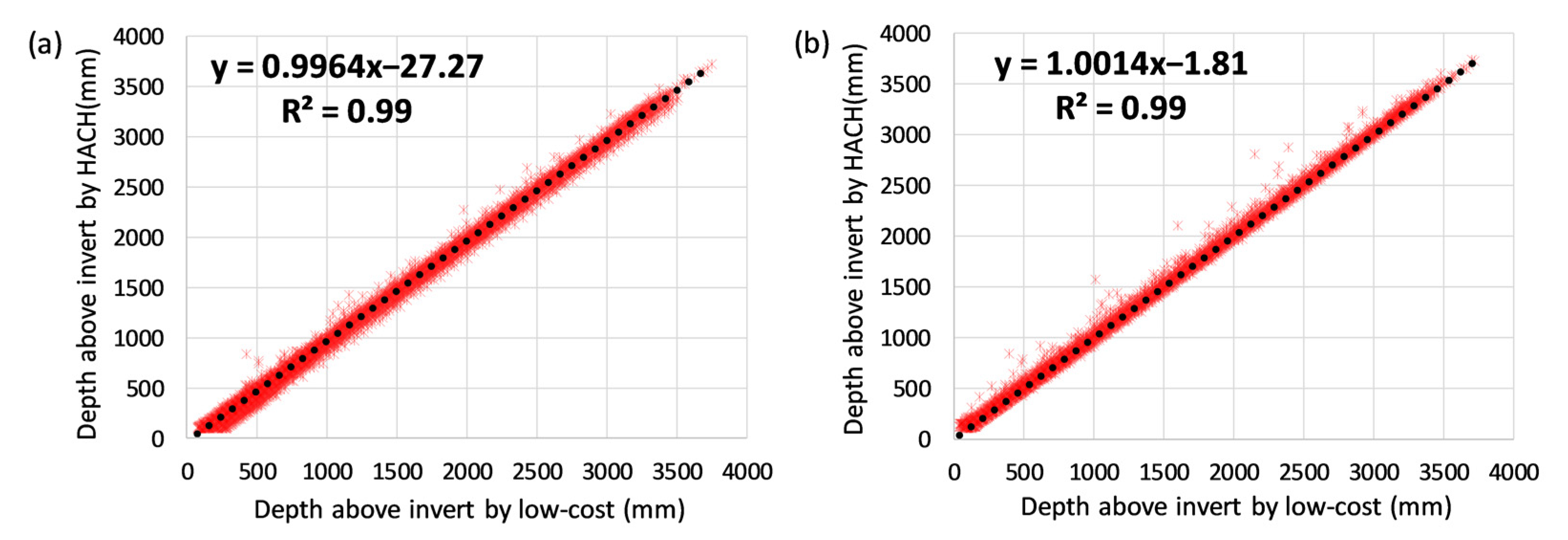
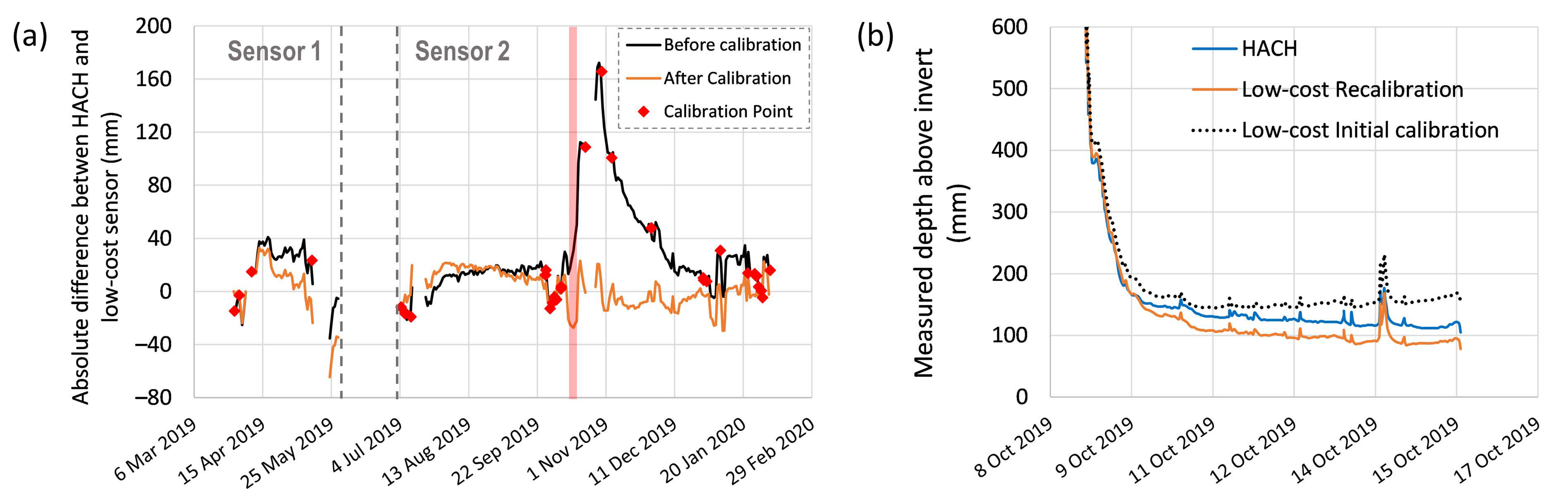
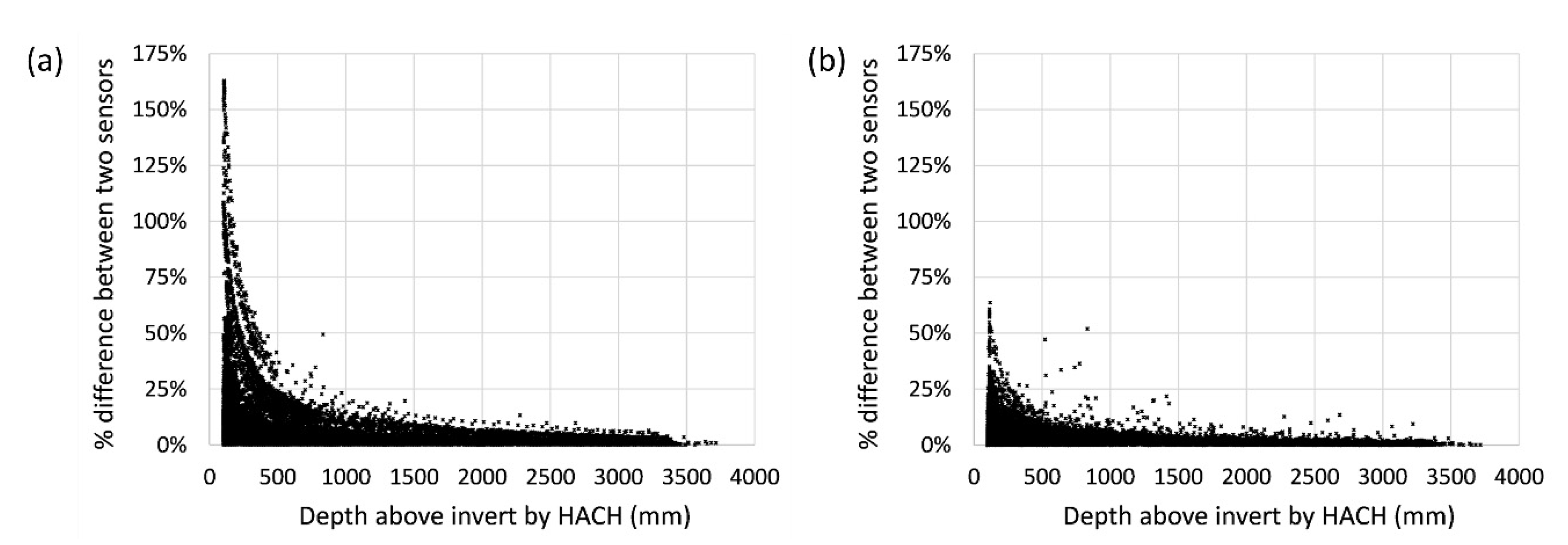
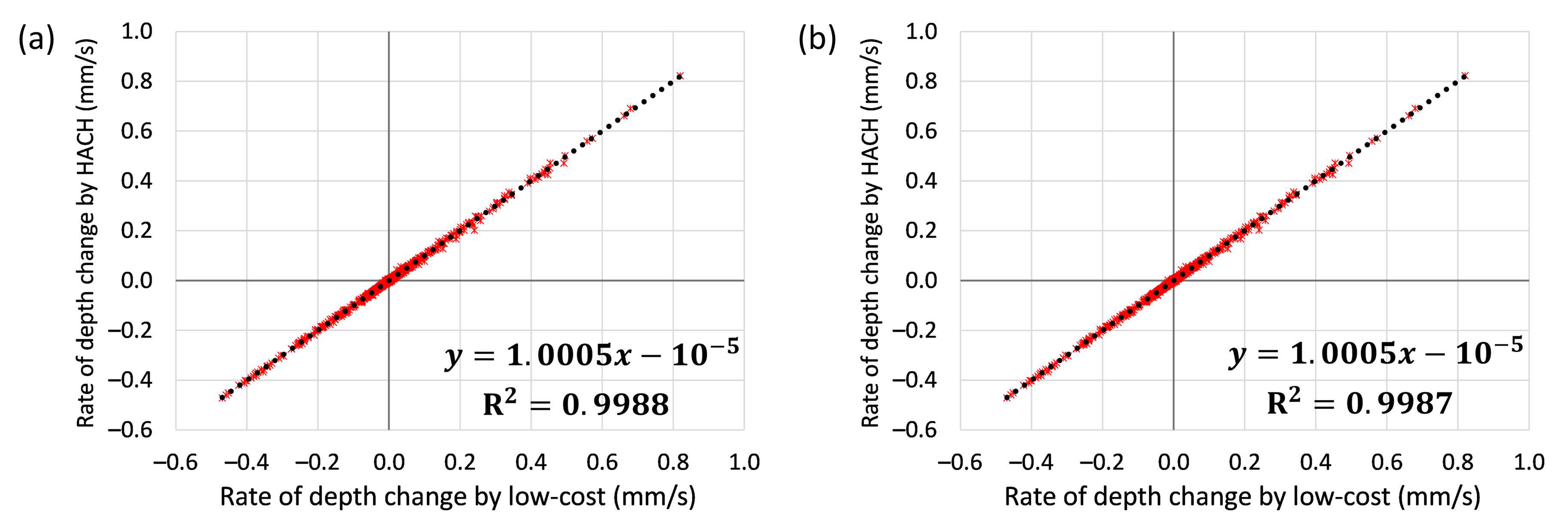
4.1.2. Field Deployment
4.1.3. Application of the Low-Cost Depth Sensors
4.2. Conductivity Sensor
4.2.1. Lab Testing
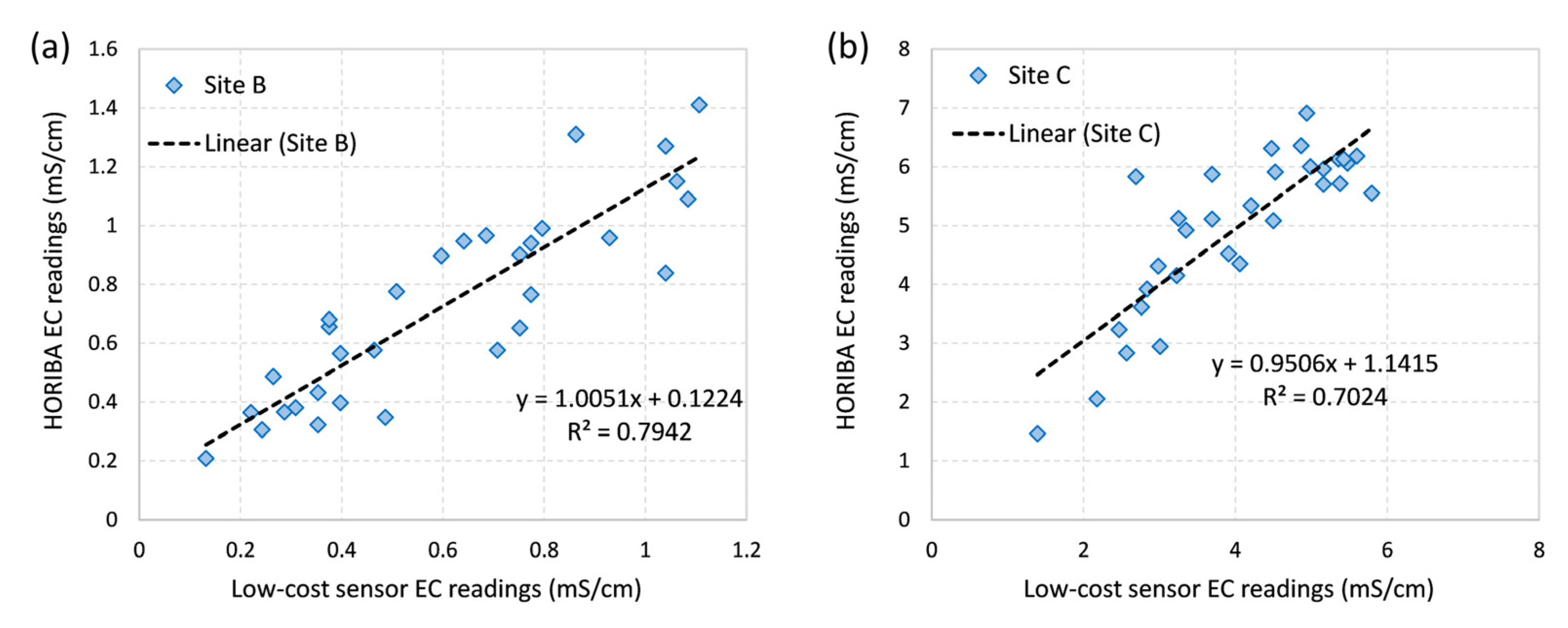
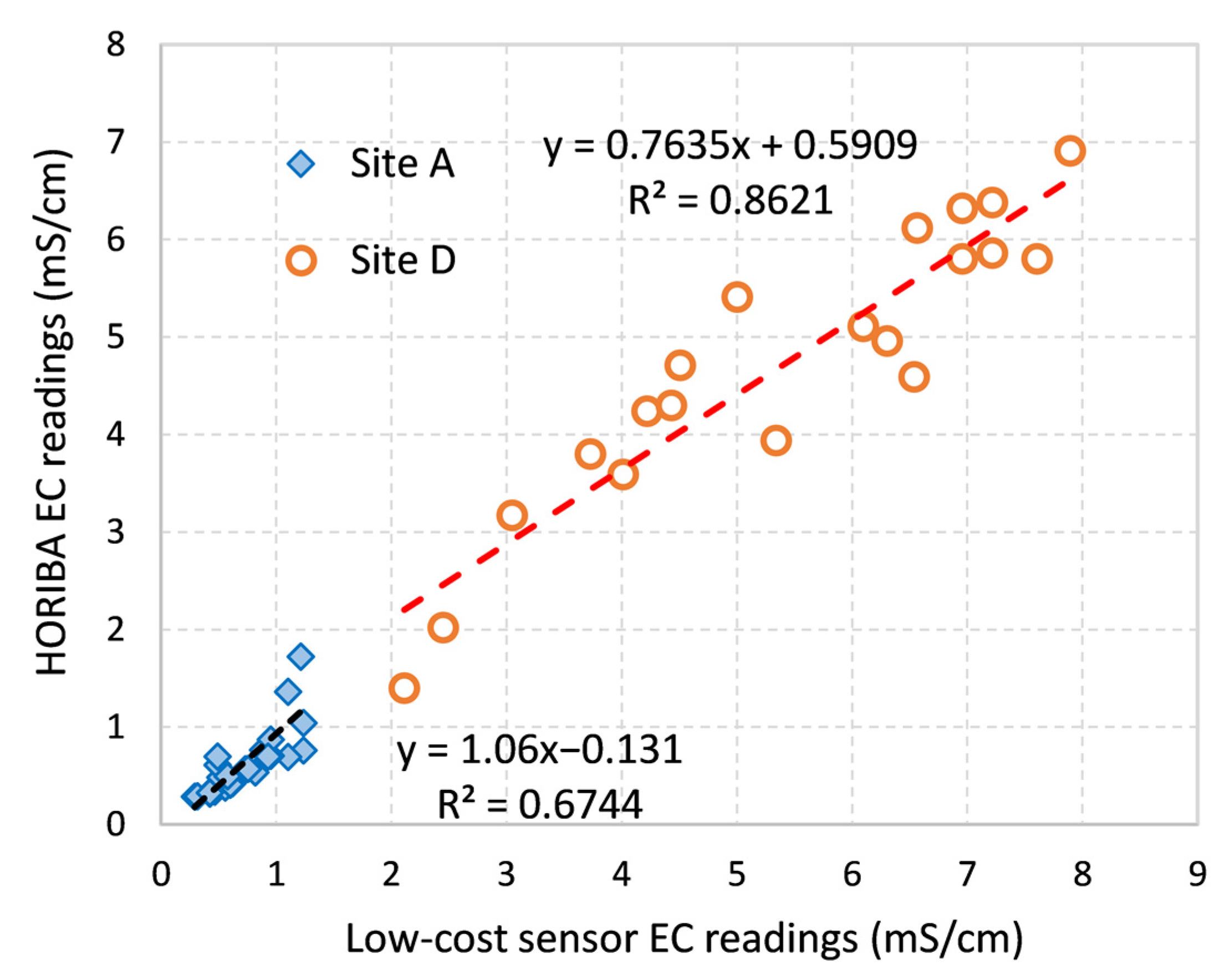
4.2.2. Field Comparison
4.2.3. Conductivity Sensor’s Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Sartor, J.D.; Boyd, C.B. Water Pollution Aspects of Street Surface Contaminants; U.S. Environmental Protection Agency: Washington, DC, USA, 1972.
- Weibel, S.R.; Anderson, R.J.; Woodward, R.L. Urban land runoff as a factor in stream pollution. Water Pollut. Control Fed. 1964, 36, 914–924. [Google Scholar]
- Shi, B.; Bach, P.M.; Lintern, A.; Zhang, K.; Coleman, R.A.; Metzeling, L.; McCarthy, D.T.; Deletic, A. Understanding spatiotemporal variability of in-stream water quality in urban environments—A case study of Melbourne, Australia. J. Environ. Manag. 2019, 246, 203–213. [Google Scholar] [CrossRef]
- Bonhomme, C.; Petrucci, G. Should we trust build-up/wash-off water quality models at the scale of urban catchments? Water Res. 2017, 108, 422–431. [Google Scholar] [CrossRef]
- Dotto, C.B.; Kleidorfer, M.; Deletic, A.; Fletcher, T.D.; McCarthy, D.T.; Rauch, W. Stormwater quality models: Performance and sensitivity analysis. Water Sci. Technol. 2010, 62, 837–843. [Google Scholar] [CrossRef]
- Kerkez, B.; Gruden, C.; Lewis, M.; Montestruque, L.; Quigley, M.; Wong, B.; Bedig, A.; Kertesz, R.; Braun, T.; Cadwalader, O. Smarter stormwater systems. Environ. Sci. Technol. 2016, 50, 7267–7273. [Google Scholar] [CrossRef]
- Deffontis, S.; Breton, A.; Vialle, C.; Montrejaud-Vignoles, M.; Vignoles, C.; Sablayrolles, C. Impact of dry weather discharges on annual pollution from a separate storm sewer in Toulouse, France. Sci. Total Environ. 2013, 452–453, 394–403. [Google Scholar] [CrossRef] [PubMed]
- McPherson, T.N.; Burian, S.J.; Stenstrom, M.K.; Turin, H.; Brown, M.J.; Suffet, I. Dry and Wet Weather Flow Nutrient Loads from a Los Angeles Watershed 1. J. Am. Water Resour. Assoc. 2005, 41, 959–969. [Google Scholar] [CrossRef]
- Ellis, J.B.; Butler, D. Surface water sewer misconnections in England and Wales: Pollution sources and impacts. Sci. Total Environ. 2015, 526, 98–109. [Google Scholar] [CrossRef] [PubMed]
- Panasiuk, O.; Hedstrom, A.; Marsalek, J.; Ashley, R.M.; Viklander, M. Contamination of stormwater by wastewater: A review of detection methods. J. Environ. Manag. 2015, 152, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Pitt, R. Illicit Discharge Detection and Elimination, a Guidance Manual for Program Development and Technical Assessments; Center for Watershed Protection: Ellicott City, MD, USA, 2004. [Google Scholar]
- Schang, C.; Henry, R.; Kolotelo, P.A.; Prosser, T.; Crosbie, N.; Grant, T.; Cottam, D.; O’Brien, P.; Coutts, S.; Deletic, A. Evaluation of techniques for measuring microbial hazards in bathing waters: A comparative study. PLoS ONE 2016, 11, e0155848. [Google Scholar] [CrossRef]
- HACH Company. Submerged AV Sensor. Available online: https://www.hach.com/flow-sensors/submerged-av-sensor/family?productCategoryId=54948588082 (accessed on 1 October 2019).
- HORIBA Scientific. D-50 Series Handheld Water Quality Meters. Available online: https://www.horiba.com/scientific/products/water-quality/conductivity-meters/details/d-50-series-handheld-water-quality-meters-72/ (accessed on 7 October 2019).
- Lockridge, G.; Dzwonkowski, B.; Nelson, R.; Powers, S. Development of a low-cost arduino-based sonde for coastal applications. Sensors 2016, 16, 528. [Google Scholar] [CrossRef]
- Kumar, M.S.; Chandra, T.R.; Kumar, D.P.; Manikandan, M.S. Monitoring moisture of soil using low cost homemade Soil moisture sensor and Arduino UNO. In Proceedings of the 2016 3rd international conference on advanced computing and communication systems (ICACCS), Coimbatore, India, 22–23 January 2016; pp. 1–4. [Google Scholar]
- Ferdoush, S.; Li, X. Wireless sensor network system design using Raspberry Pi and Arduino for environmental monitoring applications. Procedia Comput. Sci. 2014, 34, 103–110. [Google Scholar] [CrossRef]
- Zafar, S.; Miraj, G.; Baloch, R.; Murtaza, D.; Arshad, K. An IoT based real-time environmental monitoring system using Arduino and cloud service. Eng. Technol. Appl. Sci. Res. 2018, 8, 3238–3242. [Google Scholar] [CrossRef]
- Hoes, O.A.C.; Schilperoort, R.P.S.; Luxemburg, W.; Clemens, F.; Van de Giesen, N. Locating illicit connections in storm water sewers using fiber-optic distributed temperature sensing. Water Res. 2009, 43, 5187–5197. [Google Scholar] [CrossRef]
- Rocher, J.; Parra, M.; Parra, L.; Sendra, S.; Lloret, J.; Mengual, J. A Low-Cost Sensor for Detecting Illicit Discharge in Sewerage. J. Sens. 2021, 2021. [Google Scholar] [CrossRef]
- Hammond, P.; Suttie, M.; Lewis, V.T.; Smith, A.P.; Singer, A.C. Detection of untreated sewage discharges to watercourses using machine learning. NPJ Clean Water 2021, 4, 1–10. [Google Scholar]
- Fisher, D.K.; Sui, R. An inexpensive open-source ultrasonic sensing system for monitoring liquid levels. Agric. Eng. Int. CIGR J. 2013, 15, 328–334. [Google Scholar]
- Wang, G.; Gu, C.; Rice, J.; Inoue, T.; Li, C. Highly accurate noncontact water level monitoring using continuous-wave Doppler radar. In Proceedings of the 2013 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), Austin, TX, USA, 20–23 January 2013; pp. 19–21. [Google Scholar]
- Loftis, J.D.; Forrest, D.; Katragadda, S.; Spencer, K.; Organski, T.; Nguyen, C.; Rhee, S. StormSense: A new integrated network of IoT water level sensors in the smart cities of Hampton Roads, VA. Mar. Technol. Soc. J. 2018, 52, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Chetpattananondh, K.; Tapoanoi, T.; Phukpattaranont, P.; Jindapetch, N. A self-calibration water level measurement using an interdigital capacitive sensor. Sens. Actuators APhys. 2014, 209, 175–182. [Google Scholar] [CrossRef]
- Loizou, K.; Koutroulis, E.; Zalikas, D.; Liontas, G. A low-cost capacitive sensor for water level monitoring in large-scale storage tanks. In Proceedings of the 2015 IEEE international conference on industrial technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1416–1421. [Google Scholar]
- TE Connectivity. MS5837-30BA Ultra-Small, Gel-Filled, Pressure Sensor with Stainless Steel Cap. Available online: https://www.te.com/commerce/DocumentDelivery/DDEController?Action=showdoc&DocId=Data+Sheet%7FMS5837-30BA%7FB1%7Fpdf%7FEnglish%7FENG_DS_MS5837-30BA_B1.pdf%7FCAT-BLPS0017 (accessed on 15 October 2020).
- Parra, L.; Ortuño, V.; Sendra, S.; Lloret, J. Low-cost conductivity sensor based on two coils. In Proceedings of the First International Conference on Computational Science and Engineering (CSE’13), Valencia, Spain, 6–8 August 2013; p. 107112. [Google Scholar]
- Carminati, M.; Luzzatto-Fegiz, P. Conduino: Affordable and high-resolution multichannel water conductivity sensor using micro USB connectors. Sens. Actuators B Chem. 2017, 251, 1034–1041. [Google Scholar] [CrossRef]
- TE Connectivity. MS5803-01BA Miniature Variometer Module. Available online: https://www.te.com/commerce/DocumentDelivery/DDEController?Action=showdoc&DocId=Data+Sheet%7FMS5803-01BA%7FB3%7Fpdf%7FEnglish%7FENG_DS_MS5803-01BA_B3.pdf%7FCAT-BLPS0038 (accessed on 15 November 2018).
- Dallas Semiconductor. DS18B20 Programmable Resolution. Available online: https://cdn.sparkfun.com/datasheets/Sensors/Temp/DS18B20.pdf (accessed on 21 October 2019).
- Ratcliffe, M. Three Dollar EC—PPM Meter. Available online: https://hackaday.io/project/7008-fly-wars-a-hackers-solution-to-world-hunger/log/24646-three-dollar-ec-ppm-meter-arduino (accessed on 15 January 2019).
- Hayashi, M. Temperature-electrical conductivity relation of water for environmental monitoring and geophysical data inversion. Environ. Monit. Assess. 2004, 96, 119–128. [Google Scholar] [CrossRef]
- HANNA Instruments. Waterproof Portable EC/TDS/Resistivity/Salinity Meter—HI98192. Available online: https://hannainst.com.au/hi98192-waterproof-portable-ec-tds-resistivity-salinity-meter.html (accessed on 15 April 2020).
- McCarthy, D.T.; Deletic, A.; Mitchell, V.G.; Fletcher, T.D.; Diaper, C. Uncertainties in stormwater E. coli levels. Water Res. 2008, 42, 1812–1824. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Deletic, A.; Bach, P.M.; Shi, B.; Hathaway, J.M.; McCarthy, D.T. Testing of new stormwater pollution build-up algorithms informed by a genetic programming approach. J. Environ. Manag. 2019, 241, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Herngren, L.; Goonetilleke, A.; Ayoko, G.A. Understanding heavy metal and suspended solids relationships in urban stormwater using simulated rainfall. J. Environ. Eng. 2005, 76, 149–158. [Google Scholar] [CrossRef] [PubMed]




| Re-Calibration Frequency | SWITCH 1 | SWITCH 2 | SWITCH 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Absolute Difference (mm) (5th, 95th Percentiles) | Percentage Error (%) (5th, 95th Percentiles) | Relative Uncertainty (%) | Absolute Difference (mm) (5th, 95th Percentiles) | Percentage Error (%) (5th, 95th Percentiles) | Relative Uncertainty (%) | Absolute Difference (mm) (5th, 95th Percentiles) | Percentage Error (%) (5th, 95th Percentiles) | Relative Uncertainty (%) | |
| None | (−14.81, 36.99) | (0.69, 5.69) | 3.59 | (−8.33, 34.03) | (0.58, 5.36) | 3.39 | (−23.03, −6.46) | (0.96, 3.03) | 1.80 |
| 14-day | (−9.77, −2.42) | (0.38, 1.54) | 0.82 | (−6.00, 2.53) | (0.03, 0.94) | 0.35 | (−8.77, −1.82) | (0.28, 1.38) | 0.77 |
| Average 6-day | (−11.10, −2.45) | (0.36, 1.82) | 1.00 | (−6.37, 2.84) | (0.03, 1.30) | 0.41 | (−8.51, 0.63) | (0.05, 1.34) | 0.56 |
| Site | Resistance | EC = a × Measured EC + b (R2) |
|---|---|---|
| A | 100 Ω | EC = 1.0963 × measured EC − 0.2331 (0.9959) |
| B | 100 Ω | EC = 1.1075 × measured EC − 0.2004 (0.9963) |
| C | 100 Ω | EC = 1.2226 × measured EC − 0.2685 (0.9983) |
| D | 100 Ω | EC = 1.3023 × measured EC − 0.2338 (0.9990) |
| Site | HORIBA Measured EC Range (mS/cm) | Absolute Difference (mS/cm) (5th, 95th Percentiles) | Percentage Error (%) (5th, 95th Percentiles) | Relative Uncertainty (%) |
|---|---|---|---|---|
| A | (0.29, 1.72) | (−0.51, 0.44) | (4.54, 60.40) | 31.12 |
| B | (0.28, 1.34) | (−0.35, 0.16) | (0.41, 45.00) | 23.21 |
| C | (1.84, 6.55) | (−2.51, 0.17) | (3.69, 42.96) | 18.65 |
| D | (1.43, 6.88) | (−0.40, 1.94) | (0.52, 50.42) | 17.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Catsamas, S.; Kolotelo, P.; Wang, M.; Lintern, A.; Jovanovic, D.; Bach, P.M.; Deletic, A.; McCarthy, D.T. A Low-Cost Water Depth and Electrical Conductivity Sensor for Detecting Inputs into Urban Stormwater Networks. Sensors 2021, 21, 3056. https://doi.org/10.3390/s21093056
Shi B, Catsamas S, Kolotelo P, Wang M, Lintern A, Jovanovic D, Bach PM, Deletic A, McCarthy DT. A Low-Cost Water Depth and Electrical Conductivity Sensor for Detecting Inputs into Urban Stormwater Networks. Sensors. 2021; 21(9):3056. https://doi.org/10.3390/s21093056
Chicago/Turabian StyleShi, Baiqian, Stephen Catsamas, Peter Kolotelo, Miao Wang, Anna Lintern, Dusan Jovanovic, Peter M. Bach, Ana Deletic, and David T. McCarthy. 2021. "A Low-Cost Water Depth and Electrical Conductivity Sensor for Detecting Inputs into Urban Stormwater Networks" Sensors 21, no. 9: 3056. https://doi.org/10.3390/s21093056
APA StyleShi, B., Catsamas, S., Kolotelo, P., Wang, M., Lintern, A., Jovanovic, D., Bach, P. M., Deletic, A., & McCarthy, D. T. (2021). A Low-Cost Water Depth and Electrical Conductivity Sensor for Detecting Inputs into Urban Stormwater Networks. Sensors, 21(9), 3056. https://doi.org/10.3390/s21093056







