Finite-Time Dynamic Tracking Control of Parallel Robots with Uncertainties and Input Saturation
Abstract
1. Introduction
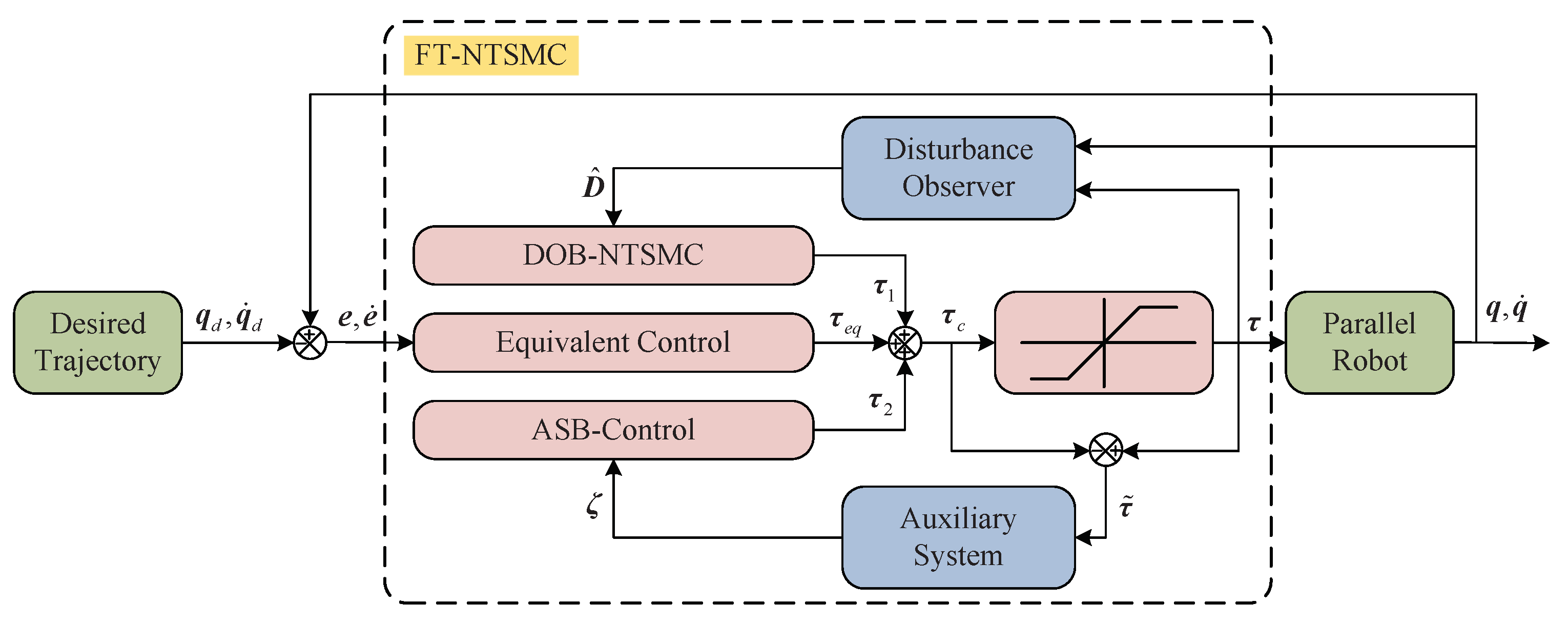
- In contrast to the existing control algorithm based on an asymptotically convergent auxiliary system [25,26,27,28,29,30,31,32,33], the proposed FT-NTSMC can realize the finite-time tracking control performance. Specifically, a novel finite-time convergent auxiliary system including fractional exponential powers is constructed to compensate for input saturation. The FT-NTSMC for parallel robots is attained by combining a disturbance observer-based NTSMC algorithm with the novel auxiliary system. Consequently, the finite-time convergence of both the sliding variable and the tracking error are ensured for parallel robots even in the presence of uncertainties and input saturation;
- The sign function is not explicitly included in the proposed control law. Moreover, due to the estimation and compensation of the lumped disturbance, the control gain merely needs to be larger than the upper bound of the disturbance estimation error. Thus, the chattering of the proposed controller can be effectively attenuated.
2. Preliminaries and Problem Formulation
2.1. Dynamic Modeling
2.2. Problem Formulation and Control Objective
2.3. Useful Lemmas
3. Design of FT-NTSMC Strategy for Parallel Robots
3.1. Design of the Disturbance Observer
3.2. Design of the Novel Auxiliary System
3.3. Design of the Proposed FT-NTSMC
3.4. Stability Analysis
4. Numerical Simulation
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, G.Q.; Ye, M.Y.; Zhang, M.C. Synchronous robust sliding mode control of a parallel robot for automobile electro-coating conveying. IEEE Access 2019, 7, 85838–85847. [Google Scholar] [CrossRef]
- Zavala-Yoe, R.; Ramírez-Mendoza, R.A.; García-Lara, S. A 3-SPS-1S parallel robot-based laser sensing for applications in precision agriculture. Soft Comput. 2016, 21, 641–650. [Google Scholar] [CrossRef]
- Ai, Q.; Zhu, C.; Zuo, J.; Meng, W.; Liu, Q.; Xie, S.Q.; Yang, M. Disturbance-Estimated Adaptive Backstepping Sliding Mode Control of a Pneumatic Muscles-Driven Ankle Rehabilitation Robot. Sensors 2018, 18, 66. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: New York, NY, USA, 2014; pp. 1–41. [Google Scholar]
- Navvabi, H.; Markazi, A.H.D. Position control of Stewart manipulator using a new extended adaptive fuzzy sliding mode controller and observer (E-AFSMCO). J. Franklin I 2018, 355, 2583–2609. [Google Scholar] [CrossRef]
- Jia, H.Y.; Shang, W.W.; Xie, F.; Zhang, B.; Cong, S. Second-order sliding-mode-based synchronization control of cable-driven parallel robots. IEEE/ASME Trans. Mech. 2020, 25, 383–394. [Google Scholar] [CrossRef]
- Yu, X.H.; Man, Z.H. Multi-input uncertain linear systems with terminal sliding-mode control. Automatica 1998, 34, 389–392. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.H.; Man, Z.H. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yu, S.H.; Yu, X.H.; Shirinzadeh, B.; Man, Z.H. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J.Y. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control. 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Hernández, J.H.; Cruz, S.S.; López-Gutiérrez, R.; González-Mendoza, A.; Lozano, R. Robust nonsingular fast terminal sliding-mode control for sit-to-stand task using a mobile lower limb exoskeleton. Control Eng. Pract. 2020, 101, 1–11. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H. Neural integral non-singular fast terminal synchronous sliding mode control for uncertain 3-DOF parallel robotic manipulators. IEEE Access 2020, 8, 65383–65394. [Google Scholar] [CrossRef]
- Galicki, M. Finite-time trajectory tracking control in a task space of robotic manipulators. Automatica 2016, 67, 165–170. [Google Scholar] [CrossRef]
- Jia, S.Y.; Shan, J.J. Finite-time trajectory tracking control of space manipulator under actuator saturation. IEEE Trans. Ind. Electron. 2020, 67, 2086–2096. [Google Scholar] [CrossRef]
- Chen, H.T.; Song, S.M.; Zhu, Z.B. Robust finite-time attitude tracking control of rigid spacecraft under actuator saturation. Int. J. Control Autom. 2018, 16, 1–15. [Google Scholar] [CrossRef]
- He, W.; Sun, Y.K.; Yan, Z.C.; Yang, C.G.; Li, Z.J.; Kaynak, O. Disturbance observer-based neural network control of cooperative multiple manipulators with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1735–1746. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.J.; Su, C.Y.; Wang, L.Y.; Chen, Z.T.; Chai, T.Y. Nonlinear disturbance observer-based control design for a robotic exoskeleton incorporating fuzzy approximation. IEEE Trans. Ind. Electron. 2015, 62, 5763–5775. [Google Scholar] [CrossRef]
- Guo, X.G.; Wang, J.L.; Liao, F.; Teo, R.S.H. CNN-based distributed adaptive control for vehicle-following platoon with input saturation. IEEE Trans. Transp. Syst. 2018, 19, 3121–3132. [Google Scholar] [CrossRef]
- Chen, M.; Tao, G.; Jiang, B. Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2086–2097. [Google Scholar] [CrossRef] [PubMed]
- Ye, N.; Song, J.C.; Ren, G.G. Model-based adaptive command filtering control of an electrohydraulic actuator with input saturation and friction. IEEE Access 2020, 8, 48252–48263. [Google Scholar] [CrossRef]
- Han, J.; Kim, T.; Oh, T.; Lee, S.; Cho, D.D. Effective disturbance compensation method under control saturation in discrete-time sliding mode control. IEEE Trans. Ind. Electron. 2020, 67, 5696–5707. [Google Scholar] [CrossRef]
- Li, H.Y.; Wang, J.H.; Shi, P. Output-feedback based sliding mode control for fuzzy systems with actuator saturation. IEEE Trans. Fuzzy Syst. 2016, 24, 1282–1293. [Google Scholar] [CrossRef]
- Xu, D.Z.; Shi, Y.; Ji, Z.C. Model-free adaptive discrete-time integral sliding-mode-constrained-control for autonomous 4WMV parking systems. IEEE Trans. Ind. Electron. 2018, 65, 834–843. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.S.; Ren, B.B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica 2011, 47, 452–465. [Google Scholar] [CrossRef]
- Du, J.L.; Hu, X.; Krstić, M.; Sun, Y.Q. Robust dynamic positioning of ships with disturbances under input saturation. Automatica 2016, 73, 207–214. [Google Scholar] [CrossRef]
- He, W.; Dong, Y.T.; Sun, C.Y. Adaptive neural impedance control of a robotic manipulator with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 334–344. [Google Scholar] [CrossRef]
- Arefinia, E.; Talebi, H.A.; Doustmohammadi, A. A robust adaptive model reference impedance control of a robotic manipulator with actuator saturation. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 409–420. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Y.Y.; Li, Z.J.; Su, C.Y.; Feng, Y. Adaptive control and optimization of mobile manipulation subject to input saturation and switching constraints. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1543–1555. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.J.; Kong, H.Y.; Ke, F. Model predictive tracking control of nonholonomic mobile robots with coupled input constraints and unknown dynamics. IEEE Trans. Ind. Inform. 2019, 15, 3196–3205. [Google Scholar] [CrossRef]
- He, W.; Li, Z.J.; Dong, Y.T.; Zhang, T. Design and adaptive control for an upper limb robotic exoskeleton in presence of input saturation. IEEE Trans. Neural Netw. Learn. 2019, 30, 97–108. [Google Scholar] [CrossRef]
- H, W.; He, X.Y.; Ge, S.S. Vibration control of flexible marine riser systems with input saturation. IEEE ASME Trans. Mechatron. 2016, 21, 254–265. [Google Scholar]
- Peng, G.Z.; Yang, C.G.; He, W.; Chen, C.L.P. Force sensorless admittance control with neural learning for robots with actuator saturation. IEEE Trans. Ind. Electron. 2020, 67, 3138–3148. [Google Scholar] [CrossRef]
- Zheng, W.W.; Feroskhan, M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances. IEEE Trans. Ind. Electron. 2017, 22, 2564–2575. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, B.; Cui, R.X. Actuator fault-tolerant control of ocean surface vessels with input saturation. Int. J. Robust Nonlin. 2016, 26, 542–564. [Google Scholar] [CrossRef]
- Min, H.F.; Xu, S.Y.; Ma, Q.; Zhang, B.Y.; Zhang, Z.Q. Composite-observer-based output-feedback control for nonlinear time-delay systems with input saturation and its application. IEEE Trans. Ind. Electron. 2018, 65, 5856–5863. [Google Scholar] [CrossRef]
- Esfandiari, K.; Abdollahi, F.; Talebi, H.A. Adaptive control of uncertain nonaffine nonlinear systems with input saturation using neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2311–2322. [Google Scholar] [CrossRef]
- Gao, Y.H.; Sun, X.M.; Wen, C.Y.; Wang, W. Adaptive tracking control for a class of stochastic uncertain nonlinear systems with input saturation. IEEE Trans. Automat. Control 2017, 62, 2498–2540. [Google Scholar] [CrossRef]
- Cai, J.P.; Qian, F.; Yu, R.; Shen, L.J. Output feedback control for pneumatic muscle joint system with saturation input. IEEE Access 2020, 8, 83901–83906. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Qu, Y.H.; Zhang, Y.M. Distributed fault-tolerant cooperative control for multi-uavs under actuator fault and input saturation. IEEE Trans. Control Syst. Technol. 2019, 27, 2417–2429. [Google Scholar] [CrossRef]
- Gao, Y.F.; Sun, X.M.; Weng, C.Y.; Wang, W. Observer-based adaptive nn control for a class of uncertain nonlinear systems with nonsymmetric input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1520–1530. [Google Scholar] [CrossRef]
- Jiang, B.Y.; Hu, Q.L.; Friswell, M.I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults. IEEE Trans. Control Syst. Technol. 2016, 24, 1892–1898. [Google Scholar] [CrossRef]
- Ding, S.H.; Liu, L.; Zheng, W.X. Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Nuño, E.; Moreno, J.A. Finite-time regulation of robots: A strict lyapunov function approach. In Proceedings of the 2nd IFAC Conference on Modelling, Identification and Control of Nonlinear Systems, Guadalajara, Mexico, 20–22 June 2018; pp. 279–284. [Google Scholar]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Connecting rod length | |
| Diameter of gear dividing circle d | |
| Radius of driving wheel | |
| Radius of driving wheel | |
| Connecting rod length | |
| Reduction ratio of reducer | 1:20 |
| Screw lead s | |
| Base length |
| Controllers | Parameters |
|---|---|
| FT-NTSMC | , |
| , | |
| , | |
| . | |
| Controller-1 | , |
| . | |
| Controller-2 | , |
| . |
| FT-NTSMC | Controller-1 | Controller-2 | |
|---|---|---|---|
| Joint 1 | |||
| Joint 2 | |||
| Joint 5 | |||
| RMSE |
| FT-NTSMC | Controller-1 | Controller-2 | |
|---|---|---|---|
| Joint 1 | |||
| Joint 2 | |||
| Joint 5 |
| FT-NTSMC | Controller-1 | |
|---|---|---|
| Z | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Gao, G.; Zhong, J.; Qin, Q. Finite-Time Dynamic Tracking Control of Parallel Robots with Uncertainties and Input Saturation. Sensors 2021, 21, 2996. https://doi.org/10.3390/s21092996
Ye M, Gao G, Zhong J, Qin Q. Finite-Time Dynamic Tracking Control of Parallel Robots with Uncertainties and Input Saturation. Sensors. 2021; 21(9):2996. https://doi.org/10.3390/s21092996
Chicago/Turabian StyleYe, Mengyang, Guoqin Gao, Junwen Zhong, and Qiuyue Qin. 2021. "Finite-Time Dynamic Tracking Control of Parallel Robots with Uncertainties and Input Saturation" Sensors 21, no. 9: 2996. https://doi.org/10.3390/s21092996
APA StyleYe, M., Gao, G., Zhong, J., & Qin, Q. (2021). Finite-Time Dynamic Tracking Control of Parallel Robots with Uncertainties and Input Saturation. Sensors, 21(9), 2996. https://doi.org/10.3390/s21092996







