Nonlinear T-Wave Time Warping-Based Sensing Model for Non-Invasive Personalised Blood Potassium Monitoring in Hemodialysis Patients: A Pilot Study
Abstract
1. Introduction
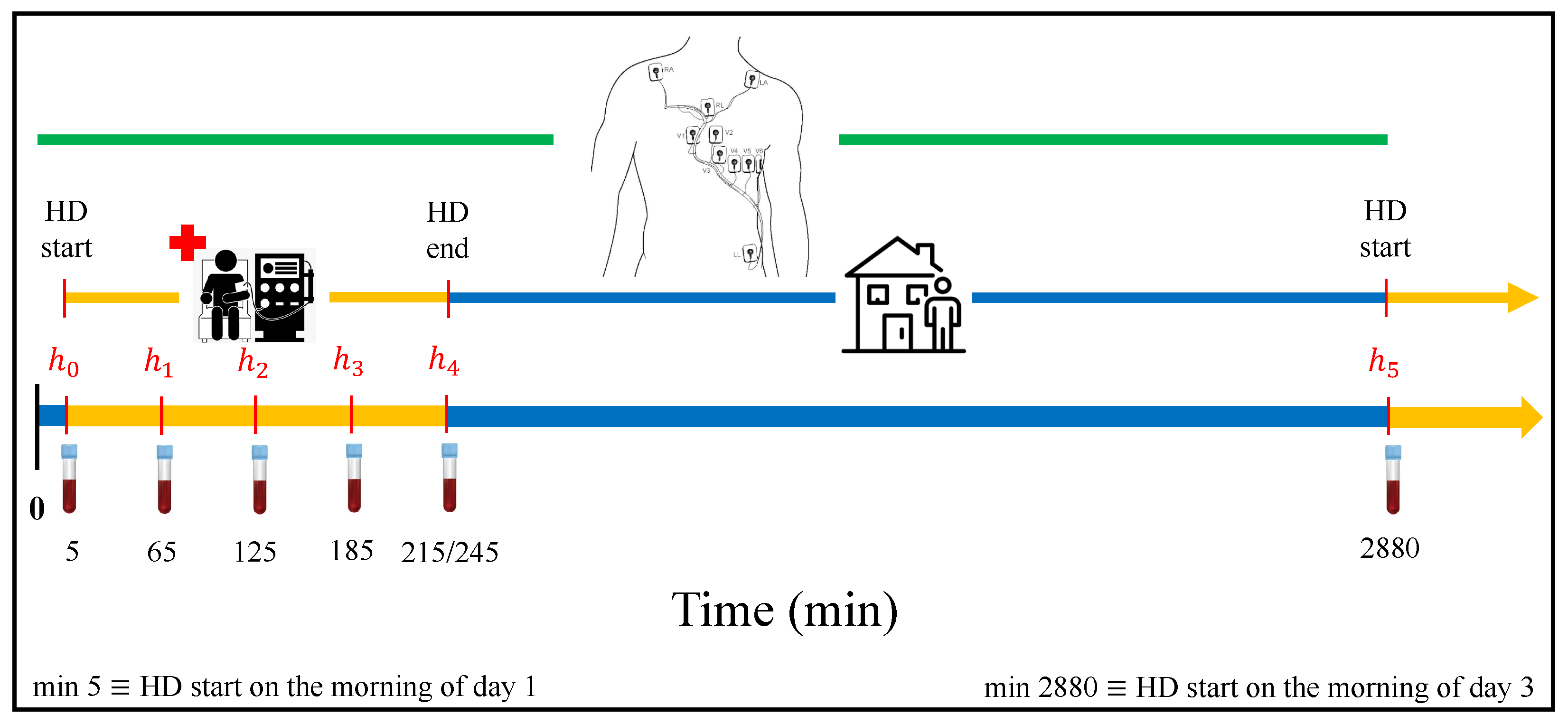
2. Materials
3. Methods
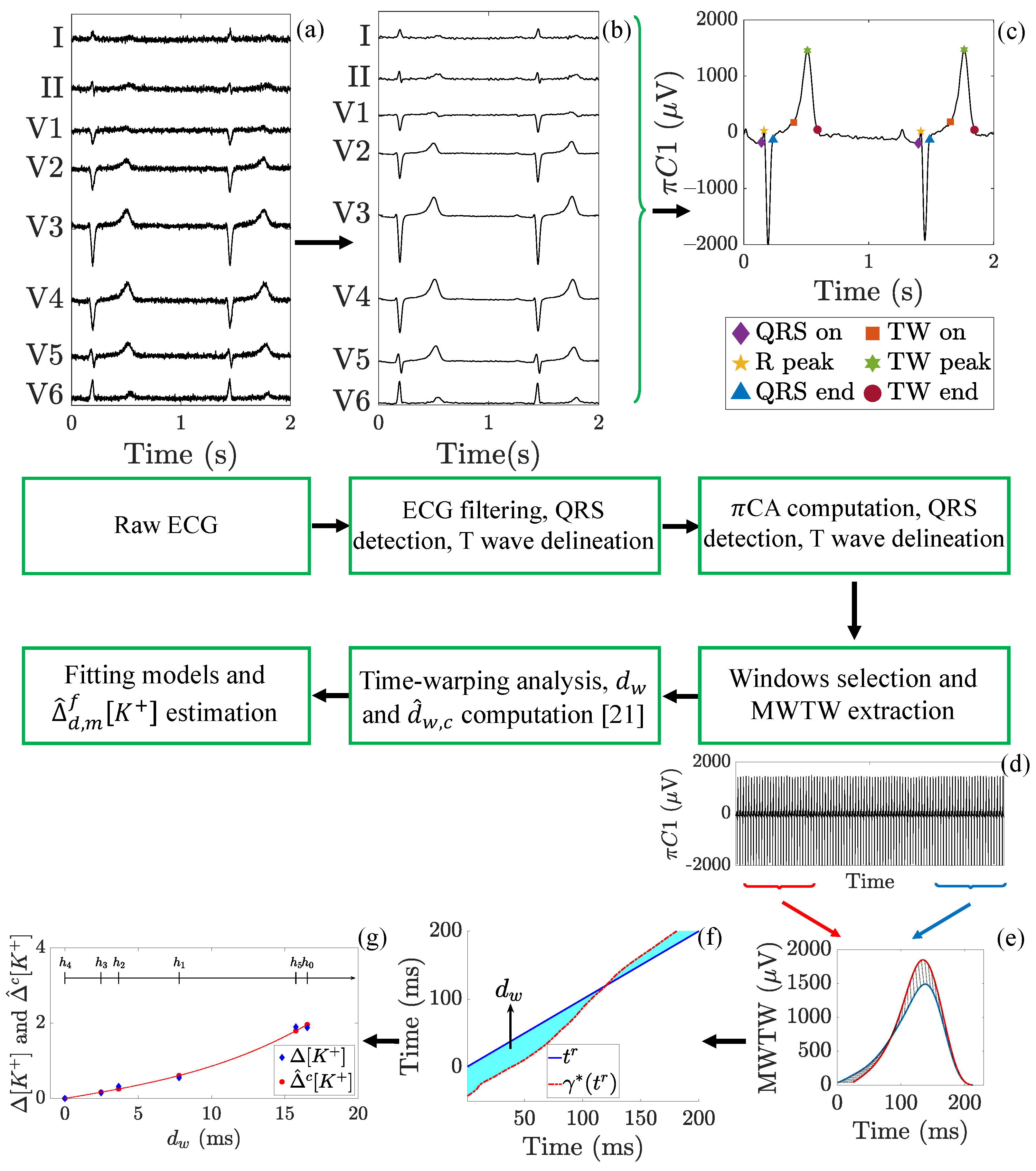
3.1. ECG Pre-Processing
3.2. Lead Transformation by Periodic Component Analysis, CA
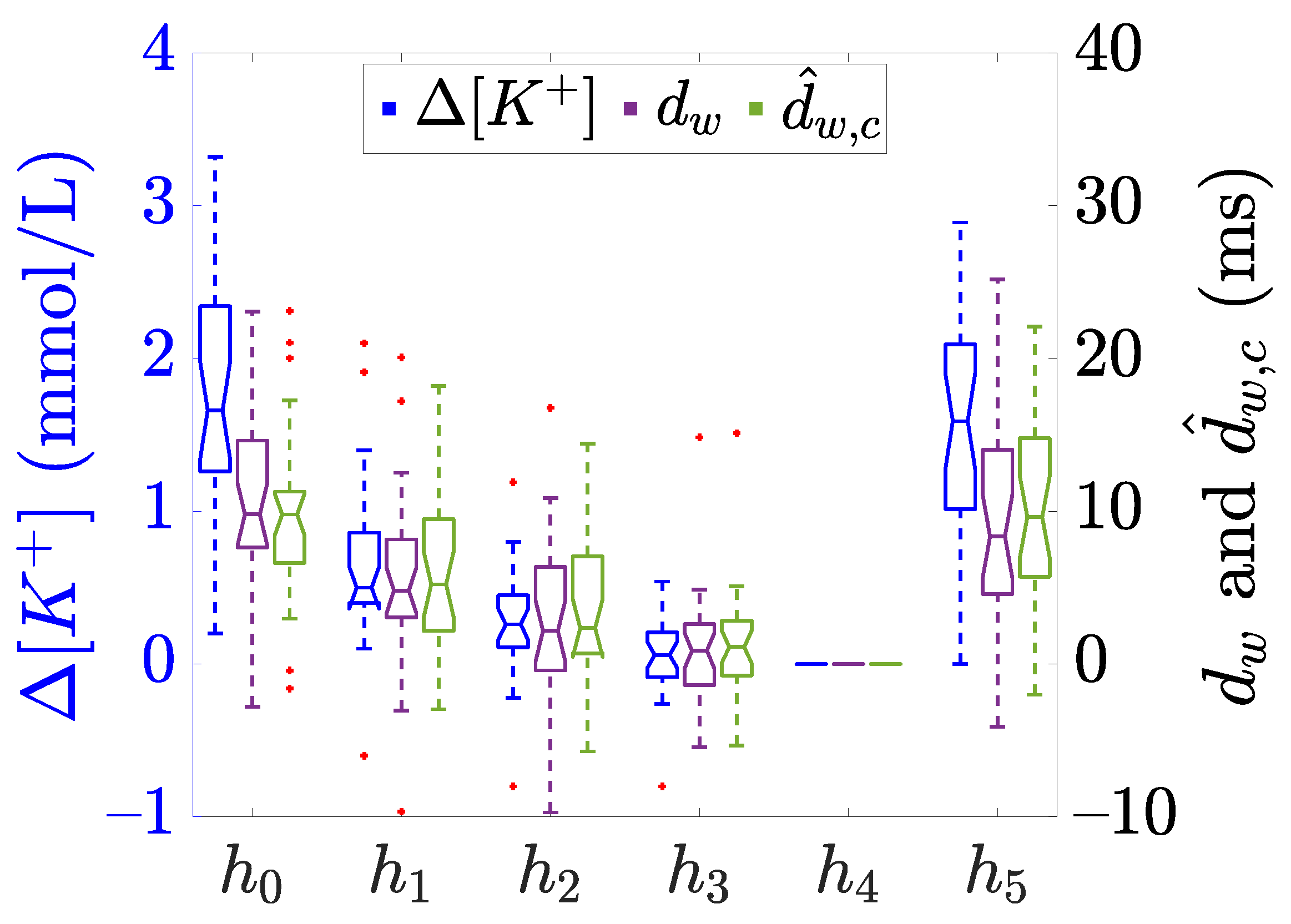
3.3. Warping-Based T-Wave Morphology Markers
3.4. Blood Potassium Concentration Variations
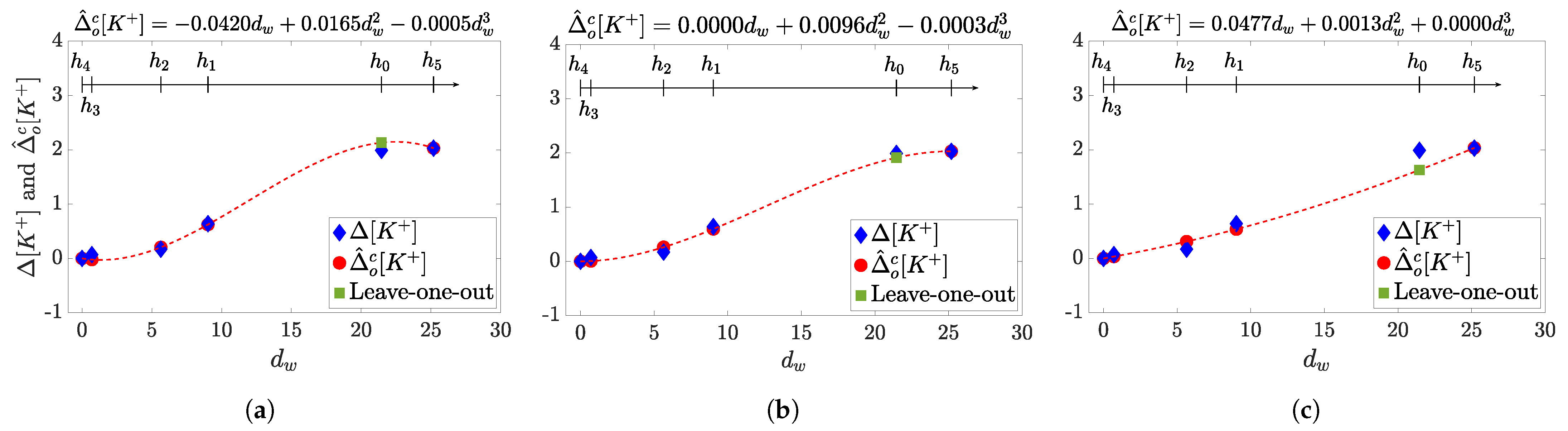
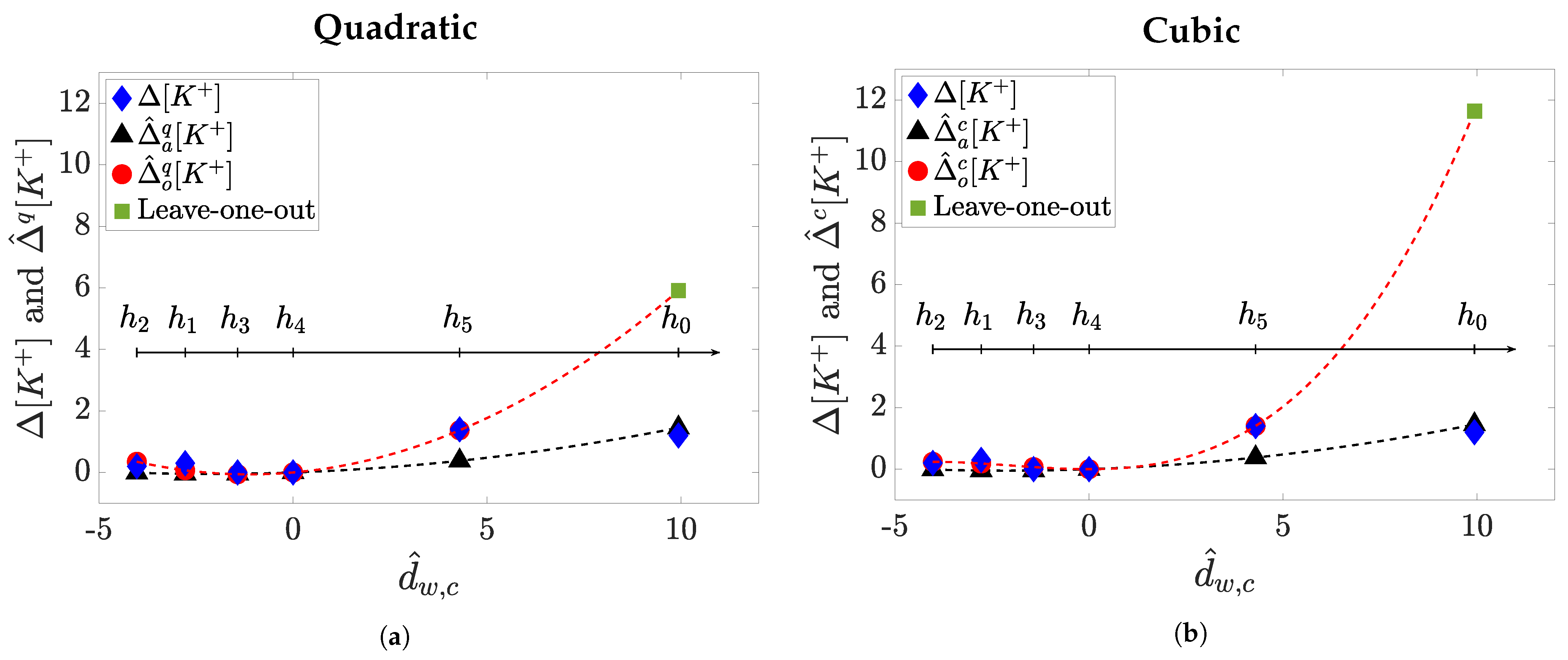
3.5. Marker Fitting Models for Estimation
3.6. Statistical Analysis
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Transformation matrix to perform Periodic Component Analysis | |
| Blood potassium concentration | |
| Blood potassium concentration variations | |
| ECG | Electrocardiogram |
| ESRD | End Stage Renal Disease |
| ESRD-HD patients | End Stage Renal Disease patients undergoing hemodialysis |
| HD | Hemodialysis |
| IQR | Interquartile range |
| MWTW | Mean Warped T-wave |
| PCA | Principal Component Analysis |
| CA | Periodic Component Analysis |
| Periodic Component Analysis evaluated over the T-wave | |
| Spearman’s correlation coefficient | |
| r | Pearson’s correlation coefficient |
References
- Segall, L.; Nistor, I.; Covic, A. Heart Failure in Patients with Chronic Kidney Disease: A Systematic Integrative Review. BioMed Res. Int. 2014, 2014. [Google Scholar] [CrossRef]
- Collins, A.J.; Foley, R.N.; Herzog, C.; Chavers, B.; Gilbertson, D.; Ishani, A.; Kasiske, B.; Liu, J.; Mau, L.-W.; McBean, M.; et al. US Renal Data System 2010 Annual Data Report. Am. J. Kidney Dis. 2011, 51 (Suppl. 1), e1–e526. [Google Scholar] [CrossRef] [PubMed]
- London, G.M. The Clinical Epidemiology of Cardiovascular Diseases in Chronic Kidney Disease: Cardiovascular Disease in Chronic Renal Failure: Pathophysiologic Aspects. Semin. Dial. 2003, 16, 85–94. [Google Scholar] [CrossRef]
- Johnson, D.W.; Craven, A.M.; Isbel, N.M. Modification of cardiovascular risk in hemodialysis patients: An evidence-based review. Hemodial. Int. 2007, 11, 1–14. [Google Scholar] [CrossRef]
- Perl, J.; Chan, C. Timing of sudden death relative to the hemodialysis procedure. Nat. Rev. Nephrol. 2006, 2, 668–669. [Google Scholar] [CrossRef] [PubMed]
- Turakhia, M.P.; Blankestijn, P.J.; Carrero, J.J.; Clase, C.M.; Deo, R.; Herzog, C.A.; Kasner, S.E.; Passman, R.S.; Pecoits-Filho, R.; Reinecke, H.; et al. Chronic kidney disease and arrhythmias: Conclusions from a kidney disease: Improving global outcomes (KDIGO) controversies conference. Eur. Heart J. 2018, 39, 2314–2325. [Google Scholar] [CrossRef] [PubMed]
- Gumz, M.L.; Rabinowitz, L.; Wingo, C. An Integrated View of Potassium Homeostasis. N. Engl. J. Med. 2015, 373, 60–72. [Google Scholar] [CrossRef] [PubMed]
- Welch, A.; Maroz, N.; Wingo, C.S. Hyperkalemia: Getting to the heart of the matter. Nephrol. Dial. Transplant. 2013, 28, 15–16. [Google Scholar] [CrossRef][Green Version]
- Van Mieghem, C.; Sabbe, M.; Knockaert, D. The clinical value of the ECG in noncardiac conditions. Chest 2004, 125, 1561–1576. [Google Scholar] [CrossRef]
- Bleyer, A.J.; Hartman, J.; Brannon, P.C.; Reeves-Daniel, A.; Satko, S.G.; Russell, G. Charact. Sudd. Death Hemodial. Patients. Kidney Int. 2006, 69, 2268–2273. [Google Scholar] [CrossRef] [PubMed]
- Levis, J.T. ECG Diagnosis: Hypokalemia. Perm. J. 2012, 16, 57. [Google Scholar] [CrossRef] [PubMed]
- Diercks, D.B.; Shumaik, G.M.; Harrigan, R.A.; Brady, W.J.; Chan, T.C. Electrocardiogr. Manifestations: Electrolyte Abnorm. J. Emerg. Med. 2004, 27, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Severi, S.; Grandi, E.; Pes, C.; Badiali, F.; Grandi, F.; Santoro, A. Calcium Potassium Chang. Haemodial. Alter Ventricular Repolarization Duration: Vivo Silico Analysis. Nephrol. Dial. Transplant. 2008, 23, 1378–1386. [Google Scholar] [CrossRef] [PubMed]
- Severi, S.; Vecchietti, S.; Cavalcanti, S.; Mancini, E.; Santoro, A. Electrocardiogr. Chang. Hemodiafiltration Differ. Potassium Remov. Rates. Blood Purif. 2003, 21, 381–388. [Google Scholar] [CrossRef]
- Frohnert, P.P.; Giuliani, E.R.; Friedberg, M.; Johnson, W.J.; Tauxe, W.N. Statistical investigation of correlations between serum potassium levels and electrocardiographic findings in patients on intermittent hemodialysis therapy. Circulation 1970, 41, 667–676. [Google Scholar] [CrossRef]
- Corsi, C.; Cortesi, M.; Callisesi, G.; De Bie, J.; Napolitano, C.; Santoro, A.; Mortara, D.; Severi, S. Noninvasive Quantif. Blood Potassium Conc. ECG Hemodial. Patients. Sci. Rep. 2017, 7, 42492. [Google Scholar] [CrossRef]
- Krogager, M.L.; Kragholm, K.; Skals, R.K.; Mortensen, R.N.; Polcwiartek, C.; Graff, C.; Nielsen, J.B.; Kanters, J.K.; Holst, A.G.; Søgaard, P.; et al. Relatsh. Serum Potassium Conc. Electrocardiogr. Charact. 163,547 Individ. Prim. Care. J. Electrocardiol. 2019, 57, 104–111. [Google Scholar] [CrossRef]
- Palmieri, F.; Gomis, P.; Ferreira, D.; Ruiz, J.E.; Bergasa, B.; Martín-Yebra, A.; Bukhari, H.A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; et al. T-Wave Morphol. Chang. Surrog. Blood Potassium Conc. Hemodial. Patients. 2019 Comput. Cardiol. (CinC) 2019, 46. [Google Scholar] [CrossRef]
- Bukhari, H.A.; Palmieri, F.; Ferreira, D.; Potse, M.; Ramírez, J.; Laguna, P.; Sánchez, C.; Pueyo, E. Transmural Ventricular Heterog. Play A Major Role Determ. T-Wave Morphol. Differ. Extracell. Potassium Levels. 2019 Comput. Cardiol. (CinC) 2019, 46. [Google Scholar] [CrossRef]
- Palmieri, F.; Gomis, P.; Ruiz, J.E.; Ferreira, D.; Martín-Yebra, A.; Pueyo, E.; Laguna, P.; Martínez, J.P.; Ramírez, J. Potassium Monit. Multilead T-Wave Morphol. Chang. Hemodyalisis: Period. Versus Princ. Compon. Analysis. 2020 Comput. Cardiol. (CinC) 2020, 47. [Google Scholar] [CrossRef]
- Palmieri, F.; Gomis, P.; Ferreira, D.; Ruiz, J.E.; Bergasa, B.; Martín-Yebra, A.; Bukhari, H.A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; et al. Monitoring Blood Potassium Concentration in Hemodialysis Patients by Quantifying T-waveMorphology Dynamics. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Bukhari, H.; Palmieri, F.; Ramírez, J.; Laguna, P.; Ruiz, J.E.; Ferreira, D.; Potse, M.; Sanchez, C.; Pueyo, E. Characterization of T Wave Amplitude, Duration and Morphology Changes During Hemodialysis: Relationship with Serum Electrolyte Levels and Heart Rate. IEEE Trans. Biomed. Eng. 2020. [Google Scholar] [CrossRef]
- Ramírez, J.; Orini, M.; Tucker, J.D.; Pueyo, E.; Laguna, P. Variability of Ventricular Repolarization Dispers. Quantified Time-Warping Morphol. T-Wave. IEEE Trans. Biomed. Eng. 2017, 64, 1619–1630. [Google Scholar] [CrossRef]
- Monasterio, V.; Clifford, G.D.; Laguna, P.; Martínez, J.P. A Multilead Scheme Based Period. Compon. Anal. T-Wave Alternans Anal. ECG. Ann. Biomed. Eng. 2010, 38, 2532–2541. [Google Scholar] [CrossRef]
- Sörnmo, L.; Laguna, P. Electrocardiogram (ECG) Signal Processing. In Wiley Encyclopedia of Biomedical Engineering; Akay, M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 1298–1313. ISBN 0-471-24967-X (CL). [Google Scholar] [CrossRef]
- Martínez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A Wavelet-Based ECG Delin. Eval. Stand. Databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef] [PubMed]
- Sameni, R.; Jutten, C.; Shamsollahi, M.B. Multichannel electrocardiogram decomposition using periodic component analysis. IEEE Trans. Biomed. Eng. 2008, 55, 1935–1940. [Google Scholar] [CrossRef] [PubMed]
- Liamis, G.; Liberopoulos, E.; Barkas, F.; Elisaf, M. Diabetes Mellit. Electrolyte Disorders. World J. Clin. Cases 2014, 2, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, M.R.; Reza Jabbari, R.; Glinge, C.; Stampe, N.K.; Butt, J.H.; Blanche, P.; Lønborg, J.; Nielsen, O.W.; Køber, L.; Torp-Pedersen, C.; et al. Potassium Disturbances Risk Ventricular Fibrillation Patients ST-Segment—Elevation Myocard. Infarction. JAHA 2020, 4, 488–496. [Google Scholar] [CrossRef]
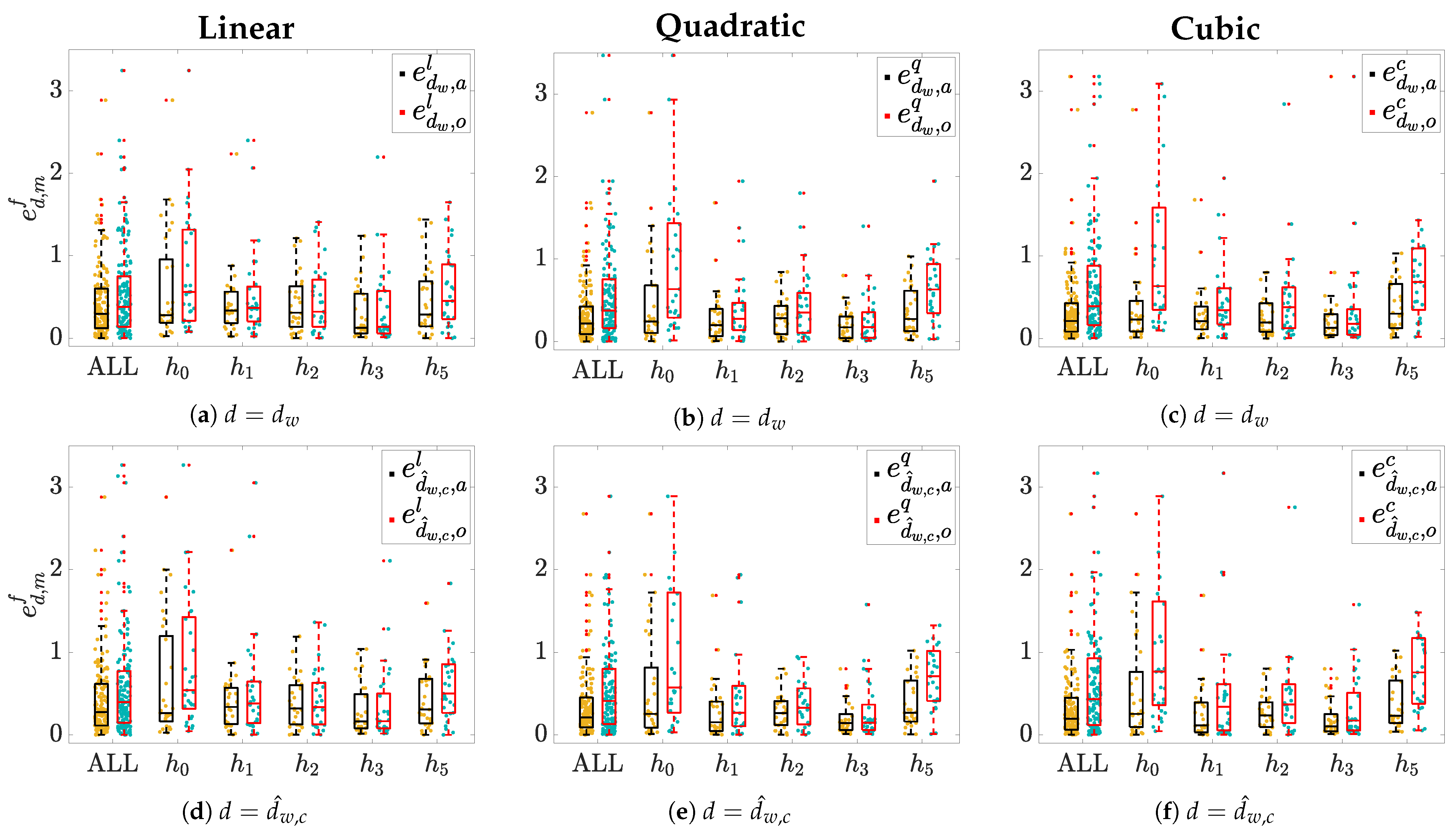
| d | f | m | r | ||||
|---|---|---|---|---|---|---|---|
| ALL | |||||||
| l | a | 0.83 (0.33) | 0.86 (0.35) | 0.30 (0.48) | 0.28 (0.77) | 0.29 (0.55) | |
| o | 0.77 (0.48) | 0.76 (0.47) | 0.38 (0.61) | 0.56 (1.10) | 0.45 (0.66) | ||
| q | a | 0.83 (0.36) | 0.91 (0.29) | 0.22 (0.34) | 0.24 (0.58) | 0.27 (0.49) | |
| o | 0.83 (0.49) | 0.77 (0.51) | 0.38 (0.59) | 0.64 (1.15) | 0.63 (0.60) | ||
| c | a | 0.89 (0.35) | 0.92 (0.27) | 0.21 (0.34) | 0.23 (0.37) | 0.30 (0.54) | |
| o | 0.83 (0.49) | 0.79 (0.61) | 0.39 (0.72) | 0.64 (1.24) | 0.69 (0.75) | ||
| l | a | 0.83 (0.31) | 0.88 (0.34) | 0.27 (0.50) | 0.26 (1.03) | 0.31 (0.54) | |
| o | 0.80 (0.44) | 0.81 (0.34) | 0.40 (0.63) | 0.54 (1.11) | 0.50 (0.59) | ||
| q | a | 0.83 (0.35) | 0.90 (0.27) | 0.21 (0.36) | 0.25 (0.73) | 0.27 (0.50) | |
| o | 0.80 (0.53) | 0.77 (0.39) | 0.41 (0.67) | 0.57 (1.45) | 0.71 (0.61) | ||
| c | a | 0.83 (0.31) | 0.90 (0.25) | 0.20 (0.39) | 0.25 (0.67) | 0.23 (0.52) | |
| o | 0.80 (0.49) | 0.72 (0.45) | 0.43 (0.81) | 0.77 (1.25) | 0.76 (0.80) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmieri, F.; Gomis, P.; Ruiz, J.E.; Ferreira, D.; Martín-Yebra, A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; Laguna, P. Nonlinear T-Wave Time Warping-Based Sensing Model for Non-Invasive Personalised Blood Potassium Monitoring in Hemodialysis Patients: A Pilot Study. Sensors 2021, 21, 2710. https://doi.org/10.3390/s21082710
Palmieri F, Gomis P, Ruiz JE, Ferreira D, Martín-Yebra A, Pueyo E, Martínez JP, Ramírez J, Laguna P. Nonlinear T-Wave Time Warping-Based Sensing Model for Non-Invasive Personalised Blood Potassium Monitoring in Hemodialysis Patients: A Pilot Study. Sensors. 2021; 21(8):2710. https://doi.org/10.3390/s21082710
Chicago/Turabian StylePalmieri, Flavio, Pedro Gomis, José Esteban Ruiz, Dina Ferreira, Alba Martín-Yebra, Esther Pueyo, Juan Pablo Martínez, Julia Ramírez, and Pablo Laguna. 2021. "Nonlinear T-Wave Time Warping-Based Sensing Model for Non-Invasive Personalised Blood Potassium Monitoring in Hemodialysis Patients: A Pilot Study" Sensors 21, no. 8: 2710. https://doi.org/10.3390/s21082710
APA StylePalmieri, F., Gomis, P., Ruiz, J. E., Ferreira, D., Martín-Yebra, A., Pueyo, E., Martínez, J. P., Ramírez, J., & Laguna, P. (2021). Nonlinear T-Wave Time Warping-Based Sensing Model for Non-Invasive Personalised Blood Potassium Monitoring in Hemodialysis Patients: A Pilot Study. Sensors, 21(8), 2710. https://doi.org/10.3390/s21082710










