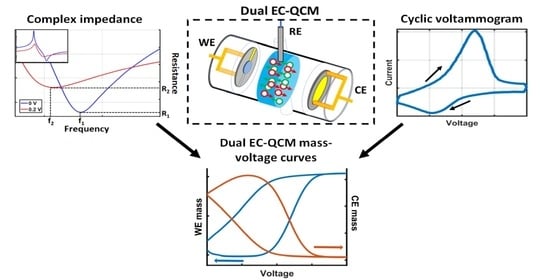
High-Sensitivity Dual Electrochemical QCM for Reliable Three-Electrode Measurements
Abstract
1. Introduction
2. Materials and Methods
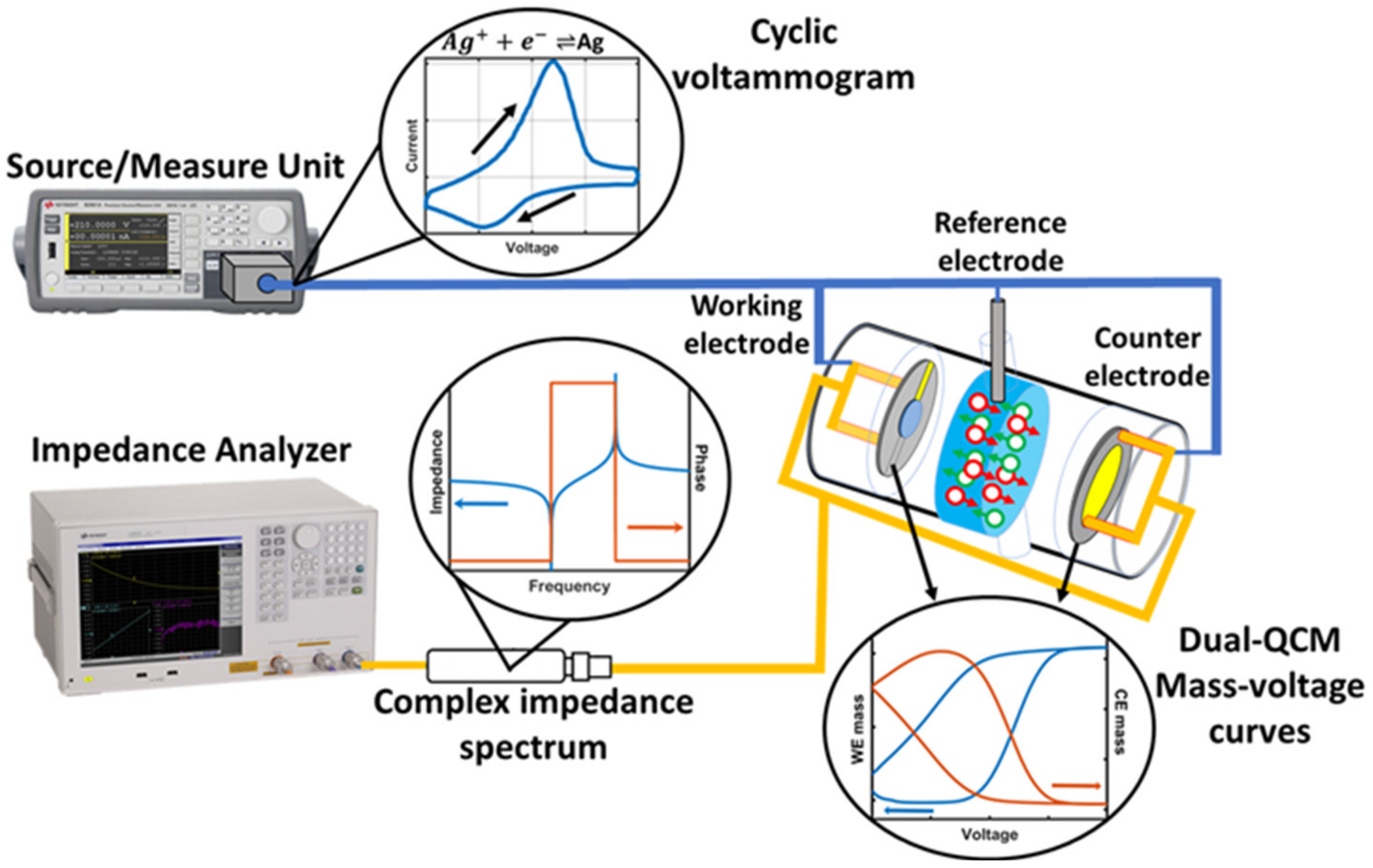
2.1. Dual EC-QCM Connection Scheme
2.2. Dual EC-QCM Cell
2.3. Electrochemical Test System
2.4. Dual EC-QCM Software Control
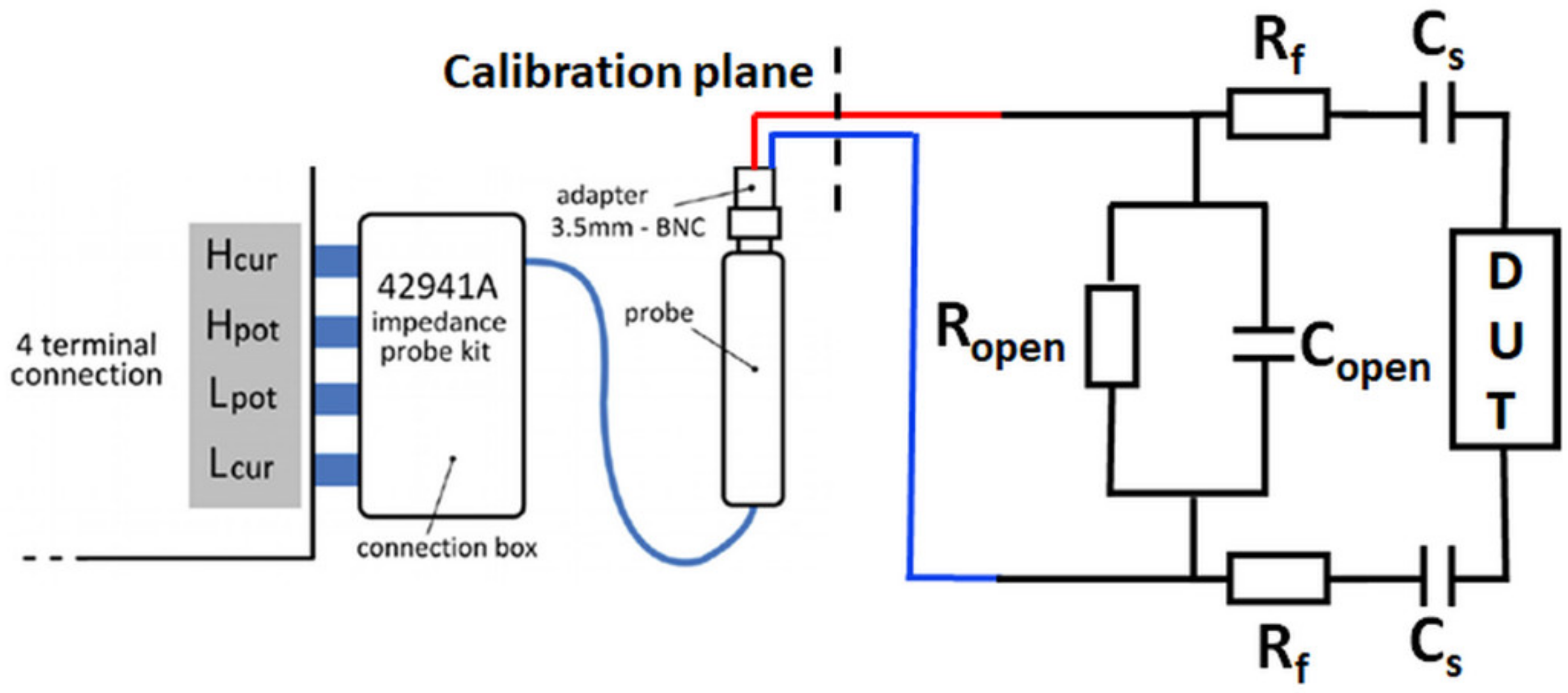
2.5. Complex Impedance Correction
2.6. Higher Harmonics
3. Results and Discussion
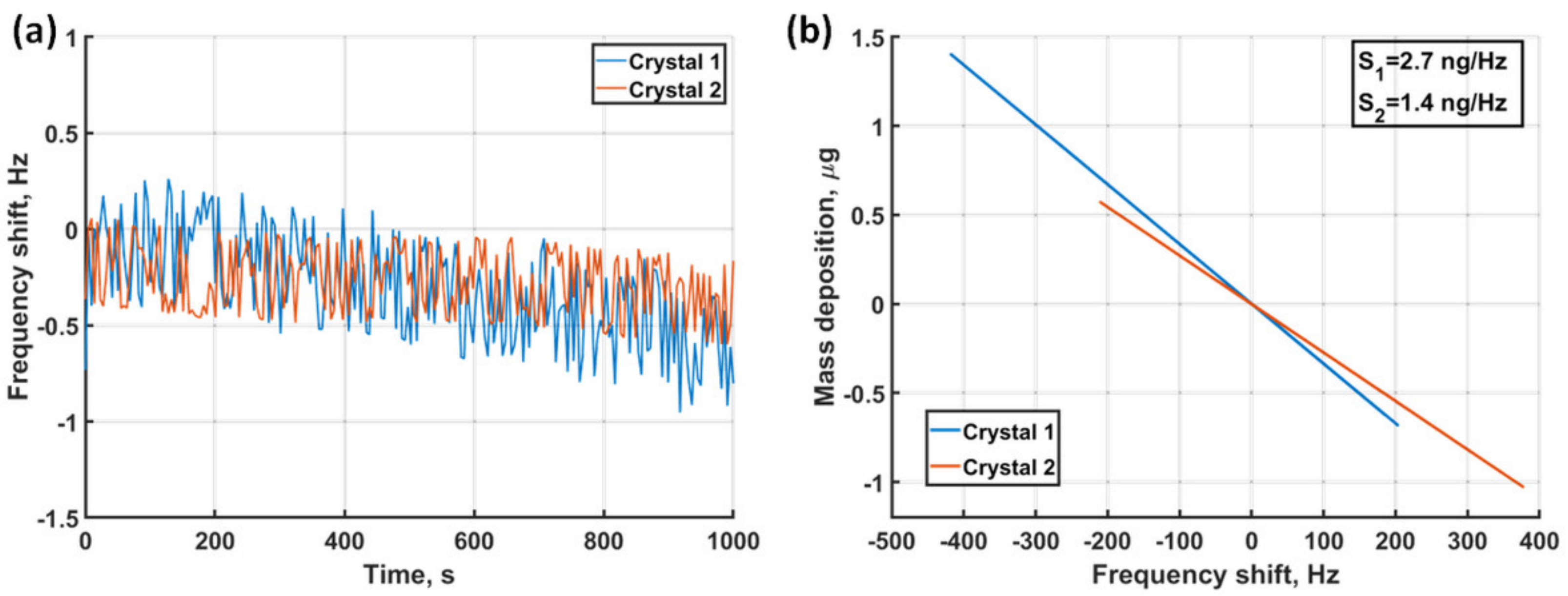
3.1. Dual EC-QCM Sensitivity and Stability
3.2. Electrochemical Characterization
3.3. Loading Separation for Accurate Mass Quantification
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Strasser, J.; De Jong, R.N.; Beurskens, F.J.; Schuurman, J.; Parren, P.W.H.I.; Hinterdorfer, P.; Preiner, J. Weak Fragment Crystallizable (Fc) Domain Interactions Drive the Dynamic Assembly of IgG Oligomers upon Antigen Recognition. ACS Nano 2020, 14, 2739–2750. [Google Scholar] [CrossRef] [PubMed]
- Malecha, K.T.; Cai, Z.; Nizkorodov, S.A. Photodegradation of Secondary Organic Aerosol Material Quantified with a Quartz Crystal Microbalance. Environ. Sci. Technol. Lett. 2018, 5, 366–371. [Google Scholar] [CrossRef]
- Lee, J.; Jang, J.; Akin, D.; Savran, C.A.; Bashir, R. Real-time detection of airborne viruses on a mass-sensitive device. Appl. Phys. Lett. 2008, 93, 4–6. [Google Scholar] [CrossRef]
- Dixon, M.C. Quartz crystal microbalance with dissipation monitoring: Enabling real-time characterization of biological materials and their interactions. J. Biomol. Tech. 2008, 19, 151–158. [Google Scholar] [PubMed]
- Lu, C.S.; Lewis, O. Investigation of film-thickness determination by oscillating quartz resonators with large mass load. J. Appl. Phys. 1972, 43, 4385–4390. [Google Scholar] [CrossRef]
- Cao-Paz, A.M.; Rodríguez-Pardo, L.; Fariña, J.; Marcos-Acevedo, J. Resolution in QCM sensors for the viscosity and density of liquids: Application to lead acid batteries. Sensors 2012, 12, 10604–10620. [Google Scholar] [CrossRef] [PubMed]
- Dargel, V.; Shpigel, N.; Sigalov, S.; Nayak, P.; Levi, M.D.; Daikhin, L.; Aurbach, D. In situ real-time gravimetric and viscoelastic probing of surface films formation on lithium batteries electrodes. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrey, G. Use of oscillating crystals for thin film characterization and for micro-range mass measurements. Zeitschrift Fuer Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Keiji Kanazawa, K.; Gordon, J.G. The oscillation frequency of a quartz resonator in contact with liquid. Anal. Chim. Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a Quartz Crystal Microbalance with Simultaneous Mass and Liquid Loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Deakin, M.R.; Buttry, D.A. Electrochemical applications of the quartz crystal microbalance. Anal. Chem. 1989, 61, 1147A–1154A. [Google Scholar] [CrossRef]
- Kasper, M.; Traxler, L.; Salopek, J.; Grabmayr, H.; Ebner, A.; Kienberger, F. Broadband 120 MHz impedance quartz crystal microbalance (QCM) with calibrated resistance and quantitative dissipation for biosensing measurements at higher harmonic frequencies. Biosensors 2016, 6, 23. [Google Scholar] [CrossRef] [PubMed]
- Arnau, A. A review of interface electronic systems for AT-cut quartz crystal microbalance applications in liquids. Sensors 2008, 8, 370–411. [Google Scholar] [CrossRef] [PubMed]
- Levi, M.D.; Shpigel, N.; Sigalov, S.; Dargel, V.; Daikhin, L.; Aurbach, D. In Situ Porous Structure Characterization of Electrodes for Energy Storage and Conversion by EQCM-D: A Review. Electrochim. Acta 2017, 232, 271–284. [Google Scholar] [CrossRef]
- Ogaki, K.; Itaya, K. In situ scanning tunneling microscopy of underpotential and bulk deposition of silver on gold (111). Electrochim. Acta 1995, 40, 1249–1257. [Google Scholar] [CrossRef]
- Bruckenstein, S.; Swathirajan, S. Potential dependence of lead and silver underpotential coverages in acetonitrile using a piezoelectric crystal oscillator method. Electrochim. Acta 1985, 30, 851–855. [Google Scholar] [CrossRef]
- Hachiya, T.; Itaya, K. In situ scanning tunneling microscopy of underpotential deposition in aqueous solution III. Silver adlayers on Au(111). Ultramicroscopy 1992, 42–44, 445–452. [Google Scholar] [CrossRef]
- Arnau, A.; Jiménez, Y.; Sogorb, T. Thickness-shear mode quartz crystal resonators in viscoelastic fluid media. J. Appl. Phys. 2000, 88, 4498–4506. [Google Scholar] [CrossRef]
- Keysight Technologies. Impedance Measurement Handbook A Guide to Measurement Technology and Techniques, 6th ed.; Keysight Technologies: Santa Clara, CA, USA, 2016. [Google Scholar]
- Tsionsky, V.; Daikhin, L.; Gileadi, E. Response of the Electrochemical Quartz Crystal Microbalance for Gold Electrodes in the Double-Layer Region. J. Electrochem. Soc. 1996, 143, 2240–2245. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tóth, D.; Kasper, M.; Alic, I.; Awadein, M.; Ebner, A.; Baney, D.; Gramse, G.; Kienberger, F. High-Sensitivity Dual Electrochemical QCM for Reliable Three-Electrode Measurements. Sensors 2021, 21, 2592. https://doi.org/10.3390/s21082592
Tóth D, Kasper M, Alic I, Awadein M, Ebner A, Baney D, Gramse G, Kienberger F. High-Sensitivity Dual Electrochemical QCM for Reliable Three-Electrode Measurements. Sensors. 2021; 21(8):2592. https://doi.org/10.3390/s21082592
Chicago/Turabian StyleTóth, Dávid, Manuel Kasper, Ivan Alic, Mohamed Awadein, Andreas Ebner, Doug Baney, Georg Gramse, and Ferry Kienberger. 2021. "High-Sensitivity Dual Electrochemical QCM for Reliable Three-Electrode Measurements" Sensors 21, no. 8: 2592. https://doi.org/10.3390/s21082592
APA StyleTóth, D., Kasper, M., Alic, I., Awadein, M., Ebner, A., Baney, D., Gramse, G., & Kienberger, F. (2021). High-Sensitivity Dual Electrochemical QCM for Reliable Three-Electrode Measurements. Sensors, 21(8), 2592. https://doi.org/10.3390/s21082592