Optimization of Imminent Labor Prediction Systems in Women with Threatened Preterm Labor Based on Electrohysterography
Abstract
1. Introduction
2. Materials and Methods
2.1. EHG Database and Characterization
2.2. Classifiers Design and Assessment
3. Results
3.1. Random Forest (RF)
3.2. Extreme Learning Machine (ELM)
3.3. K-Nearest Neighbors (KNN)
3.4. Comparison of Classifiers
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| RF Hyperparameters | ELM Hyperparameters | KNN Hyperparameters |
|---|---|---|
| Number of trees (100, 200, 500, and 750) | Number of neurons in the hidden layer (100, 500, 750, 1000, 2000, and 30,000); | Number of neighbors (1, 3, 5, and 7) |
| Maximum depth of these trees (6, 10, and unlimited) | Activation function (hyperbolic tangent and sigmoid). | Kernel used for weighting the distances (triangular, Biweight and Epanechnikov). |
| Cost of division based on the criterion of gain of information were optimized (0.001, 0.2, and 0.5) |
| Opt. Criterion | Inputs | Classifier | Number of Neurons | Activation Function |
|---|---|---|---|---|
| F1-score | EHGP10–P90 + Obs | ELMF1_1 | 500 | Sigmoid |
| EHGP50 + Obs | ELMF1_2 | 500 | Sigmoid | |
| EHGP10–P90 | ELMF1_3 | 500 | Sigmoid | |
| EHGP50 | ELMF1_4 | 500 | Sigmoid | |
| Sensitivity | EHGP10–P90 + Obs | ELMSEN_1 | 750 | Sigmoid |
| EHGP50 + Obs | ELMSEN_2 | 1000 | Sigmoid | |
| EHGP10–P90 | ELMSEN_3 | 750 | Sigmoid | |
| EHGP50 | ELMSEN_4 | 500 | Sigmoid |
| Opt. Criterion | Inputs | Classifier | Number of Neurons | Activation Function |
|---|---|---|---|---|
| F1-score | EHGP10–P90 + Obs | ELMF1_1 | 500 | Sigmoid |
| EHGP50 + Obs | ELMF1_2 | 500 | Sigmoid | |
| EHGP10–P90 | ELMF1_3 | 500 | Sigmoid | |
| EHGP50 | ELMF1_4 | 500 | Sigmoid | |
| Sensitivity | EHGP10–P90 + Obs | ELMSEN_1 | 750 | Sigmoid |
| EHGP50 + Obs | ELMSEN_2 | 1000 | Sigmoid | |
| EHGP10–P90 | ELMSEN_3 | 750 | Sigmoid | |
| EHGP50 | ELMSEN_4 | 500 | Sigmoid |
| Opt. Criterion | Inputs | Classifier | Number of Neighbors | Kernel |
|---|---|---|---|---|
| F1-score | EHGP10–P90 + Obs | KNNF1_1 | 2 | Triangular |
| EHGP50 + Obs | KNNF1_2 | 7 | Biweight | |
| EHGP10–P90 | KNNF1_3 | 2 | Triangular | |
| EHGP50 | KNNF1_4 | 7 | Biweight | |
| Sensitivity | EHGP10–P90 + Obs | KNNSEN_1 | 7 | Triangular |
| EHGP50 + Obs | KNNSEN_2 | 7 | Epanechnikov | |
| EHGP10–P90 | KNNSEN_3 | 5 | Triangular | |
| EHGP50 | KNNSEN_4 | 7 | Triangular |
References
- Behrman, R.E.; Butler, A.S. Preterm Birth: Causes, Consequences, and Prevention. Preterm Birth: Causes, Consequences, and Prevention; National Academies Press: Washington, DC, USA, 2007. [Google Scholar] [CrossRef]
- Levels and Trends in Child Mortality Report 2019. United Nations Children’s Fund; UN Inter-agency group for child mortality estimation.United Nations Children’s. Available online: https://www.unicef.org/media/79371/file/UN-IGME-child-mortality-report-2020.pdf.pdf (accessed on 1 April 2021).
- Howson, C.P.; Kinney, M.V.; McDougall, L.; Lawn, J.E.; Born Too Soon Preterm Birth Action Group. Born too soon: Preterm birth matters. Reprod. Health 2013, 10 (Suppl. 1), S1. [Google Scholar] [CrossRef] [PubMed]
- Godeluck, A.; Godeluck, A.; Gérardin, P.; Lenclume, V.; Mussard, C.; Robillard, P.Y.; Sampériz, S.; Benhammou, V.; Truffert, P.; Ancel, P.Y.; et al. Mortality and severe morbidity of very preterm infants: Comparison of two French cohort studies. BMC Pediatr. 2019, 19, 360. [Google Scholar] [CrossRef] [PubMed]
- Roberts, D.; Brown, J.; Medley, N.; Dalziel, S.R. Antenatal Corticosteroids for Accelerating Fetal Lung Maturation for Women at Risk of Preterm Birth. Cochrane Database of Systematic Reviews; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2017; Volume 2017. [Google Scholar] [CrossRef]
- Garfield, R.E.; Maner, W.L. Physiology and electrical activity of uterine contractions. Semin. Dev. Biol. 2007, 18, 289–295. [Google Scholar] [CrossRef] [PubMed]
- E Esplin, M.S.; Elovitz, M.A.; Iams, J.D.; Parker, C.B.; Wapner, R.J.; Grobman, W.A.; Simhan, H.N.; Wing, D.A.; Haas, D.M.; Silver, R.M.; et al. Predictive accuracy of serial transvaginal cervical lengths and quantitative vaginal fetal fibronectin levels for spontaneous preterm birth among nulliparous women. JAMA J. Am. Med. Assoc. 2017, 317, 1047–1056. [Google Scholar] [CrossRef] [PubMed]
- Berghella, V.; Hayes, E.; Visintine, J.; Baxter, J.K. Fetal Fibronectin Testing for Reducing the Risk of Preterm Birth. Cochrane Database of Systematic Reviews; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Lucovnik, M.; Chambliss, L.R.; Garfield, R.E. Costs of unnecessary admissions and treatments for ‘threatened preterm labor’. Am. J. Obstet. Gynecol. 2013, 209, 217.e1–217.e3. [Google Scholar] [CrossRef]
- Grover, C.M.; Posner, S.; Kupperman, M.; Washington, E.A. Term delivery after hospitalization for preterm labor: Incidence and costs in california. Prim. Care Update Ob Gyns 1998, 5, 178. [Google Scholar] [CrossRef]
- Most, O.; Langer, O.; Kerner, R.; Ben David, G.; Calderon, I. Can myometrial electrical activity identify patients in preterm labor? Am. J. Obstet. Gynecol. 2008, 199, 378. [Google Scholar] [CrossRef]
- Maner, W.L.; Garfield, R.E. Identification of human term and preterm labor using artificial neural networks on uterine electromyography data. Ann. Biomed. Eng. 2007, 35, 465–473. [Google Scholar] [CrossRef]
- Devedeux, D.; Marque, C.; Mansour, S.; Germain, G.; Duchêne, J. Uterine electromyography: A critical review. Am. J. Obstet. Gynecol. 1993, 169, 1636–1653. [Google Scholar] [CrossRef]
- Chkeir, A.; Fleury, M.J.; Karlsson, B.; Hassan, M.; Marque, C. Patterns of electrical activity synchronization in the pregnant rat uterus. BioMedicine 2013, 3, 140–144. [Google Scholar] [CrossRef]
- Mas-Cabo, J.; Ye-Lin, Y.; Garcia-Casado, J.; Alberola-Rubio, J.; Perales, A.; Prats-Boluda, G. Uterine contractile efficiency indexes for labor prediction: A bivariate approach from multichannel electrohysterographic records. Biomed. Signal Process. Control 2018, 46, 238–248. [Google Scholar] [CrossRef]
- Vinken, M.P.G.C.; Rabotti, C.; Mischi, M.; Oei, S.G. Accuracy of frequency-related parameters of the electrohysterogram for predicting preterm delivery: A review of the literature. Obs. Gynecol. Surv. 2009, 64, 529–541. [Google Scholar] [CrossRef]
- Horoba, K.; Jezewski, J.; Matonia, A.; Wrobel, J.; Czabanski, R.; Jezewski, M. Early predicting a risk of preterm labour by analysis of antepartum electrohysterographic signals. Biocybern. Biomed. Eng. 2016, 36, 574–583. [Google Scholar] [CrossRef]
- Mischi, M.; Chen, C.; Ignatenko, T.; de Lau, H.; Ding, B.; Oei, S.G.G.; Rabotti, C. Dedicated Entropy Measures for Early Assessment of Pregnancy Progression From Single-Channel Electrohysterography. IEEE Trans. Biomed. Eng. 2018, 65, 875–884. [Google Scholar] [CrossRef]
- Fele-Zorz, G.; Kavsek, G.; Novak-Antolic, Z.; Jager, F.; Fele-Žorž, G.; Kavšek, G.; Novak-Antolič, Ž.; Jager, F.; Fele-Zorz, G.; Kavsek, G.; et al. A comparison of various linear and non-linear signal processing techniques to separate uterine EMG records of term and pre-term delivery groups. Med. Biol. Eng. Comput. 2008, 46, 911–922. [Google Scholar] [CrossRef]
- Mas-Cabo, J.; Ye-Lin, Y.; Garcia-Casado, J.; Díaz-Martinez, A.; Perales-Marin, A.; Monfort-Ortiz, R.; Roca-Prats, A.; López-Corral, Á.; Prats-Boluda, G.; Diaz-Martinez, A.; et al. Robust Characterization of the Uterine Myoelectrical Activity in Different Obstetric Scenarios. Entropy 2020, 22, 743. [Google Scholar] [CrossRef]
- Fergus, P.; Idowu, I.; Hussain, A.; Dobbins, C. Advanced artificial neural network classification for detecting preterm births using EHG records. Neurocomputing 2016, 188, 42–49. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sudarshan, V.K.; Rong, S.Q.; Tan, Z.; Lim, C.M.; Koh, J.E.; Nayak, S.; Bhandary, S.V.; Qing, S.; Tan, Z.; et al. Automated detection of premature delivery using empirical mode and wavelet packet decomposition techniques with uterine electromyogram signals. Comput. Biol. Med. 2017, 85, 33–42. [Google Scholar] [CrossRef]
- Borowska, M.; Brzozowska, E.; Kuć, P.; Oczeretko, E.; Mosdorf, R.; Laudański, P. Identification of preterm birth based on RQA analysis of electrohysterograms. Comput. Methods Programs Biomed. 2018, 153, 227–236. [Google Scholar] [CrossRef]
- Degbedzui, D.K.; Yüksel, M.E. Accurate diagnosis of term–preterm births by spectral analysis of electrohysterography signals. Comput. Biol. Med. 2020, 119, 1–8. [Google Scholar] [CrossRef]
- Mas-Cabo, J.; Prats-Boluda, G.; Perales, A.; Garcia-Casado, J.; Alberola-Rubio, J.; Ye-Lin, Y. Uterine electromyography for discrimination of labor imminence in women with threatened preterm labor under tocolytic treatment. Med. Biol. Eng. Comput. 2019, 57, 401–411. [Google Scholar] [CrossRef] [PubMed]
- Mas-Cabo, J.; Prats-Boluda, G.; Ye-Lin, Y.; Alberola-Rubio, J.; Perales, A.; Garcia-Casado, J. Characterization of the effects of Atosiban on uterine electromyograms recorded in women with threatened preterm labor. Biomed. Signal Process. Control 2019, 52, 198–205. [Google Scholar] [CrossRef]
- Mas-Cabo, J.; Prats-Boluda, G.; Garcia-Casado, J.; Alberola-Rubio, J.; Monfort-Ortiz, R.; Martinez-Saez, C.; Perales, A.; Ye-Lin, Y. Electrohysterogram for ann-based prediction of imminent labor in women with threatened preterm labor undergoing tocolytic therapy. Sensors 2020, 20, 2681. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Hao, Y. Feature Extraction and Classification of EHG between Pregnancy and Labour Group Using Hilbert-Huang Transform and Extreme Learning Machine. Comput. Math. Methods Med. 2017, 1–9. [Google Scholar] [CrossRef]
- Peng, J.; Hao, D.; Yang, L.; Du, M.; Song, X.; Jiang, H.; Zhang, Y.; Zheng, D. Evaluation of electrohysterogram measured from different gestational weeks for recognizing preterm delivery: A preliminary study using random Forest. Biocybern. Biomed. Eng. 2020, 40, 352–362. [Google Scholar] [CrossRef]
- Chen, L.; Hao, Y.; Hu, X. Detection of preterm birth in electrohysterogram signals based on wavelet transform and stacked sparse autoencoder. PLoS ONE 2019, 14, 1–16. [Google Scholar] [CrossRef]
- Ren, P.; Yao, S.; Li, J.; Valdes-Sosa, P.A.; Kendrick, K.M. Improved Prediction of Preterm Delivery Using Empirical Mode Decomposition Analysis of Uterine Electromyography Signals. PLoS ONE 2015, 10, 1–16. [Google Scholar] [CrossRef]
- Mas-Cabo, J.; Prats-Boluda, G.; Garcia-Casado, J.; Alberola Rubio, J.; Perales Marín, A.J.; Ye Lin, Y. Design and Assessment of a Robust and Generalizable ANN-Based Classifier for the Prediction of Premature Birth by means of Multichannel Electrohysterographic Records. J. Sens. 2019, 1–13. [Google Scholar] [CrossRef]
- Terrien, J.; Marque, C.; Karlsson, B. Spectral characterization of human EHG frequency components based on the extraction and reconstruction of the ridges in the scalogram. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007, 2007, 1872–1875. [Google Scholar]
- Alamedine, D.; Diab, A.; Muszynski, C.; Karlsson, B.; Khalil, M.; Marque, C. Selection algorithm for parameters to characterize uterine EHG signals for the detection of preterm labor. Signal Image Video Process. 2014, 8, 1169–1178. [Google Scholar] [CrossRef]
- Lemancewicz, A.; Borowska, M.; Kuć, P.; Jasińska, E.; Laudański, P.; Laudański, T.; Oczeretko, E.; Kuc, P.; Jasinska, E.; Laudanski, P.; et al. Early diagnosis of threatened premature labor by electrohysterographic recordings—The use of digital signal processing. Biocybern. Biomed. Eng. 2016, 36, 302–307. [Google Scholar] [CrossRef]
- Vrhovec, J.; Macek-Lebar, A.; Rudel, D. Evaluating Uterine Electrohysterogram with Entropy. In 11th Mediterranean Conference on Medical and Biomedical Engineering and Computing; Springer: Berlin/Heidelberg, Germany, 2007; Volume 16, pp. 144–147. [Google Scholar]
- Ahmed, M.U.; Chanwimalueang, T.; Thayyil, S.; Mandic, D.P. A multi variate multiscale fuzzy entropy algorithm with application to uterine EMG complexity analysis. Entropy 2017, 19, 1–18. [Google Scholar]
- Zhang, X.S.X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans. Biomed. Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef]
- Moslem, B.; Hassan, M.; Khalil, M.; Marque, C.; Diab, M.O. Monitoring the progress of pregnancy and detecting labor using uterine electromyography. In Proceedings of the 2009 International Symposium On Bioelectronics; Bioinformatics; RMIT University: Melbourne, Australia, 2009; pp. 160–163. [Google Scholar]
- Diab, A.; Hassan, M.; Marque, C.; Karlsson, B. Performance analysis of four nonlinearity analysis methods using a model with variable complexity and application to uterine EMG signals. Med. Eng. Phys. 2014, 36, 761–767. [Google Scholar] [CrossRef]
- Karmakar, C.K.; Khandoker, A.H.; Gubbi, J.; Palaniswami, M. Complex correlation measure: A novel descriptor for Poincaré plot. Biomed. Eng. Online 2009, 8, 1–12. [Google Scholar] [CrossRef]
- Roy, B.; Ghatak, S. Nonlinear Methods to Assess Changes in Heart Rate Variability in Type 2 Diabetic Patients. Arq. Bras. Cardiol. 2013, 10, 317–327. [Google Scholar] [CrossRef]
- Naeem, S.M.; Seddik, A.F.; Eldosoky, M.A. New technique based on uterine electromyography nonlinearity for preterm delivery detection New technique based on uterine electromyography nonlinearity for preterm delivery detection. J. Eng. Technol. Res. 2014, 6, 107–114. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Smrdel, A.; Jager, F. Separating sets of term and pre-term uterine EMG records. Physiol. Meas. 2015, 36, 341–355. [Google Scholar] [CrossRef]
- Naeem, S.M.; Ali, A.F.; Eldosok Mohamed, M.A. Comparison between Using Linear and Non-linear Features to classify Uterine Electromyography Signals of Term and Preterm Deliveries. In Proceedings of the National Radio Science Conference, NRSC, Cairo, Egypt, 16–18 April 2013; pp. 1–11. [Google Scholar]
- Bekkar, M.; Akrouf Alitouche, T. Imbalanced Data Learning Approaches Review. Int. J. Data Min. Knowl. Manag. Process. 2013, 3, 15–33. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. Ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Hechenbichler, K.; Schliep, K. Weighted k-Nearest-Neighbor Techniques and Ordinal Classification Projektpartner Weighted k-Nearest-Neighbor Techniques and Ordinal Classification; 2004 Discussion Paper 399, SFB 386; Ludwig-Maximilians-Universität München: München, Germany, 2004. [Google Scholar] [CrossRef]
- Flach, P.A.; Kull, M. Precision-Recall-Gain Curves: PR Analysis Done Right. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Alamedine, D.; Khalil, M.; Marque, C. Comparison of different EHG feature selection methods for the detection of preterm labor. Comput. Med. 2013, 2013, 1–9. [Google Scholar] [CrossRef]
- Esteves, G.; Mendes-Moreira, J. Churn perdiction in the telecom business. In Proceedings of the 11th International Conference on Digital Information Management, ICDIM 2016, Porto, Portugal, 19–21 September 2016; pp. 254–259. [Google Scholar]
- Kayabasi, A.; Yildiz, B.; Aslan, M.F.; Durdu, A. Comparison of ELM and ANN on EMG Signals Obtained for Control of Robotic-Hand. In Proceedings of the 10th International Conference on Electronics, Computers and Artificial Intelligence, ECAI 2018, Iasi, Romania, 28–30 June 2018; pp. 1–5. [Google Scholar]
- Fergus, P.; Cheung, P.; Hussain, A.; Al-Jumeily, D.; Dobbins, C.; Iram, S. Prediction of preterm deliveries from EHG signals using machine learning. PLoS ONE 2013, 8, e77154. [Google Scholar] [CrossRef]
- Mohamed Bedeeuzzaman, A.S. Preterm Birth Prediction Using EHG Signals. Int. J. Sci. Res. Eng. Trends 2019, 5, 2395–2566. [Google Scholar]
- Idowu, I.O.; Fergus, P.; Hussain, A.; Dobbins, C.; Khalaf, M.; Casana Eslava, R.V.; Keight, R. Artificial Intelligence for Detecting Preterm Uterine Activity in Gynacology and Obstertric Care. In Proceedings of the 2015 IEEE International Conference on Computer and Information Technology; Ubiquitous Computing and Communications; Dependable, Autonomic and Secure Computing; Pervasive Intelligence and Computing, Liverpool, UK, 26–28 October 2015; pp. 215–220. [Google Scholar] [CrossRef]
- You, J.; Kim, Y.; Seok, W.; Lee, S.; Sim, D.; Suk, K.P.; Park, C. Multivariate Time–Frequency Analysis of Electrohysterogram for Classification of Term and Preterm Labor. J. Electr. Eng. Technol. 2019, 14, 897–916. [Google Scholar] [CrossRef]
- Murthy, H.S.N.; Meenakshi, D.M. ANN, SVM and KNN Classifiers for Prognosis of Cardiac Ischemia—A Comparison. Bonfring Int. J. Res. Commun. Eng. 2015, 5, 7–11. [Google Scholar] [CrossRef]
- Aditya, S.; Tibarewala, D.N. Comparing ANN, LDA, QDA, KNN and SVM algorithms in classifying relaxed and stressful mental state from two-channel prefrontal EEG data. Int. J. Artif. Intell. Soft Comput. 2012, 3, 143. [Google Scholar] [CrossRef]
- Pandey, M.; Chauhan, M.; Awasthi, S. Interplay of cytokines in preterm birth. Indian J. Med. Res. 2017, 146, 316–327. [Google Scholar]
- Van Zijl, M.D.; Koullali, B.; Mol, B.W.J.; Pajkrt, E.; Oudijk, M.A. Prevention of preterm delivery: Current challenges and future prospects. Int. J. Womens Health 2016, 8, 633–645. [Google Scholar] [CrossRef] [PubMed]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015, 198363. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.C.; Dewi, C.; Huang, S.W.; Caraka, R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data 2020, 7, 1–26. [Google Scholar] [CrossRef]
- Rostami, M.; Forouzandeh, S.; Berahmand, K.; Soltani, M. Integration of multi-objective PSO based feature selection and node centrality for medical datasets. Genomics 2020, 112, 4370–4384. [Google Scholar] [CrossRef]
- Ye-Lin, Y.; Garcia-Casado, J.; Prats-Boluda, G.; Alberola-Rubio, J.; Perales, A. Automatic Identification of Motion Artifacts in EHG Recording for Robust Analysis of Uterine Contractions. Comput. Math. Methods Med. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Happillon, T.; Muszynski, C.; Zhang, F.; Marque, C.; Istrate, D. Detection of Movement Artefacts and Contraction Bursts Using Accelerometer and Electrohysterograms for Home Monitoring of Pregnancy. IRBM 2018, 39, 379–385. [Google Scholar] [CrossRef]
- Hao, D.; Peng, J.; Wang, Y.; Liu, J.; Zhou, X.; Zheng, D. Evaluation of convolutional neural network for recognizing uterine contractions with electrohysterogram. Comput. Biol. Med. 2019, 113, 1–8. [Google Scholar] [CrossRef]
- Muszynski, C.; Happillon, T.; Azudin, K.; Tylcz, J.-B.; Istrate, D.; Marque, C. Automated electrohysterographic detection of uterine contractions for monitoring of pregnancy: Feasibility and prospects. BMC Pregnancy Childbirth 2018, 18, 1–8. [Google Scholar] [CrossRef]

 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters.
50th percentile of EHG parameters.
 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters.
50th percentile of EHG parameters.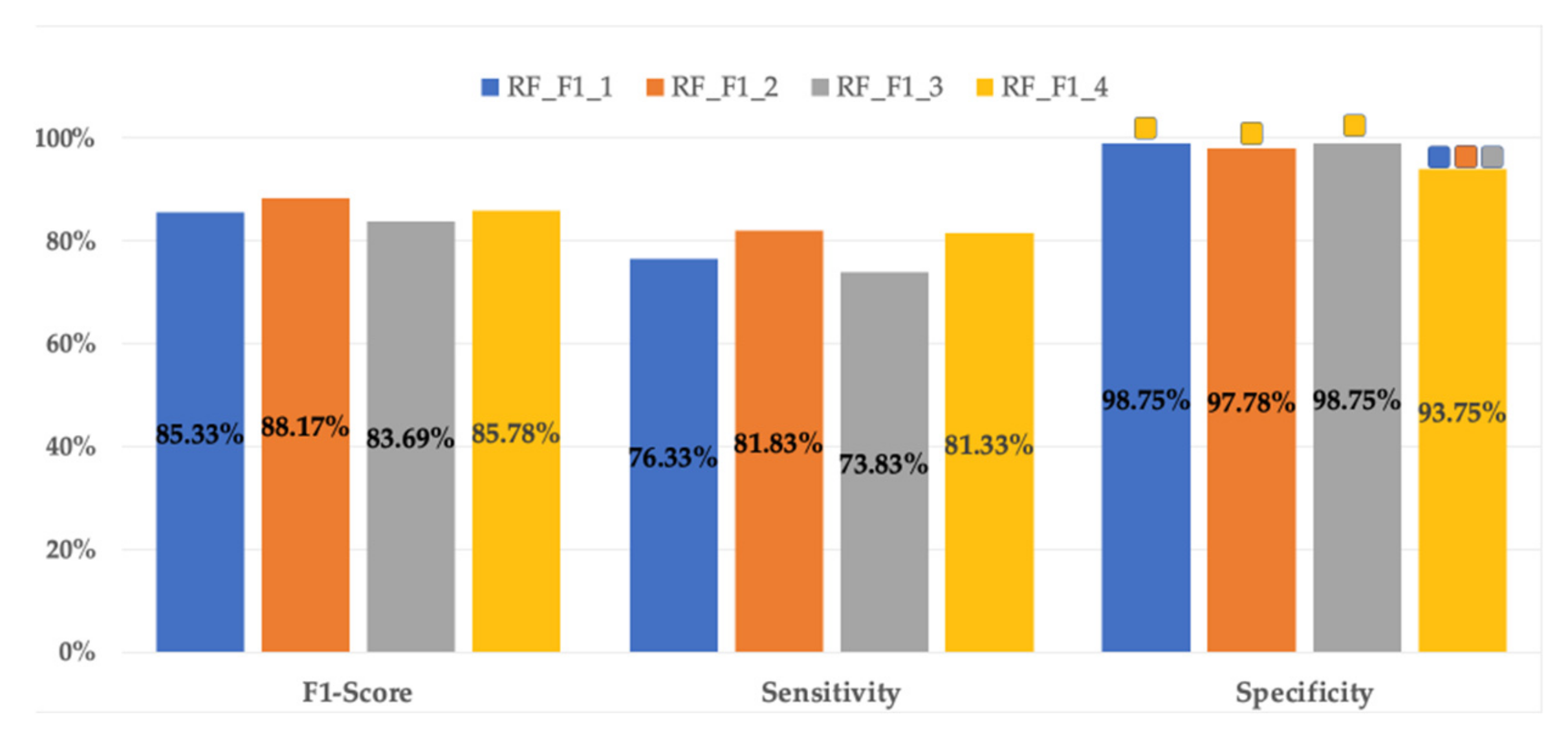
 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input data set are marked with *.
50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input data set are marked with *.
 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input data set are marked with *.
50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input data set are marked with *.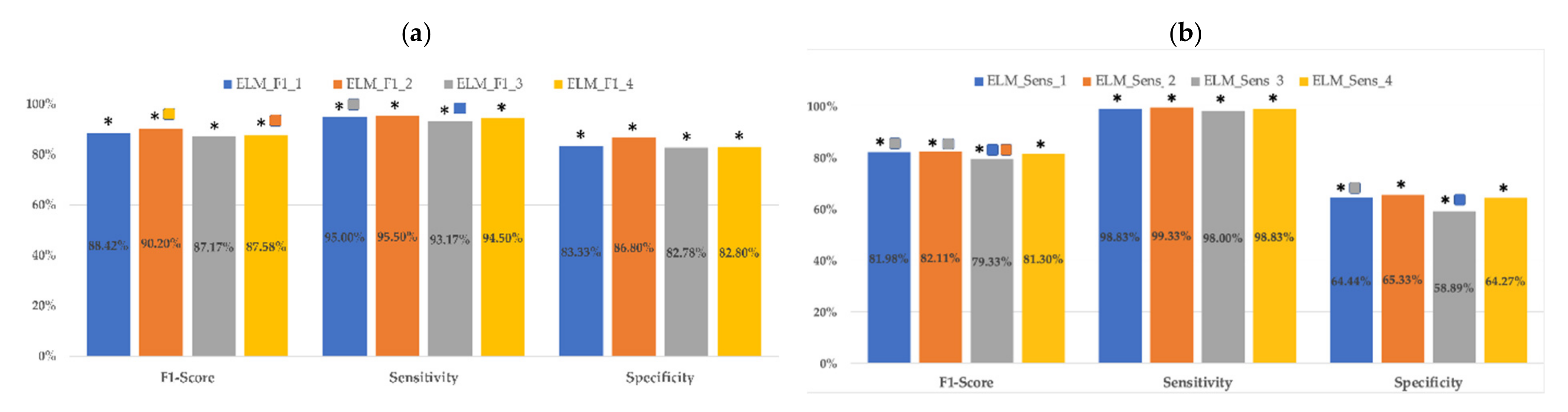
 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input dataset are marked with *.
50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input dataset are marked with *.
 10th–90th percentiles of EHG parameters + obstetric input data;
10th–90th percentiles of EHG parameters + obstetric input data;  50th percentile of EHG + obstetric input data;
50th percentile of EHG + obstetric input data;  10th–90th percentiles of EHG parameters;
10th–90th percentiles of EHG parameters;  50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input dataset are marked with *.
50th percentile of EHG parameters. Significant differences between the two optimization criteria for the same input dataset are marked with *.
 RFF1_2;
RFF1_2;  ELMF1_2;
ELMF1_2;  KNNF1_2.
KNNF1_2.
 RFF1_2;
RFF1_2;  ELMF1_2;
ELMF1_2;  KNNF1_2.
KNNF1_2.
| EHG Temporal Parameters | EHG Spectral Parameters | EHG Nonlinear Parameters | Obstetric Data |
|---|---|---|---|
| Peak-to-peak amplitude | DF1 DF2 H/L ratio Deciles [D1–D9] SMR | Binary Lempel-Ziv Multistate Lempel-Ziv (n = 6) Sample entropy Spectral entropy Fuzzy entropy Time reversibility SD1 SD2 SD1/SD2 | Cervical length Gestational age at moment of recording Maternal age Gestations Parity Abortions |
| RF | ELM | KNN | |||||
|---|---|---|---|---|---|---|---|
| Criterion | F1-Score | Sensitivity | F1-Score | Sensitivity | F1-Score | Sensitivity | |
| Input Features | |||||||
| EHG 10th–90th percentiles + Obstetric data | RFF1_1 | RFSEN_1 | ELMF1_1 | ELMSEN_1 | KNNF1_1 | KNNSEN_1 | |
| EHG 50th + Obstetric data | RFF1_2 | RFSEN_2 | ELMF1_2 | ELMSEN_2 | KNNF1_2 | KNNSEN_2 | |
| EHG 10th–90th percentiles | RFF1_3 | RFSEN_3 | ELMF1_3 | ELMSEN_3 | KNNF1_3 | KNNSEN_3 | |
| EHG 50th percentile | RFF1_4 | RFSEN_4 | ELMF1_4 | ELMSEN_4 | KNNF1_4 | KNNSEN_4 | |
| Opt. Criterion | Inputs | Classifier | Test_F1 | Test_Sens | Test_Spec |
|---|---|---|---|---|---|
| F1-Score Sensitivity | EHGP10–P90 + Obs | RFF1_1 | 77.51 ± 7.58% (9.8%) | 66.22 ± 11.70% (17.7%) | 97.12 ± 4.13% (4.3%) |
| EHGP50 + Obs | RFF1_2 | 80.35 ± 6.78% (8.4%) | 74.00 ± 10.41% (14.1%) | 92.25 ± 5.35% (5.8%) | |
| EHGP10–P90 | RFF1_3 | 77.81 ± 8.71% (11.2%) | 65.78 ± 11.61% (17.6%) | 98.29 ± 2.51% (2.6%) | |
| EHGP50 | RFF1_4 | 77.7 ± 6.6% (8.5%) | 71.44 ± 10.99% (15.4%) | 90.72 ± 4.58% (5.0%) |
| Opt. Criterion | Inputs | Classifier | Test_F1 | Test_Sens | Test_Spec |
|---|---|---|---|---|---|
| F1-score | EHGP10–P90 + Obs | ELMF1_1 | 80.00 ± 4.98% (6.0%) | 87.56 ± 8.53% (9.7%) | 74.77 ± 7.32% (9.8%) |
| EHGP50 + Obs | ELMF1_2 | 82.14 ± 5.88% (7.2%) | 89.89 ± 7.14% (7.9%) | 76.40 ± 8.12% (10.6%) | |
| EHGP10–P90 | ELMF1_3 | 78.41 ± 4.55% (5.8%) | 85.89 ± 7.91% (9.2%) | 73.24 ± 6.93% (9.5%) | |
| EHGP50 | ELMF1_4 | 79.00 ± 5.06% (6.4%) | 86.22 ± 6.65% (7.7%) | 73.87 ± 8.64% (11.7%) | |
| Sensitivity | EHGP10–P90 + Obs | ELMSEN_1 | 74.83 ± 3.88% (5.2%) | 95.44 ± 4.59% (4.8%) | 51.35 ± 9.28% (18.1%) |
| EHGP50 + Obs | ELMSEN_2 | 75.42 ± 3.96% (5.3%) | 96.00 ± 5.13% (5.3%) | 52.25 ± 9.58% (18.3%) | |
| EHGP10–P90 | ELMSEN_3 | 73.13 ± 3.10% (4.2%) | 94.78 ± 4.61% (4.9%) | 47.57 ± 8.83% (18.6%) | |
| EHGP50 | ELMSEN_4 | 73.83 ± 3.24% (4.4%) | 94.89 ± 5.01% (5.3%) | 49.37 ± 9.63% (19.5%) |
| Opt. Criterion | Inputs | Classifier | Test_F1 | Test_Sens | Test_Spec |
|---|---|---|---|---|---|
| F1-score | EHGP10–P90 + Obs | KNNF1_1 | 84.18 ± 9.47% (11.2%) | 79.33 ± 13.23% (16.7%) | 93.42 ± 6.34% (6.8%) |
| EHGP50 + Obs | KNNF1_2 | 74.16 ± 5.07% (6.8%) | 93.33 ± 6.37% (6.8%) | 52.43 ± 9.59% (18.3%) | |
| EHGP10–P90 | KNNF1_3 | 84.67 ± 8.46% (10.0%) | 80.56 ± 12.57% (15.6%) | 92.70± 8.81% (9.5%) | |
| EHGP50 | KNNF1_4 | 74.13 ± 4.57% (6.2%) | 90.89 ± 6.55% (7.2%) | 55.77 ± 9.67% (17.3%) | |
| Sensitivity | EHGP10–P90 + Obs | KNNSEN_1 | 79.8 ± 8.29% (10.4%) | 82.78 ± 12.13% (14.7%) | 80.36 ± 9.76% (12.1%) |
| EHGP50 + Obs | KNNSEN_2 | 72.98 ± 4.00% (5.5%) | 94.22 ± 5.67% (6.0%) | 47.93 ± 8.98% (18.7%) | |
| EHGP10–P90 | KNNSEN_3 | 78.63 ± 8.60% (10.9%) | 83.56 ± 12.47% (14.9%) | 76.58 ± 14.2% (18.5%) | |
| EHGP50 | KNNSEN_4 | 73.19 ± 4.31% (5.9%) | 91.78 ± 7.15% (7.8%) | 52.07 ± 9.39% (18.0%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prats-Boluda, G.; Pastor-Tronch, J.; Garcia-Casado, J.; Monfort-Ortíz, R.; Perales Marín, A.; Diago, V.; Roca Prats, A.; Ye-Lin, Y. Optimization of Imminent Labor Prediction Systems in Women with Threatened Preterm Labor Based on Electrohysterography. Sensors 2021, 21, 2496. https://doi.org/10.3390/s21072496
Prats-Boluda G, Pastor-Tronch J, Garcia-Casado J, Monfort-Ortíz R, Perales Marín A, Diago V, Roca Prats A, Ye-Lin Y. Optimization of Imminent Labor Prediction Systems in Women with Threatened Preterm Labor Based on Electrohysterography. Sensors. 2021; 21(7):2496. https://doi.org/10.3390/s21072496
Chicago/Turabian StylePrats-Boluda, Gema, Julio Pastor-Tronch, Javier Garcia-Casado, Rogelio Monfort-Ortíz, Alfredo Perales Marín, Vicente Diago, Alba Roca Prats, and Yiyao Ye-Lin. 2021. "Optimization of Imminent Labor Prediction Systems in Women with Threatened Preterm Labor Based on Electrohysterography" Sensors 21, no. 7: 2496. https://doi.org/10.3390/s21072496
APA StylePrats-Boluda, G., Pastor-Tronch, J., Garcia-Casado, J., Monfort-Ortíz, R., Perales Marín, A., Diago, V., Roca Prats, A., & Ye-Lin, Y. (2021). Optimization of Imminent Labor Prediction Systems in Women with Threatened Preterm Labor Based on Electrohysterography. Sensors, 21(7), 2496. https://doi.org/10.3390/s21072496








